在工程施工中,通常采用爆破的施工工艺进行巷道掘进及土石方开挖。炸药起爆后,不同性质的爆炸应力波会与爆破介质中的运动裂纹发生极其复杂的相互作用。在此过程中,不同性质的爆炸应力波会抑制或促进运动裂纹的扩展。在某些情况下,爆炸应力波甚至会引起运动裂纹分叉或者改变运动裂纹扩展方向。利用爆炸应力波与运动裂纹相互作用的理论能够优化爆破参数、改进爆破工艺、提高破碎作业效率,进而降低施工作业成本并提高施工效果。爆炸应力波与运动裂纹作用理论对断裂动力学理论的发展也具有重要的意义。
一些学者对爆炸应力波的传播问题进行了实验测试和理论分析研究[1-2],针对平面波和柱面波的反射、透射、衍射问题取得了一定研究成果[3]。窦林名等[4]根据岩爆与煤层岩体的应力状态关系,将弹性波CT技术应用于岩爆等地质灾害的预测当中。关于应力波与运动裂纹相互作用问题,也有科研人员对其进行了理论研究和实验探索。RAVI-Chandar和KNAUSS[5]采用高速相机研究了边界反射应力波和电磁加载装置激发产生的压缩应力波对裂纹传播方向、裂纹扩展速度和裂纹分叉进程的影响。YI-SHYONG ING和CHIEN-CHINGMA[6]利用理论研究和焦散线实验方法,研究了应力波荷载下扩展裂纹瞬态全场解,对比分析了理论计算和焦散线实验测得的应力强度因子数据。BONAMY和RAVI-CHANDAR[7]研究了由超声换能器产生的剪切波对动态扩展裂纹前沿阵面的影响,研究表明裂纹前沿响应与扰动波的大小和频率成线性相关。DALLY[8]讨论了动态光弹性实验方法在应力波传播、振动与冲击、断裂传播和准静态瞬态四个弹性动力学领域中的应用。ROSSMANITH和SHUKLA[9]将动光弹性实验方法与高速摄像技术结合,研究了应力波与预拉伸所生成运动裂纹的相互作用,分析了运动裂纹尖端波的绕射效应,研究表明应力波对裂纹传播和分叉行为有强烈的影响。FOURNEY[10]研究了层状介质中脆性-脆性连接处静态界面裂纹尖端应力波的散射问题,利用动光弹实验方法将高度复杂的应力波与裂纹相互作用过程可视化,并用线弹性断裂力学理论分析了裂纹起裂动力源高应力强度因子作用区。朱振海[11-13]利用动态光弹性实验方法,探讨了入射P波与不同角度静态裂纹作用的机理,分析了应力波对裂纹扩展速度及扩展方向的影响。李夕兵[14]对应力波在软弱结构面的传播问题进行研究,分析了入射角度不同时,结构面对波传播特性的影响,得出了应力波作用下结构面是否滑移的判据以及相应的应力波透反射系数。郭占起等[15]分析讨论了裂纹与应力波波源的相对位置、炮孔装药量、边界反射波对裂纹尖端应力场的影响,给出裂纹尖端在应力波作用过程中应力强度因子的变化规律。王明洋等[16]利用应力波传播理论分析了应力波通过节理裂隙带的衰减规律,断层裂隙带破碎程度越大,应力波经过断层破碎带所消耗的能量越多。岳中文等[17]研究了板条边界斜裂纹在爆炸动载作用下的传播规律,分析了裂纹扩展过程的动态变化参数,指出引起裂纹起裂及扩展的推动力是裂纹端部的拉伸应力。
目前关于应力波与裂纹作用关系的研究,前人已经做了大量工作并取得丰硕成果,但对于爆炸应力波与运动裂纹相互作用的实验研究相当有限。本文将动态光弹性实验技术与数字化高速相机相结合研究正入射爆炸应力波与运动裂纹的相互作用关系,利用同步控制系统实现对波与裂纹作用过程的控制。通过处理高速相机实时采集的光弹等差条纹数据,分析爆炸应力波与运动裂纹作用过程中裂纹扩展速度和裂纹尖端应力场的变化,进而深入了解断裂机理。
1 实验原理
1.1 光弹性实验原理
动态光弹性法主要利用光弹性材料的暂时双折射现象,以应力-光学定律[18]为基础,通过偏振光场获得全场随时间变化的等差条纹图。当一束平面偏振光垂直入射平面应力模型时,偏振光通过模型后产生的光程差与模型的厚度和主应力差成正比,其数学表达为
(1)
式中,τm为最大剪应力;(σ1-σ2)为主应力差;N为条纹级数;h为模型厚度;fσ为材料条纹值。
1.2 裂纹尖端应力强度因子
根据文献[19-20]复合型裂纹尖端应力场表达式为
KⅡ![]()
(2)
KⅡ![]()
(3)
KⅡ![]()
(4)
最大剪应力与应力分量之间的关系表示为
(2τm)2=(σy-σx)2+(2τxy)2
(5)
将式(1)~(4)代入式(5)即得到等差条纹级数N与复合型断裂应力场的关系表达式为
2cos θ)+KⅡ![]()
(6)
裂纹尖端等差条纹图形示意图如图1所示,其中θm表示条纹倾斜角度;rm表示最大径向距离;σox表示远场应力。

图1 裂纹尖端等差条纹图形示意
Fig.1 Isochromatic fringe pattern of crack tip
1.3 入射爆炸应力波与运动裂纹作用
弹性波在非均匀介质中传播时,会在裂纹或杂质等几何不连续处发生绕射,绕射过程会在几何不连续处产生高应力集中,导致裂纹的不稳定传播。图2为运动裂纹与入射弹性波相对位置。入射波在裂纹尖端A处发生衍射和绕射,无论入射波的性质如何,是P波或SV波,绕射波都会产生绕射P波和绕射SV波。总的应力场σij(x,y,t)由入射应力场![]() 和绕射P波、绕射SV波应力场
和绕射P波、绕射SV波应力场![]() 所组成[8]。
所组成[8]。
(7)
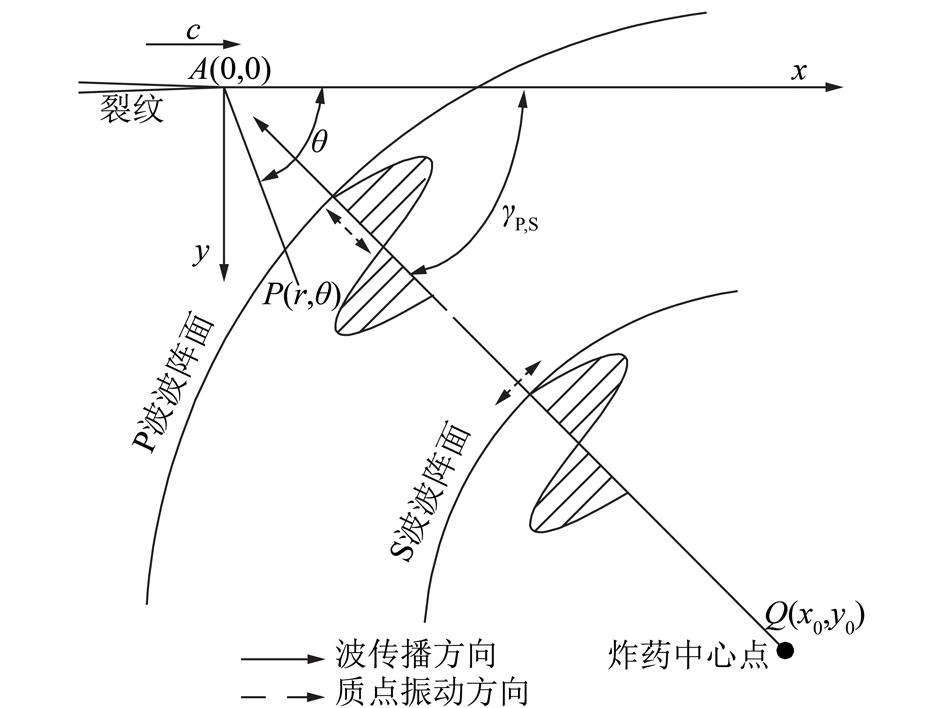
图2 运动裂纹与入射弹性波相对位置
Fig.2 Position of moving crack and incident elastic waves
如果入射P波和SV波对应力强度因子K1和K2的影响是分开的,则P波和SV波可用如下公式表示:
P波入射:
![]()
(8)
S波入射:
![]()
(9)
式中,ω为角频率;σ,τ为入射P波和S波幅值;γP,γS为P波,S波入射角;c为裂纹传播速度;MP,MS为P波和S波马赫数;SP=![]() 1/2,SS=
1/2,SS=![]() 1/2;T为入射波时间。
1/2;T为入射波时间。
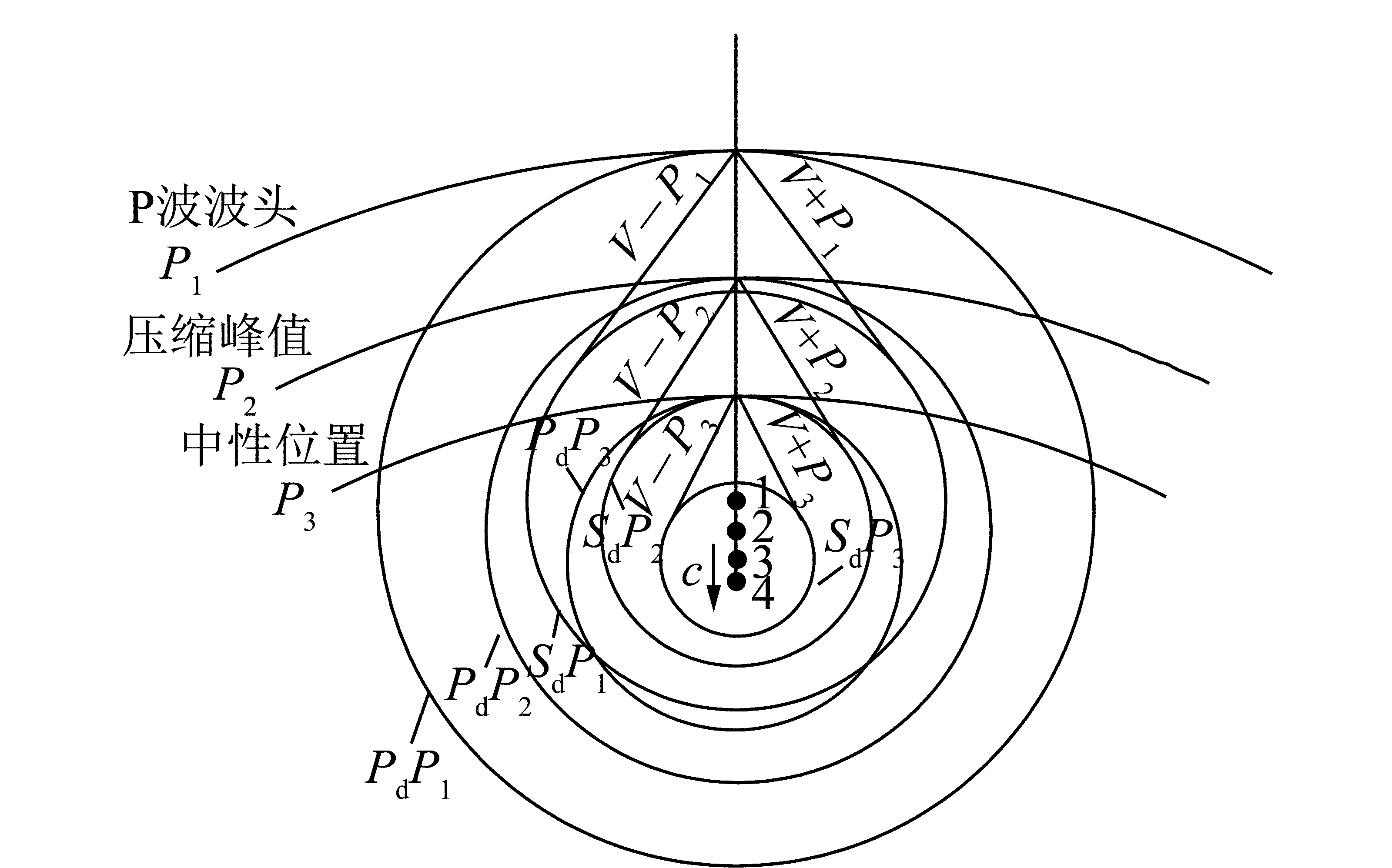
图3 P波在运动裂纹尖端绕射波阵面重构
Fig.3 Wave front reconstruction associated with P-wave scattering about a running crack
图3为P波在裂纹尖端绕射波阵面重构的示意图,可以看出,绕射P波和S波在瞬态裂纹尖端位置呈轴对称,由于运动裂纹尖端与绕射波的相对运动,绕射P波和S波的波形不再是同心圆环。
2 实验设计
2.1 冲击爆破同步加载系统
本实验利用冲击、爆破同步加载实验系统,在试件中先后产生运动裂纹和爆炸应力波,从而研究二者的作用机理。本系统由金属冲击头、金属落锤、砝码、导线、信号线、自动跟踪式同步、多通道脉冲点火器、夹具和支架组成。图4为冲击、爆破同步加载系统的结构示意。由图4可知,系统通过落锤自由下落击中冲击头,冲击头对试件施加冲击荷载,使试件中预制裂纹起裂并产生运动裂纹。在落锤与冲击头接触的瞬间,落锤、冲击头、导线形成闭合电路,产生脉冲电信号,该电信号通过导线传递到自动跟踪式同步机,自动跟踪式同步机发出触发信号至多通道脉冲点火器,多通道脉冲点火器接到触发信号后立即放电引爆炸药,在试件中产生爆炸应力波。自动跟踪式同步机收到电信号到发出触发信号的间隔时间可以预先设置。
2.2 实验材料及实验方案
实验采用自制的环氧树脂板制作试件,其基本力学参数见表1。试件模型示意图如图5所示,其尺寸L×W×T=320 mm×200 mm×8 mm,炮孔直径6 mm,试件预制裂纹C长度为5 mm,宽度为0.5 mm。实验设计方案:① 试件在冲击加载装置下产生运动裂纹,无爆炸应力波与运动裂纹相互作用,记为试件S-1;② 试件在冲击载荷加载下产生运动裂纹,正入射爆炸应力波在设定时间间隔产生并与运动裂纹相互作用,记为试件S-2。
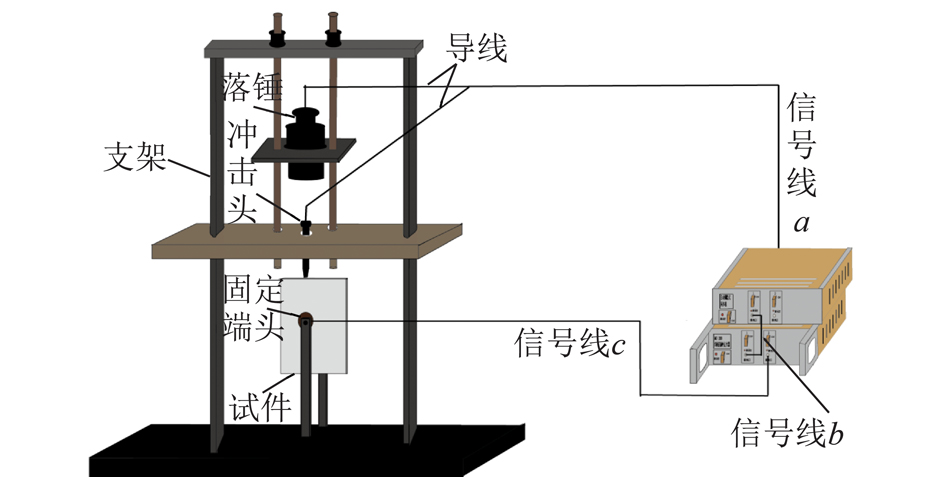
图4 冲击爆破同步加载系统结构示意
Fig.4 Schematic of impact and blasting synchronous loading experimental system
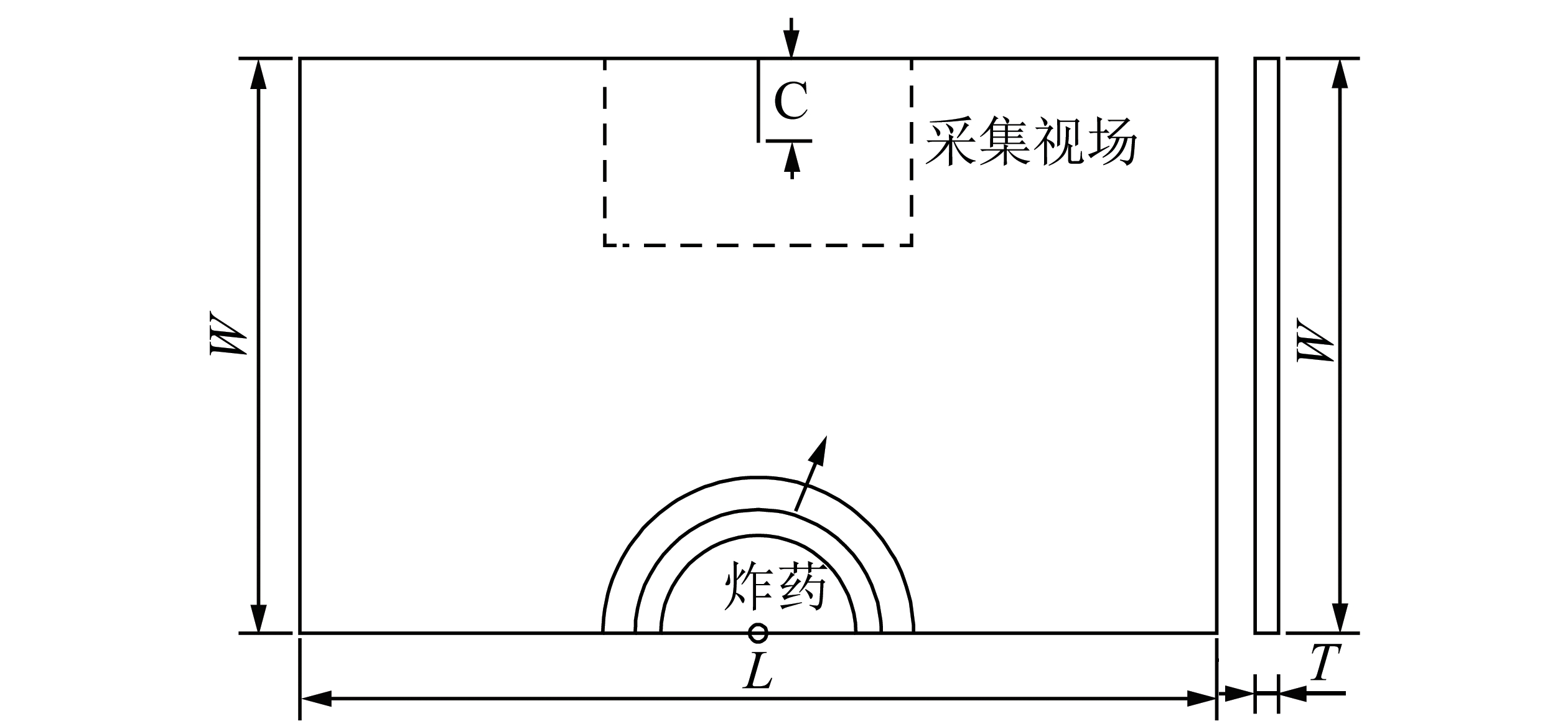
图5 试件模型示意
Fig.5 Sample size diagram
表1 光弹模型基本力学参数
Table 1 Basic mechanical parameters of photoelastic model

进行方案②时,炸药采用叠氮化铅,装药量为30 mg,采用的落锤质量为2.062 kg,下落高度为331 mm。自动跟踪式同步机的延时时间设置为300 μs。动光弹光路调整为圆偏振光场暗场,激光器输出频率设置为230 mW,高速相机拍摄频率设置为105 fps,拍摄视场范围为108 mm×65 mm,采集视场区域为图5中虚线方框区域。高速相机快门速度设置为1/100 000 0 s。方案①进行实验时,炮孔中未装入炸药,其它实验条件与方案②一致。
3 实验结果及分析
3.1 裂纹扩展光弹等差条纹图
图6(a)为试件S-1光弹等差条纹系列,图6(b)为试件S-2光弹等差条纹系列。由于P波与S波传播速度相差较大(P波波速约为2 347 m/s,S波波速约为1 468 m/s),当P波传播到运动裂纹尖端时,P波与S波已经分离。实验光路采用圆偏振光暗场,在t=0时,视场中呈黑暗状态。冲击荷载作用下裂纹不断扩展,在t=300 μs时,运动裂纹两侧条纹呈对称状,其前端0级条纹呈扇形。在t=380 μs时,S-2中裂纹前端0级条纹扇形区域面积减小,裂纹尖端应力场受到爆炸应力波的扰动。在t=390 μs时,S-2中P波前端波阵面1级条纹呈下凹状,爆炸应力波P波前端压缩应力场与运动裂纹尖端拉伸应力场叠加,作用区域内条纹级数降低。
试件S-1在t=400~470 μs,裂纹壁两侧1级条纹与裂纹尖端处1级条纹相互融合,裂纹尖端处1.5级条纹和2级条纹呈对称蝴蝶状,裂纹扩展主要受拉应力作用。t=510 μs以后,裂纹尖端1级等差条纹不断从融合条纹中解离出来,随着裂纹的不断扩展,边界应力场对裂纹尖端应力场的影响不断减弱。

图6 运动裂纹扩展光弹等差条纹
Fig.6 Running crack propagation photoelastic isochromatic fringe patterns
试件S-2在t=400 μs时,P波前端应力场与运动裂纹尖端应力场叠加并重构,在作用处出现拐点,形成蝴蝶状等差条纹,裂纹前端等差条纹由扇形状0级条纹转变为环状1级条纹,裂纹尖端产生应力集中。在t=410 μs时,随着爆炸应力波P波的不断传播,拐点位置也在不断移动,同时裂纹尖端等差条纹级数由2级上升为3级。在t=430 μs时,P波在顶端自由面处发生反射,等差条纹图呈菱形,上边沿处等差条纹发生反转。在t=440和450 μs时,图像中再次出现拐点,并由上而下运动,这是由于P波在边界处反射产生的PP波与PS波、入射波以及运动裂纹应力场相互叠加的综合作用效果,裂纹尖端处等差条纹与裂纹扩展方向所成角度近似为90°。在t=460和470 μs时,由波传播速度计算和裂纹尖端及周围的等差条纹呈现出不对称性,判定出裂纹尖端受到S波及边界处反射波扰动的影响。在t=510和550 μs时,裂纹尖端等差条纹呈现出对称性,其裂纹面所成角度近似等于90°。
通过对比图6(a),(b)可以看出,由于正入射爆炸波波动应力场的影响,爆炸应力波在运动裂纹尖端发生强烈的绕射和衍射作用。同时,由于运动裂纹尖端应力场的存在,使得爆炸波波动应力场受到影响;在正入射爆炸应力波与运动裂纹的作用过程中,运动裂纹扩展路径未发生明显偏转,爆炸应力波P波未影响等差条纹的对称性,而S波使得等差条纹呈现出不对称性。
3.2 裂纹的运动特征分析
图7(a),(b)分别为试件S-1和试件S-2裂纹扩展速度随时间变化曲线。在图7(a)中,随着时间推移,裂纹扩展速度在波动中不断上升。根据试件S-1中运动裂纹所扩展速度稳定范围,将其分为Ⅰ(130~300 μs),Ⅱ(310~380 μs),Ⅲ(390~450 μs),Ⅳ(460~550 μs)4个阶段,在4个阶段中裂纹平均扩展速度分别维持在68,113,147,203 m/s。在图7(b)中,根据爆炸应力是否到达运动裂纹尖端将运动裂纹扩展速度随时间变化过程分为2个阶段。第1阶段(130~390 μs),在此阶段正入射爆炸应力波尚未到达运动裂纹尖端;第2阶段(400~600 μs),在此阶段正入射爆炸应力波与运动裂纹相互作用。
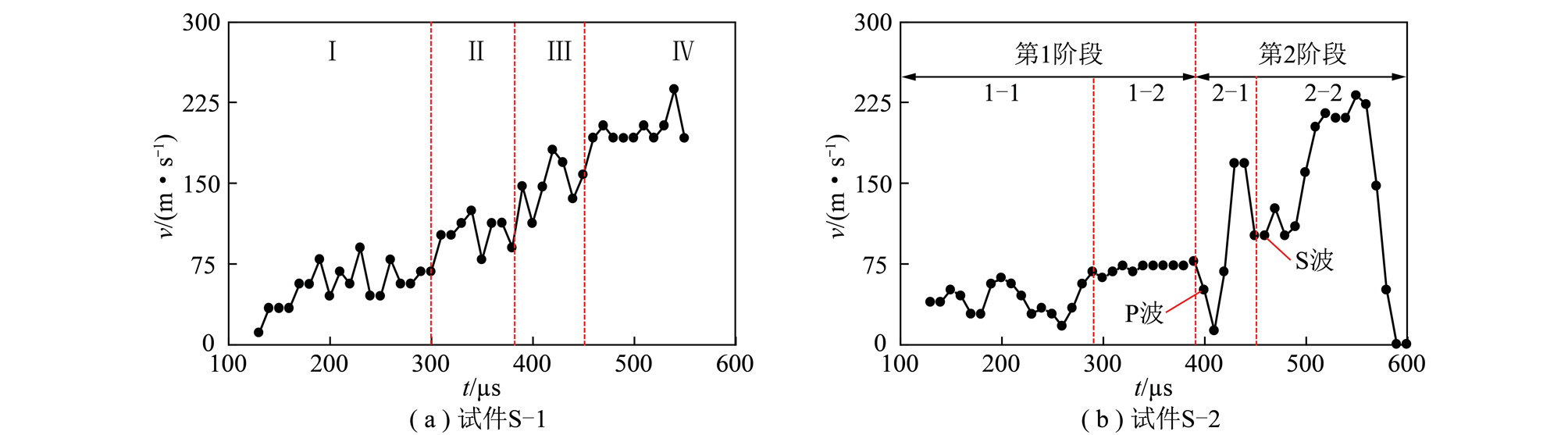
图7 裂纹扩展速度-时间曲线
Fig.7 Curves of crack growth velocity with time
在1-1阶段中,运动裂纹扩展速度呈波动状上升。在t=130 μs时,裂纹以39 m/s的速度扩展,从t=150 μs开始,裂纹扩展速度先减小,在t=170 μs时达到谷值28 m/s,后逐渐上升,在t=200 μs时达到峰值62 m/s,随后逐渐减小,在t=260 μs时达到谷值17 m/s,之后又不断上升,在t=290 μs时达到峰值68 m/s。
在1-2阶段,裂纹的平均扩展速度稳定在73 m/s,其扩展速度与试件S-1第1阶段裂纹平均扩展速度相近,但远小于其第2阶段的平均速度,结合图6相应时刻等差条纹图可以看出其差异性主要是受到落锤冲击装置的影响。
在2-1阶段,裂纹尖端受正入射爆炸应力波P波作用,裂纹扩展速度先迅速减小,在t=410 μs时达到谷值13 m/s,爆炸应力波P波前端的压缩波抑制了动态裂纹的扩展;然后,运动裂纹扩展速度迅速增加,在t=430 μs时达到峰值169 m/s,大于1-2阶段中平均扩展速度73 m/s,原因是P波尾部的拉伸波对裂纹的扩展起到积极的促进作用;随后,运动裂纹扩展速度逐渐减小,在t=450 μs时达到谷值102 m/s,这是由于P波尾部拉伸波作用的不断减弱,同时正入射爆炸应力波S波到达裂纹尖端。
在2-2阶段,运动裂纹扩展速度先逐渐增加,在t=550 μs时达到峰值233 m/s,是S波以及边界处反射的SP波、SS波综合作用的结果,随后,裂纹扩展速度迅速下降,在t=590 μs裂纹止裂。对比图7(a)和(b)可以看出,由于受到正入射爆炸波动场的作用,爆炸应力波与运动裂纹作用阶段,裂纹扩展速度剧烈的变化,爆炸应力波P波抑制了裂纹的扩展,爆炸应力波S波及边界处反射波对裂纹的扩展起到促进作用。
3.3 裂纹尖端应力特征分析
图8(a)和(b)分别为试件S-1和S-2中裂纹尖端应力强度因子随时间变化曲线,其各个阶段时间划分区间与3.2节中相同。在图8(a)中,整条曲线在波动中先上升后逐渐下降。在t=130~280 μs,裂纹尖端应力强度因子不断增加,在t=280 μs时达到峰值0.65 MPa·m1/2,随后,应力强度因子不断下降,在t=340 μs时第1次达到谷值0.49 MPa·m1/2,在t=360 μs时第2次达到谷值0.51 MPa·m1/2。在t=460~550 μs时间段内,裂纹尖端应力强度因子维持在0.47 MPa·m1/2上下浮动。在图8(b)中,在第1阶段,随着时间的推移,裂纹尖端应力强度因子不断增加,由t=130 μs时的0.49 MPa·m1/2增长至t=390 μs时的0.87 MPa·m1/2,在此阶段运动裂纹由冲击载荷驱动。在2-1阶段中,裂纹尖端应力强度因子先迅速减小然后迅速增加。在t=420 μs时达到谷值0.51 MPa·m1/2,这是由于正入射爆炸应力波P波压缩脉冲相与运动裂纹相互作用,使裂纹尖端应力强度因子不断下降;然后,应力强度因子不断增加,在t=450 μs时达到峰值0.78 MPa·m1/2,这是P波尾部拉伸脉冲相与运动相互作用的结果,使裂纹尖端应力强度因子不断增加。在2-2阶段中,裂纹尖端应力强度因子先不断增加再逐渐下降,在t=540 μs时达到最大值1.0 MPa·m1/2,这是由于正入射爆炸应力波中S波以及边界反射的PS波、SS波对运动裂纹尖端应力场的影响;然后,裂纹尖端应力强度因子不断降低,在t=590 μs时达到谷值0.5 MPa·m1/2,此时裂纹停止扩展。

图8 动态应力强度因子-时间曲线
Fig.8 Curves of dynamic stress intensity factor with time
将图8(a)和(b)进行对比分析,在爆炸波与运动裂纹相互作用阶段中,裂纹尖端应力强度因子呈现剧烈的变化,爆炸应力波P波使得应力强度因子减小,爆炸应力波S波及边界处反射波使得应力强度因子增加。
4 结 论
(1)正入射爆炸应力波不改变运动裂纹扩展方向。
(2)当正入射爆炸应力波P波前端压缩脉冲相与运动裂纹相互作用时,裂纹扩展速度会受到抑制,达到谷值13 m/s,同时裂纹尖端应力强度因子会降低,达到谷值0.51 MPa·m1/2。
(3)当正入射爆炸应力波P波尾部拉伸脉冲相与运动裂纹相互作用时,裂纹扩展速度会增加,增加后的速度169 m/s大于未受爆炸应力波作用时运动裂纹的平均稳定扩展速度73 m/s,同时裂纹尖端应力强度因子不断增加,达到峰值0.78 MPa·m1/2。
(4)正入射爆炸应力波S波以及边界反射波使裂纹扩展速度和裂纹尖端应力强度因子都呈现先增大后减小的趋势。
参考文献(References):
[1] ACHENBACH J D.Wave propagation in elastic solids[M].Amsterdam:North-Holland Co.,1973.
[2] EWING W M,JARDETZKY W S,PRESS F.Elastic waves in layered media[M].New York:McGraw-Hill Book Company,Inc.,1957.
[3] RINEHART,JOHN S.Stress transients in solids[M].Santa Fe:Hyper Dynamics,1975.
[4] DOU Linming,MU Zonglong,LI Zhenlei,et al.Research progress of monitoring,forecasting,and prevention of rockburst in underground coal mining in China[J].International Journal of Coal Science & Technology 2014,1(3):278-288.
[5] RAVI-Chandar K,KNAUSS W G.An experimental investigation into dynamic fracture:IV.On the interaction of stress waves with propagating cracks[J].International Journal of Fracture,1984,26(3):189-200.
[6] ING Y S,MA C C.Theoretical simulations of a propagating crack subjected to in-plane stress wave loading by caustic method[J].International Journal of Fracture,1997,85(4):313-331.
[7] BONAMY D,RAVI-Chandar K.Interaction of shear waves and propagating cracks[J].Physical Review Letters,2003,91(23):235502
[8] DALLY J W.An introduction to dynamic photoelasticity[J].Experimental Mechanics,1980,20(12):409-416.
[9] ROSSMANITH H P,SHUKLA A.Dynamic photoelastic investigation of interaction of stress waves with running cracks[J].Experimental Mechanics,1981,21(11):415-422.
[10] ROSSMANITH H P,FOURNEY W L.Fracture initiation and stress wave diffraction at cracked interfaces in layered media I.brittle/brittle transition[J].Rock Mechanics and Rock Engineering,1982,14(4):209-233.
[11] 朱振海.爆炸应力波与径向裂纹相互作用的动光弹研究[J].解放军理工大学学报,自然科学版,1987,3(2):81-88..
ZHU Zhenhai.Dynamic photoelastic study of stress wave interacting with radial cracks[J].Journal of PLA University of Science and Technology,Natural Science Edition,1987,3(2):81-88.
[12] 朱振海.应力波对裂纹扩展影响的动光弹研究[J].解放军理工大学学报,自然科学版,1988,4(4):78-84.
ZHU Zhenhai.Dynamic photoelastic research of stress wave influence to crack[J].Journal of PLA University of Science and Technology,Natural Science Edition,1988,4(4):78-84.
[13] 朱振海.爆炸应力波对高速扩展裂纹影响的动态光弹性试验研究[J].爆炸与冲击,1993,13(2):178-184.
ZHU Zhenhai.Dynamic photoelastic investigations of the effect of explosive stress waves on an extending-high speed crack[J].Explosion and Shock Waves,1993,13(2):178-184.
[14] 李夕兵.论岩土软弱结构面对应力波传播的影响[J].爆炸与冲击,1993,13(4):334-342.
LI Xibing.Influence of the structural weakness planes in rock mass on the propagation of stress waves[J].Explosion and Shock Waves,1993,13(4):334-342.
[15] 郭占起,费志中,吴明棣.不同爆炸加载参数下含裂纹试件的动光弹数值分析[J].北方交通大学学报,1994,18(1):81-88.
GUO Zhanqi,FEI Zhizhong,WU Mingdi.Dynamic photoelastic numerical analysis of specimens contairing cracks[J].Journal of Northern Jiaotong University,1994,18(1):81-88.
[16] 王明洋,钱七虎.爆炸应力波通过节理裂隙带的衰减规律[J].岩土工程学报,1995,17(2):42-46.
WANG Mingyang,QIAN Qihu.Attenuation law of explosive wave propagation in cracks[J].Chinese Journal of Geotechnical Engineering,1995,17(2):42-46.
[17] 岳中文,杨仁树,董聚才,等.爆炸载荷下板条边界斜裂纹的动态扩展行为[J].爆炸与冲击,2011,31(1):75-80.
YUE Zhongwen,YANG Renshu,DONG Jucai,et al.Dynamic propagation behaviors of an oblique edge crack in material under blast loading[J].Explosion and Shock Waves,2011,31(1):75-80.
[18] 苏先基,励争.固体力学动态测试技术[M].北京:高等教育出版社,1997:115-158.
[19] DALLY J W,SANFORD R J.Classification of stress-intensity factors from isochromatic-fringe patterns[J].Experimental Mechanics,1979,19(5):175-175.
[20] 高家美,刘益河,宋育仁.光弹性法在矿山工程中的应用[M].北京:煤炭工业出版社,1989:330-336.>