悬臂式部分断面掘进机外形尺寸和质量小,工作方式灵活,对巷道的形状和煤岩的赋存情况适用性强,并能实现选择性切削,而广泛应用于煤巷及半煤岩巷道掘进。目前,悬臂式部分断面掘进机的工作机构采用多截齿配置的切削头,从切削性能上,难以高效切削f>8以上全岩巷。每年巷道掘进总长约为9 000 km,其中硬岩巷道占总长20%~30%,90%的硬岩巷道采用炮掘,研制适用于全岩巷道的悬臂式部分断面掘进机工作机构十分迫切。
硬岩破碎一直是硬岩巷道高效掘进和悬臂式掘进机面临的难题,切削理论是煤岩高效破碎的理论基础。别隆等[1]提出的“密实核”学说,认为切割煤岩的过程是接触压碎形成密实核与煤崩落不断交替的过程。EVANS[2]提出最大拉应力理论,指出煤岩破碎是由于刀具切入煤岩时的拉应力造成的,引起材料脆性断裂破坏的因素是最大拉应力。Y.NISHIMATSU[3]给出煤岩体破碎面遵守库仑-摩尔准则。H.LAN[4]结合动量守恒和质量守恒三大定律,建立了岩石多场耦合分析模型。牛东民[5]建立断裂力学的模型,认为煤岩在刀具作用下沿着煤岩本身的层理和节理方向破碎。王成勇等[6]采用激光散斑法测量切削应变场,研究了花岗岩和细粒花岗岩的切削断裂应力性质,建立切削花岗岩的力学模型。
切削刀具的运动方式也是影响煤岩破碎效率的重要因素。B.STEVERDING等[7]通过振动截齿切削煤岩实验,采用正弦波式振动切削比三角波形式有效。徐小荷等[8]指出刀具侵入岩石的破碎煤岩过程具有跃进式侵入、承压核和破碎角稳定等规律。赵明阶[9]基于压剪裂纹,研究了岩石在三轴卸载过程中微裂纹的变形特点。陈忠辉等[10]利用连续介质损伤力学理论,建立了各向同性岩石损伤模型及弹脆性本构方程。PRAKASH等[11]对透水石英砂岩进行了截齿切削测试实验,得出截齿受力和能耗随岩石的饱和度增大而增发。姜永东等[12]实验研究了岩石应力-应变全过程的声发射特征,指出岩石微裂纹的损伤演化具有混沌特征。王春华等[13]进行了刀形截齿切削煤岩实验,指出采用单一破碎强度准则,不能准确描述煤岩破碎机理。BILGIN等[14]利用镐型截齿切削实验研究不同特性的煤岩,发现煤岩的轴向抗压强度对切削机构性能的影响最大,抗拉强度、静态和动态弹性模量对切削机构性能的影响较大。刘春生等[15-16]通过多截齿破碎煤岩试验,获得截割载荷谱,建立了分形盒维数和能耗的破碎性能评价模型与方法。
通过研究切削理论与切削刀具运动的研究现状发现合理的刀具及其破碎煤岩理论是提高破碎煤岩效率的基础。笔者在文中探讨一种在轴向振动与径向切削复合破碎煤岩的边缘牙齿碟盘刀具,着重研究刀具与煤岩作用分区过程、力学机理、载荷模型及破碎煤岩特性。
1 碟盘破碎煤岩力学机理
1.1 边缘牙齿形碟盘刀具
边缘牙齿形碟盘是可安装在悬臂式掘进机上的一种切削刀具,如图1所示。在碟盘的边缘上均匀分布多个牙齿,从结构上碟盘刀具分为齿尖与碟盘楔面两部分,在运动方式上分为径向切削vj与轴向振动vs。刀具在径向与轴向共同作用下挤压、切削破碎岩石。

图1 碟盘刀具破碎煤岩模型
Fig.1 Disc cutter tooth rock model
1.2 单牙齿破碎煤岩的力学特征
边缘牙齿碟盘破碎煤岩时,取等效单牙齿宽度为研究对象,分析与煤岩的相互作用关系,刀具在不同运动条件下,破碎煤岩各阶段的主导作用。在奥斯特洛乌什柯[17]和刀形截齿切削煤岩的机理[18]等观点的基础上,将刀具齿尖等效为以r为半径的球体,给出刀具破碎煤岩过程的各阶段力学模型,为研究刀具整体受力及结构设计提供理论依据。
1.2.1 弹塑性挤压阶段
刀具初接触煤岩时,随载荷的增加接触面煤岩受压变形,在接触面出现裂纹。由弹塑性理论,当除去载荷时,接触面煤岩的挤压变形也会消失。随载荷的增大,接触面煤岩裂纹迅速扩展直至被压碎形成密实核。此时,刀具齿尖与煤岩体接触球面压力为
(1)
式中,r0为压力体作用面的半径,![]() 为与岩体接触的球面平均压强,MPa。
为与岩体接触的球面平均压强,MPa。
根据抛物线形压力分布最大压强与平均压强的关系
(2)
式中,σ为与岩体接触的最大压强,MPa。
1.2.2 压裂阶段
随刀具载荷进一步增加接触面上裂纹开始增多,并向深部扩展,最终裂纹相互贯通,载荷影响深度加深,在等效刀具齿尖中心处载荷最大,从中心向两侧减小,最终在刀具下方形成锥形的压力体,如图2中阴影区域所示。当达到煤岩抗剪强度时,压力锥体与边界处的煤岩因剪切而产生滑移。根据剪切理论,在压裂阶段形成主压力锥体载荷Py的力学关系如图2所示。
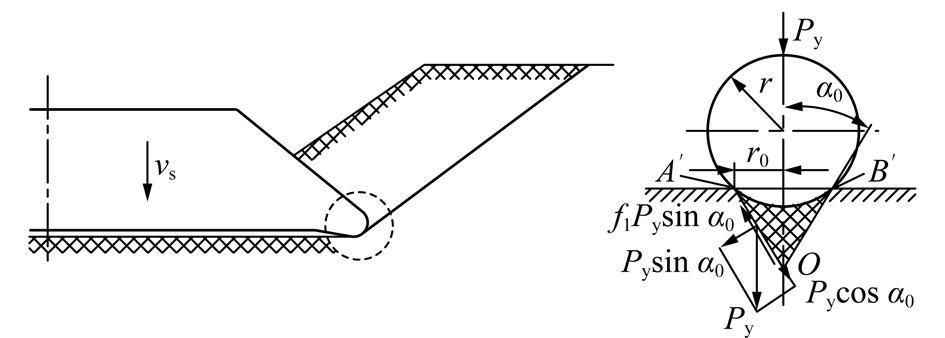
图2 球形压头形成主压力体
Fig.2 Spherical head forms the main pressure body
主压力体剪切破碎面载荷
Pycos α0-f1Pysin α0=σjS
(3)
式中,f1为煤岩的内摩擦因数;σj为煤岩的抗剪强度,MPa;α0为压力锥体半锥角,(°)。
压力锥体A′OB′表面积
可得
(4)
1.2.3 破碎阶段
主压力体随刀具载荷的继续增加,与主压力体接触边界面上开始出现裂纹,主压力体增大并指向AO,BO面。当达到煤岩的抗剪强度时,裂纹扩展、连接直至贯通,最终形成的剪切体A′OA,B′OB开始崩离,A′OB′主压力体被压碎,形成AOB破碎坑。在体积破碎阶段,破碎载荷PT的力学关系如图3所示。

图3 体积破碎阶段
Fig.3 Volume crushing stage
剪切体AOB被剪切产生位移时,可得
式中,![]() 为压力锥体面A′O与AO的夹角,(°)。
为压力锥体面A′O与AO的夹角,(°)。
则剪切体AOB的表面积S1:
由图2和3可得体积破裂面AOB的受力方程,可得沿剪切体锥面总阻力Fz:
Fz=S1σj+Pm
(5)
式中,Pm为内摩擦力,Pm=f1PTsin α0sin ![]() ,kN。
,kN。
沿锥面的有效作用力Px:
Px=PTcos α0cos ![]()
(6)
由式(5)和(6)可得,剪切体AOB破碎时的力学条件:
(7)
1.2.4 大块崩落阶段
大块崩落阶段,如图4所示。刀具齿尖侵入到煤岩体中,随刀具vj>0径向进给。在碟盘刀具楔面的作用下,楔面上的煤岩受挤压变形,然后在与刀具楔面成一定角度上形成破碎面,当破碎面上的力达到煤岩的抗剪强度时,破碎面上煤岩发生滑移错动,从岩体中分离,即产生大块崩落时,按剪切强度准则,可得碟盘楔面与煤岩的力学模型。
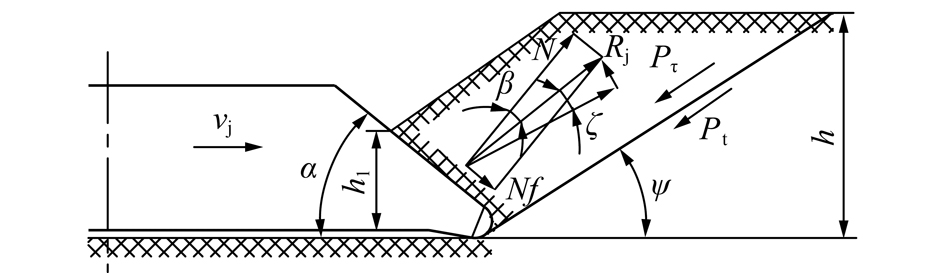
图4 大块崩落阶段
Fig.4 Large chunks of caving
崩落体底面的抗剪阻力Pt:
(8)
式中,h为切削厚度,mm;b为碟盘刀具单个牙齿的等效宽度,mm;ψ为煤岩体崩落面倾角,(°)。
崩落体两侧产生的抗剪阻力:
(9)
式中,α为碟盘楔面倾角,(°);h1为碟盘楔面与煤岩的接触高度,mm。
碟盘楔面对煤岩的合力Rj:
(10)
式中,f为刀具与煤岩之间的摩擦因数;N为碟盘楔面与岩石接触面之间的正压力,kN。
当碟盘楔面上的煤岩产生大块崩落时,满足:
Rjcos ξ>Pt+Pτ
(11)
式中,ξ为碟盘楔面合力与崩落楔面之间的夹角,ξ=90°-α-β-ψ,(°)。
1.3 压力锥体半锥角α0
煤岩体发生剪切裂纹与破坏时,符合能量最小原则[19],即由于剪切应力τ所产生的切向位移所消耗的能量最小,能量是剪力与位移的乘积,位移与剪力成正比,因此,主压力体产生压裂破坏能量与τ2成正比,则有![]() 即
即![]() 时有最小值,由式(4)可得
时有最小值,由式(4)可得
![]()
(12)
2 碟盘牙齿齿尖的受力分析
2.1 径向切削
摆动切削时,即vj>0,vs=0,碟盘刀具的齿尖等效球形压头压力体破碎时的合力Pj力学关系如图5所示。

图5 切削形成主压力体的力学关系
Fig.5 Cutting forms the stress relation of the main pressure body
等效刀头压力体作用面半径r0j:
r0j=rcosα1/2
式中,![]() 为刀具齿尖压力锥体合力的水平夹角,(°);r为边缘牙齿碟盘单齿齿尖等效球头半径,mm。
为刀具齿尖压力锥体合力的水平夹角,(°);r为边缘牙齿碟盘单齿齿尖等效球头半径,mm。
由式(7)可得
(13)
根据煤岩体破碎机理可知,当刀具齿尖达到体积破碎时,在与刀具楔面共同作用下使岩石大块崩落。此时,刀具齿尖体积破碎的载荷与压力体的压力面(A′B′)达到抗压强度等价,为计算简单可靠,则有
(14)
2.2 轴向振动
当vj=0,vs≠0,刀具在轴向上下往复振动时的载荷为Ps1和Ps2,等效球形压头形成主压力体的力学模型如图6所示。

图6 轴向振动形成压力体的力学模型
Fig.6 Force relation of the axial vibration to the diagram pressure body is formed
上下往复轴向振动时,等效压力体作用面A′B′半径r0s1和r0s2为
r0s1=rsin φ
式中,φ为刀具轴向向上运动,刀具齿尖压力锥体合力与水平面之间的夹角,![]() 为刀具轴向最大振幅,mm。
为刀具轴向最大振幅,mm。
刀具在轴向上下往复振动时,体积破碎阶段的载荷Ps1和Ps2,由式(7)可知:
式中,Sos1,Sos2为刀具轴向向上和向下时破碎锥体的表面积,mm2。
同理,由式(14)简化算法的载荷为
2.3 复合运动切削
当vs≠0,vj>0时,由图5和6阐述的单独作用结果进行叠加,其力学关系如图7所示。
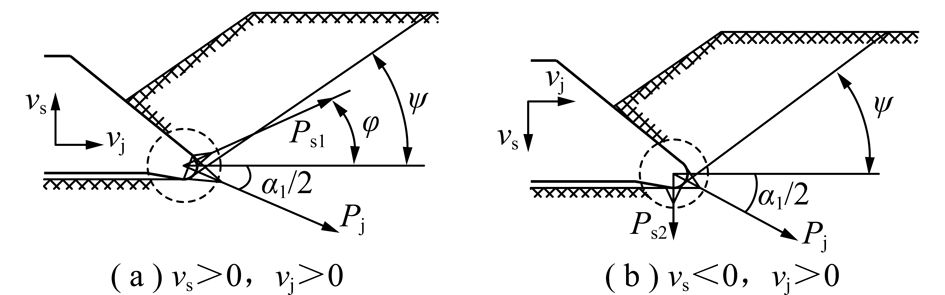
图7 复合运动形成主压力体的受力关系
Fig.7 Composite motion forms the stress model of the main pressure body
由图7(a)所示,当刀具复合轴向向上振动时,由径向摆动切削与轴向向上振动两种工况下进行矢量叠加,刀具齿尖的径向和轴向载荷Tj1和Ts1分别为
由图7(b)所示,同理,当刀具复合轴向向下时,其径向与轴向载荷Tj2和Ts2分别为
3 破碎煤岩的力学模型
根据刀具的运动状态,分析在单切削作用与振动切削复合作用下刀具的载荷关系,把刀具在齿尖与碟盘楔面上的载荷矢量叠加,建立刀具径向载荷与轴向载荷的数学模型。
3.1 单切削楔劈破碎煤岩
当摆动切削速度vj>0,vs=0时,刀具切削破碎岩石齿尖与碟盘楔面上力学关系如图8所示。

图8 剪切破碎岩石的力学关系
Fig.8 Mechanical relation of shear fracture rock
由式(8),(9)可知,岩石崩落底面和侧面的总阻力Fc:
岩体崩落面的总阻力Fα:
![]()
(15)
刀具作用到岩体的有效作用力Fy:
(16)
![]() 和
和![]() 对大块崩落作用不明显,为计算的可靠和方便,可略去此项,由式(15)和(16)可得
对大块崩落作用不明显,为计算的可靠和方便,可略去此项,由式(15)和(16)可得
碟盘齿尖与碟盘楔面处的载荷进行矢量叠加,建立刀具径向载荷Fj与轴向载荷Fs的数学模型。
3.2 复合剪切破碎煤岩
当vj>0,vs>0时,碟盘刀具轴向向上运动由刀具楔面对煤岩形成剪切作用。碟盘齿尖和碟盘楔面与煤岩的力学关系如图9所示。
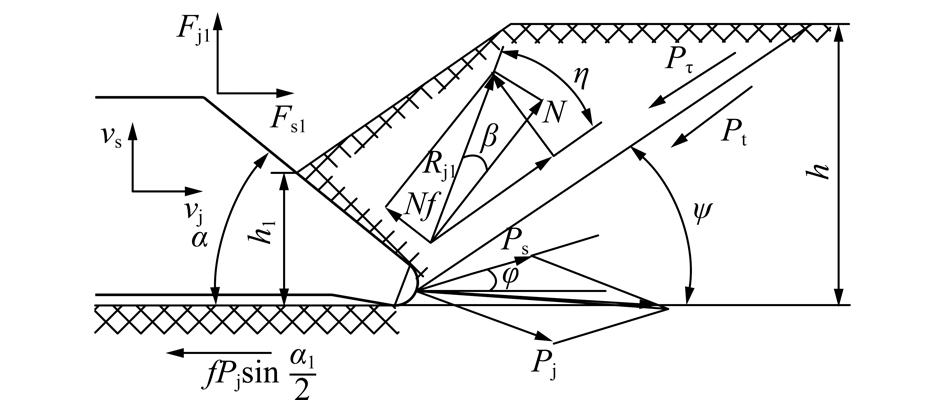
图9 剪切破碎煤岩的力学关系
Fig.9 Mechanical relation of shear fracture rock
同理,由式(8),(9)可得,煤岩崩落底面与侧面的总阻力Ff:
煤岩体崩落面的总阻力Fs:
![]()
(17)
刀具作用到煤岩体的有效作用力Fo:
Ps1cos(ψ-φ)
(18)
同理,当大块崩落计算峰值载荷时,忽略
![]() 和
和![]() 由式(17)和(18)可得:
由式(17)和(18)可得:
φ)[sin(α+ψ-β)-f1cos(α+ψ-β)]
同理,由图9可知,建立刀具径向载荷Fj1与轴向载荷Fs1的数学模型。
4 边缘牙齿碟盘破碎煤岩的数值模拟
利用有限元仿真软件ABAQUS模拟边缘牙齿碟盘破碎煤岩时的径向与轴向载荷的变化规律[20]。刀具破碎煤岩的有限元模型如图10所示。刀具与煤岩参数见表1。

图10 破碎岩石有限元模型
Fig.10 Finite element model of broken rock
表1 刀具与煤岩参数
Table 1 Parameters of cutter and coal rock

4.1 单作用破碎煤岩的载荷特性
当vj>0,vs=0刀具单作用径向切削破碎煤岩仿真时,刀具的切削厚度h=10~18 mm,径向载荷和轴向载荷变化规律如图11所示。

图11 单切削破碎煤岩载荷曲线
Fig.11 Load curves of the single crushing coal rock
由图11(a)看出,径向载荷由两部分组成,一是碟盘楔面与煤岩作用的结果,径向载荷幅值变化大。随切削厚度的增加而增加;二是刀具齿尖产生的载荷幅值缓慢变化具有明显的稳态值和挤压特性,与前述的理论模型的叠加算法一致。径向的载荷随切削厚度的增加而增加。
由图11(b)看出,与径向载荷相同,轴向载荷也由两部分叠加构成,但2者方向相反。随切削厚度的增大,齿尖处的轴向载荷分量变化不大,当切削厚度较小时,碟盘楔面载荷小于齿尖处载荷,轴向载荷的方向取决于齿尖处载荷(如h=10 mm)。而当切削厚度增较大时,碟盘楔面载荷大于齿尖处载荷,其大小与方向取决于碟盘楔面载荷(如h=18 mm),碟盘楔面载荷随切削厚度的增加而增加,而齿尖处载荷随切削厚度的增加变化不大。轴向载荷随切削厚度的增加而增加。
4.2 复合作用破碎煤岩的载荷特性
当vj>0,vs≠0刀具振动切削复合破碎煤岩,刀具切削厚度由h=10~18 mm。刀具径向和轴向载荷曲线如图12所示。

图12 复合破碎煤岩载荷曲线
Fig.12 Load curves of the composite crushing coal rock
如图12(a)所示,径向载荷与图11(a)同样有两部分构成,碟盘楔面径向载荷幅值变化大,随切削厚度的增加而增加。由于刀具轴向往复运动,刀具齿尖等效球形压头产生的载荷的幅值稳态值明显小于图11(a)单作用情况,。
如图12(b)所示,随刀具轴向上下往复振动,其轴向载荷与振动周期同步明显的变化特性,轴向的幅值随切削厚度的增加越趋于对称性变化,表现出大块煤岩崩落碟盘楔面的显著作用。
由图11,12可知,刀具单切削作用与复合轴向向上时,径向载荷与轴向载荷均随切削厚度的增加而增加;径向载荷齿尖处载荷变化缓慢,具有稳态值;复合轴向向上时径向载荷小于单切削作用载荷;轴向载荷大于单切削作用载荷。
5 分析与讨论
煤岩大块崩落时,刀具齿尖处载荷计算有两种算法:一种是按式(13)剪切准则建立的体积破碎载荷Ⅰ,另一种是按式(14)等效抗压准则建立的简化载荷Ⅱ,得出刀具在两种不同算法下的径向与轴向载荷随切削厚度的变化规律。刀具单切削作用时,径向和轴向载荷的理论值与模拟值随切削厚度的变化规律,如图13所示。
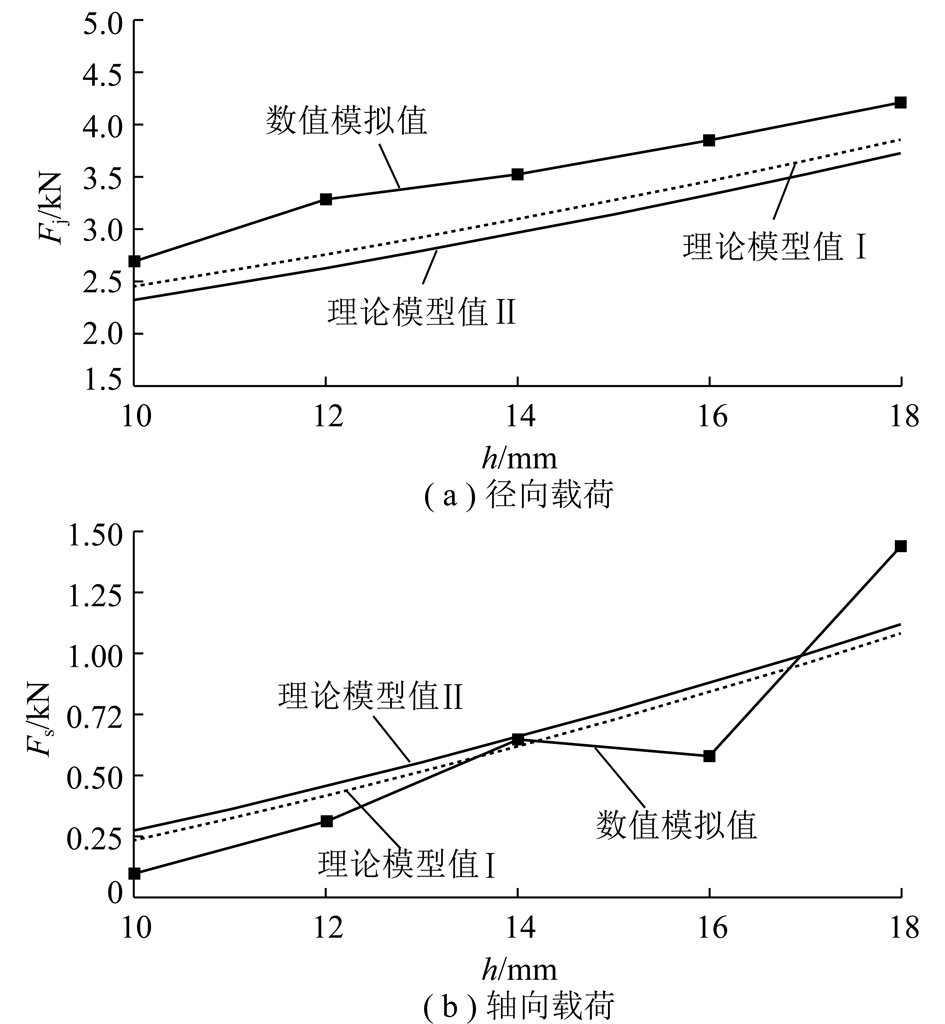
图13 单切削作用时载荷随切削厚度的变化
Fig.13 Load varies with the cutting thickness of a single acting cutting
由图13可知,刀具在单切削作用煤岩时,由两种理论模型计算得出径向载荷与轴向载荷基本一致。数值模拟与理论模型计算的径向载荷与轴向载荷变化规律相同。
刀具复合轴向向上时,径向载荷和轴向载荷的理论值与模拟值随切削厚度的变化规律,如图14所示。

图14 复合作用时载荷随切削厚度的变化
Fig.14 Load varies with the cutting thickness of composite acting cutting
由图14可知,刀具复合轴向向上运动破碎煤岩时,理论模型两种算法计算得出的载荷的变化规律基本一致。数值模拟与理论模型得出的径向载荷与轴向载荷均随切削厚度的增加而增加。
由图13,14可知,刀具单切削作用与复合轴向向上时,由数值模拟与理论模型计算得出的径向载荷与轴向载荷均随切削厚度的增加而增加;单切削作用数值模拟与理论模型计算径向载荷大于复合轴向向上时的载荷。轴向载荷小于复合轴向向上时的载荷。
刀具单切削作用破碎煤岩时,刀具数值模拟径向和轴向平均载荷与理论模型计算结果相差11%和4%。刀具复合轴向向上破碎煤岩时,刀具数值模拟径向与轴向平均载荷与理论模型计算结果相差3%和18%。
6 结 论
(1)通过分析边缘牙齿形碟盘破碎煤岩的力学过程,提出不同阶段主导作用相结合的方法,将等效单刀齿破碎煤岩的过程分为弹性变形,压裂、体积破碎和大块崩落4个阶段,揭示碟盘刀具各阶段破碎煤岩时受力状态与运动方式的关系,阐明了碟盘单刀齿宽度刀具破碎岩石的力学机理。
(2)运用复合效应叠加原理,通过碟盘刀具楔面与齿尖上载荷的矢量叠加,建立了单刀具在单切削作用与复合轴向向上时径向载荷与轴向载荷的数学模型。
(3)复合轴向向上时轴向载荷大于单切削作用时载荷,而径向载荷小于单切削作用时的径向载荷,说明复合作用方式更加有利于煤岩破碎。
(4)刀具数值模拟与理论模型均随切削厚度的增加而增加,2者的变化规律具有一致性。刀具单切削作用时,数值模拟径向与轴向载荷平均值与理论模型计算结果相差11%和4%;刀具复合轴向向上破碎煤岩时,数值模拟径向与轴向载荷与理论模型计算结果相差3%和18%。
参考文献(References):
[1] 别隆 A И.煤炭切削原理[M].王兴祚,译.北京:中国工业出版社,1965.
[2] EVANS I.A theory of the cutting force for point-attack picks[J].International Journal of Mining Science,1984,2(1):67-71.
[3] NISHIMATSU Y.The mechanics of rock cutting[J].International Journal of Rock Mechanics and Mining Science and Geomechanics Abrstracts,1972,9(2):261-270.
[4] LAN H,MARTIN C D,ANDERSSON J C.Evolution of in situ rock mass damage induced by mechanical-thermal loading[J].Rock Mechanics and Rock Engineering,2013,46(1):153-168.
[5] 牛东民.刀具切削破煤机理研究[J].煤炭学报,1993,18(5):48-54.
NIU Dongmin.Study of coal cutting mechanism of cutting tool[J].Journal of China Coal Society,1993,18(5):48-54.
[6] 王成勇,刘培德,胡荣生.花岗岩切削破碎过程研究[J].岩石力学与工程学报,1991,10(2):189-196.
WANG Chengyong,LIU Peide,HU Rongsheng.Study of granite cutting process[J].Chinese Journal of Rock Mechanics and Engineering,1991,10(2):189-196.
[7] STEVERDING B,LEHNIGK S H.Respongse of cracks to impact[J].Journal of Applied Physics,1970,41(5):2096-2099.
[8] 徐小荷,余静.岩石破碎学[M].北京:煤炭工业出版社,1984.
[9] LAN H,MARTIN C D,ANDERSSON J C.Evolution of in situ rock mass damage induced by mechanical-thermal loading[J].Rock Mechanics and Rock Engineering,2012,46(1):153-168.
[10] 陈忠辉,林忠明,谢和平,等.三维应力状态下岩石损伤破坏的卸荷效应[J].煤炭学报,2004,18(4):31-35.
CHEN Zhonghui,LIN Zhongming,XIE Heping,et al.Damage study of brittle rock failure under complicated stress[J].Journal of China Coal Society,2004,18(4):31-35.
[11] ABU Bakar M Z,GERTSCH L S.Evaluation of saturation effects on drag pick cutting of a brittle sandstone from full scale linear cutting tests[J].Tunnelling and Underground Space Technology,2013,34:124-134.
[12] 姜永东,鲜学福,尹光志,等.岩石应力应变全过程的声发射及分形与混沌特征[J].岩土力学,2010,31(8):2413-2418.
JIANG Yongdong,XIAN Xuefu,YIN Guangzhi,et al.Acoustic emission fractal and chaos characters in rock stress-strain procedure[J].Rock and Soil Mechanics,2010,31(8):2413-2418.
[13] 王春华,李贵轩,姚宝恒.刀型截齿切削煤岩的实验研究[J].辽宁工程大学学报,2001,20(4):487-488.
WANG Chunhua,LI Guixuan,YAO Baoheng.The experiment study of flat pick cutting coal and rock[J].Journal of Liaoning Technology University,2001,20(4):487-488.
[14] SHEN Hou-Lun Warren.Acoustic emission potential for monitoring cutting and breakage characteristics of coal[D].Pennsylvania,USA:Pennsylvania State University,1996.
[15] 刘春生,靳立红.基于截槽非对称条件镐型截齿的切削力学模型[J].煤炭学报,2009,34(7):983-987.
LIU Chunsheng,JIN Lihong.The cut mechanical model of pick-shaped cutter under conditions of dissym metrical slotting[J].Journal of China Coal Society,2009,34(7):983-987.
[16] 刘春生,王庆华,李德根.镐型截齿切削阻力谱的分形特征与比能耗模型[J].煤炭学报,2015,40(11):2623-2628.
LIU Chunsheng,WANG Qinghua,LI Degen.Fractal characteristic and specific energy model of conical picks cutting resistance spectrum[J].Journal of China Coal Society,2015,40(11):2623-2628.
[17] 张祖培,刘宝昌.碎岩工程学[M].北京:地质出版社,2004.
[18] 刘春生,李德根.截齿切削煤岩的力学模型与性能评价[M].哈尔滨:哈尔滨工业大学出版社,2017.
[19] 刘春生,于信伟,任昌玉.滚筒式采煤机工作机构[M].哈尔滨:哈尔滨工业大学出版社,2010.
[20] 刘春生,徐玉芸,李德根,等.碟盘刀齿冲击与切削复合破碎煤岩的载荷特性[J].黑龙江科技大学学报,2017,27(2):97-103.
LIU Chunsheng,XU Yuyun,LI Degen,et al.Load characteristics behind disc cutter teeth impacting and cutting composite broken coal rocks[J].Journal of Heilongjiang University of Science and Technology,2017,27(2):97-103.>