新修订的《煤矿安全规程》要求矿井应装备具有煤矿井下人员精确定位功能的矿井人员定位系统[1]，同时，煤矿井下人员精确定位也是实施煤矿快速有效应急救援所必须解决的问题[2]，因此，研究煤矿井下人员精确定位技术与方法对于煤矿安全生产无疑具有重要意义[3-5]。 无线定位技术的发展使得具有更高定位精度的基于到达时间(Time of Arrival,TOA)的定位方法，逐渐成为矿井人员定位系统的主流技术[6]。由于井下空间狭小，电磁环境恶劣，多径效应严重，导致测得的到达时间受非视距(Non Line of Sight，NLOS)信号的影响，TOA测量出现超量时延现象，所测距离具有正测量误差，严重降低定位精度。抑制NLOS误差是优化矿井人员定位系统定位精度所要解决的关键问题[7]。针对矿井定位环境，一些学者对人员精确定位系统做出了富有成效的研究，并取得了具有一定代表性的研究成果[8-12]，其代表了3种典型的处理和抑制NLOS影响的定位方法:第1种是非视距识别法，如文献[8]，识别出NLOS信号，然后对视距传播的测量值增大权值用于位置估计，其本质是剔除NLOS信号的影响;第2种是增加空间观测维度法，如文献[9]，分别采用超声波和无线电测量巷道横向距离和纵向距离，观测信息的丰富能大幅度减少NLOS的影响;第3种是数据平滑法，如文献[10-11]，分别采用均值滤波和卡尔曼滤波对测量结果进行滤波以对NLOS信号造成的误差进行抑制。第1种方法，识别过程要求必须有LOS信号，实际应用定位结果不理想，且市面上的通用测距芯片并不提供NLOS信号的辨别功能[13]，因此，算法的实现需要专用芯片或自行开发的接收装置，这对大规模推广是不利的。第2种方法毫无疑问能有效避免NLOS误差，但因此付出的硬件成本是实际应用中难以接受的，很难在实际应用中推广。性价比最高的当属第3种方法，采用滤波处理抑制NLOS误差是一种有效的方法。但文献[10-11]所述方法与其他大多数矿井定位方法一样，偏重于理想情况，只能应用于直线型巷道，而实际巷道往往是弯曲的[14];另外，虽然文献[10-11] 重视解决NLOS所带来的定位误差问题，但在解决过程中，对NLOS数据只是简单的摒弃处理，没有充分挖掘其中的有用信息。因此，井下定位方法还有较大的改进空间，如何挖掘NLOS信号所蕴含的有用信息并加以合理利用，在矿井环境下统一NLOS与LOS场景，将定位方法应用于更一般的曲线巷道，值得进一步研究。

针对上述技术问题，本文采用扩频测距的方式研究了多径时延测距误差产生机制，并分析了由此导致的TOA测量值正向误差的分布特点，在此基础上，提出一种基于测距值二次重构的弯曲巷道目标定位方法，该方法利用巷道空间位置信息重构测量数据，统一处理NLOS和LOS的测距信息，适用于更为一般的曲线型巷道的定位。

1 巷道测距误差分析

1.1 巷道扩频测距模型

扩频信号有出色的抗电磁干扰、抗多径的能力，有着良好的测距功能，相对于WiFi,Bluetooth等其他测距方式具有明显的优势[15]，且具有低功耗、低成本的特点，适用于矿井人员定位。下面就以直接序列扩频方式来研究矿井环境下的无线电TOA测距误差机制，所得出的结论亦能适用于其他基于TOA的无线测距方式。

在巷道密集多径的环境下，定位系统对多径效应的研究，不但要注重对信号幅度的影响，更需要注重多径效应对信号相位测量的影响。因此，不失一般性，将巷道视为时变的系统，表征该时变信道模型的系统函数可表示为

(1)

其中，hi(t)和 τi(t)分别表示 t 时刻第 i 条路径的幅度和相对于直达信号的传播延迟，直达信号可认为是第1条到达路径;δ(t)表示单位冲激响应;η表示多径衰减因子。

矿井环境下，每个hi的幅度服从瑞利分布[16]，考虑延迟主要是信号多次反射造成的影响，加上延迟衰减因子η，延迟衰减因子符合指数分布[17]，因此可合理确定表示平均时延，考虑信道的变化速率与扩频码速率相比很慢，多径信道可以认为是稳定的，可视为线性系统[18]，那么，式(1)可合理地简化为

(2)

无论采取何种扩频方式，扩频测距本质上都是利用扩频信号自身良好的自相关性，通过接收信号与本地信号的相关运算，判断两者的最大相关峰值输出以实现接收信号相对于发射信号时间延迟的测量。为说明问题方便，简化其他因素，下面设发射机发射信号为c(t)，c(t)为以m序列作为扩频的伪随机(Pseudo Noise,PN)码，其波形可由式(3)描述:

(3)

其中，Tc为PN码一个码片持续时间;PT(t)为脉宽为Tc的矩形单位脉冲，ck∈{-1，1}。该发射信号经式(2)所描述信道传输后，接收端所接收信号可表示为

r(t)=h(t,τ)c(t-td-t′)dt′

(4)

其中，td为直达信号传播时延。测距装置通过码时钟驱动产生本地信号c(t-τ)，与接收信号按式(5)进行相关运算:

(5)

其中，NTc为m序列周期，联合式(2)～(4)，则相关运算式(5)可更为具体地表示为式(6)。当τ=td时，相关运算出现峰值，表示本地码与接收码相位一致，从而可以获得接收信号延迟时间td。

td-τi)c(t-td-t′)dt′c(t-τ)dt

(6)

式(6)作为井下扩频测距模型，模型不关心信号在传播过程中的具体行为，而是从统计的角度来确定信号被接收的特性，特别突出了接收信号的时延特性，能够准确刻画矿井密集多径环境下各时延信号对相关运算的影响，为扩频测距误差的产生提供了理论分析的依据。

1.2 巷道扩频测距误差分析

根据式(6)，可以客观地观察多径对扩频测距的影响，设置如下仿真参数:扩频码速为40 Mb/s，即Tc=1/4×10-7 s，采样时间设为1.25 ns，直达径传播时延td=50 ns，参考矿井相关参数[16]，设置信道莱斯因子为-8，多径延迟分辨时间为2.5 ns，平均时延设为12.5 ns，最大延迟信号与直达信号功率之比设为-20 dB，进行相关运算仿真，结果如图1所示。

从仿真结果图1中可以观察到，在没有多径干扰的情况下，即使信道是衰减的，相关峰依然呈尖锐的三角形;在多径存在的情况下，相关值不再呈尖锐的峰值性质，而是一种类似正态分布的钟型曲线，峰值往时间轴正向偏移，偏移有4～5 ns，这表明，相应的测距结果具有非零均值误差，会有1.2～1.5 m的正向偏差;进一步在无直达信号情况下，峰值往时间轴上偏移更大，但其相关图与有直达信号存在时形状类似，这表明两者除偏离程度不同外，其时延的统计规律是相似的;同时仿真结果也揭示了多径造成的测距误差无法通过提高系统接收机的测量精度来消除。

仿真结果提供了统一NLOS与LOS场景的理论依据，如果没有直达信号，在处理好正向偏差的前提下，可以充分利用NLOS信号，实现目标定位。

2 定位方法描述

2.1 方法的定位场景

本文讨论更为一般的曲线型巷道目标定位问题，直线巷道作为曲线巷道的特例，所提出的算法对直线巷道亦能适用，文中对直线巷道的定位场景不再赘述。图2所示的是弯曲巷道场景的俯视示意。

定位采用双基站进行二维平面定位，基站B1,B2设置在巷道的同一侧，以B1为坐标原点，以B1与B2的连线为x轴建立平面坐标系。移动节点rP在巷道两基站间随机移动，基站与移动节点间通过测量TOA方式获得彼此之间的距离(所测量的距离值并不是准确的距离值，文后叙述称为伪距)。rP与B1间不存在电磁波直达路径，属于NLOS场景，隧道和煤矿井下巷道都可看作是波导[19]，所测出的距离L1近似rP与B1间巷道的实际长度，带有较大的正向测距误差。rP与B2间则存在着直达径，由于多径影响，所测得两者间距离d2依然具有正向误差。下面将根据此定位场景及所建立的坐标系展开算法。

2.2 有偏测距值的二次重构

2.2.1 NLOS伪距重构

弯曲巷道下，当移动目标点rP与其中的一个基站处于NLOS状态时，两者通过TOA所测的距离L1并不是两者之间的直线距离，若使之能提供定位有效信息，则必须对此伪距合理重构。重构需要额外的信息，在巷道中确定若干标志点，如图2所示的点M1，M2，…，M5。它们的连线就能较为准确地描述巷道的走向及位置信息，这样处理可将曲线巷道近似划分成若干段直线型巷道，为数据处理带来方便。为了重构伪距L1，需要利用两基站间巷道的总长度信息，设两基站间巷道长度为Ls，考虑到伪距具有正向偏差，有L1+d2>Ls，则可按如下步骤重构伪距L1:

(1)由Δε=L1+d2-Ls,求出rP两端的偏差区间Δε;

(2)由标志点M4,M5确定的直线，求出偏差区间的中点位置R1;

(3)求出R1与B1直线距离d1作为L1的重构值。

根据重构的d1及d2，即可得到描述待定位的移动节点rP与定位基站位置关系的观测方程:

(7)

其中，(x1,y1)和(x2,y2)分别表示2个定位基站B1和B2的位置坐标，(x,y)是待测目标节点rP的位置坐标，方程(7)的解点mP即是伪距d1,d2所确定的位置估计点。考虑到泰勒级数展开算法是有效求解非线性方程的最优估计方法，适用于所有的定位系统[20]，可由泰勒展开方法直接解算出观测方程(7)的解点mP。

2.2.2 位置估计值的精重构

由于并未能完全消除伪距误差所造成的影响，观测方程(7)的解点是粗糙估计，依然具有较大误差。需要对该估计值进行第2次重构，重构的目的是提高估计点的精度。重构的方法主要依据巷道的位置信息。继续以图2为例，阐述重构步骤如下:

(1)设定巷道标志点，将巷道抽象表示成由标志点M1-M2-M3-M4-M5表示的线型巷道;

(2)确定解点mP所在的线段区域M4-M5;

(3)采用线性插值法，将点mP向线段区域M4-M5投影。获得的投影点R2作为解点mP的重构点。

2.2.3 重构后位置参量误差特性

伪距d1和d2是造成位置估计误差的根本原因，考察观测方程(7)，由于在NLOS状态下伪距正向误差要比LOS状态下大，伪距L1重构得到d1并不能完全消除正向偏差，现定性考察伪距d1和d2对方程解点mP所造成的影响，首先考虑对x方向位置偏差的影响，由于移动节点处于两个基站之间，伪距d1和d2在x方向的误差值是相反的，这样所求出的位置交叉点在x方向的正向偏差会互相抵消，两个伪距在x方向的定位误差均值为0，x方向的误差分布可合理设为高斯模型[21]。而对于y方向，由于移动节点位于两定位基站的同一侧，所求出的位置交叉点在y方向的正向偏差会互相叠加，误差均值不为0，导致解点基本落在巷道沿y正方向的一侧，影响定位精度。第2次重构能够解决y方向误差均值不为0的问题。第2次重构将解点投影到巷道中心线上，使得y方向的估计值亦为巷道中心线的y值。考虑到巷道内人员或者其他移动目标的行走路线一般是沿巷道中心线，因此，移动目标的真实位置y值会在巷道中心线上下随机变化，因而它与投影点的y估计值的差均值为0，且亦能合理视为高斯分布。

二次重构不但提升了精度，而且重构后x,y误差均值为0，并能合理视为高斯分布，方法下一步设计卡尔曼滤波对其进一步优化。

2.3 卡尔曼滤波优化方法

卡尔曼滤波算法主要是对目标的位置、速度以及加速度等运动参数进行估计，其状态方程可以描述任何复杂多维的运动学方程，不但能对静止目标定位，同时也能对运动目标进行跟踪，这些优势使得卡尔曼滤波成为定位系统广泛应用的一种有效方法[22]。一般情况下巷道内人员移动速度在2 m/s以下，由于巷道内移动节点运动速度相对较慢，有一定的规律性，而定位方法关心位置信息，前面的重构工作已直接给出了位置的估计值，因此降低了运动描述的复杂性，卡尔曼状态方程可采用如式(8)所示的一阶运动学方程，能够很好地描述巷道移动目标的随机运动状态。

S(k)=Φk/k-1S(k-1)+GW(k-1)

(8)

其中，表示x方向和y方向的位移、速度;Φk/k-1为tk-1时刻至tk时刻的一步状态转移阵，在此，状态转移阵视做常量处理，因此可去掉下标，按常规的一阶运动学方程表示成式(9):

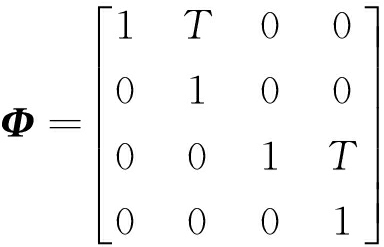
(9)

其中，T为卡尔曼滤波的采样时间;G为系统噪声驱动阵，移动节点在巷道内随机移动，随机性体现在位置的变化上，故将移动节点运动的位置随机变化视为系统噪声，噪声驱动阵设为常量，只影响位置，可表示成式(10):

(10)

系统噪声不难由经验确定:由于巷道是狭长的，巷道宽一般不超过5 m，沿x方向伸展，可以认为移动目标正常情况下是在巷道中心线及偏离中心线0.5 m的两侧区域上移动，因此，y方向系统噪声可设定标准差为0.5 m的高斯噪声，而移动过程中，停止、启动、加减速等行为，可视为x方向上的扰动，考虑巷道内目标移动速度较低，在一个采样周期内，比照y方向，x方向亦可设定标准差为0.5 m的高斯噪声，亦即认为移动目标在一般情况下维持原有的运动状态。据此确定系统噪声序列为

卡尔曼滤波的观测方程由式(11)确定:

Z(k)=HS(k)+Q(k)

(11)

其中观测矩阵由式(12)确定:

(12)

Q(k)为观测噪声方差阵。在此是针对重构点的观测，观测误差显然与系统噪声序列一致，可设置为

2.4 方法总体设计方案

根据以上分析，本方法的总体设计方案如流程图3所示，方法整体设计方案以测量数据二次重构为关键步骤，辅以卡尔曼滤波为实现基础。

针对流程图作以下几点说明:

(1)巷道位置信息，包括事先确定的若干标志点以及两基站之间的巷道长度。所确定的标志点的连线能够近似表示所定位巷道段的走向及其他点的位置信息。

(2)卡尔曼滤波初始参数包括:状态估计初值设为S0=[x0,0,y0,0,0,0],其中，(x0,y0)为初始位置，可由第1个重构的观测值Z0确定;滤波增益阵作为独立计算回路，其中主要是均方误差阵Pk 的递推算法，均方误差阵P初始值可设为系统的噪声方差阵，即

(3)非视距重构是指移动节点与基站间不存在直达路径的伪距重构，不包括遮挡引起的NLOS状况。遮挡与否对方法的定位效果影响不大。

3 仿真与实测

3.1 算法性能仿真

为了检验算法在各种曲率的弯曲巷道下的定位精度，设置如下内容的仿真。以二次抛物线型来近似模拟一段定位的曲线型巷道，由于井下巷道的弯曲部分基本上设计为圆曲线，在该抛物线顶点左右两侧各取一个点，以所取的这两点之间的弧线代表巷道的弯曲部分，以这段弧线的平均曲率来表示弯曲程度。定位的基站BS1与BS2的坐标分别为(0,0)与(100,0)。为说明问题方便，取该抛物线顶点在两基站中点位置。移动目标位置由BS1向BS2沿抛物线随机产生，对于所产生的每一个位置点，对其y坐标加上一个均值为0标准差为0.5的随机数，以表示移动路径并非完全落在抛物线上。

仿真的曲率范围设为0.013≤ki<0.46，根据大量实测数据显示，伪距的误差均值及方差均随曲率的增大而增大，因而在仿真过程中，通过式(13)所确定的均值与方差产生定位所需的距离数据。

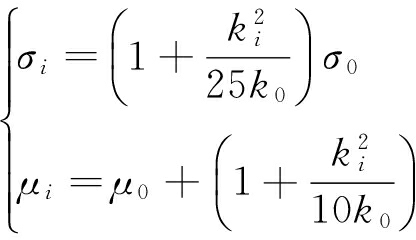
(13)

式中，k0为基准曲率，k0=0.013，大致对应于直线状况;ki为仿真中的第i个曲率;σ0为在k0状态下伪距的标准差;μ0为k0状态下伪距的均值。

从上述曲率范围平均选取了25组曲率的曲线，每组曲线随机产生100个位置点，每组曲率各做了100次的蒙特卡洛仿真，为了比较算法性能，同时也仿真了普通的平面位置线交叉定位方法，两者定位效果如图4所示。

仿真结果显示，在曲率小于0.3部分，定位平均误差接近于1，且非常平稳，表明该方法在此间具有良好的定位效果，对曲率变化不敏感。曲率大于0.35，平均误差有明显上升，特别是在超过0.4时有急剧上升趋势，算法性能下降，即便如此，定位误差依然在2 m以下，特别需要提出的是，实际弯曲巷道绝大部分曲率在0.25以下。因此，总体上算法性能优越。与之形成鲜明对比的是，地面定位常用的位置线交叉定位方法定位误差一直高居10 m左右，误差上升趋势明显，大曲率下更是急剧上升到50 m左右，这从另一方面说明了地面一些经典的定位方法并不能直接应用于矿井巷道定位。

3.2 实测验证

实验选择北京某地铁站一处较典型的曲线型地下通道，通道宽约4.0 m，高约2.5 m，长约80 m，其中弧线通道部分长约4.1 m，平均曲率0.192，实验场景如图5所示。

实验中收发装置均采用线性扩频(Chirp Spread Spectrum,CSS)无线节点，节点使用的射频芯片为NA5TR1，该 CSS 射频芯片工作于80 MHz带宽模式，采用双边对等两次测距法测量收发双方间的距离。实验中需要3个节点，其中两个做为基站，两基站间直线距离43.29 m，非视距安置，分处弧线两端，其中第1个基站到巷道弧线端距离为22.8 m，另一个基站距巷道弧线端距离为20.4 m，移动节点与电脑相连，在两基站间移动。实验中标定5个标志点(包含两基站，弧线两端点及弧线中心点)。实验中共对36个位置点进行定位，表1列出了其中奇数位置点的定位数据。

表1 定位数据
Table 1 Positioning data

为了显示清晰，将表1中的位置序列进行定位效果显示，如图6所示。

效果图(图6)直观显示了方法各个步骤逐步优化定位精度的过程，随定位方法每一步的执行，估计点随之向实际位置点接近，显示了采用二次重构联合卡尔曼滤波设计方法的科学性和有效性。

为了更准确地评价方法性能，下面考虑误差累积分布和均方根误差两个定位精度指标。图7显示了方法的误差累积分布，误差大部分落在1.5 m之内，误差在2 m以内接近90%，表明方法有较高的确定性。为了更直观体现方法的稳定性，图8显示了方法的定位性能，列出了定位误差与相应的伪距误差对比，在弯曲巷道情况下，由于非视距影响，伪距具有更大的测量误差，但定位误差线明显靠近零线，表明方法具有很强的误差抑制能力，能够有效地利用NLOS信号测距信息实现定位。

考查表1中的定位误差，发现有若干序列点的定位误差在2 m以上，现考虑定位精度另一重要指标均方根误差，定位均方根误差由式(14)定义:

(14)

其中，表示位置估计值;x,y表示移动目标的真实位置值，尽管有一些位置点定位误差偏大，从总体考虑方法的定位精度，则由式(14)所确定的定位均方根误差在1 m以下，达到0.891 m，表明方法在实现弯曲巷道目标定位上具有较高的定位精度。

4 结 论

(1)在巷道密集多径环境下，NLOS信号一方面会影响测距精度，另一方面它与LOS信号在接收端的时延统计规律是相似的，同样蕴含有可用的测距信息。在井下人员精确定位方法的设计中，由于非视距现象普遍，需要注重NLOS信号的利用，使定位方法能够在更为复杂的环境下应用。

(2)所提出的方法充分挖掘NLOS信号中的测距信息，不但能显著抑制了NLOS信号测距误差所造成的定位精度下降的影响，而且与LOS信号统一应用于巷道目标定位，能够实现更为一般的弯曲巷道下目标的定位，相比现有的矿井定位方法，具有更大的普适性。

(3)所提出的方法在仅采用二基站，无冗余定位信息的情况下，充分利用巷道位置信息，定位误差累积分布理想，定位均方根误差为0.891 m，具有高性价比，适用于井下移动目标定位。

参考文献(References):

[1] 孙继平.2016年版《煤矿安全规程》监控与通信条款解析[J].工矿自动化,2016,42(5):1-7.

SUN Jiping.Explanations for part of monitoring and communication of coal mine safety regulations of,2016 Edition[J].Industry and Mine Automation,2016,42(5):1-7.

[2] 孙继平,钱晓红.煤矿事故与应急救援技术装备[J].工矿自动化,2016,42(10):1-5.

SUN Jiping,QIAN Xiaohong.Coal mine accident and emergency rescue technology and equipment[J].Industry and Mine Automation,2016,42(10):1-5.

[3] 孙继平.煤矿安全生产监控与通信技术[J].煤炭学报,2010,35(11):1925-1929.

SUN Jiping.Technologies of monitoring and communication in the coalmine[J].Journal of China Coal Society,2010,35(11):1925-1929.

[4] 孙继平.煤矿物联网特点与关键技术研究[J].煤炭学报,2011,36(1):167-171.

SUN Jiping.Research on characteristics and key technology in coal mine internet of things[J].Journal of China Coal Society,2011,36(1):167-171.

[5] 孙继平.煤矿井下人员位置监测技术与系统[J].煤炭科学技术,2010,38(11):1-5.

SUN Jiping.Personnel position monitoring technology and system in underground mine[J].Coal Science and Technology,2010,38(11):1-5.

[6] 孙继平.煤矿事故特点与煤矿通信、人员定位及监视新技术[J].工矿自动化,2015,41(2):1-5.

SUN Jiping.Characteristics of coal mine accidents and new technologies of coal mine communication,personnel positioning and monitoring[J].Industry and Mine Automation,2015,41(2):1-5.

[7] 胡青松,张申,吴立新,等.矿井动目标定位:挑战、现状与趋势[J].煤炭学报,2016,41(5):1059-1068.

HU Qingsong,ZHANG Shen,WU Lixin,et al.Localization techniques of mobile objects in coal mines:Challenges,solutions and trends[J].Journal of China Coal Society,2016,41(5):1059-1068.

[8] 田子建,王宝宝,张向阳.一种基于非视距鉴别加权拟合的矿井超宽带定位方法[J].煤炭学报,2013,38(3):512-516.

TIAN Zijian,WANG Baobao,ZHANG Xiangyang.Mine ultra-wideband positioning method based on non line-of-sight identification weighted fitting[J].Journal of China Coal Society,2013,38(3):512-516.

[9] 田子建,李宗伟,刘晓阳,等.基于电磁波及超声波联合测距的井下定位方法[J].北京理工大学学报,2014,34(5):490-494.

TIAN Zijian,LI Zongwei,LIU Xiaoyang,et al.A positioning method in mine tunnel based on joint electromagnetic wave and ultrasonic distance measurement[J].Transactions of Beijing Institute of Technology,2014,34(5):490-494.

[10] 孙继平,李晨鑫.基于卡尔曼滤波和指纹定位的矿井TOA 定位方法[J].中国矿业大学学报,2014,43(6):1127-1133.

SUN Jiping,LI Chenxin.Mine time of arrival positioning method based on Kalman filtering and fingerprint positioning[J].Journal of China University of Mining & Technology,2014,43(6):1127-1133.

[11] 孙继平,李晨鑫.基于改进均值滤波和参数拟合的矿井 TOA 几何定位方法[J].煤炭学报,2015,40(5):1206-1212.

SUN Jiping,LI Chenxin.Mine TOA geometric positioning method based on improved mean filtering and parameter fitting[J].Journal of China Coal Society,2015,40(5):1206-1212.

[12] 赵志信,李加君,江晓林,等.狭长空间环境下改进的WSN节点质心定位算法[J].黑龙江科技大学学报,2016,26(5):577-580.

ZHAO Zhixin,LI Jiajun,JIANG Xiaolin,et al.Improved WSN node centroid localization algorithm in long and narrow space environment[J].Journal of Heilongjiang University of Science & Technology,2016,26(5):577-580.

[13] 谷战垒,何诚,宁月松.基于NA5TR1的无线定位节点的设计[J].电子设计工程,2011,19(9):189-192.

GU Zhanlei,HE Cheng,NING Yuesong.Design of wireless location node based on NA5TR1[J].Electronic Design Engineering,2011,19(9):189-192.

[14] 石庆冬,孙继平.弯曲矩形隧道电磁波衰减特性[J].中国矿业大学学报,2001,30(1):91-93.

SHI Qingdong,SUN Jiping.Attenuation characteristic of guided EM waves in curved rectangular mine tunnel[J].Journal of China University of Mining & Technology,2001,30(1):91-93.

[15] YOON Chanmin,CHA Hojung.Experimental analysis of IEEE 802.15.4a CSS ranging and its implications[J].Computer Communications,2011,34(11):1361-1374.

[16] 王艳芬,于洪珍,张传祥.矿井超宽带复合衰落信道建模及仿真[J].电波科学学报,2010,25(4):805-810.

WANG Yanfen,YU Hongzhen,ZHANG Chuanxiang.Modeling and simulation of mine ultra-wideband composite fading channel[J].Chinese Journal of Radio Science,2010,25(4):805-810.

[17] 杨维,李滢,孙继平.类矩形矿井巷道中UHF宽带电磁波统计信道建模[J].煤炭学报,2008,33(4):467-472.

YANG Wei,LI Ying,SUN Jiping.A statistical channel model of wideband UHF radio waves along rectangular-like mine tunnel[J].Journal of China Coal Society,2008,33(4):467-472.

[18] 张天骐,苗圃,马国宁,等.多径环境下的直扩信号伪码周期估计[J].电波科学学报,2009,24(5):973-978.

ZHANG Tianqi,MIAO Pu,MA Guoning,et al.Period estimation of the PN sequence for direct sequence spread spectrum in multipath environment[J].Chinese Journal of Radio Science,2009,24(5):973-978.

[19] 孙继平,张长森.异型波导截止频率的研究[J].煤炭学报,2003,28(2):210-213.

SUN Jiping,ZHANG Changsen.Study on cut-off frequency of abnormity wave-guide[J].Journal of China Coal Society,2003,28(2):210-213.

[20] 田孝华,廖桂生,赵修斌,等.面向CDMA蜂窝网的无线定位技术术[J].电子学报,2005,33(12):2196-2203.

TIAN Xiaohua,LIAO Guisheng,ZHAO Xiubin,et al.Wireless location technologies for CDMA cellular radio networks[J].Acta Electronica Sinica,2005,33(12):2196-2203.

[21] 田孝华,周义建.无线电定位理论与技术[M].北京:国防工业出版社,2011:52-53.

TIAN Xiaohua,ZHOU Yijian.Theory and technology of wireless location[M].Beijing:National Defense Industry Press,2011:52-53.

[22] PELKA Mathias,HELLBRÜCK Horst.Introduction,discussion and evaluation of recursive Bayesian filters for linear and nonlinear filtering problems in indoor localization[A].2016 International Conference on Indoor Positioning and Indoor Navigation[C].Madrid Spain,2016:1-8.>