
邓正定1,2,吴建奇1,2,尚佳辉1,2,谢 栎1,2
(1.江西理工大学 建筑与测绘工程学院,江西 赣州 341000; 2.江西省环境岩土与工程灾害控制重点实验室,江西 赣州 341000)
摘 要:基于等效弹性模型的方法,构建综合考虑含贯通—非贯通交叉节理岩体宏细观缺陷的复合损伤模型。首先,将贯通节理部分看成一定厚度的独立材料,其主要产生闭合变形及沿节理面的剪切变形,其储存弹性应变能及剪切应变能;其次,基于断裂力学及应变能理论相结合,将交叉节理中的非贯通节理岩体部分看成岩体内部宏观损伤,对节理尖端的应力强度因子进行了计算,推导得出了储存在非贯通节理中的应变能计算公式,并将岩体内部的细观损伤按Weibull分布描述,建立综合考虑宏细观缺陷的节理岩体复合损伤模型;再次,对交叉节理岩体的强度准则进行了讨论,构建考虑交叉节理不同强度准则的等效弹性模型;最后,将计算结果与试验结果进行了比较分析,模型计算结果与试验结果吻合较好,证明了模型的合理性,同时讨论了贯通节理倾角、非贯通节理倾角对岩体峰值强度及破坏准则的影响,以及非贯通节理贯通率对初始损伤变量影响规律。
关键词:贯通;非贯通;交叉节理岩体;等效弹性模型;强度
中图分类号:TD315
文献标志码:A
文章编号:0253-9993(2018)11-3098-09
DENG Zhengding1,2,WU Jianqi1,2,SHANG Jiahui1,2,XIE Li1,2
(1.School of Architectural and Surveying and Mapping Engineering,Jiangxi University of Science and Technology,Ganzhou 341000,China; 2.Jiangxi Provincial Key Laboratory of Environmental Geotechnical and Engineering Disaster Control,Ganzhou 341000,China)
Abstract:Based on the method of the equivalent elastic model,the composite damage model was constructed to consider comprehensively the mac-roscopic and microscopic defects of the rock mass containing persistent and non-persistent joints.Firstly,the part of persistent joint was considered as an independent material with a certain thickness,which mainly produces closed deformation and shear deformation along the joint surface,which can store elastic strain energy and shear strain energy.Secondly,based on the combination of fracture mechanic and strain energy theory,the non-persistent joint rock part of the cross joint was regarded as the internal macro damage of rock mass.Therefore,the joint point of stress intensity factor was calculated,and the formula of strain energy stored in non-persistent joint was derived.The microscopic damage was described according to the Weibull distribution within the rock mass,and the comprehensive consideration macro and micro defects of joint rock damage model was established.Thirdly,the strength criterion of cross jointed rock mass was discussed,and the equivalent elastic model of different strength criterion was constructed.Finally,the calculated results were compared with the test results,the model calculation results are in good agreement with the experiment results,which proves the rationality of the model.In addition,the influence of persistent joint angle and non-persistent joint angle on the peak strength and failure criterion of rock mass,and the influence law of initial damage variables affected by penetration rate of non-persistent joint were discussed.
Key words: persistent;non-persistent;cross-jointed rock;the equivalent elastic model;strength

移动阅读
邓正定,吴建奇,尚佳辉,等.含贯通-非贯通交叉节理岩体等效弹性模型及强度特性[J].煤炭学报,2018,43(11):3098-3106.doi:10.13225/j.cnki.jccs.2017.1819
DENG Zhengding,WU Jianqi,SHANG Jiahui,et al.Equivalent elastic model and strength properties for cross-jointed rock mass containing persistent and non-persistent joints[J].Journal of China Coal Society,2018,43(11):3098-3106.doi:10.13225/j.cnki.jccs.2017.1819
收稿日期:2017-12-24
修回日期:2018-07-03
责任编辑:常 琛
基金项目:江西省教育厅科学技术研究资助项目(GJJ170562);江西理工大学博士科研基金资助项目(3401223293)
作者简介:邓正定(1987—),男,江西萍乡人,博士,讲师。E-mail:dengzhengding@126.com
节理裂隙的几何分布形态特征及力学参数对岩石的强度特征及力学特性都有重要的影响[1]。自然界中岩体的节理由于地质构造应力坏境的差异而形态各异,其中以交叉节理而存在的岩体是其主要赋存形式之一,其交叉节理的几何形态对岩体工程特性有较大影响。
目前,国内外学者对完整岩石、含单节理或多条平行节理岩体的力学特性无论试验还是理论方面都进行了较多研究。如在试验研究方面,刘红岩等[2]通过按一定比例配置的水泥砂浆类岩石相似材料进行试验研究,其在岩体内预置单组及多组平行节理在不同应变率下进行试验,得出了节理的几何特征对节理岩体的强度及破坏模式的影响规律;张平等[3]采用静、动三轴伺服材料试验机,对预制断续裂隙砂岩试件进行单轴动载试验,结果表明:裂隙的空间位置、贯通方式等与静载下有明显区别,在动载下更容易在非贯通裂隙尖端产生直接贯通。 在理论研究方面,D.Zhao等[4]基于连续介质损伤力学把岩体内的节理定义为初始损伤,采用二阶张量作为岩体损伤变量,建立了节理岩体的弹性损伤模型;WANG等[5]利用等效方法建立了含有数组平行节理岩体的连续型本构模型;张力民等[6]基于断裂力学和应变能理论相结合,对单个节理存在引起的附加应变能增量与损伤力学的损伤应变能释放量相关联,推导出了含非贯通节理岩体的损伤变量计算公式,进而提出了含多条平行节理岩体的损伤本构模型。
对于含交叉节理岩体,相关学者对此方面也进行了部分研究,但大多侧重于试验研究。如刘东燕等[7]研究了主节理角度变化对含X型交叉节理岩体力学性能的影响,认为含X型交叉节理岩体强度高于含单一节理岩体;熊飞等[1]通过对含尖端相交裂隙砂岩试样进行单轴压缩试验,研究了2 条相交裂隙分布方向角β和两节理间夹角α的关系对砂岩强度、变形及破裂演化特征的影响。试验结果表明:随着β角的增大,试样峰值强度逐渐增大,平均模量先增大后减小。张波等[8-9]以类岩石材料模拟岩体,考虑主次多裂隙、等长多裂隙2类交叉多裂隙形式,制作含交叉多裂隙试件,对试件进行单轴压缩静载试验,研究了含交叉多裂隙岩体在单轴压缩下的力学性能。刘学伟等[10]对含不同预制裂隙形式(单、双、T形交叉及X形交叉裂隙)的类岩石试样进行了单轴压缩试验,系统地研究了裂隙形式对试样强度特征及失稳模式的影响。
对于岩体中的节理,学者们大多都已认为节理的几何特征(倾角、节理长度等)对岩体的力学特性有较大影响。同时由于地质构造作用的方向及不同位置作用程度的差异,导致自然界中的节理岩体既含有处于贯通状态也有处于非贯通状态。当岩体中同时含贯通及非贯通的交叉型节理时,其交叉节理对强度准则如何影响,对其损伤如何演化,都是值得研究的问题。因此本文针对实际工程中含贯通-非贯通组合的交叉型节理岩体,对其在单轴压剪作用下的强度准则及本构关系进行研究,具有较大的工程应用价值。
节理岩体的破坏模式主要分为完整岩块的张拉和剪切破坏、沿贯通节理面剪切滑移破坏、非贯通节理面剪切破坏及组合破坏等4种形式[11]。

图1 含贯通-非贯通交叉节理岩体模型
Fig.1 Jointed rock mass model containing persistent and non-persistent
对于含贯通-非贯通的交叉节理岩体,如图1所示。倾角为α的节理为贯通状态,倾角为β的节理为非贯通状态。对于贯通节理,其将岩体分割成独立的两部分,在压力作用下,一定厚度节理主要发生闭合变形及沿节理面的剪切变形;对于非贯通节理,因存在部分未贯通的岩桥,当节理面切应力达到一定值时,节理尖端会产生应力集中,裂隙沿节理面尖端扩展,因此对于非贯通节理,可以看成是岩块内部的宏观损伤;此外,岩体内部还存在许多微孔洞,微裂纹等细观损伤,且随着应力的增加,微裂隙会继续扩展,此部分可看成是岩体内部的细观损伤。因此,含贯通-非贯通的交叉节理岩体可看成是非贯通节理宏观缺陷、微裂隙细观缺陷及有一定厚度的贯通节理的复合地质材料。基于此,本文通过等效弹性模型的方法,将应变能理论与损伤理论相结合,研究交叉节理岩体的力学特性。
假定完整岩石的弹性模量为E0、体积为V,在受到均匀压应力σ作用下,则储存在岩体内的弹性应变能U0为
(1)
根据能量互易定理,岩体因节理存在而引起附加应变能,同时导致岩体的等效弹性模量的弱化,假定因交叉节理存在而使岩体发生宏观初始损伤的损伤变量为D0,则有
(2)
E=E0(1-D0)
(3)
式中,E为岩体损伤后等效弹性模量;ΔU为节理存在后的附加应变能。
由于交叉节理中包含贯通节理及非贯通节理,则附加应变能ΔU可分为贯通节理法向应变引起的附加弹性应变能ΔU1,贯通节理剪切变形引起的弹性应变能ΔU2,储存在贯通节理上部非贯通节理的弹性应变能ΔU3,储存在贯通节理下部非贯通节理弹性应变能ΔU4,满足式(4):
ΔU=ΔU1+ΔU2+ΔU3+ΔU4
(4)
则根据式(2),(3),(4)可得到岩体因交叉节理存在而引起的初始损伤变量:
(5)
式(5)反映了岩体存在贯通节理和非贯通节理宏观缺陷而产生的初始损伤变量。实际上节理岩体除存在宏观损伤外,还存在微孔洞等细观缺陷,且在加载过程中,宏细观损伤均会发生损伤演化。对于细观缺陷,结合袁小清等的研究成果认为细观损伤D服从Weibull分布[12]:
(6)
式中,ε为应变;ε0,m为拟合常数。
假定岩体在加载过程中,仍服从胡克定律,则据此建立本构模型为
![]()
(7)
由式(7)可知,本构模型主要参数为求解弹性应变能ΔU,而弹性应变能ΔU主要由4部分组成。同时,式(7)建立的本构模型没有考虑强度准则的影响,下文基于以上两方面进行讨论。
贯通节理面的变形主要由一定厚度的节理法向压缩变形和沿剪切面切向变形所组成,其方向变形规律可用节理面的闭合变形来表示,其遵循衰减法则[13],即
(8)
式中,dεα为偏应变;dσα为法向偏应力;Eα为节理面弹性模量;εm为节理面最大法向应变;εα为节理面法向应变。
对式(8)进行积分可得
(9)
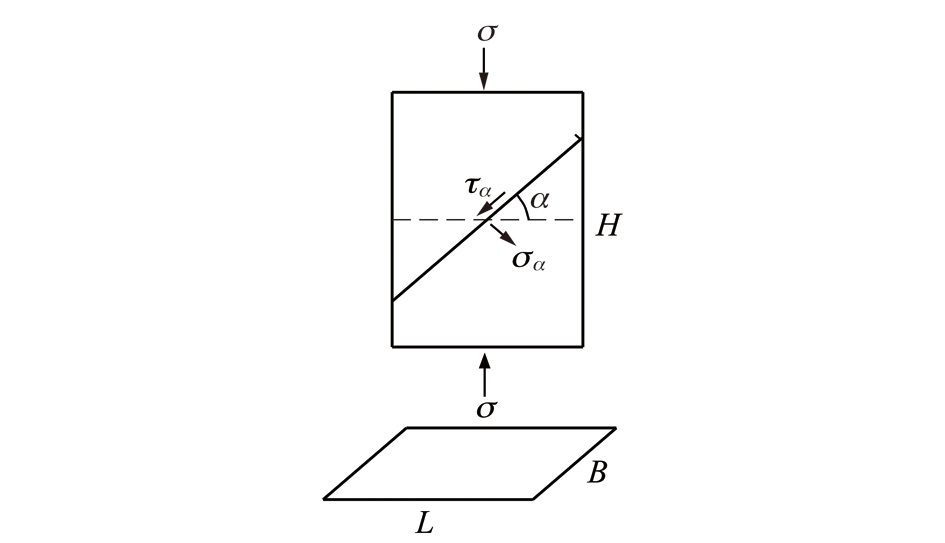
图2 贯通节理岩体模型
Fig.2 Rock mass model containing persistent joint
图2为含倾角α的贯通节理岩体模型,不考虑非贯通节理滑动驱动力的影响,其贯通节理面上的正应力σα及切应力τα分别为
σα=σcos2α
(10)
![]()
(11)
将式(10)代入式(9)中可得
(12)
则在压应力作用下储存在贯通节理内的弹性应变能ΔU1为
(13)
同样,在剪切应力τα作用下,储存在贯通节理的剪切弹性应变能ΔU2为
(14)
式中,ks为贯通节理切向刚度;L为试件在平面内宽度;B为试件垂直于平面宽度。
与贯通节理面主要发生闭合变形和剪切滑移不同,含非贯通节理岩体除沿节理面产生剪切滑移外,主要表现为非贯通岩桥部分的裂纹扩展断裂及岩块部分的微裂纹扩展问题。目前,基于应变能及断裂力学相结合的方法[15]同时考虑了非贯通节理岩体几何参数及节理面力学参数的影响。
如图1所示,交叉节理岩体中的贯通节理将整个岩体分割成含非贯通节理的上下两部分独立岩体,因此需分别考虑上下岩体的断裂损伤问题。
根据断裂力学理论,对于平面应变问题,贯通节理上部岩体因非贯通节理存在而引起的附加应变能ΔU3[15]为
(15)
式中,A1分别为上部岩体非贯通节理表面积;ν为完整岩石的泊松比;KI为上部岩体节理尖端翼裂纹的I型应力强度因子;KII为上部岩体节理尖端翼裂纹的II型应力强度因子。

图3 上部非贯通节理岩体模型
Fig.3 Rock mass model above containing non-persistent joint
如图3所示,受远场应力σ的影响,作用于非贯通节理面上的法向应力σβ及切应力τβ分别为
σβ=σcos2β
(16)
![]()
(17)
在压缩荷载作用下,作用于非贯通节理面上的剪应力使上部岩块产生向下滑动的趋势,而作用于节理面的法向应力则会产生与剪应力相反方向的摩擦力,当节理面剪应力超过节理面上的摩擦力时,两者之差称为有效剪切应力![]()
(18)
根据郑安兴等[16]的研究成果,节理尖端的I,II型应力强度因子为
(19)
![]()
(20)
式中,L1为上部非贯通节理长度。
将式(16),(18)代入式(19),(20)中,可得压剪状态下上部节理尖端应力强度因子:
(21)
![]()
(22)
将式(21),(22)代入式(15)中即可得到上部岩体因节理存在而引起的附加应变能ΔU3:
(sin2β-cos2βtan φ)]2
(23)
对于贯通节理下部的非贯通节理岩体的断裂损伤问题,同样可参照贯通节理以上含非贯通节理岩体应变能计算方法,区别在于上部岩块的轴向应力及切向应力经贯通节理再传递到下部岩块时需考虑贯通节理面压剪传递系数的影响。

图4 下部非贯通节理岩体模型
Fig.4 Rock mass model on the bottom containing non-persistent joint
如图4所示,作用在贯通节理面上的正应力及切应力经贯通节理传递至下部岩块分别受传压系数Cn及传剪系数Cs的影响,直接作用于下部岩体上的正应力![]() 及切应力
及切应力![]() 分别为
分别为
(24)
![]()
(25)
对于传压系数Cn及传剪系数Cs的选取,可参照文献[17]的经验公式:
(26)
![]()
(27)
式中,Kn为贯通节理面法向刚度;Ks为贯通节理面切向刚度;E′为岩块的有效弹性模量;G′为岩块有效剪切模量。
结合式(24),(25)可得作用于下部岩块的等效轴向应力为σ*为
σ*=Cnσcos2α+Csσsin2α
(28)
下部非贯通节理岩体的附加应变能计算方法与上部岩体相同,只需将轴向应力σ替换为σ*即可。结合式(23),(28),可得下部岩体附加应变能ΔU4为
[cos4β+(sin2β-cos2βtan φ)]2
(29)
诸多研究结果表明[11]:当节理倾角较大时,岩体常沿节理面特别是贯通节理面首先发生剪切破坏,从而使岩体发生失稳破坏,因此需考虑贯通节理剪切强度对岩体整体强度的影响。对于贯通节理面的剪切破坏准则,目前常有的屈服准则有Mohr-Coulomb强度准则、Barton强度准则及Drucker-Prager强度准则等。由于大多数节理都为无充填或黏结力较小,因此贯通节理部分的强度准则可采用Barton强度准则表示[17-18]:
(30)
式中,δ为贯通节理表面粗糙度系数;σα为贯通节理表面法向应力;σs为完整岩块单轴抗压强度;φ1为贯通节理面基本摩擦角。
将式(10)代入式(30)中,可得贯通节理部分发生剪切破坏时所对应的单轴抗压强度σg为节理倾角及强度参数的函数:
(31)
目前非贯通节理岩体的强度理论中,应用最广的主要有Jennings准则和Lajtai岩桥破坏理论。其中Jennings准则遵守Mohr-Coulomb强度准则,将非贯通节理及岩桥部分抗剪强度参数按贯通率进行加权平均,将得到的加权平均强度作为抗剪强度。但该方法没有考虑岩桥在剪切过程中靠近节理尖端会首先发生剪切破坏进而导致岩桥力学参数弱化的影响。夏才初等[19]在此基础上进行了试验研究,并得到了考虑非贯通岩桥部分弱化的剪切破坏准则:
τ=kc2+λ(1-k)cb+σn[ktan φ2+(1-k)tan φb]
(32)
式中,τ为切应力;σn为法向正应力;c2为节理面黏结力;cb为非贯通岩桥部分黏结力;φ2为节理面摩擦角;φb为非贯通岩桥部分内摩擦角;k为节理为贯通率;λ为岩桥黏结力折减系数,取0.81[19]。
由于节理间的抗剪强度主要取决节理间的粗糙程度,即摩擦角的影响,且节理间的黏结力远远小于岩桥部分黏结力,因此此处不考虑节理间黏结力的影响,式(32)可简化为
τ=λ(1-k)cb+σn[ktan φ2+(1-k)tan φb]
(33)
将式(10)代入式(33)中,可得上部岩体单轴抗压强度σf:
(34)
式中,k1为上部岩体非贯通节理连通率。
同理考虑压剪系数影响,可得下部岩体单轴抗压强度![]()
(35)
式中,k2为下部岩体非贯通节理连通率。
岩体中同时存在贯通节理及非贯通节理时,其强度准则决定于起控制性作用的节理面。如贯通节理面倾角较小时(如0°时),其贯通节理部分很难发生剪切破坏,岩体整体强度取决于非贯通节理部分或完整岩块,其强度准则遵循非贯通节理强度准则,反之亦然;当贯通节理面及非贯通节理面倾角均较小时(如均接近0°时),此时两交叉节理均难以发生沿节理面的剪切破坏,其岩体强度取决于完整岩块的强度。因此这里应包括4个单轴抗压强度参数,分别为贯通节理面发生剪切破坏所对应的抗压强度σg、非贯通节理剪切破坏所对应的单轴抗压强度![]() 以及完整岩块张拉破坏所对应的单轴抗压强度σs。显然,4个抗压强度中的最小值即为整个交叉节理岩体的单轴抗压强度,其所对应的强度准则即为整个岩体的强度准则。
以及完整岩块张拉破坏所对应的单轴抗压强度σs。显然,4个抗压强度中的最小值即为整个交叉节理岩体的单轴抗压强度,其所对应的强度准则即为整个岩体的强度准则。
当![]() 时,此时岩体强度准则即遵循贯通节理部分的剪切破坏准则,即单轴最大压应力达到σg时,岩体达到峰值强度;同样,当
时,此时岩体强度准则即遵循贯通节理部分的剪切破坏准则,即单轴最大压应力达到σg时,岩体达到峰值强度;同样,当![]() 时,此时岩体抗剪强度准则遵循非贯通节理部分的破坏准则,其抗压强度由非贯通节理几何形态及岩桥的力学特性所决定。据此建立考虑强度准则的等效弹性模型为
时,此时岩体抗剪强度准则遵循非贯通节理部分的破坏准则,其抗压强度由非贯通节理几何形态及岩桥的力学特性所决定。据此建立考虑强度准则的等效弹性模型为

(36)
为验证等效弹性模型的合理性及讨论含贯通-非贯通交叉节理几何特征对岩体力学特性的影响。以文献[20]试验资料为例,对本文提出的等效弹性模型进行讨论。试验采用的岩石相似材料,弹性模量E0=1.907 GPa,泊松比为0.3,ε0=0.20,m=3.2,含有如图1所示的倾角α=30°的贯通节理,倾角β=135°、上下非贯通节理连通率均为0.5的非贯通节理组合而成的交叉节理岩体试件。由于采用的是水泥砂浆相似材料[21],取节理面基本摩擦角20°,完整试件黏聚力cb为5.5 MPa,完整试件内摩擦角φb为30°,贯通节理表面粗糙度系数δ=0.35,切向刚度ks=2 GPa/m,法向刚度kn=9 GPa/m,Eα=198 MPa,εm=0.023,L=0.1 m,则用本文所提的等效弹性模型方法得到岩体在压剪作用下的应力-应变曲线如图5所示。

图5 交叉节理岩体试验与理论计算结果比较
Fig.5 Comparison between the experimental result and theoretical results of the cross joints rock mass
图5为对交叉节理岩体模型计算结果与试验结果的比较曲线,由图5可看出,完整岩石、含30°贯通节理岩体、含45°非贯通节理的试验结果与模型计算结果基本吻合。当含α=30°贯通节理时,岩体的峰值强度为10.4 MPa,较完整岩石的峰值强度20.2 MPa降低了48.5%,主要原因为贯通节理的存在致使岩体沿贯通节理面发生剪切破坏,整个岩体的强度准则遵循贯通节理剪切强度准则;同时含贯通节理岩体达到峰值强度时轴向总应变也较完整岩石大34%,主要原因为贯通节理弹性模量远小于岩石弹性模量,因此加载前期轴向应变主要源自贯通节理面的闭合变形,这说明节理的存在削弱了岩体强度,使其刚度降低,增大了其柔度。当含β=45°、贯通率为0.5的非贯通节理时,岩体的峰值强度为17.8 MPa,较完整岩石的峰值强度20.2 MPa降低了11.7%,此时岩体强度遵循非贯通节理及岩桥剪切破坏所控制的强度准则。当岩体中含α=30°,β=135°的贯通-非贯通交叉节理时,岩体除贯通节理发生闭合变形外,非贯通节理岩体部分也发生较大应变,故达到峰值强度时岩体总应变较只含贯通节理时岩体的总应变更大,但含交叉节理岩体峰值强度与只含贯通节理时岩体峰值强度基本一致,分析原因为此时岩体强度准则仍然遵循贯通节理剪切破坏强度准则,故非贯通节理的存在只对总应变有影响,而对岩体整体峰值强度无影响。
以下结合等效弹性模型及相关参数,分析含贯通-非贯通交叉节理岩体的节理倾角、连通率等对岩体力学特性的影响。
由于与单节理及平行节理不同,交叉节理倾角涉及两条节理面的角度,因此在其他参数相同的情况下,分别以非贯通节理β=0°,β=30°及β=60°为例,非贯通节理贯通度均为0.5,通过改变贯通节理倾角α,研究节理倾角对岩体力学特性的影响。同时将非贯通节理倾角β=0°时,针对不同倾角的贯通节理岩体峰值强度理论计算结果与文献[20]中的试验结果进行对比。

图6 岩体峰值强度随贯通节理倾角的变化规律
Fig.6 Variation of peak strength of rock mass along with the angle of persistent joint
由图6可知,当非贯通节理倾角为0°时,通过改变贯通节理倾角,由本文理论模型计算得到的节理岩体峰值强度与文献[20]中试验得到节理岩体峰值强度吻合较好,且峰值强度随倾角的变化趋势也基本一致。
由图6所示的本文理论模型计算结果可知,当非贯通节理倾角为0°及30°时,且贯通节理为0°及15°时,岩体的峰值强度均为20.2 MPa,说明在此时贯通节理及非贯通节理倾角均较小,均难以发生剪切破坏,岩体强度由完整岩石强度所控制;当贯通节理倾角继续增大时,贯通节理起控制性节理作用,岩体强度由贯通节理剪切强度所决定,且随着贯通节理倾角的增加而减小。
当非贯通节理倾角为60°时,贯通节理倾角为0°,15°,30°时,其峰值强度均为5.2 MPa,说明岩体强度均由非贯通节理强度控制;当贯通节理倾角继续增大时,贯通节理所控制的剪切强度小于非贯通节理所控制的剪切强度,岩体强度由贯通节理所决定,且随着贯通节理倾角的增加而减小。
在其他参数相同的情况下,分别以贯通节理倾角α=0°,α=30°及α=45°为例,非贯通节理贯通度均为0.4,通过改变非贯通节理倾角β,研究非贯通节理倾角对岩体力学特性的影响。同时将贯通节理倾角α=0°时,针对不同倾角的非贯通节理岩体峰值强度理论结果与文献[22]中的试验结果进行对比。由于文献[22]所采用的试验材料力学参数与本文理论模型所计算的材料力学参数有一定差异,而此部分主要研究非贯通节理倾角与岩体峰值强度的内在关系,因此将文献[22]中的节理岩体试样峰值强度与其完整岩石试样的峰值强度之比作为无量纲参数,再乘以本文理论模型计算所得的完整岩石峰值强度作为节理岩体试验峰值强度,如图7所示。

图7 岩体峰值强度随非贯通节理倾角的变化规律
Fig.7 Variation of peak strength of rock mass along with the angle of non-persistent joint
由图7可知,当贯通节理倾角为0°时,通过改变非贯通节理倾角,由本文理论模型计算得到的节理岩体峰值强度与文献[22]中试验得到节理岩体峰值强度随倾角的变化趋势基本一致。但当非贯通节理倾角较小时,由本文理论模型计算得到的峰值强度与试验结果存在一定差异,这是因为本文理论模型主要考虑非贯通节理的节理面及岩桥的剪切破坏,而没有考虑非贯通节理的存在对岩体的张拉强度影响。实际上,非贯通节理倾角较小时,虽不会发生沿非贯通节理面的剪切破坏,但由于节理结构面间刚度远小于岩桥刚度,从而造成岩桥的应力集中,加速岩桥的张拉破坏强度。当非贯通节理倾角较大时,岩体主要发生岩桥及节理面的剪切破坏,所以非贯通节理倾角较大时,理论模型结果与试验结果吻合较好。
由图7所示的本文理论模型计算结果可知,当贯通节理为0°时,非贯通节理倾角为0°,15°,30°时,非贯通节理及贯通节理均不发生剪切破坏,岩体强度由完整岩石强度所控制;当贯通节理倾角继续增加时,岩体强度由非贯通节理所控制,其中倾角为60°时强度最小;但当非贯通节理倾角为75°时强度开始增大,主要非贯通节理倾角较大时,作用于非贯通节节理面及对应岩桥上的正应力较大,而切向应力相对较小,是非贯通节理面抗剪强度提高所致。
当贯通节理倾角为30°时,岩体强度只在非贯通节理倾角为60°时遵循非贯通节理剪切强度准则,其余均遵循贯通节理剪切强度准则;当贯通节理倾角为45°时,岩体强度均遵循贯通节理强度准则。
在其他参数相同的情况下,取非贯通节理面倾角β分别为45°,60°,通过改变非贯通节理连通率,研究初始损伤变量随连通率的变化规律,如图8所示。

图8 初始损伤变量随连通率的变化规律
Fig.8 Change of the initial injury variable with the connectivity rate
由图8可知,岩体的损伤变量随节理连通率的增加而增大。当节理连通率较小时,损伤变量增加幅度较小;节理连通率较大时,损伤变量增加幅度较大,但随着节理接近于贯通,增加幅度又变小。
(1)针对自然界大量赋存的含贯通-非贯通交叉节理岩体。在前人工作的基础上,基于复合损伤的观点,综合考虑交叉节理岩体宏细观缺陷,将节理面闭合剪切变形理论、断裂力学理论与能量理论相结合,构建了单轴压缩下交叉节理岩体多尺度组合模型,但三轴压缩下的力学特性有待进一步研究。
(2)讨论了交叉节理中的贯通节理及非贯通节理对强度准则的影响,岩体强度受贯通节理倾角、非贯通节理倾角、连通率等因素影响。
(3)本文提出的本构模型综合考虑了节理的几何特征、岩体力学参数的影响,需确定的材料参数较少,且均通过常规试验即可确定。
参考文献:
[1] 熊飞,靖洪文,苏海健.尖端相交裂隙砂岩强度与破裂演化特征试验研究[J].煤炭学报,2017,42(4):886-895.
XIONG Fei,JING Hongwen,SU Haijian,et al.Strength and fracture behaviors of sandstone samples containing intersect fissures under uniaxial compression[J].Journal of China Coal Society,2017,42(4):886-895.
[2] 刘红岩,邓正定,王新生.节理岩体动态破坏的SHPB相似材料试验研究[J].岩土力学,2014,35(3):659-665.
LIU Hongyan,DENG Zhengding,WANG Xinsheng.Similar material test study of dynamic failure of jointed rock mass with SHPB[J].Rock and Soil Mechanics,2014,35(3):659-665.
[3] 张平,李宁,李贺兰.动载下3条断续裂隙岩样的裂缝贯通机制[J].岩土力学,2006,27(9):1457-1464.
ZHANG Ping,LI Ning,LI Helan.Fracture coalescence mechanism of three-intermittent-flaws rock specimen under dynamic loading[J].Rock and Soil Mechanics,2006,27(9):1457-1464.
[4] ZHAO D,SWOBODA G,LAABMAYR F.Damage mechanics and its application for the design for an underground theater[J].Tunnelling and Underground Space Technology,2004,19:567-575.
[5] WANG T T,HUANG T H.A constitutive model for the deformation of a rock mass containing sets of ubiquitous joints[J].International Journal of Rock Mechanics & Mining Sciences,2009,46(3):521-530.
[6] 张力民,张慧,刘红岩.单轴压缩荷载下非贯通闭合节理岩体损伤本构模型[J].煤田地质与勘探,2016,44(1):79-84.
ZHANG Limin,ZHANG Hui,LIU Hongyan.A damage constitutive model for rock mass with non-persistently closed joints under uniaxial compression load[J].Coal Geology & Exploration,2016,44(1):79-84.
[7] 刘东燕,朱可善,范景伟.双向应力作用下X型断续节理岩体的强度特性研究[J].重庆建筑工程学院学报,1991,13(4):40-46.
LIU Dongyan,ZHU Keshan,FAN Jingwei.Strength properties of rock mass joints[J].Journal of Chongqing Institute of Architecture and Engineering,1991,13(4):40-46.
[8] 张波,李术才,杨学英,等.含交叉裂隙岩体相似材料试件力学性能单轴压缩试验[J].岩土力学,2012,33(12):3674-3679.
ZHANG Bo,LI Shucai,YANG Xueying,et al.Uniaxial compression tests on mechanical properties of rock mass similar material with cross-cracks[J].Rock and Soil Mechanics,2012,33(12):3674-3679.
[9] 张波,李术才,杨学英,等.含交叉多裂隙类岩石材料单轴压缩力学性能研究[J].岩石力学与工程学报,2015,34(9):1777-1785.
ZHANG Bo,LI Shucai,YANG Xueying,et al.Mechanical property of rock-link material with intersecting multi flaws under uniaxial compression[J].Chinese Journal of Rock Mechanics and Engineering,2015,34(9):1777-1785.
[10] 刘学伟,刘泉声,陈元,等.裂隙形式对岩体强度特征及破坏模式影响的试验研究[J].岩土力学,2015,36(S2):208-214.
LIU Xuewei,LIU Quansheng,CHEN Yuan,et al.Experimental study of effects of fracture type on strength characteristics and failure modes of fractured rockmass[J].Rock and Soil Mechanics,2015,36(S2):208-214.
[11] 刘红岩,张力民,苏天明,等.节理岩体损伤本构模型及工程应用[M].北京:冶金工业出版社,2016.
[12] 袁小清,刘红岩,刘京平.基于宏细观损伤耦合的非贯通裂隙岩体本构模型[J].岩土力学,2015,36(10):2804-2814.
YUAN Xiaoqing,LIU Hongyan,LIU Jingping,et al.Constitutive model of rock mass with non-persistent joints based on coupling macroscopic and mesoscopic damages[J].Rock and Soil Mechanics,2015,36(10):2804-2814.
[13] 孙广忠,孙毅.岩体力学原理[M].北京:科学出版社,2011:44-50.
[14] 夏才初,孙宗颀.工程岩体节理力学[M].上海:同济大学出版社,2002:133-140.
[15] 刘红岩,王新生,张力民,等.非贯通节理岩体单轴压缩动态损伤本构模型[J].岩土工程学报,2016,38(3):426-436.
LIU Hongyan,WANG Xinsheng,ZHANG limin,et al.A dynamic damage constitutive model for rock mass with nonpersistent joints under uniaxial compression[J].Chinese Journal of Geotechnical Engineering,2016,38(3):426-436.
[16] 郑安兴,罗先启.压剪应力状态下岩石复合型断裂判据的研究[J].岩土力学,2015,36(7):1892-1898.
ZHENG Anxing,LUO Xianqi.Research on combined fracture criterion of rock under compression-shear stress[J].Rock and Soil Mechanics,2015,36(7):1892-1898.
[17] BANDIS S C.Experimental studies of scale effect on the shear behaviour of rock joint[J].International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts,1981,18(1):1-21.
[18] BARTON N.Review of a new shear strength criterion for rock joints[J].Eng.Geol.,1973,7:287-332.
[19] 夏才初,肖维民,丁增志.非贯通节理Jennings 强度准则的岩桥弱化和节理面起伏角修正[J].岩石力学与工程学报,2010,29(3):485-493.
XIA Caichu,XIAO Weimin,DING Zengzhi.Modification of Jennings strength criterion for intermittent joints considering rock bridge weakening and joint surface undulating angle[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(3):485-493.
[20] 刘红岩,黄妤诗,李楷兵,等.预制节理岩体试件强度及破坏模式的试验研究[J].岩土力学,2013,34(5):1235-1243.
LIU Hongyan,HUANG Yushi,LI Kaibing,et al.Test study of strength and failure mode of pre-existing jointed rock mass[J].Rock and Soil Mechanics,2013,34(5):1235-1243.
[21] 邓正定,王桢,刘红岩.基于复合损伤的节理岩体动态本构模型研究[J].岩土力学,2015,36(5):1368-1374.
DENG Zhengding,WANG Zhen,LIU Hongyan.Dynamic constitutive model of jointed rock mass based on the theory of composite damage[J].Rock and Soil Mechanics,2015,36(5):1368-1374.
[22] 陈新,廖志红,李德建.节理倾角及连通率对岩体强度、变形影响的单轴压缩试验研究[J].岩石力学与工程学报,2011,30(4):781-789.
CHEN Xin,LIAO Zhihong,LI Dejian.Experimental study of effects of joint inclination angle and connectivity rate on strength and deformation properties of rock masses under uniaxial compression[J].Chinese Journal of Rock Mechanics and Engineeing,2011,30(4):781-789.
[23] 张波,杨学英,李术才,等.含两组叠置X型裂隙类岩石材料单轴拉伸破坏特征[J].煤炭学报,2017,42(8):1987-1993.
ZHANG Bo,YANG Xueying,LI Shucai,et al.Uniaxial tensile failure properties of rock-like specimens with two overlapped X-type flaws[J].Journal of China Coal Society,2017,42(8):1987-1993.
[24] XUE Junhua,WANG Hanpeng,ZHOU Wei,et al.Experimental research on overlying strata movement and fracture evolution in pillarless stress-relief mining[J].International Journal of Coal Science & Technology,2015,2(1):38-45.