
徐 渊1,宾光富1,2,叶桂林3,李学军2
(1.湖南科技大学 机电工程学院,湖南 湘潭 411201; 2.湖南科技大学 机械设备健康维护湖南省重点实验室,湖南 湘潭 411201; 3.泰富国际工程有限公司,湖南 湘潭 411201)
摘 要:输送倾角是圆管带式输送机直线爬坡段设计中的关键难点,过大会发生胀管事故,过小则需重新布局管线导致整机成本大幅增加。基于相对滑移理论,构建了管带中物料的力学模型,采用导来摩擦因数表征物料与管带之间的滑移状态,推导不同填充率下导来摩擦因数与极限输送倾角之间的关系。然后针对50%,62%,75%三种典型填充率下某型圆管带式输送机运行工况,分析得出导来摩擦因数与输送倾角的函数关系,根据物料与圆管之间不发生相对滑移的基本准则,从而分别确定管带机的极限输送倾角为32°,34°,36°。该方法可为圆管带式输送机直线爬坡段物料输送倾角的设计与分析提供参考。
关键词:圆管带式输送机;相对滑移理论;填充率;导来摩擦因数;极限输送倾角
中图分类号:TD528
文献标志码:A
文章编号:0253-9993(2018)11-3240-07
XU Yuan1,BIN Guangfu1,2,YE Guilin3,LI Xuejun2
(1.School of Mechanical Engineering,Hunan University of Science and Technology,Xiangtan 411201,China; 2.Hunan Provincial Key Laboratory of Health Maintenance for Mechanical Equipment,Hunan University of Science and Technology,Xiangtan 411201,China; 3.Tidfore International Engineering Co.,Xiangtan 411201,China)
Abstract:Conveying inclination is the key difficulty in the design of straight-line climbing section of pipe belt conveyor.Expansion accidents occur during assembly if the inclination is too large.It will be necessary to re-layout the pipeline if the inclination is too small,so that the cost of the whole machine will increase significantly.In this paper,the relative slip theory is used to build a mechanical model of the material in the pipe.The friction coefficient is used to characterize the slippage between the material and the pipe.The relationship between the friction coefficient and the ultimate transport angle under different loading rates is deduced.Then,the transport inclination of the belt conveyor under three typical filling rates of 50%,62% and 75% were analyzed,respectively.The coefficient of friction coefficient and the transport inclination angle were derived.According to the relative slip between the material and the tube,the ultimate conveying inclination of the belt conveyor are determined as 32°,34° and 36°,respectively.The method has some reference values for the design and analysis of material conveying inclination in the straight line climbing section of pipe belt conveyor.
Key words:pipe belt conveyor;relative sliding theory;filling rate;friction coefficient;extreme delivery angle

移动阅读
徐渊,宾光富,叶桂林,等.基于相对滑移理论的管带机直线爬坡段极限输送倾角研究[J].煤炭学报,2018,43(11):3240-3246.doi:10.13225/j.cnki.jccs.2018.0194
XU Yuan,BIN Guangfu,YE Guilin,et al.Research on limit conveying inclination in circular climbing section of pipe belt conveyor based on relative slip theory[J].Journal of China Coal Society,2018,43(11):3240-3246.doi:10.13225/j.cnki.jccs.2018.0194
收稿日期:2018-02-05
修回日期:2018-08-21
责任编辑:毕永华
基金项目:湖南省科技重大专项资助项目(2015GK1003);国家自然科学基金资助项目(51575176,51775030)
作者简介:徐 渊(1993—),男,湖南汨罗人,硕士研究生。E-mail:1624209866@qq.com
通讯作者:宾光富(1981—),男,湖南衡山人,教授,博士生导师。E-mail:abin811025@163.com
圆管带式输送机将物料包围在输送带的圆形截面内,增加了物料与输送带内表面的相互摩擦力以及物料本身的内摩擦力,从而使输送物料的倾角提高。在工程实际应用中普通带式输送机的最大输送倾角为18°,而圆管带式输送机的最大输送倾角远大于普通带式输送机的输送倾角[1-3]。因此,圆管带式输送机被广泛应用于矿山、发电、港口、化工、冶金等行业。但是由于带速、托辊间距、物料与圆管带之间的相互作用力等各种复杂因素对输送倾角大小会产生影响,难以得出一个确定的并且可靠的极限输送倾角,因此在工程实际中往往会根据以往经验保守的采用较小的输送倾角输送物料,这样就导致整体管线布局过长、能耗过大、整机成本增加等一系列问题。郭永存等研究了在不同的物料填充率以及不同颗粒粒度的边界条件下,物料对管带侧压力的影响[4-5]。蒋卫良对新型托辊装置进行了研究,推导出5辊深槽型输送带与物料之间的导来摩擦因数[6]。孙可文等对锁边圆管带式输送机物料在管带中的受力进行理论分析[7-8]。边永梅利用EDEM软件离散元仿真对管状带式输送机极限运行倾角进行分析[9]。宾光富等得出了在匀速运行的工况下,圆管输送带与托辊组间的动态接触力变化规律特性[10]。然而,从皮带与物料之间相对滑移角度出发,开展圆管带式输送机填充率、导来摩擦因数、输送倾角相互关系的研究目前鲜有报道。
笔者以某型圆管带式输送机直线爬坡段为例,基于相对滑移理论,从理论上推导不同填充率下,物料与管带间导来摩擦因数与极限输送倾角的函数关系式。采用离散元DEM仿真方法分析不同填充率下的导来摩擦因数与极限输送倾角的关系并对理论推导进行验证。最后通过仿真与理论推导相结合的方法得出了不同填充率下圆管带式输送机的极限输送倾角,该种方法能够给工程实际中如何确定圆管带式输送机直线爬坡段的输送倾角提供指导。
由散体力学理论可知,散体物料具有固体和液体的双重物理力学属性。容器中的液体能够向四周施加水平压力,散体具有类似的性质,但其水平压力不同于液体,不是完全由深度决定,而是要在垂直压力上乘以<1的侧压力系数[11],即
σx=λσy
(1)
式中,σx为散体水平压应力;σy为垂直压应力;λ为侧压系数λ=(1-sin φ)/(1+sin φ);φ为物料内摩擦角。
对于任意倾角为β的直线爬坡段圆管输送带,在垂直于圆管轴心线取一段微元体2的管内物料,分析其受力情况,如图1所示:① 微元体2自身重力所产生下滑分力G1;② 上端物料3对微元体2所产生的压力Fp1;③ 下端物料1对微元体2所产生的反力Fp2,胶带对微元体2的挤压力Fj及产生相应的摩擦力f1;④ 微元体2重力分量对胶带产生的正压力G2,以及产生阻止下滑的摩擦力f2[6]。
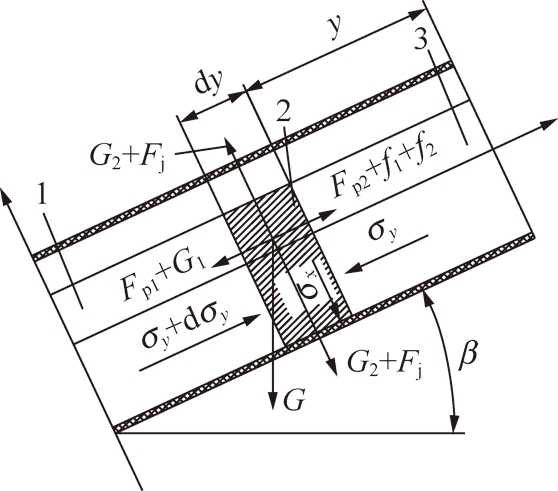
图1 微元在管带中的受力
Fig.1 Force of the microelement in the pipe
由以上受力分析得出物料对圆管压应力的应力截面分布图如图2所示,物料4对管壁5的压应力可分为:① 物料填充圆管所产生挤压管壁的压应力σx;② 物料对管壁的正压力所产生的压应力σθ[7]。为了便于研究物料在管带中的填充率对管带机输送倾角的影响,因此,忽略物料堆积角的影响,假设物料在管带中的堆积角为0°。
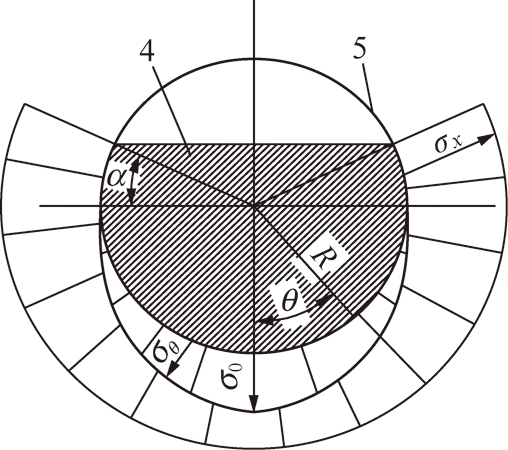
图2 物料对圆管的压应力分布截面
Fig.2 Material on the circular tube compressive stress distribution section
以上的受力计算如下。微元体2自身重力所产生下滑分力G1:
G1=ψπR2ρgdysin β
(2)
上端物料3对微元体2所产生的压力Fp1:
Fp1=ψπR2σy
(3)
下端物料1对微元体2所产生的反力Fp2:
Fp2=ψπR2(σx+dσy)
(4)
胶带对微元体2的挤压力Fj及其相应摩擦力f1:
(5)
![]()
(6)
微元体2的重力分量对胶带产生的正压力G2,以及产生阻止下滑的相应摩擦力f2:
2ψπR2ρgdycos β
(7)
f2=2μψπR2ρgdycos β
(8)
根据力的平衡得
Fp1+G1=Fp2+f1+f2
(9)
将式(2)~(6),(8)代入式(9)得
(10)
解式(10),可得
(11)
将式(11)带入式(1),可得σx为
(12)
式中,y为微元体在圆管带中的深度;σy为物料沿圆管的轴向压应力;σx为物料作用于管壁的压应力;dσy为物料沿圆管轴向压应力增量;ρ为物料的堆积密度;g为重力加速度;R为管带内径;μ为物料与管带间的静摩擦因数;β为管带直线爬坡段的倾角;θ为图2所示,圆管截面中圆管水平中心线以下圆管上任意一点与圆管垂直中心线的夹角;α为如图2所示圆管截面中圆管水平中心线以上物料与管壁接触弧段所对应的圆心角;ψ为如图2阴影部分所示物料在管带中的填充率,ψ=α/180+sin αcos α/π+0.5;h为如图2所示在圆管截面中物料与管壁接触的弧长,h=(α/90+1)πR,若设l=(α/90+1),则h=lπR。
摩擦力一般可用f= kFN表示。其中f为摩擦力,FN为产生摩擦力的压力,k为导来摩擦因数,k通常都是接触面摩擦因数乘一系列的几何关系,如图3所示实际上就是把不同的摩擦形式最终转化成最普通的斜面滑块形式时对应的摩擦角[6]。
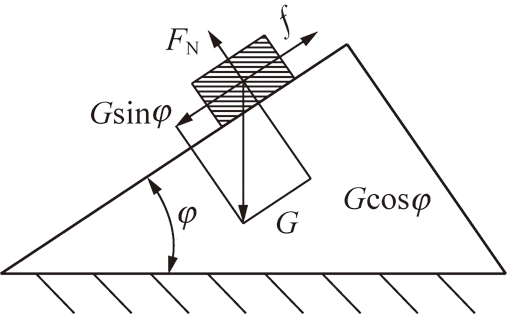
图3 斜面上物体的受力
Fig.3 Bevel on the force of the object
由图3可知,当斜面的倾角一定时,且摩擦力f刚好等于下滑分Gsin φ,此时滑块有往下滑移的趋势,但是滑块相对于斜面仍然处于静止状态,滑块的受力处于一个临界状态,那么在该临界状态下求得的导来摩擦因数k是一个临界值。如果滑块与斜面间的导来摩擦因数值大于该临界值时,摩擦力f大于或等于下滑分力Gsin φ,则滑块不会在斜面上滑移,反之如果小于该临界值时,则滑块将会在斜面上滑移。根据以上分析可得:可以通过滑块与斜面间的导来摩擦因数来表征它们之间的相对滑移状态,滑块与斜面间导来摩擦因数的临界值增大,那么摩擦力将会增大,就会使斜面的倾角增大,同时滑块在斜面也不会往下滑移。同理推断,物料与管带间的导来摩擦因数可用于表征物料在管带中的滑移状态,如果要最大限度的增大物料的输送倾角,并且要使物料在管带中不发生滑移,就得通过增大物料与管带间的导来摩擦因数来实现。
根据导来摩擦因数定义,结合式(6),(7),(8)和(12),可得物料与管带间的导来摩擦因数k为
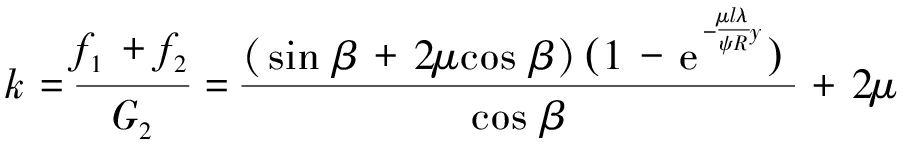
(13)
由式(13)可得输送倾角β与k的函数关系式:
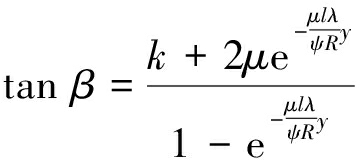
(14)
当输送倾角一定时,且其他参数不变时,由式(13)可通过改变填充率ψ大小来改变导来摩擦因数k,图4为输送倾角为30°,k随ψ变化时的函数图,可得ψ越大k也越大。当填充率一定时,由式(14)可得物料与管带间导来摩擦因数k越大,则输送倾角β越大。因此,通过以上理论推导与分析得出填充率、导来摩擦因数、输送倾角3者间的影响关系为:填充率增大,使导来摩擦因数增大,从而使输送倾角增大。

图4 导来摩擦因数与填充率函数
Fig.4 Leads to the friction coefficient and the central angle function diagram
离散元素法是分析与求解复杂离散系统的动力学问题的一种数值方法,离散元素法的基本原理是,将研究对象划分为相互独立的单元,根据单元之间的相互作用和牛顿运动定律,采用动态松弛法或静态松弛法进行循环迭代计算,确定每一个时间步长所有单元的受力及位移[12]。采用基于离散元素法的分析软件EDEM可有效处理圆管带式输送机中管带与物料之间的约束问题,从而比较合理地描述管带与物料之间的相对运动关系。目前在工程实际中由于物料粒度和输送量等因素影响,物料在管带中的填充率一般设定范围为50%~75%。因此,本文将在三种典型填充率下(50%,62%,75%)进行圆管带式输送机极限输送倾角的仿真分析。
颗粒仿真计算中颗粒的模型是影响颗粒仿真结果的关键因素,颗粒外形会影响物料与管带间的相对滑移状态。当要对复杂形状的颗粒进行离散元仿真分析时,如果单纯用球形颗粒进行模拟,那么就会导致最终的仿真结果不准确。而在实际工程中块状的散体物料以四面体居多[13]。以块煤为仿真物料,设定仿真颗粒的外形为正四面体,颗粒的粒度为30~90 mm,颗粒外形和填充如图5所示。

图5 块煤颗粒的外形和填充
Fig.5 Lime coal particle shape and filling
工程实际中圆管带式输送机大倾角输送物料管线布置情况如图6所示。尾部机架2安装了改向滚筒1和槽形的过度托辊组,使输送带在尾部机架1从展开状到卷成圆管状,头部机架4安装了驱动滚筒5和槽形的展开托辊组,使输送带在头部机架4从圆管状变成展开状,只有在中部机架3输送带一直为圆管状。因头部机架5和尾部机架2的输送倾角不能过大,圆管带式输送机主要是通过提升中部机架3直线爬坡段的输送倾角来达到大倾角输送物料的目的,故本文选取中部机架3直线爬坡段的圆管输送带进行建模,对极限输送倾角进行研究。

图6 管带机整体管线布置
Fig.6 Pipe belt conveyor with the overall pipeline layout
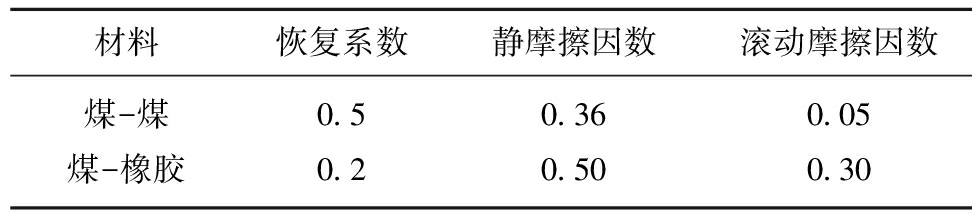
仿真物料的材料为块煤,块煤的堆积密度为700~900 kg/m3,静堆积角为45°,动堆积角为25°,管径为400 mm,带速为3 m/s,圆管输送带的材料为橡胶。表1为煤和橡胶的材料属性,表2为煤与煤,煤与橡胶的接触属性[14]。
表1 材料属性
Table 1 Material properties
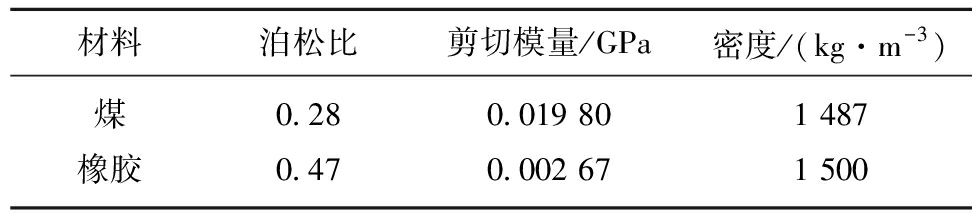
表2 接触属性
Table 2 Contact attributes
为确保仿真颗粒建模和圆管带式输送机运行参数的准确性,需要对物料的静堆积角、动堆积角、堆积密度以及管带机的带速和输送量等参数进行验证。堆积角的验证过程如下:建立一个无厚的圆筒,圆筒半径为700 mm,高度为500 mm。圆筒的正上方设有圆形平面作为产生颗粒的颗粒工厂,圆形平面半径为900 mm,与圆筒最上端的距离为1 000 mm。颗粒从颗粒工厂生成,然后自由下落到圆筒,直到在圆筒上端形成了一个外形不变的圆锥体状的颗粒堆。此时形成的堆积角为静堆积角,测量出静堆积角为46.01°。然后在圆筒上的垂直方向和水平方向加入振动幅值为1 mm,频率为50 Hz的振动,振动时间为10 s,待振动停止,颗粒不往下滑,此时形成的堆积角为动堆积角,测量出动堆积角为26.57°。堆积密度的验证如下:创建一个长宽高都为1 m封闭的立方体,然后将物料填满立方体,然后测量出立方体内物料总质量862.14 kg,即物料的堆积密度为862.14 kg/m3[15-17]。以上所验证的仿真物料的静堆积角、动堆积角以及堆积密度都与参考值较接近。因此,证明了仿真颗粒与实际物料颗粒相符合。
由以上所得出物料的堆积密度为862.14 kg/m3,设定的带速为3 m/s以及管径为400 mm。经计算得,当物料在管带中的填充率分别为50%,62%,75%时,实际工况下的输送量理论值为162.51,201.51,243.14 kg/s。分析图7可知实际输送量分别在相应的理论值范围内,符合参数验证要求。当输送倾角为30°时,虽然填充率不同但是测得物料的速度都最终都稳定在3 m/s,与设定带速符合。由以上可得仿真设定参数均符合实际工况。
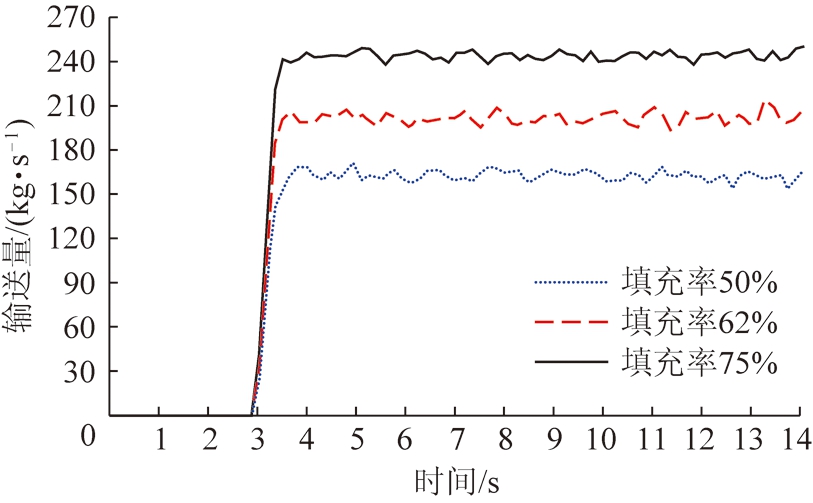
图7 输送量变化曲线
Fig.7 Delivery volume curves
圆管带式输送机的输送倾角越大,物料的稳定性越差,越容易引起物料在管带中发生相对滑移。当物料与管带间发生相对滑移时,物料与管带间的摩擦力小于物料下滑的分力,物料的速度就会明显低于带速。因此,在仿真时可通过物料在管带中的速度,来判断物料在管带中是否发生滑移,由此来确定圆管带式输送机的极限输送倾角。图8为填充率75%,输送倾角分别为37°,38°时,物料运行速度平稳后,管带中的上层物料、下层物料以及整体物料平均速度变化曲线。通过对比分析,当输送倾角为38°时,整体物料的平均速度已经小于2.9 m/s,且物料的速度波动明显大于输送倾角为37°时的波动,说明输送倾角为38°时物料在管带中的状态不稳定,而且物料在管带中明显发生了滑移,此时不能满足物料在管带中平稳输送的条件了。因此,填充率为75%时圆管带式输送机物料的极限输送倾角为37°。进一步分析,在输送倾角分别为37°,38°时,圆管输送带中的上层物料速度的变化曲线和下层物料的速度变化曲线分别与整体物料速度变化曲线相比较,它们的变化趋势与整体物料的变化趋势大体一致,并且下层物料的平均速度随着输送倾角的增大也会减小。因此,说明随着输送倾角的增大,导致物料整体在管带中速度降低的主要原因是由于物料与管带间的摩擦力不足引起的,而不是由于物料与物料间内部的摩擦力不足所导致。
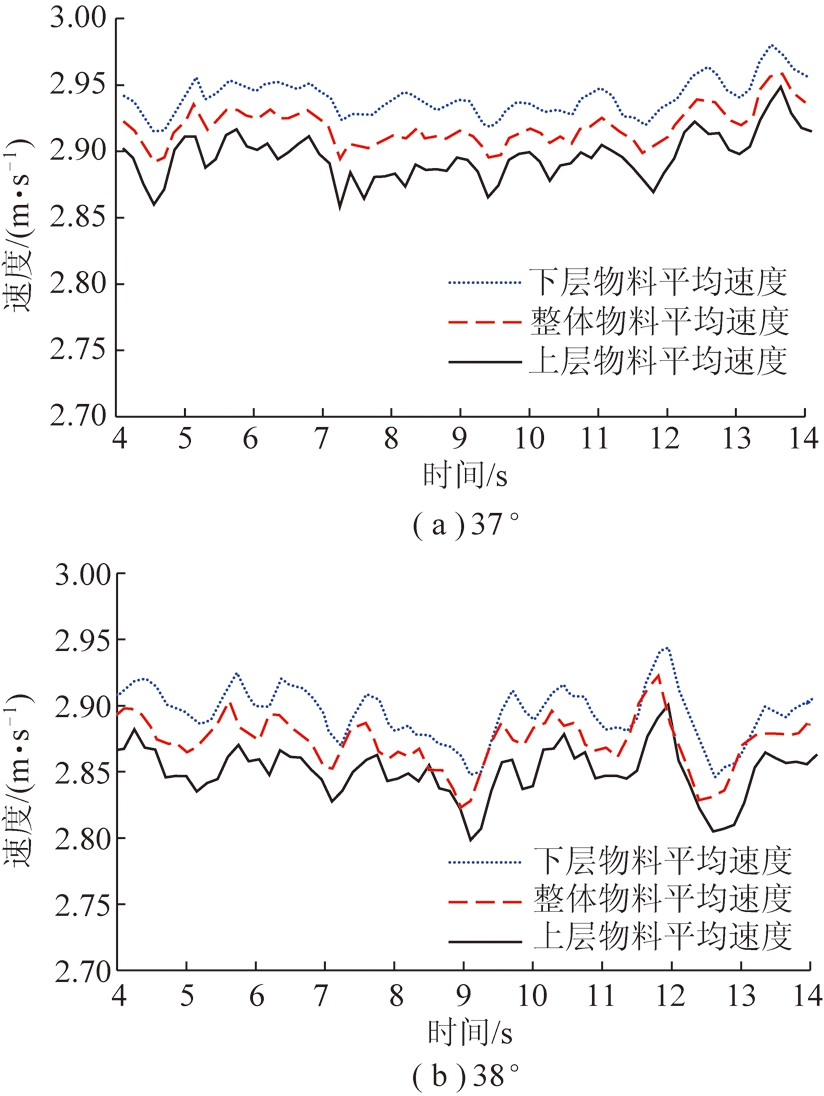
图8 填充率75%输送倾角为37°,38°时物料速度
Fig.8 Material velocity of fill rate 75% and delivery angle 37°,38°
图9为填充率50%,62%,75%时,整体物料平均速度值随输送倾角变化的曲线图,同样以物料在管带中不发生滑移为判定准则,得出填充率为50%,62%时圆管带式输送机极限输送倾角分别为32°,34°。因此,填充率越大圆管带式输送机的极限倾角越大,并且填充率越小随着输送倾角的增大物料在管带中速度下降的越快。随着输送倾角的变化,等物料在管带中平稳运行后,获取圆管输送带与物料间的摩擦力和正压力的平均值,然后根据导来摩擦因数的定义求出物料与圆管输送带间导来摩擦因数的仿真值,表3为在3种典型填充率下导来摩擦因数在输送倾角不同时的仿真值。由表3可知,当输送倾角相同时,填充率越大导来摩擦因数越大。通过仿真分析得出:填充率增大,使导来摩擦因数增大,从而使输送倾角增大。

图9 物料随输送倾角变化速度平均值
Fig.9 Average velocity of the material changes with the delivery angle
基于相对滑移理论,以导来摩擦因数来表征物料与管带之间的相对滑移状态,当导来摩擦因数的仿真值大于或等于理论推导的临界值时,则物料在管带中不发生滑移,反之小于,物料将会在管带中发生滑移。因此,将表3中导来摩擦因数的仿真值与导来摩擦因数理论推导的临界值进行对比,如图10所示。
表3 导来摩擦因数仿真值
Table 3 Leads to the friction coefficient simulation value
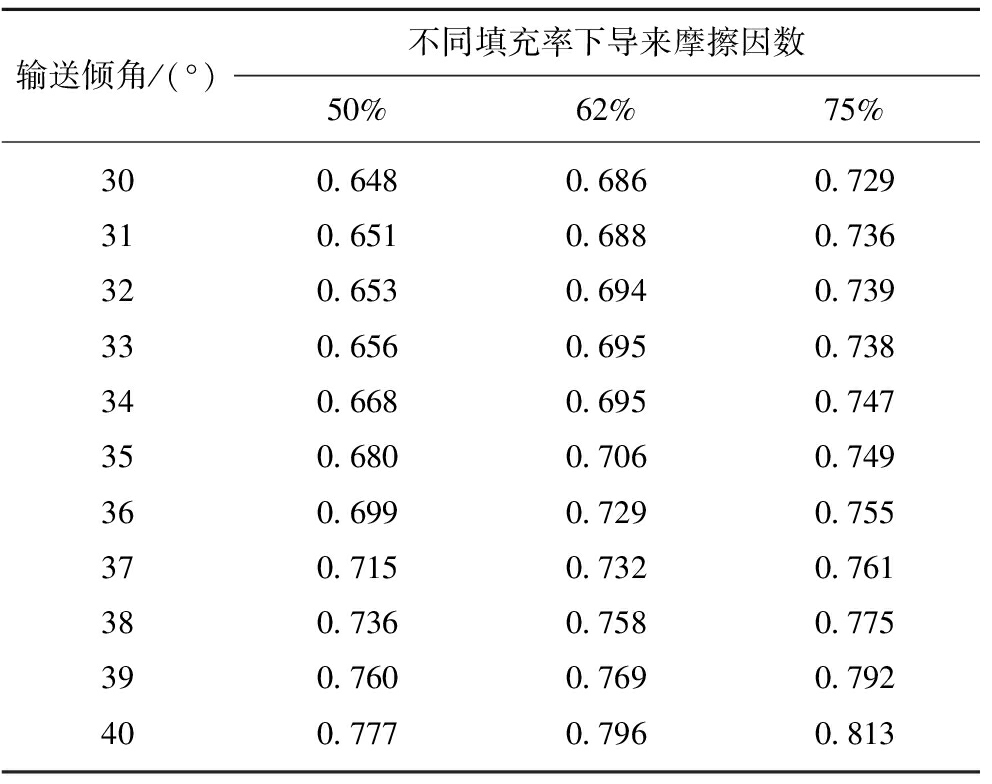
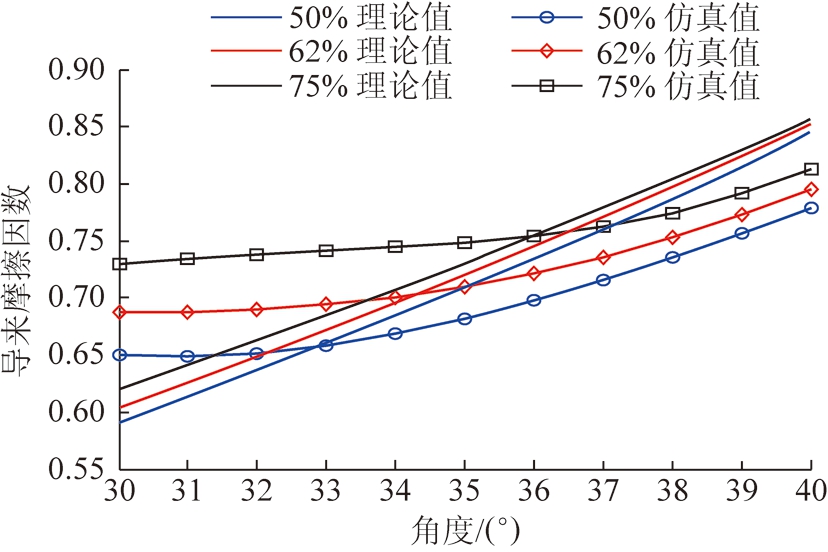
图10 导来摩擦因数随输送倾角变化曲线
Fig.10 Leads to the friction coefficient with delivery angle
由图10可得在3种典型的填充率下,仿真所得拟合曲线与理论推导的函数曲线3个交点所对应的输送倾角的值分别为32.7°,34.2°,36°,与仿真得出的极限输送倾角32°,34°,37°基本一致。如图10所示,在交点之前导来摩擦因数的仿真拟合值大于理论推导值,在交点之后导来摩擦因数的仿真拟合值小于理论推导值,而且在仿真中当输送倾角大于极限输送倾角时物料在管带发生了明显的滑移。因此,就证明了以导来摩擦因数来表征物料与管带之间的相对滑移状态的合理性。如果要保证物料在管带中不发生相对滑移,那么物料与管带间导来摩擦因数的仿真值必须要大于或等于理论推导值的临界值,如果小于则物料将在管带中发生相对滑移。由以上分析得,以导来摩擦因数来表征物料与管带之间的相对滑移状态,结合理论与仿真分析得出圆管带式输送机在填充率分别为50%,62%,75%时,其极限输送倾角分别为32°,34°,36°。
(1)基于相对滑移理论推导不同填充率下导来摩擦因数与极限输送倾角的函数关系。采用离散元法分析不同填充率下导来摩擦因数与极限输送倾角的拟合函数关系。采用导来摩擦因数表征物料与管带间相对滑移状态,理论与仿真相结合分析不同填充率下圆管带式输送机直线爬坡段极限输送倾角。
(2)通过该方法得出当物料为块煤,管径为400 mm,物料填充率分别为50%,62%,75%时,某型圆管带式输送机直线爬坡段的极限输送倾角分别为32°,34°,36°。
(3)由于圆管带式输送机的实际运行工况条件复杂,今后还需结合物料内部相互作用力、管径、带速、托辊间距、输送带压陷阻力等因素对圆管带式输送机直线爬坡段极限输送倾角展开深入研究。
参考文献:
[1] 朱立平,蒋卫良.适用于我国煤矿带式输送机典型机型的研究[J].煤炭学报,2010,35(11):1916-1920.
ZHU Liping,JIANG Weiliang.Study on typical belt conveyor in coal mine of China[J].Journal of China Coal Society,2010,35(11):1916-1920.
[2] 多斯桑托斯 J A,许升阳.大倾角双层带式输送机研制进展[J].江苏煤炭,1990(2):52-55.
DOS SANTOS J A,XU Shengyang.Development of double-dip belt conveyor with large dip angle[J].Jiangsu Coal,1990(2):52-55.
[3] 王鹰,杜群贵,韩刚,等.环保型连续输送设备——圆管状带式输送机[J].机械工程学报,2003,39(1):149-158.
WANG Ying,DU Qungui,HAN Gang,et al.Environment-protecting continual conveyor-pipe belt conveyor[J].Chinese Journal of Mechanical Engineering,2003,39(1):149-158.
[4] GUO Yongcun,WANG Shuang,HU Kun,et al.Optimization and experimental study of transport section lateral press of pipe belt conveyor[J].Advanced Powder Technology,2016,27(4):1318-1324.
[5] GUO Yongcun,WANG Shuang,HU Kun,et al.Optimizing the pipe diameter of the pipe belt conveyor based on discrete element method[J].3d Research,2016,7(1):85.
[6] 蒋卫粮.大倾角下运带式输送机新型托辊装置试验研究[J].煤矿机械,1999(8):16-18.
JIANG Weiliang.Test of new belt conveyor idlers under the new large angle[J].Coal Mining Machinery,1999(8):16-18.
[7] 孙可文,肖林京,梁兆正,等.锁边圆管带式输送机运转理论分析[J].煤炭学报,1996(6):655-660.
SUN Kewen,XIAO Linjing,LIANG Zhaozheng,et al.Theoretical study of side locked tube belt conveyor[J].Journal of China Coal Society,1996(6):655-660.
[8] 肖林京,徐锦诚,孙可文.锁边圆管带式输送机弯曲处的力学分析[A].中国机械工程学会物料搬运分会学术年会[C].1996:263-269.
XIAO Linjing,XU Jincheng,SUN Kewen,et al.Dynamics analysis of pipe belt conveyor with locked edges at its turning point[A].The Proceedings of Third Annual Conference of Material Handling Professional Society of Chinese Mechanical Engineering Society[C].1996:263-269.
[9] 边永梅.管状带式输送机极限运行倾角分析[J].煤矿机电,2017(4):53-55.
BIAN Yongmei.Analysis of the extreme operation inclination of tubular belt conveyor[J].Coal Mining Machinery,2017(4):53-55.
[10] 宾光富,张文强,李学军,等.考虑圆管输送带弹性的托辊组动态接触力特性分析[J].煤炭学报,2017,42(9):2483-2490.
BIN Guangfu,ZHANG Wenqiang,LI Xuejun,et al.Dynamic contact force analysis considering pipe conveyor belt elasticity[J].Journal of the China Coal Society,2017,42(9):2483-2490.
[11] 黄松元.散体力学[M].北京:机械工业出版社,1993:10-13.
[12] 胡国明.颗粒系统的离散元素法分析仿真:离散元素法的工业应用与EDEM软件简介[M].武汉:武汉理工大学出版社,2010:7-8.
[13] 李勤良.颗粒堆积性质和散状物料转载过程的DEM仿真研究[D].沈阳:东北大学,2010:30-32.
LI Qinliang.The research of granular piling and bulk material transfer process using DEM simulation[D].Shenyang:Northeastern University,2010:30-32.
[14] 宋伟刚,徐亚美,王雷克.深槽托辊组大倾角输送机理分析的仿真方法[J].煤炭学报,2014,39(S2):563-568.
SONG Weigang,XU Yamei,WANG Leike.Simulation method of transport mechanism analysis of deep groove idlers belt conveyor in large in-clination angle[J].Journal of China Coal Society,2014,39(S2):563-568.
[15] 宋伟刚,王天夫.散状物料转载系统设计DEM仿真方法的研究[J].工程设计学报,2011,18(6):428-436.
SONG Weigang,WANG Tianfu.The research on DEM method to design bulk material transfer system[J].Journal of Engineering Design,2011,18(6):428-436.
[16] 贾富国,韩燕龙,刘扬,等.稻谷颗粒物料堆积角模拟预测方法[J].农业工程学报,2014,30(11):254-260.
JIA Fuguo,HAN Yanlong,LIU Yang,et al.Simulation prediction method of repose angle for rice particle materials[J].Transactions of the Chinese Society of Agricultural Engineering,2014,30(11):254-260.
[17] 宋伟刚,张书杰,王丛.堆料机转载站结构参数设计的离散单元法的仿真[J].中国工程机械学报,2012,10(4):421-428.
SONG Weigang,ZHANG Shujie,WANG Cong.DEM simulation method for structural parameter design on stacker transfer stations[J].Chinese Journal of Construction Machinery,2012,10(4):421-428.