文志杰1,5，张瑞新1，杨 涛2，陈连军1，蒋宇静1，谭云亮1，陈 结3，陈 艾1,4
(1.山东科技大学 矿山灾害预防控制省部共建国家重点实验室培育基地，山东 青岛 266510; 2.华北科技学院 安全工程学院，河北 廊坊 065201; 3.重庆大学 资源及环境科学学院，重庆 400030; 4.神华宁夏煤业有限公司 羊场湾煤矿，宁夏 灵武 750409; 5.山东大学 岩土与结构工程研究中心，山东 济南 250061)
摘 要:巷道围岩的稳定性不仅与岩体强度有关，还与围岩应力场梯度密切相关。为研究锚杆在巷道围岩支护中合理支护强度的确定方法，在特定的地质条件中提出合理的预紧力，以连续损伤力学模型为基础并引入材料力学领域中的应力梯度理论，推导出了考虑围岩塑性区与弹性区交界面处的平衡方程和边界条件，建立了基于Mohr-Coulomb准则、Drucker-Prager准则以及Hoek-Brown准则下的围岩应力梯度求解模型;以Mohr-Coulomb准则为例，借助FLAC3D对比出模拟结果与理论计算值吻合度为93%且变化趋势一致，验证了提出的应力梯度求解方式适用性，发现随着锚杆预紧力的增加，巷道围岩的塑性区应力梯度相应增加，弹性区应力梯度不断减小，岩体劣化程度减弱。提出应力补偿系数，模拟计算出不同锚杆预紧力下巷道围岩应力梯度分布规律和支护效果，发现预紧力的变化与巷道围岩的锚固效果呈正相关趋势，塑性区范围随预紧力的增加不断减小，围岩稳定性随应力梯度的增加不断提高，并据此得出了锚杆预紧力与围岩应力梯度的对应补偿关系并提出最优补偿比。在现场实践中对巷道变形控制效果提高40%以上，并且应力梯度补偿系数高于0.65，高于该矿围岩变形安全控制要求，为确定锚杆合理支护强度提供了一种研究思路。
关键词:应力梯度;预紧力;应力补偿;锚杆支护;支护强度
移动阅读
文志杰，张瑞新，杨涛,等.基于应力梯度理论的锚杆合理预紧力[J].煤炭学报,2018,43(12):3309-3319.doi:10.13225/j.cnki.jccs.2018.1269
WEN Zhijie,ZHANG Ruixin,YANG Tao,et al.Reasonable pre-tightening force of bolt based on the theory of stress gradient[J].Journal of China Coal Society,2018,43(12):3309-3319.doi:10.13225/j.cnki.jccs.2018.1269
中图分类号:TD322;TD353
文献标志码:A
文章编号:0253-9993(2018)12-3309-11
收稿日期:2018-09-21
修回日期:2018-11-15
责任编辑:郭晓炜
基金项目:国家重点研发计划资助项目(2016YFC0600708);山东省自然科学基金资助项目(ZR2018MEE001);山东省高等学校科技计划资助项目(J15LH04)
作者简介:文志杰(1982—)，男，山东平度人，副教授。Tel:0532-86057329，E-mail:sdust0532@gmail.com
通讯作者:张瑞新(1993—)，男，山东阳谷人，硕士研究生。E-mail:zhangruixinchn@gmail.com
WEN Zhijie1,5,ZHANG Ruixin1,YANG Tao2,CHEN Lianjun1,JIANG Yujing1,TAN Yunliang1,CHEN Jie3,CHEN Ai1,4
(1.State Key Laboratory of Mining Disaster Prevention and Control Co-founded by Shandong Province and the Ministry of Science and Technology,Shandong University of Science and Technology,Qingdao 266590,China; 2.College of Safety Engineering,North China Institute of Science and Technology,Langfang 065201,China; 3.College of Resources and Environmental Science,Chongqing University,Chongqing 400030,China; 4.Yangchangwan Coal Mine,Shenhua Ningxia Coal Group Co.，Ltd.，Lingwu 750409，China; 5.Geotechnical and Structural Engineering Research Center,Shandong University,Jinan 250061,China)
Abstract:The stability of roadway surrounding rock is not only related to the strength of rock mass,but also closely related to the stress field gradient of surrounding rock.In order to study the determination method of reasonable support strength of bolt in roadway surrounding rock support,a reasonable pre-tightening force is put forward in some specific geological conditions.This paper is based on the continuum damage mechanics model and introduces the stress gradient theory in the field of material mechanics.The equilibrium equation and boundary conditions of the interface between the plastic zone and the elastic zone of the surrounding rock are derived,and the stress gradient solution model of surrounding rock is established based on Mohr-Coulomb criterion,Drucker-Prager criterion and Hoek-Brown criterion.Taking the Mohr-Coulomb criterion as an example,using the FLAC3D numerical software,the simulation results are compared with the theoretical values,which are 93 percent consistent with the change trend,which verifies the applicability of the stress gradient solution method proposed in this paper.It is found that the stress gradient in the plastic area of roadway surrounding rock increases correspondingly with the increase of the pre-tightening force of bolt,the stress gradient in the elastic area decreases continuously,and the degradation degree of rock mass decreases.The authors put forward the stress compensation coefficient.The stress gradient distribution law and supporting effect of roadway surrounding rock under different bolt preloads are calculated by simulation.It’s found that the change of pre-tightening force is positively correlated with the bolting effect of roadway surrounding rock,and the range of plastic zone decreases with the increase of pre-tightening force,and the stability of sur-rounding rock increases with the increase of stress gradient.Based on these conclusions,the corresponding compensation relation between the bolt’s pretension force and the stress gradient of surrounding rock is obtained and the optimal compensation ratio is proposed.In the field practice,the control effect of roadway deformation is improved by more than 40%,and the stress gradient compensation coefficient is higher than 0.65,which is higher than the safety control requirements of surrounding rock deformation,and provides a research idea for determining the reasonable support strength of the bolt.
Key words:stress gradient;pre-tightening force;stress compensation;rock bolting;support strength
地下工程开挖过程中产生结构体自由面，导致开挖边界附近的应力重新分布，使围岩形成一种新的多轴向应力状态。大量研究[1-5]证实了围压对岩石力学行为的显著影响，特别是在强度和断裂特性方面，围压在某一方向上变化的快慢程度直接决定着围岩的破坏方式。在高地应力条件下，径向应力受垂向应力的影响在围岩中表现出明显的梯度变化，进而影响围岩稳定性。
由于各向同性的特性和应用的广泛性，学者对于应力梯度理论的研究集中在金属材料领域[6-9]，尤其基于细观尺度在对金属构件疲劳程度的评估以及材料受梯度应力作用下裂纹的扩展等的研究应用较多(ANTUNES M A[6]，VANTADORI S[7]，ARA
JO J A[8]，GATES N[9])。应力梯度在岩土工程领域的研究较少，HE Jiang[10]建立了水平应力梯度诱导层错型岩爆发生的判据。SU Guoshao[11]探究了径向应力梯度对花岗岩应变型岩爆的影响，并得出了随着径向应力梯度的增加岩石力学特征的变化规律。CARTER B J[12]从实验的角度对应力梯度理论开展了初步探索，得出了应力梯度和尺寸效应对孔洞周围裂隙扩展的影响系数。在岩体劣化失稳的理论研究中,CHAPPELL B A[13]，JESSLL M[14]，GERÇEK H[15]证明岩体劣化带内存在着明显的应力梯度效应，并且梯度的阈值区间对岩体的劣化损伤特征起着控制作用。
开挖以后，岩体因所处应力环境不同发生劣化失稳现象[16-21]。围岩失稳或者岩体损伤多出现在具有显著应力梯度的应力集中区域。因此，应力梯度是岩体稳定性分析中着重考虑的主要因素之一。笔者在已有研究的基础上，推导出不同岩体强度准则下的应力梯度，并提出了锚杆合理预紧力确定方法，为围岩锚固支护强度的判定提供了一种研究思路。
图1 巷道围岩破坏
Fig.1 Failure of surrounding rock
岩体中天然裂隙的存在使得岩体无法满足经典连续介质力学连续性假设[22-23]，将岩石视为理想弹塑性材料，在线弹性范围内假定εij和σij符合广义Hooke定律:
式中，σi(j,k)，σj(k,i)，σk(i,j)为应力分量;εi(j,k)为应变分量;γjk(ki,ij)为剪应变分量;τjk(ki,ij)为剪应力分量;G为拉梅常量;E为弹性模量。
计算过程中考虑静力过程，平衡方程为
σij,i-τijk,ij+fi=0
其中，fi为体力，即物理内部微元体所受外力;σij,i，τijk,ij分别为材料所受正应力和剪应力。用岩体相当小而非无穷小体积上的应力变化统计平均值表示应力分量并计算应力梯度T(x,y)，即
应力梯度诱发巷道围岩产生离层、滑动及拉伸、剪切裂纹等不连续、渐变型扩容变形[24]。为保持围岩完整性和自承能力，降低由应力梯度导致的岩体扩容劣化与损伤，通常采用锚杆与喷浆混凝土协同支护方式加固围岩。因此提出用应力梯度补偿系数评价劣化岩体支护后效果。根据应力梯度的分布规律，应力梯度补偿系数η可表示为
式中，σij为不同预紧力支护条件下的水平应力;σ0为初始开挖条件下岩体水平应力;P0为原岩应力。
把岩石假定为由无数微元组成的各向同性结合体，使用锚杆锚固后的微元体间距和体积相比初始开挖采动状态下更小，微元体间相互作用力的增加导致应力梯度爬升(图2)。基于实际岩体中力学参数的差异性以及岩石材料属性的离散性，本文提出应力梯度有效补偿系数
和η的数值关系为
式中，Ts为岩体应力梯度的实际值;Tl为岩体应力梯度理论值。
图2 应力梯度补偿示意
Fig.2 Stress gradient compensation
同时，巷道围岩应力重分布的过程中，围岩的稳定性明显降低，用应力梯度损伤变量表征岩体的稳定程度，稳定系数Y表示为
式中，T(x)为应力梯度。
2.1.1 基本假设
① 深埋圆形平巷、无限长;② 原岩应力各向等压;③ 岩体为理想弹塑性材料;④ 巷道埋深≥20R0[25-28]。
图3 巷道围岩力学模型及本构关系
Fig.3 Mechanical model and constitutive relation of surrounding rock
塑性区的本构关系采用增量型本构关系，即Levy-Mises关系确定。轴对称圆巷的力学模型及本构关系如图3所示，其中，Re为弹性区半径;Rp为塑性区半径;σs为屈服应力。
2.1.2 弹性解
根据前人的研究成果[29-31]有
(1)
(2)
式中，σr，σθ分别为围岩弹性区的径向应力和切向应力;R0为圆巷的半径;r为围岩任意一点的半径。
根据广义Hooke定律:
则在巷道开挖之后的原岩应力区有
P0=ν(P0+P0)+Eεz
(3)
式中，ν为泊松比。
在巷道开挖之后的弹性应力区，对于无限长巷道可以简化为平面应变问题，有
σz=ν(σr+σθ)+Eεz
(4)
式(4)减式(3)并整理，可得
σz=ν(σr+σθ-2P0)+P0
(5)
把式(1)，(2)代入式(5)得
σz=P0
(6)
式中，σz，εz分别为围岩弹性区沿巷道轴向方向的应力和应变。
2.1.3 围岩开始屈服时的原岩应力
根据M-C屈服条件，有
τ=c+σntan φ
(7)
式中，τ，σn分别为破坏面上的剪应力和正应力;c，φ分别为黏聚力和摩擦角。
将其与莫尔圆结合转化为
(8)
式中，σ1和σ3分别为加载过程中
达到峰值时对应的最大压应力和最小压应力。
为表述切向应力和径向应力的关系，引入剪切应力
得
(9)
式中，σc为抗压强度。
2.1.4 弹塑性解
在弹性区，积分常数待定的弹性区应力解为
(10)
其中，A，B分别为未知表达式。在塑性区，当达到M-C屈服条件即原岩应力
时，巷道围岩屈服范围，即弹塑性界面半径不断增大，其中
为在M-C屈服条件下计算得的原岩应力。根据Levy-Mises本构关系有
(11)
(12)
式中，εr为径向应变。
式(12)代入式(7)得
σr-σθ=(1-ε)σr-σc
(13)
式(11)代入平衡方程得
(14)
求解得
(15)
式(15)积分得
(16)
式中，C1为未知表达式。
边界条件为
弹性区:
外边界r→
;σr=σθ=P0
(17)
内边界(弹塑性交界面):
(18)
塑性区:
外边界(弹塑性交界面)
(19)
(20)
式中，
为塑性区径向应力;
为弹性区径向应力;
为塑性区切向应力;
为弹性区切向应力;上角p为塑性区相关参数;上角e为弹性区相关参数。
内边界σr=0
所以
(21)
式(12)，(13)，(16)，(21)联合求解得塑性区应力为
(22)
(23)
(24)
由式(10)和式(17)得
(25)
(26)
式(19),(22)，(25)联合求解得
(27)
(28)
式(12)，(25)，(26)，(28)联合求解得
(29)
(30)
(31)
由式(20),(23)，(30)得弹塑性交界面处应力平衡关系为
(32)
求解式(30)得塑性区半径为
(33)
令
式(33)可以简化为Rp=R0β。
式(25)，(26)，(28)，(33)联合求解得弹性区应力为
(34)
令
则式(34)可以简化为
(35)
把极坐标转换成直角坐标为
(36)
有
(37)
根据式(7)设
f(x,y,z)=τ-c+σntan φ
(38)
可得出基于M-C准则的另一种表达式:
f(x,y,z)=τ-c+σntan φ=0
式(37)代入式(38)得
(39)
对式(39)求其梯度场，得
(40)
式(40)则是基于M-C准则的应力场梯度。巷道内围岩应力场视为平面应变问题，所以式(40)可简化为
(41)
平面应变条件下，基于M-C准则的应力场梯度值为
(42)
弹性区:
塑性区:
计算过程与M-C准则计算过程一致，下面列出求解结果。
根据D-P屈服条件，有
(43)
式中，α，k为仅与岩石的内摩擦角和黏聚力有关的试验常数;I1为第1应力不变量。
计算得塑性区应力为
(44)
(45)
(46)
计算得弹性区应力为
(47)
基于D-P准则的应力场梯度值为
(48)
式中，
为第2应力偏量不变量。
计算过程与M-C准则计算过程一致，下面列出求解结果。
根据H-B屈服条件，有
(49)
式中，S为量纲为1的参数，对于连续介质可取S=1。
计算得塑性区应力为
(50)
弹性区应力为
(51)
式中,
平面应变条件下，应力场梯度值为
(52)
羊场湾煤矿130205轨道巷埋深-495 m，运输巷与回风巷两帮变形严重，影响了矿井的正常生产，需要合理分析围岩的锚固支护强度以确保巷道正常使用。
将实际岩体力学参数赋值于构建的应力梯度求解模型，以Mohr-Coulomb准则为例，其计算参数如下:巷道半径R0=2.5 m，水平原岩应力P0=12.8 MPa，围岩弹性模量E=5 GPa，切变模量G=2.14 GPa，泊松比μ=0.17，黏聚力C=6 MPa。应用上述计算参数，按照本文第二部分求解流程求得基于Mohr-Coulomb准则在未支护条件下巷道围岩的径向应力梯度(图8)，其中塑性区半径rp=3.25 m;即在2.5 m≤r≤3.25 m内围岩处于峰后塑性状态，在3.25 m≤r≤10 m内围岩处于峰前弹性状态。
在130205工作面轨道巷靠近掘进工作面处选取一试验段使用锚杆加固围岩，间排距为600 mm×600 mm，并且每3排锚杆预紧力增加25 kN，预紧力阈值为0～200 kN。被锚固岩体稳定后，监测不同预紧力下的围岩水平应力，数据记录如图4所示，计算出实测应力梯度如图5所示。
图4 实测水平应力
Fig.4 Measured horizontal stress
图5 实测水平应力梯度
Fig.5 Measured horizontal stress gradient
分析监测数据得出，水平应力梯度沿围岩径向方向逐渐降低并最终趋近于0。以25 kN支护预紧力监测数据分析为例，同一监测路径由浅至深会出现梯度变化折点，在该折点前应力梯度随预紧力的升高逐渐增加，折点后应力梯度随着预紧力的增加逐渐降低。
数值模型尺寸为x方向50 m;y方向0.5 m;z方向50 m，模型网格划分33 360个单元;模型中部进行加密划分，加密区位于模型中心，半径为10 m，加密区网格划分为24 000个单元，力学参数见表1，数值模型如图6所示，不同锚杆预紧力下的围岩应力梯度模拟结果如图7所示。由图7可知，未支护条件下巷道围岩应力梯度从巷道壁至岩体内部平缓小幅增加至塑性区边界，越过边界后应力梯度逐渐降低至0。
随着预紧力从25 kN增加至200 kN，塑性区水平应力梯度峰值从8 MPa/m逐渐增加至15.5 MPa/m，塑性区范围从3.5 m缩减至3 m，可见锚杆预紧力的增加使得围岩劣化范围减小，塑性区边界向围岩外侧偏移。应力梯度变化折点与围岩弹塑性交界面几乎重合，并且会随着锚杆预紧力的增加逐渐向巷道围岩浅部偏移，塑性区范围也会随之缩小，显著提高了巷道围岩稳定性。根据提出的围岩稳定系数Y求解条件，得出在巷道围岩浅部(r<10 m)围岩稳定系数Y与应力梯度T(x)成正相关，验证了提出的围岩稳定模型评估方式的有效性。
表1 材料参数
Table 1 Material properties
图6 模型示意
Fig.6 Schematic diagram
图7 模拟水平应力梯度
Fig.7 Simulated horizontal stress gradient
对未支护条件下巷道变形数值模拟、理论计算以及现场实测结果进行对比分析(图8)，模拟值、理论值与实测值相关性分析见表2。
图8 理论、模拟与现场监测结果对比
Fig.8 Comparison of theoretical,simulated and field monitoring results
表2 模拟值、理论值与实测值的相关性分析
Table 2 Correlation analysis of simulated value,theoretical value and measured value
由表2可以得出模拟值拟合相关性为0.930 13>0.9，理论值拟合相关性为0.963 27>0.9，所以可用二阶拟合方式对该巷道围岩进行应力梯度进行求解，关系式为
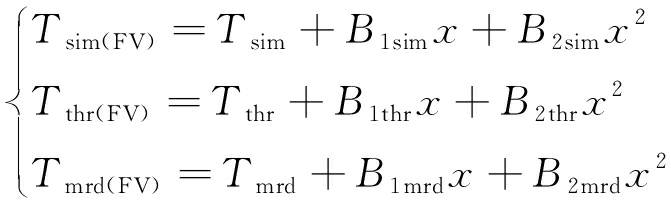
(53)
根据曲线修正为
Tthr(FV)=Tsim+B1simx+0.9B2simx2=Tmrd+
B1mrdx+1.2B2mrdx2
(54)
式中，FV为拟合值;sim为模拟值;thr为理论值;mrd为实测值;Tsim(FV)为模拟应力梯度的拟合值;Tthr(FV)为理论应力梯度的拟合值;Tmrd(FV)为实测应力梯度的拟合值。
式(54)可用于理论值、模拟值与实测值之间的求解，以及根据理论值对实测值进行正确的评估。获得未支护条件下围岩的应力梯度后，借助模拟运算结果(图9(b))，分析知当锚杆预紧力为150 kN时，该支护形式下巷道围岩变形量相较于未支护条件下减少40%，即巷道变形补偿比为40%;断面塑性区范围缩减60.4%。应力梯度补偿系数计算方式如下:
图9 应力梯度补偿效果
Fig.9 Effect of stress gradient compensation
理论方式获得的应力梯度基准为T0，不同预紧力锚杆支护状态下的围岩应力梯度为Tx，则补偿系数计算准则为
(55)
有效补偿系数为
(56)
现场应力梯度折损值为(0.65-0.604)/0.65=0.07,以数值模拟应力梯度补偿系数为依据，得到相应的应力梯度补偿效果(图9(a))，不同预紧力下应力梯度补偿系数变化趋势(图9(c))。
锚杆预紧力对围岩应力梯度的补偿呈正相关关系(图9(c))，对曲线段进行线性拟合得到补偿系数，即
η=0.001 16Fn+0.477 17(R2=0.964 27)
(57)
式中，Fn为预紧力。
基于该计算准则可以较准确的计算出现场条件下巷道围岩进行锚杆支护时所需最合适预紧力。计算及分析流程如图10所示。
图10 应力梯度计算及分析流程
Fig.10 Stress gradient calculation and analysis process
根据理论分析结果，选取应力梯度补偿系数0.65为最优补偿比，对应预紧力为150 kN。根据该地质条件下现场实测值相较于理论计算值0.07的预估折损比，对锚杆设计的最优支护强度需施加161 kN的预紧力，在130205轨道巷共设置3组巷道围岩变形及应力监测区域，监测设备如图11所示，施工完成后支护优化效果如图12所示。
图11 围岩监测设备
Fig.11 Surrounding rock monitoring equipment
图12 优化效果统计
Fig.12 Statistical chart of application effect
依据本文提出的应力梯度补偿方式在同等围岩条件下，对巷道变形控制效果提高40%以上，并且应力梯度补偿系数高于0.65，高于该矿围岩变形安全控制要求。
综上所述，基于Mohr-Coulomb强度理论及该理论指导下提出的围岩应力梯度理论模型求解的巷道围岩径向应力梯度与数值模拟、现场实测数据基本一致，且变化趋势吻合，为确定现场条件下的应力梯度及变化规律提供了计算依据;同时，根据不同预紧力作用下的巷道围岩应力梯度变化规律，可以优化应力梯度补偿值及锚杆预紧力，改进支护参数。
(1)应力梯度变化是一种在巷道围岩中普遍存在的现象;在理论上研究巷道围岩的应力梯度应从塑性区和弹性区不同的应力平衡关系切入，并且根据不同的围岩条件选取合适的岩石强度理论。
(2)基于应力梯度理论及连续损伤力学模型推导了在平面应变条件下塑性区与弹性区交界面的力学平衡方程和边界条件，并提出了在Mohr-Coulomb准则、Drucker-Prager准则以及Hoek-Brown准则下巷道围岩应力梯度的理论求解方法。
(3)基于Mohr-Coulomb破坏准则及该准则指导下提出的巷道围岩应力梯度理论求解模型求解的围岩径向应力梯度与数值模拟、现场实测数据基本一致，且变化趋势吻合，验证了本文提出的应力梯度求解方式适用性:锚杆预紧力增加，巷道围岩的塑性区应力梯度相应增加，弹性区应力梯度不断减小，岩体劣化程度减弱;对巷道围岩的锚固效果呈正相关趋势，塑性区范围会随预紧力的增加不断减小，围岩稳定性随应力梯度的增加不断提高。
(4)利用FLAC3D数值模拟软件模拟不同锚杆预紧力下巷道围岩应力梯度的变化，得出了应力梯度补偿值与锚杆预紧力之间的对应关系，提出了应力梯度补偿系数并用以优化锚杆预紧力施加值，为巷道围岩的锚固设计提供了一种新的研究思路。
参考文献
[1] ALAM A K M B,NIIOKA M,FUJII Y,et al.Effects of confining pressure on the permeability of three rock types under compression[J].International Journal of Rock Mechanics and Mining Sciences,2014,65(1):49-61.
[2] SUKPLUM W,WANNAKAO L.Influence of confining pressure on the mechanical behavior of Phu Kradung sandstone[J].International Journal of Rock Mechanics and Mining Sciences,2016,86:48-54.
[3] LI Xibing,TAO Ming,WU Chenqing,et al.Spalling strength of rock under different static pre-confining pressures[J].International Journal of Impact Engineering,2017,99:69-74.
[4] SCHMIDT R A,HUDDLE C W.Effect of confining pressure on fracture toughness of Indiana limestone[J].International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts,1977,14(5):289-293.
[5] CHI T N,NGUYEN G D,DAS A,et al.Constitutive modelling of progressive localised failure in porous sandstones under shearing at high confining pressures[J].International Journal of Rock Mechanics and Mining Sciences,2017,93:179-195.
[6] ANTUNES M A,SILVA C R M D,Rêgo E M F D.Stress intensity factor solutions for fretting fatigue using stress gradient factor[J].Engineering Fracture Mechanics,2017,186:331-346
[7] VANTADORI S,FORTESE G,RONCHEI C,et al.A stress gradient approach for fretting fatigue assessment of metallic structural components[J].International Journal of Fatigue,2017,101:1-8.
[8] ARA
JO J A,ALMEIDA G M J,FERREIRA J L A,et al.Early cracking orientation under high stress gradients:The fretting case[J].International Journal of Fatigue,2017,100:611-618.
[9] GATES N,FATEMI A.Notch deformation and stress gradient effects in multiaxial fatigue[J].Theoretical and Applied Fracture Mechanics,2016,84:3-25.
[10] HE Jiang,DOU Linming.Gradient principle of horizontal stress inducing rock burst in coal mine[J].Journal of Central South University,2012,19(10):2926-2932.
[11] SU G,ZHAI S,JIANG J,et al.Influence of radial stress gradient on strainbursts:An experimental study[J].Rock Mechanics and Rock Engineering,2017,50(10):2659-2676.
[12] CARTER B J.Size and stress gradient effects on fracture around cavities[J].Rock Mechanics and Rock Engineering,1992,25(3):167-186.
[13] CHAPPELL B A.Size effects,stress and couple stress gradients in jointed rock[J].Mining Science and Technology,1990,11(1):1-18.
[14] JESSLL M.The failure of rock[J].International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts,1965,2:389-403.
[15] GERÇEK H.An elastic solution for stresses around tunnels with conventional shapes[J].International Journal of Rock Mechanics and Mining Sciences,1997,34(3-4):96.
[16] BARTON N,LIEN R,LUNDE J.Engineering classification of rock masses for the design of tunnel support[J].Rock Mechanics,1974,6(4):189-236.
[17] CAI Y,ESAKI T,JIANG Y.A rock bolt and rock mass interaction model[J].International Journal of Rock Mechanics and Mining Sciences,2004,41(7):1055-1067.
[18] MOORE I D.Analysis of rib supports for circular tunnels in elastic ground[J].Rock Mechanics and Rock Engineering,1994,27(3):155-172.
[19] KANG Hongpu.Support technologies for deep and complex roadways in underground coal mines:A review[J].International Journal of Coal Science & Technology,2014,1(3):261-277.
[20] BOBET A.Elastic solution for deep tunnels application to excavation damage zone and rockbolt support[J].Rock Mechanics and Rock Engineering,2009,42(2):147-174.
[21] LIU G F,FENG X T,FENG G L,et al.A method for dynamic risk assessment and management of rockbursts in drill and blast tunnels[J].Rock Mechanics and Rock Engineering,2016,49(8):3257-3279.
[22] BARPI F,VALENTE S,CRAVERO M,et al.Fracture mechanics characterization of an anisotropic geomaterial[J].Engineering Fracture Mechanics,2012,84:111-122.
[23] 左建平,魏旭,王军,等.深部巷道围岩梯度破坏机理及模型研究[J].中国矿业大学学报,2018,47(3):478-485.
ZUO Jianping,WEI Xu,WANG Jun,et al.Investigation of failure mechanism and model for rocks in deep roadway under stress gradient effect[J].Journal of China University of Mining and Technology,2018,47(3):478-485.
[24] 张绪涛,张强勇,向文,等.基于应变梯度理论的分区破裂机制分析研究[J].岩石力学与工程学报,2016,35(4):724-734.
ZHANG Xutao,ZHANG Qiangyong,XIANG Wen,et al.Zonal disintegration mechanism based on strain gradient theory[J].Chinese Journal of Rock Mechanics and Engineering,2016,35(4):724-734.
[25] 王明洋,解东升,李杰,等.深部岩体变形破坏动态本构模型[J].岩石力学与工程学报,2013,32(6):1112-1120.
WANG Mingyang,XIE Dongsheng,LI Jie,et al.Dynamic constitutive model for deformation and fracture of deep rock mass[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(6):1112-1120.
[26] 刘会波,肖明,陈俊涛.复杂地下洞室围岩开挖扰动空间效应参数化研究[J].四川大学学报(工程科学版),2012,44(3):47-54.
LIU Huibo,XIAO Ming,CHEN Juntao.Parametric analysis of spatial effect of excavation damaged/disturbed zone around complex underground openings[J].Journal of Sichuan University (Engineering Science Edition),2012,44(3):47-54.
[27] CHEN Z H.Stress distribution characteristics in rock surrounding heading face and its relationship with temporary supporting[J].Applied Mechanics and Materials,2014,568-570:1684-1689.
[28] 侯公羽,牛晓松.基于Levy-Mises本构关系及Hoek-Brown屈服准则的轴对称圆巷理想弹塑性解[J].岩石力学与工程学报,2010,29(4):765-777.
HOU Gongyu,NIU Xiaosong.Perfect elastoplastic solution of axisymmetric cylindrical cavity based on levy-mises constitutive relation and Hoek-Brown failure criterion[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(4):765-777.
[29] IX C.Fundamentals of rock mechanics[M].Blackwell:Blackwell publishing,1976:132-166.
[30] OBERT L，DUVALL W I.Rock mechanics and the design of structure in rock[M].New York:John Wiley and Sons,1967,71-78.
[31] 蔡美峰.岩石力学与工程[M].北京:科学出版社，2013:21-41.