
张向东,任 昆
(辽宁工程技术大学 土木工程学院,辽宁 阜新 123000)
摘 要:为研究煤渣改良土强度及屈服特性,通过不同冻融循环次数下的三轴试验,获得了配合比及冻融循环次数对煤渣改良土强度特性及屈服面的影响。通过引入配合比影响因子及冻融次数影响因子对改良土屈服面的表达形式进行了修正,推导了改良土的双屈服本构关系。研究表明:随着煤渣掺量的提高,改良土的黏聚力先增大后减小,内摩擦角稍有增加。剪应变屈服面及体应变屈服面出现先扩张后收缩的变化规律。随冻融次数的增加改良土的黏聚力降低明显,内摩擦角的变化不大。剪应变屈服面及体应变屈服面随冻融次数的增加而逐渐向原点收缩。采用配合比影响因子及冻融次数影响因子可较好的反映改良土屈服面的演化规律,据此建立的本构关系具有一定的精度。
关键词:改良土;配合比;冻融循环;强度;屈服面;影响因子

移动阅读
张向东,任昆.冻融循环下煤渣改良土的强度及屈服特性[J].煤炭学报,2018,43(12):3371-3378.doi:10.13225/j.cnki.jccs.2018.0447
ZHANG Xiangdong,REN Kun.Strength and yield characteristics of cinder improved soil under freeze-thaw cycles[J].Journal of China Coal Society,2018,43(12):3371-3378.doi:10.13225/j.cnki.jccs.2018.0447
中图分类号:TU43
文献标志码:A
文章编号:0253-9993(2018)12-3371-08
收稿日期:2018-04-05
修回日期:2018-09-19
责任编辑:毕永华
基金项目:国家自然科学基金资助项目(51774166);高等学校博士学科点专项科研基金资助项目(20112121110004)
作者简介:张向东(1962—),男,吉林榆树人,教授,博士。Tel:0418-3350627,E-mail:jwd101@126.com
ZHANG Xiangdong,REN Kun
(School of Civil Engineering,Liaoning Technical University,Fuxin 123000,China)
Abstract:To study the strength and yield characteristics of cinder-improved soil,the triaxial tests under different freeze-thaw cycles were carried out.The influence of mix proportion and freeze-thaw cycles on the strength characteristics and yield surface of cinder-improved soil were obtained through the tests.The expression of yield surface was modified by introducing the influence factor of mix proportion and freeze-thaw cycles,and the double yield constitutive relation of improved soil was obtained.The results show that with the increase of cinder content,the cohesion of the improved soil increases first and then decreases,the internal friction angle increases slightly.Shear strain yield surface and volumetric strain yield surface exhibit the rule of first expansion and then shrinkage.With the increase of freeze-thaw cycles,the cohesion of the improved soil decreases obviously,while the internal friction angle changes little.Shear strain yield surface and volumetric strain yield surface gradually shrink to the origin with the increase of freeze-thaw cycles.The influence factors of mix proportion and freeze-thaw cycles can better reflect the evolution of the yield surface of the improved soil.The constitutive relationship based on the results has a better accuracy.
Key words:improved soil;mix proportion;freeze-thaw cycles;strength;yield surface;influence factors
辽宁省位于我国东北部,属于季节性冻土区,当地的道路工程受季节变化的影响较大。与常温土相比,季节性冻土的物理力学性能随季节的改变会出现较大的变动,出现冬季冻胀、春季融陷的现象,对路基结构会造成较大破坏,影响行车安全。目前,对于道路工程中性质的不良土体,常使用石灰、水泥等进行化学改良,大量的使用石灰和水泥必将增加工程的成本。阜新地区具有较为丰富的煤炭资源,火力发电及冬季供暖需要大量的燃烧煤炭。煤炭燃烧后产生的煤渣大多进行填埋处理,对环境的影响较大。煤渣的主要成分是SiO2和Al2O3,其成分与粉煤灰相似[1-2]。若能将煤渣用于阜新地区的道路工程建设,既能保护环境又可以降低工程的成本,具有巨大的环境效益和社会效益。因此,研究煤渣改良土在冻融循环作用下的物理力学性质就显得极为重要。
对于煤渣、矿渣等大宗固体废弃物,刘栋等[3-4] 研究了以生活垃圾焚烧炉渣部分替代碎石对路面基层材料产生的影响。张互助等[5]对水泥煤渣稳定煤矸石基层的温缩性进行了研究,发现水泥煤渣稳定煤矸石基层的温缩系数较低,适合作为寒冷地区的路面基层。国外也有一些学者[6-7]使用炉渣作为混凝土骨料,并对炉渣混凝土的性能进行了研究。
对于常见的路基填料,常丹等[8-10]研究了冻融循环对青藏地区的粉砂土物理力学性质的影响,分析了不同冻融次数下土体屈服面的演化规律并采用非相关联流动法则建立了土体的双屈服面本构关系。刘建坤等[11]研究了冻融循环对粗细颗粒分布不均匀的铁路路床土屈服强度及静强度的影响。邓国华等[12]通过向修正的剑桥模型中引入结构性参数建立了结构性黄土的本构关系。李顺群等[13]研究了K0固结条件下原状土的剑桥模型与修正剑桥模型。张坤勇等[14]考虑了土体的各向异性,对椭圆-抛物线双屈服面模型进行了修正,并通过试验进行了验证。
在岩土体材料的本构关系研究过程中,对于原状土及重塑土在一般条件下的研究较为充分。而以改良土为研究对象,考虑配比及外界环境对土体性质的影响的研究较为缺乏。笔者以煤渣改良土为研究对象,对不同配比的煤渣改良土在较低围压下经历数次冻融循环后的物理力学特性及屈服面的演化规律进行了研究,通过引入配合比及冻融次数影响因子对沈珠江双屈服面模型[15]进行了改进。
试验中采用的风积砂土取自辽宁省阜新市某道路施工现场,属于级配不良的细砂,其级配曲线如图1所示。煤渣为阜新市第五供热公司燃煤的废弃炉渣,经过破碎处理后取粒径小于2.36 mm的燃煤炉渣备用,其主要化学成分为Al2O3及SiO2,堆积密度为921 kg/m3。水泥选用“阜新鹰山”牌42.5级普通硅酸盐水泥。

图1 风积砂的级配曲线
Fig.1 Particle size distribution curve
试验中改良土的质量配合比及基本物理性质见表1,将试验中使用的土样加水搅拌均匀,在φ39.1 mm×80 mm的三瓣饱和器内分5层振捣压实。试样制备完成后,立即使用保鲜膜对试件进行包裹,放置在(20±2)℃、湿度≥95%的标准养护环境下养护7 d,养护完成后进行相关物理力学试验。
表1 试验配合比设计
Table 1 Test proportion design

为研究煤渣改良土在经历数次冻融循环后物理力学性质的变化,在试件养护完成后放入-15℃的冷冻箱内冻结12 h,冻结完成后放置在20℃的室温环境中融化12 h,这样便完成了一次冻融循环。为防止冻融过程中水分的散失,在冻结过程中不移除养护阶段所设置的保鲜膜。在试件历经1,3,5,7,10次冻融循环后,利用GDS三轴试验系统(图2)开展常规三轴剪切试验,该系统围压范围为0~2 MPa,最大轴向荷载25 kN,最大轴向位移90 mm,满足试验的需求。
由于需要测定改良土在试验过程中的体积变化,在验开始前先对试件进行反压饱和,饱和过程完成后采用固结排水(CD试验)方式进行试验,饱和度控制在95%以上,轴向剪切速率为0.02%/min。考虑到路基填土的工作环境,试验过程中围压设置为30,50,70,100和150 kPa。

图2 GDS三轴试验系统
Fig 2 GDS triaxial test system
图3为不同煤渣掺量的改良土在经历不同冻融循环次数后的应力-应变关系曲线,受文章篇幅限制文中仅给出了部分试验数据,其他情况下改良土的应力-应变关系与其大致相同。

图3 围压为50 kPa不同煤渣掺量下改良土的应力-应变关系
Fig.3 Stress-strain relationship of modified soil under different cinder content under 50 kPa confining pressure
通过图3可以发现,在煤渣掺量相同的条件下,随着冻融循环次数的增加改良土的应力-应变关系曲线出现逐渐降低的趋势,前5次冻融循环对改良土的应力-应变关系影响较大,最大可使得改良土的强度的降低32.5%。当冻融循环次数超过5次后这种影响逐渐减弱,应力-应变关系曲线基本相同。这是因为改良土内的水分在低温的环境下发生冻结产生体积膨胀,在冻胀力的作用下使得土体内部产生许多细小的裂隙,对改良土结构造成不可逆转的破坏,从而造成改良土承载能力的降低。在冻融循环次数相同的条件下,随着煤渣掺量的增加改良土的抗剪强度出现先增大后减小的变化趋势,当煤渣掺量为15%时改良土的强度可以达到最大值为1 085 kPa。这是由于煤渣中具有活性的氧化硅和氧化铝与水泥水解产生的氢氧化钙发生火山灰反应在土中形成了水化硅酸钙及水化铝酸钙,在土中起胶结作用,提高了改良土的承载能力,即
2(2CAO·SiO2)+4H2O=3CaO·2SiO2·3H2O+
Ca(OH)2
xCa(OH)2+SiO2+(m-x)H2O=
xCaO·SiO2·mH2O
yCa(OH)2+Al2O3+(n-y)H2O=
yCaO·Al2O3·nH2O
(1)
随着煤渣掺量的提高活性氧化硅和氧化铝的含量逐渐提高,反应产生胶结物的量也逐渐增大,但由于煤渣自身强度较低掺入过多时会降低改良土的承载能力,最终使得改良土的抗剪强度出现先增大后减小的变化趋势。
在应力平面上以剪应力τ=(σ1-σ3)/2为纵轴,正应力σ=(σ1+σ3)/2为横轴,绘制不同煤渣掺量下改良土试样的摩尔应力圆,根据改良土的抗剪强度包络线可以得出黏聚力及内摩擦角的大小,图4为煤渣掺量及冻融循环对改良土黏聚力及内摩擦角的影响。

图4 改良土的黏聚力与内摩擦角
Fig.4 Cohesion and internal friction angle of improved soil
通过图4可知,随着煤渣掺量的增加改良土的黏聚力出现先增大后减小的变化趋势。当煤渣掺量为15%时,黏聚力达到最大为276.3 kPa。内摩擦角随煤渣掺量的增加略有增加,但增加幅度不大。这是因为随着煤渣掺量的增加,水化反应产生的胶结物的量逐渐增加,使得土颗粒之间的结合更为紧密,出现黏聚力增大的现象。由于水泥的用量一定,随着煤渣的继续增加反应产生的胶结物已经不能继续增加,过多的煤渣反而会减弱土颗粒之间的联系,造成黏聚力的降低。煤渣的加入在一定程度上改善了风积砂的级配,使土颗粒之间的咬合能力增强,出现内摩擦角略有增大的现象。
随着冻融循环次数的增加改良土的黏聚力有较大程度衰减。前5次冻融循环的影响最为明显,最大可造成124.7 kPa的黏聚力衰减。冻融循环对内摩擦角的影响则较为有限,随冻融次数的增加内摩擦角稍有减小,但总体变化不大。这是因为改良土中的水分在冻结过程中发生体积膨胀产生冻胀力,在冻胀力的作用下,改良土内部产生细小裂隙,使得水化反应产生的胶结物发生破坏,降低了土颗粒之间的胶结及咬合作用。在融化过程中水分渗入到裂隙中,在下一次冻结过程中再次对改良土结构造成破坏。由于试样处于封闭系统之中水分得不到补充,使得这种破坏作用逐渐减弱最终趋于稳定。
土体的屈服面分为单屈服面与多屈服面两种,沈珠江双屈服面模型作为多屈服面模型的一种,由于其形式简单,模型中各参数容易确定,在工程中得到了广泛的应用[16]。沈珠江双屈服面模型的两个屈服面为
(2)
式中,p为平均主应力;q为偏应力;r,s为模型系数。
p=(σ1+σ2+σ3)/3
沈珠江模型中两个屈服面分别以塑性剪应变![]() 及塑性体应变
及塑性体应变![]() 为硬化参量,所以弹塑性应变的分离是构建屈服面的关键,由三轴CD试验可以得到试验过程中试件体积应变和轴向应变的关系(图5)。
为硬化参量,所以弹塑性应变的分离是构建屈服面的关键,由三轴CD试验可以得到试验过程中试件体积应变和轴向应变的关系(图5)。

图5 未冻融水泥改良土的体应变
Fig.5 Volumetric strain of unfrozen cement improved soil
则剪应变可以表示为
εs=ε1-εV/3
(3)
式中,ε1为轴向应变。
应变中弹性部分可以表示为
(4)
式中,G为剪切模量;K为体积模量。
通过不同围压下的三轴CD试验,可以获得q与εs的关系,进而求出剪切模量G,剪切模量与围压的关系如图6所示,可以由式(5)来进行描述。
(5)
式中,Pa为大气压强,Pa=101.33 kPa;L,n为试验参数,L=152.569,n=0.287 6。
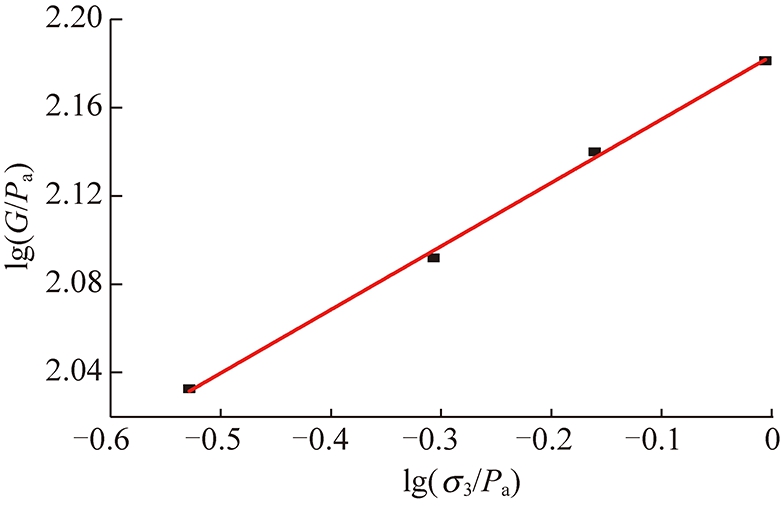
图6 剪切模量与围压的关系
Fig.6 Relationship between shear modulus and confining pressure
改良土在冻融循环的作用下会出现性质的弱化[17-18],不同的煤渣掺量使改良土表现出不同的弱化规律。综合考虑配比及冻融循环次数对改良土剪切模量的影响,可以利用式(6)来进行修正。
G′=α(ω,N)G
(6)
式中,G′为不同配比的改良土在经历N次冻融循环后的剪切模量;α(ω,N)为考虑配比及冻融的剪切模量修正系数。
α(ω,N)=0.952 2-0.070 1N+0.029 9ω+
0.003 5N2-0.000 8ω2,R2=0.907
式中,ω为煤渣掺量,%;N为冻融循环次数。
则塑性剪应变与塑性体应变为
(7)
对试验数据进行处理,将不同围压下无煤渣掺入的改良土产生塑性体应变为0.1%,0.3%,0.5%,0.7%时的数据点绘制在p-q平面上,如图7所示(图中直线CSL为改良土的临界状态线)。
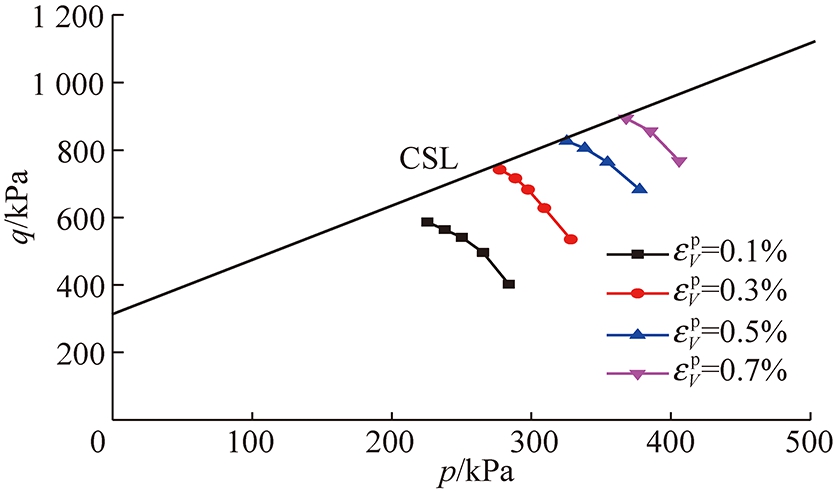
图7 水泥改良土的体应变屈服面
Fig.7 Volumetric strain yield surface of cement improved soil
通过图7可以看出,在三轴试验的过程中随着荷载的施加,改良土的屈服面逐渐扩张,改良土的塑性体应变逐渐增长,各塑性体应变相等的试验数据点所构成的屈服轨迹大致呈椭圆走势,对数据点用椭圆函数进行拟合,取沈珠江模型中参数r=3,则椭圆屈服面的表达式为:![]() 对硬化参量
对硬化参量![]() 进行拟合得:
进行拟合得:
提取塑性剪应变数据,将不同围压下无煤渣掺入的改良土产生塑性剪应变为2%,4%,6%,8%时的数据点绘制在p-q平面上,如图8所示。

图8 水泥改良土的剪应变屈服面
Fig.8 Shear strain yield surface of cement improved soil
由图8可知,随着试验的进行塑性剪应变屈服面逐渐扩张,改良土的塑性剪应变逐渐增大。各塑性剪应变相同的数据点在p-q平面上构成的屈服轨迹大致呈抛物线型,采用抛物线函数继续拟合。取沈珠江模型中参数s=2,则改良土的剪应变屈服面为:![]() 对硬化参量
对硬化参量![]() 进行拟合得:
进行拟合得:
当煤渣掺量及冻融循环次数不同时,将塑性体应变为0.3%的屈服面绘制在p-q平面上可得不同煤渣掺量及冻融循环次数的屈服面,如图9所示。

图9 煤渣掺量及冻融次数对体应变屈服面的影响
Fig.9 Effect of cinder content and freeze-thaw cycles on the yield surface of the volumetric strain
从图9(a)可以看出,在冻融循环次数相同的情况下,煤渣改良土的体积应变屈服面随着煤渣掺量的增加出现先扩张后收缩的现象,当煤渣掺量为15%时,改良土屈服面最大。试验结果表明,随着煤渣掺量的增加,改良土的物理力学性质先增强后减弱,达到相同塑性体应变的屈服面越靠外,改良土的承载能力越好,产生相同塑性体应变所需的荷载越大。为描述煤渣掺量对改良土屈服面演化的影响,引入体应变配合比影响因子ki(ω)(i=1,2,…,n),则不同煤渣掺量下改良土屈服面的演化规律可表示为:
![]()
(8)
硬化参量![]() 可表示为
可表示为
(9)
式中,k1(ω)=17 631 148+9 112.509 2ω+13 921.846 1ω2-577.751 8ω3,R2=0.976,k2(ω)=1.139 5-0.000 392ω+0.000 139ω2-0.000 005ω3,R2=0.982。
从图9(b)可以发现,当改良土煤渣掺量相同时,随着冻融循环的增加达到相同塑性体应变时屈服面所围成的面积越小,土体弹性工作范围逐渐减小。这是因为在低温环境中,改良土中的水分发生冻结发生体积膨胀,在冻胀力的作用下使得土体内部产生许多细小裂缝,对改良土的结构造成了损害,与式(6)中剪切模量的衰减相对应,从另一方面说明冻融循环对改良土的结构产生了不可恢复破坏,在相同荷载作用时提前进入塑性工作范围产生不可恢复的塑性变形,从而影响道路工程的正常使用。为描述冻融循环对改良土体应变屈服面的演化规律引入体应变冻融循环影响因子ki(N)(i=1,2,…,n),则冻融循环条件下改良土屈服面的演化可以表示为
(10)
硬化参量![]() 可以表示为
可以表示为
(11)
式中,k1(N)=14 795 786+2 835 362e-0.451 8N,R2=0.979,k2(N)=1.074 7+0.064 8e-0.925 4N,R2=0.988。
将改良土配比及冻融循环综合考虑,则某配比下改良土经N次冻融循环,体应变屈服面的演化规律为
(12)
![]()
(13)
当煤渣掺量及冻融循环次数不同时,将塑性剪应变为4%的屈服面绘制在p-q平面上可得不同煤渣掺量及冻融循环次数的屈服面,如图10所示。

图10 煤渣掺量及冻融次数对剪应变屈服面演化的影响
Fig.10 Effect of cinder content and freeze-thaw cycles on the yield surface of the shear strain
由图10(a)可知,当冻融循环次数相同的情况下,改良土的剪应变屈服面随着煤渣掺量的增加出现先上升后下降的变化趋势,当煤渣掺量为15%时可以获得最大的剪应变屈服面,当煤渣掺量超过15%,剪应变屈服面开始降低,达到相同塑性剪应变时所能承受的荷载减小,屈服面的演化规律与改良土强度的变化基本一致。引入改良土剪应变配合比影响因子si(ω)(i=1,2,…,n),则剪应变屈服面可表示为
(14)
硬化参量![]() 为
为
(15)
式中,s1(ω)=161.639 5-0.126 6ω+0.133 9ω2-0.005 5ω3,R2=0.998;s2(ω)=968.120 7-4.913 2ω+2.890 0ω2-0.115 4ω3,R2=0.995。
通过图10(b)可以看出,改良土的剪切屈服面随着冻融循环次数的增加而逐渐向原点靠近,前5次冻融循环使得屈服面由较大程度的收缩,之后冻融循环的影响逐渐减弱,表现出达到相同塑性剪应变时改良土的承载能力随冻融次数的增加而逐渐减弱,说明冻融循环对改良土结构造成了损伤。引入剪应变冻融循环影响因子si(N)(i=1,2,…,n),则剪应变屈服面可表示为
(16)
硬化参量![]() 为
为
(17)
式中,s1(N)=149.447 7+12.191 8e-0.443 2N,R2=0.989;s2(N)=779.396 8+188.723 9e-0.477 1N,R2=0.991。
综合考虑配合比和冻融循环对改良土塑性剪切应变屈服面演化的影响,则剪切屈服面为
(18)
![]()
(19)
根据弹塑性理论,改良土的总应变增量dε可以表示为弹性应变与塑性应变之和的形式,即:
(20)
式中,dεe为弹性应变增量;dεp为塑性应变增量。
采用相关联的流动法则[19],塑性应变增量可表达为
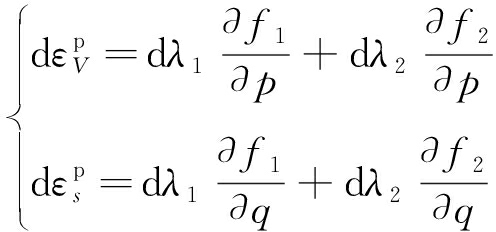
(21)
式中,dλ1,dλ2为塑性因子。
根据一致性条件有:

(22)
由式(21)和式(22)可得
(23)
式中,
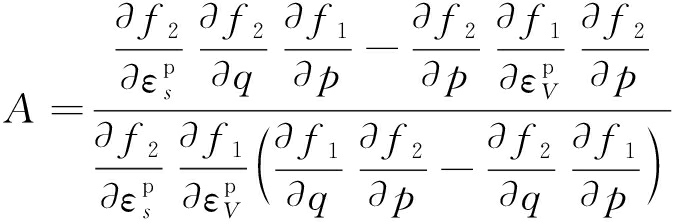


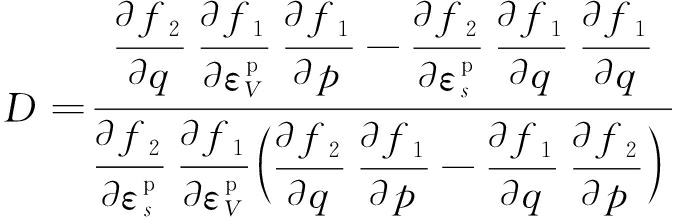
则剪应变与体应变增量可表示为
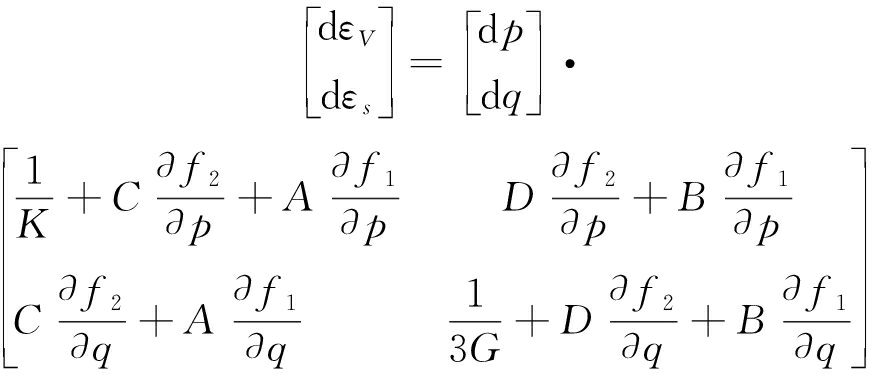
(24)
利用MATLAB数值计算软件对应力应变关系进行求解,图11为不同试验条件下应力应变关系计算值与试验值的对比。可见计算结果与实测结果较为接近,具有较高的精度。可以较好的反映出煤渣改良土在经历不同冻融循环次数有的应力应变关系,为季冻区工程建设提供参考。

图11 改良土应力-应变关系试验值与计算值的对比
Fig.11 Comparison of test value and calculated value of improved soil stress-strain relation
(1)煤渣改良土的强度随着煤渣掺量的增加出现先增大后减小的变化趋势,当煤渣掺量为15%时,可获得最大的抗剪强度。改良土随冻融循环次数的增加强度逐渐衰减,前5次冻融循环对改良土强度的影响较大,最大可造成32.5%的强度衰减。当冻融循环次数超过5次后,其对强度的影响逐渐趋于稳定。
(2)随着煤渣掺量的增加,改良土的剪应变屈服面和体应变屈服面都出现先扩张后收缩的变化趋势,当煤渣掺量为15%时可以获得最大的屈服面,是改良土获得最优的物理力学性能。
(3)随着冻融循环次数的增加,改良土的剪应变屈服和体应变屈服面都呈现出逐渐收缩、逐渐向原点靠近的趋势,前5次冻融循环对改良土造成较大程度的影响。屈服面的演化从另一个方面说明了冻融循环对土体结构的破坏作用。
(4)通过引入配合比影响因子和冻融循环影响因子可以较好的反映出不同配合比的改良土在冻融循环作用下屈服面的演化过程,具有一定的精度,可以为季冻区工程建设提供参考。
(5)根据屈服面演化所建立的双屈服面本构关系可以较好的反映出煤渣改良土在经历不同冻融循环次数有的应力应变关系,具有较高的精度,可为季冻区工程建设提供参考。
参考文献
[1] 王红鑫,周承京,陈群.煤渣掺量对灰渣混合料力学性质的影响[J].水电能源科学,2015,33(9):113-116.
WANG Hongxin,ZHOU Chengjing,CHEN Qun.Impact of coal cinder content on mechanical properties of ash residue mixture[J].Water Resources and Power,2015,33(9):113-116.
[2] HALDUN Kurama,MINE Kaya.Usage of coal combustion bottom ash in concrete mixture[J].Construction and Building Materials,2008(22):1922-1928.
[3] 刘栋,李立寒,崔华杰.水泥稳定炉渣碎石的强度性能[J].建筑材料学报,2014,17(3):538-542.
LIU Dong,LI Lihan,CUI Huajie.Strength performance of cement stabilized aggregate containing bottom ash aggregate(BAA)[J].Journal of Buliding Material,2014,17(3):538-542.
[4] 刘栋,李立寒,崔华杰.水泥稳定炉渣碎石基层路用性能[J].同济大学学报(自然科学版),2015,43(3):405-409,415.
LIU Dong,LI Lihan,CUI Huajie.Pavement performance of cement stabilized municipal solid waste incineration bottom ash aggregate and crushed stones[J].Journal of Tongji University (Natural Science),2015,43(3):405-409,415.
[5] 张互助,程培峰,邵洪杰,等.水泥煤渣稳定煤矸石基层材料温缩性能的试验研究[J].公路交通科技,2007,24(11):29-32.
ZHANG Huzhu,CHENG Peifeng,SHAO Hongjie,et al.Test research on temperature shrinkage performance of cement and cinder stabilized coal gangue base course materials[J].Journal of Highway and Transportation Research and Development,2007,24(11):29-32.
[6] PECQUEUR G,CRIGNON C,QUÉNÉE B.Behaviour of cement-treated MSWI bottom ash[J].Waste Management,2001,21(3):229-233.
[7] MÜLLER U,RÜBNER K.The microstructure of concrete made with municipal waste incinerator bottom ash as an aggregate component[J].Cement and Concrete Research,2006,36(8):1434-1443.
[8] 常丹,刘建坤,李旭,等.冻融循环对青藏粉砂土力学性质影响的试验研究[J].岩石力学与工程学报,2014,33(7):1496-1502.
CHANG Dan,LIU Jiankun,LI Xu,et al.Experiment study of effects of freezing-thawing cycles on mechanical properties of Qinghat-Tibet silty sand[J].Chinese Journal of Rock Mechanics and Engineering,2014,33(7):1496-1502.
[9] 常丹,刘建坤,李旭.冻融循环下青藏粉砂土双屈服面本构模型研究[J].岩石力学与工程学报,2016,35(3):623-630.
CHANG Dan,LIU Jiankun,LI Xu.A constitutive model with double yielding surfaces for silty sand after freeze-thaw cycles[J].Chinese Journal of Rock Mechanics and Engineering,2016,35(3):623-630.
[10] 常丹,刘建坤,李旭.冻融循环下粉砂土屈服及强度特性的试验研究[J].岩石力学与工程学报,2015,34(8):1721-1728.
CHANG Dan,LIU Jiankun,LI Xu.Experimental study on yielding and strength properties of silty sand under freezing-thawing cycles[J].Chinese Journal of Rock Mechanics and Engineering,2015,34(8):1721-1728.
[11] 刘建坤,于钱米,刘景宇等.细粒土不均匀分布对粗粒土力学特性的影响[J].岩土工程学报,2017,39(3):562-572.
LIU Jiankun,YU Qianmi,LIU Jingyu,et al.Influence of non-uniform distribution of fine soil on mechanical properties of coarse-grained soil[J].Chinese Journal of Geotechnical Engineering,2017,39(3):562-572.
[12] 邓国华,邵生俊,佘芳涛.结构性黄土的修正剑桥模型[J].岩土工程学报,2012,34(5):834-841.
DENG Guohua,SHAO Shengjun,SHE Fangtao.Modified Cam-clay model of structured loess[J].Chinese Journal of Geotechnical Engineering,2012,34(5):834-841.
[13] 李顺群,张建伟,夏锦红.原状土的剑桥模型和修正剑桥模型[J].岩土力学,2015,36(S2):215-310.
LI Shunqun,ZHANG Jianwei,XIA Jinhong.An improvement on Cam-clay model and modified Cam-clay model for intact soil[J].Rock and Soil Mechanics,2015,36(S2):215-310.
[14] 张坤勇,文德宝,马奇豪.椭圆抛物双屈服面弹塑性模型三维各向异性修正及其试验验证[J].岩石力学与工程学报,2013,32(8):1692-1700.
ZHANG Kunyong,WEN Debao,MA Qihao.Three-dimensional anisotropic revision and experimental verifcation of elliptic parabolic double yield surface elastoplastic model[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(8):1692-1700.
[15] 罗刚,张建民.邓肯-张模型和沈珠江双屈服面模型的改进[J].岩土力学,2004,25(6):887-890.
LUO Gang,ZHANG Jianmin.Improvement of Duncan-Chang nonlinear modeland Shen Zhujiang’s elastoplastic model for granular soils[J].Rock and Soil Mechanics,2004,25(6):887-890.
[16] 屈智炯,刘恩龙.土的塑性力学(第二版)[M].北京:科学出版社,2011.
[17] 张英,邴慧.基于压汞法的冻融循环对土体孔隙特征影响的试验研究[J].冰川冻土,2015,37(1):169-174.
ZHANG Ying,BING Hui.Experimental study of the effect of freezing-thawing cycles on porosity characters of silty clay by using mercury intrusionporosimetry[J].Journal of Glaciology and Geocryology,2015,37(1):169-174.
[18] 王静,吕翔,张云龙,等.季冻区路基土静动模量关系研究[J].公路交通科技,2016,33(9):25-30.
WANG Jing,LÜ Xiang,ZHANG Yunlong,et al.Study on relationship static and dynamic moduli of subgrade soil in seasonal frozen area[J].Journal of Highway and Transportation Research and Development,2016,33(9):25-30.
[19] 钱家欢,殷宗泽.土工原理与计算(第二版)[M].北京:中国水利水电出版社,1996.