
成景旺1,常锁亮2,张友源1
(1.长江大学 地球物理与石油资源学院,湖北 武汉 430100; 2.太原理工大学 矿业工程学院,山西 太原 030024)
摘 要:时间域全波形反演采用全频带地震数据时容易陷入局部极值,通过滤波器对地震数据分频段开展时间域的多尺度反演研究。从一阶导数的高阶交错网格有限差分格式出发,给出了不同差分阶数下不同频段反演时可取的空间步长;采用巴特沃斯自相关滤波器将地震数据滤波成一系列不同频段的地震数据,从低频到高频依次反演,上一个低频段反演的结果作为下一个高频段反演的初始模型。考虑到不同频段反演时采用的空间步长不是简单的倍数关系,通过引入三次卷积插值技术来实现不同频段之间的插值。理论模型试算证明:在不同的反演频带下分别选择合适的空间步长,同时相应改变时间步长,能最大程度减少反演所需时间;三次卷积插值技术可实现粗网格大小与细网格大小为任意倍数的插值,基于三次卷积插值法反演可得到与常规统一网格步长反演法精度相当的结果。
关键词:三次卷积插值;时间域;多尺度;全波形反演

移动阅读
成景旺,常锁亮,张友源.基于三次卷积插值的时间域多尺度全波形反演[J].煤炭学报,2018,43(12):3480-3487.doi:10.13225/j.cnki.jccs.2018.0310
CHENG Jingwang,CHANG Suoliang,ZHANG Youyuan.Multiscale time domain full waveform inversion based on cubic convolution interpolation[J].Journal of China Coal Society,2018,43(12):3480-3487.doi:10.13225/j.cnki.jccs.2018.0310
中图分类号:P631
文献标志码:A
文章编号:0253-9993(2018)12-3480-08
收稿日期:2018-03-08
修回日期:2018-06-18
责任编辑:韩晋平
基金项目:国家自然科学基金青年科学基金资助项目(41504102);湖北省“地球内部多尺度成像”重点实验室开放基金资助项目(SMLL-2015-08);长江大学长江青年基金资助项目(2015cqn32)
作者简介:成景旺(1987—),男,山西吕梁人,讲师,博士。E-mail:chjw2008@126.com
CHENG Jingwang1,CHANG Suoliang2,ZHANG Youyuan1
(1.Geophysics and Oil Resource Institute,Yangtze University,Wuhan 430100,China; 2.College of Mining Engineering,Taiyuan University of Technology,Taiyuan 030024,China)
Abstract:The time domain full waveform inversion using the full band data is usually unsuccessful because the misfit error is easily trapped into local minima value.This problem can be solved with filter technique to realize the time domain multiscale inversion.Starting from the high-order staggered grid finite difference scheme,the space step corresponding to different frequency bands at different difference orders is given.The seismic data is filtered into different frequency-bands by the Butterworth autocorrelation filter to realize multiscale inversion.In the inversion,the low-frequency inversion result is used as the starting model in the high-frequency inversion.Considering that the spatial step of different frequency bands is not a simple multiple relation,the interpolation between different frequency-bands is realized by using the cubic convolution interpolation.The test of theoretical model proves that it can reduce the time required for the inversion,when the appropriate space step in different inversion bands is selected and the time step is changed correspondingly.The cubic convolution interpolation technique can realize the interpolation with discretionary ratio between coarse mesh and fine mesh.This method can not only realize the multi-scale inversion quickly,but also can get the same accuracy inversion result as the tra-ditional fixed-spatial-step method.
Key words:cubic convolution interpolation;time-domain;multiscale;full waveform inversion
地震勘探技术目前被广泛应用于煤矿开采研究中[1],地层速度是其主要研究参数之一。全波形反演利用了地震数据的所有信息(振幅、相位和走时等),已被证明是一种建立高精度速度模型的有效方法[2]。按实现方法分类,主要有时间域、频率域和Laplace域等[3]。全波形反演最早在时间域中实现,TARANTOLA[4]利用伴随状态法求取反演梯度实现了二维时间域全波形反演;随后,PRATT[5]将全波形反演理论推广到频率域,形成频率域全波形反演;SHIN[6]针对地震数据带宽有限、初始模型获取困难等问题,利用阻尼波场零频分量反演低频模型作为频率域波形反演的初始模型,即Laplace域全波形反演。其中,频率域全波形反演由于固有的多尺度特征,其相关理论研究和实际应用得到快速发展[7-11]。然而,频率域反演最大的问题为大型稀疏方程组的求解及巨大的内存需求,国内外学者大多借用MUMPS(MUltifrontal Massively Parallel sparse direct Solver)线性方程组求解软件包进行求解[12-13]。但当模型较大尤其为三维模型时,一般的计算机集群难以满足频率域正演所需的内存,故近年来时间域全波形反演得到了快速发展[14-16]。时间域全波形反演是全频带反演,反演容易陷入局部极值导致反演失败。该问题可通过两种方法解决:时间域正演联合频率域反演的混合域全波形反演[16]和基于滤波器处理的多尺度反演。BUNKS[17]最早利用汉明窗低通滤波器将观测数据和地震子波分解成不同频段的数据,实现了由低频带到高频带的多尺度反演,不同频带之间的模型采用简单方法进行插值,插值过程中相邻反演频带对应的网格步长需满足两倍关系,该方法明显不能满足大多数实际情况。随后,BOONYASIRIWAT[18]选择了滤波效果更好的低通维纳滤波器,同时根据SIGURE[19]提出的频率域全波形反演的频率选择策略,给出了相应的频率选择策略,但无论是低频段反演还是高频段反演,均采用固定的空间网格大小,导致计算时间较长。
根据交错网格有限差分的离散性分析可知,有限差分阶数一定时,单位波长内含有一定的网格点数便可得到较高的模拟精度。因此在低频段反演时可采用较大网格,同时根据稳定性条件时间步长也可适当增加。从低频到高频依次反演时,相应的减小空间网格步长和时间步长,既可实现多尺度反演,又可减少计算量,快速提高反演效率。
笔者首先对交错网格有限差分的精度进行分析,给出不同情况下正演网格大小的选择策略;采用巴特沃斯自相关滤波进行多尺度反演,根据频率选择策略给出不同反演频段的各个截止频率值,并结合该频段的最大频率,选择合适的空间网格大小和时间步长,通过理论模型数据进行的时间域多尺度全波形反演,验证本文方法的正确性和可行性。
全波形反演是一个非线性问题。非线性问题的最优化求解,需要通过多次迭代逐步逼近目标函数的全局极小值。目标函数为正演模拟数据与实际数据残差的L2范数,正演模拟的精度直接影响全波形反演的结果。因此,基于滤波器的时间域多尺度全波形反演的主要研究内容包括正演模拟、不同频段模型的插值和最优化反演3个方面。
基于波动方程的正演模拟是全波形反演的基础。空间网格间距是影响正演模拟精度和正演效率的关键因素,可通过对空间一阶导数的误差分析来选择合适的空间步长。交错网格有限差分法被广泛应用于波动方程正演模拟中[20]。根据交错网格有限差分格式,在x=0处2N阶精度一阶导数可近似为
(1)
式中,cn为交错网格有限差分系数。
对式(1)进行傅里叶变换,并将等式两边相减得到近似误差[21]:
(2)
其中,kx为圆波数;Δx为空间步长;波长λ=1/kx。令G为单位波长内的网格点数,则1/G=Δx/λ=kxΔx。表1给出了近似误差error≤0.1%时,不同差分阶数下单位波长内大约需要的网格点数。
表1 不同阶数下单位步长内所需网格点数
Table 1 Grid points required in a step for different orders

为了减少数值频散,保证正演模拟的精度,不同阶数下的离散网格步长应满足如下条件:
(3)
式中,vmin为介质最小传播速度;fmax为震源子波最大频率。
低频段反演采用粗网格,高频段反演采用细网格,低频段的反演结果需经过插值才能作为下一高频段反演的初始模型。由式(3)可知,粗网格与细网格大小非倍数关系,BUNKS[17]的插值方式不再适用,需采用其他的插值方式。目前常用的插值方法有最邻近插值法、双线性插值法及三次卷积插值法等[22]。其中三次卷积插值法考虑了周围16个点对插值点的影响,插值精度最高。
图1为三次卷积插值法示意,(i+u,j+v)表示需要进行插值的插值点,i和j代表已知的规格网格点的坐标。根据连续信号采样定理可知,若对等间隔离
散采样值用归一化插值内核函数s(x)=sin(πx)/(πx)进行插值时,则可以准确地恢复原函数,即可准确得到采样点间任意点的值。三次卷积插值法实质上利用一个三次多项式来近似理论最佳插值内核函数。

图1 三次卷积插值示意
Fig.1 Sketch map of Cubic convolution interpolation
插值点(i+u,j+v)处的值可以表示为
(4)
式中,

x=[Δx3 Δx2 Δx 1]T,z=[Δz3 Δz2 Δz 1]

式(4)中c为3次多项式的系数,即在三次卷积插值过程中,需根据插值点与已知规则点的距离,使用不同的权系数。Δx和Δz分别为已知规则网格的横向和纵向网格间距。
以网格间距为10 m的Marmousi模型为例,将该模型首先抽稀成网格间距为30 m的模型。对抽稀后的模型分别用最邻近插值法、双线性插值法和三次卷积插值法,依次进行插值成网格间距为10 m的模型,如图2所示。其中最邻近插值法插值后的模型边缘产生锯齿效应且误差值较大;双线性插值法误差虽然比最邻近插值小,但相对来说依然较大;三次卷积插值法计算精度高,能够较好的保持图像的细微结构,且误差最小。
全波形反演是一个全局最优化问题,笔者采用预条件共轭梯度迭代法进行求解,其模型参数迭代公式可表示为
mn+1=mn-αnPn mE(mn)
mE(mn)
(5)
其中,m为模型空间;Pn为第n次迭代的梯度预处理算子;αn为第n次迭代的步长; mE(mn)表示目标函数对模型参数的梯度。由式(5)可知,全波形反演主要解决问题:迭代步长、预条件算子以及反演梯度。其中迭代步长求取采用抛物线曲线拟合法[23],预条件算子通过地震正传波场与残差反传波场的能量来构造[24],梯度主要采用伴随状态法求取。由于采用一阶应力-速度声波波动方程进行正演模拟,故目标函数关于纵波速度的反演梯度[25-26]可表示为
mE(mn)表示目标函数对模型参数的梯度。由式(5)可知,全波形反演主要解决问题:迭代步长、预条件算子以及反演梯度。其中迭代步长求取采用抛物线曲线拟合法[23],预条件算子通过地震正传波场与残差反传波场的能量来构造[24],梯度主要采用伴随状态法求取。由于采用一阶应力-速度声波波动方程进行正演模拟,故目标函数关于纵波速度的反演梯度[25-26]可表示为
(6)
式中,P表示的是声压;![]() 为拉梅参数;ρ为密度;vp为纵波速度。
为拉梅参数;ρ为密度;vp为纵波速度。
从低频到高频依次进行反演,滤波器的高截频率应按照一定的策略来选择。为了保证地震信号垂直

图2 3种插值方法的插值误差
Fig.2 Interpolation error of three interpolation methods
覆盖充分,反演选择的两个相邻频率应满足[18]:
fn+1=fn/αmin
(7)
这样能保证当前频率的最大波数刚好是下一个频率的最小波数(图3),其中αmin为入射波在目的层反射角的余弦最小值。假设反演目的层深度为z,观测系统最大半偏移距为h,则αmin=1/[1+(h/z)2]1/2。
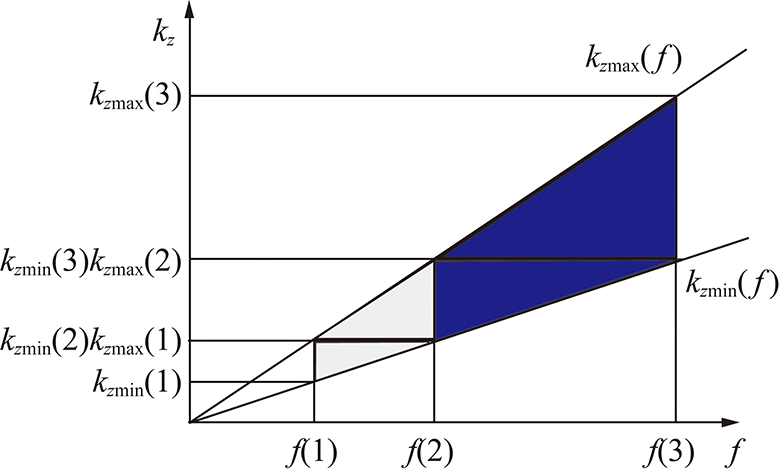
图3 频率选择策略示意
Fig.3 Sketch map of Cubic convolution interpolation
笔者利用该频率选择准则逐渐改变巴特沃斯自相关滤波器的截止频率。给定初始截止频率f1,根据观测系统计算αmin,根据式(7)依次计算f2,f3,f4,……。每一个频带反演结果作为下一个频带反演的初始模型,逐步实现从低频到高频的反演,每一次更换高频截止频率意味着反演中多加入了不同颜色区域表示的地震信号。
为验证本文方法的正确性,采用Marmousi模型进行试算,该模型纵向3 000 m,横向9 000 m,网格间距为10 m×10 m,网格点数为300×900,如图4(a)所示。首先采用空间网格大小为10 m的模型进行正演模拟得到炮集记录,并将此作为全波形反演的观测数据。正演过程中模型四周均加上一定的网格点来用于边界条件的实施。震源采用20 Hz雷克子波,震源选择在地表激发(z=0,实际地表上面增加了相应的边界网格点),一共激发19炮,炮间距为450 m,第1炮位于300 m处,最后一炮位于8 400处,炮集记录时间为3.6 s,时间采样间隔为0.6 ms。所有炮的检波器均匀的固定在地表,一共有899道接收。第1道位于10 m处,最后一道位于8 990 m处。计算过程采用并行计算,基于区域分解将模型分解为多个进程同时进行正演和反演[27],本次数值测试采用10个进程并行计算。
正演模拟采用6阶有限差分精度,根据表1可知,一个步长至少需要6个网格点。Marmousi模型纵波最小速度1 500 m/s,最大速度为5 750 m/s,故空间网格步长选择应满足:
(8)
根据交错网格有限差分稳定性条件,对应时间步长应满足:

图4 基于三次卷积插值法的多尺度反演结果
Fig.4 Multi-scale inversion result based on cubic convolution interpolation method

(9)
式中,vmax为正演模型的最大传播速度;L代表2L阶有限差分精度(此处2L=6);al为对应的差分系数。
取初始截止频率为5 Hz,根据频率选择策略计算出反演高截频率依次为f1=5 Hz,f2=9 Hz,f3=16.36 Hz和f4=29.2 Hz。由于每个频带滤波后,大于高截频的频率成分并没有完全滤波掉,依然存在一部分高频。因此当高截止频率小于主频时,式(8)中最大频率计算方法为fmax=1.5fn(n=1,2,3,4)。当截止频率大于主频时,式(8)中最大频率采用fmax=fn(n=1,2,3,4)计算得到。最终该模型对应的多尺度反演参数见表2,其中实际反演空间步长和时间步长根据具体情况适当修改。
首先进行高截频带为5 Hz的反演。在反演前,将观测数据进行抽样,根据该频带下对应的空间步长和时间步长,空间上每3道进行抽样,时间上每5点进行抽样(在满足稳定性条件前提下,采用整数倍抽样),抽样后每一炮共有296道,第1道位于30 m,最后一道位于8 880 m。反演初始模型首先将10 m网
表2 多尺度反演参数
Table 2 Multiscale inversion parameters

格大小的Marmousi模型抽样成网格大小为30 m的模型,然后进行高斯光滑得到(图4(b))。5 Hz高截频带反演结束后,将反演结果(图4(c))采用三次卷积插值方法进行插值,得到网格大小为15 m的新模型(图4(d))作为高截频带9 Hz的初始模型;同样,在反演之前,需要对观测数据进行抽样。此时网格大小与理论模型不是倍数关系,为了反演数据的匹配,空间上仍然采用每3道进行抽样(每炮道数跟上一个反演频带一样),时间上每两点进行抽样。9 Hz高截频带反演结束后,将反演得到的速度模型(图4(e))进行三次卷积插值,得到16.36 Hz反演的初始模型(图4(f))。最后两个反演频段不需要进行任何抽样,直接进行反演,反演结果如图4(g),(h)所示。从反演结果可以看出:从低频段反演到高频段反演,反演得到的速度模型分辨率越来越高。低频带反演只能得到模型的大尺度结构,高频带反演则反映了模型的细节部分。低频带的反演结果为下一高频段反演提供了较好的初始模型。
为进一步说明本文方法的有效性,对同样的Marmousi模型做另外两个反演试算。一是固定空间网格大小的常规多尺度全波形反演,即从低频带到高频带的反演空间步长均取10 m,时间步长均取0.6 ms;另外一个是采用最邻近插值法进行多尺度反演,反演参数与三次卷积插值多尺度反演相同。两个试算采用的初始模型均与上述实验相同,每个频带反演的结果当作下一个反演频带的初始模型。
图5为3种反演结果与真实模型的误差。可以看出,由于最大偏移距有限,反映模型两侧有关的地震信息较少,且反演方法本身的问题导致模型两侧和底部误差较大。3种方法的反演结果中浅层部分的误差值接近于0。三次卷积插值反演法的反演误差与常规固定空间步长法相似,而最邻近插值反演法的浅层部分误差较大,具有不连续性,有明显的锯齿效应。图6和7(局部放大)为横向位置750,1 500以及2 000 m处的纵剖面反演速度对比图,可得到与图5相同的结论。

图5 反演结果与真实模型误差
Fig.5 Errors between inversion results and real model

图6 不同横向位置处的反演速度曲线
Fig.6 Inversion velocity curve at different positions

图7 图6局部放大
Fig.7 Detail with enlarged scale of Fig.6
表3给出了3种反演方法不同频带的反演次数和反演所用时间。可以看出:在5 Hz高截频和9 Hz高截频反演时,由于网格点少,计算较快,与后面的16.36 Hz和29.2 Hz高截频反演相比较,所用时间明显减少。两种基于插值法的全波形反演所用时间大致相同,均明显少于常规固定空间步长所用时间。从不同高截频带反演所用时间可以看出:反演所减少的时间主要体现在低频带反演时间的减少,也说明了插值法能有效提高多尺度反演效率。
表3 不同反演法的反演时间对比
Table 3 Inversion times of different inversion methods

(1)通过对一阶空间导数的交错网格有限差分公式分析,给出了不同差分阶数、不同滤波频率下合适的空间网格步长,为基于滤波器处理的时间域多尺度反演提供理论基础。
(2)三次卷积插值法计算精度高,误差低,可实现粗网格大小与细网格大小呈任意倍数的插值,能适用于多尺度反演中不同频段模型之间的插值。
(3)低频段反演采用较大网格步长,高频段采用较小网格步长,同时相应改变时间步长。以低频段反演模型经过三次卷积插值,作为下一步高频段反演的初始模型,能显著减少计算量,提高反演效率,并能得到与常规统一网格反演法精度相当的反演结果。
参考文献
[1] DU Wenfeng,PENG Suping,ZHU Guowei,et al.Time-lapse geophysical technology-based study on overburden strata changes induced by modern coal mining[J].International Journal of Coal Science & Technology,2014,1(2):184-191.
[2] 杨勤勇,胡光辉,王立歆.全波形反演研究现状及发展趋势[J].石油物探,2014,53(1):77-82.
YANG Qinyong,HU Guanghui,WANG Lixin.Research status and development trend of full waveform inversion[J].Geophysical Prospecting for Petroleum,2014,53(1):77-82.
[3] VIRIEUX J,OPERTO S.An overview of full-waveform inversion in exploration geophysics[J].Geophysics,2009,74(6):WCC1-WCC26.
[4] TARANTOLA A.Inversion of seismic reflection data in the acoustic approximation[J].Geophysics,1984,9(8):1259-1266.
[5] PRATT R G.Seismic waveform inversion in the frequency domain,Part 1:Theory and verification in a physical scale model[J].Geophysics,1999,64(3):888-901.
[6] SHIN C,CHA Y H.Waveform inversion in the Laplace domain[J].Geophysics,2008,173(3):922-931.
[7] 成景旺,吕晓春,顾汉明,等.基于柯西分布的频率域全波形反演[J].石油地球物理勘探,2014,49(5):940-945.
CHENG Jingwang,LÜ Xiaochun,GU Hanming,et al.Full waveform inversion with Cauchy distribution in the frequency domain[J].Oil Geophysical Prospecting,2014,49(5):940-945.
[8] 张广智,孙昌路,盘新朋,等.快速共轭梯度法频率域全波形反演[J].石油地球物理勘探,2016,51(4):730-737.
ZHANG Guangzhi,SUN Changlu,PAN Xinpeng,et al.Acoustic full waveform inversion with Cauchy in the frequency domain based on fast conjugate gradient method[J].Oil Geophysical Prospecting,2016,51(4):730-737.
[9] HAN M,HAN L G,LIU C C,et al.Frequency-domain auto-adapting full waveform inversion with blended source and frequency-group encoding[J].Applied Geophysics,2013,10(1):41-52.
[10] 曹书红,陈景波.频率域全波形反演中关于复频率的研究[J].地球物理学报,2014,57(7):2302-2313.
CAO Shuhong,CHEN Jingbo.Studies on complex frequencies in frequency domain full waveform inversion[J].Chinese J.Geophys.,2014,57(7):2302-2313.
[11] 高凤霞,刘财,冯暄,等.几种优化方法在频率域全波形反演中的应用效果及对比分析研究[J].地球物理学进展,2013,28(4):2060-2068.
GAO Fengxia,LIU Cai,FENG Xuan,et al.Comparisons and analyses of several optimization methods in the application of frequency-domain full waveform inversion[J].Process in Geophys.,2013,28(4):2060-2068.
[12] BEN-HADJ-ALI H,OPERTO S,VIRIEUX J.Velocity model building by 3D frequency-domain,full-waveform inversion of wide-aperture seismic data[J].Geophysics,2008,73(5):VE101-VE117.
[13] 李媛媛,李振春,张凯,等.基于双级并行的弹性波频率域全波形多尺度反演方法[J].应用地球物理,2015,12(4):545-554.
LI Yuanyuan,LI Zhenchun,ZHANG Kai,et al.Frequency-domain elastic full-waveform multiscale inversion method based on dual-level parallelism[J].Applied Geophysics,2015,12(4):545-554.
[14] 苗永康.基于L-BFGS算法的时间域全波形反演[J].石油地球物理勘探,2015,50(3):469-474.
MIAO Yongkang.Full waveform inversion in time domain based on limited-memory BFGS algorithm[J].Oil Geophysical Prospecting,2015,50(3):469-474.
[15] 白璐,韩立国,张盼,等.最小平方滤波时间域全波形反演[J].石油地球物理勘探,2016,51(4):721-729.
BAI Lu,HAN Liguo,ZHANG Pan,et al.Time-domain full waveform inversion based on least square filter[J].Oil Geophysical Prospecting,2016,51(4):721-729.
[16] SIGURE L,ETGEN J T,ALBERTIN U.3D frequency-domain wav-eform inversion using time-domain finite-difference methods[A].70th EAGE Conference & Exhibition[C].Rome,2008,F022.
[17] BUNKS C,SCALECK F M,ZALESKI S,et al.Multiscale seismic waveform inversion[J].Geophysics,1995,60(5):1457-1473.
[18] BOONYASIRIWAT C,VAUL V,ROUTH P,et al.An efficient multiscale method for time-domain waveform tomography[J].Geophysics,2009,74(6):WCC59-WCC68.
[19] SIGURE L,PRATT R.Efficient waveform inversion and imaging:A strategy for selecting temporal frequencies[J].Geophysics,2004,69(1):231-248.
[20] 董良国,马在田,曹景忠,等.一阶弹性波方程交错网格有限差分解法[J].地球物理学报,2000,43(3):411-418.
DONG Liangguo,MA Zaitian,CAO Jingzhong,et al.A staggered-grid high-order difference method of one-order elastic wave equation[J].Chinese J.Geophys.,2000,43(3):411-418.
[21] CHU C,STOFFA P L.Determination of finite-difference weights using scaled binomial windows[J].Geophysics,2012,77(3):W17-W26.
[22] 韩复兴,孙建国,杨昊.基于二维三次卷积插值算法的波前扩散构建射线追踪[J].吉林大学学报(地球科学版),2008,38(2):336-346.
HAN Fuxin,SUN Jianguo,YANG Hao.Ray-tracing of wavefront construction by bicubic convolution interpolation[J].Journal of Jilin University(Earth Science Edition),2008,38(2):336-346.
[23] VIGH D,STARR E,KAPOOR J.Developing Earth models with full waveform inversion[J].The Leading Edge,2009,28(4):432-435.
[24] ZHANG Z,LIN Y,HUANG L.Full-waveform inversion in the time domain with an energy-weighted gradient[A].81st SEG Annual International Meeting[C].San Antonio,2011:2772-2776.
[25] KOHN D,DENIL D,KURZMANN A,et al.On the influence of model parameterization in elastic full waveform tomography[J].Geophysics Journal International,2012,191(1):325-345.
[26] SHIPP R,SINGH S.Two-dimensional full wavefield inversion of wide-aperture marine seismic streamer data[J].Geophysics Journal International,2002,151(2):325-344.
[27] BOHLEN T.Parallel 3-D viscoelastic finite difference seismic modeling[J].Computers & Geosciences,2002,28:887-899.