冲击地压是煤矿重大灾害之一。随着开采深度的增加,初始地应力越来越大,冲击地压发生的频度及其对井下工程的破坏程度均呈上升趋势,对煤矿深部开采构成严重威胁。据不完全统计全国101处矿井发生的2 083次冲击地压事件中,发生在巷道位置的冲击地压事件为1 880次,占90.3%。可见绝大多数冲击地压事件发生在巷道,因此对巷道冲击地压进行深入研究具有特别重要的意义。
煤矿井下巷道施工前,煤岩体处于初始应力平衡状态。巷道施工过程中,围岩应力重新分布,受开挖面空间效应影响[1],掘进工作面附近煤岩体应力不能充分释放,围岩变形受到一定限制。随着掘进工作面的推进,虚拟支护力逐渐降低,围岩变形受到的限制逐渐解除。
在初始应力较小的条件下,考虑巷道围岩发生弹性变形,不会发生冲击地压。随着进入深部开采,地质条件变得复杂,初始应力加大,巷道内壁附近部分煤岩体将发生塑性变形,进入塑性变形状态。根据冲击地压失稳理论[2],当塑性区范围达到临界值时,巷道围岩变形系统处于非稳定平衡状态,遇外部扰动将失稳而发生冲击地压。
具有冲击危险性矿井,为防止冲击地压的发生,应采取有效支护手段,如支架支护、锚索支护等行之有效的措施手段,限制塑性区范围过度扩大。巷道支护产生的支护力能够在一定程度上起到限制围岩塑性区过度扩大的作用,选择合适的支护时机,限制塑性区范围过度扩大,即可达到防治冲击地压的目的。因此选择合适的支护时机成为防冲支护是否有效的关键。
为解决以上问题,首先要分析虚拟支护条件下巷道围岩的应力与变形,确定塑性区范围,得到巷道冲击地压的发生条件。如果满足冲击地压的发生条件,必须采取一定的支护措施,并选择合适的支护时机,避免或最大程度降低冲击地压危险程度。
以往有关煤矿巷道围岩变形规律研究主要借鉴公路(铁路)隧道的研究成果。吴创周[3]、曾开华[4-5]、饶平平[6]、张常光等[7-12]等分别推导了圆形隧道应力和洞壁位移解析解。其特点是基于统一强度理论[13]和非关联线性流动法则,考虑了塑性区的中间主应力效应和围岩剪胀特性的影响,文献[9]和[12]考虑了塑性区弹性模量的劣化,其不足是采用的弹-脆-塑性软化模型不能完全反映塑性区强度和变形参数的变化;范鹏贤等[14]以材料模型为主线,对圆形隧洞围岩的应力位移问题的研究成果进行了归纳总结和评述;刘夕才等[15-17]采用非相关联塑性流动法则模拟软岩的塑性扩容特性,推导了软岩巷道围岩塑性区位移理论解;张强等[18]将后继破坏岩体分为多个塑性区,给出围岩准应变软化弹塑性应力解析式,其不足在于人为划分塑性区的个数及其大小造成强度和变形参数是离散的;徐栓强等[19]利用衬砌与围岩的位移协调条件对地下圆形洞室进行了弹塑性分析,其不足是采用了塑性区体积不可压缩假设,并且没有考虑塑性区与弹性区力学参数的区别。
为建立圆形巷道冲击的发生条件,必须给出巷道围岩-支护变形系统失稳判别准则,以往一般采用能量判别准则或扰动响应判别准则。这两种判别准则本质上是一致的,但扰动响应判别准则形式简单,便于进行解析分析。基于巷道围岩-支护相互作用规律,得到不同支护条件下巷道围岩应力和变形分析规律,应用扰动响应判别准则,即可得到巷道冲击地压发生条件及其影响因素。这方面研究成果的文献报道尚不多见。潘一山等[20-23]提出了洞室岩爆发生的扰动响应判别准则,得到了发生岩爆的洞室临界塑性区深度及临界作用应力,指出岩石弹性模量和峰值后降模量之比是决定洞室稳定性的重要参数,根据稳定性动力准则,得到了采场巷道受静水压力作用下发生冲击的临界峰值应力深度和发生冲击地压的临界开采深度,给出了回采巷道冲击地压危险指标的确定方法;其不足之处在于没有考虑中间主应力效应和剪胀特性的影响;郭延华等[24]基于统一强度理论和塑性应变损伤模型,考虑中间主应力效应和剪胀特性,对高地应力下的圆形巷道进行弹塑性分析,由冲击地压扰动失稳理论建立了圆形巷道临界冲击地压解析解,但忽略了塑性区的弹性应变及塑性区强度和变形参数的变化;马念杰等[25]以均质圆形巷道为研究对象,从巷道围岩塑性破坏区的产生、发展和爆炸式的破坏力学机制入手,研究了巷道蝶形冲击地压的发生机理;成云海等[26]以华丰矿为研究对象,研究巷道沿空防冲机制,以广义库伦理论计算为依据,采用微震、地音、应力在线预警系统和钻屑法监测,最终实现了深超千米无区段煤柱开采;胡少斌等[27]从理论解释了扰动引力波在煤岩空间的传播规律,并探讨附加应力场特征规律,以数值模拟分析煤岩系统对扰动频率与振幅的响应特征及能量变化规律;刘洪涛等[28]为研究冲击地压发生机理,以耿村矿“12.22”冲击地压事故为背景进行了分析验证,得到沿巷道轴向的主应力曲线;刘烨等[29]为研究治理巷道诱发型冲击地压灾害,从力学机制方面作了具体阐述,将煤层巷道围岩二次静力与震源动应力叠加,得到叠加后产生的最大主应力与最小主应力表达式,提出了巷道诱发型冲击地压的判断方法,分析了山东某矿掘进工作面发生冲击的原因。但是其均没有考虑塑性区裂化参数的变化对巷道围岩的影响。
综上所述,目前有关巷道冲击地压的理论研究尚存在许多不足,需要对此做进一步研究。笔者基于统一强度理论和塑性软化本构模型,综合考虑开挖面空间效应、中间主应力效应、塑性区剪胀特性、塑性区强度和变形参数的变化,分析巷道围岩应力与位移分布规律,应用扰动响应判别准则,建立圆形断面巷道冲击地压发生的临界条件,分析相关因素对临界条件的影响规律。
1 基本假设与基本方程
1.1 基本假设
为获得圆形巷道冲击地压发生的临界条件,为简化求解难度(实际巷道围岩地质条件过于复杂),且不影响规律分析,做如下假设:
(1)巷道围岩视为均匀、连续的各向同性煤岩体;
(2)埋深H0≥20a, a为巷道半径。忽略体力(自重);
(3)考虑巷道掘进工作面附近的开挖面空间效应;
(4)考虑中间主应力效应,采用统一强度理论描述塑性软化特征;
(5)考虑塑性区剪胀效应及宏观强度与变形参数的劣化特性;
(6)采用扰动响应判别准则确定冲击地压发生的临界条件。
1.2 基本方程
如图1所示,以开挖面处巷道轴心为坐标原点建立柱坐标系(r,θ,x),R为塑性区半径。初始地应力为p0,作用在无穷远处。支护力pi均匀地作用在巷道内壁r=a处。支护力在不同巷道断面位置含义不同,在未开挖断面(x<0)和已开挖未支护断面(0≤x<L)为因开挖面空间效应而产生的虚拟支护力[1],在已开挖已支护断面(x>L)支护力为巷道围岩与支护达到平衡时接触面处的相互作用力,随着支护力的增加,虚拟支护力逐渐减小,直至消失。

图1 巷道冲击地压分析简化模型
Fig.1 Simplified model analysis of roadway rock burst model
考虑开挖面空间效应,位移释放系数u*(x)为巷道壁处径向位移ua(x)与无支护下最大位移uamax之比,采用E.HOEK的拟合公式
(1)
在任一断面位置x处沿轴向取单位巷道长度计算,以压应力、压应变为正,指向巷道内部的位移为正。径向应力、环向应力、轴向应力分别为σr,σθ,σz,径向应变、环向应变、轴向应变分别为εr,εθ,εz,轴向位移为u。
平衡微分方程为
(2)
几何方程为
(3)
弹性区弹性模量和泊松比分别为E,ν,本构方程为

塑性区应变εθ,εr分解为弹性应变![]() 与塑性应变
与塑性应变![]() 之和,即
之和,即
(5)
由于煤岩材料具有应变软化特性,而理想弹塑性模型与“弹-脆-塑”性模型均不能真实反映峰后应变软化特性。文献[17]指出岩石的破坏过程实际上是其宏观强度(黏聚力和内摩擦角)劣化并逐渐丧失的过程,变形参数也产生一定的衰减。文献[9]假设塑性区泊松比与弹性区泊松比相等,塑性区弹性模量Ep简化为半径相关函数形式。本文假设塑性区泊松比等于初始泊松比ν、内摩擦角等于初始内摩擦角φ,塑性区弹性模量Ep、黏聚力cp简化为半径相关函数形式,即
(6)
![]()
(7)
式中,c0为初始黏聚力;η,n,s为试验拟合参数,可通过采集同一地点煤样,采用常规三轴循环加载试验获得。
由广义虎克定律,得应变弹性分量![]() 即
即
![]()
(8)
采用线性非关联流动法则描述围岩的剪胀特性,应变塑性分量![]() 与
与![]() 间的关系为
间的关系为
(9)
式中,β为剪胀特性参数,![]() 为围岩剪胀角,一般≤内摩擦角φ。
为围岩剪胀角,一般≤内摩擦角φ。
文献[23]提出的统一强度理论考虑了中间主应力效应,令中间主应力![]() 为中间主应力系数,则统一强度理论由下式表示
为中间主应力系数,则统一强度理论由下式表示
σθ=qpσr+σcp
(10)
式中,![]() 为统一强度理论参数,反映中间主应力效应,0≤b≤1;φp为塑性区内摩擦角。
为统一强度理论参数,反映中间主应力效应,0≤b≤1;φp为塑性区内摩擦角。
2 巷道围岩应力与位移
2.1 巷道围岩只发生弹性变形的虚拟支护断面
由于开挖面空间效应的影响,在x≤xe范围的巷道围岩只发生弹性变形。由式(2)~(4)和应力边界条件σr( )
)![]() 为虚拟支护力,得应力与位移分布规律为
为虚拟支护力,得应力与位移分布规律为
(12)
在巷道周边r=a处,![]() 由式(1)得虚拟支护力
由式(1)得虚拟支护力
(13)
在r=a,x=xe处满足初始屈服条件,由式(10)~(13)得
(14)

(15)
式中,σc0为实际支护初始应力;py为巷道壁处刚好屈服时虚拟支护力![]()
2.2 巷道围岩发生弹塑性变形的虚拟支护断面
在xe≤x≤L范围的巷道围岩发生弹塑性变形。
由式(2)~(10)和应力边界条件σr( )
)![]() 及r=R处的应力与位移连续条件,得应力与位移分布规律为
及r=R处的应力与位移连续条件,得应力与位移分布规律为
弹性区(r≥R)
(16)
塑性区(a≤r≤R)

(17)
![]()
(18)
式中,
塑性区半径R由下式确定
(19)
巷道壁r=a处的位移为
![]()
(20)
由式(1),(19),(20)可确定虚拟支护力![]()
在x→ 处,
处,![]() 塑性区半径为R可由式(19)得到,无支护下最大位移uamax可由式(20)得到。
塑性区半径为R可由式(19)得到,无支护下最大位移uamax可由式(20)得到。
2.3 巷道围岩发生弹塑性变形的实际支护断面
支护起点为x=L。在x≥L的各巷道断面,在虚拟支护力![]() 与实际支护pc的共同作用下,巷道围岩发生弹塑性变形。将式(19)中的
与实际支护pc的共同作用下,巷道围岩发生弹塑性变形。将式(19)中的![]() 以
以![]() 替换,得塑性区半径R。代入式(20),得巷道壁r=a处的位移ua。
替换,得塑性区半径R。代入式(20),得巷道壁r=a处的位移ua。
假设实际支护为线弹性结构,刚度系数为Kc,则支护结构的径向位移
(21)
巷道壁r=a处的位移ua由支护起点位移uas和支护结构的径向位移uc构成,即
ua=uas+uc
(22)
由式(1)得
uas=uamaxf(L)
(23)
与虚拟支护力![]() 对应的位移由式(1)确定,进而由式(19),(20)即可得到虚拟支护力
对应的位移由式(1)确定,进而由式(19),(20)即可得到虚拟支护力![]()
3 巷道冲击地压临界条件及其影响因素
根据冲击地压发生的扰动响应判别准则dp0/dR=0,由式(19)得冲击地压发生的临界塑性区半径Rcr和临界载荷p0cr

(24)
![]()
(25)
可见,巷道发生冲击地压的临界条件与支护力pi、初始强度参数c及φ、塑性区黏聚力参数η及s有关。
为了验证结论的可靠性,采用相似模拟试验验证分析,讨论相关参数对临界条件的影响规律。
3.1 模拟试验验证
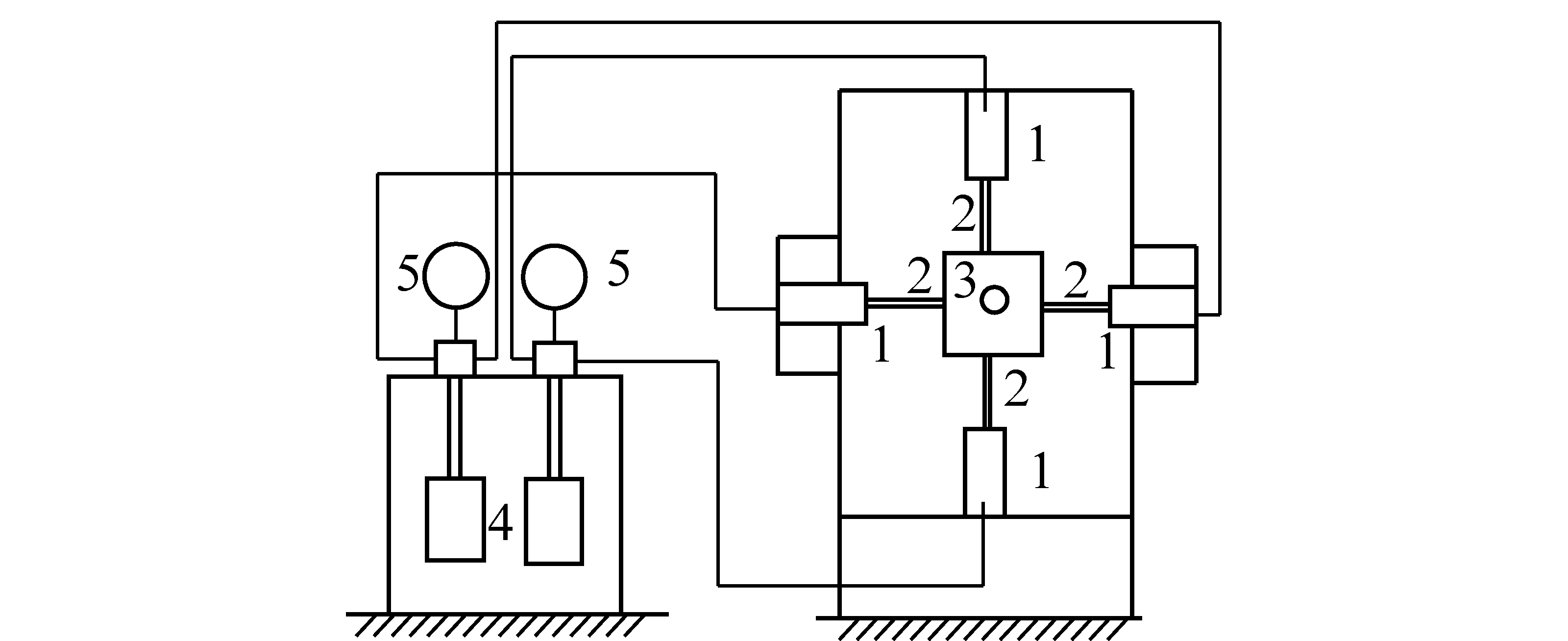
图2 巷道冲击地压模拟实验装置示意
Fig.2 Schematic diagram of experimental facility about Impact ground pressure simulation of roadway
1—油缸;2—模型加压板;3—巷道模型;4—油泵;5—油压表
依据图2试验方式进行试验[24],试验采用石膏、砂、松香材料混合进行模拟实验,按照砂∶石膏∶水∶酒精∶松香=78∶9∶8∶2∶3的比例混合,建立尺寸25 cm×25 cm×7 cm的相似模型,圆形巷道半径 5 cm。在巷道模型上下左右4个面通过油路进行等压加载,当载荷达到P=1.53 MPa时,突然发生冲击。混合材料力学参数如下:峰值强度1.41 MPa,内摩擦角30°。

图3 巷道位移载荷曲线
Fig.3 Load curve of tunnel displacement
对于本文得到的冲击地压临界条件,当初始黏聚力0.351 MPa、内摩擦角30°、b=0.1、m=1时,计算得到σc0=1.41 MPa。根据相似模拟的试验条件,制作了多组相似材料试件,在刚性试验机上进行不同围压条件下的三轴循环加载试验,获得不同围压条件下的全应力应变曲线。通过试验结果数据拟合,得到式(7)中的峰后塑性区参数,s=1.05、η=1.74时,得到冲击地压临界载荷理论值为1.528 MPa,与试验结果吻合。
3.2 支护对临界条件的影响
在其他参数不变的条件下,分别取η=1.0,1.5,2.5,得到临界塑性半径、临界载荷与支护力关系曲线,如图4所示。临界塑性半径、临界载荷均随支护力的增大而单调增加,表明加强支护是防治冲击地压的有效手段。

图4 临界塑性半径、临界载荷与支护力关系曲线
Fig.4 Relation curves of plastic critical radius,critical load and supporting force
由2.1节可知,在开挖面附近(x<xe)范围,由于虚拟支护力较大,巷道围岩只发生弹性变形,发生冲击地压概率极低。只有在距开挖面较远位置(x>xe),虚拟支护力逐渐降低,巷道围岩出现塑性区,才有发生冲击地压的可能性。如果塑性区较小,R<Rcr,也不会发生冲击地压;只有当塑性区达到一定临界值,R=Rcr,才会发生冲击地压。
3.3 初始强度参数对临界条件的影响
在其他参数不变的条件下,分别取φ=20°,30°,40°,得到临界塑性半径、临界载荷与初始黏聚力关系曲线,如图5所示。临界塑性半径随初始黏聚力增大而降低,临界载荷随初始黏聚力增大而增加。结果表明,当初始黏聚力较大时,虽然临界塑性区半径有所减小,但临界载荷较大,不容易发生冲击地压。

图5 临界塑性半径、临界载荷与初始黏聚力关系曲线
Fig.5 Relation curves of plastic radius,critical load and plastic zone cohesion

图6 临界塑性半径,临界载荷与塑性区黏聚力参数关系曲线
Fig.6 Relation curves of plastic critical radius,critical load and plastic zone cohesion
3.4 塑性区黏聚力参数对临界条件的影响
在其他参数不变的条件下,分别取η=1.0,1.5,2.5,得到临界塑性半径、临界载荷与塑性区黏聚力参数关系曲线,如图6所示。临界塑性半径、临界载荷随黏聚力参数s和η的增大而降低。结果表明,当塑性区黏聚力劣化较快时,容易发生冲击地压。
当η=0时,cp=c,为理想弹塑性情况,Rcr→ ,p0cr→
,p0cr→ ,则不会发生冲击地压。
,则不会发生冲击地压。
当η>0时,Rcr>a。临界条件下,将式(23)代入式(7),且令cp=0,得![]() 其中rs为黏聚力降为0的径向位置。可见,在冲击地压发生时,巷道壁附近a<r<rs区域的黏聚力已降为0,煤体内裂隙丛集(类似于散体结构),当冲击地压发生时将会向巷道内部空间迅速抛出。
其中rs为黏聚力降为0的径向位置。可见,在冲击地压发生时,巷道壁附近a<r<rs区域的黏聚力已降为0,煤体内裂隙丛集(类似于散体结构),当冲击地压发生时将会向巷道内部空间迅速抛出。
4 结 论
(1)为建立巷道冲击地压发生的临界条件,首先要分析巷道围岩应力与位移分布规律。综合考虑开挖面空间效应、中间主应力效应、塑性区剪胀特性、塑性区强度和变形参数的变化,得到的巷道围岩应力与位移分布规律更加符合工程实际。
(2)基于统一强度理论和塑性软化本构模型,应用扰动响应判别准则,建立了圆形断面巷道冲击地压发生的临界条件。结果表明,巷道冲击地压的临界条件主要与支护方式、围岩的初始强度参数及塑性区强度参数的变化密切相关。
(3)临界塑性半径、临界载荷均随支护力的增大而单调增加,表明加强支护是防治冲击地压的有效手段。在开挖面附近,由于虚拟支护力较大,巷道围岩只发生弹性变形,不会发生冲击地压,只有在距开挖面一定距离位置,虚拟支护力逐渐降低,巷道围岩出现塑性区,才有发生冲击地压的可能性。但是如果塑性区很小也不会发生冲击地压;只有当塑性区达到一定值时才会发生冲击。
(4)临界塑性半径随初始黏聚力增大而降低,临界载荷随初始黏聚力增大而增加。当初始黏聚力较大时,虽然临界塑性区半径有所减小,但临界载荷较大,不容易发生冲击地压。临界塑性半径、临界载荷随黏聚力参数的增大而降低。当塑性区黏聚力劣化较快时,容易发生冲击地压。以塑性区黏聚力参数变化作为冲击地压临界条件的主要依据,结果与工程实际符合较好。
参考文献(References):
[1] 侯公羽.基于开挖面空间效应的围岩-支护相互作用机制[J].岩石力学与工程学报,2011,30(1):2871-2877.
HOU Gongyu.Interaction mechanism between surrounding rock and support based on spatial effect of excavation face[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(1):2871-2877.
[2] 章梦涛.冲击地压失稳理论与数值模拟计算[J].岩石力学与工程学报,1987,6(3):197-204.
ZHANG Mengtao.Instability theory and numerical simulation of Rockburst[J].Chinese Journal of Rock Mechanics and Engineering,1987,6(3):197-204.
[3] 吴创周,杨林德,李秋实.弹脆塑性围岩应力和位移的广义SMP准则解[J].工程力学,2013,30(8):223-228
WU Chuangzhou,YANG Linde,LI Qiushi.Perfect elastic-brittle-plastic solution of axisymmetric circular openings in rock mass on extended SMP criterion[J].Engineering Mechanics,2013,30(8):223-228.
[4] 曾开华,鞠海燕,张常光.深埋圆形隧道弹塑性位移统一解及其比较分析[J].岩土力学,2011,32(5):1315-1319.
ZENG Kaihua,JU Haiyan,ZHANG Changguang.Elastoplastic unified solution for displacements around a deep circular tunnel and its comparative analysis[J].Rock and Soil Mechanics,2011,32(5):1315-1319.
[5] 曾开华,鞠海燕,盛国君,等.巷道围岩弹塑性解析解及工程应用[J].煤炭学报,2011,36(5):752-755.
ZENG Kaihua,JU Haiyan,SHENG Guojun,et al.Elastic-plastic analytical solutions for surrounding rocks of tunnels and its engineering applications[J].Journal of China Coal Society,2011,36(5):752-755.
[6] 饶平平,李镜培,张常光,等.考虑拉压模量及主应力顺序的隧洞应力解析解[J].同济大学学报(自然科学版),2011,39(4):512-516.
RAO Pingping,LI Jingpei,ZHANG Changguang,et al.Analytical solutions of hydraulic tunnel with a consideration of variation of principal stresses orders and different elastic moduli in tension and compression[J].Journal of Tongji University(Natural Science),2011,39(4):512-516.
[7] 张常光,张庆贺,赵均海.考虑应变软化、剪胀和渗流的水工隧洞解析解[J].岩土工程学报,2009,31(12):1941-1946.
ZHANG Changguang,ZHANG Qinghe,ZHAO Junhai.Analytical solutions of hydraulic tunnels considering strain softening,shear dilation and seepage[J].Chinese Journal of Geotechnical Engineering,2009,31(12):1941-1946.
[8] 张常光,张庆贺,赵均海,等.具有衬砌的圆形水工隧洞弹塑性应力统一解[J].同济大学学报(自然科学版),2010,38(1):50-53,134.
ZHANG Changguang,ZHANG Qinghe,ZHAO Junhai,et al.Elastic-plastic stress unified solutions of a circular hydraulic tunnel with lining[J].Journal of Tongji University (Natural Science),2010,38(1):50-53,134.
[9] 张常光,徐飞,张庆贺,等.岩石隧道塑性位移新解[J].岩石力学与工程学报,2011,30(S2):3551-3556.
ZHANG Changguang,XU Fei,ZHANG Qinghe,et al.New plastic solution for displacement of rock tunnels[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(S2):3551-3556.
[10] 张常光,赵均海,张庆贺.基于统一强度理论的深埋圆形岩石隧道收敛限制分析[J].岩土工程学报,2012,34(1):110-114.
ZHANG Changguang,ZHAO Junhai,ZHANG Qinghe.Convergence-confinement analysis of deep circular rock tunnels based on unified strength theory[J].Chinese Journal of Geotechnical Engineering,2012,34(1):110-114.
[11] 张常光,赵均海,孙珊珊.隧道围岩弹-脆-塑性应力的三剪统一解[J].应用力学学报,2012,29(5):530-534.
ZHANG Changguang,ZHAO Junhai.SUN Shanshan.An analytical solution for tunnel stress in an elastic-brittle-plastic rock based on the triple-shear unified strength criterion[J].Chinese Journal of Applied Mechanics,2012,29(5):530-534.
[12] 张常光,范文,赵均海.深埋圆形巷道围岩塑性区位移及特征曲线新解和参数分析[J].岩土力学,2016,37(1):12-24,32.
ZHANG Changguang,FAN Wen,ZHAO Junhai.New solutions of rock plastic displacement and ground response curve for a deep circular tunnel and parametric analysis[J].Rock and Soil Mechanics,2016,37(1):12-24,32.
[13] 俞茂宏.岩土类材料的统一强度理论及其应用[J].岩土工程学报,1994,16(2):1-10.
YU Maohong.Unified strength theory for geomaterials and its applications[J].Chinese Journal of Geotechnical Engineering,1994,16(2):1-10.
[14] 范鹏贤,王明洋,李文培.岩土介质中圆形隧洞围岩压力理论分析进展[J].现代隧道技术,2010,47(2):1-7.
FAN Pengxian,WANG Mingyang,LI Wenpei.Progress in theoretical analysis of ground response to circular excavations in rock & soil medium[J].Modern Tunneling Technology,2010,47(2):1-7.
[15] 刘夕才,林韵梅.软岩巷道弹塑性变形的理论分析[J].岩土力学,1994,15(2):27-36.
LIU Xicai,LIN Yunmei.Theoretic analysis of elastoplastic deformation for the tunnel in soft rocks[J].Rock and Soil Mechanics,1994,15(2):27-36.
[16] 刘夕才,林韵梅.软岩扩容性对巷道围岩特性曲线的影响[J].煤炭学报,1996,21(6):596-601.
LIU Xicai,LIN Yunmei.Effect of dilatancy of soft rocks on rock characteristic curves of tunnels[J].Journal of China Coal Society,1996,21(6):596-601.
[17] 刘夕才.轴对称巷道变形的弹塑性理论分析[J].力学与实践,1994,16(5):20-22.
LIU Xicai,Elastic-plastic analysis of axisymmetric deformation of roadway[J].Mechanics in Engineering,1994,16(5):20-22.
[18] 张强,王水林,葛修润.圆形巷道围岩应变软化弹塑性分析[J].岩石力学与工程学报,2010,29(5):1031-1035.
ZHANG Qiang,WANG Shuilin,GE Xiurun.Elastoplastic analysis of circular openings in strain-softening rock masses[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(5):1031-1035.
[19] 徐栓强,俞茂宏,胡小荣.基于双剪统一强度理论的地下圆形洞室稳定性的研究[J].煤炭学报,2003,28(5):522-526.
XU Shuanqiang,YU Maohong,HU Xiaorong.The stability analysis of circular tunnel based the twin shear unified strength theory[J].Journal of China Coal Society,2003,28(5):522-526.
[20] 潘一山,章梦涛,李国臻.稳定性动力准则的圆形洞室岩爆分析[J].岩土工程学报,1993,15(5):59-66.
Pan Yishan,ZHANG Mengtao,LI Guozhen.Analysis on circular chamber rockburst by dynamic stability criterion[J].Journal of Geotechnical Engineering,1993,15(5):59-66.
[21] 潘一山,章梦涛.冲击地压失稳理论的解析分析[J].岩石力学与工程学报,1996,15(S1):504-510.
Pan Yishan,ZHANG Mengtao.The exact solution for rockburst in coal mine by unstabilityrockburst theory[J].Journal of geotechnical engineering,1996,15(S1):504-510.
[22] 潘一山,李国臻,章梦涛.回采巷道冲击地压危险指标的确定[J].矿山压力与顶板管理,1994(1):56-59.
PAN Yishan,LI Guozhen,ZHANG Mengtao.Determination of the rockburst hazardous indices in mining work[J].Ground Pressure and Strata Control,1994(1):56-59.
[23] 潘一山.冲击地压发生和破坏过程研究[D].北京:清华大学,1999.
PAN Yishan.Study on rockburst initiation and failure propagation[D].Beijing:Qinghua University,1999.
[24] 郭延华,姜福兴,张常光.高地应力下圆形巷道临界冲击地压解析解[J].工程力学,2011,28(2):118-122.
GUO Yanhua,JIANG Fuxing,ZHANG Changguang.Analytical solution for critical rockburst of a circular chamber subjected to high in-situ stress[J].Engineering Mechanics,2011,28(2):118-122.
[25] 马念杰,郭晓菲,赵志强,等.均质圆形巷道蝶型冲击地压发生机理及其判定准则[J].煤炭学报,2016,41(11):2679-2688.
MA Nianjie,GUO Xiaofei,ZHAO Zhiqiang,et al.Occurrence mechanisms and judging criterion on circular tunnel butterfly rock burst in homogeneous medium[J].Journal of China Coal Society,2016,41(11):2679-2688.
[26] 成云海,姜福兴,胡兆锋,等.埋深千米综放采场沿空巷道冲击地压防治研究[J].岩石力学与工程学报,2016,35(S1):3000-3007.
CHENG Yunhai,JIANG Fuxing,HU Zhaofeng,et al.Prevention and control of coal burst on gob-side entry in deep coal seam with fully mechanized sublevel caving mining[J].Chinese Journal of Rock Mechanics and Engineering,2016,35(S1):3000-3007.
[27] 胡少斌,王恩元,沈荣喜.深部煤岩动力扰动响应特征及数值分析[J].中国矿业大学学报,2013,42(4):540-546.
HU Shaobin,WANG Enyuan,SHEN Rongxi,Characteristics of dynamic disturbance response in deep coal and rock and its numerical analysis[J].Journal of China University of Mining & Technology,2013,42(4):540-546.
[28] 刘洪涛,镐振,吴祥业,等.塑性区瞬时恶性扩张诱发冲击灾害机理[J].煤炭学报,2017,42(6):1392-1399.
LIU Hongtao,HAO Zhen,WU Xiangye,et al.Mechanism of blast disaster induced by instantaneous malignant expansion of plastic zone[J].Journal of China Coal Society,2017,42(6):1392-1399.
[29] 刘晔,姜福兴,冯宇.巷道诱发型冲击地压的发生机制及危险性分析[J].岩土力学,2015,36(S2):201-220.
LIU Ye,JIANG Fuxing,FENG Yu.Study of occurrence mechanism and risk analysis of induced rockburst in roadway[J].Rock and Soil Mechanics,2015,36(S2):201-220.