微震技术是监测煤矿岩爆、矿震等灾害的一种区域性预测手段,能够对煤岩体微震活动实时、连续、在线监测,并形成微震数据。煤矿井下噪声污染严重,微震数据中包含了大量外部噪声,需将微震有效信号从噪声中分离出来。因此,研究微震信号的降噪问题具有重要的意义。
微震信号具有随机性、非平稳性特点,传统基于经典傅里叶变换的降噪方法[1],虽然能在一定程度上抑制噪声,但其主要对周期性平稳信号有效,对包含有尖峰和突变的微震信号降噪效果不佳[2-3];目前常用的非平稳信号的降噪方法有小波变换[4-7]和经验模态分解(Empirical Mode Decomposition,EMD)[8-11]等方法,小波变换因其具有良好的多分辨率特性而广泛应用于信号降噪中,但需选取合适的基波函数和阈值才能达到较好的降噪效果,且不同的小波基分析同一个信号会产生不同的结果;EMD方法是一种自适应的时频分析方法,EMD认为一个时间序列由多个时间尺度的振荡波构成[12],设法从经验资料中逐级分离出固有的、内在的本征模态函数(Intrinsic Mode Function,IMF)分量,通过时频分析,最终得到原序列的多尺度振荡特征,但该方法存在边界效应及模态混叠现象[13],导致EMD具有不稳定性和不唯一性,EMD的这些缺陷使得在信号降噪时难免存在弊端;总体平均经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)虽然可以在一定程序上抑制模态混叠现象,但其计算量大、频谱剖分效果不理想。
变分模态分解(Variational Mode Decomposition,VMD)[14]是一种新的非递归的信号分解方法,该方法在获取分解分量的过程中通过迭代搜寻变分模型最优解来确定每个分量的频率中心及带宽,从而能够自适应地实现信号的频域部分及各分量的有效分离。与EMD相比较,VMD具有坚实的理论基础,克服了EMD等递归分解算法出现的模态混叠和频率效应等缺点,具有很好的噪声鲁棒性和降噪效果。目前,VMD已经被应用于脑肌信号分析[15]和故障诊断[16]中,基于VMD分解的微震信号降噪研究还鲜见报道。
笔者尝试利用VMD对微震信号分解时,克服了模态混叠和虚假分量的缺点,自适应地将微震信号分解为一组具有中心频率的窄带分量,计算各分量的能量熵值,获取信号和噪声的分界点,剔除高频噪声分量,最终实现对微震信号的降噪滤波功能。仿真信号和实测信号实验结果表明,该方法可以有效分离微震信号及噪声,具有良好的降噪效果。
1 相关理论基础
1.1 变分模态分解
VMD是由DRAGOMIRETSKIY和ZOSSO于2014年提出的一种新的非递归的信号分解方法,VMD方法将模态的估计转变为变分问题,通过在频率内不断搜索约束变分模型的最优解实现将信号自适应分解为各模态及其中心频率,最后各模态经傅立叶逆变换到时域。首先,本征模态函数IMF被重新定义为调频-调幅信号,表达式为
uk(t)=Ak(t)cos(φk(t))
(1)
其中,模态分量uk(t)可以看作一个幅值为Ak(t)、瞬时频率为ωk(t)的谐波信号,Ak(t)为uk(t)的瞬时幅值,Ak(t)≥0;相位φk(t)是一个递增函数,![]() (t)>0;ωk(t)=
(t)>0;ωk(t)=![]() (t),ωk(t)为uk(t)的瞬时频率,ωk(t)≥0。假设每个模态分量uk(t)都具有中心频率和有限带宽,约束条件为各模态分量之和等于输入信号x,且每个模态分量的估计带宽之和最小,则对应的约束变分模型描述为:
(t),ωk(t)为uk(t)的瞬时频率,ωk(t)≥0。假设每个模态分量uk(t)都具有中心频率和有限带宽,约束条件为各模态分量之和等于输入信号x,且每个模态分量的估计带宽之和最小,则对应的约束变分模型描述为:
![]()
(2)
式中,uk={u1,…,uK}为分解得到的K个有限带宽的变分模态分量;ωk={ω1,…,ωK}为各模态分量的频率中心;δ(t)为狄拉克(Dirac)函数;*代表卷积;x为含噪微震信号![]() 为对所有的变分模态求和。
为对所有的变分模态求和。
为求取式(2)的最优解,引入扩展的Lagrange函数,将约束性变分问题变换为非约束性变分问题,其表达式为
![]()
(3)
式中,α为二次惩罚因子,用于保证信号的重构精度,α值越大,各模态分量的频率带宽就越小;λ(t)为拉格朗日乘法算子,使约束条件保持严格性。
利用交替方向乘子算法求取上述扩展的Lagrange函数的鞍点,即求取约束变分模型的最优解,其中模态分量uk及中心频率ωk分别为
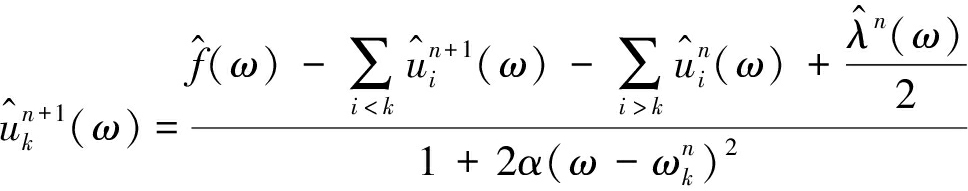
(4)
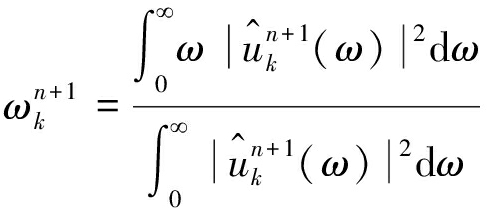
(5)
式中,ω=ω-ωk。
1.2 模态分量的能量熵分析
1948年,香农第1次将熵的概念引入信息论中,熵值反映了信号的不确定性和复杂程度。能量熵表征信号能量的分布情况[17],能量熵大,对应信号在总能量中的比重小,能量熵小,对应信号在总能量中的比重大。目前,能量熵作为特征量已经广泛应用于语音降噪等领域[18]。
笔者利用能量熵值的变化找到噪声和微震的分界点。在微震信号经VMD分解后得到的从高频到低频依次排列的K个模态分量u1,u2,…,uK中,噪声对每个分量的支配作用逐渐降低,信号对每个分量的支配作用不断加强。确定分界模态分量ui的方法是:首先计算各模态分量的能量熵;其次,搜索第一个能量熵取局部极小值时对应的模态分量ui;最后,将前i-1个模态分量作为噪声滤除,对剩余模态分量ui,ui+1,…,uK进行重构,即可得到降噪后的微震信号。
各模态分量的能量熵计算公式为
H(uk)=-Pklog2Pk
(6)
式中,H(uk)为分量uk的能量熵值;Pk表示第k个分量uk的能量在总能量中的比重;Ek为各分量的能量,E为K个分量能量之和,其中,![]()
2 基于VMD和能量熵的微震降噪算法
对含噪微震信号进行VMD分解,计算各分量的能量熵值,在分解得到的K个分量中找出噪声与信号的分界分量uj,将u1~ui-1共i-1个高频分量剔除,对剩余分量进行重构,从而得到降噪后的信号。微震信号的降噪过程如图1所示。

图1 基于VMD和能量熵的微震信号降噪方法流程
Fig.1 Process of denoising of micro-seismic signals based on VMD and energy entropy
综上所述,基于VMD和能量熵的微震信号自适应降噪算法步骤如下。
步骤1:定义变分模态分量个数K值与惩罚因子α的值。
步骤2:对含噪微震信号x(t)进行VMD分解,得到K个变分模态分量,记为Q={u1,u2,…,uk,…,uK}。
(1)初始化![]()
(2)令n=n+1,执行整个循环;
(3)执行内层第1个循环,根据式(7)更新uk:
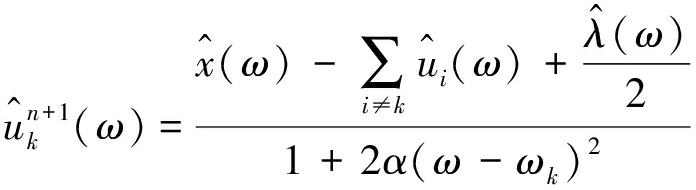
(7)
式中,![]() 为信号x(t)的傅立叶变换,
为信号x(t)的傅立叶变换,![]()
(4)令k=k+1,重复(3),直到k=K,结束内层第1个循环;
(5)执行内层第2个循环,根据式(8)更新ωk;
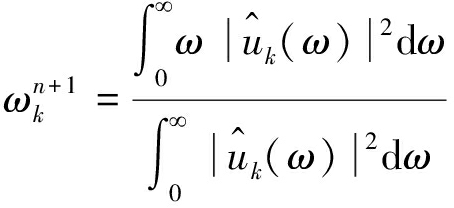
(8)
(6)令k=k+1,重复步骤(5),直到k=K,结束内层第2个循环;
(7)执行外层循环,根据式(9)更新λ:
(9)
式中,τ为拉格朗日乘法算子λ(t)的更新步长参数;
(8)重复步骤(2)~(7),直到满足迭代停止条件如公式(10)所示,结束整个循环,输出结果,得到K个变分模态分量,
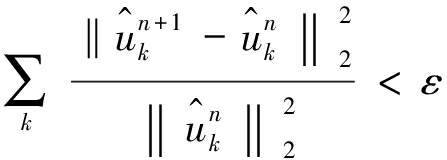
(10)
式中,ε为求解精度;
步骤3:按式(6)计算各分量的能量熵值{H(u1),H(u2),…,H(uk),…,H(uK)}。
步骤4:根据各分量的能量熵值,应用1.2节所述方法搜索第1个局部能量熵最小值,确定噪声和信号的分界分量ui。
步骤5:将u1~ui-1共i-1个高频分量剔除,对剩余分量ui~uK进行重构,从而得到降噪后的信号x(t)′。
3 实验分析
为验证本文方法的有效性,本文用仿真信号和实际微震数据在MATLAB平台上进行了多组实验。其中仿真实验1组,实际微震信号4组,并对本文方法与EMD方法的降噪效果进行对比分析。
3.1 实验结果评价指标
本文采用信号降噪前后的信噪比SNR、降噪后信号占原信号的能量百分比ESN和原信号与降噪后信号的均方根误差RMSE三个参数评价降噪效果。其中信噪比SNR定义为

(11)
其中,x(t)为含噪信号;x(t)′为降噪后信号;N为采样点数。信噪比越高表明信号中的真实微震信号的信息量越多,降噪效果越好。
降噪后信号占原信号的能量百分比ESN定义为
ESN=E′/E
(12)
其中,E′为降噪后信号的能量[19];E为原信号的总能
量,其中,![]() 值越大,说明降噪后的信号更多地保持了原信号特征,更接近原信号。
值越大,说明降噪后的信号更多地保持了原信号特征,更接近原信号。
原始信号和降噪后信号的均方根误差RMSE定义[20] 为
(13)
均方根误差是降噪后的微震数据偏离原始数据平均值的度量,均方根误差越小表示降噪信号就越接近原始信号,降噪效果就越好。
3.2 仿真实验与结果分析
采用模拟地震的Ricker子波对本文方法进行仿真分析,Ricker子波可表达为
(14)
其中,f(t)为振幅;t为时间;fp为谱峰频率。仿真分析中取fp=25 Hz,采样频率为1 kHz,采样点个数为1 000。在Ricker子波中加入随机噪声,未加噪声和加入随机噪声的Ricker子波波形及其频谱如图2所示。

图2 Ricker子波、加噪Ricker子波波形及其频谱
Fig.2 Waveform and spectrum of the Ricker wavelet and the noise Ricker wavelet
对加噪Ricker子波进行EMD分解并对分解得到的每个IMF分量进行快速傅里叶变换(Fast Fourier Transfer,FFT),各IMF分量波形及其FFT频谱如图3所示。对加噪Ricker子波使用VMD分解并对分解得到的每个模态分量uk进行快速傅里叶变换,各模态分量uk波形及其FFT频谱如图4所示。对比图2~4可知,由于随机噪声干扰,且原Ricker子波的频率位于0~50 Hz的较小范围内,使得EMD分解结果产生了模态混叠现象;由图3可以看出,相邻2个IMF分量之间均产生了模态混叠,且每个IMF分量中均包含了部分Ricker子波波形;由图4可以看出,VMD分解有效地去除了模态混叠和虚假模态。因此,EMD算法本身具有一定的缺陷,而VMD方法具有很好的噪声鲁棒性和分解效果。
使用EMD降噪后的Ricker子波波形及频谱如图5所示,使用本文方法降噪后的Ricker子波波形及频谱如图6所示。对比图5,6可知,使用EMD降噪后的Ricker子波中还存在大量噪声,与原Richer子波波形相比差别较大,如在三个极值点处的幅值绝对值均明显变小;而使用VMD降噪后信号波形中仅存在少量噪声,原Ricker子波波形被完整地分离并保留下来。

图3 含噪Ricker子波EMD分解结果及频谱
Fig.3 EMD decomposed results of the noise Ricker wavelet and IMFS’ corresponding spectrum

图4 含噪Ricker子波VMD分解结果及频谱
Fig.4 VMD decomposed results of the noise Ricker wavelet and IMFS’ corresponding spectrum

图5 EMD降噪后Ricker子波波形及频谱
Fig.5 Ricker waveform and spectrum after EMD denoised

图6 VMD降噪后Ricker子波波形及频谱
Fig.6 Ricker waveform and spectrum after VMD denoised
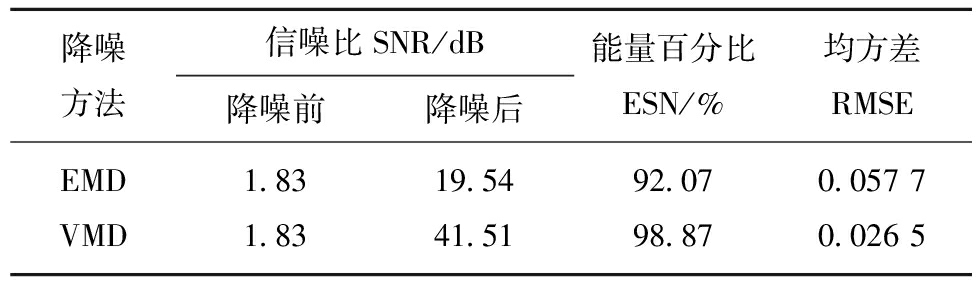
分别应用式(11)~(13)计算含噪Ricker子波使用EMD方法降噪和本文方法降噪前后的SNR,ESN以及RMSE,计算结果见表1。分析表1可知,含噪Ricker子波的信噪比为1.83 dB,应用EMD降噪后信噪比为19.54,降噪后信号占原信号能量百分比为92.07%,均方根误差为0.057 7,可见因EMD分解法本身存在的模态混叠等问题,噪声和信号同时混叠在多个IMF分量中,降噪后的Ricker子波与真实的Ricker子波差异较大,信噪比较低,降噪后的信号中依然存在大量随机噪声,降噪效果不理想;采用本文方法降噪后信噪比提升至41.51,均方根误差为0.026 5且其能量百分比仍保持在原信号的98.87%,说明用本文方法降噪后的Ricker子波更接近真实的Ricker子波,定量说明了本文降噪方法的合理性及有效性。
表1 EMD和VMD降噪效果对比分析
Table 1 Comparative analysis of denoised effect of EMD and VMD
4 应用实例
4.1 模态的选取
VMD分解前需要确定模态分量个数K,K值不同,分解后各模态分量的中心频率也不同,本文采用观察各模态分量中心频率的方法确定K。选取一个典型含噪信号进行VMD分解,采样频率为1 000 Hz,采样点个数为5 000,不同K值下的中心频率见表2,应用本文方法对该典型含噪信号在不同K值下进行降噪处理,降噪后信号的SNR值如图7所示。
表2 不同K值对应的中心频率
Table 2 Center frequency corresponding to different K
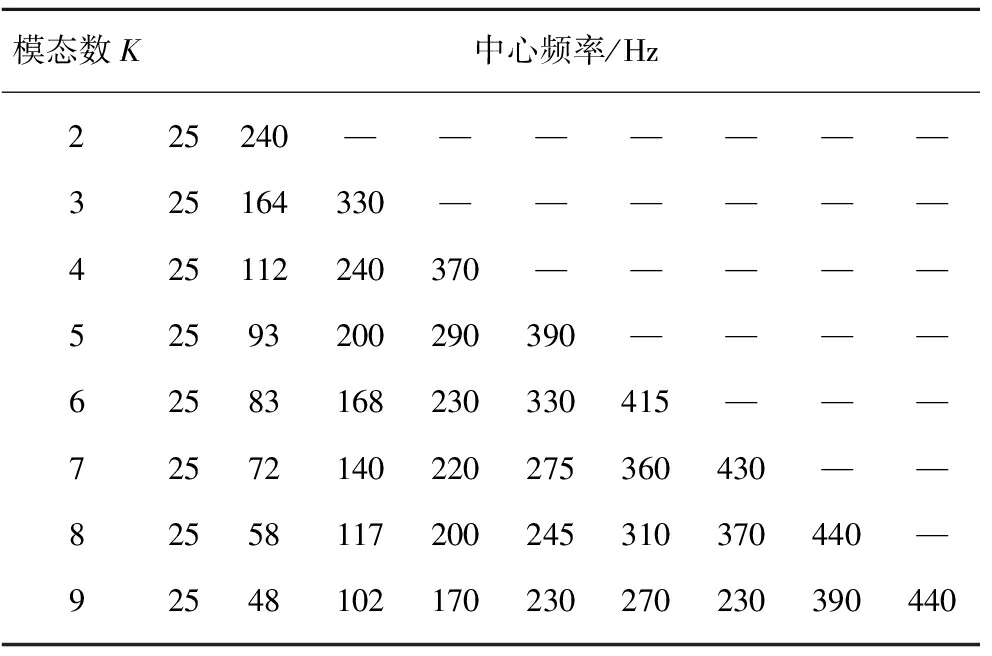

图7 不同K值对应的信噪比
Fig.7 SNR to different K
微震信号是随机性、非平稳的低频信号,其频率分布较为分散,主频及能量分布于0~250 Hz频带,对于大于250 Hz的高频分量将作为噪声剔除。表1中,从K=7开始,出现了对中心频率大于250 Hz过分解的现象。图7中,降噪后信号的SNR在K=6时均达到最优,因此,本文模态个数K选为6,α采用VMD默认值2 000。
4.2 实验结果及分析
实验数据来源于我国西部某煤矿微震监测系统,该系统具有捕捉微弱微震信号的能力,主要用于冲击地压灾害预测。笔者从2010年6月份的监测数据中随机选择4组含噪微震信号,应用Matlab编程对信号进行频谱分析,4组含噪微震信号及其频谱如图8所示。从图8可以看出,4组微震信号中均存在大量的随机噪声,优势频谱分布不明显,尤其是微震信号RF3中微弱的微震信号几乎淹没于噪声中,因而需要进行降噪处理。

图8 4组微震信号降噪前后波形及其频谱
Fig.8 Waveform and spectrum of four rock fracture(RF) micro-seismic signals before and after denoised
采用本文方法对4组微震信号进行降噪处理,降噪后的信号波形及其频谱如图9所示。对比含噪信号和降噪后信号波形及频谱可知,降噪后的4组微震波形较降噪前清晰,优势频谱分布明显,可见,本文方法在充分保留微震信号随机性和非平稳的特征的基础上,最大程度上对微震信号进行滤波,降噪效果明显。
分别采用基于EMD方法和本文方法对上述4组含噪微震信号进行降噪处理,计算降噪后信号的SNR,ESN和RMSE值,计算结果见表3。
表3 4组微震信号降噪效果分析
Table 3 Comparative analysis on denoised effect of four rock fracture(RF) micro-seismic signals

由表3可知,两者都对含噪微震信号进行了一定程度的降噪,利用本文方法降噪后微震信号的信噪比均高于EMD降噪方法,本文方法降噪后信号占原信号的能量百分比均高于EMD降噪方法,本文方法降噪后信号和原始信号的均方根误差值均低于EMD降噪方法。实验结果表明,本文方法降噪效果更好,且降噪后信号在形态上更接近原始信号。为了进一步说明降噪效果,我们又随机抽取了50组微震数据做上述分析,应用本文方法对50组微震信号降噪后,其信噪比均介于20~56 dB,降噪后信号占原信号能量百分比均介于88%~99.9%,原信号与降噪后信号的均方根误差均围绕在0.02×10-3左右。总之,基于变分模态分解和能量熵的微震信号降噪方法,从3个评价参数上均定量说明本文方法具有良好的降噪效果。
5 结 论
(1)仿真实验表明,VMD能够更准确的分解信号并有效避免模态混叠现象,与EMD方法相比较,VMD预处理结果更加准确和理想。
(2)基于VMD和能量熵的降噪方法处理后的微震信号,与原始信号有很好的相似性,较少的抑制了信号的有用成分,最大程度的保留了原始信号的尖峰、突变等波形特征。
(3)实验结果表明,基于VMD和能量熵的降噪方法对微震信号具有很好地降噪效果,降噪后微震信号的信噪比均介于20~56 dB,效果优于EMD降噪法,说明本文方法有较高的可行性与应用价值。
参考文献(Reference):
[1] 李振春,张军华.地震数据处理方法[M].东营:石油大学出版社,2004:23-54.
[2] ALVANITOPOULOS P F,PAPAVASILEIOU M,ANDREADIS I,et al.Seismic intensity feature construction based on the Hilbert-Huang transform[J].IEEE Transactions on Instrumentation and Measurement,2012,61(2):326-337.
[3] GASI S.The use of wavelet-based denoising techniques to enhance the first-arrival picking on seismic traces[J].IEEE Transactions on Geoscience and Remote Sensing,2014,52(8):4558-4563.
[4] 李夕兵,张义平,刘志祥,等.爆破震动信号的小波分析与HHT变换[J].爆炸与冲击,2005,25(6):528-535.
LI Xibing,ZHANG Yiping,LIU Zhixiang,et al.Wavelet analysis and Hilbert-Huang transform of blasting vibration signal[J].Explosion and Shockwaves,2005,25(6):528-535.
[5] 刘敏,王恩元,刘贞堂,等.小波降噪在煤岩微震信号处理中的应用[J].矿业研究与开发,2011,31(2):67-70.
LIU Min,WANG Enyuan,LIU Zhentang,et al.Application of wavelet denoising in processing the micro-seismic signal of coal-rock[J].Mining Research and Development,2011,31(2):67-70.
[6] 徐宏斌,李庶林,陈际经.基于小波变换的大尺度岩体结构微震监测信号去噪方法研究[J].地震学报,2012,34(1):85-86.
XU Hongbin,LI Shulin,CHEN Jijing.A study on method of signal denoising based on wavelet transform for micro-seismicity monitoring in large-scalerockmass structures[J].Acta Seismologica Sinica,2012,34(1):85-86.
[7] BEENAMOL M,PRABAVATHY S,MOHANALIN J.Wavelet based seismic signal de-noising using Shannon and Tsallis entropy[J].Computer & Mathematics with Application,2013,64(11):3580-3593.
[8] 梁喆,彭苏萍,郑晶.基于EMD和互信息熵的微震信号自适应去噪[J].计算机工程与应用,2014,50(4):7-11.
LIANG Zhe,PENG Suping,ZHENG Jing.Self-adaptive denoising for microseismic signal based on EMD and mutual information entropy[J].Computer Engineering and Applications,2014,50(4):7-11.
[9] BATTISTA B M,KNAPP C C,MCGEE T,et al.Application of the empirical mode decomposition and Hilbert-Huang transform to seismic reflection data[J].Geophysics,2007,72(2):29-37.
[10] 贾瑞生,赵同彬,孙红梅,等.基于经验模态分解及独立成分分析的微震信号降噪方法[J].地球物理学报,2015,58(3):1013-1023.
JIA Ruisheng,ZHAO Tongbin,SUN Hongmei,et al.Micro-seismic signal denoising method based on empirical mode decomposition and independent component analysis[J].Chinese Journal of Geophysics,2015,58(3):1013-1023.
[11] 李月,彭蛟龙,马海涛,等.过渡内蕴模态函数对经验模态分解去噪结果的影响研究及改进算法[J].地球物理学报,2013,56(2):626-634.
LI Yue,PENG Jiaolong,MA Haitao,et al.Study of the influence of transition IMF and EMD de-noising and the improved algorithm[J].Chinese Journal of Geophysics,2013,56(2):626-634.
[12] 郑祖光.经验模态分析与小波分析及应用[M].北京:气象出版社,2010:83-88.
[13] 胡爱军,孙敬敬,向玲.经验模态分解中的模态混叠问题[J].振动、测试与诊断,2011,31(4):429-434.
HU Aijun,SUN Jingjing,XIANG Ling.Mode mixing in empirical mode decomposition[J].Journal of Vibration,Measurement & Diagnosis,2011,31(4):429-434.
[14] KONSTANTIN D,DOMINIQUE Z.Variation mode decomposition[J].IEEE Transactions on Signal Processing,2014,62(3):531-544.
[15] 谢平,杨芳梅,李欣欣,等.基于变分模态分解-传递熵的脑肌电信号耦合分析[J].物理学报,2016,65(11):118701-1-9.
XIE Ping,YANG Fangmei,LI Xinxin,et al.Functional coupling analyses of electroencephalogram and electromyogram based on variational mode decomposition-transfer entropy[J].Acta Physica Sinica,2016,65(11):118701-1-9.
[16] 唐贵基,王晓龙.参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用[J].西安交通大学学报,2015,49(5):73-81.
TANG Guiji,WANG Xiaolong.Parameter optimized variational mode decomposition method with application to incipient fault diagnosis of rolling bearing[J].Journal of Xi’an Jiaotong University,2015,49(5):73-81.
[17] 张超,陈建军,郭迅.基于EEMD能量熵和支持向量机的齿轮故障诊断方法[J].中南大学学报(自然科学版),2013,43(3):932-939.
ZHANG Chao,CHEN Jianjun,GUO Xun.Gear fault diagnosis method based on ensemble empirical mode decomposition energy entropy and support vector machine[J].Journal of Central South University(Science and Technology),2013,43(3):932-939.
[18] 徐望,丁琦,王炳锡.一种基于特征空间能量熵的语音信号端点检测算法[J].通信学报,2003,24(11):125-132.
XU Wang,DING Qi,WANG Bingxi.A speech endpoint detector based on eigenspace-energy-entropy[J].Journal of China Institute of Communications,2003,24(11):125-132.
[19] 朱权洁,姜福兴,于正光,等.爆破震动与岩石破裂微震信号能量分布特征研究[J].岩石力学与工程学报,2012,31(4):723-730.
ZHU Quanjie,JIANG Fuxing,YU Zhengguang,et al.Study on energy distribution characters about blasting vibration and rock fracture microseismic signal[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(4):723-730.
[20] 李学龙,李忠辉,王恩元,等.矿山微震信号干扰特征及去噪方法研究[J].中国矿业大学学报,2015,44(5):788-792.
LI Xuelong,LI Zhonghui,WANG Enyuan,et al.Study of mine microseismic signals interference characteristic and its de-noising method[J].Journal of China University of Mining & Technology,2015,44(5):788-792.
