岩石作为一种复杂的非均质地质材料[1-2],其变形破坏规律与岩土工程质量、寿命和动力灾害的发生休戚相关[3]。在实际的工程实践中,岩石材料往往处于一种往复的加卸载状态下,如受采掘影响的矿山巷道(硐室),隧洞开挖与支护,铁路、公路及桥梁基岩所受车辆载重往复影响、水库的蓄放水、波浪对大坝往复冲击等等,故研究岩石材料在往复加卸载下的变形演化规律有助于正确认识岩石在循环荷载作用下的破坏机理,进而科学地评价工程岩体的长期稳定性[4],对工程设计、施工及防护具有重要的理论意义和实用价值。
对循环加卸载下岩石材料的力学响应规律,相关专家开展了相应的研究工作,陈运平等[5-6] 为了研究不同孔隙流体和不同性质的岩石在循环荷载下应力-应变曲线的细微差异开展了饱和砂岩和大理岩的循环荷载实验,分析了饱和岩石在循环荷载下的应力-应变滞回线、瞬时杨氏模量、泊松比的“X”形变化曲线,杨氏模量随应变振幅的增加而减少等滞后现象,以及施加外力的应变振幅对衰减的影响。许江等[7-9]从不同加载速率、不同荷载水平、不同含水状态、不同岩石孔隙性等角度对岩石在循环加卸载条件下的滞回曲线演化规律进行了研究。苏承东和杨圣奇[10]从平均变形模量的角度对循环加卸载下岩石的变形特征进行了研究。上述研究工作取得了很多有价值的成果,但仍存在一些问题尚未解决。一般认为,岩石的非均匀变形演化,即岩石的变形局部化导致了岩石的最终破坏[11-15],以前研究中鲜有对循环加卸载过程中岩石的变形局部化演化与循环加卸载次数、加卸载应力之间的关系开展研究,较少涉及岩石材料在循环加卸载条件下的试件非均匀变形、局部化带特征参数演化规律分析。
本文开展单轴循环加卸载下花岗岩试件非均匀变形演化试验研究,探讨循环加卸载条件下岩石试样非均匀变形规律及局部化带形成后对其附近位移宽度影响规律。
1 单轴循环加卸载试验
试验选用花岗岩制作标准方形试件,试件尺度为50 mm×50 mm×100 mm;试件表面采用喷漆制作人工散斑场。试验过程中利用伺服压力机对试样进行单轴循环加卸载试验,运用CCD相机、计算机和压力机组成试验系统,试验系统示意图如图1所示,试验系统实物如图2所示。
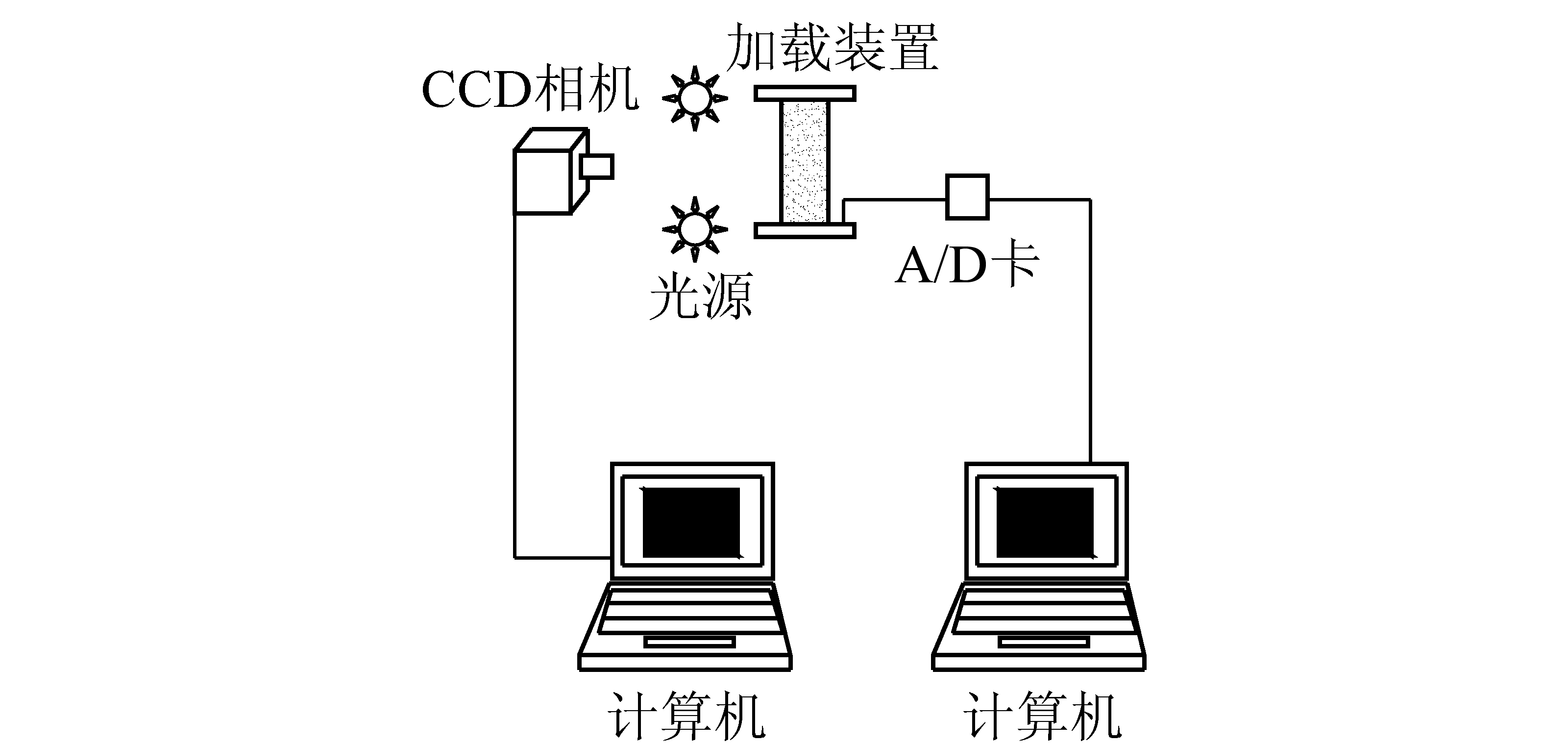
图1 试验系统示意
Fig.1 Schematic diagram of test system

图2 试验系统实物
Fig.2 Physical diagram of test system
采用荷载控制的方式进行加卸载,加卸载速率为0.1 kN/s。考虑试验测试数据的存储问题,试验中共进行6次完整加卸载循环,第7次直接加载到试样破坏;每次循环加载顶点其荷载依次递增37.5 kN,每次卸载到25 kN后重新加载。试件加卸载全过程的荷载与时间关系曲线如图3所示(本文选取其中一组典型试件的试验结果进行详细分析),在该曲线上选取12个典型时刻进行标识,即图3中的标识点A至L。其中A,C,E,G,I,K为每次循环卸载的起始点(也即加载的顶点)。B,D,F,H,J,L为每次循环卸载的最低点(也即加载的起始点)。

图3 荷载与时间曲线
Fig.3 Curve of load and time
试验过程中试件表面的变形图像采用CCD相机进行采集,采集速率为2帧/s,图像分辨率为1 600 pixel×1 200 pixel,其物面分辨率为0.1 mm/pixel。在试验开始阶段,压力机与CCD相机同时启动。压力机自动记荷载、位移、时间等数据,CCD相机在单轴循环加卸载全过程中对试件表面的散斑图像进行连续采集,同时拍摄下试样破坏后的照片,如图4所示。从图4可以看出,该试件的破坏以张拉破坏为主。

图4 试样破坏图片
Fig.4 Picture of damaged sample
2 花岗岩试样非均匀变形规律试验结果分析
2.1 循环加卸载试样变形演化分析
(1)非均匀变形演化分析
以图3中标识点O作为参考点,以此点对应的变形图像作为参考图像,以A~L作为变形图像,采用白光数字散斑相关方法分析计算可以得到加卸载全过程中相应时刻的应变场云图。
由图5中点A~L可知,在加载到卸载过程中,试件出现变形恢复现象,最大变形量值减小。每次循环加卸载加载到最高点(图3中的A,C,E,G,I,K)时,试件的变形集中区域基本在同一位置,例如试件上端x=5 mm,x=20 mm,x=30 mm附近,试件左端y=3 mm,y=40 mm,y=68 mm附近均存在变形集中,且在G点于试件上端x=20 mm附近形成比较明显的变形局部化带。随着循环加卸载的进行,变形局部化带愈加明显,最终导致试样发生接近平行于荷载方向的破坏形式,说明循环加卸载条件下,试样的破坏以张拉破坏为主,如图4所示。从图5中可以看出,前3次循环(点A~F)过程中,在上端x=20 mm处变形集中区域变形量值极小,尚未形成明显的变形局部化带;第4次循环加载到G点即60 MPa时,变形局部化区域形成长度约为14 mm,宽度约为4 mm的条带,变形量值约为4.5×10-4;第5次循环加载到I点即75 MPa时,变形局部化区域形成长度约为18 mm,宽度约为7 mm的条带,变形量值约为7×10-4;第6次循环加载到K点即90 MPa时,变形局部形成长度约为20 mm,宽度约为12 mm的条带,变形量值约为9×10-4,峰值后沿着该局部化条带产生宏观裂纹,发生破坏。试件破坏后中下部也存在一条拉伸裂纹,但由于其启动较晚,在前6次循环加卸载中尚未启动,由于岩石材料的非均质性及试件本身原因,受试件左下端变形影响较大。

图5 非均匀变形场演化云图
Fig.5 Evolution nephogram of non-uniform deformation field
从循环加卸载试样变形演化云图中比较相同荷载条件下的变形演化可以看出:在相同的加卸荷载作用下,循环次数对试样变形影响不明显、不直观,考虑非均匀变形的空间特点,引入非均匀变形指标进一步进行分析。
(2)变形场非均匀指标分析
岩石的非均匀变形演化为局部化变形,局部化现象是材料从该区域破坏的前兆信息。岩石类材料多为脆性破坏,其破坏前兆信息大都不明显,即在材料破坏前其局部化变形场与均匀变形场对比不明显,但二者存在以下区别[16-17]:一是变形场中少数(局部化带内)点的变形量远远大于其它(局部化带外)点的变形量,这些点可以称为变形局部化的“数值特征”;二是变形量大的少数点集中在一个(或少数几个)连通的带内,这可以称为变形局部化的“空间特征”。故引入一种可以同时描述变形局部化“数值”和“空间”两种特征的统计指标Sw,对非均匀变形场演化进行分析。其统计指标公式为
Sw=wsS
(1)
式中,S为某一时刻变形场的方差;ws为考虑变形局部化“空间特征”的一种加权,且有
(2)
![]()
(3)
![]()
(4)
X*=X⊗B
(5)
式中,Xk为变形场中每个点的变形量![]() 为Xk的平均值;X*为经过“空间化处理”的变形场,是X(变形场数据矩阵)与一个元素全为1且大小为m×m的矩阵B(卷积核)的卷积。
为Xk的平均值;X*为经过“空间化处理”的变形场,是X(变形场数据矩阵)与一个元素全为1且大小为m×m的矩阵B(卷积核)的卷积。
由上述公式可知,一般情况下,局部化变形区域即非均匀变形场的方差S会大于没有发生变形局部化的变形场的S,且局部化带出现时刻,变形场方差S随时间(或名义应变)的演化曲线会发生突变,体现了变形局部化出现比较突然的特征(相对于均匀变形阶段)。所以变形场的方差S能描述变形局部化的“数值特征”。而描述变形局部化“空间特征”的ws是卷积后变形场的方差,根据卷积的性质可知,变形场的空间集中程度越厉害,ws越大。所以由S与ws相乘得到的统计指标Sw能同时考虑变形局部化即非均匀变形的“数值特征”和“空间特征”,能够描述变形场的非均匀性特征。
通过计算得到试验过程中的Sw值,将统计指标Sw进行归一化处理,得到Sw随时间的变化曲线如图6所示。从图6可以看出,Sw曲线在循环加卸载过程中呈波动变化,且随着局部化带的明显出现(G点以后),其非均匀变形指标随加卸载应力值的增大发生对应的增大。在每一个循环加卸载过程中,Sw值随着加载应力的增大而增大,随卸载应力的减小数值逐渐减小。

图6 循环加卸载过程中Sw演化曲线
Fig.6 Evolution curves of Sw during cyclic loading
为了研究循环加卸载对其非均匀变形的影响,选取典型标识点对应时刻的Sw值进行对比分析。分别选取每次循环卸载起始点(加载顶点A,C,E,G,I,K)的统计指标Sw值和每次卸载最低点(B,D,F,H,J,L)即10 MPa时的统计指标Sw值绘制变化曲线如图7和8所示。
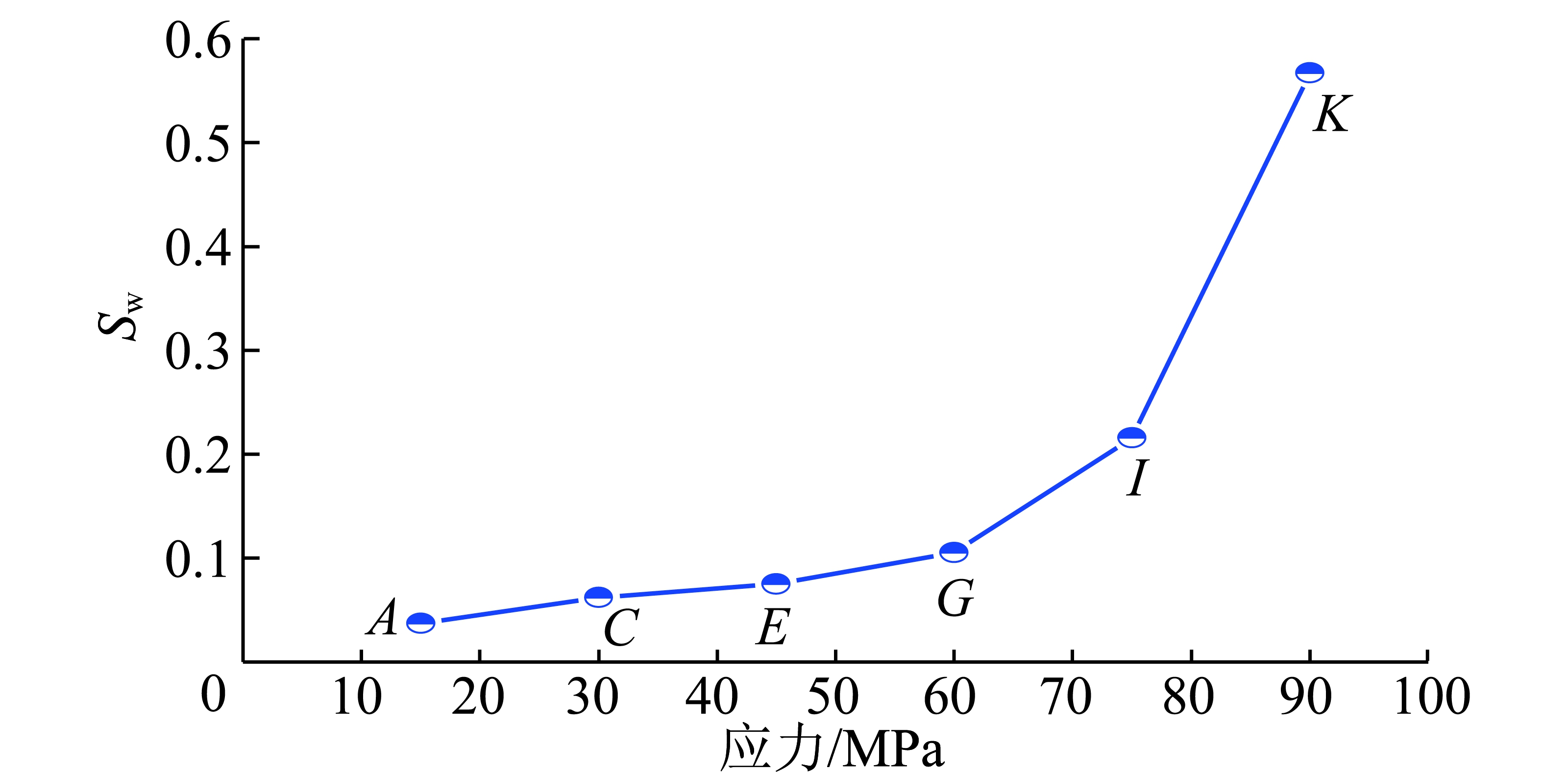
图7 加载最高点统计指标Sw变化曲线
Fig.7 Change curve of Sw at the highest loading points
从图7可知,前3次循环卸载起始点的Sw值呈增大趋势,但数值皆较小,说明前3次循环变形较为均匀。从第4次循环加载到G点及之后,Sw值增加较大。对应图5可知,因为从G点起,在试件上端x=20 mm附近变形局部化带已经启动,且随着荷载增大,变形局部化带不断拓展延伸,变形量值也逐渐增大,同时在试件左端y=3 mm,y=40 mm,y=68 mm附近均存在变形集中;I,K点的非均匀变形指标数值相对于G点明显增大,说明自局部化开始形成以来,后两个循环荷载加载到最大点I,K时局部化变形越明显,非均匀变形程度越大。整体而言,随着循环加载荷载的逐渐增大,非均匀变形指标增大,说明试样的非均匀变形程度随着荷载的增大非均匀程度加剧。
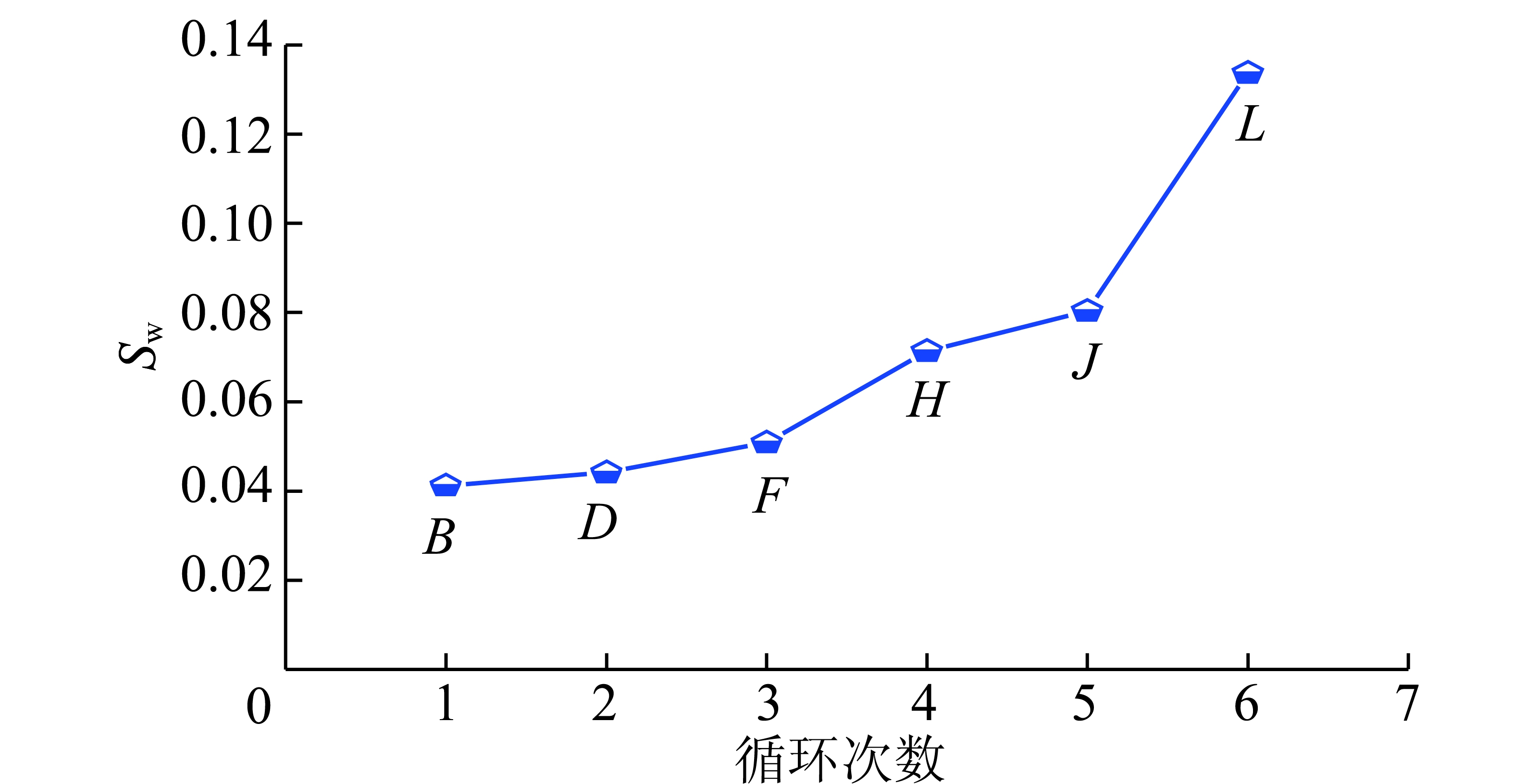
图8 卸载最低点统计指标Sw值变化曲线
Fig.8 Change curve of Sw at the lowest unloading points
图8为每次循环卸载到最低点相同应力值时非均匀变形指标随循环次数变化的关系曲线,从图8可以看出:每次卸载到相同的应力值10 MPa时,随着循环次数增多,对应的Sw值呈现增长趋势,这说明岩石试件在没有超过其抗压强度的循环加卸载过程中,在相同的荷载量值下,试件内部由于循环荷载作用已经产生非均匀变形积聚,且随着循环次数的增加其非均匀变形程度越大;另外,也可从损伤力学角度来解释该现象,随着循环次数的增多,试样内部损伤程度越来越大,局部非均匀变形现象从宏观上体现为试样损伤程度的加剧。
上述能从定性上解释循环加卸载对非均匀变形的影响,下文将进一步开展循环加卸载对非均匀变形的定量分析。
2.2 循环荷载下局部化带位移演化分析
由上文可知,在循环加卸载到G点时,试样开始出现明显的局部化现象,即初次出现局部化带。采用相关方法对循环加卸载过程中的局部化带演化规律与加卸载应力及循环次数之间的关系进行分析。
(1)局部化带位移演化分析方法
根据试件最终的破坏形态以及破坏之前的变形场,确定局部化带的位置。局部化带位移演化分析方法如图9所示,局部化带中心位置两侧对称地选取3组像素点(以图中p1点和p2点为中心点的对应区域),两点距离局部化带的距离分别为a=3,4,5,6,7 mm(目的在于研究局部化带出现后对其平行区域位移的影响规律),将水平位移u和竖直位移v分别沿着平行局部化带和垂直局部化带进行分解,并求出其差值,分别作为局部化带的位移错动分量和位移挤压分量,其中规定沿局部化带逆时针方向错动为正,垂直局部化带挤压为正。

图9 变形局部化带位移演化分析方法
Fig.9 Analytical method of displacement evolution of deformation localization band
(2)变形局部化带位移演化分析
为避免a值过大或过小对分析局部化带位移演化规律的影响,将a值选为3 mm,按照此方法对6次循环加卸载过程中的每个位移场进行处理,得到其错动位移演化曲线、挤压位移演化曲线与加卸载应力的对应关系如图10所示。

图10 循环加卸载过程中变形局部化带位移演化曲线
Fig.10 Displacement evolution curves of deformation localization band during cyclic loading and unloading
从图10(a)可以看出,在前5次循环加卸载过程中,变形局部化带在整体趋势上于加载阶段沿变形局部化带逆时针方向发生错动,于卸载阶段沿变形局部化带顺时针方向发生错动,其错动位移演化与加卸载应力基本成对应关系。但在第6次循环过程中,变形局部化带于加载过程改变了错动方向,在t=9 935 s变形局部化带由逆时针方向错动向顺时针方向错动转变。这主要是由于该变形局部化带以挤压张拉为主,错动方向的位移受挤压张拉影响较大,故在不同循环过程中,其数值也没有明显的变化规律。在后文分析局部化带影响宽度变化时,也只分析挤压张拉方向的影响宽度。
由图10(b)可知,在循环加卸载过程中,变形局部化带在整体趋势上于加载阶段发生挤压,在卸载阶段发生张拉,其挤压张拉位移演化也与加卸载应力基本呈对应关系。局部化带在卸载初始点处由挤压状态向张拉状态转变,在卸载最低点处开始由张拉状态向挤压状态转变。且在6次循环加卸载中,随着循环次数的增加,在加载顶点与卸载最低点处其挤压位移在整体趋势上均逐渐增大。但在具体时刻增幅略有不同,例如第2次循环到第3次循环过程中,加载顶点的挤压位移由0.002 6 mm变成0.002 9 mm,卸载最低点的挤压位移由0.001 9 mm到0.002 1 mm,数值增加不大。而在第4次循环中,其加载顶点(加载到60 MPa)的挤压位移增加到0.004 6 mm,其卸载最低点的挤压位移增加到0.002 7 mm,位移增幅均较大,对应图5可知,这是因为在第4次循环过程中,在试件上端x=20 mm附近处的局部化带已经启动。从第4次循环开始,加载顶点的挤压位移增加变缓,由第4次循环的0.004 6 mm增加到第5次循环的0.004 9 mm,增加到第6次循环的0.005 1 mm;卸载最低点的挤压位移也逐次增加,由第4次循环的0.002 7 mm增加到第5次循环的0.002 75 mm、第6次循环的0.002 9 mm。由此可见,在试件没有出现明显局部化带前,加载顶点的位移随着荷载的增加略有增加,卸载最低点随着循环次数的增加位移略有增加,但试件一旦出现明显局部化变形后,局部化前后位移增加明显;在局部化带出现后,加载顶点的位移随着荷载的增加略有增加,卸载最低点随着循环次数的增加位移略有增加,即在局部化带出现前后位移演化明显,且循环加卸载能影响局部化带位移演化规律。
(3)变形局部化带影响宽度演化分析
在循环加卸载过程中,变形局部化带出现后,其影响宽度也不断发生变化。变形局部化带的影响宽度是指变形场中变形量大的少数点(变形量远大于周围其它点的变形量)集中在一个(或少数几个)连通的带状范围内,垂直该条带方向大变形点的影响范围。下面分析变形局部化带影响宽度的演化规律,首先按照局部化带位移演化分析方法绘制不同a值(a=4,5,6,7 mm)下的挤压位移曲线如图11所示。

图11 不同a值下挤压位移演化曲线
Fig.11 Evolution curves of extrusion displacement under different a
根据岩石试件破坏前的变形场以及最终的破坏形态,将试件表面分为变形局部化带影响区域与变形局部化带外区域,变形局部化带外区域可以近似认为是弹性区域。弹性区域在加载过程中其位移变形随荷载(或应力)基本保持线性增加,当荷载达到材料强度极限后,其位移增加出现明显非线性,认为此时试件发生了局部化变形。在本文中,当a取某一定值时,在某一加卸载过程中,如果位移随应力线性增加到最大值后又线性减小到最小值,说明a值范围的边界位于弹性区域;如果位移存在非线性增加或减少,说明a值范围的边界位于局部化带的影响范围内。
对比图11(a),图10(b)可知,在第4次循环过程中,挤压位移较第3次循环过程有较大增加,此时局部化带已经启动,且挤压位移在加载过程上升,卸载过程立即下降,即此时可以认为在第4次循环加卸载过程中,距离局部化带两侧a=3 mm外为弹性区域,局部化带影响宽度小于等于6 mm。对于第5次循环,当a=3 mm时,其挤压位移在t=6 334 s斜率随时间增长发生变化,且在卸载过程中其位移减小斜率不断发生变化,可以认为在第5次循环过程中,距离局部化带两侧a=3 mm处在局部化带影响区域内,在该应力作用下局部化带的影响宽度大于6 mm,同样第6次循环时,该宽度更大。
对比图10(b),11(a)~(d)可知,当a=4 mm时,在第5次循环过程中,挤压位移随加卸载应力基本呈线性变化,可以认为局部化带两侧a=4 mm处的位移处于局部化带影响区域之外,即在第5次循环加卸载过程中局部化带影响宽度大于6 mm小于8 mm,即试件在75 MPa压力下,其局部化带影响宽度小于8 mm。对于第6次循环,当a分别为3,4,5,6 mm时,挤压位移在加载顶点前后某一时间段出现位移起伏段,例如当a=3 mm时,在10 052~10 795 s之间共间隔743 s;当a=4 mm时,在10 279~10 908 s之间共间隔629 s;当a=5 mm时,在10 337~10 879 s之间共间隔542 s;当a=6 mm时,在10 451 s~10 794 s之间共间隔343 s,该时间段内挤压位移数值变化不大,其原因是由于受到变形局部化带的影响,在a≤6 mm时的区域皆处于局部化带影响范围内。当a=7 mm时,挤压位移随加卸载应力近似发生线性变换,可以认为a=7 mm的两侧区域为弹性区域。故可以认为在第6次循环加卸载过程中局部化带影响宽度大于12 mm小于14 mm,即在应力为90 MPa时,局部化带影响宽度达到12 mm。由上述分析可知,随应力水平增大及循环次数增多,变形局部化带影响范围逐渐演化,其宽度逐渐增大。
根据前面变形局部化带影响宽度演化规律可知,当变形局部化带影响宽度近似为6 mm时,局部化带两侧平行区域挤压位移为0.004 7 mm;当变形局部化带影响宽度近似为8 mm时,局部化带两侧平行区域挤压位移为0.005 6 mm;当变形局部化带影响宽度近似为12 mm时,局部化带两侧平行区域挤压位移为0.006 3 mm。从中可以看出,变形局部化带影响宽度越大,其两侧平行区域挤压位移越大。
3 结 论
(1)在循环加卸载条件下,随着循环次数的增加,试件变形局部化现象越来越明显。
(2)表征试件非均匀变形程度的指标Sw在数值上随加载应力增大而增大;随着循环次数的增加,Sw在卸载最低点(荷载值相同时)也逐渐增大,试件非均匀变形程度加剧。
(3)试件破坏以张拉为主,在局部化带出现前,局部化带挤压位移增幅不大,当出现局部化现象时,挤压位移明显增大,之后随着循环次数的增加挤压位移逐渐增大。
(4)局部化带影响宽度随加载应力的增加而增大、随循环加卸载次数增多而逐渐增大,且局部化带两侧平行区域的挤压位移随局部化带影响宽度的增加而增加。
参考文献(References):
[1] 谢和平,彭瑞东,鞠杨.岩石变形破坏过程中的能量耗散分析[J].岩石力学与工程学报,2004,23(21):3565-3570.
XIE Heping,PENG Ruidong,JU Yang.Energy dissipation of rock deformation and fracture[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(21):3565-3570.
[2] 赵忠虎,谢和平.岩石变形破坏过程中的能量传递和耗散研究[J].四川大学学报(工程科学版),2008,40(2):26-31.
ZHAO Zhonghu,XIE Heping.Energy transfer and energy dissipation in rock deformation and fracture[J].Journal of Sichuan University (Engineering Science Edition),2008,40(2):26-31.
[3] BIENIAWSKI Z T.Mechanism of brittle fracture of rocks:part I[J].International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts,1967,4(4):395-404.
[4] 李树春.周期荷载作用下岩石变形与损伤规律及其非线性特征[D].重庆:重庆大学,2008:1-2.
LI Shuchun.Deformation and damage law and its nonlinear characteristics of rock under cyclic load[D].Chongqing:Chongqing University,2008:1-2.
[5] 陈运平,席道瑛,薛彦伟.循环荷载下饱和岩石的应力-应变动态响应[J].石油地球物理勘探,2003,38(4):409-413.
CHEN Yunping,XI Daoying,XUE Yanwei.Dynamic stress-strain response in saturated rocks under cycling load[J].Oil Geophysical Prospecting,2003,38(4):409-413.
[6] 陈运平,席道瑛,薛彦伟.循环荷载下饱和岩石的滞后和衰减[J].地球物理学报,2004,47(4):672-679.
CHEN Yunping,XI Daoying,XUE Yanwei.Hysteresis and attenuation of saturated rocks under cyclic loading[J].Oil Geophysical Prospecting,2004,47(4):672-679.
[7] 许江,王维忠,杨秀贵,等.细粒砂岩在循环加、卸载条件下变形实验[J].重庆大学学报(自然科学版),2004,27(12):60-62.
XU Jiang,WANG Weizhong,YANG Xiugui,et al.Experimental study on the deformation characteristics of fine-sandstone under the loading and unloading conditions[J].Journal of Chongqing University(Natural Science Edition),2004,27(12):60-62.
[8] 许江,鲜学福,王鸿,等.循环加、卸载条件下岩石类材料变形特性的实验研究[J].岩石力学与工程学报,2006,25(S1):3040-3045.
XU Jiang,XIAN Xuefu,WANG Hong,et al.Experimental study on rock deformation characteristics under cyclingloading and unloading conditions[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(S1):3040-3045.
[9] 许江,杨红伟,李树春,等.循环加、卸载孔隙水压力对砂岩变形特性影响实验研究[J].岩石力学与工程学报,2009,28(5):892-899.
XU Jiang,YANG Hongwei,LI Shuchun,et al.Experimental study of effects of cyclic loading and unloading pore water pressures on deformation characteristic of sandstone[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(5):892-899.
[10] 苏承东,杨圣奇.循环加卸载下岩样变形与强度特征试验[J].河海大学学报(自然科学版),2006,34(6):667-671.
SU Chengdong,YANG Shengqi.Experimental study on deformation and strength characteristics of rock specimens under cyclic loading and unloading[J].Journal of Hohai University(Natural Sciences),2006,34(6):667-671.
[11] MOGI K.Source locations of elastic shocks in the fracturing processes in rocks[J].Bulletin of the Earthquake Research Institute Tokyo Imperial University,1968,46:1103-1125
[12] SCHOLZ C H.Experimental study of the fracturing process in brittle rocks[J].Journal of Geophysical Research,1968,73(4):1447-1454.
[13] WU L X,LIU S J,WU Y H,et al.Changes in IR with rock deformation[J].International Journal of Rock Mechanics and Mining Sciences,2002,39(6):825-831.
[14] 董玉芬,王来贵,刘向峰,等.岩石变形过程中红外辐射的实验研究[J].岩土力学,2001,22(2):134-137.
DONG Yufen,WANG Laigui,LIU Xiangfeng,et al.The experimental research of the infrared radiation in the process of rock deformation[J].Rock and Soil Mechanics,2001,22(2):134-137.
[15] 宋义敏,马少鹏,杨小彬,等.岩石变形破坏的数字散斑相关方法研究[J].岩石力学与工程学报,2011,30(1):170-175.
SONG Yimin,MA Shaopeng,YANG Xiaobin,et al.Experimental investigation on failure of rock by digital speckle correlation methods[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(1):170-175.
[16] 宋义敏,邢同振,赵同彬,等.岩石单轴压缩变形场演化的声发射特征研究[J].岩石力学与工程学报,2017,36(3):534-542.
SONG Yimin,XING Tongzhen,ZHAO Tongbin,et al.Acoustic emission characteristics of deformation field development of rock under uniaxial loading[J].Chinese Journal of Rock Mechanics and Engineering,2017,36(3):534-542.
[17] 杨小彬,宋义敏,赵同彬.岩石变形破坏演化力学分析[M].北京:煤炭工业出版社,2016:47-54.
YANG Xiaobin,SONG Yimin,ZHAO Tongbin.Mechanics analysis of deformation and failure of rock[M].Beijing:China Coal Industry Publishing House,2016:47-54.