钢管混凝土结构是在充分地利用钢管的套箍作用和混凝土良好承压性能的基础上,在钢管中灌注混凝土形成的一种复合支护结构,现在主要应用于深井软岩巷道、地铁车站、桥梁以及高层建筑等结构工程中[1]。在钢管混凝土结构的性能方面,研究主要集中在轴压承载能力与抗弯能力两个方面。国内外诸多学者,主要以钢管混凝土短柱和直梁作为研究对象,通过室内实验和线性回归分析的方法将钢管混凝土短柱的轴向承载力计算公式与直梁的抗弯承载力进行了拟合。李学彬等[2]在软岩巷道采用钢管混凝土支架联合辅助金属网支护和混凝土喷层支护,共同维持巷道围岩的稳定,成功解决了巷道非对称变形太大的问题。李学彬等[3]还通过改进设计复合支护方案,通过对钢管混凝土支架的承载力以及支护反力的计算,来验证巷道围岩向巷道空间的移动,结合锚网喷临时支护及围岩注浆手段,监测并分析了巷道围岩表面的变化速率和变化量。
对钢管混凝土支架在现场应用过程中的认识大多只是停留在理论和工程经验方面。而灌注式钢管混凝土支护体系由于加载系统、平面失稳控制以及反力支架的装配存在很大困难,因此,利用数值仿真手段,研究整架的钢管混凝土支架的承载力和力学性能,是一种既简易又科学的研究方法。而且核心混凝土的承载力,也是直接影响构件力学性能的一个重要参数,虽然传统的有限元模拟手段能够很好的模拟出材料的宏观力学行为,如荷载-位移曲线、应力分布情况等,但是从微观角度来看,传统的有限元手段无法从直观上模拟混凝土裂缝的数量和裂纹的扩展范围。另外,对于不同让压层厚度条件下钢管混凝土支架的承载力与位移的关系具体公式,相关研究并未形成统一的理论。此外,对于ABAQUS中涉及混凝土本构模型的裂缝扩展以及裂面行为等重要影响因素的研究甚少。
钢管混凝土支架与围岩的相互作用还依赖于相互间的接触状态,因此,支架与围岩间应设置让压层,确保支架均匀受力,以避免受到围岩的集中力影响。本文将利用数值模拟软件ABAQUS模拟钢管混凝土支架整体结构在类均布荷载,不同边界条件下的压弯力学性能,并结合一种无厚度黏聚力粘结单元的混凝土塑形损伤模型,从微观上对钢管核心混凝土压密过程、弹性变形过程、弹塑性变形过程、破坏过程的裂纹扩展和剥落程度进行模拟并与相关实验进行对比,从而得出了适合本文的钢管混凝土支架的荷载—位移曲线,来确定黏结单元的有效性,对钢管混凝土支架的现场应用有一定的工程指导意义。
1 圆形支架抗弯性能实验研究
1.1 圆形支架模型介绍
本次圆弧拱压弯性能实验在山东建筑大学结构工程与振动教育部重点试验室进行,实验室内配有含大型反力架的实验台,以及相关配套的不同吨位的千斤顶,能够满足室内实验的相关要求,如图1所示[4]。

图1 钢管混凝土支架实验台[4]
Fig.1 CFST stent structural experiment tab[4]
支架主要由两帮段、顶弧段、底弧段4部分组成[5-8],且由4段1/4圆弧拱拼接而成,内充填C40的混凝土,4段圆弧拱由4个规格均为φ152 mm×60 mm的套管绑定连接,在每段圆弧拱上的4个5等分点布置4个刚性垫块,同时各支架之间采用连杆连接,使巷道轴线方向的支架能形成整体,不偏斜失稳,保证支架的稳定性,如图2所示。

图2 钢管混凝土支架结构[4]
Fig.2 CFST stent structural model[4]
钢管应变监测时,首先利用打磨仪器预先处理位于跨中位置处的钢管外壁,并沿着应变片的贴片位置同步交叉进行打磨,除去已有的锈迹和污垢从而活化钢管表面,既增加了钢管外壁的表面面积,又提高了其粘结的强度。然后划线定位并粘贴经过改性丙烯酸酯胶做密封防护处理过的应变片,同时接入补偿片并粘贴在与试件材料相同而不受应力的补偿块上(应变片要求型号相同且规格一致,补偿块要求材料相同且不受力),并以固化处理工艺作为温度补偿,从而保证应变片的性能稳定,如图3(a)所示。此外,核心混凝土应变监测装置采用结构简易、持久耐用、高频响高精度的电阻应变式传感器,将核心混凝土应变测试装置预埋入小型预制试件中,如图3(b)所示。

图3 预埋式混凝土应变监测装置[4]
Fig.3 Schematic of pre-buried concrete monitoring device[4]
1.2 圆形支架位移监测
钢管混凝土支架在考虑均布加载和两帮段考虑让压层厚度条件下,沿支架垂直中心线和水平中心线布置位移传感器,采用液压千斤顶配套的压力传感器收集荷载。对圆形支架顶弧段和两帮段位置处的位移、荷载以及试件跨中位置处钢管外壁和内部核心混凝土的应变进行监测,并对其破坏形态进行分析,位移计的具体布置如图4所示。

图4 位移计布置效果[4]
Fig.4 Arrangement diagram of displacement meter[4]
1.3 实验操作步骤与设定
首先将由4段圆弧拱组合而成的钢管混凝土支架在实验室场地上组装完好,并通过放样和对中的方式找出各段弧拱中点的位置。其次,在钢管表面标识出平面假设的对应线,并沿着预先刻画出的平面假设对应线粘贴应变片。然后对圆形钢管混凝土支架的四周焊接承载板,并吊装支架到实验操作台。最后,连接应变片电线,安装位移传感器,并调整液压千斤顶就绪后开始实验。此外,按照实验要求对圆形支架进行分步加载,并记录实验数据,待实验结束后将支架再重新吊落到地面上,并及时对后期数据进行监测并做好记录。
有限元模型的建立与实验、巷道现场实际情况保持一致,同时限制整个支架的平面外位移,控制其平面外失稳。3个支架左右两帮段留有大小不同的空隙,这个空隙用来模拟在巷道支护中设置的均压空间,该均压空间会在第一步加载过程中逐渐压实。3种不同边界条件的支架具体情况见表1。
表1 各个试件的边界条件
Table 1 Boundary conditions of each specimen

1.4 圆形支架实验结果分析
分别通过顶弧段、两帮段的四等分点的刚性加载块对支架加载,3段圆弧拱施加的荷载大小相同,分8级进行加载,每步50 kN。在第1步加载过程中,2号,3号支架左右两帮段会向圆弧外变形,直到支架左右两帮段预留的让压空隙被完全压实,第一步加载结束;从第2步加载开始,3个支架的荷载方式、大小与边界条件均相同,即在顶弧段和左右两帮段的五等分4个刚性垫块点施加均布荷载,底弧段的4个垫块完全固定。
沿着支架的拱轴线,取拱轴线的40等分点,每个等分点为一个测点,1号测点为支架顶弧段跨中位置,从1号测点开始,按照顺时针方向依次对应每个监测编号,在荷载为50 kN和极限荷载两种荷载条件下监测每个测点的轴力、弯矩,支架的测点布置方案如图5所示。

图5 圆弧拱支架弯矩、轴力监测点布置
Fig.5 Arrangement of monitoring points for moment and axial force of circular arch
荷载-位移曲线波峰位置是支架的4个套管所在的位置,即每段圆弧拱的拱脚位置,而1号支架波谷位置,位于四段圆弧拱跨中附近的两个加载垫块位置。2号、3号支架的波谷位置,位于圆弧拱的跨中区域;3个支架波谷区域的轴力大小基本相同,说明在加载过程中,不论是否存在让压滑移,构成支架的4段圆弧拱跨中附近的轴力均最小。
由于支架变形属于对称变形,如图6,7所示,3个支架的两组荷载-位移曲线看出,在均布加载条件下,支架整体的变形趋势:左右帮段向弧内变形、顶弧段向弧外变形。支架的变形阶段主要分为3个阶段,即弹性阶段、弹塑性阶段和塑性屈服阶段。

图6 支架顶弧段跨中荷载-位移曲线
Fig.6 Load displacement curves of the middle top arc section of support structure

图7 支架左右帮段跨中荷载-位移曲线
Fig.7 Load displacement curves of the middle left-right side section of support structure
如图6,7所示,荷载在0~50 kN范围内,支架顶弧段与左右帮段的弹性变形对支架后期的变形产生了让压作用,这是导致2号、3号支架的承载力大于1号支架的承载力的主要原因。当荷载达到250 kN以后,随着荷载的增加,支架各部分的位移明显增大,支架发生了明显的塑性变形;但2,3号支架变形量远远小于1号支架。
如图8,9所示,达到极限荷载以后,支架的左右两帮段跨中区域的测点轴力增加幅度最大,说明当支架两帮段均压让压层压密以后,随着荷载的增加,两帮段的整体轴力上升;支护体的局部轴压达到极限轴压值,说明以圆弧拱为主的支护体(包括圆弧拱和由圆弧拱组成的支架)达到极限承载力。1~3号支架在荷载为50 kN和极限荷载时的弯矩分布如图10~11所示。

图8 荷载50 kN支架轴力分布
Fig.8 Distribution of axial force with 50 kN load of support structure

图9 极限荷载支架轴力分布
Fig.9 Distribution axial force with ultimate load of support structure

图10 荷载50 kN支架弯矩分布
Fig.10 Distribution of moment with load 50 kN of support structure

图11 极限荷载条件下弯矩分布
Fig.11 Distribution of bending moment with ultimate load of support structure
如图10,11所示,荷载在0~50 kN范围内,曲线波峰位置是支架的4个套管所在的位置,即每段圆弧拱的拱脚位置。3台支架的极限载荷数值分别为50,1 380和1 460 kN。达到极限荷载以后,让压空间的存在可以有效的降低支架上部两个套管的弯矩增加速度。
由于支架钢管与套管绑定为一体,所以支架在模拟加载过程不会发生突然断裂。因此,支架的左右肩部的套管位置和左右帮段的跨中位置发生屈曲。在巨大的弯矩作用下,支架顶弧段不断向弧内外变形,承载力降低,支架发生破坏,周围油漆脱落,对应下方位置出现较大鼓包,如图12所示。

图12 支架破坏形态
Fig.12 Failure pattern of support structure
2 钢管混凝土支架承载数值分析
研究1~3号这3个试件从开始加载到支架屈曲、破坏的全过程,分析钢管混凝土圆弧拱在不同的让压厚度情况下的受载变形情况,从圆形支架的荷载-位移曲线、轴力与弯矩分布、钢管内核心混凝土的应力分布、钢管表面的应力分布、圆弧拱屈曲、破坏后的形态等几方面分析,得出让压层厚度对圆弧拱承载力的影响。
2.1 力学模型建立与边界约束
室内实验仅能对支架的承载力、位移、应变等参数进行监测[9-12],对于支架内的应力分布、轴力、弯矩等变量的监测,仍需要借助数值模拟手段对其进行分析。故本文选用ABAQUS模拟软件,对0.26矢跨比钢管混凝土圆形支架影响因素进行分析[13-15]。
所选用的减缩积分单元为C3D8R进行非线性分析时[16-19],满足塑性变形规则的较大区而且尽量适当,细化提高求解精度的要求。试件力学模型如图13所示。由于,计算机模拟与实验加载相比可以更加稳定的对试件进行加载,因此,0~400 kN范围内按每级50 kN对每个垫块进行加载,从400 kN以后按每级25 kN进行加载。

图13 圆形支架力学模型
Fig.13 Supports mechanical model
2.2 钢管与混凝土本构选取
(1)钢管本构选取
本文对混凝土塑性损伤模型中参数设置见表2。
(2)混凝土本构选取
本文对混凝土塑性损伤模型参数设置见表3。
混凝土塑性损伤模型的屈服面函数为[20-22]
表2 20号无缝钢管弹塑性模型参数
Table 2 Elastic-plastic damage model parameters of No.20 seamless steel tube
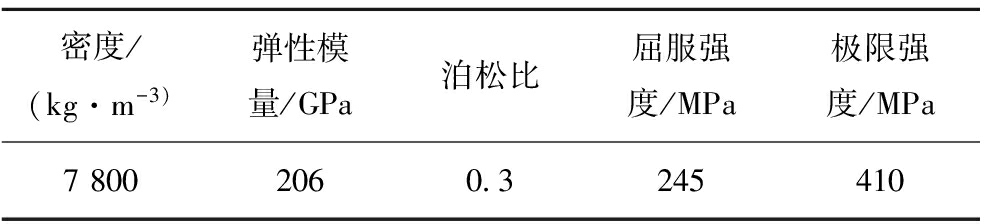
表3 混凝土塑性损伤模型参数
Table 3 Parameters of concrete plastic damage model

注:ρ为密度;λ为泊松比;M为流动势偏心率;φ为剪胀角;α为双轴等压与单轴强度之比;γ为第二应力比值;c为黏性系数; E为弹性模量。
(1)
其中,I1,J2分别为应力张量第一不变量和偏应力张量第二不变量,其余各参数的计算公式如下:
![]()
(2)
其中,σb0为混凝土双轴抗压强度;σc0为混凝土单轴抗压强度;KC为控制混凝土屈服面在偏平面上的投影形状的参数,若KC=1.0,则混凝土屈服面在偏平面上的投影为圆形,类似于经典弹塑性理论中的Drucker-Prager准则;若KC=0.5,则混凝土屈服面在偏平面上的投影为三角形,类似于经典弹塑性理论中的Rankine准则。对于正常配筋的混凝土,建议KC=0.67。
3 钢管混凝土短柱实验与模拟
为了更加清晰明了的观察核心混凝土的剥落与裂纹破坏,本文对核心混凝土受压过程添加了粘结单元并与实验对比。待混凝土坍落度符合试验要求后,批量成模并对立方体试块力学强度进行测试。随后将相同水灰比配制的钢管混凝土短柱和混凝土成各2组,进行单轴抗压强度测试,如图14所示。

图14 相同水灰比配制的CFST短柱(左)和混凝土(右)单轴抗压强度测试
Fig.14 Uniaxial compressive strength test with the same water-cement ratio for CFST Short columns (left) and concrete (right)
以0.4水灰比核心混凝土立方体为例,将在实验室实测的钢管混凝土短柱轴向压缩数据及混凝土轴向压力的破坏形态与模拟实验结果进行对比分析。选取实验室实测的有代表性的2个试块的位移-荷载曲线与Abaqus软件模拟分析计算后得到的位移-荷载曲线进行对比,从三条曲线可以明显发现实验与模拟对比曲线如图15所示。

图15 钢管混凝土试块单轴荷载-位移曲线
Fig.15 Uniaxial load displacement curves of CFST short column test block
在单轴压缩实验中由于受到设备等因素的影响,如图15所示,当试块达到屈服临界值以后,荷载略有下降,随后呈缓慢上升趋势,说明试件已开始进入塑性强化阶段。在数值模拟中支架的3个变形阶段:弹性阶段、弹塑性阶段和塑性屈服阶段分布较为明显。如图16所示,当试块到达屈服荷载后,进入塑性阶段,随着应变增加,紧箍作用加强,说明试件开始逐渐进入塑性强化阶段。

图16 钢管混凝土短柱变形过程对比
Fig.16 Deformation process of CFST short column
由图17可以看出,数值模拟结果与实验结果相吻合。试件表面产生的裂缝大多数已经贯通,混凝土单元逐渐开始剥离试件。试件的破坏是从顶部面棱角区域开始的,当试件破坏时伴随着部分混凝土实体单元崩离试件,无厚度粘结单元挤压严重,与崩离试件的混凝土单元无厚度粘结单元消失。

图17 核心混凝土变形过程对比
Fig.17 Deformation process of core concrete
4 支架钢管表面应力分布
钢管混凝土圆弧拱试件受载破坏后,钢管表面会发生屈曲、鼓包,一般此区域的应力集中明显,而且钢材又属于各向同性材料,所以只需研究钢管表面的综合应力即可。
当荷载达到50 kN时,3个支架的跨中、拱脚,均出现了应力集中现象,且加载点处由于垫块的包裹作用而成为应力降低区。但是,3个支架的钢管表面Mises应力变化和支架的变形不是很明显,所以不做讨论。
当达到极限荷载,对比此状态下3个支架的钢管表面Mises应力分布云图(图18)可以发现:
(1)3个支架的钢管表面应力大小关系为1号>2号>3号,最大应力区域为组成支架的4段圆弧拱的拱脚;达到极限荷载时,支架的套管位置处由于受到强烈的弯矩、挤压作用,支架表面应力最大。钢管在此处发生弯曲破坏。

图18 极限荷载支架钢管表面应力云图
Fig.18 Distribution of steel tube surface stress cloud atlas of the support structure
(2)试件的加载垫块所在的位置位应力降低区域。
(3)由于对底弧段的约束为完全固定,3个支架的底弧段的钢管表面应力最小。
5 支架核心混凝土应力分布
由于混凝土是属于各向异性材料,其极限抗拉强度仅为抗压强度的1/10~1/20,所以相对于压应力而言,拉应力更容易引起混凝土材料的破坏。将支架核心混凝土沿着支架轴线,将核心混凝土沿着竖直方向做剖面,随着荷载的增加,观察核心混凝土的应力分布情况,分析核心混凝土内在的破坏机理,ABAQUS软件后处理中,Mises-S11,Mises-S22应力云图表示支架横向受力分布,通过分析核心混凝土的Mises-S11应力分布来判断支架顶弧段的核心混凝土拉压应力分布情况,通过分析核心混凝土的Mises-S22应力分布来判断支架左右帮段的核心混凝土拉压应力分布情况。S11,S22为正表示横向受拉、S11,S22为负表示横向受压。动态观察三榀支架的核心混凝土的横向应力S11分布,寻找核心混凝土拉压应力区随着荷载的变化规律,进而得出核心混凝土的破坏原理。
5.1 荷载为50 kN时,核心混凝土应力分布
取3个支架的核心混凝土在50 kN荷载下的应力分布情况的研究,来判断核心混凝土的变形情况。当荷载为50 kN时,支架的S11,S22应力分布云图如图19所示。
根据支架的S11,S22应力分布图,当荷载为50 kN时,3个支架顶弧段核心混凝土拉应力区位置基本相同,分别在顶弧段圆弧拱跨中拱顶侧和拱脚的拱外侧,1号支架两帮段核心混凝土的拉应力分布在跨中弧内侧区域,2,3号支架两帮段的核心混凝土拉应力区分布在跨中下方。1号支架的底弧段拱脚的弧外侧也存在拉应力。
由上述发现:当荷载为50 kN时,2,3号支架的拉应力区域明显大于1号支架,区域内拉应力大小相差不大。

图19 1~3号支架S11,S22应力分布
Fig.19 Distribution of stress cloud atlas of the S11,S22 support structure from Nos.1~3 support structure
5.2 极限荷载时,核心混凝土的Mises应力分布
当3个支架的承载力达到其极限荷载时,研究核心混凝土整体的Mises应力分布情况,分析支架核心混凝土的破坏原因。3个支架的核心混凝土的竖向剖面应力分布、表面应力分布如图20,21所示。

图20 1~3号支架核心混凝土的Mises竖向剖面应力分布
Fig.20 Distribution of stress cloud atlas of core concrete for Nos.1~3 support structure

图21 1~3号支架核心混凝土的Mises表面应力分布
Fig.21 Distribution of stress cloud atlas of core concrete for Nos.1~3 support structure
通过对3个支架在达到极限荷载以后的支架核心混凝土的竖向剖面应力云图及表面应力分布图对比发现:
(1)达到极限荷载时,3个支架的核心混凝土应力分布情况相似,套管位置处的混凝土应力最大,而且应力集中主要分布在核心混凝土外表面,所以支架核心混凝土的弯曲破坏最初从支架套管位置处发展。
(2)由于支架变形量的不同,核心混凝土的应力大小与支架变形量成正比。
5.3 有限元模型验证
为了能够更加清晰的说明此荷载下,3个支架的弯矩分布情况,做支架结构的竖向截面图,同时等比例的将各个测点的弯矩绘制到截面图上,然后用平滑的曲线将各个测点的弯矩连接。再利用本文建模方法建立3个钢管混凝土支架的对应模型,最后对比分析试验和模拟结果,对比结果如图22所示。

图22 支架顶弧段与两帮段的模拟与实际弯矩对比截面
Fig.22 Sectional drawing of bending moment of three support structure
从图22可以发现按照本节建模方法进行有限元分析所得钢管混凝土支架的最大弯矩分布曲线与试验结果比较吻合,支架各测点的应变分布误差均小于13%。从弯矩截面图中可以明显观察出,2,3号支架虽然在顶弧段套管处的弯矩大于1号支架,但是其两帮弯矩明显小于1号支架,所以两帮段让压层可以明显降低两帮段弯矩,进而提高支架的承载力。从而证明,本文所述的方法正确合理,能够反映钢管混凝土支护结构的真实受力特点。
6 结 论
(1)首先从整体上分析了整个试件的核心混凝土拉、压应力区的分布情况,钢管的早期变形已反映在位移计监测到的竖向位移上,而核心混凝土在轴压作用下,其内部的孔隙与缝隙正被逐渐压实。故混凝土发生横向“爆裂”并逐渐变形。短柱试验中立方体核心混凝土试件的破坏是先从试件顶底面的棱角开始,侧面的混凝土也剥离了试件,对比结合粘结单元的模拟试件破坏后的云图发现,两者结果基本吻合。
(2)其次通过试验可以得到2,3号支架的承载力、核心混凝土拉应力分布区域、4个套管处的轴力和顶弧段的两个套管处的弯矩明显大于1号支架。说明由于两帮段的均压让压层可以有效的提高支架的承载能力,且在一定范围内,同等型号的支架的承载能力的大小与让压层的厚度成正比且支架整体变形较小。此外,在让压层逐渐压密的过程中,引起了左右两帮段的变形,减弱了支架4段圆弧拱的整体的轴力,核心混凝土拉应力作用区并未发生非弹性形变,其整体的承载能力并未降低。由于底弧段完全固定,所以仅仅加大了支架顶弧段两个套管处的弯矩。
(3)通过室内抗弯实验对钢管混凝土支架顶弧、两帮段施加荷载,类比巷道实际围岩应力,让压层在压密过程中的让压变形的机理是两帮段主动向弧外变形降低其核心混凝土的弯矩,由于让压层厚度并不大,不会导致顶弧段变形太大使支架整体破坏,证实了钢管混凝土支架在巷道支护的有效性。
致谢 感谢王军,刘珂铭以及何晓生对文中试验部分的指导和大力支持。
参考文献(References):
[1] 韩林海.钢管混凝土结构-理论与试件[M].北京:科学出版社,2000.
[2] 李学彬,杨仁树,高延法,等.大断面软岩斜井高强度钢管混凝土支架支护技术[J].煤炭学报,2013,38(10):1743-1747.
LI Xuebin,YANG Renshu,GAO Yanfa,et al.High-strength steel tubular confined concrete supports support technology for large section soft rock inclined shaft[J].Journal of China Coal Society,2013,38(10):1743-1747.
[3] 李学彬,杨仁树,高延法,等.杨庄矿软岩巷道锚杆与钢管混凝土支架联合支护技术研究[J].采矿与安全工程学报,2015,32(2):286-290.
LI Xuebin,YANG Renshu,GAO Yanfa,et al.Study on combined support technology of bolt-mesh-shotcrete and concrete filled steel tubular supports for soft rock roadway in Yangzhuang mine[J].Journal of Mining & Safety Engineering,2015,32(2):286-290.
[4] 王军.钢管混凝土圆弧拱的抗弯力学性能实验研究与工程应用[D].北京:中国矿业大学(北京),2014.
WANG Jun.Research on mechanical properties of anti-bendingt for Concrete filled Steel Tube circular arch and its application[D].Beijng:China University of Mining and Technology (Beijng),2014.
[5] 曲广龙.钢管混凝土支架结构抗弯性能研究及应用[D].北京:中国矿业大学(北京),2013.
QU Guanglong.Research on flexural performance of concrete-filled steel tubular support and its application[D].Beijing:China University of Mining and Technology (Beijng),2013.
[6] 李华为,王文达.ABAQUS二次开发在钢管混凝土结构有限元分析中的应用[J].建筑结构学报,2013,34(8):353-358.
LI Huawei,WANG Wenda.Application of ABAQUS secondary development in finite elementanalysis of concrete filled steel tubular structures[J].Journal of Building Structures,2013,34(8):353-358.
[7] 禚一,李忠献.钢筋混凝土纤维梁柱单元实用模拟平台[J].工程力学,2011,28(4):102-108.
ZHUO Yi,LI Zhongxian.A practical simulation platform of reinforced concrete fiber beam-column element[J].Engineering Mechanics,2011,28(4):102-108.
[8] 张文福,陈克珊,李明亮,等.方钢管混凝土拱侧倾屈曲计算公式适用范围的有限元验证[J].工业建筑,2016,46(S1):962-970.
ZHANG Wenfu,CHEN Keshan,LI Mingliang,et al.Research and application of flexural behavior of concrete filled steel tubular support structure[J].Industrial Construction,2016,46(S1):962-970.
[9] 韩军,李英民,陈伟贤,等.基于ABAQUS三维梁单元的混凝土材料子程序次开发[J].建筑结构,2011,41(5):111-114.
HAN Jun,LI Yingmin,CHEN Weixian,et al.Development of concrete materialsubroutines based on ABAQUS three-dimensional beam element[J].Building Structure,2011,41(5):111-114.
[10] 聂建国,王宇航.基于ABAQUS的钢-凝土组合结构纤维梁模型的开发及应用[J].工程力学,2012,29(1):70-80.
NIE Jianguo,WANG Yuhang.Development and application of steel-concrete composite fiber beam model in ABAQUS platform[J].Engineering Mechanics,2012,29(1):70-80.
[11] HIBBIT T,KARLSSON B,SORENSEN R.ABAQUS/Standard User Subroutines Reference Manual[M].New Yourk:The Pennsylvania State University,1998:1-200.
[12] HU H T,HUANG C S,WU M H,et al.Nonlinear analysisof axially loaded concrete-filled tube columnswith confinement effect[J].Journal of Structural Engineering,ASCE,2003,129(10):1322-1329.
[13] MANDER J B,PRIESTLEY M J N,PARK R.Theoreticalstress-strain model for confined concrete[J].Journal of Structural Engineering ASCE,1988,114(8):1804-1826.
[14] 沈聚敏,王传志,江见鲸.钢筋混凝土有限元与板壳极限分析[M].北京:清华大学出版社,1993:50-51.
[15] 汪训流,陆新征,叶列平.往复荷载下钢筋混凝土柱受力性能的数值模拟[J].工程力学,2007,24(12):76-81.
WANG Xunliu,LU Xinzheng,YE Lieping.Numerical simulation for the hysteresis behavior of RC columns under cyclic loads[J].Engineering Mechanic,2007,24(12):76-81.
[16] ESMEILY A,XIAO Y.Behavior of reinforced concrete columns under variable axial loads:analysis[J].ACI Structure Journal,2005,102(5):736-744.
[17] LGERON F.PAULTRE P,MAZAR J.Damage mechanics modeling of nonlinear seismic behavior of concrete structures[J].Journal of Structural Engineering,ASCE,2005,131(6):946-954.
[18] HAN L H,YANG Y F,Cyclic performanceof concrete-filled steel CHS columns under flexural loading[J].Journal of Constructional Steel Research,2005,61(4):423-452.
[19] VECCHIO F J,COLLINS M P.The modified compression-field theory for reinforcedconcrete elements subjected to shear[J].ACI Structural Journal,1986,83(2):219-231.
[20] KANG H P.Support technologies for deep and complex roadways in underground coal mines:A review[J].International Journal of Coal Science & Technology,2014,1(3):261-277.
[21] 韩林海,游经团,杨有福,等.往复荷载作用下矩形钢管混凝土构件力学性能的研究[J].土木工程学报,2004,37(11):11-22.
HAN Linhai,YOU Jingtuan,YANG Youfu,et al.Behaviorofconcrete filled steel rectangular hollow sectionalcolumns subjected to cyclic loading[J].China Civil Engineering Journal,2004,37(11):11-22.
[22] 张晓楠,史三元,路漫,等.既有砖混结构在软土地区迫降纠倾法分析[J].建筑结构,2016,46(8):89-94.
ZHANG Xiaonan,SHI Sanyuan,LU Man,et al.Analysis of forced settlement rectification method of available brick-concrete structures in soft soil area[J].Building Structures,2016,46(8):89-94.