锚杆支护作为一种经济有效的支护手段,已经在矿山与隧道工程、边坡防护工程、堤坝加固工程等大型工程中得到广泛的应用,并取得了较为理想的应用效果。几十年来,随着锚杆支护技术的不断发展与完善,逐渐形成了以端锚、加长锚固和全锚为代表的锚杆锚固方式[1-3]。但是随着我国煤矿开采深度的不断增加,深部高应力巷道、极松软破碎巷道、易膨胀围岩巷道、强动压影响巷道等复杂困难巷道开始不断出现,对巷道支护强度要求更加苛刻,仅采用端锚和加长锚固的方式难以控制此类巷道有害变形。而全长锚固锚杆因其具有应力扩散范围广、支护强度高、与围岩结构黏结性好等优点,在此类巷道支护设计中得到了广泛的应用与认可[4-6]。
近几年,国内外学者对于端锚或加长锚固锚杆受力特性研究较多。例如,王洪涛等[7]从理论方面推导了端锚预应力锚杆应力分布规律,分析了不同直径、预紧力和围岩弹性模量对锚杆应力分布的影响;SHOWKATI A等[8]研究了含有垂直节理岩体中端部锚固锚杆受力特性及产生的应力场在围岩中的分布;康红普等[9]采用数值模拟手段研究了预应力对端锚锚杆支护效果的影响。但是以上研究均将锚杆锚固的围岩结构视为理想的弹性体,忽略了围岩峰后破坏后的力学特性对锚杆杆体受力的影响。同时,对于深部极为破碎的围岩结构而言,端锚或加长锚固锚杆对围岩变形的控制效果并不是特别理想,尤其在巷道大变形条件下极易造成此类锚杆发生拉伸破断或锚固端滑移脱锚失效等严重工程问题。因此开展全长锚固锚杆的研究依然尤为重要。
关于全长锚固锚杆的受力特性研究方面,国内外学者也取得一定成果。其中,李冲等[10]将围岩视为理想弹塑性体,分析了全长锚固锚杆杆体轴向正应力与剪应力分布规律以及两者与锚杆尺寸之间的关系;RANJBARNIA M等[11]通过理论研究了全长锚固锚杆在圆形巷道中的分布,并分析了预紧力、支护密度等对围岩应力场分布规律的影响;黄明华等[12]通过建立锚固界面的非线性剪切滑移模型以及锚杆锚固段荷载传递的非线性微分方程,获得了锚杆锚固段的轴力和界面剪应力解析解,并对其剪应力分布规律进行了分析;文献[13-15]也对全长锚固锚杆受力特性进行了部分理论与试验研究,并取得了一定研究成果。但以上研究过程均没有考虑围岩峰后应变软化、脆性破坏或塑性流动、剪胀扩容等特点对锚杆杆体受力分布的影响。而在实际工程中,受外部地质环境的影响,围岩表现出不同的峰后破坏形式(图1),根据其特点,可将围岩结构简化为理想弹塑性围岩、弹脆性围岩以及应变软化围岩;然而受其峰后破坏形式的影响,岩体内锚杆受力特征也不尽相同,所产生的锚杆支护效果也会有所差异,因此笔者通过建立不同围岩性质条件下的全长锚固锚杆力学模型,考虑岩体峰后残余黏聚力、应变软化及剪胀性等特点,推导了全长锚固锚杆轴向正应力与剪应力计算式,系统化地分析了不同围岩参数及孔口处锚杆端头轴力对锚杆受力的影响,可为复杂条件下的锚杆支护设计提供理论依据。
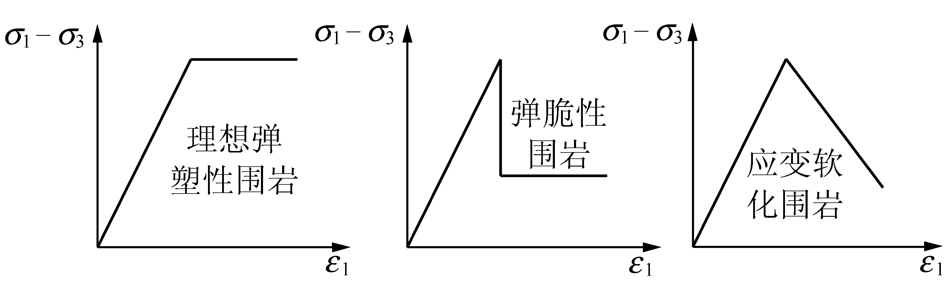
图1 围岩峰后破坏简化模型
Fig.1 Post-peak failure model of surrounding rock
1 全锚锚杆-围岩相互作用力学模型
全长锚固锚杆杆体受力情况不但与锚杆直径、长度、预紧力大小等参数有关,还与巷道埋深、围岩参数及性质、支护阻力等外在条件密切相关。根据锚杆与围岩相互作用原理,建立如图2所示全长锚固锚杆杆体受力计算力学模型,图2(a)中峰后破坏区代表围岩破坏后处于的3种不同围岩状态,即理想塑性状态、脆性破坏状态以及应变软化状态;图2(b)为锚杆杆体受力分布情况,其中A点代表锚杆杆体中性点位置;图2(c)为锚杆微单元体的受力情况。建立的力学模型应满足以下假设条件:
(1)视围岩结构为无限大各向同性地质体,开挖巷道足够长,可按平面应变问题进行求解。
(2)忽略锚杆杆体对围岩结构的破坏,且处于围岩弹性区和峰后破坏区的杆体剪应力均可用锚杆与围岩之间相对位移的函数来表示。
(3)忽略峰后岩体劣化的渐进式破坏过程,认为围岩峰值前后的剪切刚度分别为一定值。
(4)认为图2围岩-锚杆相互作用状态为最终稳定平衡状态,此时锚杆在孔口处的轴力即为托盘对其反作用力(F),忽略中间非稳态变化过程对围岩-锚杆受力状态的影响。
(5)围岩-锚杆协调变形过程中,其相互作用形式仅与锚杆托盘提供的作用力(对围岩的支护阻力和对锚杆端头的张拉力)有关,忽略围岩内部锚杆杆体剪应力对围岩状态变化影响,故稳态下锚杆与围岩受力计算过程可分别独立进行考虑。
全长锚固锚杆是通过锚杆与围岩之间的黏结力来控制围岩变形的。AC段锚杆通过对围岩产生压应力,达到阻止围岩变形的目的;AB段锚杆通过对围岩产生拉应力,调动深部岩层自承能力,达到控制下部岩层变形的目的。因此根据力的相互作用原理,以中性点为界,可将全长锚固锚杆杆体剪应力分为两个部分,即(图2)靠近外端点侧向上的剪应力和靠近内端点侧向下的剪应力。
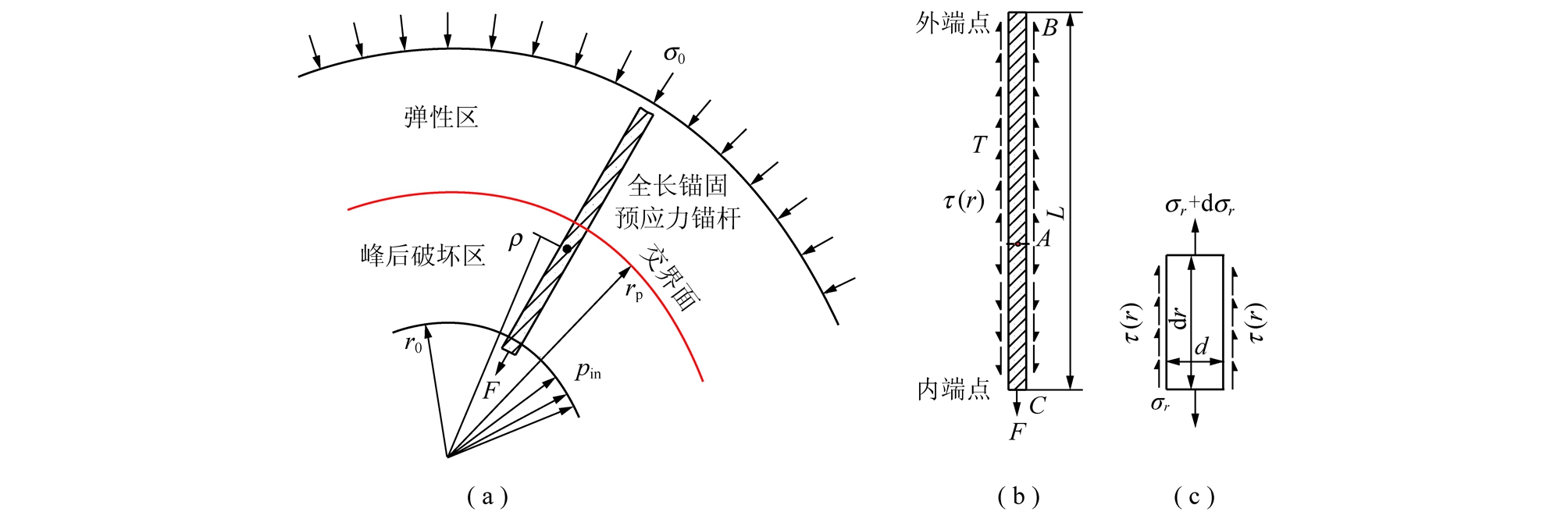
图2 稳态下全长锚固锚杆杆体受力计算力学模型
Fig.2 A mechanical model of a fully anchored pre-stressed bolt under the condition of stable equilibrium state
图2中,σ0为地应力;pin为围岩达到稳定时锚杆对其产生的支护阻力;r0为巷道开挖半径;rp为围岩弹性区与峰后破坏区交界处半径,F和ρ分别表示围岩稳定平衡状态下锚杆端头轴力大小和中性点位置;L和 d分别表示锚杆长度和直径;T和τ(r)分别表示锚杆杆体所受剪力和剪应力的大小,它们是围岩与锚杆之间相对位移的函数。
2 全锚锚杆-围岩相互作用受力分析
2.1 基本方程
(1)围岩变形满足的基本方程
平衡方程:
(1)
几何方程:
(2)
式中,σr和σθ分别为围岩径向和环向应力;εr和εθ分别为围岩径向和环向应变;u为围岩径向位移。
(2)锚杆杆体受力满足的基本方程
根据假定条件,结合文献[10]所述方法,弹性区和峰后破坏区锚杆杆体剪力均可表示为
Ti=KiΔui=Ki(uρ-ui)
(3)
式中,Ki表示锚杆与围岩之间剪切刚度,Ki=Giπd;Δui表示锚杆中性点位置与围岩之间相对位移;uρ表示锚杆杆体中性点位置位移;Gi表示岩体剪切模量;ui表示“i”区围岩位移;下标“i”表示弹性区(e)和峰后破坏区(p)。
稳态下锚杆杆体剪力与端头轴力之间的关系满足的表达式为
∑Tidr=∑Ki(uρ-ui)dr=
Kp(uρ-up)dr+
Ke(uρ-ue)dr=F
(4)
2.2 围岩应力、变形与峰后破坏区半径的确定
(1)围岩弹性区应力及变形
结合弹性力学理论可得围岩弹性区应力及变形表达式为
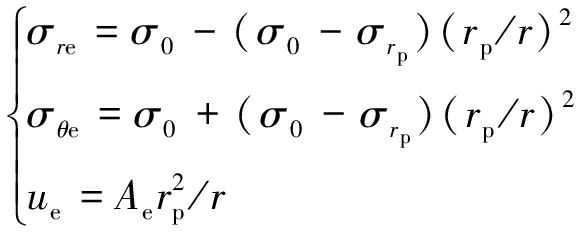
(5)
式中,Ae=(σ0-σrp)/2Ge;σrp=(2σ0-Y)/(1+N);N=(1+sin φ)/(1-sin φ);Y=2ccos φ/(1-sin φ);c和φ分别为围岩弹性区黏聚力和内摩擦角。
(2)围岩峰后破坏区应力及变形
① 围岩峰后破坏区应力
当围岩应力满足Mohr-Colomb准则时,开始进入峰后破坏区,此时围岩环向和径向应力满足关系:
(6)
式中,上标角符号“P”，“B”，“S”分别代表理想弹塑性围岩、弹脆性围岩以及应变软化围岩;Yr=2crcos φ/(1-sin φ),cr为弹脆性围岩残余黏聚力;Yrs(r)为应变软化围岩软化区任一点抗压强度。其中Yrs(r)可表达为
(7)
式中,λ为岩石应变软化系数;β为峰后破坏区剪胀系数,且β=(1+sin ψ)/(1-sin ψ);ψ为岩石剪胀角;εs和εe分别为应变软化区任一点处环向应变和峰值点处环向应变。
将式(7)代入式(6),然后联立式(1),结合应力接触条件(σrp)r=rp=σrp可得3种不同围岩状态下峰后破坏区径向应力表达式为
(8)
将式(8)代入式(6)即得围岩峰后破坏区环向应力表达式。
② 围岩峰后破坏区变形
假定围岩峰后破坏区应变仅有塑性应变组成,且满足如下关系
(9)
式中,
和
分别表示峰后破坏区径向和环向应变。联立式(2)和(9),结合位移边界条件(ue)r=rp=(up)r=rp,可得3种不同围岩状态下峰后破坏区位移表达式为
(10)
(3)围岩峰后破坏区半径的求解
联立式(8)和边界条件(σrp)r=r0=pin,即得3种不同围岩状态下峰后破坏区半径表达式
(11)
2.3 全长锚固锚杆受力计算
(1)中性点位置的求解
将式(11)分别代入式(5),(10),然后结合式(4),可得出3种不同围岩状态下锚杆中性点位置表达式。
当忽略剪胀效应影响时,3种不同围岩状态下锚杆中性点位置表达式均为
(12)
求解式(12)得
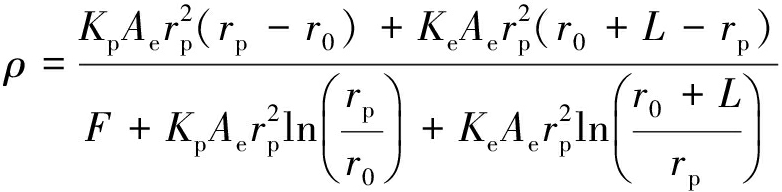
(13)
当考虑剪胀效应影响时,为简化计算,仅对应变软化围岩锚杆中性点位置表达式进行求解
(14)
求解式(14)得
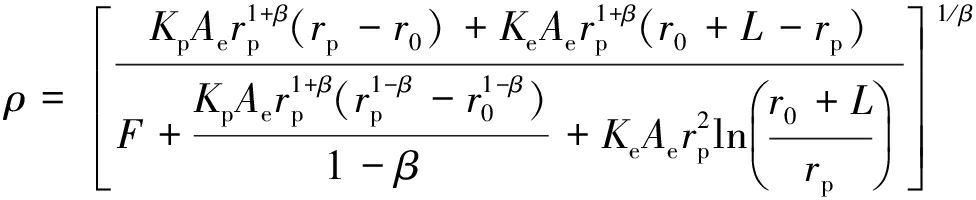
(15)
(2)锚杆剪应力的求解
如图2(b)所示,将剪力沿锚杆横截面平均分配至杆体周围,即得锚杆杆体剪应力表达式τ=T/πd,然后将式(3),(5),(7),(11)代入该式中即得3种不同围岩状态下锚杆剪应力表达式
(16)
式中,当β=1时,即为不考虑剪胀效应影响的情况。由式(16)可以分析出,在弹塑性交界rp处锚杆剪应力连续与否与围岩剪胀系数和剪切刚度密切相关。当β=1,Ke=Kp时,在r=rp处,式(16)两式相等,此时锚杆杆体剪应力具有连续性;反之,则表现出间断性变化特征。
(3)锚杆轴向正应力的求解
如图2(c)所示,分别取弹性区和峰后破坏区锚杆杆体上一段微元进行受力分析,根据微元体受力平衡条件得
(17)
化简后得
(18)
联立式(16),(18),结合锚杆轴向正应力连续条件
即得锚杆轴向正应力分布表达式。
不考虑围岩剪胀效应的锚杆轴向正应力表达式:
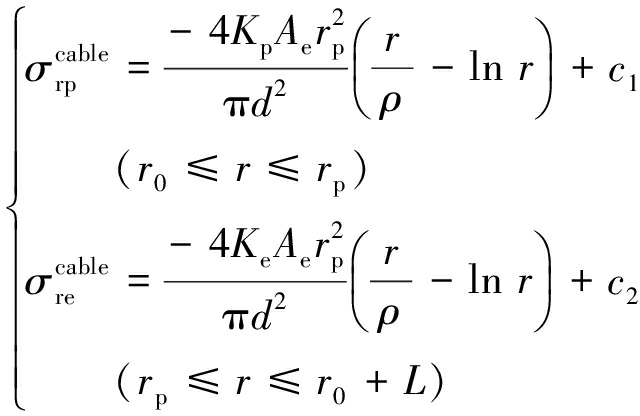
(19)
式中,
和
分别表示锚杆位于围岩峰后破坏区及弹性区部分的锚杆轴向正应力;
考虑围岩剪胀效应锚杆轴向正应力表达式:
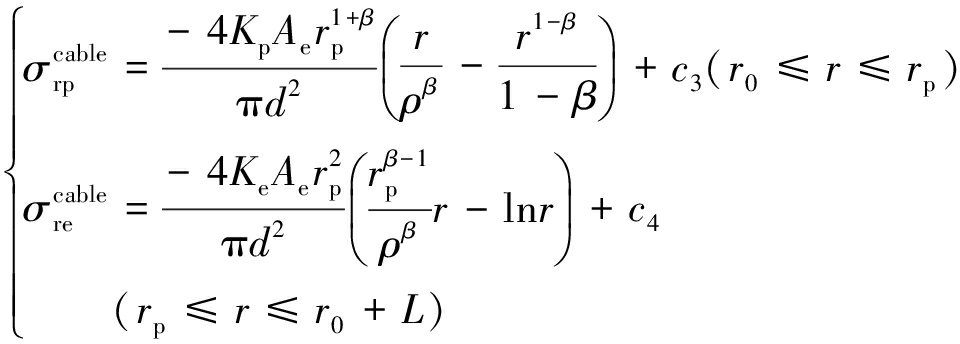
(20)
式中,
由式(19)和(20)可知,锚杆轴向正应力在其弹性区与峰后破坏区交界处是连续变化的。此外,计算结果表明:锚杆受力的大小不仅与锚杆自身尺寸有关,也与稳态下锚杆端头轴力的大小以及围岩参数等密切相关。
3 全长锚固锚杆受力影响因素
3.1 工程条件
以文献[10]所示工程背景为例,某矿回采巷道半径r0=3 m,围岩应力σ0=10 MPa,泊松比μ=0.25,初始黏聚力c=2 MPa,内摩擦角φ=30°,弹性区和峰后破坏区剪切刚度分别为Ke=10 GPa和Kp=5 GPa,全长锚固锚杆长度L=2.4 m,直径d=22 mm。取稳定状态下锚杆对围岩支护力pin=1 MPa,锚杆端头轴力F=20 kN。忽略峰后围岩剪胀性对锚杆杆体受力的影响,取剪胀系数β=1。采用控制变量法,分别分析孔口处锚杆端头轴力、残余黏聚力、剪胀系数和应变软化系数对锚杆受力特性的影响。
3.2 残余黏聚力对锚杆受力的影响
如图3所示,随着cr的不断增加,rp不断减小,而ρ却表现出先增大后减小的变化特征,且当cr达到临界值
时,ρ=rp。此时,若
中性点处于峰后破坏区;若
中性点处于弹性区。当中性点位于弹性区时,ρ随着cr的增大而减小,说明锚杆杆体外端点侧剪应力范围增大,进而说明围岩受拉范围增大,受压范围减小;当中性点位于峰后破坏区时,ρ却随着cr的增大而增大,说明锚杆杆体内端点侧剪应力范围增大,围岩受拉范围减小。
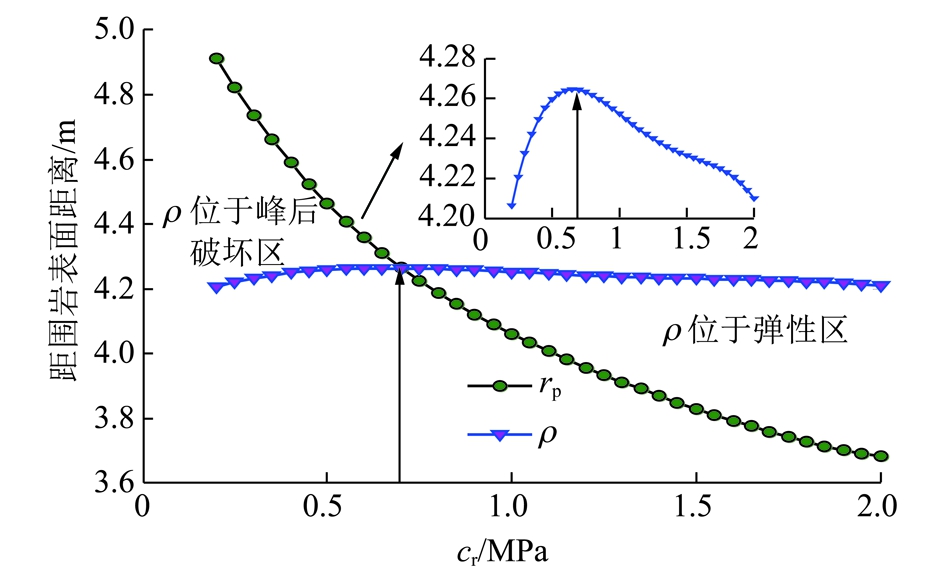
图3 中性点位置与破坏区范围随残余黏聚力变化曲线
Fig.3 Change curves of neutral point position and post-peakfailure radius with the change of residual cohesion
由图4～5可总结出如下4部分内容:① 锚杆轴向正应力从锚杆内端点至外端点呈现出先增大后减小的变化特征,且应力曲线在弹性区与峰后破坏区呈现出明显差异性,这与锚杆杆体剪应力分布特点密切相关。② 锚杆剪应力从杆体内端点至外端点呈现出先减小后增大的变化特征,且在中性点处锚杆剪应力为0。③ 忽略剪胀效应的影响,在围岩弹塑性分界处锚杆杆体剪应力的连续性与否与其分界面两侧围岩剪切刚度密切相关,当其剪切刚度满足Ke≠Kp时,锚杆杆体剪应力表现出明显间断性,反之则呈现出连续变化特征。④ 锚杆轴向正应力和剪应力均随着cr增大而减小,且剪应力在锚杆端点处取得最大值。
图4 残余黏聚力对锚杆轴向正应力的影响
Fig.4 Influence of residual cohesion on bolt axial stress
图5 残余黏聚力对锚杆剪应力的影响
Fig.5 Influence of residual cohesion on bolt shear stress
3.3 剪胀系数对锚杆受力的影响
由图6～7可知,剪胀系数对锚杆受力和中性点位置变化均产生重要影响。锚杆轴向正应力和剪应力均随着β的增大而增大,例如当β由1.1变化至1.4时,相对于β=1.0锚杆轴向正应力增大了9.96%～41.89%,内端点剪应力增大了17.87%～62.53%,外端点剪应力增大了15.01%～39.39%。这是由于β 越大,围岩破坏程度越高,巷道变形越剧烈,锚杆与围岩之间相对位移也就越大,进而锚杆受力也就越大。由表1可知,ρ随着β的增大而逐渐减小,例如当β由1.1变化至1.4时,ρ减小了25 mm,中性点位置逐渐向锚杆内端点移动,其杆体外端点侧剪应力范围增大,说明锚杆在围岩内产生的拉应力扩散范围增加,充分调动了锚杆外端点侧完整围岩自承能力和锚杆支护潜能。
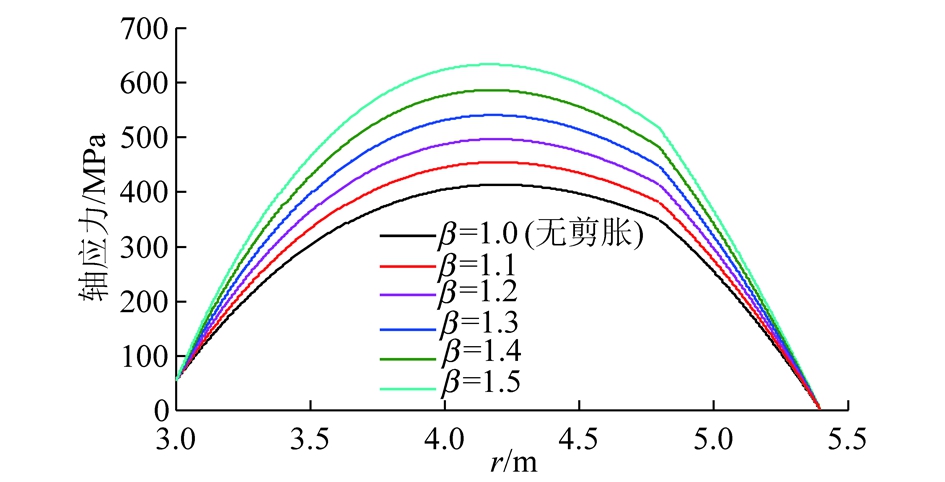
图6 剪胀系数对锚杆轴向正应力的影响
Fig.6 Influence of dilatant coefficient on bolt axial stress
图7 剪胀系数对锚杆剪应力的影响
Fig.7 Influence of dilatancy on bolt shear stress
表1 剪胀系数对锚杆中性点位置的影响
Table 1 Influence of dilatant coefficient on the location of neutral point
3.4 应变软化系数对锚杆受力的影响
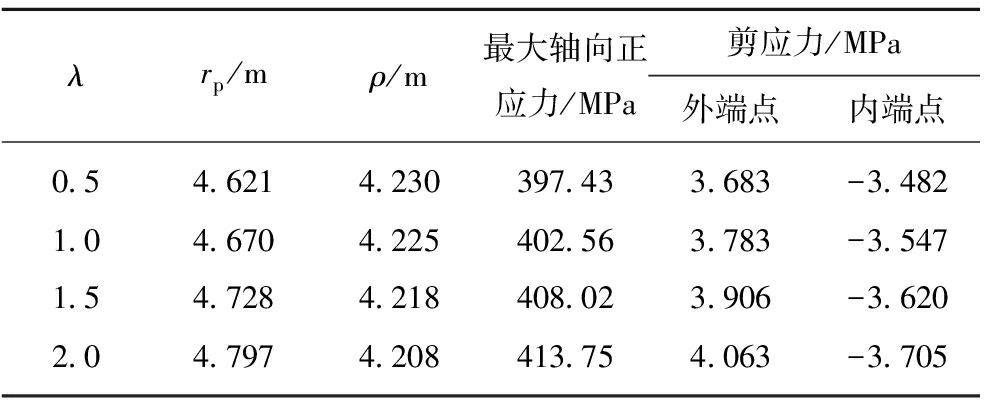
由图8可知,锚杆轴向正应力和剪应力均随着λ的增大而增大,例如,当λ由0.5变化至2时,锚杆轴向正应力、内端点剪应力和外端点剪应力分别增加了16.32,0.22和0.38 MPa,提高了4.1%,6.3%和10.32%。这是由于围岩峰后软化程度的提高加剧了巷道围岩变形,增大了锚杆与围岩之间相对位移。由表2可知,随着λ的不断增大,rp不断增大,ρ却不断减小,例如当λ由0.5变化至1.5时,rp增大了107 mm,提高了2.32%;ρ却减小了12 mm,降低了0.28%。此时,锚杆中性点位置逐渐向其内端点移动,围岩受压范围减小,受拉范围增大。分析表明:围岩应变软化程度对锚杆支护潜能的发挥具有直接作用关系,围岩应变软化程度越高,锚杆轴力越大,其控制围岩变形能力也就越强,但锚杆轴力也不宜过大,以防杆体受力超过其极限破断载荷而发生拉伸破断。因此对于极松软应变软化围岩,应适当提高锚杆极限破断载荷和延伸率来适应巷道变形较大的特点。
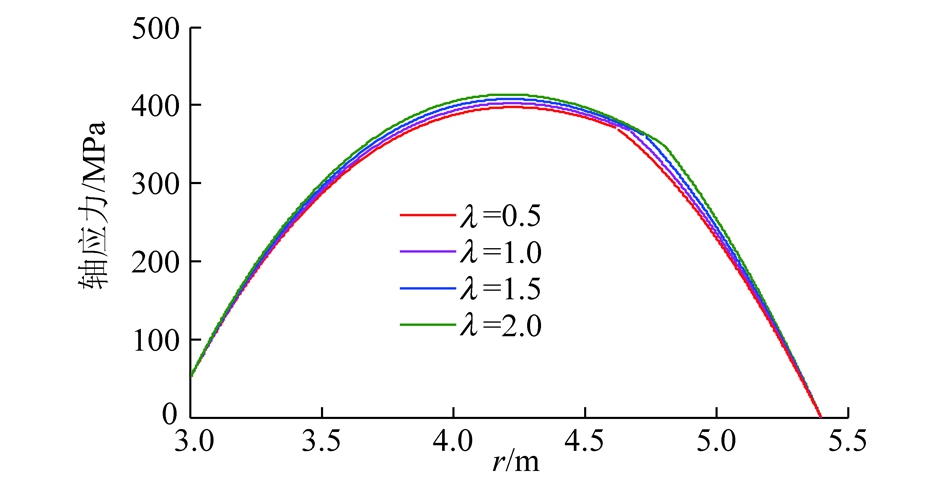
图8 应变软化系数对锚杆轴向正应力的影响
Fig.8 Influence of strain softening coefficient on bolt
axial stress
表2 应变软化系数对锚杆受力及峰后破坏范围的影响
Table 2 Influence of strain softening coefficient on bolt stress and post-peak failure radius
3.5 稳态下锚杆端头轴力对其受力的影响
由图9～10可知,锚杆杆体轴向正应力和外端点剪应力均随着F的增大而增大,内端点剪应力随着F的增大而减小。例如,当F由20 kN增加至60 kN时,锚杆轴向正应力和外端点剪应力分别增加了64.43和0.37 MPa,提高了15.57%和9.78%;内端点剪应力减小了0.19 MPa,降低了5.36%。在中性点处,锚杆轴向正应力取得最大值,剪应力取值为0,并在此处剪应力开始改变方向,远离围岩表面部分指向锚杆外端点方向,靠近围岩表面部分指向锚杆内端点方向。由表3可知,随着锚杆端头轴力的增大,中性点位置也逐渐向锚杆内端点移动。分析表明:在实际工程应用中锚杆设计应与其支护强度相匹配,使锚杆与围岩形成合理的锚固支护系统。若锚杆强度设计过小,则易发生拉伸破断,反之,则易使围岩因变形过大而发生失稳破坏。
图9 端头轴力对锚杆轴向正应力的影响
Fig.9 Influence of the end axial force on bolt axial stress
图10 端头轴力对锚杆剪应力的影响
Fig.10 Influence of the end axial force on bolt shear stress
表3 端头轴力对锚杆中性点位置的影响
Table 3 Influence of the end axial force on the location of neutral point
4 结 论
(1)建立了稳态下全长锚固锚杆杆体受力计算力学模型,考虑围岩峰后破坏特征,推导了全长锚固锚杆轴向正应力与剪应力计算表达式。
(2)锚杆轴向正应力从锚杆内端点至外端点呈现出先增大后减小的变化特征,且应力曲线在弹性区与峰后破坏区呈现出明显的差异性。
(3)中性点位置随着残余黏聚力的增大呈现出先增大后减小的变化特征,当残余黏聚力大于某一临界值时中性点位于弹性区,反之,位于峰后破坏区。锚杆轴向正应力和剪应力均随着残余黏聚力的增大而减小;在弹塑性交界处锚杆剪应力的连续性与否与围岩剪胀系数和剪切刚度密切相关,且在锚杆端点处杆体剪应力取得最大值。
(4)剪胀系数、应变软化系数及锚杆端头轴力均对锚杆轴向正应力和剪应力产生重要影响;锚杆强度设计应与其支护强度相匹配,才能使其与围岩形成合理的锚固支护系统,否则,易使锚杆发生拉伸破断或围岩发生失稳破坏。
参考文献(References):
[1] 康红普,王金华,林健.煤矿巷道锚杆支护应用实例分析[J].岩石力学与工程学报,2010,29(4):649-664.
KANG Hongpu,WANG Jinhua,LIN Jian.Case studies of rock bolting in coal mine roadways[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(4):649-664.
[2] 辛亚军,勾攀峰,贠东风,等.非软顶底板煤巷锚杆支护及围岩松动规律[J].采矿与安全工程学报,2012,29(2):203-208.
XIN Yajun,GOU Panfeng,YUN Dongfeng,et al.Loose regularity of bolting and surrounding in a non-soft floor and roof gateway[J].Journal of Mining & Safety Engineering,2012,29(2):203-208.
[3] 候朝炯,郭励生,勾攀峰.煤巷锚杆支护[M].徐州:中国矿业大学出版社,1999.
[4] 王强,吴拥政.煤矿井下锚杆预紧力控制研究[J].煤炭科学技术,2011,39(1):29-32.
WANG Qiang,WU Yongzheng.Study on bolt pretension control in underground mine[J].Coal Science and Technology,2011,39(1):29-32.
[5] LI Chong,XU Jinhai,FU Chunsheng,et al.Mechanism and practice of rock control in deep large span cut holes[J].Mining Science and Technology,2011,21(6):891-896.
[6] HOU Chaojiong.Review of roadway control in soft surrounding rock under dynamic pressure[J].Journal of Coal Science & Engineering(China),2003,9(1):1-7.
[7] 王洪涛,王琦,王富奇,等.不同锚固长度下巷道锚杆力学效应分析及应用[J].煤炭学报,2015,40(3):509-515.
WANG Hongtao,WANG Qi,WANG Fuqi,et al.Mechanical effect analysis of bolts in roadway under different anchoring lengths and its application[J].Journal of China Coal Society,2015,40(3):509-515.
[8] SHOWKATI A,MAAREFVAND P,HASSANI H.Stresses induced by post-tensioned anchor in jointed rock mass[J].Journal of Central South University,2015,22(4):1463-1476.
[9] 康红普,姜铁明,高富强.预应力锚杆支护参数的设计[J].煤炭学报,2008,33(7):721-726.
KANG Hongpu,JIANG Tieming,GAO Fuqiang.Design for pre-tensioned rock bolting parameter[J].Journal of China Coal Society,2008,33(7):721-726.
[10] 李冲,徐金海,李明.全长锚固预应力锚杆杆体受力特征分析[J].采矿与安全工程学报,2013,30(2):188-193.
LI Chong,XU Jinhai,LI Ming.The mechanical characteristics analysis of fully anchored pre-stressed bolts in coal mines[J].Journal of Mining & Safety Engineering,2013,30(2):188-193.
[11] RANJBARNIA M,FAHIMIFAR A,ORESTE P.A simplified model to study the behavior of pre-tensioned fully grouted bolts around tunnels and to analyze the more important influencing parameters[J].Journal of Mining Science,2014,50(3):533-548.
[12] 黄明华,周智,欧进萍.全长黏结式锚杆锚固段荷载传递机制非线性分析[J].岩石力学与工程学报,2014,33(2):3992-3997.
HUANG Minghua,ZHOU Zhi,OU Jinping.Nonlinear analysis on load transfer mechanism of wholly grouted anchor rod along anchoring section[J].Rock and Soil Mechanics,2014,33(2):3992-3997.
[13] 尤春安.全长黏结式锚杆的受力分析[J].岩石力学与工程学报,2000,19(3):339-341.
YOU Chunan.Mechanical analysis of wholly grouted anchor[J].Chinese Journal of Rock Mechanics and Engineering,2000,19(3):339-341.
[14] 文志杰,石永奎,崔增娣,等.全长黏结型预应力锚杆受力特性研究[J].岩土力学,2010,31(1):177-181.
WEN Zhijie,SHI Yongkui,CUI Zengdi,et al.Study of stress features of fully grouted prestressed anchors[J].Rock and Soil Mechanics,2010,31(1):177-181.
[15] 林健,任硕,杨景贺.树脂全长锚固锚杆外形尺寸优化实验室研究[J].煤炭学报,2014,39(6):1009-1015.
LIN Jian,REN Shuo,YANG Jinghe.Laboratory research of resin full-length anchoring bolts dimension optimization[J].Journal of China Coal Society,2014,39(6):1009-1015.
07