按照厚煤层定义,当单一煤层厚度超过3.5 m时为厚煤层,而单一煤层厚度超过8 m则为特厚煤层[1]。综放开采技术很好地解决了厚与特厚煤层矿井的高效和安全开采问题,凡是条件允许综放开采技术已经成为了我国厚及特厚煤层矿区的主要采煤方法[2]。山西、内蒙等地区赋存厚与特厚煤层的矿井较多,且大多采用综放开采技术,特厚煤层综放开采一次性采放煤层厚度大,工作面推进速度快,开采强度大;该地质采矿条件特征也使得地表沉陷规律表现出特殊性。
地表沉陷预计可定量研究开采沉陷影响反映至地表移动变形在时间和空间上的分布规律[3];地表沉陷预计既是沉陷机理研究的目标,也是理论应用于工程的实际需要,而科学、合理的预计模型是保证预测准确的前提[4-5]。
随着煤矿开采沉陷学的发展,相关学者针对不同地质采矿条件提出了新的预计方法或进行了一定程度的改进与修正,使得地表沉陷预计理论更加丰富、预计结果的精确性更加提高。何万龙等[6]运用叠加原理讨论了采动滑移与地形的关系,并建立了山区地表移动预计数学模型;戴华阳等[7-8]提出了基于倾角变化的矢量法开采沉陷预计模型;吴侃等[9]提出添加修正项的方法,提高了概率积分法的预计精度;郭文兵[10]提出了全采多工作面预计与条带开采预计参数相结合的方法,提高了深部大采宽条带开采的预计精度;郝延锦等[11]基于托板理论、刘玉成和曹树刚[12]基于关键层理论并都假定沉陷盆地边界为椭圆形状,建立了地表沉陷预测模型。以上研究成果在一定程度上弥补了已有模型的部分缺陷,然而或未考虑到岩层的沉陷控制作用,或适用条件有限,限制了沉陷预计方法的实践应用。
在特厚煤层综放开采地表移动变形过程中,不能简单的将原上覆岩层看作均质松散体,需要考虑到覆岩的强度特征、层状结构与沉陷控制作用,提高地表沉陷的预计精度。本文从此角度出发进行了公式推导和理论研究,并初步建立了地表沉陷预计模型。
1 特厚煤层综放开采地表沉陷规律特殊性分析
1.1 沉陷盆地特殊性分析
特厚煤层综放开采地表移动变形实测资料表明,特厚煤层综放开采在开切眼和终采线两侧的下沉分布差异较大,盆地非对称性分布特别明显;开切眼处下沉盆地边缘较终采线处陡峭,地表倾斜值较大。其原因可归纳为
(1)岩梁破断结构不同:工作面自开切眼处向前推进,随着采空区空间的增加,部分顶板垮落,形成暂时稳定的承重拱形结构,由于一次采出煤体厚度大,垮落后的岩块不能充满采空区,由冒落岩块组成的铰接拱形结构向前并向上扩展,垮落带、裂缝带高度也逐渐变大,此过程岩梁为两端固定支承的固支梁结构[13]。
工作面推进至终采线附近时,顶板自下而上的破断形状沿走向剖面为倒阶梯形,终采线煤柱侧岩梁约束形式为固支;工作面后方,因为垮落岩块的堆砌作用,使得一定高度的岩梁末端接矸,因此可认为终采线处岩梁为悬臂梁[13]。
岩梁在不同约束形式下的破断距离与破断位置的差异,将逐步扩展到上覆岩层,从而影响到地表的盆地形状、角值大小及盆地两侧的非对称性。
(2)中上部基岩移动方向不同:基本顶初次破断后,工作面前方为煤岩体,后方是采空区,工作面前方为固定约束,后方自由约束,伸向采空区的岩梁有竖直下沉和向工作面推进方向的位移分量,带动着上部岩层向停采线侧移动。
(3)扰动影响后稳定时间不同:工作面自开切眼向终采线方向推进,终采线侧稳定时间比开切眼侧少1~2 a,稳定时间对盆地两侧的岩层移动变形也有差异。
1.2 主要影响角正切特殊性分析
特厚煤层高强度综放开采条件下,主要影响半径变小,盆地边缘更加陡峭,碗形盆地现象更加明显,主要影响角正切值偏大。原因为
(1)覆岩移动结构差异:采出空间的加大,垮落带范围大,覆岩沿煤壁的切落现象明显,岩层向煤壁两侧的传递效应与传播范围减小;同时,导水裂缝带发育高度大,弯曲下沉带内的弹性层状岩层厚度相对减小,拉伸变形向采空区外侧传播距离变小,使得特厚煤层综放开采地表沉陷的主要影响半径变小。
(2)松散层阻碍了岩层向盆地外传播的能力:研究区域黄土层厚度约45 m,黄土抗拉强度较低,易形成地表裂缝,裂缝阻隔了地表移动变形的传递,使得沉陷主要影响区域小而集中。
(3)工作面推进速度快:工作面推进速度快使得上覆岩层下沉速度加快,采空区覆岩悬空的时间减小,向采空区外侧传递的梁板移动变形时间变短。
1.3 拐点偏移距特殊性分析
近浅埋特厚煤层综放开采拐点偏移距较小。由于工作面上方边界附近的岩层并非沿煤壁切断冒落或呈阶梯状弯曲下沉,覆岩中的厚硬岩层使得采空区边缘的冒落空间呈悬臂梁支撑形式,在四周煤层未开采时,拐点略偏向采空区一侧;并且岩层越硬,顶板悬臂梁越长,拐点偏移距越大。
特厚煤层综放开采一次性采出煤层厚度大,顶板沿煤壁切断的岩层范围大,支撑上部基岩的悬臂梁位置高,使得地表下沉向采空区中心传播的能力降低,拐点偏向采空区侧的距离变小。
2 近浅埋深特厚煤层综放开采沉陷预计模型构建
基于以上分析可知,近浅埋深特厚煤层综放开采条件下覆岩移动变形及地表沉陷机理与常规条件下的地表沉陷有所不同,在砌体梁结构和覆岩挠曲岩梁结构的共同作用下,覆岩移动不仅表现出随机介质特征,同时也表现出较强的板壳挠曲特征。特别是开采边界附近,受厚硬岩层的控制作用明显,采用随机介质理论的地表沉陷预计与实测值在沉陷盆地边缘区域吻合程度有一定偏差。因此,需要将弹性梁板理论和随机介质理论相耦合,建立适用于水平煤层、矩形工作面开采、特厚煤层综放开采条件下的地表沉陷预计模型,并进行实例应用。
2.1 概率积分法预计理论
概率积分法沉陷预计模型假定上覆岩层介质颗粒是由体积大小相同、质量均一的小球构成的,当煤层某区域被移出后,上部岩层球体将服从随机概率向下、向中部移动并达到新的稳定;并且同一层位内,被移出区域正上方小球填补空缺概率最大、最外侧的小球移动概率最小,如图1所示。在图1(a)中,根据岩块的相对空间位置对小球进行编号;图1(b)中数字表示将a1球下部煤层采出后,上部各小球移动并填补空缺的概率值。
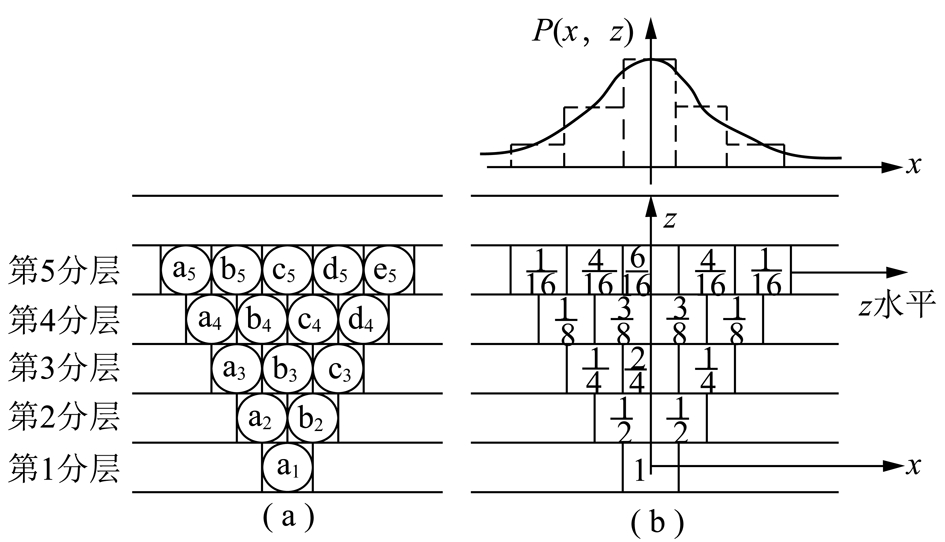
图1 随机介质体理论预计模型
Fig.1 Prediction model of random medium theory
2.2 基于弹性梁板和随机介质理论耦合作用的沉陷预计模型
2.2.1 弹性梁板控制地表沉陷理论基础
由近浅埋深特厚煤层综放开采条件下岩层移动变形特征、开采空间、覆岩与地表沉陷空间的变化规律可近似认为:岩层移动变形对地表的沉陷控制作用比较明显;开采空间较小(非充分采动)时,覆岩及地表移动变形可认为是弹性梁板控制的挠曲变形;当开采空间较大(充分采动)时,覆岩及地表的移动变形表现为岩梁协调移动变形与随机介质体共同作用的移动特征;并且在近浅埋深特厚煤层综放开采这种深厚比值较小的开采条件,岩层对地表沉陷控制特征更加明显。
2.2.2 预计模型的构建
(1)沉陷预计坐标系统的建立
以水平煤层倾向充分采动的半无限开采为例,其走向主断面坐标系统如图2所示,包括岩层沉陷控制坐标系和地表沉陷坐标系;前者以开采边界作为原点O1,X轴指向采空区,Z1轴指向地表;地表沉陷坐标系以开采边界正上方的地表为原点O2,横轴X表示沿走向主断面的坐标位置,Z2表示地表移动变形值,如下沉值W(x)向下为正,水平移动值U(x)向上为正。
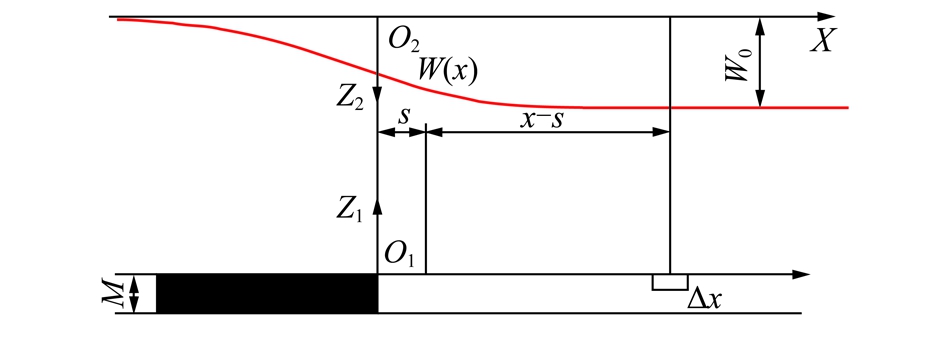
图2 沉陷预计坐标系统示意
Fig.2 Diagram of surface subsidence prediction coordinated system
(2)层状弹性梁板和随机介质理论耦合作用地表沉陷预计模型
若煤层位置采出微小单元Δx,地表对应下沉记为ΔW可由沉陷影响函数F(x)表示为
ΔW=F(x)Δx
(1)
并且认为地表移动变形是弹性层状岩体与随机介质体概率移动的共同作用结果,其移动概率及量值由弹性层状岩体与随机介质体的作用关系及沉陷影响函数共同决定。则式(1)可用层状结构岩体与随机介质颗粒体的耦合函数表示为
ΔW=n1W1(x)+n2W2(x
(2)
式中,W1(x),W2(x)分别为弹性层状岩体的地表沉陷函数与随机介质体的沉陷计算函数;n1,n2分别为两种介质体的沉陷比率系数,且n1+n2=1。
2.2.3 地表沉陷函数的推导
弹性岩梁控制的地表沉陷函数
对矩形开采工作面,设上覆岩层自上而下共有m层(第0层为松散层),取第i层作为研究对象,岩层厚度为hi,由于岩层厚度hi远小于水平方向上的尺寸。根据沉陷盆地主断面的弹性梁理论,岩层移动变形可看作由沉陷控制层的挠曲引起,对于两端简支的弹性岩梁[14],其挠曲函数为
(3)
式中,qi为作用于第i层岩梁的均布荷载;l为研究主断面方向受扰岩梁长度;Ei为岩梁弹性模量;Ii为岩梁截面矩,且岩梁最大挠度![]() 可表示为
可表示为
(4)
将式(4)代入式(3)可得到不涉及岩梁物理力学参数方程为
(5)
由式(5)可知,任意点沉陷量可由岩梁最大挠度和受扰岩梁长度两个参数构成的方程表示。
(2)随机介质理论的地表沉陷计算函数
根据随机介质理论,采出煤层倾角为α、法向厚度为M的任意微小煤层块段,地表点的沉陷函数为
(6)
其中,q为充分采动时地表下沉系数;r为主要影响半径。开采x1-x2块段后,地表任意点下沉可表示为
(7)
充分采动条件下的地表最大下沉值![]() 由于弹性岩梁最大挠曲值应与随机介质理论最大下沉值一致,则式(5)可简化为
由于弹性岩梁最大挠曲值应与随机介质理论最大下沉值一致,则式(5)可简化为
![]()
(8)
若将非充分采动条件下的最大下沉值与煤层沿法向厚度的比值记为η。即开采未充分采动时η<q;当开采达到充分采动后η=q。因此式(8)可化为式(9)
(9)
其中,Mηcos α为根据随机介质理论计算最大下沉值,或者是实际开采产生的最大下沉值![]() 将式(7)和(9)代入到式(2)可以得到开采任意块段煤层x1-x2地表走向主断面任意点下沉函数:
将式(7)和(9)代入到式(2)可以得到开采任意块段煤层x1-x2地表走向主断面任意点下沉函数:
![]()
(10)
(3)地表任意点(x,y)的下沉计算函数
岩层在横向载荷作用下,弹性弯曲变形一般小于它的厚度,认为符合弹性薄板的基本要求,能够采用弹性薄板小挠度弯曲理论[15-17]进行研究,将上覆岩层沿走向受扰长度记为l1,沿倾向尺寸记为l2,则第i岩层面挠度方程为
(11)
根据积分相乘原理,可以求出开采走向长度L1=x1-x2与倾向长度L2=y1-y2煤层,地表任意点A(x,y)的下沉可表示为
![]()
(12)
由式(11)与式(12)可得出适用于水平煤层、矩形工作面开采条件下的层状弹性梁板和随机介质共同作用下地表点(x,y)的下沉计算公式:
![]()
(13)
2.2.4 沉陷比率系数n1与n2值分析
地表沉陷比率系数n1与n2是关键参数,它们的变化直接影响着层状厚硬岩层对随机介质体概率移动变形的作用结果,为此,绘制了不同沉陷比率系数条件下的地表下沉曲线,如图3所示。
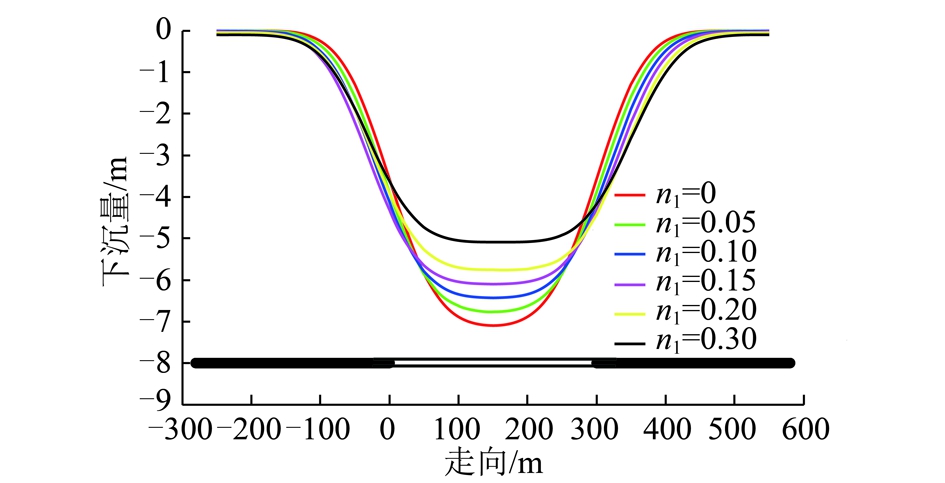
图3 不同岩层沉陷比率系数条件地表下沉曲线
Fig.3 Surface subsidence curves for different subsidence ratio coefficient of rock stratum
由岩层梁板与松散介质耦合作用地表下沉曲线可知,从岩层力学控制地表沉陷角度讲,相同荷载时硬岩承载能力强,其挠曲量值较小;在相同挠曲时,坚硬岩层的受扰动岩梁较长,地表沉陷盆地范围较大,沉陷盆地边界收敛速度变慢,但沉陷量值较小。该模型可适当修正概率积分法边界收敛快与沉陷盆地两侧非对称性等问题。
由前述特厚煤层综放开采沉陷特征分析可知,当开采范围较小时,覆岩尚未破断垮落,覆岩主要以岩梁的挠曲为主,岩层的板梁控制作用明显,且岩层沉陷比率系数值较大;随开采空间加大,上覆岩层坚硬顶板初次垮落后,煤壁两侧为悬臂空间,采空区中部形成的“短砌体梁”结构,岩层沉陷比率系数有所减小;当工作面继续推进,随机介质移动变形逐渐占主体,岩层沉陷比率系数进一步减小;当达到充分采动时,岩层对地表沉陷的控制系数趋于常数。
3 参数选取及应用实例
在上述地表沉陷预计公式推导过程中,采用空间变形叠加原理,可分别计算出概率积分法移动变形和弹性梁板的挠曲变形,然后根据各沉陷控制函数及其概率进行叠加。岩层受扰长度(l1与l2)一般由采深、岩性、采厚等决定。
3.1 弹性梁板参数选择
3.1.1 覆岩受扰动高度范围
试验区位于山西省朔州市,工作面平均采深260 m,采出煤层厚度为14.5 m,煤层倾角约为2.3°,综放开采一次采全高。为确定上覆岩层受扰动影响高度范围,应用FLAC3D对上覆岩层塑性区破坏特征和最大主应力分布特征进行了模拟研究。
图4为试验区工作面达到充分采动时覆岩的塑性区破坏情况,由数值模拟结果可知,由于煤壁两侧的切割作用和垮落岩块支撑作用覆岩的导水裂缝带高度较工作面中部高;“两带”高度沿煤层走向方向似“马鞍形”。

图4 充分采动时覆岩的塑性破坏场
Fig.4 Plastic damage field for fully mining
根据试验数据可知开切眼侧导水裂缝带高度约为162 m,终采线侧导水裂缝带高度约为156 m,工作面中部导水裂缝带高度约为95 m。
3.1.2 上覆岩层扰动角度
由数值模拟结果可知(图5),采空区上部一定区域内为减压区,该减压区常认为是垮落带范围;垮落带之上为类似“马鞍形”的拉应力区;“马鞍形”的区域上部由于厚硬岩层的支撑作用,出现了应力缓冲区;减压区上部即为弯曲下沉带,该区域中部有呈“倒钝角三角形”分布的压应力区。
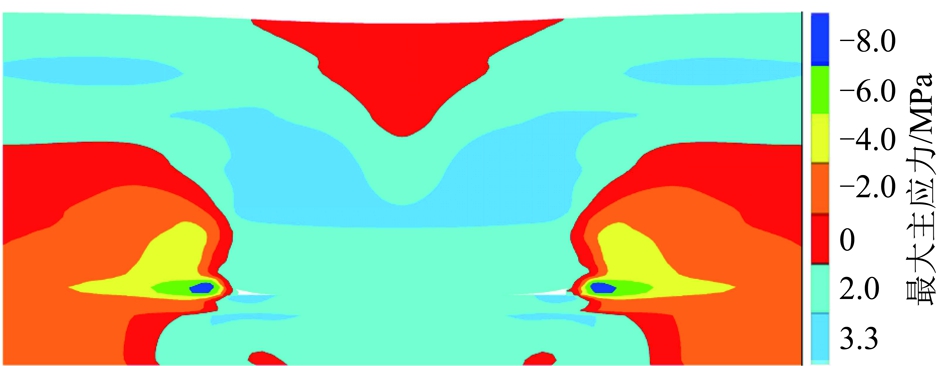
图5 充分采动时覆岩内部最大主应力
Fig.5 Maximum principal stress nephogram of overlying strata
for fully mining
工作面两侧的煤岩体内部,则分别出现了横向应力升高区和应力降低区。由模拟结果数据求得试验区工作面开切眼侧岩层扰动区与煤柱侧夹角约为58.2°,工作面终采线侧岩层扰动区与煤柱侧夹角约为57.0°。
3.1.3 上覆岩层扰动长度
由以上结果数据可知,位于煤层顶板约159 m以上的上覆岩层沿走向主断面方向受扰动长度l1=工作面长度+162 m/tan 58.2°+156 m/tan 57.0°。
3.2 应用效果对比分析
将该模型算法应用于试验区地表移动观测线的曲线拟合求参中,并将计算结果和实测数据及概率积分法曲线拟合求参结果相比较,如图6所示。
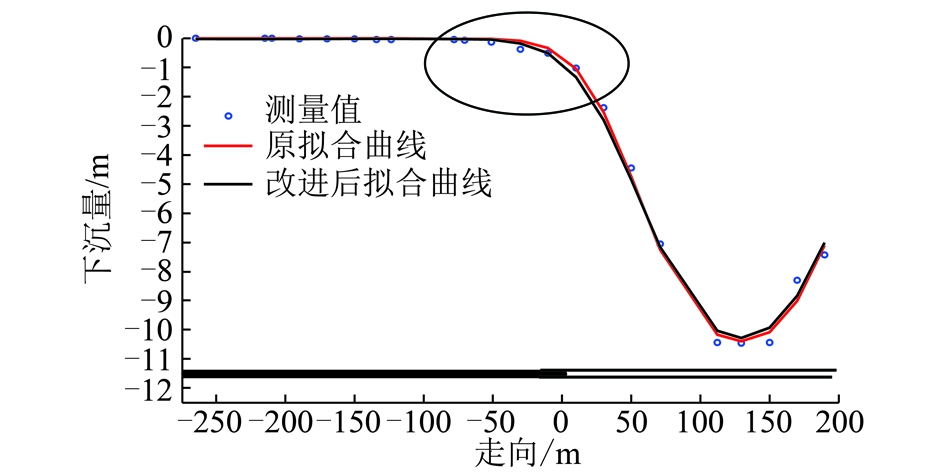
图6 原概率积分法与改进算法曲线拟合求参对比曲线
Fig.6 Correlation curves between probability integral
method and algorithm improvement
由对比结果可知,基于层状弹性梁板岩层变形和随机介质理论耦合作用预计模型算法对特厚煤层综放开采地表沉陷边界控制作用较概率积分法沉陷算法与实测结果吻合程度好,说明该模型适合于特厚煤层综放开采地表沉陷;同时该模型较好地解决了概率积分法边界收敛迅速、下沉盆地两侧非对称性(盆地两侧的岩梁扰动长度差异)等问题,使得地表沉陷预计精度有所提高。
4 结 论
(1)依托于朔州某试验区地表移动变形实测数据,分析了近浅埋深特厚煤层综放开采的地表沉陷规律特殊性。
(2)考虑厚硬岩层对地表沉陷的控制作用,并基于层状弹性梁板岩层沉陷控制理论和随机介质理论,建立了适合近浅埋深特厚煤层综放开采沉陷预计模型。
(3)该沉陷预计模型算法与实测结果吻合程度较好,适合于特厚煤层综放开采地表沉陷预计应用;较好地解决了概率积分法边界收敛迅速与下沉盆地两侧非对称性等问题,地表沉陷预计精度有所提高。
参考文献(References):
[1] 杨永康.特厚煤层大采高综放采场覆岩移动规律及围岩控制研究[M].北京:煤炭工业出版社,2014.
[2] 滕永海,唐志新,郑志刚.综采放顶煤地表沉陷规律研究及应用[M].北京:煤炭工业出版社,2009.
[3] 何国清,杨伦,凌赓娣,等.矿山开采沉陷学[M].徐州:中国矿业大学出版社,1991.
[4] 乔世范.随机介质变形破坏判据研究及其工程应用[D].长沙:中南大学,2006.
QIAO Shifan.Study on the deformation failure criterion of stochastic medium and its application[D].Changsha:Central South University,2006.
[5] 煤炭科学科学究院北京开采所.煤矿地表移动与覆岩破坏规律及其应用[M].北京:煤炭工业出版社,1982.
[6] 何万龙,康建荣.山区地表移动与变形规律的研究[J].煤炭学报,1992,17(4):1-15.
HE Wanlong,KANG Jianrong.Laws of ground movement and deformation in mountainous areas[J].Journal of China Coal Society,1992,17(4):1-15.
[7] 戴华阳,王金庄,蔡美峰.岩层与地表移动的矢量预计法[J].煤炭学报,2002,27(5):473-478.
DAI Huayang,WANG Jinzhuang,CAI Meifeng.Extraction-vectorized prediction method for rock and surface movement[J].Journal of China Coal Society,2002,27(5):473-478.
[8] 戴华阳,王金庄.急倾斜煤层开采沉陷[M].北京:中国科学技术出版社,2005.
[9] 吴侃,葛家新,周鸣,等.概率积分法预计模型的某些修正[J].煤炭学报,1998,23(1):33-36.
WU Kan,GE Jiaxin,ZHOU Ming,et al.Some modifications of using probability integral method to predicate model[J].Journal of China Coal Society,1998,23(1):33-36.
[10] 郭文兵.深部大采宽条带开采地表移动的预计[J].煤炭学报,2008,33(4):368-372.
GUO Wenbing.Surface movement predicting problems of deep strip pillar mining[J].Journal of China Coal Society,2008,33(4):368-372.
[11] 郝延锦,吴立新,戴华阳.用弹性板理论建立地表沉陷预计模型[J].岩石力学与工程学报,2006,25(S1):2958-2961.
HAO Yanjin,WU Lixin,DAI Huayang.Establishing a ground settlement prediction model with elastic slab theory[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(S1):2958-2961.
[12] 刘玉成,曹树刚.基于关键层理论的地表下沉盆地模型初探[J].岩土力学,2012,33(3):719-724.
LIU Yucheng,CAO Shugang.Preliminary study of surface subsidence model based on theory of key rock stratum[J].Rock and Soil Mechanics,2012,33(3):719-724.
[13] 钱鸣高,缪协兴.采场上覆岩层结构形态与受力分析[J].岩土力学与工程学报,1995,14(2):97-106.
QIAN Minggao,MIAO Xiexing.Theoretical analysis on the structural form and stability of overlying strata in longwall mining[J].Chinese Journal of Rock Mechanics and Engineeing,1995,14(2):97-106.
[14] 刘鸿文.材料力学:第4版[M].北京:高等教育出版社,2004.
[15] 徐芝纶.弹性力学:第4版[M].北京:高等教育出版社,2006.
[16] 王焕定,王伟.有限单元法教程[M].哈尔滨:哈尔滨工业大学出版社,2003.
[17] 吴立新,王金庄.托板控制下开采沉陷的滞缓和集中现象研究[J].中国矿业大学学报,1994,13(4):10-19.
WU Lixin,WANG Jinzhuang.Study of mining subsidence delay and concentration under the control of holding-plate[J].Journal of China University of Mining & Technology,1994,13(4):10-19.
汤伏全,李庚新,原一哲.煤矿采空区地表重力异常效应模拟研究[J].煤炭学报,2018,43(4):945-950.doi:10.13225/j.cnki.jccs.2017.1578
TANG Fuquan,LI Gengxin,YUAN Yizhe.Simulation and study on ground gravity anomaly effect in goaf of coal mine[J].Journal of China Coal Society,2018,43(4):945-950.doi:10.13225/j.cnki.jccs.2017.1578