我国煤炭资源丰富,其开采方式主要为地下开采。多年来的大规模高强度开采形成了大量的地下采空区[1],在上覆岩层的自重作用下顶板将逐层垮落导致空洞效应向上传递,直至地表形成塌陷盆地。地表塌陷的程度取决于煤层开采深度、工作面大小、覆岩特性等多种因素。由于受岩层垮落碎胀影响和基岩关键层的控制作用,多数采空区上覆岩层并未充分垮落和压实,不同层位上(包括采空区)存在大量的空洞,尤其是一些建筑物下的条带开采和地方小煤窑,以及在巨厚坚硬岩层下进行采煤时,采空区的垮落基本上被上覆岩层所阻隔,并未传递到地表。一些小煤窑的盗采和滥采使得老采空区的空间位置亦无法确定。这种长期存在的地下空洞效应导致老采空区地面发生持续的残余变形或突然塌陷等安全隐患,严重影响了矿区的安全生产和各种工程的选址与建设[2]。目前,对于老采空区的探测一般采用钻探方法或物探方法。常用物探技术有电阻率法、探地雷达法、电磁法、三维地震法、放射性法、重力法等[3-8]。其中,重力法是通过重力场变化判定和解读地球内部结构构造、矿产资源分布规律等的一种重要手段。老采空区的空洞效应会引起地面重力场发生变化,但由于这种重力异常较小,一般只有50~500 μGal的量级。因此多数学者认为,通过地表获得的重力异常数据来反演地下采空区的空间分布和变化特征在技术上难以实现。而近年来,随着重力测量仪的精度不断提高,如CG-5型相对重力仪的测量随机误差在5 μGal左右,展开上述问题研究已具有现实可能性。为此,本文以现有的布格重力理论模型为基础,将地下采空区简化为立方体空洞,分析采空区地表的重力异常与采空区特征之间的关系,通过数值模拟方法探讨基于重力异常效应进行采空区反演的可行性,为煤矿采空区探测和地面长期稳定性监测提供一种新的技术途径。
1 煤矿采空区地表重力异常计算模型
地下岩层、矿产密度分布不均匀或因矿产开发等质量亏损会导致地表重力发生变化,称为重力异常[9]。本文采用布格重力模型来模拟计算规则采空区地表的重力变化[10]。如图1所示,以采空区左边界中央在地表的垂直投影作为地表坐标系原点,地水平面内沿采空区延伸方向为X轴,沿采空区宽度方向为Y轴,垂直向下为Z轴正向。采空区长、宽、高分别A,B,C,埋深为H。
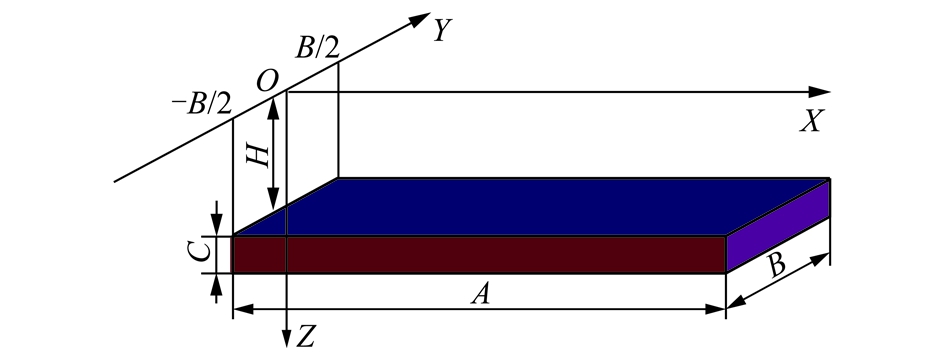
图1 计算模型坐标系
Fig.1 Coordinate system of calculation
根据重力场的计算公式,该采空区的重力场可表示为
(1)
式中,G为万有引力常数;ρ为场源密度;(x,y,z)为观测点的坐标;(ξ,η,ζ)为采空区场源点的坐标。
对式(1)的积分求解,许多学者都进行了研究[11],本文使用式(2)来计算该积分。
Δg=-Gρ‖(ξ-x)ln[(η-y)+R]+(η-
y)ln[(ξ-x)+R]-(ζ-z)×
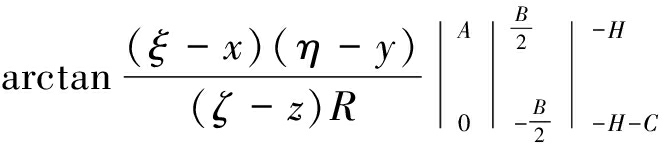
(2)
2 采空区地表的重力异常分布特征
为分析采空区特征对于地表重力异常的影响,以矩形工作面开采条件建立模拟计算的基准模型,设采空区长度A、宽度B、高度C及埋深H分别为:2 000,200,4,300 m。剩余密度为ρ =2 680 g/cm3,在其它尺度参数不变的情况下,地表重力异常随采空区长度A变化的分布曲线如图2(图中地表点位置坐标零点在采空区左边界正上方,向右为正)所示。当采空区长度达到1 000 m后,重力异常峰值大小趋于不变,在采空区中央地表达到最大重力异常值,在该基准模型条件下约为90 μGal。重力异常曲线呈现以采空区中心为对称的分布形态,这对于通过重力异常分布来反演采空区边界具有参考意义。

图2 不同采空区长度A的重力异常分布曲线
Fig.2 Distribution curves of surface gravity anomalies at different length

图3 不同采深H的地表重力异常分布曲线
Fig.3 Distribution curves of surface gravity anomalies at different mining depth
当采空区深度H从300 m变化到100 m时,地表重力异常分布曲线如图3所示。各曲线变化形态基本相似,在采空区边界附近的地表有所不同。随着空洞深度变小,重力异常峰值由59 μGal增大到156 μGal,其发生位置由采空区中央向边界方向偏移。
当采空区宽度B从100 m变化到300 m时,地表重力异常分布曲线如图4所示,随着开采宽度的增大,重力异常峰值由49 μGal增大到122 μGal,各曲线分布形态基本呈一致。

图4 不同采宽B的地表重力异常分布曲线
Fig.4 Distribution curves of surface gravity anomalies at different mining width
当采空区高度C从3 m变化到7 m时,地表重力异常分布曲线如图5所示。重力异常峰值由68 μGal增大到158 μGal,其发生位置位于采空区内侧地表,各曲线分布形态基本呈一致。
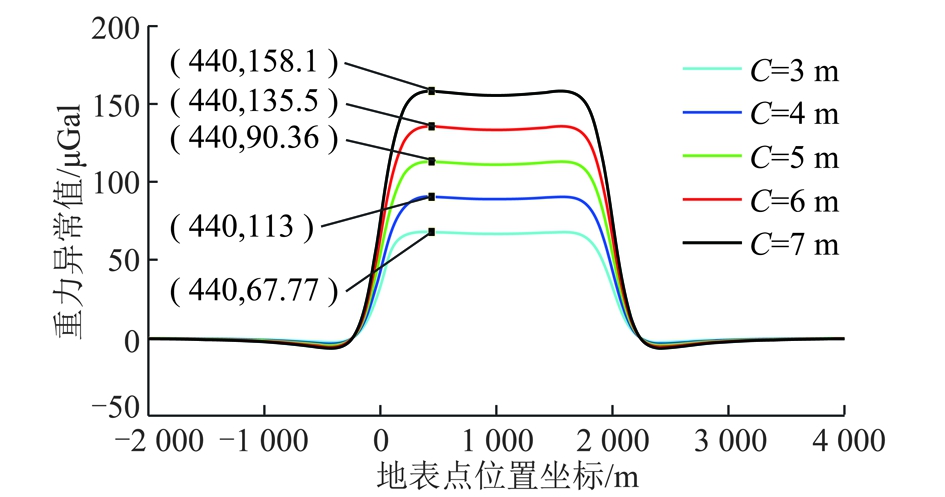
图5 不同采高C的地表重力异常分布曲线
Fig.5 Distribution curves of surface gravity anomalies at different mining depths
分析图4和图5可知,在基准模型条件下地表重力异常峰值与采宽、采高均呈线性正相关。分析图3可知,地表重力异常峰值与采空区埋深呈非线性的负相关,如图6所示。
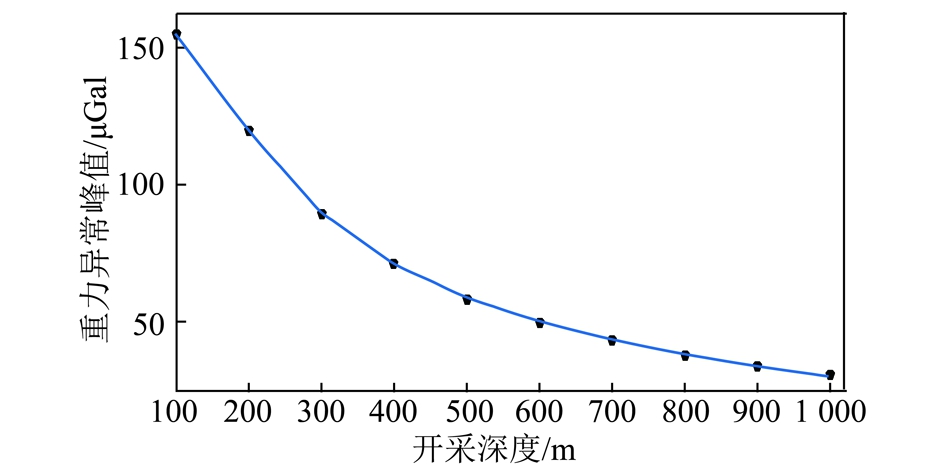
图6 采空区埋深与重力异常峰值的关系
Fig.6 Relationship between different mining depths and maximum gravity anomalies
在基准模型条件下,采空区重力异常分布曲线(图7(a))的形态较为简单,在采空区边界位置的地表重力异常未见明显特征。所以,仅依据重力异常曲线难以反演确定重力变化与采空区边位置的关系。为此,对重力异常曲线(图7(a))进行一次差分处理来分析其变化特征[12-13]。由于传统的有限差分格式在步长较大的情况下精度偏低,若要提高精度则需要增加网格点。因此,这里采用计算物理学中广泛应用的紧致差分格式[14-15]逼近算法来进行一次差分处理。该方法所需的网格点较少,且截断误差系数较小,其基本算法如下:对于区间[a,b]上的离散函数F(x),节点为x1,x2,…,xn,步长h=xi-xi-1,i=1,2,…,n。节点处的函数值为f(i),一阶导数值为df(i),对于节点xi,设一阶导数与函数值之间满足式(3):
![]()
(3)
式中,al为差分格式的待定系数,l=1,2,3,…,n。

图7 基准模型下地表重力异常及其一阶导数曲线
Fig.7 Ground gravity anomaly and its first derivative curve under the normal model
则函数F(x)具有三阶逼近精度的一次差分。即其一阶导数df(i)可通过对式(3)采用Taylor级数展开,根据精度需要得到待定系数al的代数方程,用追赶法求解该代数方程得到相应的待定系数。本文采用计算步长为h=10 m,并对边界点使用5点偏差逼近(i=1和i=n时),求得三阶紧致差分逼近算法满足:
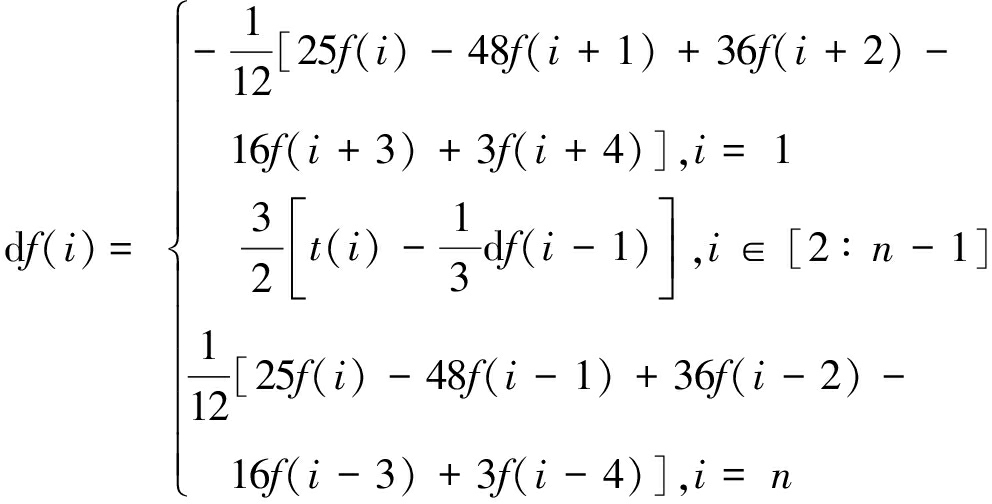 (4)
(4)
式中,![]() 为步长。
为步长。
对图7(a)的曲线函数值利用上述算法计算其一次差分,得到基准模型下地表重力异常分布的一次差分曲线,如图7(b)所示。
由图7(b)可以看出,重力异常一次差分曲线的两个峰值正好位于采空区边界正上方附近。两峰值之间的距离与采空区长度相等。因此在理论模型下,可根据采空区地表重力异常的一次差分曲线的峰值位置来判断采空区边界位置并确定采空区范围。
3 基于重力异常模拟数据反演采空区边界位置
由于实地观测的重力异常数据中不可避免会存在一定的随机误差,使得重力异常曲线偏离图7所示的标准形态。在大地测量及岩土工程领域,常通过数值模拟和加入随机误差的方法来研究实际工程问题[16]。因此,本文在重力异常曲线中加入一定的随机误差后,来分析基于重力异常反演采空区边界位置的可行性。
首先,根据目前高精度相对重力仪(如CG-5型仪器)的测量精度情况,在理论重力异常曲线中加入±5 μGal的随机测量误差,得到地表重力g异常模拟测量值的散点分布,分别采用有理数拟合法、正弦曲线逼近法、平滑样条拟合法和傅立叶变换拟合法对模拟测量值进行拟合和平滑处理,得到拟合曲线及其残差分布,如图8所示。将图8的拟合平滑曲线利用三阶紧致差分逼近算法,计算其一阶导数得到地表重力异常的一阶差分曲线,如图9所示。
为了衡量上述拟合方法的优劣程度,采用确定系数(R-square)和回归拟合标准差(RMSE)来评价拟合优度。R-square为预测数据与原始数据均值之差的平方和除以原始数据与均值之差的平方和。R-square的变化范围为[0,1],其值越大表明拟合程度越好。RMSE为预测数据和原始数据对应点误差的平方和之均值的平方根。上述4种拟合方法的拟合优度系数见表1。
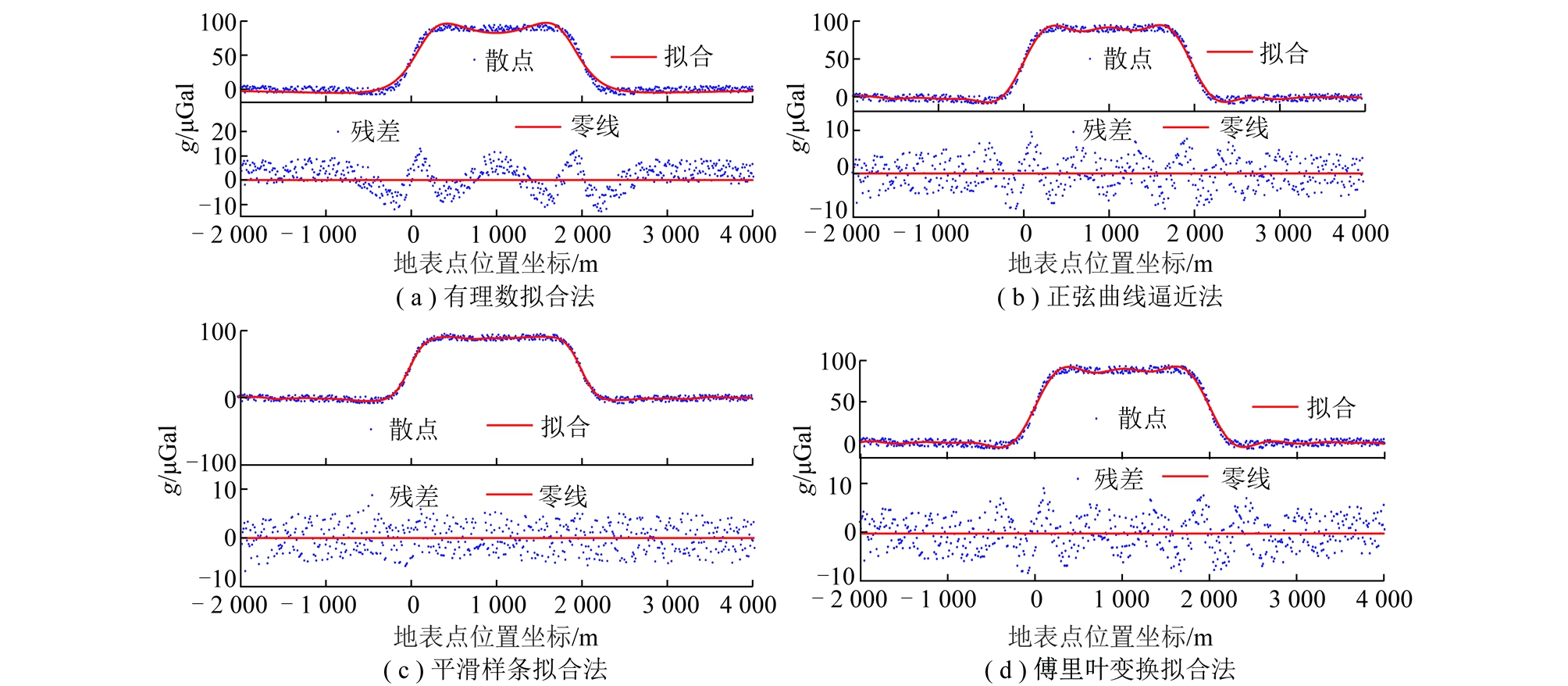
图8 不同方法拟合的重力异常模拟曲线
Fig.8 Fitting curves and residuals of gravity anomaly values by different methods

图9 加±5 μGal随机误差的重力异常一阶差分曲线
Fig.9 First order difference curve of gravity anomaly with 5 μGal random error
表1 4种拟合方法的拟合优度参数
Table 1 Goodness of fit parameters for four fitting methods
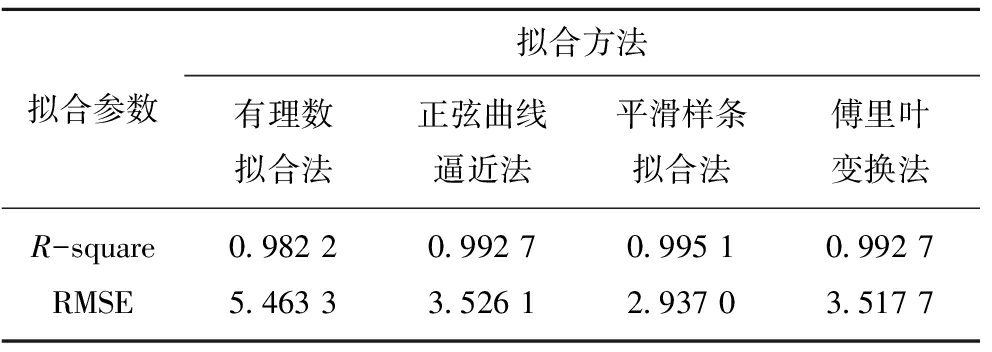
对图8和表1的拟合效果参数分析可得:在加入±5 μGal随机误差情况下,采用平滑样条拟合方法得到最佳拟合效果,傅里叶变换法次之,正弦曲线逼近法和有理数拟合法法拟合效果最差。对比图9和图7可知,平滑样条拟合法,有理数拟合法和正弦曲线逼近法的一次差分曲线与没有随机误差的标准差分曲线相比,其峰值位置相差10 m。即在±5 μGal的随机误差影响下,若采用这3种方法获取一次差分曲线,其反演的采空区位置偏离正确位置10 m。而傅里叶变换法的一次差分曲线,其分布特征和峰值位置与标准曲线(图7)一致。
将随机误差增大到±10 μGal,利用傅里叶变换法对上述重力异常模拟数值进行拟合后并得到其一阶差分曲线,如图10所示。由图10可知,其一阶差分曲线的峰值位置与采空区边界位置相一致。
为探讨随机误差对于采空区边界位置反演效果的影响,将随机误差不断增大到±50 μGal,通过上述方法得到空洞边界反演的最大位置偏差与随机测量误差的关系曲线,如图11所示。图11中当测量随机误差为±15 uGal时,所反演的空洞边界位置偏差达10 m,反演效果变差。

图10 加入±10 μGal随机误差后重力异常一阶差分曲线
Fig.10 First order difference curve of gravity anomaly with 10 μGal random error
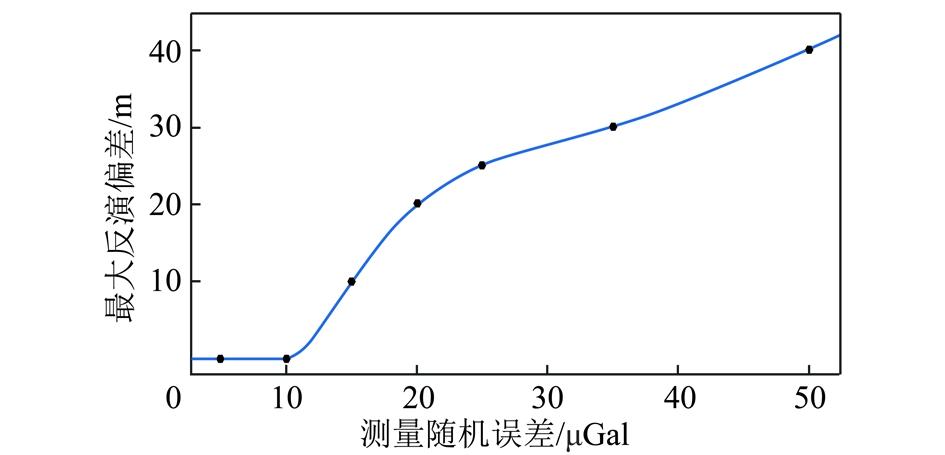
图11 最大反演偏差与测量随机误差的关系曲线
Fig.11 Relationship between the maximum inversion and measurement random error
4 结 论
(1)采空区地表的重力异常与采宽、采高呈线性正相关,与开采深度呈非线性的负相关。基于理论模型的重力异常一阶差分曲线的峰值位置与采空区边界位置相一致。
(2)对于随机误差不超过±10 μGal的模拟重力异常数据,使用傅里叶拟合方法进行平滑并利用三阶紧致差分逼近得到其一阶差分曲线,可通过该曲线峰值位置来推断地下空洞的边界位置。因此,在一定的测量误差情况下,利用地表重力异常数据反演地下空洞仍然具有可行性。
应该指出,在实际情形中当地下空洞呈非规则形状和离散分布时,也可利用数值叠加方法得到地表重力异常值。因此,在一定的边界条件和简化假设下,通过重力异常数据可反演得到诸如条带开采或小煤窑老采空区等空洞在埋深、边界、大小等方面特征的演变过程。
参考文献(References):
[1] 杜坤,李夕兵,刘伟科,等.采空区危险性评价的综合方法及工程应用[J].中南大学学报(自然科学版),2011,42(9):2803-2804.
DU Kun,LI Xibing,LIU Kewei,et al.Comprehensive evaluation of underground goaf risk and engineering application[J].Journal of Central South University(Science and Technoogy),2011,42(9):2803-2804.
[2] 魏晓刚,麻凤海,刘书贤,等.煤矿采空区地震安全防护的若干问题[J].地震研究,2016,39(1):151-152.
WEI Xiaogang,MA Fenghai,LIU Shuxian,et al.Problems of safety control of seismic dynamic disasters in doal mine goaf[J].Journal of Seismological Research,2016,39(1):151-152.
[3] 刘菁华,王祝文,朱士,等.煤矿采空区及塌陷区的地球物理探查[J].煤炭学报,2005,30(6):716-717.
LIU Jinghua,WANG Zhuwen,ZHU Shi,et al.The geophysical exploration about exhausted area and singking area in coal mine[J].Journal of China Coal Society,2005,30(6):716-717.
[4] 程久龙,潘冬明,李伟,等.强电磁干扰区灾害性采空区探地雷达精细探测研究[J].煤炭学报,2010,35(2):227-228.
CHENG Jiulong,PAN Dongming,LI Wei,et al.Study on the detecting of hazard abandoned workings by ground penetrating radar on strong electromagnetic interference area[J].Journal of China Coal Society,2010,35(2):227-228.
[5] 覃思,程建远,胡继武,等.煤矿采空区及巷道的井地联合地震超前勘探[J].煤炭学报,2015,40(3):636-637.
QIN Si,CHENG Jianyuan,HU Jiwu,et al.Coal-seam-ground-seismic for advance detection of goaf and roadway[J].Journal of China Coal Society,2015,40(3):636-637.
[6] 姜志海,杨光.浅埋特厚煤层小窑采空区瞬变电磁探测技术研究及应用[J].采矿与安全工程学报,2014,31(5):770-771.
JIANG Zhihai,YANG Guang.Research and application of TEM detection technology for small mine gob area in shallowly-buried and extremely thick seam[J].Journal of Mining & Safety Engineering,2014,31(5):770-771.
[7] 李文.煤矿采空区地面综合物探方法优化研究[J].煤炭科学技术 2017,45(1):194-195.
LI Wen.Optimization study of surface comprehensive geophysical detection methods of coal mine goafs[J].Coal Science and Technology 2017,45(1):194-195.
[8] 付天光.综合物探方法探测煤矿采空区及积水区技术研究[J].煤炭科学技术,2014,42(8):90-91.
FU Tianguang.Study on technology of comprehensive geophysic method exploration of mine goaf and water accumulated area[J].Coal Science and Technology,2014,42(8):90-91.
[9] 吴亮,刘长弘,王庆宾,等.重力异常对地下异常体边界的识别算法[J].测绘科学,2015,40(12):34-35.
WU Liang,LIU Changhong,WANG Qingbin,et al.An identification method of underground anomaly boundary using gravity anomaly[J].Science of Surveying and Mapping,2015,40(12):34-35.
[10] SU Yongjun,CHENG Lizhen,MICHEL Chouteau,et al.New improved formulas for calculating gravity anomalies based on a cylinder model[J].Journal of Applied Geophysics,2012,86(2):36-43.
[11] 骆遥.两种新的长方体重力场正演表达式及其理论推导[J].工程地球物理学报,2008,5(2):211-212.
LUO Yao.New Expressions for gravitational attraction of a homogeneous rectangular prism and its deduction[J].Chinese Journal of Engineering Geophysics,2008,5(2):211-212.
[12] ZUO Boxin,HU Xiangyun.Edege detection of gravity field using eigenvalue analysis of gravity gradient tensor[J].Journal of Applied Geophysics,2015,114(1):263-270.
[13] Wu Heyu,Li Lu,Xing Congcong,et al.A new method of edge detection based on the total horizontal derivative and the modulus of full tensor gravity gradient[J].Journal of Applied Geophysics,2017,139(1):239-245.
[14] 孙建安,贾伟,吴广智.一种非均匀网格上的高精度紧致差分格式[J].西北师范大学学报(自然科学版),2014,50(4):31-33.
SUN Jian’an,JIA Wei,WU Guangzhi.A higher accurate compact difference scheme on non-uniform grid[J].Jounral of Northwest Normal University (Natural Science),2014,50(4):31-33.
[15] 李佳,罗纪生.一阶、二阶导数耦合的紧致差分格式及其应用[J].计算机工程与应用,2012,48(1):13-15.
LI Jia,LUO Jisheng.Derivation and application compact scheme of coupling of first and second derivative[J].Computer Engineering and Applications,2012,48(1):13-15.
[16] 刘惠敏,刘繁明,荆心,等.浅地表地下质量异常重力与磁探测数值模拟方法[J].中国惯性技术学报,2016,24(4):491-492.
LIU Huimin,LIU Fanming,JING Xin,et al.Numerical simulation method for gravity and magnetic observations of mass anomaly in shallow subsurface[J].Journal of Chinese Inertial Technology,2016,24(4):491-492.