露天矿排土规划是指设计露天矿各水平剥离物从采掘点出发按指定的路线运往指定的排弃点排弃，是在满足露天矿采、剥、排时空关系约束条件下，合理规划露天矿剥离物流向流量，使露天矿剥离物运输费用最小，属于目标规划问题。由于露天矿运输系统十分复杂，且随着采剥工程的推进动态变化，因此，该问题较为复杂[1]。
露天矿排土规划直接影响剥离物运输距离和运输费用。由于露天矿剥离量巨大，剥离物的运输费用占露天矿生产总费用的40%以上，不合理的排土规划可能导致露天矿剥离物运距增大，无法适时合理的利用排土空间，露天矿生产费用大幅增大[2-3]。
对于在内部排土场排土的露天矿，当矿层近水平赋存、地表起伏不大时，在开采相同量矿石的情况下，剥离量与内排空间等变化不大，仅进行排土短期规划即可满足生产要求。但当矿层倾角较大、地表起伏较大、境界不规则或者境界内存在较大断层时，在开采相同量矿石的情况下，剥离量与内排空间变动较大[4-5]，其排土工程需要长远规划的指导。否则可能导致露天矿内排土场高度频繁调整，不利于后续复垦。
目前，国内外关于露天矿规划的研究主要集中在采矿作业方面，对于露天矿排土规划、降低剥离物总运输费用的研究较少[6]。且目前对露天矿排土规划的研究多针对短期排土工程，缺少长远发展规划。一般首先建立露天矿运输系统网络模型，然后计算出各采掘点至各卸载点的最短路径，再利用物流规划模型确定剥离物的流向和流量[7-9]。物流规划模型基本相似，通常以运输功最小、运输费用最小或出动卡车数量最少为目标，以运输设备生产能力、道路通过能力、剥离量及排土空间限制等为约束条件[10-11]。如刘光和张瑞新指出了排土程序、排土量与排土运距之间的动态关系，建立了内外排流向流量优化的线性规划模型[12]。孙效玉等从图论的角度对露天矿运输道路进行了分析，分别建立了基于0-1整数规划的最短路径模型和基于线性规划的货流分配模型[13-14]。魏强等根据采剥物料的运移特征、矿山工程发展规律，建立了露天矿运输系统动态网络模型，开发了露天矿物料流规划系统[15]。李勇等以露天矿运输成本最小为目标，构建了露天矿物流规划模型，并提出了基于粒子群优化算法的模型求解方法[16]。KORTELEV O B与ALEKSANDROV A N基于采石场非均匀运输流的概念与采矿网络结构理论，提出了优化采石场运输系统的方法[17]，该方法以经济效率作为对形成运输网络及技术单元位置选择的判据，通过采用不同的运输模式及其组合运输模式对运输网络形态进行优化，实现了采石场运输网络组建和运营费用下降15%～20%。以上排土规划模型均把露天矿采掘点、排弃点看作是固定点，没有考虑采掘点、排弃点的动态变化，仅适用于短期内的露天矿排土优化。模型计算结果仅能保证短期内露天矿运输费用较低，但可能导致露天矿长期总费用较大[18]。
此外，TOPAL等讨论了露天矿开采作业过程中剥离物的排弃设计，以运输费用最小为目标建立了剥离物排弃优化模型，但由于其模型分时间段规划剥离物排弃，其计算结果可能不是全局最优[19]。LI Y等考虑排弃条件及环境约束，建立了基于混合整数规划的排土规划模型[20]，其模型没有给出剥离物运输距离的计算方法，较适用于露天矿剥离物排弃至外部排土场的情况。不同于以往短期排土规划模型，本文以剥离物总运输费用最小为目标，建立了内排长远规划模型，并提出了模型的求解方法。
1 露天矿内排长远规划模型
1.1 模型思路
长远规划主要是为了指导露天矿短期规划设计，避免出现内排土场高度频繁调整等问题。由于实际生产过程中，内排土场工作平盘宽度、内排土场边坡角、内排土场高度等参数以及运输系统动态变化，详细精确的进行内排长远规划难度较大，且意义不大。因此，建立长远规划模型时，假设采场、排土场边坡角度不变，将计算周期内的采场、排土场分别划分为若干个采剥阶段、排弃阶段，如图1所示。将各个采剥阶段、排弃阶段作为一个整体，根据采剥阶段和对应排弃阶段质心的位置变化计算得到剥离物运距，再根据露天矿单位运输成本计算得到整个计算周期内的总运输费用，得到总运输费用与各阶段排弃高度、采空区宽度的关系式，以计算周期内总运输费用最小为目标建立非线性规划模型，求解并给出各阶段的排土工程位置。
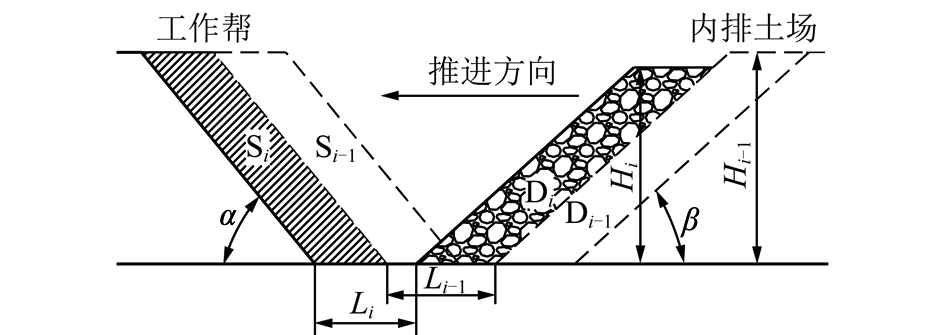
图1 长远规划模型示意
Fig.1 Schematic diagram of long-term planning model
图1中，β为内排土场边坡角，α为工作帮边坡角，Si为第i个采剥阶段，Di为第i个排弃阶段，Hi为第i阶段排土高度，Li为第i阶段采空区宽度。
1.2 约束条件
(1)采空区宽度Li不宜过大或者过小，即Lmin≤Li≤Lmax，Lmin，Lmax分别为采空区宽度的最小和最大值;
(2)各排弃阶段排土场容量
应等于对应采剥阶段剥离量
的散体体积，即
其中λ为松散系数，
(3)考虑到后续复垦以及便于剥离半连续工艺设备的工作面移设，相邻排弃阶段的排土高度不能相差太大，即|Hi-Hi-1|≤h，其中h为相邻排弃阶段的排土高度最大差值。
1.3 模型建立
根据水平运输距离与垂直提升高度可计算得出第i排弃阶段的运输成本:
(1)
式中，Ci为第i排弃阶段运输成本，元
为排弃阶段与对应采剥阶段水平运输距离，
为排弃阶段质心与采剥阶段质心高差，km。
内排长远规划模型为
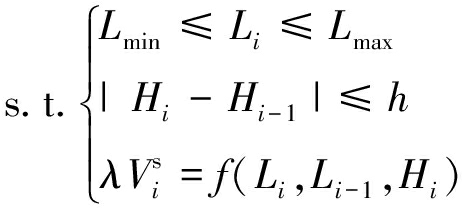
(2)
式中，C为剥离物总运输费用，元;N为求解的排弃阶段数。
模型的约束条件中仅包含采空区宽度Li和排弃高度Hi两组变量，且包含一个等式约束，因此，模型可简化为仅有采空区宽度Li一组变量。利用该模型可计算得出:最小剥离物总运输费用、各阶段的排弃高度、采空区宽度和排弃坡底位置、各阶段水平运输距离与垂直提升高度。
1.4 模型数据定义
(1)坡底位置的定义
对于矿层近水平赋存的露天矿，最下部台阶的坡底线近似为直线，其采剥阶段和排弃阶段的坡底位置容易确定。而矿层缓倾斜赋存横向开采的露天矿，当矿层沿走向有一定起伏时，采剥阶段和排弃阶段的坡底位置较难确定。为此，定义坡底位置如下:
在露天矿地表境界外推进方向前，设置一个与推进方向垂直的平面AB，定义采剥阶段坡面与坑底境界交线CE上距平面AB最远的点C为采剥阶段坡底位置，排弃阶段坡面与坑底境界交线DF上距平面AB最近的点D为排弃阶段坡底位置，如图2所示。
图2 坡底位置定义示意
Fig.2 Schematic diagram of slope toe position
采空区宽度Li=LD-LC，其中LC为点C与平面AB的距离， LD为点D与平面AB的距离。
(2)排弃阶段相关数据的定义
通过对预先建立的内排土场按设定的排弃坡面角和固定推进度进行切割，得到固定推进度条件下的排弃块段，定义为排弃块段。同时，在垂直方向上按照一定高度进行切割，得到排弃块段垂直方向切割实体，定义为切割实体，如图3所示。
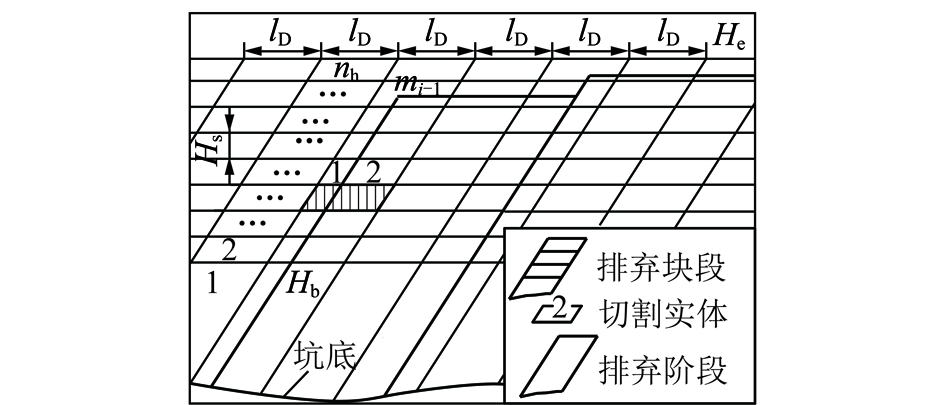
图3 排弃块段及切割实体示意
Fig.3 Dumping block and its vertical slice
上述排弃块段不与采剥阶段对应，提出排弃块段及切割实体的概念是为了辅助计算排弃高度等。模型求解的排弃阶段文中统一称为排弃阶段，排弃阶段与采剥阶段一一对应。
图3中，He为最高排弃标高，Hb为第1个切割实体上部标高，Hs为切割实体高度，lD为固定推进度，mi-1为排弃块段编号。利用相关软件可以得到切割实体的体积和质心数据。
1.5 模型求解方法
从第1个采剥阶段开始，首先根据约束条件1中采空区宽度取值范围选取一个采空区宽度，然后根据采剥阶段坡底位置确定排弃阶段坡底位置，再根据剥离量及约束条件2确定排弃高度，判断排弃高度是否满足约束条件3，当所有阶段都能满足上述约束条件时，即可求解总运输费用。采用穷举法求解不同排弃高度、采空区宽度情况下的总运输费用，总运输费用最小时对应的解即为最优解。
根据以上求解思路，确定模型求解的流程，如图4所示。
图4 模型求解流程
Fig.4 Flow chart of model solution
图4中，Cf为初始剥离物总运输费用，Lstep为采空区宽度调整步长。
2 关键问题求解算法
2.1 排弃阶段坡底位置确定
排弃阶段坡底位置根据如下公式确定:
(3)
式中，
为第i排弃阶段坡底位置，
为第i采剥阶段坡底位置，m;Li为第i阶段采空区宽度，m。
确定存在采空区的情况下，离第i采剥阶段坡底位置
最近的排弃块段，标记
在数组中的位置为Mi，
(4)
式中，Mi为离采剥阶段i坡底位置最近的排弃块段;为第j排弃块段的坡底位置，m。
与和
的位置关系存在两种情况:
如图5所示，a面为采剥阶段，其坡底位置为
面为排弃阶段坡面，对应排弃阶段坡底位置
面为存在采空区情况下排弃块段中离采剥阶段坡底位置最近的块段的坡面，坡底位置
面比d面离采剥阶段坡底位置更近。
图
与和的相对位置情况1
Fig.5 Situation one between 
如图6所示，d面为排弃块段中离采剥阶段坡底位置最近的阶段的坡面，坡底位置
排弃阶段坡底位置满足
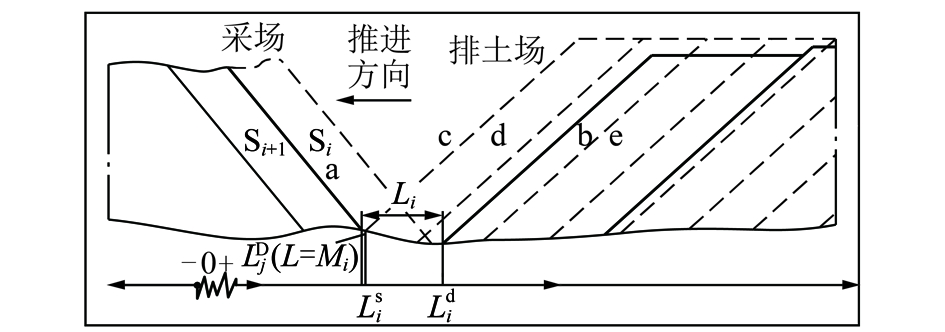
图
与和的相对位置情况2
Fig.6 Situation two between and
根据图5，6的几何关系，可以得到第i个排弃阶段坡面所处的排弃块段mi:
(5)
式中，
为第Mi个排弃块段坡底位置，m;nc为排弃阶段坡底位置处在排弃坡面和第Mi个排弃块段之间的个数。
根据mi计算第i个排弃阶段坡面与第Mi个排弃块段坡面在水平面采场推进方向上的距离
(6)
2.2 排弃阶段坡面切割实体后的质心和体积
排弃阶段坡面将其所在的排弃块段实体一分为二，如图3所示。排弃阶段与采剥阶段之间的实体部分用于下一排弃阶段，另一部分用于当前排弃阶段。这两部分的体积及质心根据排弃阶段坡面所在排弃块段坡面距离确定。
根据图3中的几何关系，计算第mi个排弃块段垂直方向上第j个实体被第i个排弃阶段坡面切割后形成的第k个实体(k=1为处在当前排弃阶段，k=2为处在下一排弃阶段)的质心坐标
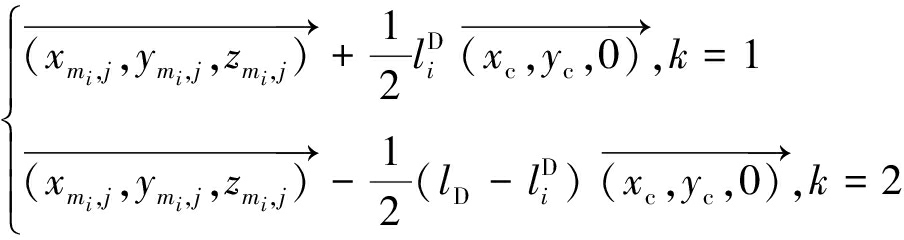
(7)
式中，
为平面AB的法向单位向量，采场推进方向为负。
排弃阶段坡面将其所在的排弃块段实体分割为两部分的各部分体积则由断面面积加权得到，即
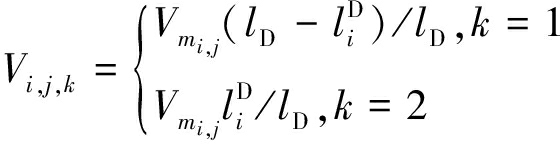
(8)
式中，Vi,j,k为第mi个排弃块段垂直方向上第j个实体被第i个排弃阶段坡面切割后形成的第k个实体(k=1为处在第i个排弃阶段范围内的实体，k=2为处在第i+1个排弃阶段范围内的实体)的体积，m3;Vmi,j为第mi个排弃块段垂直方向上第j个实体体积，m3。
2.3 排弃阶段排弃高度的计算
在第i个排弃阶段坡底位置确定的情况下，从第i个排弃阶段坡面到第i-1个排弃阶段坡面之间的排弃块段切割实体在垂直方向上从下到上逐层累计到第n层实体时的体积Vn:
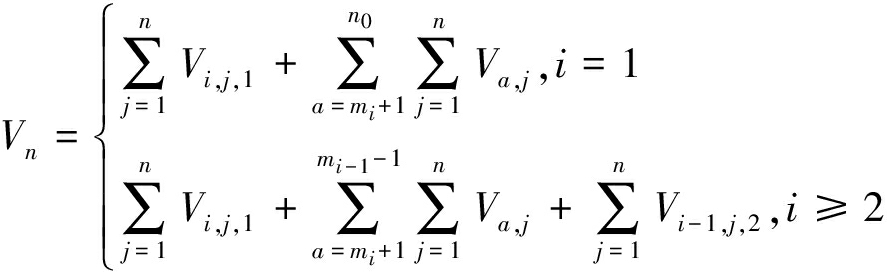
(9)
式中，n0为排弃块段的阶段数目。
当
时，第i排弃阶段排弃到第n层实体与第n层实体起始高度的高差
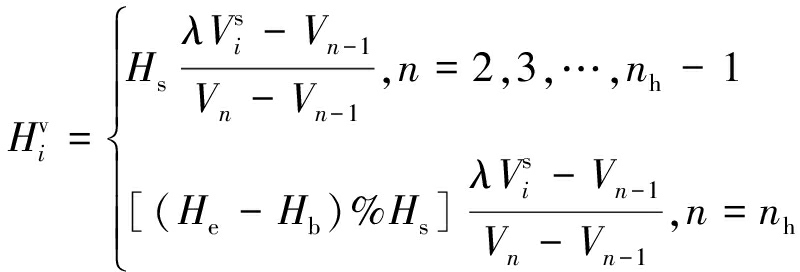
(10)
式中，nh为排弃块段垂直切割后的实体数目;%为取余数运算。
第i排弃阶段排弃高度Hi:
(11)
对排弃阶段内垂直方向上第n个实体在
高度处进行切割。切割后在第i个排弃阶段排土标高以下的部分其质心的x,y坐标不变，z坐标为切割前实体质心的坐标减去
其中Hn为第n(n≥2)层排弃块段切割实体的厚度:
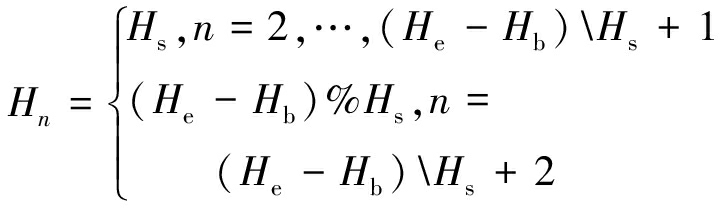
(12)
式中,“\”为整除符号。
切割后在第i个排弃阶段排弃标高以下部分的实体体积为切割前实体体积乘以
将第i个排弃阶段范围内各个实体的体积作为权重对其质心坐标加权即可得到第i个排弃阶段质心坐标
根据采剥质心、排弃质心以及运输路径，可计算得到各阶段的水平运输距离和垂直提升高度，进而进行模型求解。
3 工程实例
3.1 矿山概况
某露天煤矿位于某煤田二区露天勘探范围内，采场为窄长型，走向长13.27 km，宽1.15～3.58 km，面积31.36 km2，开采深度85～356 m。矿田内断层多、构造复杂。其核定生产能力为15 Mt/a。
目前，某露天煤矿工作线沿煤层走向布置，倾向推进，同时逐渐向西扩帮，使西帮缓帮逐渐变为工作帮。其长远规划设计采区发展方向为:加快西帮南侧推进速度，使工作线布置方向与目前西帮夹角20°，然后保持工作线布置方向不变向西推进。当采场底部推进至线段LM位置时，开始逐渐改变工作线布置方向至闭坑，如图7所示。露天煤矿能使用的排土场只有内排土场。
图7 某露天煤矿生产现状
Fig.7 Surface coal mine’s production status
3.2 模型数据的获取
(1)采剥阶段的矿岩量、质心及坡底位置
建立露天煤矿三维地质模型，采场工作帮坡角取11°，推进度取150 m，沿规划推进方向计算固定推进度下的采剥块段矿岩量及质心。各块段位置如图8所示，图中标志的位置为896水平。
图8 采场推进方向及采剥块段位置
Fig.8 Advancing direction and toe position of stripping block
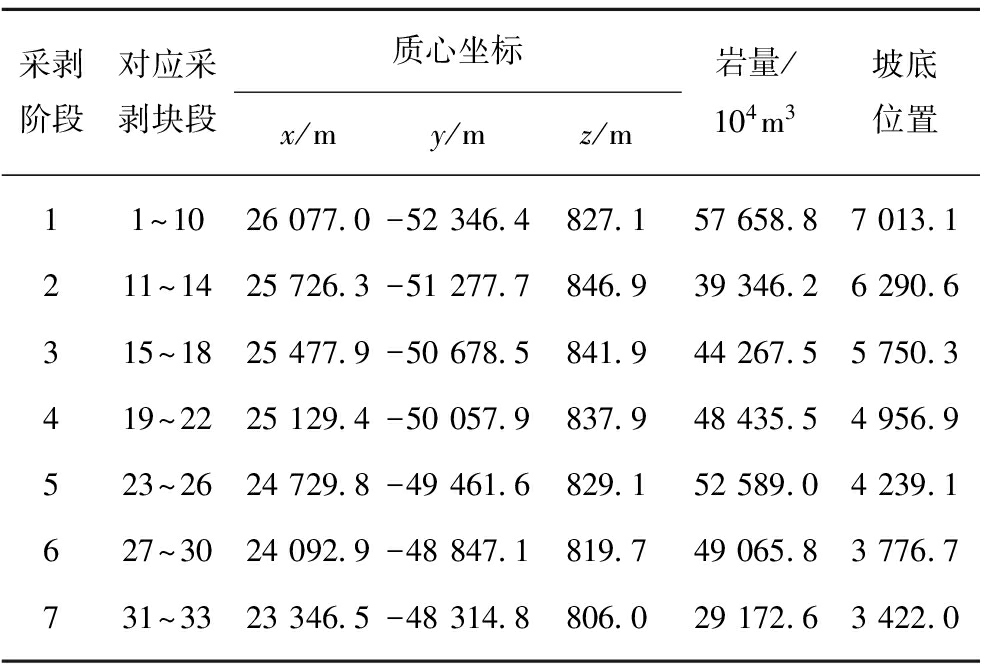
由于是长远规划，因此每隔几个块段选取一个位置，累计其矿岩量作为计算数据，对应的质心根据体积进行加权。选取位置为图8中加粗实线块段，即块段1、块段10、块段14、块段18、块段22、块段26、块段30和块段33，各标志块段之间合并形成7个采剥阶段。各选取位置之间累计矿岩量及加权质心见表1。
表1 累计剥离量及加权后质心
Table 1 Cumulative stripping volume and weighted centroid
(2)排弃块段切割实体体积及质心
建立排土场块体模型，取排土场帮坡角12°，推进度150 m，推进方向与采场方向一致，各排弃块段位置如图9所示，计算各排弃块段的排弃量，在垂直方向上按照高程进行切割，得到各块段按照高程切割后的实体的质心坐标及体积，计算结果见表2。
(3)排弃块段的坡底位置
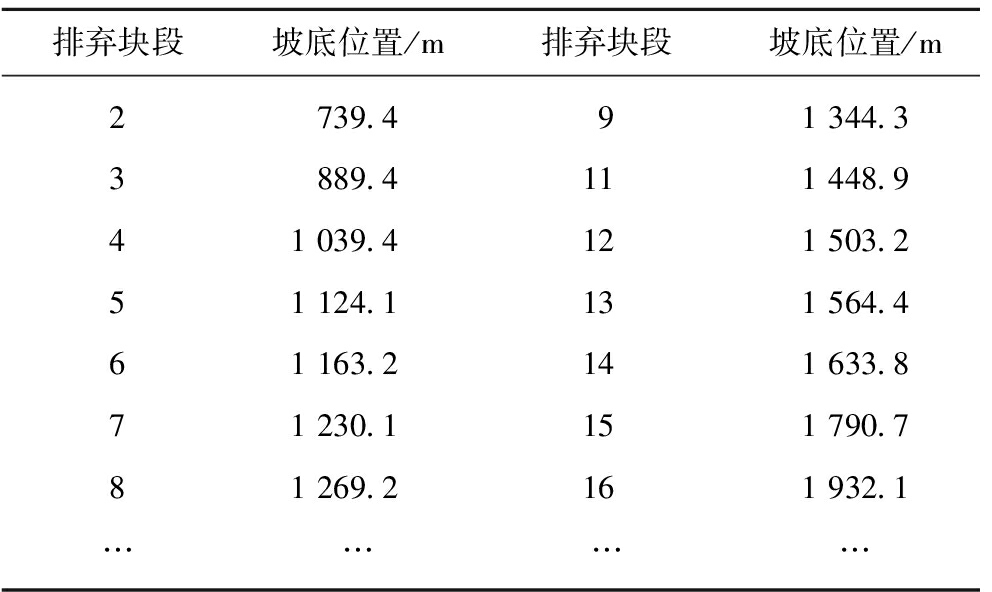
根据坡底位置的定义，先得出各排弃块段与最终境界的交线，再得出交线上离采空区最近的点，得到排弃块段的坡底位置，见表3。
图9 排弃块段位置
Fig.9 Dumping block position
表2 排弃块段切割实体的质心及体积
Table 2 Volume and centroid of dumping block cutting entity
表3 排弃块段的坡底位置
Table 3 Toe position of dumping block slope
3.3 模型计算结果
设置采空区宽度调整步距、相邻排弃阶段最大高差、单位运输成本等参数后，进行求解可得最优运输费用为820.4亿元，优化的排土长远规划见表4和图10。
由图10及表4可知，本文模型计算的排土标高呈先下降后上升的趋势。各期采空区宽度与相邻阶段有一定的均衡。如计算结果中第2阶段与第3阶段，其排土高度基本相同，推进度基本相同，而前者采空区宽度为180 m，后者采空区宽度为20 m。前者排弃容量较为富余，为了给后者预留排土空间，扩大了采空区宽度，提高了排弃高度。但即使这种情况下，后者的排土空间仍较为紧张，如果露天矿不做长远排土规划，可能导致第3阶段排土空间不足，需要大幅提高内排高度或者进行外排，大大增加运输费用。
表4 模型计算结果
Table 4 Calculation results of the model
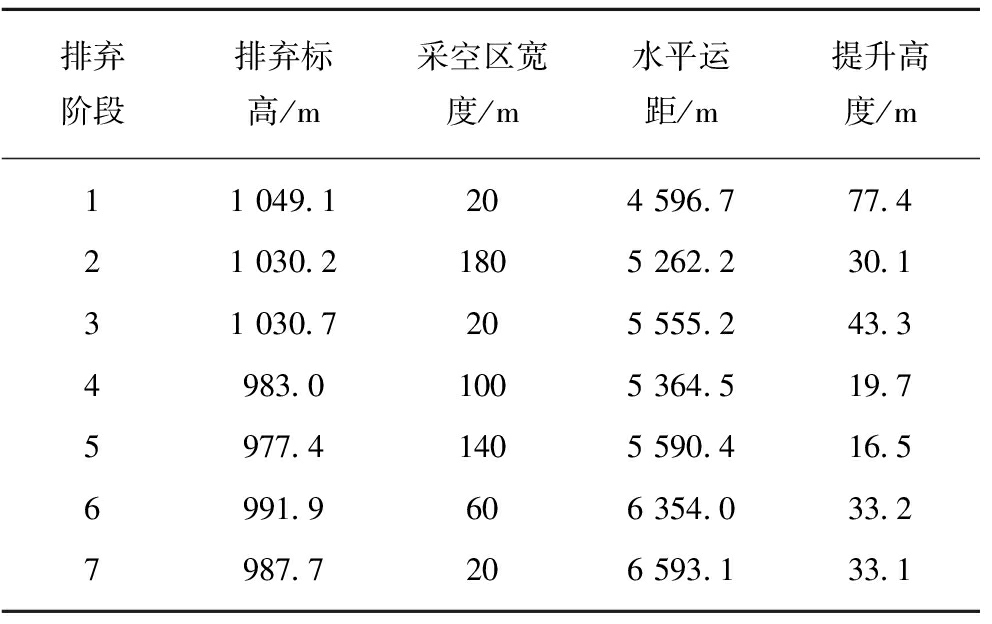
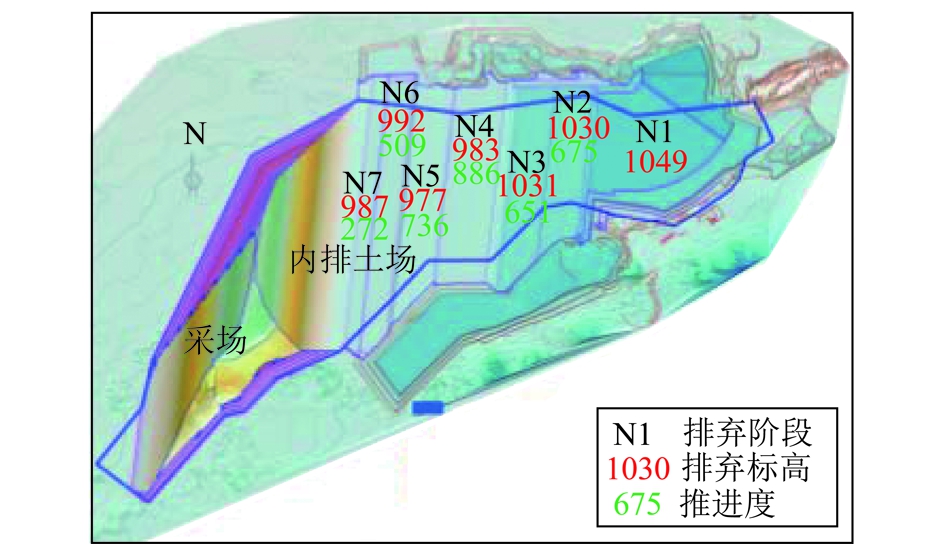
图10 计算结果三维示意
Fig.10 3D effect of calculation results
传统情况下的排土设计，只考虑当前阶段排土费用最小而不考虑后续的排土规划，使采空区宽度取最小值，对排土标高不做限制，得到当期排弃阶段最小费用条件下的排土规划，与本文模型计算结果相比，剥离物总运输费用增加17.8亿元，单位运输成本提高0.56 元/m3。两者各阶段排弃标高如图11所示。
图11 各阶段排弃标高
Fig.11 Height of each dump stage
由图11可知，本文模型各阶段排弃标高波动较小，有利于排土及后续复垦作业，本文模型计算结果较优。
4 结 论
(1)对露天矿内排工程进行长远规划，能够充分利用内排空间，减少外排量，降低剥离物运输费用，并能够避免内排土场高度频繁调整，有利于后续复垦。
(2)内排土场长远规划过程中应该满足以下约束条件:采空区宽度宜在合理取值范围内，各排弃阶段排土场容量应等于对应采剥阶段剥离量的散体体积，相邻排弃阶段的排土高度不能相差太大。
(3)以总运输费用最小为目标，建立了露天矿内排长远排土规划模型，提出了模型的求解思路及算法流程。在某露天煤矿的应用表明:与传统方法设计结果相比，本文模型计算结果能够降低剥离物运输费用17.8亿元，各阶段排弃标高波动较小，有利于排土及后续复垦作业。
参考文献(References):
[1] JAEHO S,KRIS G M,DONALD S M.Determination of haul distance and direction in mass excavation[J].Journal of Construction Engineering and Management,2005,131(3):302-309.
[2] ALARIE S,GAMACHE M.Overview of solution strategies used in truck dispatching systems for open pit mines[J].International Journal of Surface Mining,Reclamation and Environment,2002,16(1):59-76.
[3] MOSELHI O,ALSHIBANI A.Optimization of earthmoving operations in heavy civil engineering projects[J].Journal of Construction Engineering and Management,2009,135(10):948-954.
[4] SAKANTSEV G G,CHESKIDOV V I.Application range of internal dumping in opencast mining of steep mineral deposits[J].Journal of Mining Science,2014,50(3):501-507.
[5] ZAITSEVA A A,ZAITSEV G D.Influence of geological and technological factors on the internal dump capacity in flat deposits[J].Journal of Mining Science,2009,45(4):380-389.
[6] SOUZA M J F,COELHO I M,RIBAS S,et al.A hybrid heuristic algorithm for the open-pit-mining operational planning problem[J].European Journal of Operational Research,2010,207(2):1041-1051.
[7] 李富平,杨福海,马宪福.露天矿排土规划优化方法研究[J].金属矿山,2001,30(10):15-17.
LI Fuping,YANG Fuhai,MA Xianfu.Study on the optimization of disposal programs for open-pit mines[J].Metal Mine,2001,30(10):15-17.
[8] 孙效玉,田凤亮,张航,等.兼顾固定配车需要的露天矿车流规划模型[J].煤炭学报,2016,41(S2):583-588.
SUN Xiaoyu,TIAN Fengliang,ZHANG Hang,et al.Traffic flow model in open pit mine for needs of fixed assignment of truck[J].Journal of China Coal Society,2016,41(S2):583-588.
[9] 孙效玉,赵松松,刘恒,等.露天矿车流路网均衡分配模型[J].煤炭学报,2017,42(6):1607-1613.
SUN Xiaoyu,ZHAO Songsong,LIU Heng,et al.Equilibrium distribution model of traffic flow on road network for traffic flow of open pit[J].Journal of China Coal Society,2017,42(6):1607-1613.
[10] 卢雯雯,叶义成,刘明,等.露天矿排岩优化的物流调度规划方法探讨[J].资源环境与工程,2007,21(4):466-470.
LU Wenwen,YE Yicheng,LIU Ming,et al.A research of dumping optimization in strip mine based on logistics programming[J].Resources Environment and Engineering,2007,21(4):466-470.
[11] 狄卫民,云庆夏.应用网络流规划编制露天矿最优排土计划[J].黄金科学技术,1999,7(45):78-81.
DI Weimin,YUN Qingxia.Planning of surface mine optimum dumping based on network flow programming[J].Gold Science and Technology,1999,7(45):78-81.
[12] 刘光,张瑞新.露天矿排土及土岩流向流量优化模型[J].化工矿物与加工,1991,20(3):6-8.
LIU Guang,ZHANG Ruixin.Dump planning and rock flow-direction and flow rate model of surface mines[J].Industrial Minerals and Processing,1991,20(3):6-8.
[13] 孙效玉,张维国,贾荣军.矿山运输系统优化模型及解算方式探讨[J].金属矿山,2012,41(5):133-136.
SUN Xiaoyu,ZHANG Weiguo,JIA Rongjun.Discussion on the model optimization and solution for mining pit transportation system[J].Metal Mine,2012,41(5):133-136.
[14] 孙效玉,张维国.满足各种矿岩配车需求的露天矿车流规划模型[J].东北大学学报(自然科学版),2012,33(10):1487-1491.
SUN Xiaoyu,ZHANG Weiguo.Traffic flow programming model for various matchs of hauling fleet and materials in open-pit mine[J].Journal of Northeastern University (Natural Science),2012,33(10):1487-1491.
[15] 魏强,李克民,姚绍武.露天矿物料流规划系统的设计与实现[J].中国矿业大学学报,2003,32(2):180-182.
WEI Qiang,LI Keming,YAO Shaowu.Design and realization of surface mining materiel-stream programming system[J].Journal of China University of Mining and Technology,2003,32(2):180-182.
[16] 李勇,胡乃联,李国清.基于改进粒子群算法的露天矿运输调度优化[J].中国矿业,2013,22(4):98-101.
LI Yong,HU Nailian,LI Guoqing.Open pit hauling dispatching optimization based on improved PSO algorithm[J].China Mining Magazine,2013,22(4):98-101.
[17] KORTELEV O B,ALEKSANDROV A N.Method to optimize location of technological units in a quarry in view of non-uniform haulage streams[J].Journal of Mining Science,2006,42(2):145-150.
[18] 黄甫.内排条件下露天矿长远排土规划研究[D].徐州:中国矿业大学,2017:22-28.
HUANG Fu.Long-term planning of internal dumping in surface coal mining[D].Xuzhou:China University of Mining and Technology,2017:22-28.
[19] TOPAL E,WILLIAMS D J,ZHANG N.Development and validation of a waste rock dumping optimisation model[A].Securing the Future and 8th International Conference on Acid Rock Drainage[C].Skelleftea,Sweden:SveMin/INAP,2009:1-11.
[20] LI Y,TOPAL E,WILLIAMS D.Waste rock dumping optimisation using mixed integer programming (MIP)[J].International Journal of Mining,Reclamation and Environment,2013,27(6):425-436.
07