全部垮落法开采过程中,随着采煤工作面不断地向前推进,顶板岩层不断垮落不仅可以及时减少工作面的控顶面积,而且因顶板垮落后破碎岩石对采空区的充填,对上覆岩层起到了一定的支承作用,从而减轻了工作面顶板压力,同时对上覆岩层运动和地表沉陷具有一定的抑制作用。采空区内垮落的破碎岩石处于一种长期承压变形的状态,时间效应极为显著,随着时间的推移,破碎岩石会因承载能力降低而减弱对覆岩的支承作用,极易加剧采空区围岩结构失稳,引发矿井突水和地表塌陷等动力灾害。对此,我国学者开展了针对破碎岩石承载变形特性的系列研究。
缪协兴等[1]采用特制的刚性圆筒配以万能试验机,试验研究了煤(岩)碎胀与压实特性;马占国等[2-4]、卜万奎[5]和杜春志等[6]采用破碎岩石压实渗透试验装置,试验分析了粒径、强度对饱和破碎岩石应力-应变特性的影响;陈占清等[7]和马占国等[8]采用破碎岩体多相耦合蠕变实验装置,试验研究了饱和破碎岩石蠕变过程中孔隙率的变化规律;张振南等[9]进行了松散岩块压实破碎的试验研究,得出了松散岩块的压实破碎规律;苏承东等[10]和陈晓祥等[11]采用压实试验装置配以RMT-150B型试验系统,试验研究了压实过程含水和不含水状态下破碎岩石强度、块径、压实力与碎胀性、压实度、密度以及能耗的关系;樊秀娟和茅献彪[12]采用破碎岩石承压变形仪配以普通摆锤机械式压力机,试验研究了破碎砂岩蠕变变形与轴向载荷、破碎块径的关系;冯梅梅等[13]采用自制破碎岩石压实装置,试验研究了满足连续级配的饱和破碎岩石压实特性及压实前后岩石粒径的分布规律;张季如等[14-15]采用自制的侧限压缩试验装置进行压缩试验,建立描述粒状岩土材料的应力水平与孔隙比、体应变、相对破碎率等相关关系的数学模型;郁邦永等[16]建立轴向位移、压缩模量和粒度分布分形维数与轴向应力之间的关系式,讨论Talbol 幂指数对压实变形和粒度分布的影响规律。
通过总结分析发现,现有的实验装置普遍存在有效容积小这一缺陷,随着破碎岩石粒径的增大,边界效应问题越发突出,且现有成果中大多进行的是单一级配破碎岩石或者是Talbol 连续级配破碎岩石的相关研究。笔者研制了大尺寸(φ40 cm×68 cm)破碎岩石承压变形试验系统,利用其进行了破碎岩石初始颗粒粒径满足正态分布的承压变形试验,分析了不同轴向应力下破碎岩石的承压变形特性、试验前后粒径的变化情况,研究了破碎岩石的承压变形机制。
1 试验装置及试验方案
1.1 试验装置
大尺寸破碎岩石承压变形试验系统主要由主体承载支架、试验舱、承压水仓、储能罐、水压水量双控伺服系统和位移应力双控伺服系统组成,其主体结构如图1 所示。
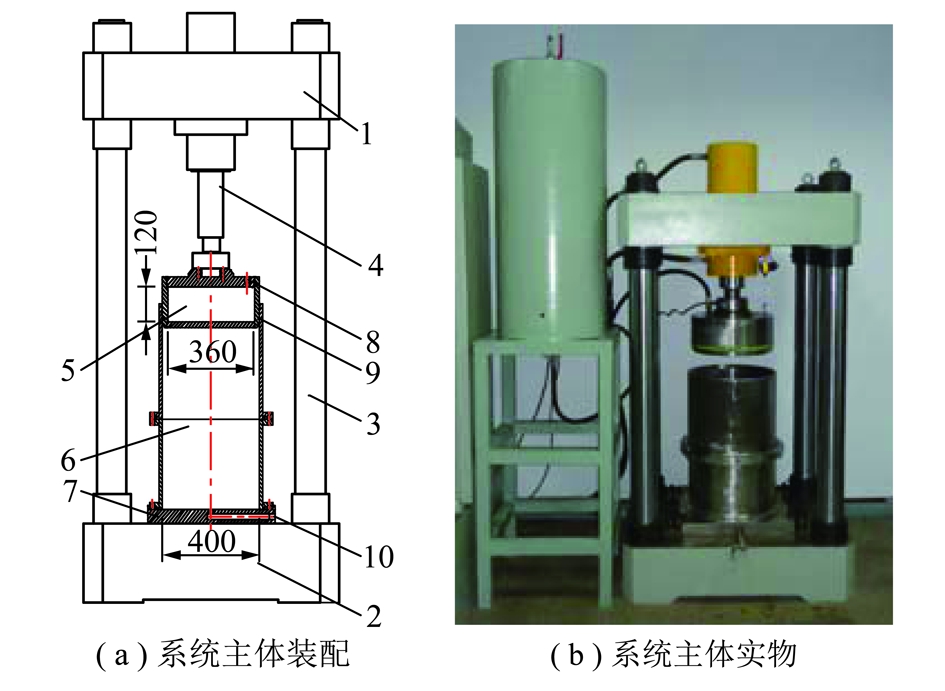
图1 试验装置主体结构
Fig.1 Structural diagrams of mechanical system
1—试验系统横梁;2—试验系统底座;3—立柱;4—加载油缸;5—加载压头兼承压水仓;6—试验舱;7—试验舱底座;8—进水口;9—密封圈;10—出水口
(1)主体承载支架:主要包含了底座、横梁,加载油缸固定架和立柱,主要起固定和支撑作用。
(2)试验舱:外形呈圆筒状,内径为40 cm、高度为68 cm。为便于试验材料的填装,试验舱由上下两个舱体组成。
(3)承压水仓:兼做加载压头,通过活塞杆与加载油缸相连,在底部均匀分布着34个直径为10 mm的出水孔。
(4)储能罐:位于水压水量双控伺服加载系统和试验舱之间,可提高输入试验舱内水压和水流量的稳定性,如图1(b)所示。
(5)控制系统:包括操作台和伺服加载系统两部分,其中伺服加载系统由水压水量双控伺服加载系统和位移应力双控伺服加载系统组成,全程实现自动控制,采集的数据包含时间、位移、压力、水压和流量5种类型,最小采集频率为10个/s,试验控制系统整体如图2所示。

图2 试验控制系统
Fig.2 Testing control system
需要指出的是,本次试验未使用水压水量双控伺服加载系统,仅仅利用了该试验装置的位移应力双控伺服加载系统。位移应力双控伺服加载系统可以实现位移和应力的双重控制,加载油缸的最大行程为400 mm、精度为0.01 mm,可施加的最大载荷为600 kN、精度为0.01 kN,既可实现连续加卸载也可实现分级加卸载。
1.2 试验方案
试验岩样为采自山东能源岱庄煤矿的顶板砂岩,自然含水状态下单轴抗压强度96.87 MPa,弹性模量16.1 GPa,泊松比0.199,密度为2 540 kg/m3。根据国内外学者的研究[17-19],考虑到尺寸效应的影响,要求试样直径与岩石最大粒径比值D/dmax≥5,由于试验舱内径为40 cm,因此试验机可取的岩石最大粒径为80 mm。为将尺寸效应对试验结果的影响降到尽可能低,试验中选取的岩石最大粒径为40 mm。这与现有的试验装置有效尺寸(内径≤150 mm,高度≤200 mm)相比,在有效容积上优势较明显。将完整岩石人工破碎后,按照粒径大小分成5~10,10~15,15~20,20~25,25~30,30~35和35~40 mm七种级别。考虑到顶板岩石垮落后的块度级配近似满足正态分布,因此将7种粒径的破碎岩石按照质量分数5%,10%,20%,30%,20%,10%,5%进行组合。配制完成的破碎岩石试样粒径级配近似满足正态分布,如图3所示。
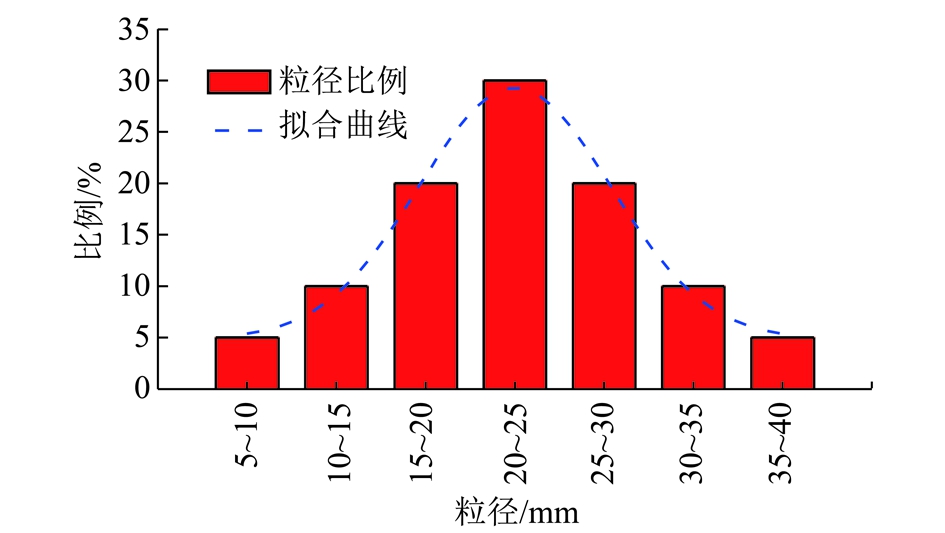
图3 破碎岩石级配设计
Fig.3 Gradation design of broken rock
某种级别粒径岩石所占比例与粒径的关系为
(1)
式中,A为某种粒径岩石所占比例,%;D为某种级别粒径岩石的最小粒径值,mm。
考虑到试验舱直径为40 cm、高度为68 cm,并且需为加载压头预留一定的活动空间,破碎岩石试样的实际装样高度为655 mm,总质量为110 kg,破碎岩石初始碎胀系数K=1.901,空隙率P=0.901。装配好的破碎岩石试样如图4所示。

图4 装配好的破碎岩石试样
Fig.4 Assembled broken rock
采空区冒落岩石承受的压力主要来自上覆岩层的压力,力的大小与断裂岩层的高度直接相关,随着断裂岩层高度的增大而增大。在顶板两次来压之间的时间段内,作用在冒落岩石上的压力可近似为不变,与上覆断裂岩层的自重应力基本相同;在顶板来压时,作用在冒落岩石上的压力会迅速增加,增量约等于此次来压过程中上覆岩层新断裂岩层的自重应力。因而冒落岩石在采空区内的受力状态不是线性增加的,而是呈现阶梯状增大的趋势,因此在破碎岩石承压变形试验中,设计采用梯形分级加载的方式。
各级轴向载荷分别为100,200,300,400,500 kN,加载梯度为100 kN,可反映采空区内垮落的破碎岩石在4 MPa压力以内的变形特性。试验正式开始之前对破碎岩石施加20 kN的预压力,待破碎岩石变形稳定后(约15 min),采用0.5 kN/s的加载速率将轴向载荷增至一级载荷100 kN,并维持100 kN轴向载荷4 h,而后采用0.5 kN/s的加载速率将轴向载荷增至二级载荷200 kN,并维持200 kN轴向载荷4 h,依次逐级增加轴向载荷直至试验完成。需要指出的是,在实际工作面开采过程中,考虑周期来压步距和工作面推进速度的关系,采空区冒落矸石的变形往往未达到所受维持恒力的稳定状态,便会因为顶板的来压导致作用在冒落矸石上的压力的增加,因此,在进行每级加载维持恒力时间设计时,并未刻意追求待破碎岩石变形状态稳定后再进行下一级的加载;此外,由于此试验开始便不可中断,在时间设定上还考虑了试验系统连续运转稳定性和实验员需长时不间断看护的问题,最后将每一级的加载维持时间确定在4 h。
试验过程中,通过试验系统的位移应力双控伺服加载系统对破碎岩石试样承压变形过程中的压力和变形进行实时监测和记录。
破碎岩石试样初始碎胀系数为
K=V1/V0
(2)
式中,V0为完整岩块的体积;V1为完整岩块破碎后自然堆积状态下的体积。
破碎岩石试样初始空隙率为
P=(V1-V0)/V0=K-1
(3)
破碎岩石试样承压变形后的残余高度为
h1=h0-u
(4)
式中,h0为破碎岩石试样的实际装样高度,mm;u为破碎岩石试样承压后的变形量,等于试验系统加载压头位移值,mm。
破碎岩石试样承压变形后的残余碎胀系数为
K1=h1S/V0
(5)
式中,S为试验系统试验舱的有效底面积,S=πd2/4,d=400 mm。
2 试验结果及分析
2.1 碎胀及变形特征
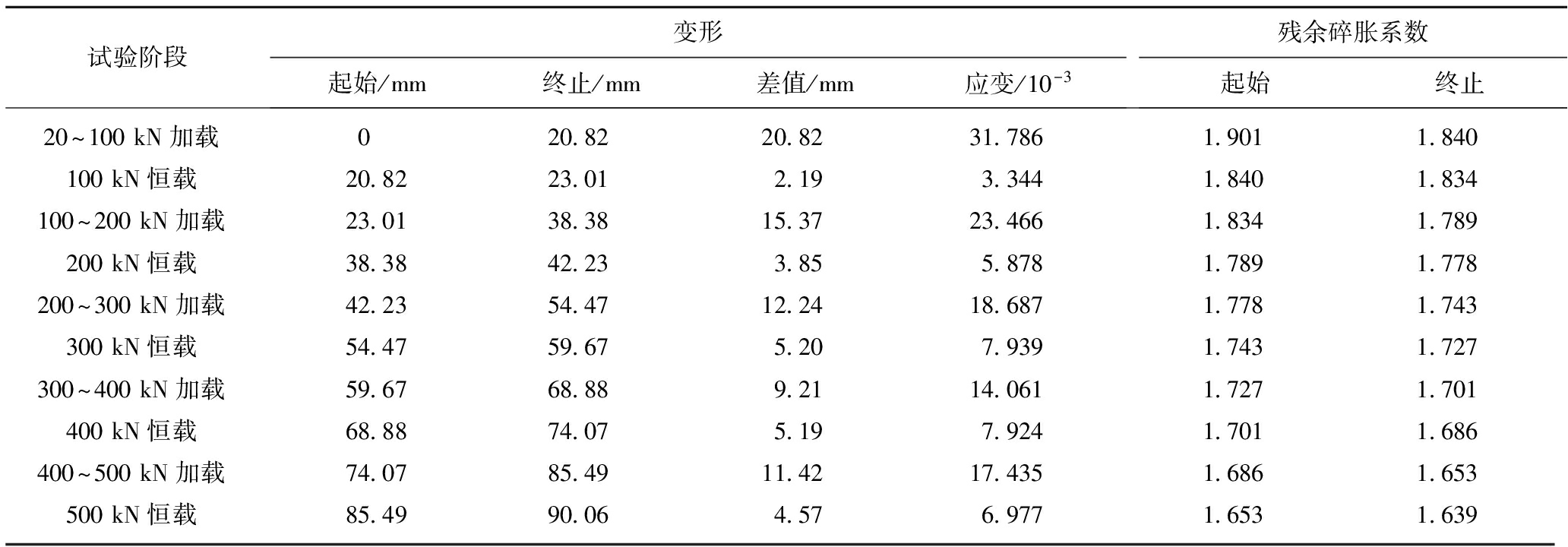
随着轴向载荷的增加,破碎岩石轴向变形呈现逐渐增大的趋势,500 kN恒载结束时轴向变形最终值为90.06 mm,相应的轴向应变最终值为137.5×10-3;残余碎胀系数和空隙率呈现逐渐减小的趋势,破碎岩石残余碎胀系数由1.901降为1.639,空隙率由0.901变为0.639;试验过程中,加载阶段较恒载阶段破碎岩石轴向变形更为明显,占全部变形的76.7%。
轴向载荷与时间的关系曲线、轴向变形与时间的关系曲线如图5所示,残余碎胀系数-时间、空隙率-时间曲线如图6所示。加载过程自然状态破碎岩石参数变化情况见表1。
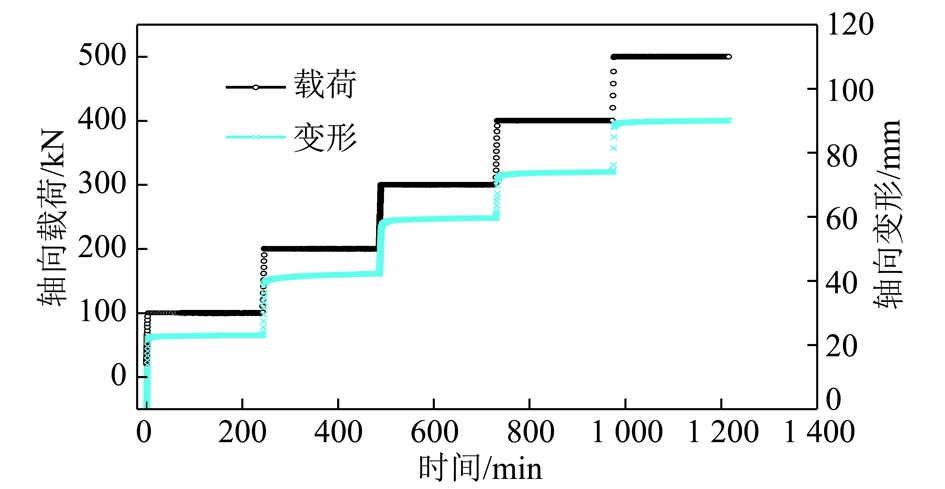
图5 破碎岩石载荷、变形-时间曲线
Fig.5 Load-time and deformation-time curves of broken rock
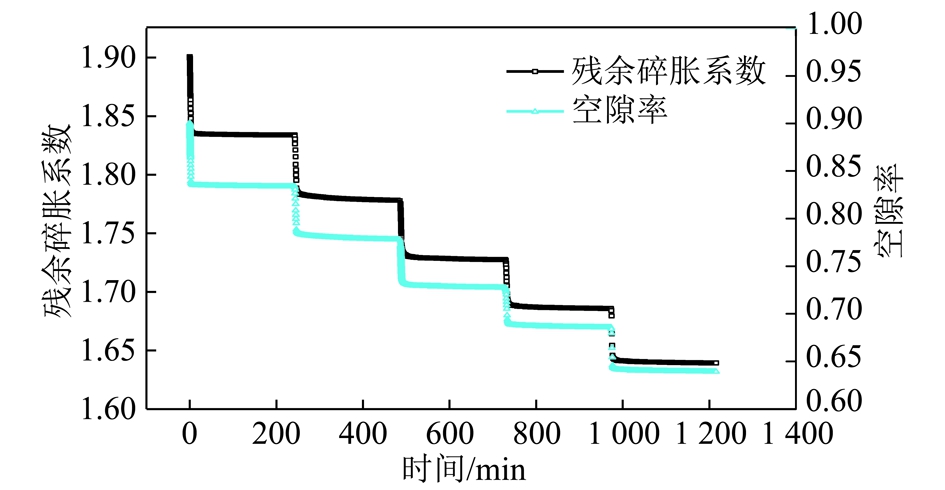
图6 破碎岩石残余碎胀系数、空隙率-时间曲线
Fig.6 Residual bulking factor-time curve and porosity-time curves of broken rock
表1 破碎岩石试验过程中参数变化统计
Table 1 Parameter variation of broken rock during the test
为了更直观地展现恒载阶段自然状态破碎岩石轴向变形的变化特征,将恒载情况下的轴向应变随时间的变化情况做曲线。恒载初期轴向应变增长较快,而后增长趋势逐渐变缓,恒载末期轴向应变趋于平稳。恒载情况下的应变-时间典型曲线如图7所示。

图7 破碎岩石恒载阶段应变-时间曲线
Fig.7 Deformation-time curves of broken rock under constant load
恒载载荷为200 kN情况下,破碎岩石试样的应变与时间的关系为
ε=54.55+1.036ln(t+210.82),R=0.994
(6)
式中,ε为破碎岩石试样的应变,10-3;t为时间,s。
恒载载荷为400 kN情况下,破碎岩石试样的应变与时间的关系为
ε=107.56+0.579ln(t-2.115),R=0.948
(7)
将自然状态破碎岩石轴向载荷加载阶段和恒载阶段应变差分别作曲线如图8所示。
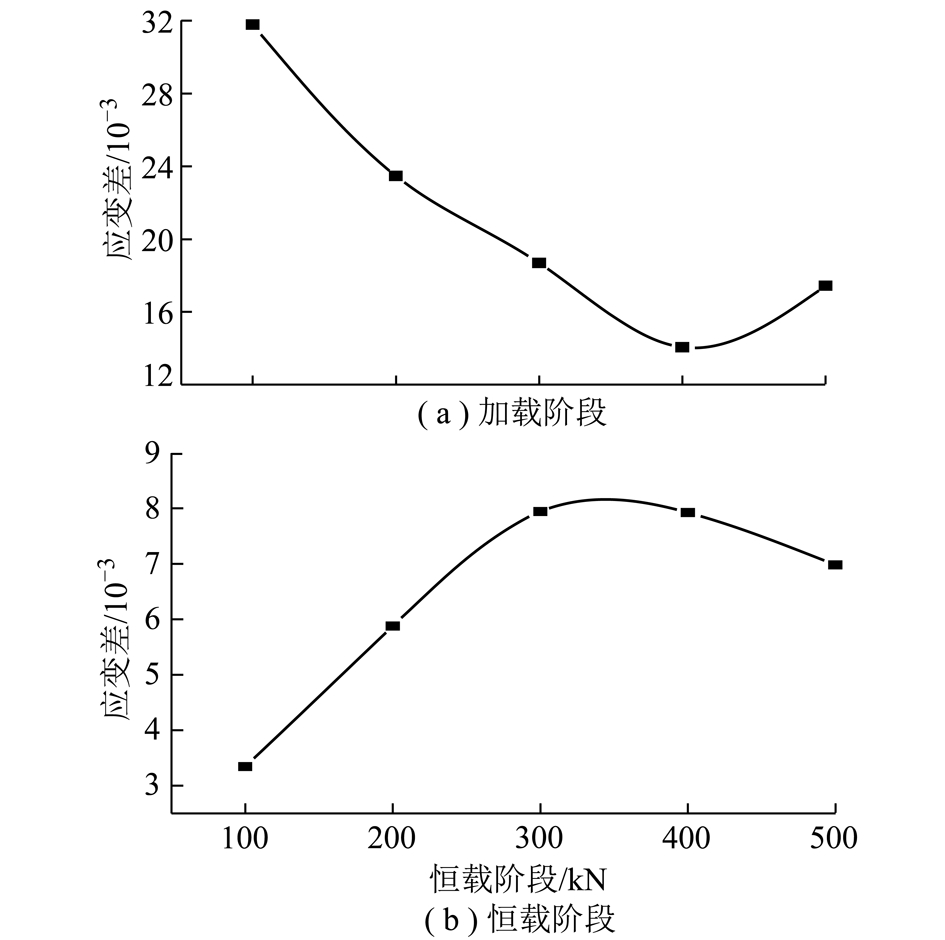
图8 破碎岩石加载阶段和恒载阶段应变差变化曲线
Fig.8 Strain difference of broken rock in loading stage and constant load stage
加载阶段:在加载阶段初期,轴向应变差值随着载荷的增大呈现减小的趋势,且试验过程中试验盒中无明显岩石破裂的声音,表明在该载荷加载阶段破碎岩石未出现明显破裂,轴向应变增大主要是由破碎岩石中较大颗粒位置调整及小颗粒滑动填充空隙引起的;经过初期加载之后,载荷作用后的破碎岩石形成一个较稳定的支撑结构,在轴向载荷由300 kN加载至400 kN过程中,轴向应变差值达到最小值14.06×10-3;在轴向载荷由400 kN加载至500 kN过程中,轴向应变差值出现反弹增大趋势,且试验过程中试验盒中有明显岩石破裂的声音,表明在该载荷加载阶段破碎岩石出现集中破坏现象,轴向应变增大的原因除了破碎岩石中颗粒位置调整及小颗粒滑动填充空隙,还包括破碎岩石压碎产生的小颗粒滑入岩块空隙。
恒载阶段:在恒载阶段初期,轴向应变差值随着恒定载荷的增大呈现增大的趋势,在恒定载荷为300 kN过程中,轴向应变差值达到最大值7.94×10-3;在恒定载荷为400 kN和500 kN过程中,随着恒定载荷的增大,轴向应变差值反而逐渐减小,这也从另一个角度说明,轴向载荷较小时,轴向应变增大主要是由破碎岩石中颗粒位置调整及小颗粒滑动填充空隙引起的,轴向载荷较大时,轴向变形增大的原因还包括破碎岩石压碎产生的小颗粒滑入空隙中。但由于前期的加载形成的破碎岩石试样的累积变形已经较大,空隙率显著降低,抵抗变形的能力大大增强,因此在恒载阶段后期应变差出现下降现象。
2.2 粒径变化特征
对破碎岩石试验后的粒径重新进行筛分和称量,试验前后不同粒径破碎岩石质量变化见表2,破碎岩石中不同粒径所占比例变化情况如图9(a)所示。破碎岩石试验前后级配变化曲线如图9(b)所示。
试验后,粒径<15 mm的破碎岩石含量均有不同程度的增加,合计增加18.44 kg;粒径15~20 mm的破碎岩石含量基本不变,可作为破碎岩石试样承压变形过程中的稳定粒径,但是试验前后此粒径范围内的破碎岩石肯定不是绝对不发生变化的,而是一个动态平衡的过程,即破碎的部分与新形成的部分基本相等,重新筛分后该粒径范围内的破碎岩石具有明显的新的断裂摩擦痕迹即是很好的证明;粒径>20 mm的破碎岩石含量则均有不同程度的减小,合计减小18.64 kg,与粒径<15 mm的破碎岩石增加量18.44 kg基本相等,为破碎岩石试样总质量的16.76%。
表2 破试验前后不同粒径破碎岩石质量变化统计
Table 2 Mass variation of broken rock with different size before and after the test
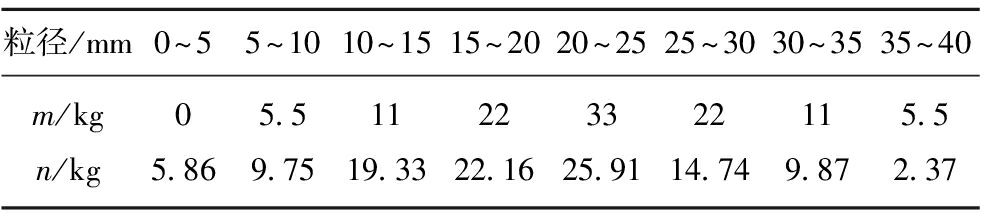
注:m为试验前,破碎岩石试样中该粒径岩石的质量;n为试验后,破碎岩石试样中该粒径岩石的质量。
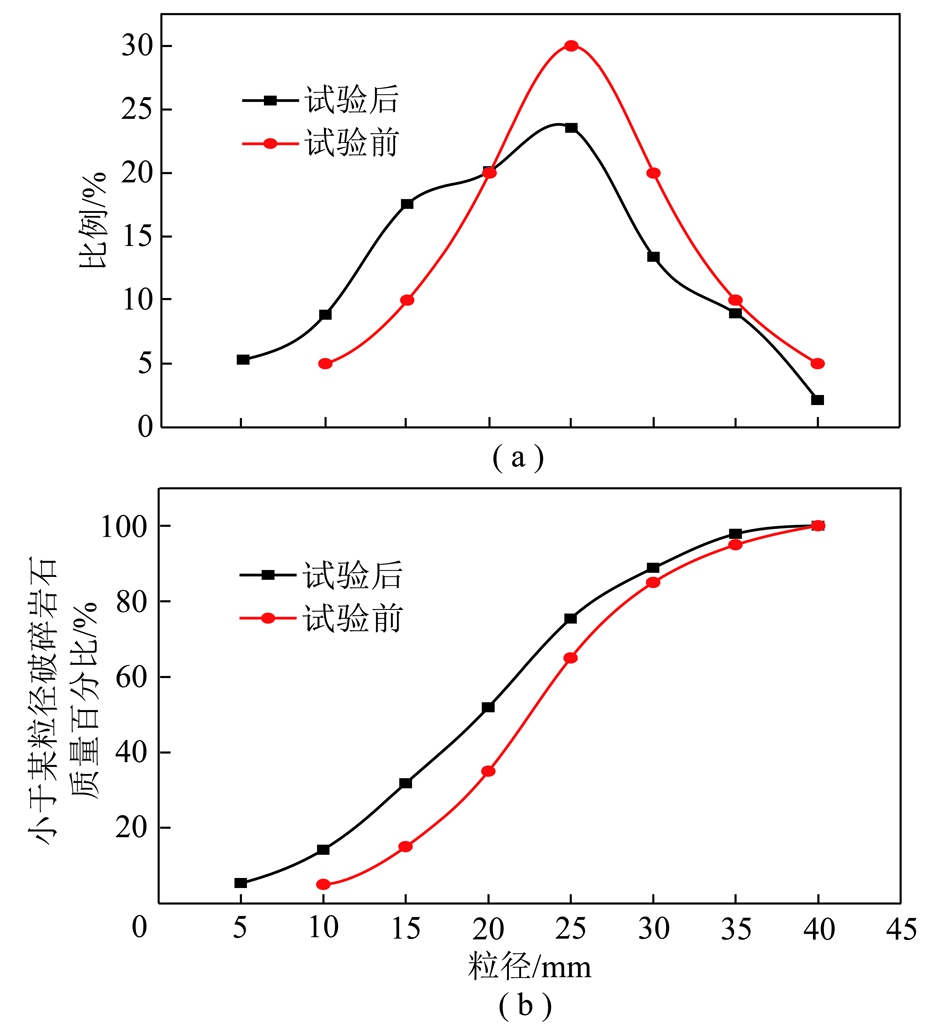
图9 破碎岩石试验前后粒径和级配变化曲线
Fig.9 Grain size variation and graduation variation of broken rock before and after the test
2.3 破碎岩石变形机制
在破碎岩石承压变形试验过程中,沿试验舱内壁将产生向上的较大摩擦力[20],同时在破碎岩石传递力的过程中会消耗减弱,这使试验舱底部破碎岩石承受的压应力比加载在破碎岩石体上表面的载荷要小。考虑到试验舱直径为400 mm,装样高度初始值为655 mm,因此试验舱属于窄而高的容器。设h为试验舱中破碎岩石的高度,A为试验舱的横截面积,L为截面周长。破碎岩体的侧壁和底部的压应力分布如图10所示[21]。

图10 破碎岩体侧壁和底部的压应力分布
Fig.10 Compressive stress distribution of side wall and bottom of broken rock
侧压应力[20-21]为
(8)
式中,σb为破碎岩石对侧壁的压应力;ρ为破碎岩体密度;g为重力加速度;μ为破碎岩石与侧壁的摩擦因数;n′为侧压应力与平均垂直压应力的比值,![]() 为平均垂直压应力。
为平均垂直压应力。
垂直压力[20-21]为
(9)
式中,μ0为破碎岩体内摩擦因数,μ0=tan φ;φ为近试验舱壁处极坐标应力图主轴偏转角;b为试验舱的半径;x为垂直压应力值计算点距试验舱中心的距离。
假定破碎岩石试样中颗粒j与其他颗粒间有n个接触,施加载荷后,第i个接触对应的作用力、接触面积分别为Pi,δi(i=1,2,…,n)。取颗粒j的某一接触面A作为研究对象,假定有m个接触,必定有m≤n,如图11所示,则接触面A上的正应力σA,剪应力τA分别为
(10)
![]()
(11)
式中,αi为接触面法线与作用力的交角。
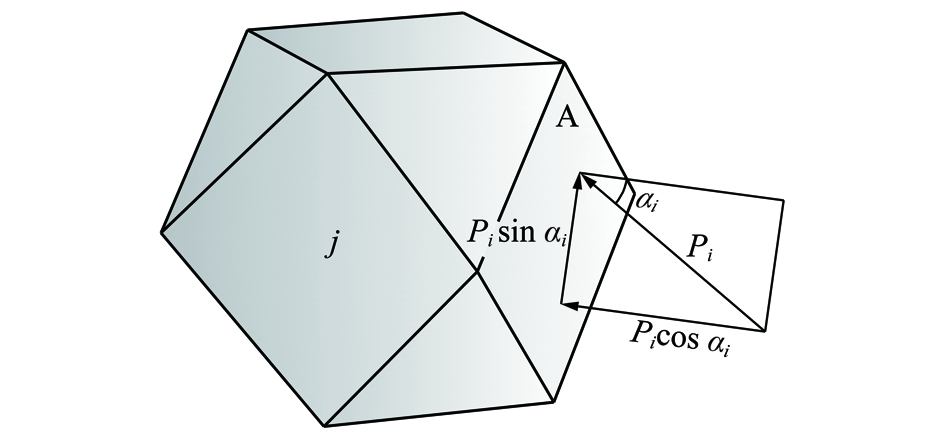
图11 颗粒j与其他颗粒的某一接触面A上的一个接触作用示意
Fig.11 Acting force between two contact surfaces belongingto particle j and other particle respectively
总正应力方向总体上对该颗粒形成压应力,在一般情况下,其值要小于破碎岩石颗粒的破损强度σs,因而不会产生颗粒间的挤压破碎。但是,在破碎岩石颗粒一些棱角或边缘接触的局部软弱界面上,其破损强度σsm常小于对应的接触挤压应力σim,其中有K个颗粒软弱界面将因受挤压而破碎、细化,即
(12)
在宏观上,破碎岩石的棱角和软弱界面将产生因压碎而引起的变形,其总量ε1为
(13)
式中,ζk为压缩柔量,等于应变与挤压应力之比。
此外,由式(11),剪应力在颗粒破损表面上形成切向应力τk,由于接触面积很小,故可将该切应力近似为均匀分布,则第k个接触面上的切应力对颗粒j重心的力矩Tk为
Tk=τkrkδk
(14)
式中,rk为接触面距颗粒重心的力矩半径。
通过颗粒重心某一局部坐标(ξ-η平面)的所有剪应力力矩矢量之和为
(15)
![]()
(16)
式中,ξk,ηk为局部坐标投影系数,分别等于剪应力在平面ξ和η上的投影值与原始值的比值。
两个力矩一般不为0,因而挤压破碎的颗粒在力矩作用下,产生细微的转动或滑移,总是向着能够移动的薄弱空间移动,进而起到填充空隙的作用。其应变ε2为
(17)
式中,θξ,θη为剪切柔量,等于应变与剪切应力之比。
则破碎岩石承压变形中的塑性应变ε为
![]()
(18)
单从应变值的数量级可以看出,ε2>ε1,因此由滑移填充空隙引起的破碎岩石变形要大于破碎岩石软弱界面被压碎引起的变形,也就是说,颗粒细化填充空隙是破碎岩石承压产生变形的主要原因[22]。
破碎岩石的承压变形试验主要分为两个阶段:瞬时压缩变形阶段和长期压缩变形阶段。
(1)瞬时压缩变形阶段:随着载荷的增加,破碎岩石逐渐变密实,其特征是变形显著,加载阶段轴向变形占到了破碎岩石试样全部变形的76.7%,时间较短,载荷停止增加,变形也基本停止。此阶段破碎岩石颗粒间以脆性接触为主,主要表现为颗粒的分解细化、滑移填充和结构调整,也伴有破碎岩石棱角的破碎,这一现象随着载荷的增加愈发显著,但细化颗粒对空隙的填充不太充分,变形也仅停留在一个相对稳定的状态。
(2)长期压缩变形阶段:载荷处于一个恒定状态,对破碎岩石冲击式的碾压虽然结束,但由于颗粒间应力的重新分布同样会导致颗粒棱角或软弱颗粒的破碎和细化,颗粒滑移、排列得到进一步调整,在宏观上表现为缓慢变形。
3 结 论
(1)研制了大尺寸破碎岩石承压变形试验系统由主体承载支架、试验舱、承压水仓、储能罐、水压水量双控伺服系统和位移应力双控伺服系统组成,具有模拟空间大、可视度优、密封性好、加载方式多样、数据精度高等特点。
(2)随轴向载荷增加,破碎顶板砂岩轴向变形逐渐增大,残余碎胀系数和空隙率逐渐减小,加载较恒载阶段尤为明显;恒载初期轴向应变增长较快,而后逐渐变缓并趋于平稳,应变-时间之间呈现对数关系;加载阶段,随载荷增大,破碎岩石试样轴向应变差值呈现先减小后增大,恒载阶段,随载荷增大,破碎顶板砂岩试样轴向应变差值则呈现先增大后减小。
(3)破碎顶板砂岩承压后的变形分为瞬时压缩变形和长期压缩变形两个阶段,主要由颗粒位置调整、原始或新生小颗粒滑动填充空隙引起的;破碎顶板砂岩试样以粒径15~20 mm为承压变形过程中粒径变化的稳定点,试验后,粒径<15 mm的含量均有增加,粒径>20 mm的含量则均有减小,为破碎顶板砂岩试样总质量的16.76%。
参考文献(References):
[1] 缪协兴,茅献彪,胡光伟,等.岩石(煤)的碎胀与压实特性研究[J].实验力学,1997,12(3):394-400.
MIAO Xiexing,MAO Xianbiao,HU Guangwei,et al.Research on broken expand and press solid characteristics of rocks and coals[J].Journal of Experimental Mechanics,1997,12(3):394-400.
[2] 马占国,郭广礼,陈荣华,等.饱和破碎岩石压实变形特性的试验研究[J].岩石力学与工程学报,2005,24(7):1139-1144.
MA Zhanguo,GUO Guangli,CHEN Ronghua,et al.An experimental study on the compaction of water-saturated over-broken rock[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(7):1139-1144.
[3] 马占国,缪协兴,李兴华,等.破碎页岩渗透特性[J].采矿与安全工程学报,2007,24(3):260-264.
MA Zhanguo,MIAO Xiexing,LI Xinghua,et al.Permeability of broken shale[J].Journal of Mining and Safety Engineering,2007,24(3):260-264.
[4] 马占国,缪协兴,陈占清,等.破碎煤体渗透特性的实验研究[J].岩土力学,2009,30(4):985-988.
MA Zhanguo,MIAO Xiexing,CHEN Zhanqing,et al.Experimental study of permeability of broken coal[J].Rock and Soil Mechanics,2009,30(4):985-988.
[5] 卜万奎.采场底板断层活化及突水力学机理研究[D].徐州:中国矿业大学,2009.
BU Wankui.Research on mechanical mechanism of fault activation and water inrush from faults in mining floor[D].Xuzhou:China University of Mining and Technology,2009.
[6] 杜春志,刘卫群,贺耀龙,等.破碎岩体压实渗透非稳态规律的试验研究[J].采矿与安全工程学报,2004,21(1):109-111.
DU Chunzhi,LIU Weiqun,HE Yaolong,et al.Experimental study on non-steady state of permeation in compacted broken rock[J].Journal of Mining & Safety Engineering,2004,21(1):109-111.
[7] 陈占清,李顺才,茅献彪,等.饱和含水石灰岩散体蠕变过程中孔隙度变化规律的实验研究[J].煤炭学报,2006,31(1):26-30.
CHEN Zhanqing,LI Shuncai,MAO Xianbiao,et al.Experimental on the porosity changing of water-saturated granular limestone during its creep[J].Journal of China Coal Society,2006,31(1):26-30.
[8] 马占国,兰天,潘银光,等.饱和破碎泥岩蠕变过程中孔隙变化规律的试验研究[J].岩石力学与工程学报,2009,28(7):1447-1454.
MA Zhanguo,LAN Tian,PAN Yinguang,et al.Experimental study of variation law of saturated broken mudstone porosity during creep process[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(7):1447-1454.
[9] 张振南,缪协兴,葛修润.松散岩块压实破碎规律的实验研究[J].岩石力学与工程学报,2005,24(3):451-455.
ZHANG Zhennan,MIAO Xiexing,GE Xiurun.Testing study on compaction breakage of loose rock blocks[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(3):451-455.
[10] 苏承东,顾明,唐旭,等.煤层顶板破碎岩石压实特征的试验研究[J].岩石力学与工程学报,2012,31(1):18-26.
SU Chengdong,GU Ming,TANG Xu,et al.Experimental study of compaction characteristics of crushed stones from coal seam roof[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(1):18-26.
[11] 陈晓祥,苏承东,唐旭,等.饱水对煤层顶板碎石压实特征影响的试验研究[J].岩石力学与工程学报,2014,33(S1):3318-3326.
CHEN Xiaoxiang,SU Chengdong,TANG Xu,et al.Experimental study of effect ofwater-saturated state on compaction property of crushed stone from coal seam roof[J].Chinese Journal of Rock Mechanics and Engineering,2014,33(S1):3318-3326.
[12] 樊秀娟,茅献彪.破碎砂岩承压变形时间相关性试验[J].采矿与安全工程学报,2007,24(3):260-264.
FAN Xiujuan,MAO Xianbiao.Experimental study of time-dependent deformation of broken sandstones under pressure[J].Journal of Mining and Safety Engineering,2007,24(4):486-489.
[13] 冯梅梅,吴疆宇,陈占清,等.连续级配饱和破碎岩石压实特性试验研究[J].煤炭学报,2016,41(9):2195-2202.
FENG Meimei,WU Jiangyu,CHEN Zhanqing,et al.Experimental study on the compaction of saturated broken rock of continuous gradation[J].Journal of China Coal Society,2016,41(9):2195-2202.
[14] 张季如,祝杰,黄文竞.侧限压缩下石英砂砾的颗粒破碎特性及其分形描述[J].岩土工程学报,2008,30(6):783-789.
ZHANG Jiru,ZHU Jie,HUANG Wenjing.Crushing and fractal behaviors of quartz sand-gravel particles under confined compression[J].Chinese Journal of Geotechnical Engineering,2008,30(6):783-789.
[15] 张季如,张弼文,胡泳,等.粒状岩土材料颗粒破碎演化规律的模型预测研究[J].岩石力学与工程学报,2016,35(9):1898-1905.
ZHANG Jiru,ZHANG Biwen,HU Yong,et al.Predicting the particle breakage of granular geomaterials[J].Chinese Journal of Rock Mechanics and Engineering,2016,35(9):1898-1905.
[16] 郁邦永,陈占清,吴疆宇,等.饱和级配破碎泥岩压实与粒度分布分形特征试验研究[J].岩土力学,2016,37(7):1887-1894.
YU Bangyong,CHEN Zhanqing,WU Jiangyu,et al.Experimental study of compaction and fractal properties of grain size distribution of saturated crushed mudstone with different gradations[J].Rock and Soil Mechanics,2016,37(7):1887-1894.
[17] 张超,展旭财,杨春和.粗粒料强度及变形特性的细观模拟[J].岩土力学,2013,34(7):2077-2083.
ZHANG Chao,ZHAN Xucai,Yang Chunhe.Mesoscopic simulation of strength and deformation characteristics of coarse grained materials[J].Rock and Soil Mechanics,2013,34(7):2077-2083.
[18] 南京水利科学研究院.SL237-1999 土工试验规程[S].北京:水利水电出版社,1999.
[19] BISHOP W A,HENKEL D J.The measurement of soils properties in triaxial test[R].London:Edward Arnold Ltd.,1962.
[20] 黄松元.散体力学[M].北京:机械工业出版社,1993.
[21] 王海龙.厚松散层薄基岩采动涌水溃砂致灾基础试验研究[D].青岛:山东科技大学,2016.
WANG Hailong.Experimental study on water and sand inrush caused by mining under thin bedrock and thick unconsolidated formations[D].Qingdao:Shandong University of Science and Technology,2016.
[22] 梁军,刘汉龙,高玉峰.堆石蠕变机理分析与颗粒破碎特性研究[J].岩土力学,2003,24(3):479-483.
LIANG Jun,LIU Hanlong,GAO Yufeng.Creep mechanism and breakage behaviour of rockfill[J].Rock and Soil Mechanics,2003,24(3):479-483.
王登科,吕瑞环,彭明,等.含瓦斯煤渗透率各向异性研究[J].煤炭学报,2018,43(4):1008-1015.doi:10.13225/j.cnki.jccs.2017.0922
WANG Dengke,LÜ Ruihuan,PENG Ming,et al.Experimental study on anisotropic permeability rule of coal bearing methane[J].Journal of China Coal Society,2018,43(4):1008-1015.doi:10.13225/j.cnki.jccs.2017.0922