含瓦斯煤渗透率是煤层气抽采过程中的关键参数,其大小影响着煤层气的高效抽采。我国煤层渗透率普遍偏低[1],在形成过程中往往受沉积环境、成煤作用和构造作用的影响,呈现渗透率各向异性的特征,因此开展含瓦斯煤渗透率各向异性应力敏感性研究对煤矿瓦斯灾害预测与防治及煤层气高效抽采具有指导意义。
为此,国内外学者针对煤岩体的透气性及瓦斯运移规律开展了相关研究。POMEROY和ROBINSON[2]在对立方体煤柱做水渗流时发现,当围压分别垂直于面割理、端割理和层理面时,水渗流速率有明显不同。在对圣胡安盆地La Plata矿井煤样进行渗流实验时,GASH等[3]发现不同方向含瓦斯煤渗透率差异较大,沿割理方向渗透率差异较小,而沿垂直层理面方位渗透率较小,也证实了煤层渗透率的各向异性。MASSAROTTO[4]定义了水平渗透率各向异性率和垂直渗透率各向异性率,并通过真三轴加载煤渗透率仪(TTSCP)对其进行了研究。基于渗流力学理论,王端平、周涌沂等[5-7]推导出了计算岩芯渗透率主值的新模型,根据计算得出的渗透率主值,就可以计算任意方位岩芯的渗透率值,并给出了详细实施步骤。利用渗透率测试仪,黄学满[8]进行不同方位含瓦斯煤渗透率的测定,针对瓦斯在平行于煤样层理方向与垂直于层理方向渗透性的不同,进行了不同瓦斯压力下的渗透率测定,发现考虑垂直与平行层理面方位下渗透率差异可达一个数量级。PAN Zhejun等[9]认为用圆柱形试样测非均质性较强岩石的各向异性渗透率不能反映真实的各向异性渗透率,于是设计了用感光性树脂,通过3D打印技术,做成直径为38.1 mm中间掏出边长约21 mm立方体空间的柱状支撑模,对四川盆地龙马溪组方形页岩试样进行了渗透率各向异性测量,并利用SIMED II模拟软件对渗透率各向异性对页岩气产量的影响进行了数值模拟,得出各向异性渗透率对页岩气产量有很大影响的结论。岳高伟[10]、亓宪寅[11]等建立了煤体各向异性渗透模型,分别研究了考虑各向异性渗流规律煤体中钻孔方位对抽采效果的影响以及煤体各向异性对气体扩散和渗透的影响。WANG Kai等[12]提出了一个基于有效应力变化和气体吸附作用煤的各向异性渗透率演变模型,并通过渗透率实验测试对模型进行了验证。高超等[13]利用瞬态渗透率测试方法,研究了正交方向CCUS场地储层砂岩渗透率差异性随围压的变化规律,并定义了渗透率各向异性系数,定量描述了渗透率各向异性变化规律。在对立方体页岩试样渗流实验研究中,MA Yong[14],TAN Yuling[15]等发现在平行层理的两个方向,渗透率也表现出了很强的各向异性。王登科等[16-18]综合考虑了气体黏性系数、压缩因子、应力路径和克氏效应对煤层瓦斯渗透性的影响,自主研发了三轴应力条件下的含瓦斯煤吸附-解吸-渗流实验系统[19],为煤层瓦斯渗透率各向异性的研究提供了理论参考和实验测试手段。
从目前的研究现状来看,有关含瓦斯煤各向异性渗流的结论还存在一些分歧,对含瓦斯煤渗透率各向异性的动态发展和瓦斯优势流动方向的研究还不够深入,本文通过开展不同有效应力条件下含瓦斯煤各向异性渗流实验,对含瓦斯煤渗透率各向异性程度进行评价,重点研究含瓦斯煤渗透率各向异性动态变化和瓦斯优势流动方向的确定,以期为我国煤矿瓦斯灾害防治和煤层瓦斯高效抽采提供借鉴。
1 煤样制备
实验所用煤样取自山西晋城泽州天安煤业苇町矿,将井下取出的煤块用保鲜膜密封,带回实验室。为钻取不同角度平行层理的原煤煤柱,选取无明显宏观裂隙、弱面,且层理性较好的大煤块(图1),假设煤层的走向方向为0°,利用立式钻床(图2)钻取平台取样。沿平行层理依次钻取0°,30°,60°,90°方向,以及垂直层理方向的柱状煤样,取样示意如图3所示,将钻取的柱状煤样,用岩石切片机切割成长度为50±0.2 mm的煤样,最后利用双端面磨岩机将煤柱两端面磨平,煤样端面的不平整度利用千分表测量,将煤样规格控制在力学试验标准之内,制备完成的煤样如图4所示。本实验共制备3组试样,分别命名为A,B,C三组,每组5个煤样,共15个煤样,各煤样的取样方向见表1。

图1 新鲜煤样
Fig.1 Fresh coal
将制备完成的煤样放入恒温干燥箱中,调整烘干温度为90 ℃,烘干24 h,去除煤样中的水分,装入密封袋备用。
2 实验原理与实验步骤
2.1 实验原理
不同煤级、不同赋存环境中的含瓦斯煤渗透率差异较大,透气性各有不同,对不同透气性的含瓦斯煤试样,各有其适合的渗透率测量方法,即瞬态法与稳态法。本文渗透率测量方法采用稳态测量法,渗透率的计算公式为

图2 立式钻床
Fig.2 Vertical drilling machine

图3 取样示意
Fig.3 Sketch map of sampling

图4 实验煤样
Fig.4 Samples for experiment
表1 所取煤样分组、编号和取样方向
Table 1 Group,numbering and drilling direction of coal samples

(1)
式中,K为煤样渗透率,10-15 m2;qa为标准状况下气体通过煤样的稳定流量,cm3/s;μ为气体动力黏度,1.08×10-5 Pa·s;L为煤样长度,cm;A为煤样横截面积,cm2;p1为煤样进气口的气体压力,MPa;pa为煤样出气端的气体压力,MPa。
假设垂直层理方向为煤层的一个渗透率主值方向,且规定垂直层理方向的渗透率主值为Kz。因此含瓦斯煤渗透率各项异性的三维问题可以转化为二维平面问题进行分析。在二维空间中,渗透率张量Kij有4个分量,表示为
(2)
式中,Kxy=Kyx,在直角坐标系中,对角线分量之和为常数,与坐标方向无关。
当渗透率主值方向与坐标轴方向一致时,将式(2)对角化处理后可得
(3)
这种形式的张量称为对角线张量,对应的两个非零分量Kx,Ky为渗透率的主值,渗透率主值所对应的方向为主渗透方向。如图5所示,x轴和y轴为主渗透方向,v为渗透速度,vx和vy为渗透速度在xoy坐标中的速度分量,vζ和vη为渗透速度在ζoη坐标中的速度分量。若已知渗透率的主值大小Kx,Ky及其方向,根据坐标变换原理(图5),就可以求得渗透率分量与渗透率主值的关系[20-23],具体公式表述如下:

(4)
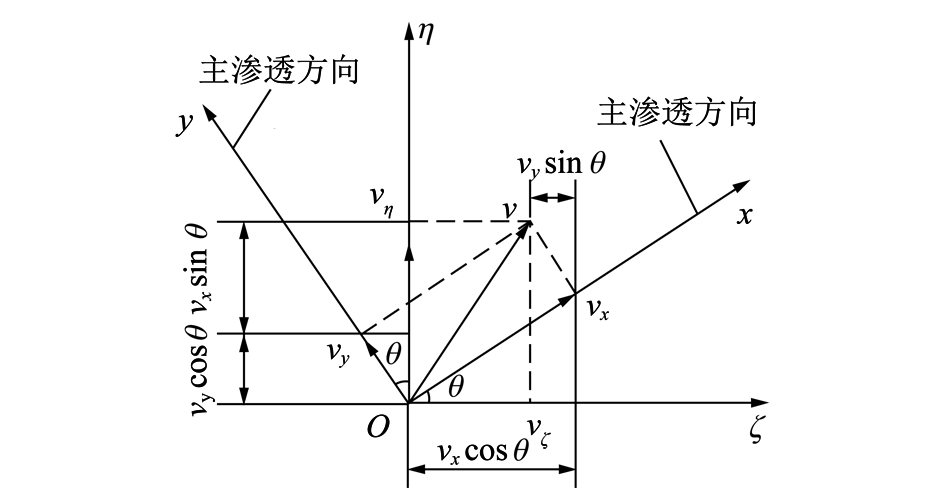
图5 渗透率主值与渗透率分量的关系
Fig.5 Relationship between the permeability and the
permeability component
其中,θ为Kx或Ky的方位角,利用三角函数的倍角关系,可以得到渗透率分量为

(5)
运用式(5)就可以在已知渗透率主值和方向的条件下,求解任意坐标系下的渗透率分量。同样,也可以在已知渗透率分量和方位角的情况下求解渗透率主值的大小和方位,具体如下:
将实验测得的不同方位角下的渗透率分量(仅需3个角度下的渗透率值)及其方位角代入式(4)可得

(6)
解方程组即可得到渗透率主值Kx,Ky及其方位角θ,θ+90°的大小。
2.2 实验步骤
本实验采用瓦斯地质与瓦斯治理重点实验室自主研发的三轴瓦斯渗流实验系统对含瓦斯煤进行各向异性渗透率的测量,实验系统基本组成部分为:煤样加持器、加卸载系统、抽真空系统、气体渗流系统、流量监测系统、位移监测系统和温度监控系统,具体实验系统详见文献[24]。
主要实验步骤如下:
(1)煤样安装。将三轴瓦斯渗流实验系统的夹持器清洁干净,把干燥好的煤样放入夹持器中,安装好左压头与右压头,通过手动高压泵对煤样施加一定的轴压与围压。
(2)渗透率测定。调节手动高压泵,将围压调节至2 MPa,轴压调节至2 MPa,打开高纯甲烷罐,及相关阀门,调节减压阀,将入口气压调节至表压0.9 MPa(绝对压力1.0 MPa),打开出气口阀门,通过外接解析仪进行记录,待甲烷气体流动稳定,打开机械秒表进行计时,记录气体累计流量,通过记录的累计流量,以及进出气口甲烷压力,可通过式(1)计算得出煤样在此围压条件下的渗透率,通过手动高压泵,将围压调节至下一实验载荷,围压逐级加载,间隔为0.8 MPa,直到围压加载至6 MPa,待瓦斯流动稳定后,通过上述方法,计算得到煤样渗透率。不断更换围压大小,完成实验。实验测试条件见表2。
表2 煤样渗透率测试条件
Table 2 Test conditions of coal sample permeabilityMPa

3 实验结果与分析
3.1 渗透率测试结果与渗透率主值求解
在流固耦合的研究中,根据实验结果,充分考虑外加载荷及孔隙压力的作用,以有效应力作为自变量,建立渗透率随有效应力变化的函数关系式是常用研究手段[25],本文利用实验测试得到了各组煤样在不同有效应力条件下的渗透率大小,具体测试结果详见表3~5。
表3 A组煤样渗透率测试结果
Table 3 Permeability results of coal samples in group A

表4 B组煤样渗透率测试结果
Table 4 Permeability results of coal samples in group B
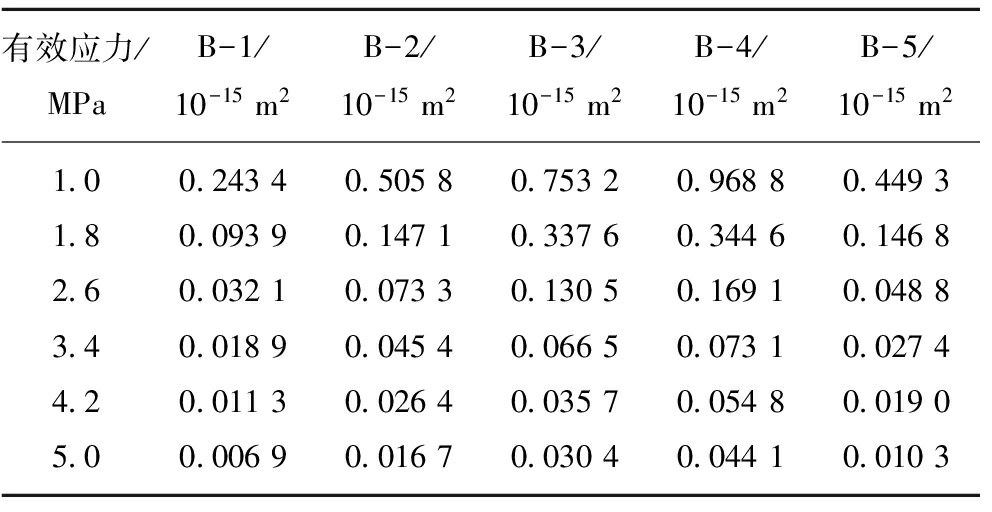
表5 C组煤样渗透率测试结果
Table 5 Permeability results of coal samples in group C

根据表1中的煤样取样方向,在平行层理方向共取了4组煤样,取平行层理0°,30°和90°方向煤样的渗透率进行渗透率主值及其方位角的求解,60°方向煤样的渗透率则用于渗透率主值及其方位角计算结果的验证。通过计算得到不同有效应力下的含瓦斯煤渗透率主值及其方位角大小见表6。
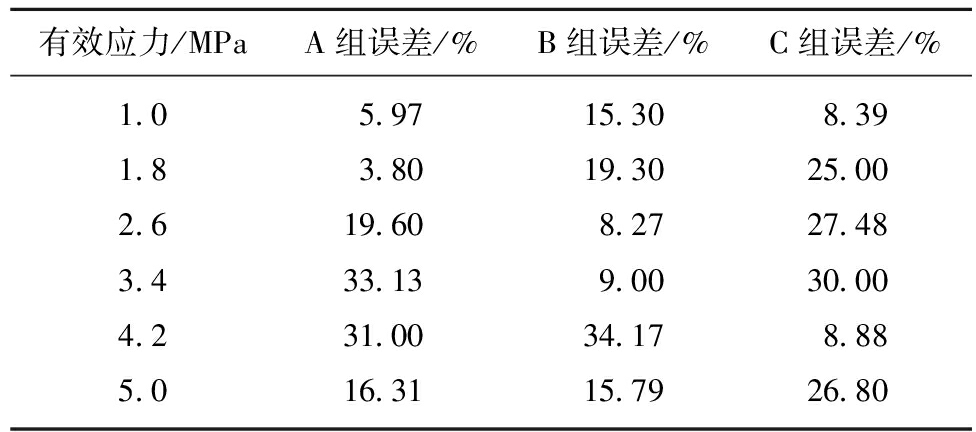
验证过程中,令θ1=60°,代入式6,利用表6中的渗透率主值及其方向的计算结果,可得到60°方向煤样渗透率的理论值,然后根据表3中A-3煤样、表4中B-3煤样和表5中C-3煤样的渗透率实测值大小,来验证煤样渗透率理论值的准确性。理论值和实测值的对比结果见表7,可以看出,计算值与理论值的相对误差维持在35%以内,表明理论计算结果较为真实可信。由于含瓦斯煤不仅具有各向异性,同时也具有非均质性,含瓦斯煤体内的孔、裂隙发育不均匀,这些均是导致实验所测值与理论计算值之间产生偏差的重要原因。由此可见,本文的解析计算法为相关科研工作者提供了一种较为有效的、简单快捷的煤体各向异性渗透率评估方法。
表6 煤样渗透率主值与方位角求解结果
Table 6 Results of anisotropic principal and position angle of coal samples

表7 渗透率理论值与实测值对比结果
Table 7 Comparison between theoretical and measured results of coal permeability
3.2 含瓦斯煤渗透率主值应力敏感性分析
通过对不同有效应力条件下煤样渗透率主值的求解,可以发现随着有效应力增加,A~C组煤样渗透率主值逐渐减小,主值方位角变化较小,基本维持在同一方位。对渗透率主值随有效应力变化的规律进行分析后,发现煤样渗透率主值随有效应力的增加呈现出负指数函数关系降低规律,如图6所示,具体见式(7),拟合参数及拟合精度的具体结果见表8。
K(Pe)=K0e-βPe(7)
式中,Pe表示所施加的有效应力;K(Pe)表示有效应力为Pe时的煤样渗透率;K0,β为拟合参数。

图6 煤样渗透率主值随有效应力变化规律
Fig.6 Changing rules of coal sample principal permeability under varying effective stress
从煤样渗透率主值随有效应力的变化规律来看,平行层理渗透率主值Kx,Ky之间在数值上差别较大,基本上有Kx>Ky,因此可确定Kx的方向为含瓦斯煤的优势流动方向。Ky,Kz之间在数值上差别相对较小,存在Kz>Ky的现象(图6(a),(b)),这表明并不是平行煤层层理方向的瓦斯渗透率就一定会大于垂直煤层层理方向的渗透率。
3.3 含瓦斯煤渗透率的各向异性程度评价
孙东生等[26]在进行低渗砂岩渗透率各向异性研究时,定义了评价低渗砂岩各向异性程度的参数,本文参考其定义,利用各向异性率αK这一参数,来评价煤体渗透率主值在3个相互垂直的主方向上的各向异性程度。各向异性率αK若为正值,则表明在有效应力作用下,瓦斯的优势流动方向未发生改变,若αK正负号发生改变,则表明优势流动方向发生了改变。
表8 渗透率主值随有效应力变化拟合参数
Table 8 Fitting parameters of permeability principal value changing over effective stress

3个平面各向异性程度可以用参数αK来表示,αK定义为
(8)
代入式(7),渗透率各向异性率可由式(9)表示。
αK(di,dj,Pe)=ln αK0+AαKPe
(9)
式中,di,dj代表方向(i,j表示x,y,z中任两个方位);Ki,Kj表示不同有效应力下的渗透率。
αK0=K0,i/K0,j
(10)
AαK=βj-βi
(11)
如前所述,假设z轴为垂直层理方向,x轴和y轴为平行层理方向。通过计算,可以得到所测3组煤样渗透率各向异性率随有效应力的变化规律如图7所示,其中,Ax,Ay和Az分别代表A组煤样渗透率主值处于x轴、y轴和z轴方位,Bx,By和Bz分别代表B组煤样渗透率主值处于x轴、y轴和z轴方位,Cx,Cy和Cz分别代表C组煤样渗透率主值处于x轴、y轴和z轴方位;图7中的Ax/Ay表示在xy平面上的A组煤样渗透率各向异性率的变化情况,Ax/Az表示在xz平面上的A组煤样渗透率各向异性率的变化情况,Ay/Az表示在yz平面上的A组煤样渗透率各向异性率的变化情况,其他组的具体情况以此类推。
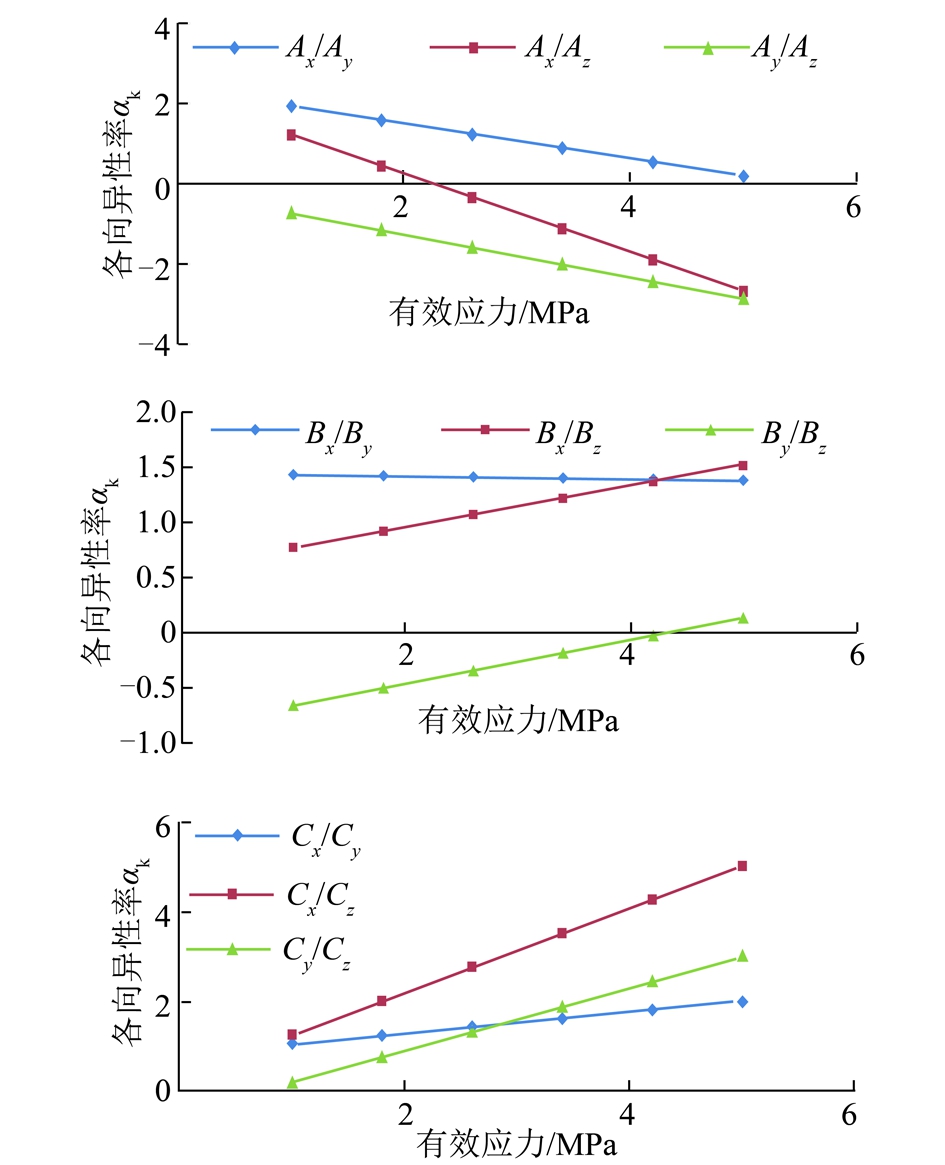
图7 不同有效应力下3组煤样各向异性率
Fig.7 Anisotropy ratio of three group under different effective stress
现以图7中的A组煤样渗透率主值的变化情况来详细说明含瓦斯煤渗透率各向异性的发展趋势。根据实验结果,在xy平面内,在有效应力小于5.0 MPa时,各向异性率αK>0,而且其数值逐渐变小,表明瓦斯优势流动方向未发生改变,一直都是x轴方向,但是含瓦斯煤的渗透率各向异性在逐渐减弱;在xz平面内,随着有效应力的增加,各向异性率由原来的αK>0变为了αK<0,说明瓦斯优势流动方向由原来的x轴方向转为了z轴方向,而且各向异性率先减小后增大,含瓦斯煤渗透率的各向异性先减弱后增强;在yz平面内,随着有效应力的增加,各向异性率αK<0且随有效应力不断增加,表明瓦斯优势流动方向一直保持在z轴方向,并且含瓦斯煤渗透率的各向异性在不断增强。
同理,在图7(b)中,在xy平面和xz平面内,瓦斯优势流动方向一直都是x轴方向;在yz平面内,当有效应力大于4 MPa时,瓦斯优势流动方向由原来的z轴方向转为了y轴方向。在图7(c)中,在xy平面和xz平面内,瓦斯优势流动方向也一直都是x轴方向,含瓦斯煤渗透率的各向异性随有效应力增大而不断增强;在yz平面内,瓦斯优势流动方向一直都是y轴方向,含瓦斯煤渗透率的各向异性随有效应力增大而增强。
通过上述分析可知,由于煤的非均质性以及应力的不断增加,对煤体结构有一定的破坏,含瓦斯煤渗透率的各向异性程度随着应力加载是动态变化的,而且可能出现瓦斯优势流动方向发生转变的现象,并不是说平行层理方向就一定是瓦斯优势流动方向,垂直层理方向就一定不是优势流动方向。
4 结 论
(1)基于三角函数所提出的含瓦斯煤的各向异性渗透率计算方法简单有效,规避了利用方形试样测试各向异性渗透率时所存在的气密性很难保证、无法准确获取含瓦斯煤的渗透率主值大小及其方向等不足。
(2)通过计算得出了平行层理方向含瓦斯煤的渗透率主值及其方位,随着有效应力的增加,含瓦斯煤的渗透率主值与有效应力之间符合负指数函数变化规律。渗透率主值Kx方向(平行层理的某个方向)基本上是煤层瓦斯优势流动方向,存在渗透率主值的Kz方向(垂直层理方向)是煤层瓦斯优势流动方向的可能。
(3)含瓦斯煤渗透率的各向异性程度不是一成不变的,而是动态变化的,随着载荷的变化会出现瓦斯优势流动方向发生转变的现象,平行层理方向不一定为煤层瓦斯绝对优势流动方向,垂直层理方向有可能成为煤层瓦斯优势流动方向。
参考文献(References):
[1] 叶建平,史保生,张春才.中国煤储层渗透性及其主要影响因素[J].煤炭学报,1999,24(2):8-12.
YE Jianping,SHI Baosheng,ZHANG Chuncai.Coal reservoir permeability and its controlled factors in China[J].Journal of China Coal Society,1999,24(2):118-122.
[2] POMEROY C D,ROBINSON D J.The effect of applied stresses on the permeability of a middle rank coal to water[J].International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts,1967,4(3):329-343.
[3] GASH B W,VOLZ R F,POTTER G,et al.The effects of cleat orientation and confining pressure on cleat porosity,permeability and relative permeability in coal[A].The 1993 International Coalbed Methane Symposiun[C].The University of Alabama,Tuscaloosa,Alabama,USA,1993.
[4] MASSAROTTO P,RUDOLPH V,GOLDING S D.Anisotropic permeability characterisation of Permian coals[A].International Coalbed Methane Symposium[C].The University of Queensland,Brisbane,Australia,2003.
[5] 周涌沂,王端平.岩石方向渗透率的确定方法研究[J].大庆石油地质与开发,2005,24(4):21-24.
ZHOU Yongyi,WANG Duanping.Research on the methods to determine directional permeability of rock[J].Petroleum Geology & Oilfield Development in Daqing,2005,24(4):21-24.
[6] 周涌沂,王端平,马泮光,等.渗透率的矢量性研究[J].新疆石油地质,2004,25(6):683-685.
ZHOU Yongyi,WANG Duanping,MA Panguang,et al.Study on vector property of permeability[J].Xinjiang Petroleum Geology,2005,25(6):683-685.
[7] 王端平,周涌沂,马泮光,等.方向性岩石渗透率的矢量特性与计算模型[J].岩土力学,2005,26(8):1294-1297.
WANG Duanping,ZHOU Yongyi,MA Panguang,et al.Vector properties and calculation model for directional rock permeability[J].Rock and Soil Mechanics,2005,26(8):1294-1297.
[8] 黄学满.煤结构异性对瓦斯渗透特性影响的实验研究[J].矿业安全与环保,2012,39(2):1-3.
HUANG Xueman.Experimental study on influence of structural anisotropy of coal upon gas permeability[J].Mining Safety & Environmental Protection,2012,39(2):1-3.
[9] PAN Z J,MA Y,CONNELL L D,et al.Measuring anisotropic permeability using a cubic shale sample in a triaxial cell[J].Journal of Natural Gas Science & Engineering,2015,26:336-344.
[10] 岳高伟,王滨宾,曹汉生,等.结构异性煤层顺层钻孔方位对有效抽采半径的影响[J].煤炭学报,2017,42(S1):138-147.
YUE Gaowei,WANG Binbin,CAO Hansheng,et al.Influence of effective drainage radius by borehole orientation along seam with anisotropic permeability[J].Journal of China Coal Society,2017,42(S1):138-147.
[11] 亓宪寅,王威.基于结构异性比的含瓦斯煤渗透各向异性研究[J].岩土工程学报,2017,39(6):1030-1037.
QI Xianyin,WANG Wei.Anisotropic permeability model for coal containing methane based on anisotropic structure ratio[J].Chinese Journal of Geotechnical Engineering,2017,39(6):1030-1037.
[12] WANG K,ZANG J,WANG G D,et al.Anisotropic permeability evolution of coal with effective stress variation and gas sorption:Model development and analysis[J].International Journal of Coal Geology,2014,130(4):53-65.
[13] 高超,谢凌志,熊伦,等.基于特低渗砂岩覆压试验渗透率方向性特征分析[J].岩土力学,2016,37(4):948-956.
GAO Chao,XIE Lingzhi,XIONG Lun,et al.Analysis of direction-dependent characteristics of permeability of sandstone with ultra-lowly permeability in confining pressure tests[J].Rock and Soil Mechanics,2016,37(4):948-956.
[14] MA Y,PAN Z J,ZHONG N N,et al.Experimental study of anisotropic gas permeability and its relationship with fracture structure of Longmaxi Shales,Sichuan Basin,China[J].Fuel,2016,180:106-115.
[15] TAN Y L,PAN Z J,LIU J S,et al.Experimental study of permeability and its anisotropy for shale fracture supported with proppant[J].Journal of Natural Gas Science & Engineering,2017,44:250-264.
[16] WANG D K,WEI J P,FU Q C,et al.Seepage law and permeability calculation of coal gas based on Klinkenberg effect[J].Journal of Central South University,2015,22(5):1973-1978.
[17] WANG D K,WEI J P,WEN Z H.Permeability characteristics of gas-bearing coal under different stress paths[J].Disaster Advances,2013,6(S2):289-294.
[18] 王登科,魏建平,付启超,等.基于Klinkenberg效应影响的煤体瓦斯渗流规律及其渗透率计算方法研究[J].煤炭学报,2014,39(10):2029-2036.
WANG Dengke,WEI Jianping,FU Qichao,et al.Coalbed gas seepage law and permeability calculation method based on Klinkenberg effect[J].Journal of China Coal Society,2014,39(10):2029-2036.
[19] 王登科,彭明,魏建平,等.煤岩三轴蠕变-渗流-吸附解吸实验装置的研制及应用[J].煤炭学报,2016,41(3):644-652.
WANG Dengke,PENG Ming,WEI Jianping,et al.Development and application of tri-axial creep-seepage-adsorption and desorption experimental device for coal[J].Journal of China Coal Society,2016,41(3):644-652.
[20] FANCHI J R.Directional permeability[J].Spe Reservoir Evaluation & Engineering,2008,11(3):565-568.
[21] 王洪涛.多孔介质污染物迁移动力学[M].北京:高等教育出版社,2008.
[22] 李亚军,姚军,黄朝琴,等.裂缝性油藏等效渗透率张量计算及表征单元体积研究[J].水动力学研究与进展,2010,25(1):1-7.
LI Yajun,YAO Jun,HUANG Chaoqin,et al.Calculation of equivalent permeability tensorand study on represent ative element volume for modeling fractured reservoirs[J].Chinese Journal of Hydro-Dynamics(series A),2010,25(1):1-5.
[23] 胡书勇,马俊修,张烈辉,等.一种各向异性渗透率张量的测试方法[P]:中国,CN101220735B.2015-04-08.
[24] 魏建平,李明助,王登科,等.煤样渗透率围压敏感性试验研究[J].煤炭科学技术,2014,42(6):76-80.
WEI Jianping,LI Mingzhu,WANG Dengke,et al.Experimental research on sensibility of coal samples permeability under confining pressure[J].Coal Science and Technology,2014,42(6):76-80.
[25] 黄远智,王恩志.低渗透岩石渗透率对有效应力敏感系数的试验研究[J].岩石力学与工程学报,2007,26(2):410-414.
HUANG Yuanzhi,WANG Enzhi.Experimental study on coefficient of sensitiveness between percolation rate and effective pressure for low permeability rock[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(2):410-414.
[26] 孙东生,李阿伟,王红才,等.低渗砂岩储层渗透率各向异性规律的实验研究[J].地球物理学进展,2012,27(3):1101-1106.
SUN Dongsheng,LI Awei,WANG Hongcai,et al.Experiment on anisotropy of permeability with tight sandstone[J].Progress in Geophysics,2012,27(3):1101-1106.