瓦斯涌出是煤巷掘进过程中的主要威胁之一，准确掌握瓦斯涌出量的变化规律为瓦斯涌出异常分析、预防瓦斯事故的发生提供理论基础。目前煤巷掘进瓦斯涌出量的确定方法多基于煤层瓦斯流动理论，按计算维度分为传统二维煤巷瓦斯涌出量计算方法和三维瓦数值计算方法[1-9]。传统二维煤巷瓦斯涌出量计算方法根据沿巷道长度方向上瓦斯涌出量与某一固定地点煤壁瓦斯涌出量随时间变化的相似性通过对时间的积分代替对巷道长度方向的积分[10]，具有模型简单、计算量少、巷道起止位置无限制、掘进速度变化函数设置灵活的特点，但对煤巷的揭露方式及煤层厚度有一定要求。三维数值计算方法相比传统二维计算方法对煤层条件具有更好的适应性，逐渐成为煤巷掘进瓦斯涌出研究的热点。高建良等[2-3]将渗透率对煤壁距离的分段函数引入到瓦斯涌出计算模型中，并研究了时空步长对煤巷壁面瓦斯涌出精度的影响;梁冰等[4]采用瓦斯流固耦合模型，研究了掘进长度对静态瓦斯涌出总量的影响;刘伟等[5]采用参数无因化及移动坐标系的方法研究了掘进速度对煤壁动态瓦斯涌出的影响。但三维数值计算方法对长距离煤巷掘进瓦斯涌出量计算要求划分大量网格，难以考虑掘进速度及时间效应对瓦斯涌出总量的影响。
为此，笔者在传统二维煤巷瓦斯涌出量计算方法中引入固气耦合模型，提出基于固气耦合及巷道断面瓦斯涌出量时间积分的煤壁瓦斯涌出计算方法。以南桐矿区兴隆煤矿被保护层工作面煤巷掘进为工程背景，对掘进过程中煤壁瓦斯涌出量的变化规律进行分析。
1 数学模型
1.1 基本假设
本文对煤巷掘进中瓦斯涌出源及煤层内瓦斯渗流模型作如下假设:
(1)煤巷掘进煤壁瓦斯涌出包括巷道两侧煤壁的瓦斯涌出和工作面前方煤壁的瓦斯涌出，均为单向流动[10];
(2)煤体为连续、均质及各向同性介质;煤层瓦斯渗流为等温过程，服从达西定律[11-13]。
1.2 煤层瓦斯流动固气耦合计算模型
(1)煤层瓦斯渗流方程
煤层瓦斯渗流服从达西方程，瓦斯流动连续性方程[12]为
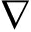
(1)
其中,
Cfree=ρgφ;ρg=pgβg
式中，pg为煤层瓦斯压力，Pa;ρg为煤层瓦斯密度，kg/m3;vg为瓦斯渗流速度，m/s;C为煤层瓦斯含量，kg/m3，Cad为吸附瓦斯含量，Cfree为游离瓦斯含量;k为有效渗透率，m2;φ为煤体孔隙率;βg为瓦斯压缩因子，kg/(Pa·m3);a，b为Langmuir吸附常数;A，B为灰分、水分。
有效渗透率k表示为体应力、瓦斯压力函数[14]:
k=(a1Θ2+a2Θ+a3)[1+c1(a1Θ2+a2Θ+a3)c2/pg]
(2)
式中，a1，a2，a3，c1，c2均为试验确定的拟合常数(a1=2.1×10-31,a2=-8.36×10-24,a3=1.02×10-16,c1=9.356 7×10-7,c2=-0.699 9);Θ为体积应力，Pa。
对式(1),(2)进行整理，得到系数形式的二阶渗流场偏微分方程:
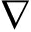(coeffc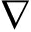
(3)
其中
(2)含瓦斯煤体的变形场方程
含瓦斯煤体的变形控制方程服从有效应力方程[15]:
σ=2Gε+λtr(ε)I-αpgI
(4)
式中，σ为有效应力，Pa;ε为应变矩阵;tr(ε)为应变矩阵ε的迹;G为剪切模量，Pa;λ为拉梅系数;I为单位矩阵;α为Biot系数，由瓦斯压力及体应力拟合式表示[16]:
α=d1p-d2Θ-d3pΘ+d4
根据南桐矿区有关有效应力的研究[14]，回归系数d1，d2，d3，d4的取值分别为0.483 2×10-6，0.008 3×10-6，0.02×10-12，0.399 1。
孔隙率与瓦斯压力的关系[15]:
(5)
(6)
式中，Ks为煤的骨架体积模量;εb为煤的体积应变;pg0为初始瓦斯压力，Pa。
1.3 煤巷掘进煤壁瓦斯涌出量计算模型
(1)煤巷掘进巷道两侧煤壁瓦斯涌出
煤巷掘进过程中沿掘进方向的每个断面上瓦斯涌出量从揭露开始均以相同趋势随时间不断衰减，可将煤巷掘进的三维空间的瓦斯渗流模型转化为煤巷断面的二维瓦斯渗流模型对时间维的积分。煤壁瓦斯涌出量的时间递推关系式[1]:
Qt=Qt,t-1+Qt-1=Qt,t-1+Qt-1,t-2+Qt-2=
(7)
式中，t为掘进时间，h;Qt为t时刻煤巷全长，lt的瞬时瓦斯涌出量;li为时刻ti的巷道距离，m;Qt-1为t时刻掘进距离为lt-1的煤壁瞬时瓦斯涌出量，m3/h;Qt,t-1为新揭露煤壁(lt-lt-1)的瓦斯涌出量;vi为ti时刻的掘进速度，m/h;δit为煤壁揭露的第ti到ti+1时间间隔，h;qt-ti为t时刻，li位置的巷道断面瓦斯涌出量，m2/h，q1=q0。
qt-ti=∮vgds
(8)
式中，vg为t时刻巷道壁瓦斯渗流速度，m/h;s为断面周长，m。
式(7)可表示为距离或时间的积分表达式[17]
Qt=
q(l-l′)dl′=
q(t-t′)v(t′)dt′
(9)
式中，l′，t′为积分变量。
对式(1)～(6)进行瓦斯流动的固气耦合模型数值计算，得到煤壁上某点随时间变化的瓦斯渗流速度vg。将该值代入式(8)及式(7)得到煤壁瓦斯涌出量随时间的变化关系。
(2)煤巷掘进工作面前方煤壁瓦斯涌出
煤巷掘进不断揭露新鲜煤体，导致工作面瓦斯涌出初始速度较高，且停掘或掘进速度放慢后瓦斯涌出速度衰减较快。将掘进1 h，两侧新鲜暴露煤壁的瓦斯涌出速度均值作为掘进工作面前方煤壁的瓦斯涌出速度。掘进工作面前方煤壁瓦斯涌出量为
(10)
式中，S为掘进工作面前方煤壁暴露面积，m2;T为掘进时间
为T时间内两侧新鲜煤壁瓦斯涌出速度均值;Q0-T为巷道掘进的T小时内两侧壁面瓦斯涌出量;v为掘进速度，m/h;h为巷道高度，m。
将式(8)，(9)代入式(10)，并假设巷道断面为矩形，顶底板不透气，得
(11)
2 煤巷断面瓦斯涌出数值计算条件
2.1 工程背景
南桐矿区兴隆煤矿4号被保护层1401N1工作面，走向长度200 m，位于6号保护层工作面的被保护范围内。矿井设计在1401N1工作面标高+310 m位置掘进回风巷，如图1所示。为检验区域防突措施消突效果，通过穿层钻孔进行1401N1工作面瓦斯压力实测，得到+310 m腰巷上下两侧20 m标高范围内平均瓦斯压力0.30 MPa。
图1 掘进巷道剖面
Fig.1 Sectional drawing of excavation roadway
2.2 计算的几何模型
为使模型具有一般性，假设煤体的物理力学性质稳定，煤巷沿直线掘进，并忽略沿煤巷掘进方向煤层厚度变化。以1401N1工作面+310 m腰巷掘进为工程背景，根据图1中掘进巷道空间关系建立平面应变有限元计算模型(图2)，研究从巷道断面揭露到巷道断面瓦斯流动逐渐稳定的过程。研究域宽×高:70 m×40 m;煤层厚2.8 m，倾角43°;巷道简化为与煤层平行的矩形断面，宽2.5 m，距下边界层面距离28 m，距上边界层面距离25 m。
图2 煤巷断面瓦斯涌出量计算几何模型
Fig.2 Geometry model of section flux calculation
2.3 模型初始条件和边界条件
(1)边界条件
模型左右两侧边界限制水平方向位移;下边界变形场约束垂直位移;上边界施加变形场垂直应力ps(top)=7.5 MPa，以模拟上覆岩层自重;煤层上下边界设置远场瓦斯压力边界条件pg=0.30 MPa;煤层顶底板为不透气边界。如图2所示。
(2)初始条件
在巷道开挖前通过稳态计算得到原始应力状态。巷道开挖时巷道壁原始瓦斯压力与大气压相同，为0.1 MPa。其他边界条件保持不变。
2.4 数值计算参数
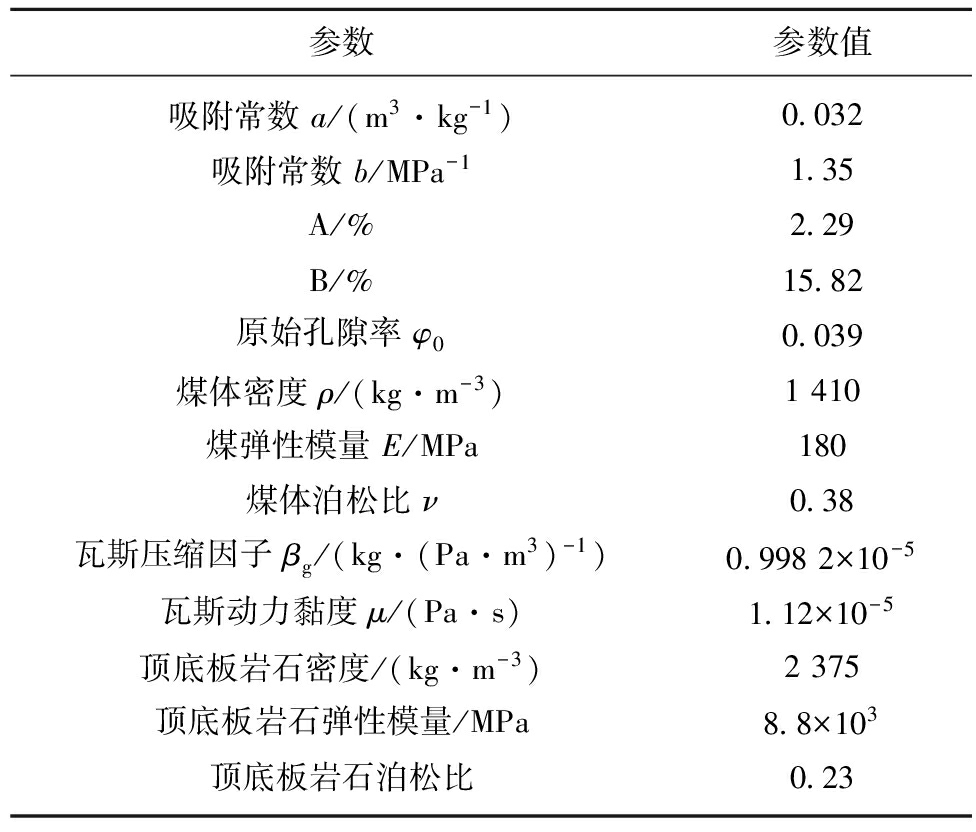
巷道掘进全长200 m，平均掘进速度2 m/d，因此选择数值计算时间为200 d，以便对巷道掘进全过程的瓦斯压力及瓦斯涌出变化规律进行研究。模型主要参数见表1。
表1 数值计算主要参数
Table 1 Model parameters for numerical calculation
3 数值计算结果与分析
在数值计算分析中，根据式(3)进行瓦斯压力场计算，通过式(5)～(6)反映变形场的影响;同时，在变形场计算中，通过Biot系数及瓦斯压力pg反映瓦斯压力场的影响，从而实现变形场和瓦斯压力场的双向耦合;然后根据确定的初边值条件和数值计算参数进行工程实例的数值计算求解，所得数值计算结果及分析如下。
3.1 巷道掘进引起断面瓦斯渗流参数变化
煤巷掘进后煤层瓦斯在瓦斯压力梯度作用下涌出巷道壁，引起煤体内瓦斯压力重新分布[9,18]，如图3所示。
图3 煤巷断面瓦斯压力分布
Fig.3 Gas pressure redistribution of seam after tunneling
图3(a)为巷道断面揭露1 d煤层瓦斯压力分布。此时瓦斯压力变化主要集中于巷道两侧约3 m范围内。图3(b)是巷道断面揭露200 d的煤层瓦斯压力分布，此时煤层瓦斯压力的改变扩展至大部分研究区域。
通过将巷道断面瓦斯压力瞬态计算结果按时间插值得到图4所示200 d时煤壁瓦斯压力的三维分布。其中z方向为时间轴，单位为d，z坐标为0对应当前时间，z坐标为200对应掘进刚开始时刻。xy平面为巷道断面。x，y轴分别对应于图3中的纵轴和横轴。
图4 煤巷掘进200 d煤壁内瓦斯压力三维分布
Fig.4 3D gas pressure redistribution around roadway
图5 煤巷掘进200 d煤层渗透率三维分布
Fig.5 3D coal seam permeability redistribution around roadway
从图4可知，从当前位置到煤巷入口，掘进引起的瓦斯压力重新分布逐渐向两帮内部扩展，呈由入口指向掘进工作面的“锥形”分布。当掘进速度恒定，根据式(9)将图4中z轴乘以掘进速度即得到煤巷掘进形成的瓦斯压力三维空间分布图。
采用相同插值的方法，将瓦斯压力p及体应力Θ的计算结果代入式(2)得到图5所示掘进过程中煤层渗透率的三维分布。
图5中，巷道开挖破坏了初始状态下以稳定梯度自下而上增加的煤层渗透率分布。巷道开挖后下侧煤体渗透率仍呈梯度分布，上侧煤体渗透率分布较复杂，从煤壁到模型边界呈先减小后增大的趋势。
煤层瓦斯含量的三维分布如图6所示。比较图4与图6，煤巷开挖后煤层瓦斯含量分布与瓦斯压力分布具有较高的相似度。
图6 煤巷掘进200 d煤层瓦斯含量三维分布
Fig.6 3D coal seam gas content redistribution after tunneling
3.2 巷道掘进速度对煤壁瓦斯涌出量的影响
根据图4和5，利用Darcy定律，得到沿掘进方向上巷道壁面的瓦斯涌出速度分布。掘进速度分别取为2 和3 m/d，通过式(9)进行时间积分得到图7(a)所示两侧煤壁瓦斯涌出量随时间的变化关系，进行距离积分得到图7(b)所示两侧煤壁瓦斯涌出量随掘进距离的变化曲线。
图7 瓦斯涌出量随速度变化曲线
Fig.7 Gas emission curves of different tunneling speed
根据式(11)，将断面煤壁瓦斯涌出的积分时间缩短为1 h以提高掘进工作面前方煤壁瓦斯涌出量计算精度，通过计算得到掘进工作面前方煤壁瓦斯涌出量恒定为0.96 m3/min，在图7表示为水平线。
从图7(a)可知，煤巷断面揭露初期的断面瓦斯涌出速度降幅剧烈，长期瓦斯涌出速度趋于平稳。随时间增加，新暴露煤壁面积不断增加，煤壁瓦斯涌出总量随时间的增加而增加，但增幅逐渐减小。在煤巷掘进初期煤壁瓦斯涌出量增幅变化较大，而长期增幅变化趋于平稳。
为对模型进行工程验证，取工程实际中的瓦斯涌出量与模型计算结果进行对比。在实际工程中，巷道掘进平均速度约为2 m/d，取巷道掘进进度正常时(数据尽量在无放炮落煤的情况下进行测定，以减少放炮落煤的影响)的瓦斯涌出量实测数据来对模型进行验证，如图7(b)所示。从图7(b)可知基于固气耦合及巷道断面瓦斯涌出量时间积分的煤壁瓦斯涌出计算方法所得预测结果与实测瓦斯涌出量较符合。
为方便将数值计算结果用于现场瓦斯涌出总量预测，采用指数衰减多项式(exponential decay)对图7中平均掘进速度2 m/d的瓦斯涌出总量数值计算结果进行拟合，得到:
(12)
式中，y为煤壁瓦斯涌出总量，m3/min;x为掘进时间，h;拟合优度R2=99.95%。
3.3 掘进循环对巷道两侧煤壁瓦斯涌出总量的影响
为研究采用不同循环掘进对瓦斯涌出总量的影响，将掘进速度表示为时间的分段函数。考虑具有相同日进尺而实际作业时间不同的两种掘进循环:一天两班掘进循环，掘进时间16 h，实际掘进速度为0.125 m/h，如式(13);1 d仅掘进1 h，实际掘进速度为2 m/h，如式(14)。
(13)
(14)
图8(a)为不同掘进循环煤壁瓦斯涌出量随时间的变化曲线。从图8(a)可知，实际掘进时煤壁瓦斯涌出量逐渐增大，停掘后逐渐减小，煤壁瓦斯涌出量曲线呈锯齿状增加;每天实际掘进1 h相比实际掘进16 h，每个循环内“锯齿”高度更高，即瞬时最大瓦斯涌出量更大，说明平均掘进速度相同，适当增加实际掘进工作时间、减小实际掘进速度有利于瞬时瓦斯涌出控制;随着掘进时间增加，“锯齿”高度与曲线高度比值逐渐减小。即间断式掘进时，单个循环内瓦斯涌出最大与最小差值几乎保持不变，但在巷道瓦斯涌出总量中所占比例逐渐减小。
将图8(a)中“锯齿”底部(每天第24 h)作为参考比较点，对两种掘进循环在参考比较点的瓦斯涌出总量作差值，如图8(b)所示。从图8(b)可以看出，该值为正且随时间呈增加趋势，但掘进约60 d后趋于稳定。且与瓦斯涌出总量的比值逐渐减小，在掘进60 d后，约为4%，因此计算掘进瓦斯涌出总量时可忽略掘进循环内瓦斯涌出量波动的影响。
图8 不同掘进循环的瓦斯涌出总量及差异
Fig.8 Total flux curves & the difference curve of different tunneling cycle
图9 不同原始瓦斯压力的瓦斯涌出速度及涌出量随时间、距离变化曲线
Fig.9 Sectional gas emission curves of different gas pressure changing with time and distance
3.4 初始瓦斯压力对巷道两侧煤壁瓦斯涌出量的影响
图9为掘进速度2 m/d，不同初始瓦斯压力条件下断面瓦斯涌出速度随时间的变化曲线及两侧煤壁瓦斯涌出量随掘进距离的变化曲线。由图9可知瓦斯压力越大，煤壁瓦斯涌出总量及其随掘进距离的增幅均越大。因此，掘进距离一定，存在煤层瓦斯压力临界值，当通风能力、掘进速度一定，瓦斯压力超过该临界值，巷道掘进后期瓦斯涌出可能超限。根据本文实例:煤巷掘进全长为200 m，掘进速度为2 m/d，掘进面局部通风机最大风量为200 m3/min，若巷道内瓦斯浓度要求小于1%，则在巷道掘进过程中，瓦斯涌出量必须保证小于2 m3/min。从图中可知该巷道掘进200 m全长内的临界瓦斯压力略小于0.3 MPa。
4 结 论
(1)在传统二维煤巷瓦斯涌出量计算方法中引入固气耦合模型，提出了基于固气耦合及巷道断面瓦斯涌出量时间积分的煤壁瓦斯涌出计算方法。
(2)掘进速度恒定，煤壁瓦斯涌出量随时间、掘进距离逐渐增大，但增幅不断减小，符合指数衰减多项式的变化规律。利用指数衰减多项式对煤壁瓦斯涌出量随时间、掘进距离的变化关系拟合，拟合效果较好。
(3)间断式掘进循环的煤壁瓦斯涌出量呈锯齿状增加，总体趋势与恒速掘进相同。随时间增加，不同掘进循环瓦斯涌出总量差异趋于稳定。长时间掘进，掘进循环内瓦斯涌出量波动对瓦斯涌出总量的影响可忽略。
(4)煤层瓦斯压力对瓦斯涌出具有较大影响。煤层瓦斯压力越大，瓦斯涌出量随掘进距离的增幅越大。且存在瓦斯压力临界值，当巷道煤层瓦斯压力超过该值后，巷道瓦斯浓度可能超限。
参考文献(References):
[1] 周世宁,林柏泉.煤层瓦斯赋存与流动理论[M].北京:煤炭工业出版社,1999:160-165.
[2] 高建良,候三中.掘进工作面动态瓦斯压力分布及涌出规律[J].煤炭学报,2007,32(11):1127-1131.
GAO Jianliang,HOU Sanzhong.Dynamic distribution of gas pressure and emission around a diving roadway[J].Journal of China Coal Society,2007,32(11):1127-1131.
[3] 高建良,吴金刚.煤层瓦斯流动数值解算时空步长的选取[J].中国安全科学学报,2006,16(7):9-12.
GAO Jianliang,WU Jingang.Determination of time step and space interval in numerical simulation of gas flow in coal seams[J].China Safety Science Journal,2006,16(7):9-12.
[4] 梁冰,刘蓟南,孙维吉,等.掘进工作面瓦斯流动规律数值模拟分析[J].中国地质灾害与防治学报,2011,22(4):46-51.
LIANG Bing,LIU Jinan,SUN Weiji,et al.Numerical simulation of flowing gas on heading face during coal mining[J].The Chinese Journal of Geological Hazard and Control,2011,22(4):46-51.
[5] 刘伟,宋怀涛,李晓飞.移动坐标下掘进工作面瓦斯涌出的无因次分析[J].煤炭学报,2015,40(4):882-887.
LIU Wei,SONG Huaitao,LI Xiaofei.Dimensionless analysis on gas emission law around tunneling face[J].Journal of China Coal Society,2015,40(4):882-887.
[6] 秦跃平,刘鹏.煤层瓦斯流动模型简化计算误差分析[J].中国矿业大学学报,2016,45(1):19-26.
QIN Yueping,LIU Peng.Research on calculation error of simplified mathematical model of gas emission in coalseam[J].Jounal of China University of Mining & Technology,2016,45(1):19-26.
[7] 郭晓华,蔡卫,马尚权,等.基于稳态渗流的煤巷掘进瓦斯涌出连续性预测[J].煤炭学报,2010,35(6):932-936.
GUO Xiaohua,CAI Wei,MA Shangquan,et al.Continuity prediction of gas emission during drivage in coal seam based on stable percolation[J].Journal of China Coal Socity,2010,35(6):932-936.
[8] WANG Zhongwei,REN Ting,CHENG Yuanping.Numerical investigations of methane flow characteristics on a longwall face Part I:methane emission and base model results[J].Journal of Natural Gas Science and Engineering,2017,45:242-253.
[9] LESZEK(LES) W LUNARZEWSKI.Gas emission prediction and recovery in underground coal mines[J].International Journal of Coal Geology,1998,35:117-145.
[10] 何学秋.煤巷瓦斯涌出规律及其连续性积分模型[J].煤炭工程师,1994,1(1):23-27.
HE Xueqiu.The gas emission rule of coal roadway and its continuous integral model[J].Coal Engineer,1994,1(1):23-27.
[11] LIU Jishan,CHEN Zhongwei,DEREK Elsworth,et al.Interactions of multiple processes during CBM extraction:A critical review[J].International Journal of Coal Geology,2011,87:175-189.
[12] 孔祥言.高等渗流力学[M].合肥:中国科技大学出版社,1999:53-55,503-508.
[13] 李志强,鲜学福,姜永东,等.地球物理场中煤层气渗流控制方程及其数值解[J].岩石力学与工程学报,2009,28(S1):3226-3233.
LI Zhiqiang,XIAN Xuefu,JIANG Yongdong,et al.Seepage control equation of coalbed methane in geo-physical field and its numerical solutions[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(S1):3226-3233.
[14] 胡国忠.急倾斜多煤层俯伪斜上保护层开采的关键问题研究[D].重庆:重庆大学,2009:28-41.
HU Guozhong.Study on key issues existed in exploiting steep incline upper protective multi-layer with a bow psedo incline technique[D].Chongqing:Chongqing University,2009:28-41.
[15] 陶云奇.含瓦斯煤THM耦合模型及煤与瓦斯突出模拟研究[D].重庆:重庆大学,2009:15-40.
TAO Yunqi.Study on the gassy coal thm coupling model and coal and gas outburst simulation[D].Chongqing:Chongqing University,2009:15-40.
[16] 赵阳升,胡耀青.孔隙瓦斯作用下煤体有效应力规律的实验研究[J].岩土工程学报,1995,17(3):26-31.
ZHAO Yangsheng,HU Yaoqing.Experimental study of the law of effective stress by methane pressure[J].Chinese Journal of Geotechnical Engineering,1995,17(3):26-31.
[17] 李红.数值分析[M].武汉:华中科技大学出版社,2010:83-111.
[18] 吴冬梅,程远平,安丰华.由残存瓦斯量确定煤层瓦斯压力及含量的方法[J].采矿与安全工程学报,2011,28(2):315-318.
WU Dongmei,CHENG Yuanping,AN Fenghua.Determination of gas pressure and gas content based on residual gas quantity of coal sample[J].Journal of Mining & Safety Engineering,2011,28(2):315-318.
07