在传统原位岩体变形监测资料分析基础上建立的现场岩体稳定性判断方法已在实际工程中得到了广泛的应用。然而,传统变形监测技术也存在两个不足[1]:其一是只能获得岩体的宏观破裂监测结果,而无法探知岩体内部的微破裂及其演化过程;其二在于只能给出局部点的监测结果,难以对岩体整体稳定性全面评价。而后发展起来的应力监测技术也没有摆脱变形监测技术的“点”测量的局限性。微震监测技术是近年来出现的一种新型监测方法,该技术的基本原理是通过监测岩石破裂时发出的地震波,并对地震波进行处理解读,计算微震活动事件发生的位置、大小、能量等信息,进而获取岩体物理力学参数的改变量,从而实现对岩体稳定性进行全面评价,该技术可视为应力监测技术的一种改进。目前认为,微震监测技术最大优点在于可实现全范围立体监测、实现超前预报,是一种具有较大潜在应用价值的监测方法[2-3]。而微震源定位是该技术的核心内容,也是其重要组成部分[4-5]。
近年来,国内外学者对微震源定位开展了大量研究。李楠等[6]认为L2范数不能很好的处理观测数据的离群点,且对检波器布置方案较为敏感,故发展了基于L1 范数的单纯形迭代定位方法;李罗兰等[7]同样认为目标函数对于定位结果影响较大,故提出了联合P波和S波的新的定位目标函数;林峰等[8]在对线性定位方法和 Geiger 定位方法分析的基础上,建议使用2种方法进行联合定位;陈炳瑞等[9]根据到时差原理,应用粒子群算法搜索震源位置;张向东等[10-11]根据特定的台站分布,应用惠更斯原理建立了相应的震源方法。
走时方程是微震源定位的理想数学模型,该模型是一个非线性方程,可通过线性化、降维及非线性反演等多种手段对其进行求解。但遗憾的是,该模型过于理想化,从控制科学的角度来说:在实际应用中,该系统的输入参数都具有一定的误差,以致输出结果不符合于实际,甚至偏差较大。另外,波速的各向异性或非均匀性在走时方程多没有得到反映,现有的研究中多采用均匀速度模型[6-9]。因此,笔者认为从控制系统角度提高微震源定位准确度要做到两点:其一在于控制各个输入参数的误差;其二在于反映波速的非均匀性。
笔者重点从波速的非均匀性对微震源定位进行了探讨,推导出了考虑非均匀速度的微震源解析解,从信息融合角度对微震源最终解获取方法上进行了初步探讨。
1 微震源定位原理
走时方程是微震源定位的基本原理。如图1所示,点O为震源位置,A~F为检波器。根据走时方程,可列出
(1)
式中,x=[xA,xB,xC,xD,xE,xF]T为各检波器在三维坐标轴下的x轴坐标;y=[yA,yB,yC,yD,yE,yF]T为各检波器在三维坐标轴下的y轴坐标;z=[zA,zB,zC,zD,zE,zF]T为各检波器在三维坐标轴下的z轴坐标;v=[vA,vB,vC,vD,vE,vF]T为震源信号传向各检波器的速度;t0为震源发震时间。

图1 微震源定位示意
Fig.1 Sketch map of micro-seismic source location
为降低计算难度和简化模型,通常将波速在各检波器方向上的传播速度简化为一均匀值,即令 vA=vB=vC=vD=vE=vF=vP,此时式(1)退化为
(2)
式(2)即为微震源定位中的均匀速度模型,该模型在微震源定位中得到了大量应用。虽然均匀速度模型降低了微震定位问题的复杂性,但其忽略了实际波速传播的非均匀性特征。为此,下文将探讨考虑速度非均匀性的微震定位方法。
2 考虑非均匀速度的微震源定位解析解
如前文所述,均匀速度假设与实际情况有较大的差异。另外,一些学者采用迭代方法(包括遗传算法、粒子群算法、单纯形法等)[6,9]进行震源的搜索,但迭代方法受到搜索区域以及搜索初值等多方面因素的影响,容易收敛于局部极值点。此外,通常迭代方法计算量较大、耗时较长。鉴于此,本节给出一种考虑非均匀速度的微震源定位的解析方法。该解析方法需要使用6个不同位置的检波器得到。
根据6个不同位置的检波器及其到时,微震源定位的控制方程写成如下形式:
![]()
(3)
![]()
(4)
![]()
(5)
![]()
(6)
![]()
(7)
![]()
(8)
式中,(xi,yi,zi)(i=1,2,…,6)为6个检波器的空间坐标;vi(i=1,2,…,6)为震源信号传向各检波器的速度。
由式(3)和(4),有
2x0(x2-x1)+2y0(y2-y1)+2z0(z2-z1)+
![]()
(9)
记:![]() 其中i=1,2,3,4,5。改写式(9),同理由式(3)~(5),式(3)~(6),式(3)~(7)和式(3)~(8),可得到
其中i=1,2,3,4,5。改写式(9),同理由式(3)~(5),式(3)~(6),式(3)~(7)和式(3)~(8),可得到
2x0(x2-x1)+2y0(y2-y1)+2z0(z2-z1)+
![]()
(10)
2x0(x3-x1)+2y0(y3-y1)+2z0(z3-z1)+
![]()
(11)
2x0(x4-x1)+2y0(y4-y1)+2z0(z4-z1)+
![]()
(12)
2x0(x5-x1)+2y0(y5-y1)+2z0(z5-z1)+
![]()
(13)
2x0(x6-x1)+2y0(y6-y1)+2z0(z6-z1)+
![]()
(14)
由式(10)~(14)可知:要求得震源坐标,需消除t0和![]() 两项,消除该两项后,5个方程只剩3个方程,则可以得到震源的惟一解。经过运算,可得到最终微震控制方程为
两项,消除该两项后,5个方程只剩3个方程,则可以得到震源的惟一解。经过运算,可得到最终微震控制方程为
![]()
(15)
![]()
(16)
![]()
(17)
式(15)~(17)中已经完全不含未知量t0和![]() 个未知数,3个方程,可求得惟一震源解。对于式(15)~(17)的求解,可以借助于符号计算数学软件进行,如Matlab等,笔者通过Matlab对式(15)~(17)进行了求解,鉴于得出的最终解过于繁多,故在此不列出。
个未知数,3个方程,可求得惟一震源解。对于式(15)~(17)的求解,可以借助于符号计算数学软件进行,如Matlab等,笔者通过Matlab对式(15)~(17)进行了求解,鉴于得出的最终解过于繁多,故在此不列出。
3 微震源最终确定方法
在式(3)~(17)中,需预先给定震源O传至各个检波器的速度vi(i=1,2,3,4,5,6)。由于震源O的位置是未知的,故理论上无法预先给定任意方向速度vi。鉴于此,笔者结合概率论的思想,在均匀速度vP生成大量速度数据,如式(18)所示。通过对多次扰动计算得到的震源位置进行统计分析,以确定最终震源位置。
vi=vP(1+ri)
(18)
其中,vi(i=1,2,3,4,5,6)为各检波器方向上的模拟速度;vP表示该区域P波的平均速度,ri(i=1,2,3,4,5,6)表示-1到1之间的随机数,可反映震源O传至各个检波器的速度的波动情况,按照标准正态分布考虑,建议取标准差1/3以下,标准差取值越大,表示波速波动性越强。由于岩体内部结构非均匀性,以及存在节理裂隙、不连续面等,应力波在岩体内部传播时可能会发生折射、反射等情况,导致波速呈现较大的波动,要通过理论计算给出各方向的波速十分困难,故采用式(18)模拟真实情况的波速变化是可行的,其可近似体现出波速的非均匀性。通过式(18)产生的大量波速vi(i=1,2,3,4,5,6),代入解析解,即可得到相应的震源解,称此时得到的震源解为备选震源解。从备选震源解获得最终震源解本质上可称之为一信息融合问题,以下探讨如何从信息融合角度[12-15]确定最终微震源的方法。
3.1 用粗大误差判别准则融合备选震源解
粗大误差定义[13]由较为明显的反常因素导致的测量数值超出正常测量误差范围的小概率误差。对粗大误差的判别方法主要有3σ准则、格拉布斯准则、肖维勒准则、狄克逊准则等。3σ准则以3倍测量数据的标准偏差为极限取舍标准,通常适用于大样本情形;而其余3种准则都适用于小样本情形。由于本文得出的震源解数据为大样本情形,故宜采用3σ准则进行异常值的剔除。3σ准则判别方法如下:
对得到的备选震源解集合{xi,yi,zi},分别计算其均值![]() 并计算标准偏差:
并计算标准偏差:
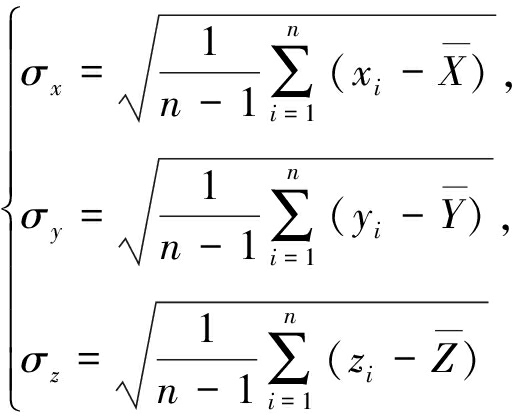
(19)
若![]() 则删除该组解;若
则删除该组解;若![]() 则删除该组解;若
则删除该组解;若![]() 则删除该组解。统计剩余的备选震源解的均值作为震源的最终解。
则删除该组解。统计剩余的备选震源解的均值作为震源的最终解。
3.2 用聚类分析方法融合备选震源解
聚类分析是一种常见的数据挖掘方法,已在多个学科中得到了广泛应用。聚类分析一般可描述为[14-15]:给定待聚类数据集X={x1,x2,…,xn},寻找聚类中心V={v1,v2,…,vc},使在某种相似性度量下能将X划分为c类。聚类分析中又具体包括多种不同的算法:如层次聚类算法、K均值聚类算法、C均值聚类算法等,各种算法有其独特的特点,已成为一种具代表性的数据驱动建模方法。备选震源解是大量的三维数据点,通过对大量备选震源解进行聚类分析,能够孤立出一些偏差样本,实现分类结果的可视化。根据聚类分析方法的原理,用聚类分析方法获得微震源最终解的方法即对备选震源解用聚类分析剔除异常值后(将所有备选震源解聚为两类,一类为异常组,一类为正常组,通过假设正常组的数据数量总是多于异常组来对两组数据进行判别)统计其均值作为震源解。
4 算例分析
4.1 模拟数据验证
(1)解析解正确性验证
假设图2所示的检波器监测系统:在某区域布置了6个检波器,各检波器坐标见表1,在图2所示坐标系下,某次微震事件的震源位置(0 m,0 m,0 m),理想情况下各检波器到时见表1,而震源传至各检波器速度都为1.73 m/ms。
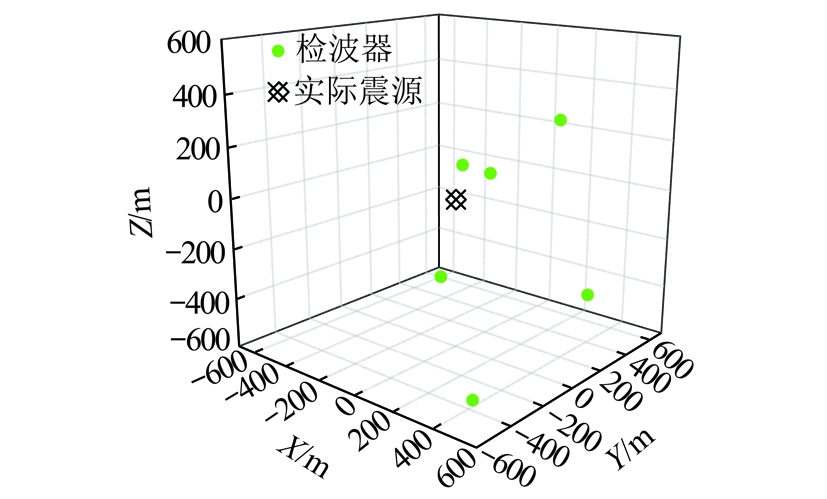
图2 检波器布设
Fig.2 Layout diagram of geophone monitoring system
表1 检波器坐标及到时参数
Table 1 Test parameters
首先验证本文所导出的解析解的正确性,将表1数据代入,将各个方向上的速度代入,求解得到震源位置为(0 m,0 m,0 m),符合实际值,表明了导出解析解的正确性。
(2)信息融合方法合理性验证
为验证本文所采用的微震源最终确定方法的合理性,在理论速度周围根据式(18)进行随机模拟生成20 000组波速(即20 000×6维向量),在这20 000组波速中,一般情况下,各检波器方向上的波速vi(i=1,2,3,4,5,6)不等,其可近似体现出波速的非均匀性,最终得到20 000个可能的震源位置。为更客观的比较各种微震源最终确定方法的合理性,共设计了5组融合方案:方案1,直接对20 000个备选震源解取均值;方案2,用聚类分析方法剔除异常解后,再取均值;方案3,用3σ准则方法剔除异常解后,再取均值;方案4,先用聚类分析去除异常值,再采用3σ准则方法进行2次筛选,取均值;方案5,先用3σ准则方法去除异常值,再用聚类分析2次筛选,取均值。为更全面比较几种融合方案的性能,分别计算在到时无误差、±5 ms、±10 ms、±20 ms下的定位结果(假定震源位置不变)。5种融合方案求得的最终结果见表2~5,其中d表示定位误差,即求得的震源位置和实际震源位置的欧式距离。
表2 计算结果(到时无误差)
Table 2 Calculation results (time error:0 ms)
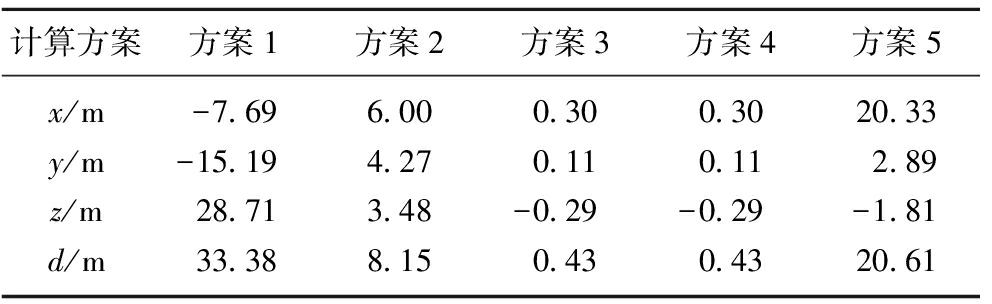
表3 计算结果(到时有误差:±5 ms)
Table 3 Calculation results (time error:±5 ms)
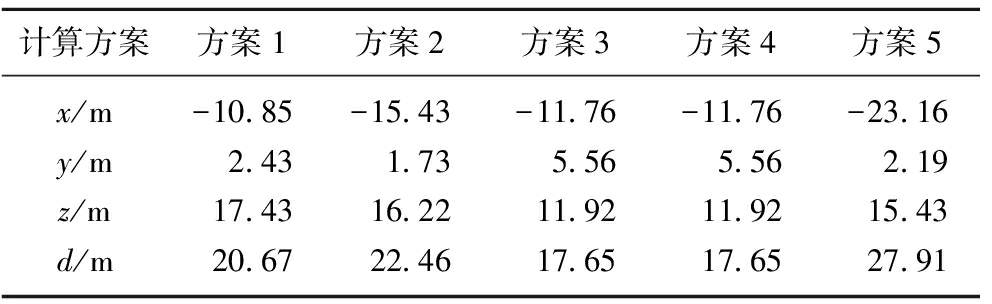
注:速度标定为1.73 m/ms时(均匀速度模型,下同),定位误差:25.98 m。
表4 计算结果(到时有误差:±10 ms)
Table 4 Calculation results (time error:±10 ms)
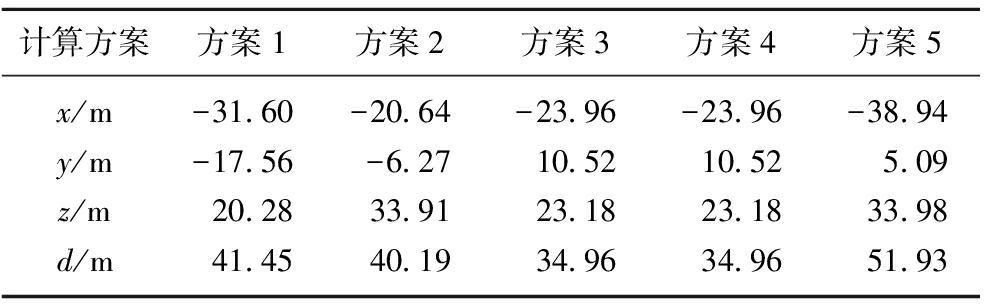
注:速度标定为1.73 m/ms时,定位误差:51.96 m。
表5 计算结果(到时有误差:±20 ms)
Table 5 Calculation results (time error:±20 ms)
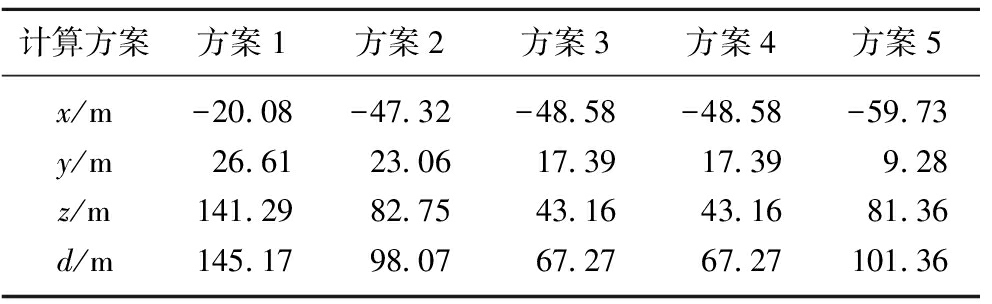
注:速度标定为1.73 m/ms时,定位误差:103.92 ms。
由表2可看出:当到时无误差时,方案2和方案3(方案4)的融合准确度较方案1和方案5佳。其中笔者在计算过程中发现方案2剔除的备选解的数量只有几个,当设置的随机模拟次数较大时,导致方案3和方案4的结果并无差别,故下文不再单独讨论方案4。相比而言,方案3剔除的备选解的数量较方案2多。
由表2~5可看出:随着到时误差的增大,几种方案的定位准确度逐渐降低。但相比而言,方案3的定位准确度仍然是几种方法中最佳的。在多数情况下,几种计算方案的定位准确度都高于均匀速度模型,这说明在震源定位中考虑速度的非均匀性是有效且必要的。通过对比几种计算方案的准确性,笔者建议在实际中采用方案3进行备选震源解的融合。
4.2 工程算例
选取某磷矿爆破试验数据[16],验证本文方法的有效性和实用性。检波器A~F坐标及对应的到时见表6,通过波速测量知该地区P波传播速度为5.0 m/ms。为展示本文方法(该例中产生15 000组速度随机数据,取粗大误差判别准则融合后的均值作为震源的最终解)的优越性,同时按照标定速度为5.0 m/ms(在表6中记为法1)和基于迭代方法的到时反演方法(采用粒子群算法实现,种群数目500,进化代数2 000),进化曲线如图3所示,(在表6中记为法2)进行定位,定位结果见表6。由表6可知,几种定位结果与实际震源位置都有一定出处,这可能是由于观测到时误差等因素造成的。定义本文方法相对于其他两种方法提高的定位准确度为
(20)
其中,d表示本文方法的定位误差;d1,d2分别表示法1和2的定位误差。将表6中的数据代入,计算可得p1=42.4%,p2=7.12%,即本文方法较法1定位准确度提高42.4%,较法2定位准确度提高7.12%。
需要说明的是:本文的微震源求解只需要6个检波器,但从算例可以看出:各个检波器的观测到时的准确性对于震源定位的准确度有较大影响,故实际工程中多使用较多的检波器对某区域的微震事件进行监测。当检波器数目大于6时,则在所有检波器中任意取6个检波器组合,按照本文的方法计算后,最后取均值即可,可称之为“六六组合定位”;而当检波器数目少于6个时,则本文的方法失效,此时可改用迭代法或作图法等。
表6 计算参数和计算结果
Table 6 Calculation parameters and results

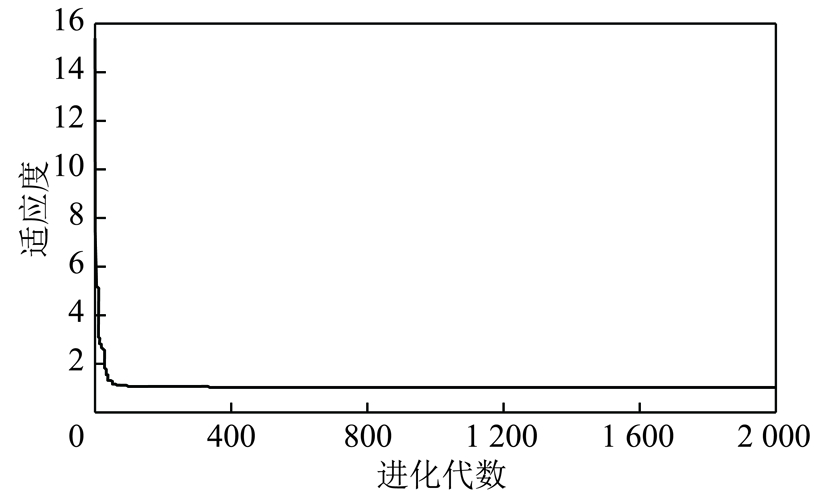
图3 粒子群算法进化曲线
Fig.3 Evolution curve of PSO
事实上,影响微震源定位准确度的因素众多[17],其中检波器布设方式对微震源定位的准确度有着较大影响,根据已有研究成果可知[7,16-19]:震源位于检波器观测系统内部时的定位准确度普遍高于震源位于外场时的准确度。检波器布设方式也取决于实际的工程地质条件。故在实际工程中,检波器的布设方案因根据具体工程地质条件而定,并尽可能的分布于潜在危险区域的周围,以保证内场定位。
5 结 论
(1)采用6个独立的检波器坐标和到时数据推导了考虑速度非均匀性的微震源解析解,通过特殊值验证了导出的解析解的正确性。和迭代方法相比,解析方法具有实现简单、计算速度较快的优点。
(2)通过随机模拟的方法给出各方向波速,并结合粗大误差判别准则和聚类分析方法两种信息融合方法获取最终结果,并通过算例验证了两种方法的有效性,相对而言,粗大误差判别准则的融合结果更加准确,在实际中建议粗大误差判别准则确定最终微震源。
(3)本文仅测试了6个独立的检波器下的微震源定位性能。当检波器数目较多时,可按照“六六组合定位方法”求取震源位置;当检波器少于6个时,则本文方法失效。
(4)对波速非均匀性特征的体现,本文仅做了一个初步探讨,更加深入的研究留待后续完成。
参考文献(References):
[1] 徐奴文.高陡岩质边坡微震监测与稳定性分析研究[D].大连:大连理工大学,2011.
[2] 姜福兴,尹永明,朱权洁,等.单事件多通道微震波形的特征提取与联合识别研究[J].煤炭学报,2014,39(2):229-237.
JIANG Fuxing,YIN Yongming,ZHU Quanjie,et al.Feature extraction and classification of mining microseismic waveforms viamulti-channels analysis[J].Journal of China Coal Society,2014,39(2):229-237.
[3] 汤国水,朱志洁,韩永亮,等.基于微震监测的双系煤层开采覆岩运动与矿压显现关系[J].煤炭学报,2017,42(1):212-218.
TANG Guoshui,ZHU Zhijie,HAN Yongliang,et al.Relationship between overburden strata movement and strata behavior during dual system seam mining based on microseismic monitoring technology[J].Journal of China Coal Society,2017,42(1):212-218.
[4] LI X B,DONG L J.Comparison of two methods in acoustic emission source location using four sensors without measuring sonic speed[J].Sensor Letters,2011,9(5):1501-1505.
[5] LI J,WU S C,GAO Y T,et al.An improved multidirectional velocity model for micro-seismic monitoring in rock engineering[J].Journal of Central South University,2015,22(6):2348-2358.
[6] 李楠,王恩元,孙珍玉,等.基于L1范数统计的单纯形微震震源定位方法[J].煤炭学报,2014,39(12):2431-2438.
LI Nan,WANG Enyuan,SUN Zhenyu,et al.Simplex microseismic source location method based on L1 norm statistical standard[J].Journal of China Coal Society,2014,39(12):2431-2438.
[7] 李罗兰,何川,谭玉阳.微地震观测系统及震源定位目标函数研究[J].北京大学学报(自然科学版),2017,53(2):329-343.
LI Luolan,HE Chuan,TAN Yuyang.Study of recording system and objective function for microseismic source location[J].Acta Scientiarum Naturalium Universitatis Pekinensis,2017,53(2):329-343.
[8] 林峰,李庶林,薛云亮,等.基于不同初值的微震源定位方法[J].岩石力学与工程学报,2010,29(5):996-1002.
LIN Feng,LI Shulin,XUE Yunliang,et al.Microseismic sources location methods based on different initial values[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(5):996-1002.
[9] 陈炳瑞,冯夏庭,李庶林,等.基于粒子群算法的岩体微震源分层定位方法[J].岩石力学与工程学报,2009,28(4):740-749.
CHEN Bingrui,FENG Xiating,LI Shulin,et al.Microseismic sources location with hierarchical strategy based on particle swarm optimization[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(4):740-749.
[10] 张向东,王帅,赵彪,等.二层水平介质中震源的精确定位[J].岩土工程学报,2014,36(6):1044-1050.
ZHANG Xiangdong,WANG Shuai,ZHAO Biao,et al.Precise positioning in double-layer horizontal media[J].Chinese Journal of Geotechnical Engineering,2014,36(6):1044-1050.
[11] 张向东,王帅,贾宝新.二层水平介质球面波正反演联用与震源定位[J].岩土工程学报,2015,37(2):225-234.
ZHANG Xiangdong,WANG Shuai,JIA Baoxin.Positioning of seismic sources combined with forward and inversion of spherical wave in double-layer horizontal media[J].Chinese Journal of Geotechnical Engineering,2015,37(2):225-234.
[12] 刘明贵,杨永波.信息融合技术在边坡监测与预报系统中的应用[J].岩土工程学报,2005,27(5):607-610.
LIU Minggui,YANG Yongbo.Application of information fusion in slope monitoring and prediction system[J].Chinese Journal of Geotechnical Engineering,2005,27(5):607-610.
[13] 熊艳艳,吴先球.粗大误差四种判别准则的比较和应用[J].大学物理实验,2010,23(1):66-68.
XIONG Yanyan,WU Xianqiu.The generalizing application of four judging criterions for gross errors[J].Physical Experiment of College,2010,23(1):66-68.
[14] 蔡国军,刘松玉,童立元,等.基于聚类分析理论的 CPTU土分类方法研究[J].岩土工程学报,2009,31(3):416-424.
CAI Guojun,LIU Songyu,TONG Liyuan,et al.Soil classification using CPTU data based upon cluster analysis theory[J].Chinese Journal of Geotechnical Engineering,2009,31(3):416-424.
[15] 朱权洁,姜福兴,缪华祥,等.基于聚类分析的微震定位二次优化研究[J].采矿与安全工程学报,2014,31(2):196-202.
ZHU Quanjie,JIANG Fuxing,MIU Huaxiang,et al.Quadratic optimization of mining microseismic source positioning based on cluster analysis[J].Journal of Mining & Safety Engineering,2014,31(2):196-202.
[16] 高永涛,吴庆良,吴顺川,等.基于误差最小原理的微震震源参数反演[J].中南大学学报(自然科学版),2015,46(8):3054-3060.
GAO Yongtao,WU Qingliang,WU Shunchuan,et al.Source parameters inversion based on minimum error principle[J].Journal of Central South University (Science and Technology),2015,46(8):3054-3060.
[17] 李绍红,吴礼舟,杨戒,等.微震源定位的两步反演方法研究[J].岩石力学与工程学报,2017,36(7):1710-1717.
LI Shaohong,WU Lizhou,YANG Jie,et al.A two-step inversion method for micro-seismic source location[J].Chinese Journal of Rock Mechanics and Engineering,2017,36(7):1710-1717.
[18] 李楠,王恩元,李保林,等.传感器台网布设对震源定位的影响规律及机制研究[J].中国矿业大学学报,2017,46(2):229-236.
LI Nan,WANG Enyuan,LI Baolin,et al.Research on the influence law and mechanisms of sensors network layouts for the source location[J].Journal of China University of Mining and Technology,2017,46(2):229-236.
[19] 巩思园,窦林名,曹安业,等.煤矿微震监测台网优化布设研究[J].地球物理学报,2010,53(2):457-465.
GONG Siyuan,DOU Linming,CAO Anye,et al.Study on optimal configuration of seismological observation network for coal mine[J].Chinese Journal of Geophysics,2010,53(2):457-465.