基于弹性波方程的多分量地震联合逆时偏移由于能够实现纵横波的深度域同步成像和具有良好的振幅保真性而受到了业界的广泛重视[1-2],有限差分求解弹性波方程是目前实现多分量联合逆时偏移的主要方法,在这一领域国内外的研究现状是:
(1)现有的多分量波场延拓技术如交错网格高阶差分技术[3-6]、紧致交错网格技术[7]等能够实现高精度正向和逆时延拓[8],但当多分量数据中高频成分丰富时需要通过提高差分阶数和减小网格剖分步长来压制频散,增加了偏移处理的内存需求且降低了计算效率;
(2)偏移噪声压制技术取得了进展,如拉普拉斯滤波技术[9-11]、基于相反传播方向的炮检波场互相关成像[12-17]等,但拉普拉斯滤波在滤除低频噪声的同时,常对有效信息造成损伤[18],而基于行波分离的成像方法要求准确获得各成像点不同时刻的纵横波传播方向,现有基于坡印廷矢量的波场传播方向求取技术只能得到纵横波混合波场的传播方向而非单纯纵波或横波的传播方向[19],导致行波分离不彻底;
(3)纵横波解耦技术达到了工业应用水准[20-22]且在保幅解耦领域[2,23]也取得了重要进展;
(4)矢量横波的标量合成技术存在较大缺陷,弹性波逆时偏移中横波的标量化处理需要求取各成像点处不同时刻炮点纵波场和接收点横波场的传播方向,目前的求取方法主要有极化向量法[24-25]和坡印廷矢量法[19]两类,其中极化向量法假设波只在炮检连线所在的竖直平面内传播[26],故该方法只适用于简单模型情况,而坡印廷矢量法只能求取混合波场的传播信息[19];
(5)在逆时偏移效率提升方面取得了许多具有应用价值的成果,如基于CPU的并行计算方法[8,27]、基于GPU的并行计算技术[28-29]和与之匹配的炮点波场随机边界重构技术[30]等;
(6)多分量地震波场的震源子波的反演技术研究进入起步阶段,如基于高阶统计量技术的子波提取方法[31-32]等;
(7)纵横波ADCIG提取技术在模型数据处理中取得了效果,如基于方位矢量法的角度域共成像点道集提取技术[33]等。
本文研究基于一阶速度-胀缩-旋转方程的多分量联合逆时偏移技术,同常规双程弹性波方程相比,Tang等[34]推导出的一阶速度-胀缩-旋转方程在逆时偏移领域具有以下应用优势:
(1)在相同的输入数据前提下不需要在偏移过程中进行显式的纵横波解耦;
(2)能够在波场延拓过程中获得各成像点在不同时刻的纯纵波和纯横波的传播方向信息,为横波极性校正、标量合成和偏移噪声压制提供了精度更高的数据。
笔者首先从一阶速度-胀缩-旋转方程出发,利用交错网格有限差分法实现了弹性波的正、反向延拓,通过求取纵、横波的坡印廷矢量获得了不同时刻各成像点处的纵、横波传播方向信息,并据此实现了纵、横波方向行波的分离,最后应用基于波场分离的归一化互相关成像条件实现了多分量地震波场的纵、横波联合逆时偏移,而横波的极性校正问题则通过在炮域利用炮点波场纵波的坡印廷矢量和接收点波场横波的坡印廷矢量的向量叉乘运算实现。模型算例表明:同基于一阶速度-应力方程的逆时偏移方法相比,本文方法在横波极性校正和偏移噪声压制等方面更具优势。
1 两种方程坡印廷矢量计算方法
1.1 一阶速度-应力弹性波方程坡印廷矢量计算方法
各向同性介质中,三维一阶速度-应力方程为

(1)
式中,vx,vy,vz为质点振动速度;σxx,σyy,σzz,σxy,σxz,σyz为应力分量;∂t,∂x,∂y,∂z分别为一阶偏微分算子∂/∂t,∂/∂x,∂/∂y,∂/∂z;ρ为密度;cp为纵波速度;cs为横波速度;t为时间。
YOON和MARFURT[35]引入电磁学中的坡印廷矢量来指示波的传播方向。常规的基于一阶速度-应力方程求取坡印廷矢量[19]的公式为
E=-Tv
(2)
式中,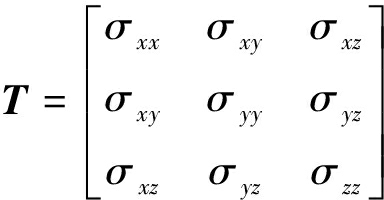 为应力张量;E为坡印廷矢量;v为质点振动速度矢量。
为应力张量;E为坡印廷矢量;v为质点振动速度矢量。
1.2 一阶速度-胀缩-旋转弹性波方程坡印廷矢量计算方法
各向同性介质中,三维一阶速度-胀缩-旋转方程[34]为
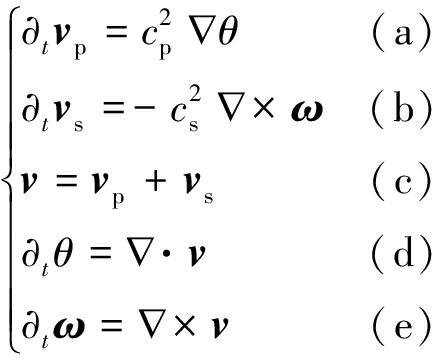
(3)
式中,v=(vx,vy,vz)为质点振动速度矢量;vp=(vpx,vpy,vpz)为质点的胀缩振动速度矢量;vs=(vsx,vsy,vsz)为质点的剪切振动速度矢量;θ为标量纵波;ω=(ωx,ωy,ωz)为矢量横波。
利用式(3)进行波场正演的具体流程为:给定一个纵波源并将之加到θ分量上,然后用式(3)中方程(a),(b)求取该时刻的vp和vs,由此可得到该时刻的v分量,再利用式(3)中方程(d),(e)求取下一个时刻的θ和ω,在时间方向上如此循环即可完成波场正演。利用式(3)进行波场逆时延拓的具体流程为:将地面三分量记录加载在v分量上,然后用式(3)中方程(d),(e)求取该时刻的θ和ω,然后由式(3)中方程(a),(b)求取上一时刻的vp和vs,进而得到v,如此在时间上循环则可实现波场的逆时传播。由上述过程可见,利用方程(3)进行多分量逆时偏移没有改变输入数据,或者说是没有对输入数据提出额外要求。
基于一阶速度-胀缩-旋转方程求取坡印廷矢量的公式[34]为
(4)
式中,Ep为纵波坡印廷矢量;Es为横波坡印廷矢量。
1.3 两种坡印廷矢量计算方法的结果比较
以图1所示二维模型的炮点波场为例比较上述两种坡印廷矢量计算方法的精度。模型中炮点位于(750 m,0 m)处,为分析问题方便,仅对模型中A点(675 m,975 m)处470 ms时刻各种类型波的传播方向进行比较。分别采用式(2),(4)计算得到的该点该时刻的坡印廷矢量和由射线追踪得到的计算结果如图2所示。由理论分析可知,A点在此时刻既有向上传播的纵波,又有向下传播的横波。采用式(2)只能求得一个坡印廷矢量,该矢量指示的方向与射线追踪得到的纵、横波传播方向均差别较大。采用式(4)可分别求得纯纵波和纯横波的坡印廷矢量,其求得的纵、横波坡印廷矢量指示的方向与射线追踪得到的纵、横波传播方向基本一致。也就是说,当空间中一点既有纵波又有横波时,利用式(2)只可得到一个坡印廷矢量,该矢量既不能准确指示纵波的方向,也不能准确指示横波的方向;而式(4)则可分别求得纯纵波和纯横波的坡印廷矢量,其中纵波的坡印廷矢量指示纵波的传播方向,横波的坡印廷矢量指示横波的传播方向,物理意义明确。

图1 二维模型
Fig.1 2D model

图2 A点在470 ms时两种坡印廷矢量的计算结果
Fig.2 Two kinds of poynting vector results of A point in 470 ms
对图1所示模型分别利用式(1)和(3)进行正演,震源位于(750 m,0 m)处,采用主频30 Hz的雷克子波。绘制两种方程在470 ms时的坡印廷矢量快照如图3所示。图3(a)为式(1)正演过程中采用式(2)得到的坡印廷矢量z分量快照,图3(b),(c)为式(3)正演过程中采用式(4)得到的同一时刻纵、横波的坡印廷矢量z分量快照。可见,基于一阶速度-胀缩-旋转方程可以分别求得纵横波的坡印廷矢量,而速度-应力方程则只能得到混合波场的坡印廷矢量,且求得的坡印廷矢量存在较大误差(图3(a)中的红圈处)。
值得注意的是:式(2)和式(4)都无法准确解决当空间某点在某时刻存在多组纵横波时的波场传播方向求取问题,此时式(4)得到的横波传播方向是该点该时刻多组横波共同作用的结果,它得到的纵波传播方向也是多组纵波共同作用的结果,而式(2)得到的是所有波共同作用的结果。这是基于坡印廷矢量理论的波场传播方向求取方法的固有缺陷,要彻底解决这一问题必须抛开坡印廷矢量理论,寻找新理论和新方法分别求取多组纵横波的传播方向,基于非坡印廷理论的纵横波传播方向求取方法不属本文的讨论范畴。

图3 两种方程的坡印廷矢量快照
Fig.3 Poynting vector snapshots based on two kinds of equations
(a)为基于一阶速度-应力方程t=470 ms时坡印廷矢量z分量快照;(b)为基于一阶速度-胀缩-旋转方程t=470 ms时的纵波坡印廷矢量z分量快照;(c)为基于一阶速度-胀缩-旋转方程t=470 ms时的横波坡印廷矢量z分量快照
2 基于一阶速度-胀缩-旋转方程的逆时偏移实现
2.1 波场逆时延拓的差分格式
二维情况下,采用与文献[34]相同的推导方法,可得到一阶速度-胀缩-旋转方程在交错网格空间中的逆时延拓差分格式,以θ分量为例,有
![]()
(5)
式中,Δx和Δz分别代表水平方向和竖直方向的空间网格步长;Δt为采样间隔;![]() 为交错网格差分系数。
为交错网格差分系数。
以地面三分量记录作为边值条件,将之加载在方程(3)中v分量上,再利用式(5)即可实现弹性波的逆时传播。
采用与文献[36]相同的推导方法得到上式的稳定性条件为
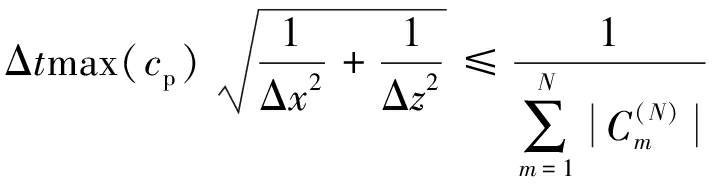
(6)
2.2 纵横波成像条件
采用基于行波分离的归一化互相关成像条件进行纵横波成像。该成像条件首先需要求得所有成像点在不同时刻的纵横波传播方向,笔者利用坡印廷矢量(式(4))来指示纵横波传播方向,求得波的传播方向后,即可分离得到不同传播方向的波,以横波为例,有

(7)
式中,ω(x,z,t)为点(x,z)在t时刻的横波波场值;ωu(x,z,t),ωd(x,z,t),ωl(x,z,t),ωr(x,z,t)分别为点(x,z)在t时刻的横波波场分离的上、下、左、右行波;Es=(Esx,Esz),Esx,Esz分别为横波坡印廷矢量的x分量和z分量。
由此可方便地应用归一化互相关成像条件进行纵横波成像:
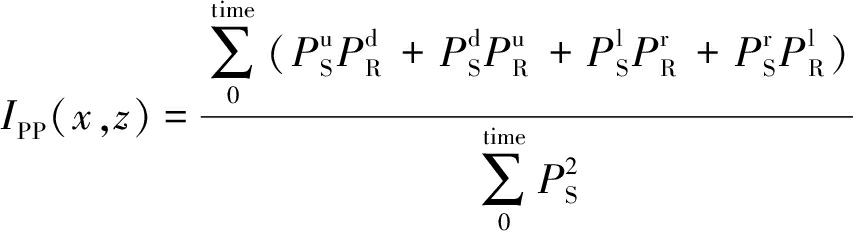
(8)
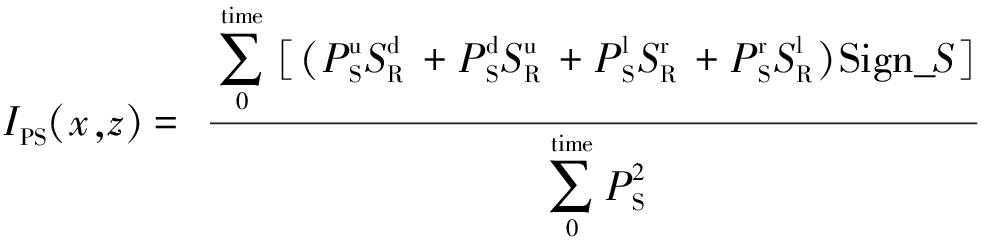
(9)
式中,IPP为PP偏移成像结果;IPS为PS偏移成像结果;PS为炮点纵波波场;![]() 分别为炮点纵波波场分离的上、下、左、右行波;
分别为炮点纵波波场分离的上、下、左、右行波;![]() 分别为接收点纵波波场分离的上、下、左、右行波;
分别为接收点纵波波场分离的上、下、左、右行波;![]() 分别为接收点横波波场分离的上、下、左、右行波;Sign_S为空间各点横波分量的极性符号,通过该符号因子与横波分量相乘即可实现横波极性校正。
分别为接收点横波波场分离的上、下、左、右行波;Sign_S为空间各点横波分量的极性符号,通过该符号因子与横波分量相乘即可实现横波极性校正。
2.3 横波极性校正
弹性波逆时偏移中,转换波成像结果的极性会随着入射方向的改变而发生反转,因此需要在偏移叠加前首先进行横波的极性校正。
本文基于DU[19]的思路进行横波的极性校正,其基本思路为:假定法向入射时横波分量为0,反射方向位于入射方向的逆时针方向时,横波分量极性为正,反之为负(图4中Di表示入射波的传播方向,Dr表示反射波的传播方向,D表示Di与Dr向量积的方向),则可通过求取入射纵波和反射横波之间传播方向的相对关系实现横波极性校正。
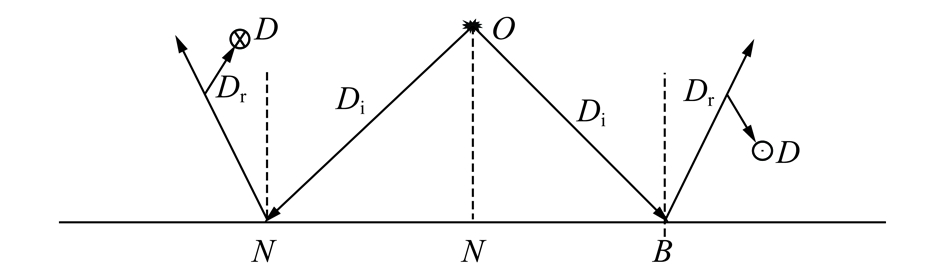
图4 横波极性示意
Fig.4 Polarity of the S-wave component
逆时偏移中,入射波传播方向即为反射点处震源波场的传播方向,反射波传播方向即为检波点波场逆时延拓得到传播方向。利用式(4)计算弹性波的传播方向,可以得到震源波场以坡印廷矢量表示的传播方向,记为ES;检波波场以坡印廷矢量表示的传播方向,记为ER。定义表征横波分量的极性符号Sign_S,则
Sign_S=Sign of(ES×ER)
(10)
令n表示震源波场的传播方向和检波波场的传播方向的向量积。二维情况下,n=(ESzERx-ESxERz)j=λj,由炮、检波场传播方向确定横波极性符号因子Sign_S有
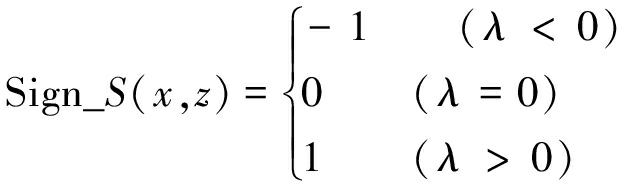
(11)
3 数值算例
3.1 两种方程不同方向行波分离效果比较
水平层状模型如图1所示,分别利用一阶速度-应力方程和一阶速度-胀缩-旋转方程进行正演并分离沿不同方向传播的纵波和横波,数值模拟时采用的参数与1.3节相同。图5为两种方程在t=470 ms的正演快照及分离得到的向下传播的纵、横波。其中图5(a),(b),(c)基于一阶速度-应力方程;图5(d),(e),(f)基于一阶速度-胀缩-旋转方程。
由图5可见:上述两个方程均可通过计算并利用其坡印廷矢量分离出下行纵、横波。但分离结果存在较大差异,为更清楚的对比两个方程的分离效果,将图5中白框部分放大并采用波形方式显示(图6,7)。
图6为两种方程分离得到的纵波快照的局部放大,由图6可见,采用速度-应力方程分离得到的结果存在部分能量缺失和地震波波形不完整等问题(图6(a)),这是该方程坡印廷矢量的计算方法带来的误差,将这一带有误差的数据应用于式(8)进行纵波成像必然会产生新的误差,降低成像精度。图6(b)克服了这一缺陷,分离结果具有更高的精度。图7为两种方程分离得到的横波快照的局部放大,比较图7(a),(b)可以得到相似的结论,且图7(a)中波形畸变更为严重,图7(b)克服了这一缺陷,为后续横波成像提供了更高精度的数据。

图5 两种方程在t=470 ms时的正演快照及分离得到的向下传播的纵、横波
Fig.5 Forward snapshots and down-ward one-way wave field separating snapshots at 470 ms
(a)由一阶速度-应力方程得到的vx分量快照;(b)由一阶速度-应力方程得到的下行纵波快照;(c)由一阶速度-应力方程得到的下行横波快照;(d)由一阶速度-胀缩-旋转方程得到的vx分量快照;(e)由一阶速度-胀缩-旋转方程得到的下行纵波快照;(f)由一阶速度-胀缩-旋转方程得到的下行横波快照

图6 局部波形显示
Fig.6 Local waveform display

图7 局部波形显示
Fig.7 Local waveform display
图5(f)分离的行波中依然存在少量误差(箭头所指处),这种误差的产生原因为:由式(4)知坡印廷矢量的符号由vp与θ或vs与ω的乘积决定,当利用交错网格有限差分数值模拟时,速度与胀缩和旋转分量在时间和空间上交错计算,使得空间中一点同一时刻的v比θ和ω超前或滞后一段时间,波形振幅正负变化不同步,因而导致波形振幅正负变化附近坡印廷矢量计算不准。
3.2 两种方程的横波极性校正效果比较
采用图8(a)所示模型的单炮偏移结果比较这两种方程的横波极性校正效果。模型数据的炮点位于(2 000 m,0 m)处,接收点深度为0,800道接收,道间距为5 m,中间放炮,最小偏移距0。对该模型数据分别利用一阶速度-应力方程和一阶速度-胀缩-旋转方程进行逆时偏移,得到单炮PS偏移剖面,并利用坡印廷矢量进行横波极性校正,校正结果如图8(b)~(f)所示。

图8 模型示意及两种方程的PS偏移剖面
Fig.8 Model and single-shot RTM PS image based two kinds of equations
(a)为弹性模型;(b),(c)分别为(e)和(f)3 000~4 000 m局部放大图;(d)为一阶速度-胀缩-旋转方程未极性校正的PS偏移剖面;(e)为一阶速度-应力方程极性校正后的PS偏移剖面;(f)为一阶速度-胀缩-旋转方程极性校正后PS偏移剖面
由于法向入射时转换横波的反射系数为0,因此无法实现这一角度的横波成像(图8(d)中箭头所指处),同时,横波的偏移结果在法向入射点处出现极性反转,在对多炮数据横波偏移结果的叠加前必须先对横波进行极性校正。笔者基于式(10),(11)进行横波的极性校正,图8(e),(f)分别为利用两种方程经极性校正后所得的PS偏移剖面,图8(b),(c)分别为两种结果斜层部分的局部放大。分析图8可见:一阶速度-应力方程极性校正后PS偏移剖面平层部分在极性反转点附近的部分能量缺失,斜层部分整体能量缺失严重,且3 000~3 100 m部分(构造突变点)极性混乱。一阶速度-胀缩-旋转方程经极性校正后所得PS偏移剖面的平层部分和斜层部分的能量均比较完整,且同相轴具有良好的连续性。
3.3 基于坡印廷矢量分离行波压制噪声
应用图8(a)模型及参数,比较两种方程基于行波分离归一化互相关成像条件压制噪声的效果(图9),以PP偏移剖面为例。
由图9(b),(c)可知,两种方程应用行波分离的归一化互相关成像条件均可以起到压制噪声的效果。但将结果增益时,图9(d)有明显的低频噪声残留,而图9(e)的低频噪声基本被消除,表明利用一阶速度-胀缩-旋转方程的坡印廷矢量可以更加精确的分离纵、横波的方向行波,进而更好的压制偏移噪声。

图9 两种方程的PP偏移剖面
Fig.9 Single-shot RTM PS image based two kinds of equations
(a)为一阶速度-应力方程应用归一化互相关成像条件所得PP偏移剖面;(b)为一阶速度-应力方程应用行波分离归一化互相关成像条件所得PP偏移剖面;(c)为一阶速度-胀缩-旋转方程应用行波分离归一化互相关成像条件所得PP偏移剖面;(d),(e)分别为(b)和(c)增益2%的PP偏移剖面

图10 两种方程应用Marmousi-II部分模型所得的偏移剖面
Fig.10 RTM images for the Marmousi-II based on two kinds of equations
(a)为纵波速度模型;(b)为横波速度模型;(c)一阶速度-应力方程PP偏移结果;(d)一阶速度-胀缩-旋转方程PP偏移结果;(e)一阶速度-应力方程未极性校正的PS偏移结果;(f)一阶速度-胀缩-旋转方程未极性校正的PS偏移结果;(g)一阶速度-应力方程极性校正后的PS偏移结果;(h)一阶速度-胀缩-旋转方程极性校正后的PS偏移结果;(i),(j)分别为(g),(h)框中的局部放大图
4 复杂模型算例
为了比较两种方程在复杂模型的偏移效果,笔者选择Marmousi-II模型的一部分进行试算,图10(a),(b)为marmousi-II部分纵、横波速度模型。具体观测系统:震源为30 Hz的雷克子波,炮点水深5 m,从模型左端点开始放炮,炮间距65 m,共100炮,检波器置于海底,道间距为5 m,共1 300道接收。
图10(c),(d)分别为两种方程应用行波分离成像条件得到的PP偏移剖面,10(c)中依然有大量的低频噪声残留,而图10(d)中的低频噪声残留明显少于图10(c),尤其浅层的低频噪声得到了较好的压制。图10(g),(h)为横波极性校正后的PS偏移剖面。10(g)中依然有大量的低频噪声,而10(h)中低频噪声得到较好的压制,具有较高的信噪比,使得构造更加清晰。
图10(e),(f)分别为两种方程未经横波极性校正的PS偏移剖面,10(g),(h)为横波极性校正后的PS偏移剖面。通过比较极性校正前后的偏移剖面,可以看出未经极性校正的剖面中同相轴连续性破坏严重,构造不够清楚。极性校正后,同相轴更加连续,偏移剖面质量得到了改善。比较图10(g)和(h),10(h)中同相轴更加连续,清晰,尤其框内部分(比较图10(i)和10(j)效果更加明显。
结果表明,在复杂模型中,基于一阶速度-胀缩-旋转方程的多分量联合逆时偏移在压制低频噪声和横波极性校正方面具有一定的优势。
5 实际资料
实测资料为某工区的海底多波地震资料,图11(a)为利用偏移速度分析方法得到的深度域纵波层速度模型,以该模型的地层架构为控制条件,由浅到深通过纵横波速度比扫描得到的横波层速度模型如图11(b)所示,密度假定为常数(1 500 g/cm3),使用本文方法得到逆时偏移剖面如图12所示。
图12初步实现了纵横波的深度域联合成像,2者在层位上基本一致,但反射纵波和转换横波的偏移结果在信噪比和分辨率方面存在较大差异,造成这一现象的可能原因包括:① 纵、横波反射机理本身不同,纵波的强反射不一定意味着横波也是强反射;② 偏移所用的纵、横波速度模型的误差不一致,由于本文中横波速度模型是在假定纵波模型准确的前提下得到的,但事实上纵波模型必定存在误差,纵波模型的误差会积累到横波模型误差中,同时本文所用横波建模方法所隐含的假设(同一地层纵、横波速度比为常数)与实际情况也不符;③ 原始单炮中横波信号主要集中在水平分量中,纵波信号主要集中在垂直分量中,而水平分量的信噪比远低于垂直分量,造成横波偏移结果的信噪比低于纵波偏移结果。因此,笔者认为更为完善的偏移预处理和纵横波层速度建模技术将是多波联合逆时偏移领域的重要研究内容和今后的研究重点之一。

图11 某工区速度模型
Fig.11 Velocity model of a work area

图12 某工区叠加偏移剖面
Fig.12 RTM images of a work area
6 结 论
(1)基于一阶速度-胀缩-旋转方程的多分量联合逆时偏移仍以三分量记录作为边值条件,该方法对输入的三分量数据的要求和常规逆时偏移算法相同,但可分别求取纵、横波的坡印廷矢量,精确指示纵、横波的传播方向,从而更加精确地分离纵、横波场的方向行波。
(2)由于能够更为准确地实现纵、横波的方向行波分离,一阶速度-胀缩-旋转方程能够更好地压制逆时偏移噪声。
(3)基于一阶速度-胀缩-旋转方程的逆时偏移使用坡印廷矢量法可以更好地解决横波的极性校正问题。
(4)基于一阶速度-胀缩-旋转方程求取坡印廷矢量方法仍有如下缺陷:利用交错网格有限差分数值模拟时,波形振幅正负变化附近坡印廷矢量计算不准;当空间某点在某时刻存在多组纵横波时,该方法无法单独求取各组纵横波波场的传播方向。
参考文献(References):
[1] DENG F,MCMECHAN G A.True-amplitude prestack depth migration[J].Geophysics,2007,72(3):S155-S166.
[2] YANG J J,LUAN X W,FANG G,et al.Elastic reverse-time migration based on amplitude-preserving P-and S-wave separation[J].Applied Geophysics,2016,13(3):500-510.
[3] CHANG W F,MCMECHAN G A.Elastic reverse-time migration[J].Geophysics,1987,52(10):1365-1375.
[4] CHANG W F,MCMECHAN G A.3D elastic prestack reverse-time depth migration[J].Geophysics,1994,59(4):597-609.
[5] 董良国,马在田,曹景忠,等.一阶弹性波方程交错网格高阶差分解法[J].地球物理学报,2000,43(3):411-419.
DONG Liangguo,MA Zaitian,CAO Jingzhong,et al.A staggered-grid high-order difference method of one-order elastic wave equation[J].Chinese J.Geophysics,2000,43(3):411-419.
[6] 何兵寿,张会星.多分量波场的矢量法叠前深度偏移技术[J].石油地球物理勘探,2006,41(4):369-374.
HE Bingshou,ZHANG Huixing.Vector prestack depth migration of multi-component wavefield[J].Oil Geophysical Prospecting,2006,41(4):369-374.
[7] DU Q Z,LI B,HOU B.Numerical modeling of seismic wavefields in transversely isotropic media with a compact staggered-grid finite difference scheme[J].Applied Geophysics,2009,6(1):42-49.
[8] 何兵寿,张会星,韩月.双程声波方程叠前逆时深度偏移及其并行算法[J].煤炭学报,2010,32(3):458-462.
HE Bingshou,ZHANG Huixing,HAN Yue.Reverse time depth migration of two way acoustic equations and its parallel algorithm[J].Journal of China Coal Society,2010,32(3):458-462.
[9] YOUN O K,ZHOU H W.Depth imaging with multiples[J].Seg Technical Program Expanded Abstracts,2001,18(1):246-255.
[10] ZHANG Y,SUN J.Practical issues of reverse time migration:True-amplitude gathers,noise removal and harmonic-source encoding[A].70th EAGE International Annual Meeting,Extended Abstracts[C].2008:F047.
[11] 刘红伟,刘洪,邹振,等.地震叠前逆时偏移中的去噪与存储[J].地球物理学报,2010,53(9):2171-2180.
LIU Hongwei,LIU Hong,ZOU Zhen,et al.The problems of denoise and storage in seismic reverse time migration[J].Chinese Journal of Geophysics,2010,53(9):2171-2180.
[12] LIU F,ZHANG G,MORTON S A,et al.An effective imaging condition for reverse-time migration using wavefield decomposition[J].Geophysics,2011,76(1):S29-S39.
[13] YE R C,JIA X F.An effective denoising strategy for wave equation migration based on propagation angles[J].Applied Geophysics,2012,9(1):33-40.
[14] ZHANG Y,XU S,ZHANG G.Imaging complex salt bodies with turning-wave one-way wave equation[J].Seg Technical Program Expanded Abstracts,2006,25(1):3541.
[15] 张宇,徐升,张关泉,等.真振幅全倾角单程波方程偏移方法[J].石油物探,2007,46(6):582-587.
ZHANG Yu,XU Sheng,ZHANG Guanquan.True amplitude turn ing-wave one-way wave equation migration[J].GPP,2007,46(6):582-587.
[16] 丁亮,刘洋.基于归一化波场拆分互相关成像条件的叠前逆时偏移方法[J].石油地球物理勘探,2012,47(3):411-417.
DING Liang,LIU Yang.Pre-stack reverse-time migration based on normalized wavefield decomposition cross-correlation imaging condition[J].Oil Geophysical Prospecting,2012,47(3):411-417.
[17] CHEN T,HE B S.A normalized wavefi eld separation cross-correlation imaging condition for reverse time migration based on Poynting vector[J].Applied Geophysics,2014,11(2):158-166.
[18] 康玮,程玖兵.叠前逆时偏移假象去除方法[J].地球物理学进展,2012,27(3):1163-1172.
KANG Wei,CHENG Jiubing.Methods of suppressing artifacts in prestack reverse time migration[J].Progress in Geophysics,2012,27(3):1163-1172.
[19] DU Q,ZHU Y,JING B.Polarity reversal correction for elastic reverse time migration[J].Geophysics,2012,77(2):31.
[20] DELLINGER J,ETGEN J.Wave-field separation in two-dimensional anisotropic media[J].Geophysics,1990,55(7):914-919.
[21] SUN R,MCMECHAN G A.Scalar reverse-time depth migration of prestack elastic seismic data[J].Geophysics,2001,66(5):1519-1527.
[22] DOU L M,MU Z,LI Z,et al.Research progress of monitoring,forecasting,and prevention of rockburst in underground coal mining in China[J].International Journal of Coal Science & Technology,2014,1(3):278-288.
[23] 胡楠,何兵寿.三维各向同性介质矢量波场保幅分离方法[J].煤炭学报,2017,42(9):2420-2426.
HU Nan,HE Bingshou.Research on the amplitude-preserving sepa ration method of 3D isotropic medium vector wavefield[J].Journal of China Coal Society,2017,42(9):2420-2426.
[24] LI Z,MA X,FU C,et al.Wavefield separation and polarity reversal correction in elastic reverse time migration[J].Journal of Applied Geophysics,2016,127:56-67.
[25] 王鹏飞,何兵寿.基于行波分离的三维弹性波矢量场点积互相关成像条件[J].石油地球物理勘探,2017,52(3):477-483.
WANG Pengfei,HE Bingshou.Vector field dot product cross-correlation imaging based on 3D elastic wave separation[J].Oil Geophysical Prospecting,2017,52(3):477-483.
[26] 公绪飞.三维多波地震资料多分量联合弹性逆时偏移[D].青岛:中国石油大学(华东),2013.
GONG Xufei.Multicomponent joint elastic reverse-time migration for 3D multi-wave seismic data[D].Qingdao:China University of Petroleum,2013.
[27] LI Z,WANG M,ZHAO J,et al.Analysis on intersections between fractures by parallel computation[J].International Journal of Coal Science & Technology,2014,1(3):356-363.
[28] 刘红伟,李博,刘洪,等.地震叠前逆时偏移高阶有限差分算法及GPU实现[J].地球物理学报,2010,53(7):1725-1733.
LIU Hongwei,LI Bo,LIU Hong,et al.The algorithm of high order finite difference pre-stack reverse time migration and GPU implementation[J].Chinese Journal of Geophysics.2010,53(7):1725-1733.
[29] SHI Y,KE X.3D VSP reverse time migration using GPU acceleration[A].Workshop:High Performance Computing[C].Beijing,2016:24-25.
[30] CLAPP R G.Reverse time migration with random boundaries[A].79th Annual International Meeting[C].SEG Expanded Abstracts,2009.
[31] LAZEAR G D.Mixed-phase wavelet estimation using fourth-order cumulants[J].Geophysics,1993,58(7):1042-1051.
[32] PETROPULU A P.Phase reconstruction from the bispectrum slices[J].IEEE Trans on SP,1998,46(2):527-530.
[33] HE B S,MOU H B,HU N.P-and S-wave angle-domain common-image gathers (ADCIGs) based on elastic-wave reverse-time migration[J].Geological Journal,2016,51(S1):669-679.
[34] TANG H G,HE B S,MOU H B.P-and S-wave energy flux density vectors[J].Geophysics,2016,81(6):357.
[35] YOON K,MARFURT K J.Reverse-time migration using the Poynting vector[J].Exploration Geophysics,2006,37(1):102-107.
[36] 董良国,马在田,曹景忠.一阶弹性波方程交错网格高阶差分解法稳定性研究[J].地球物理学报,2000,43(6):856-864.
DONG Liangguo,MA Zaitian,CAO Jingzhong.A study on stability of the staggered-grid high-order difference method of first-order elastic wave equation[J].Chinese Journal of Geophysics,2000,43(6):856-864.