相对支撑式液压支架,掩护式液压支架单排立柱直撑,平衡千斤顶辅撑的支护方式具有操作快、自重小、对煤层高度变化适应性强等优势,但其在井下作业时与围岩的适应性较差,低头、高射炮等支护失效问题时有发生[1-3]。顶梁作为液压支架与工作面顶板直接接触的承载结构,其承载特性及其对顶板载荷的适应性直接决定了液压支架的支护稳定性。基于此,众多学者对液压支架的顶梁承载特性展开了大量研究。文献[4]在分析液压支架稳定工作的力平衡条件时,首次提出了顶梁力平衡区概念,指出液压支架顶梁承载能力随外载作用位置而变化。文献[5-6]研究了掩护式液压支架的承载能力区理论,指出力平衡区的大小表明了液压支架对顶板的适应性,优化平衡千斤顶的上耳座位置有利于改善支架的支护性能。文献[7-9]将力平衡区理论应用于放顶煤液压支架,阐述了平衡千斤顶对维持放顶煤液压支架稳定性的作用。文献[10]研究了掩护式液压支架承载特性,指出液压支架力学平衡区分布随顶梁接顶条件变化而改变。
笔者在前人研究基础上,为更全面掌握掩护式液压支架与顶板的耦合适应关系,建立了单区承载条件下液压支架全高度范围载荷平衡区数学模型,分析了液压支架工作高度、顶板水平力及平衡千斤顶与立柱参数变化对载荷平衡区分布特征的影响。在此基础上,为进一步完善液压支架载荷平衡区理论及拓展其适用范围,结合液压支架实际工况,研究了顶梁双区承载条件下液压支架极限承载平衡条件,并与单区承载条件下顶梁载荷平衡区分布进行了对比分析,以准确把握顶梁承载条件与载荷平衡区分布间的关系。
1 单区承载条件下承载特性分析
1.1 全高度范围载荷平衡区数学模型
液压支架在井下工作面的实际承载状态是极其复杂的,且载荷大小及载荷作用位置随工作面顶板状态变化存在较大差异,很难找出一种完全契合的载荷规律对其真实受力状况进行理论复现。因此在对液压支架进行理论分析时,需进行一系列的简化以方便求解[11-13]:
(1)顶板载荷为空间对称分布单区(单点或单线)作用于顶梁。
(2)不考虑顶板冒落矸石施加在掩护梁上的重力载荷。
(3)将立柱及平衡千斤顶视为理想力源,不考虑立柱及平衡千斤顶受载产生的弹性变形。
论文以某型号掩护式液压支架为例,其简化后的力学分析模型如图1所示。为研究液压支架顶梁载荷平衡区在全高度范围内的分布规律,取顶梁长度方向为X轴(每隔2 mm采点),高度方向为Y轴,沿Y轴每隔110 mm取样(计41个高度点)进行分析,取样点i分布如图2所示。
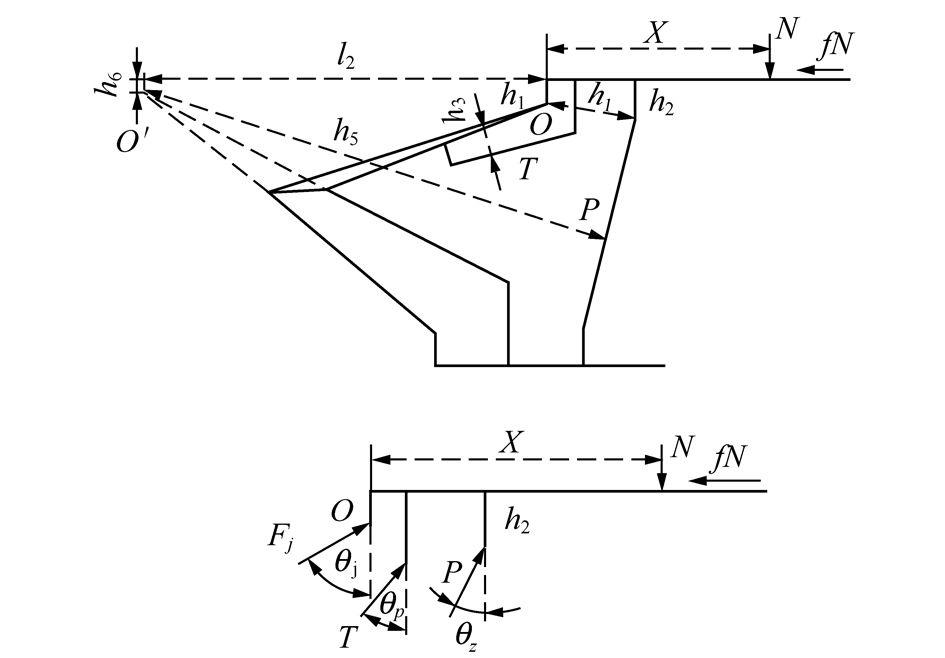
图1 单区承载条件下二柱式液压支架力学模型
Fig.1 Mechanical model of two-leggtd shield support under single region loading condition

图2 液压支架全高度范围取样点
Fig.2 Sampling points of the support during full height range
分析顶梁载荷平衡区分布特征有两种方案:
(1)取顶梁为单独受力体,构建考虑顶梁与掩护梁铰接力Fj、立柱工作阻力P及平衡千斤顶调定压力T的顶梁力平衡及力矩平衡数学模型式(1)~(3);
(2)取顶梁、掩护梁为分离受力体,构建仅考虑P及T的力矩平衡数学模型式(3)~(4)。
∑Fx=Psin θz+Tsin θP+Fjsin θj-fN=0
(1)
∑Fy=Pcos θz+Tcos θP+Fjcos θj-N=0
(2)
∑MO=Ph7+Th3+fNh1-NX=0
(3)
∑MO′=Ph5+fNh6-N(X+l2)=0
(4)
展开式(3)~(4)并引入高度变量因子i得到单区承载条件下液压支架全高度范围载荷平衡区解析:
(5)
![]()
(6)
![]()
(7)
式中,Ni为液压支架顶梁在工作高度为i时的极限平衡载荷;h1为O到顶梁的距离;h2为立柱上铰点到顶梁的距离;h3i,h7i为O到平衡千斤顶、立柱的距离;h5i为四连杆瞬心点O′到立柱的距离;h6i为O′到顶梁的距离(下为正,上为负);l2i为O′与O的水平距离;X为外载荷作用位置;T为平衡千斤顶工作阻力,推为正(活塞腔调定压力),拉为负(杆腔调定压力),f为顶板对顶梁摩擦因数,θj,θP及θz分别为Fj,T及P与竖直方向的夹角。液压支架部分参数见表1。
表1 液压支架参数
Table 1 Technical parameter of the support

1.2 定常工作位载荷平衡区分析
测取液压支架最高工作位结构参数(i=8 200 mm)代入式(5)~(7),利用MATLAB计算并绘制单区承载条件下(顶梁前端接顶或后端接顶)极限载荷平衡曲线如图3所示。由图可知(外载荷小于0的区域与正常使用工况相悖,通常不予考虑):① 极限载荷平衡曲线以X=-l2i+fh6i及(h7-h5)X+h7(l2+fh6)=0为渐进曲线呈双曲分布。沿顶梁长度方向,载荷平衡区分为两大区域:立柱主导区II(最优承载区)及平衡千斤顶主导区I(拉力作用区)和III(推力作用区)。在区域I(III),平衡千斤顶杆腔(活塞腔)达到调定压力,此时P值变化对极限平衡载荷影响较小。在区域II,平衡千斤顶由受拉转为外推,随着外载荷作用位置X不断前移,极限平衡载荷呈近线性递减。② 液压支架梁端极限支承力极小(≈1 000 kN),远远达不到其初撑顶板的实际需求(16 546 kN)。当工作面顶板较为破碎时,液压支架在升架过程中极易形成顶梁前端或后端首先触顶的单区承载姿态(图4)。此时,由于立柱升架力远大于梁端极限支承力,顶梁将绕立柱回转形成高射炮或低头位态,降低液压支架的稳定性。德国等国家针对掩护式支架的高射炮现象,在其型式试验中增加了在顶梁与掩护梁铰点处单点加载要求,指出为使顶梁保持平衡,需使P≥2T[12]。图3中匹配立柱极限载荷所需的平衡千斤顶压力曲线明确给出为平衡立柱阻力在梁端单点加载形成的载荷,平衡千斤顶有杆腔及无杆腔调定压力需达到47 720和40 000 kN。此时采用增加限位块等方式能有效提高液压支架承载能力,但难以完全满足需求。③ 立柱主导区最大极限平衡载荷为20 450 kN,小于立柱竖直分力20 908 kN(θz=5.34°)。原因在于此时液压支架不承受来自顶板的水平摩擦力(f取0),立柱的水平分力需掩护梁与顶梁铰接力F及平衡千斤顶拉力T共同承担,此时F及T竖直分力与立柱支承方向相反,故液压支架支护性能不能充分发挥。

图3 单区承载条件下液压支架顶梁承载曲线
Fig.3 Load supporting curves of shield support under single region loading condition

图4 非正常触顶条件下液压支架单区承载姿态
Fig.4 Single region support pose of a support under abnormal roof-contacted
1.3 全高度范围载荷平衡区分析
分别测取液压支架各工作位结构参数,利用MATLAB对式(5)~(7)循环求解,得到液压支架全高度范围载荷平衡区分布如图5所示。图中蓝色区域为平衡千斤顶主导区,红色区域最优承载区(立柱主导区)。
由图5可知,当液压支架工作高度变化时,顶梁最优承载区范围基本不变,最优承载区极限平衡载荷幅值存在小幅波动(22 640~19 680 kN)。随着液压支架的位态降低,最优承载区逐渐贴近煤壁(波动600 mm),促使顶梁前端支承力提高,提升液压支架端面顶板管理能力。

图5 液压支架全高度范围载荷平衡区
Fig.5 Optimal load equilibrium area of the support during full height range
2 载荷平衡区影响因素分析
2.1 水平力
依据标准“GB25974.1—2010 煤矿用液压支架”,分别取顶板对顶梁摩擦因数f为-0.2,0,0.2,0.3(采空区方向为正),研究水平力对载荷平衡区分布的影响。以f=0时液压支架的最优平衡区为基值,将f改变时高于该基值的区域视为等效最优平衡区,结果如图6所示。顶板水平力增加对等效最优平衡区覆盖范围(≈250 mm)及梁端支承力基本无影响,但能大幅提高最优平衡区极限平衡载荷,原因在于:① 在最优平衡区,外载荷主要由立柱承担,平衡千斤顶承载较小。当顶板对液压支架的水平力指向采空区并不断增大时,平衡千斤顶和顶梁与掩护梁铰点力随之增大以平衡该水平载荷,此时顶掩铰点的竖向支撑分力亦随之增大,从而间接提高了顶梁竖直方向承载能力。② 水平力促使载荷平衡区合力位置向顶梁尾端靠近,此时最优平衡区极限平衡载荷呈近线性增长。

图6 水平力变化对液压支架承载能力的影响
Fig.6 Influence of horizontal force on support capacity of support
综上可知,若顶板对液压支架形成指向采空区的水平摩擦力,不仅有利于维护端面顶板,降低底座前端比压及连杆附加力[14-15],同时能大幅提高最优承载区的极限承载能力。
2.2 平衡千斤顶及立柱工作阻力
由前述分析可知,平衡千斤顶在由受拉向外推状态过渡时能有效改善液压支架支撑合力作用位置。本节分别将平衡千斤顶工作阻力由3 458/-1 671 kN提至6 916/-3 342 kN,将立柱工作阻力由21 000 kN提至25 000,28 000 kN[8-10],量化地讨论平衡千斤顶及立柱工作阻力对载荷平衡区分布的影响(图7)。图7(a)中曲线a及b分别代表对应平衡千斤顶的额定拉、推力。由图7(a)可知,平衡千斤顶调定压力增大了一倍,最优平衡区覆盖范围及极限平衡载荷均呈等倍数增长。显然,合理提高平衡千斤顶调定压力能有效提高单区承载条件下液压支架对顶板载荷的适应性。随着立柱工作阻力的上升,液压支架载荷平衡区分布曲线如图7(b)所示。由图7(b)知,提高立柱工作阻力对顶梁梁端承载能力及最优平衡区范围基本无影响,但极限平衡载荷会随之等比增长。

图7 平衡千斤顶及立柱工作阻力对支架承载区分布的影响
Fig.7 Effect of the equilibrium and leg on the distribution of load equilibrium area
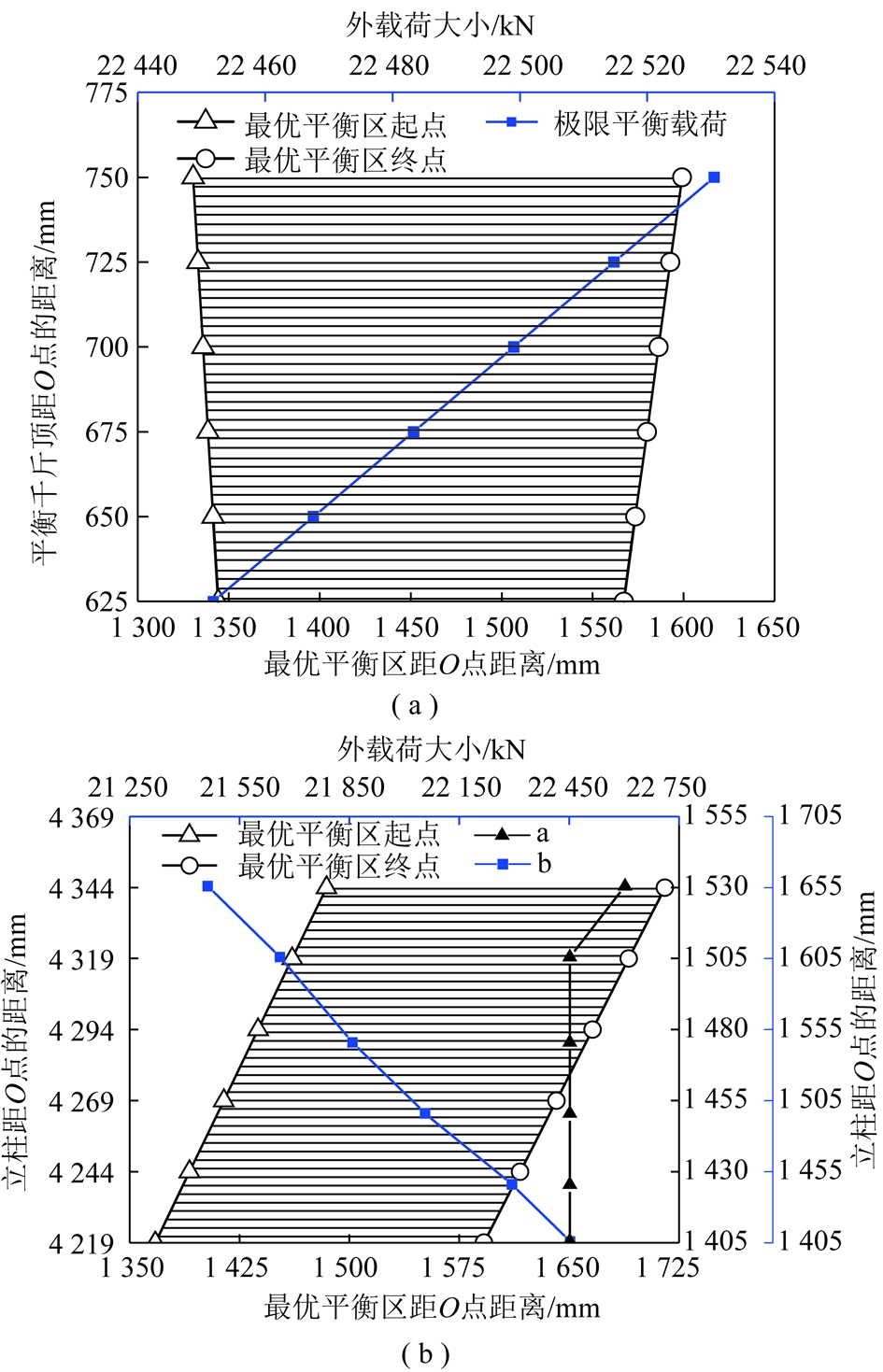
图8 平衡千斤顶及立柱定位尺寸对最优平衡区分布的影响
Fig.8 Influence of the location dimension of the equilibrium jack and leg on the distribution of the optimal load equilibrium zone
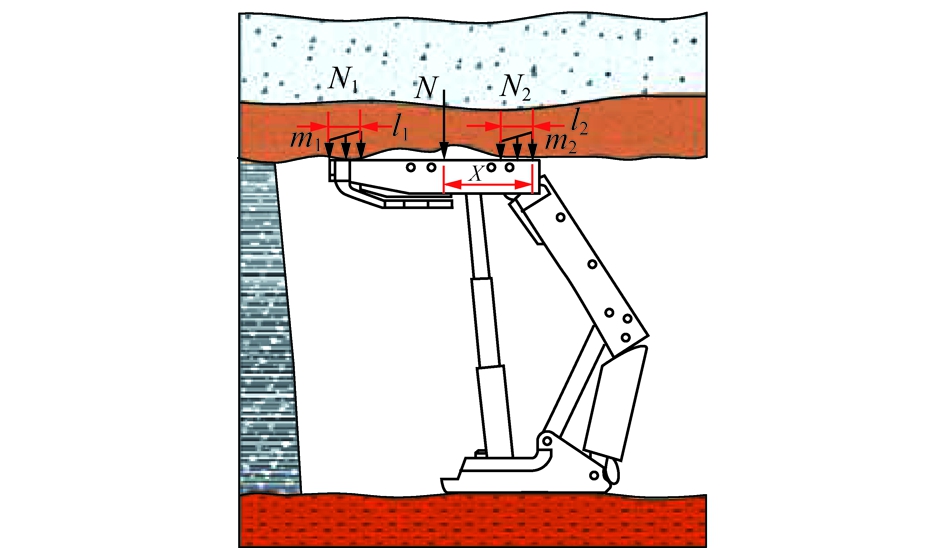
图9 正常接顶条件下支架双区承载位态示意
Fig.9 Double region support pose of the support under normal roof-contacted
2.3 立柱及平衡千斤顶定位尺寸
平衡千斤顶及立柱的上、下定位尺寸变化均影响了液压支架的承载特性,分别讨论各参数变化对支架支撑特性的影响不仅繁琐,而且难以全面把握各参数变化对支架承载特性的影响。分析式(3)~(4)不难发现,二者定位尺寸的变化最终直接影响两组参数:平衡千斤顶到O的距离(h3)及立柱到O与O′的距离(h5,h7)。图8(a)所示为增大h3时,支架最优平衡区分布。由图可知,增大h3能同时提高最优平衡区极限平衡载荷及其覆盖范围。
保持四连杆结构参数及平衡千斤顶位态不变,调节h5,h7,得到最优平衡区分布如图8(b)所示。等比例增加二者数值(立柱平行右移),顶梁最优平衡区随最优平衡区随立柱右移逐渐贴近煤壁,最优平衡区极限平衡载荷(曲线a)及覆盖范围基本无变化,初步猜测原因在于h5,h7互成反作用。为明确这一作用,在小幅增大h7的同时,较大幅增加h5,结果如曲线b所示,立柱上铰接点右移使得支架承载能力呈下降趋势,证实了假设的合理性。
3 双区承载条件下承载特性分析
当顶板处于较为完整的状态时,液压支架处于正常接顶姿态,此时由于采煤机截割顶、底板起伏不平[16],顶梁与顶板难以始终保持面接触,往往呈现为以立柱作用线为界的多区点、线或面载荷接触。在不考虑顶梁偏载、扭转条件下,液压支架多区承载条件可转化为如图9所示的双区承载条件,其中m1和m2分别为作用于梁端的分布力,可等效为距O点为X1,X2(X1,X2∈{Ⅰ,Ⅲ})的集中力N1,N2。此时液压支架载荷平衡区模型转化[12,17]为
N1=![]() m1dl
m1dl
(8)
N2=![]() m2dl
m2dl
(9)
∑MO=Ph7+Th3+fNh1-(N1X1+N2X2)=0
(10)
∑MO′=Ph5+fNh6-N1(X1+l2)-
N2(X2+l2)=0
(11)
单独分析式(8)~(11)难以直观地表征N1,N2间的数值关系,因此引入协调方程(12)~(13)构建N1与N2的映射关系,将问题转化为在单区承载特性曲线范围内寻找Max(N1)及Max(N2)的非线性寻优问题(式(14),(15))。
N1+N2=N
(12)
N1X1+N2X2=NX
(13)
![]()
(14)
Max(N2)=
![]()
(15)
分析式(14),(15),不难发现N1,N2均为隶属于N的分段函数。当X∈{Ⅰ,Ⅲ}时,Max(N1)及Max(N2)隶属于单区承载条件下平衡千斤顶主导区载荷曲线。当X∈{ΙΙ}时,Max(N1)及Max(N2)由立柱主导区载荷曲线决定。
利用MATLAB对式(14)、式(15)循环求解,得到双区承载条件下载荷平衡曲线如图10所示。图中,曲线a,b为修正的双区承载条件下液压支架承载能力曲线(Max(N1),Max(N2)),曲线c,d为形成Max(N1)及Max(N2)所需的![]() 及
及![]() 式(16),(17))。由图可知,
式(16),(17))。由图可知,![]() 小于Max(N1)(6 667 kN),Max(N2)(14 450 kN),计算结果合理。
小于Max(N1)(6 667 kN),Max(N2)(14 450 kN),计算结果合理。
(16)
![]()
(17)

图10 双区承载条件下支架承载能力曲线
Fig.10 Load supporting curve of shield support under double region loading condition
综上,液压支架在双区承载条件下的梁端承载能力远大于其单区承载条件下的梁端承载能力。通过监测顶板状态,在液压支架上方顶板冒空区域采用放置枕木等方式改善顶梁接顶状态,能大幅提高液压支架的梁端承载能力。
4 数值模拟实验
4.1 数值模型定义
本文运用多体动力学分析软件ADAMS建立液压支架的数值分析模型[18]。液压支架底座与大地固连视为刚性体,顶梁、掩护梁、四连杆机构运用Hypermesh处理为柔性体,各构件间连接采用摩擦接触定义。立柱及平衡千斤顶采用刚度弹簧阻尼系统等效替换(参数见表2),其刚度计算公式如下:
(18)
式中,K为等效刚度系数,N/m;A为液压缸有效传力面积,m2;β为乳化液体积弹性模量;L为液压缸有效行程,m。
表2 立柱和平衡千斤顶主要参数
Table 2 Main parameters of legs and equlibrium jack

依据式(18),得到平衡千斤顶、立柱一、二级缸的等效刚度分别为K1=2.06×108 N/m,K2=2.04×108 N/m,K3=1×108 N/m。当立柱一、二级缸同时工作时,将立柱等效为串联弹簧,其刚度为K4=K2×K3/(K2+K3)=6.71×107 N/m。完成定义的液压支架数值模型如图11所示。

图11 液压支架数值模型
Fig.11 Numerical model of the shield support
4.2 液压支架稳态加载测试
在顶梁上方添加模拟顶板,定义顶板与顶梁间接触为碰撞接触,给模拟顶板施加竖直向下的载荷16 000 kN,对液压支架进行稳态加载测试,结果如图12所示。由图12可知,液压支架在主动初撑阶段,外载荷小于立柱二级缸工作阻力(3 455 kN),立柱位移基本为0。在被动初撑阶段,外载荷介于立柱二级缸的主动初撑力及一级缸主动初撑力之间(3 455~6 443 kN)。此时立柱二级缸受压回缩而一级缸无动作,立柱刚度表现为二级缸刚度。当外载荷达到一级缸主动初撑力后,支架进入增阻阶段。此时立柱一、二级缸均受压回缩,立柱刚度表现为两级缸串联等效刚度。仿真结果立柱总压缩量Δx=60.5 mm,立柱理论位移可由式(19)计算得Δl=61.0 mm。综上,模拟结果与立柱实际动作规律基本一致,模型合理可信。
ΔL=ΔF1/K3+ΔF2/K4(19)
式中,ΔF1为一级缸增加压力,初始压强29 MPa;ΔF2为二级缸增加压力,初始压强28 MPa。
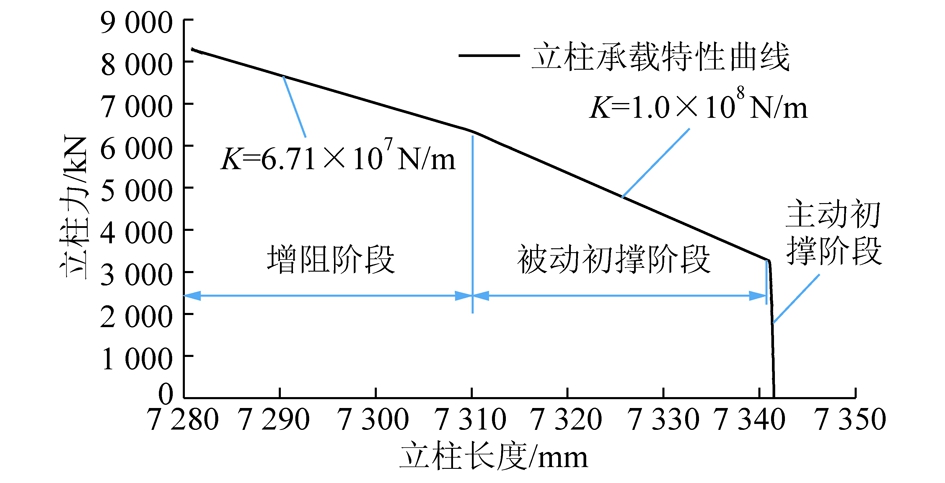
图12 液压支架载荷-位移曲线
Fig.12 Load-displacement curve of the shield support
4.3 单区承载模拟分析
基于3.2节数值模型,对支架单区承载工况进行加载分析。在顶梁顶面选取55个点进行加载,载荷大小以2.1节(f=0.3)计算结果预估并依据平衡千斤顶及立柱的响应结果进行修正(二者任何一个达到工作阻力即认定液压支架达到承载极限)。加载位置如图13所示,取顶梁长度方向为X轴,宽度方向为Y轴,其中N为施加的竖直向载荷,fN为对应载荷点水平摩擦力(fN=0.3N),ΔW=400 mm,ΔL=500 mm。图中红色点群为额外的最优平衡区探测点(位置不定,探测最优承载区边界)。
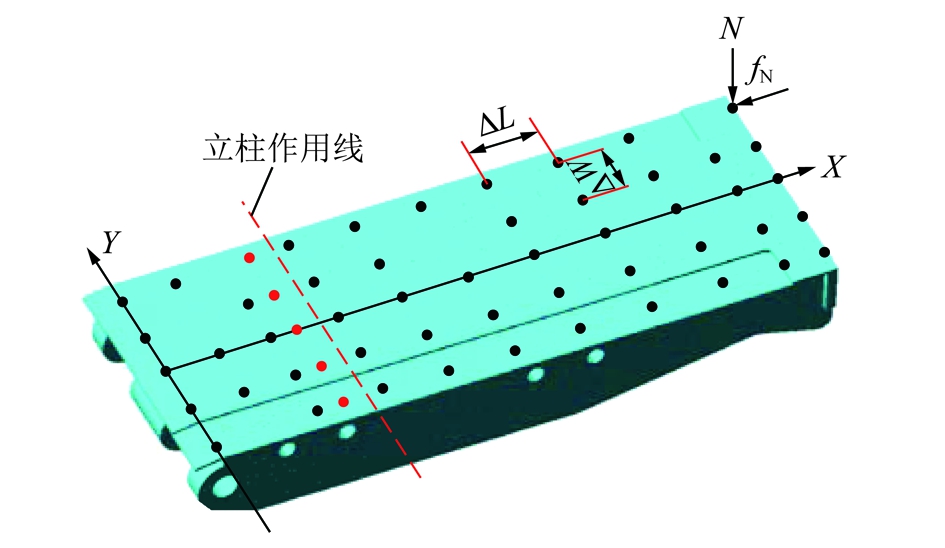
图13 单区加载位置
Fig.13 Single region loading position
图14为模型最终施加载荷,图15为对应平衡千斤顶响应曲面。由图14,15可知,① 外载荷沿顶梁宽度方向移动时,平衡千斤顶主导区承载能力基本无变化,最优承载区承载能力沿顶梁对称平面向两侧递减;② 外载荷沿顶梁长度方向由前至后移动时,平衡千斤顶由外推转为受拉,与第1节理论分析结果一致;③ 最优承载区理论计算承载能力(23 640,22 410)、作用位置(1 316~1 528 mm)及覆盖范围(212 mm)与模拟计算承载能力(23 200,22 600)、作用位置(1 256~1 470 mm)及覆盖范围(214 mm)基本一致(由于在对液压支架进行理论分析时,忽略了立柱及平衡千斤顶的液压弹性变形引起的液压支架受力状态变化,因此理论分析和数值模拟结果存在一定差异)。

图14 单区承载模拟载荷平衡区分布
Fig.14 Distribution surface of the load equilibrium area under
single region loading simulation
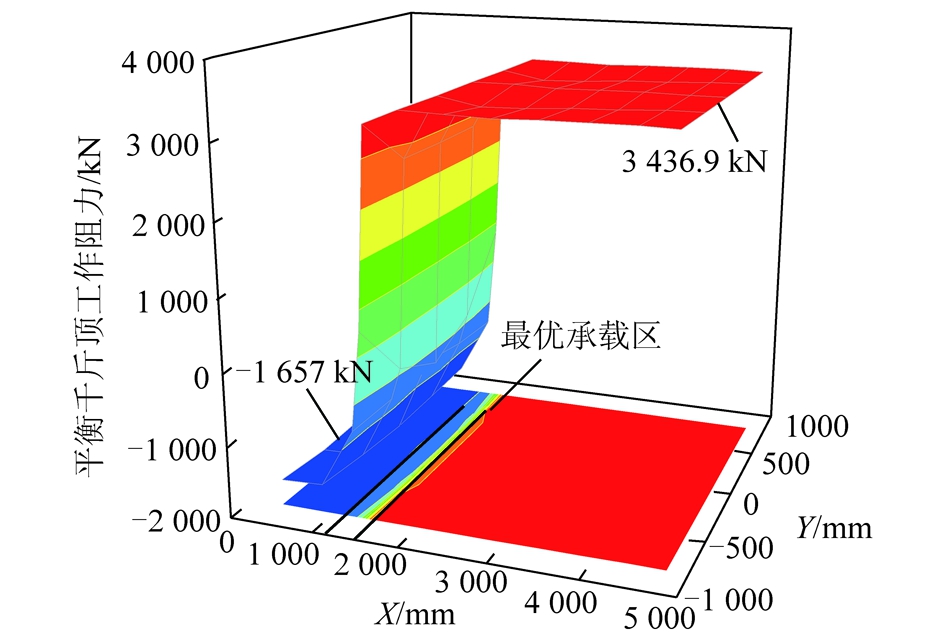
图15 平衡千斤顶响应曲面
Fig.15 Response surface of the equilibrium jack
4.4 双区承载模拟分析
考虑外载荷沿支架宽度方向移动时,平衡千斤顶工作阻力变化较小,将载荷施加位置变更为图16所示以模拟液压支架双区承载条件下承载能力。外载荷N1,N2仍以理论计算结果预估并依据平衡千斤顶及立柱响应进行修正。图17为双区承载条件下液压支架顶梁承载能力曲线。由图17可知,模拟结果能较好地对应理论分析结果。

图16 双区加载位置
Fig.16 Double region loading position

图17 双区承载模拟载荷平衡区分布
Fig.17 Distribution surface of the load equilibrium area under double region loading simulation
5 结 论
(1)根据液压支架接顶状态不同,将液压支架分为单区承载及双区承载位态,并分别构建了两种位态下液压支架承载能力区模型,指出双区承载条件下液压支架承载能力远大于其单区承载能力。通过监测顶板状态及液压支架实时姿态等方式控制其接顶状态,能大幅提高支架的支护稳定性。
(2)根据掩护式支架的承载特性,将顶梁载荷平衡区分为立柱主导区、平衡千斤顶主导区。根据平衡千斤顶作用腔不同将平衡千斤顶主导区分为拉力作用区及推力作用区,二者分别代表了顶梁抵抗抬头、低头位态的能力。
(3)掩护式支架载荷平衡区分布特征与其工作高度、平衡区千斤顶和立柱的工作阻力比、平衡千斤顶定位尺寸、顶板对支架的水平力等因素有关。通过提高平衡千斤顶与立柱的工作阻力比、优化平衡千斤顶定位尺寸等,能有效提高液压支架对顶板的适应性。
(4)首次采用数值实验方法对单、双区承载条件下液压支架载荷平衡区理论展开研究,模拟结果与理论分析一致性较高,表明了理论分析与数值模拟的合理性。
参考文献(References):
[1] 马端志,王恩鹏,王彪谋.两柱大采高强力放顶煤支架的特点与创新发展[J].煤炭科学技术,2015,43(10):111-115.
MA Duanzhi,WANG Enpeng,WANG Biaomou.Characteristics and innovation of two-legs shield powerful caving coal hydraulic support of large cutting height face[J].Coal Science and Technology,2015,43(10):111-115.
[2] FRITH Russell C.A holistic examination of the load rating design of longwall shields after more than half a century of mechanised longwall mining[J].International Journal of Mining Science and Technology,2015,25(5):687-706.
[3] 郭卫彬,刘长友,吴峰峰,等.坚硬顶板大采高工作面压架事故及支架阻力分析[J].煤炭学报,2014,39(7):1212-1219.
GUO Weibin,LIU Changyou,WU Fengfeng,et al.Analysis of support crushing accidents and support working resistance in large mining height workface with hard roof[J].Journal of China Coal society,2014,39(7):1212-1219.
[4] 周永昌.掩护式液压支架力学特性的初步分析[J].煤炭学报,1981(1):1-17.
ZHOU Yongchang.Preliminary analysis of mechanical characteristicsof shield supports[J].Journal of China Coal Society,1981(1):1-17.
[5] 王国彪.二柱掩护式支架承载能力区理论的研究[J].阜新矿业学院学报(自然科学版),1993,12(4):46-49.
WANG Guobiao.Study of two-leg shield supporting ability areas theory[J].Journal of Fuxin Mining Institute (Natural Science),1993,12(4):46-49.
[6] 王国彪,高荣.掩护式支架平衡千斤顶定位尺寸的模拟分析与优化设计[J].煤炭学报,1994,19(2):195-205.
WANG Guobiao,GAO Rong.Simulation and optimum design of locating dimensions of shield support balance ram[J].Journal of China Coal Society,1994,19(2):195-205.
[7] 杨培举,刘长友,金太.两柱掩护式综放支架的承载规律及工艺研究[J].采矿与安全工程学报,2010,27(4):512-516.
YANG Peiju,LIU Changyou,JIN Tai.Research on the load variation laws and technologic effect of two-leg sublevel caving shield support[J].Journal of Mining & Safety Engineering,2010,27(4):512-516.
[8] 杨培举,刘长友,韩纪志,等.平衡千斤顶对放顶煤两柱掩护支架适应性的作用[J].采矿与安全工程学报,2007,24(3):278-282.
YANG Peiju,LIU Changyou,HAN Jizhi,et al.Role of equilibrium jack in adaptability of 2-leg shield support of top coal caving[J].Journal of Mining & Safety Engineering,2007,24(3):278-282.
[9] 李化敏,蒋东杰,Syd S Peng,等.放顶煤液压支架承载特性及其适应性分析[J].煤炭科学技术,2015,43(6):23-28.
LI Huamin,JIANG Dongjie,SYD S Peng,et al.Analysis on loading features and suitability of hydraulic powered caving supports[J].Coal Science and Technology,2015,43(6):23-28,70.
[10] 徐亚军,王国法,刘业献.两柱掩护式液压支架承载特性及其适应性研究[J].煤炭学报,2016,41(8):2113-2120.
XU Yajun,WANG Guofa,LIU Yexian.Supporting property and adaptability of 2-leg powered support[J].Journal of China Coal Society,2016,41(8):2113-2120.
[11] OBLAK M,HARL B,BUTINAR B.Optimal design of hydraulic support[J].Structural & Multidisciplinary Optimization,2000,20(1):76-82.
[12] 王国法,史元伟,陈忠恕,等.液压支架技术[M].北京:煤炭工业出版社,1999:46-47.
[13] 牛艳奇.液压支架四连杆机构多目标优化[J].辽宁工程技术大学学报,2015,34(5):628-632.
NIU Yanqi.Hydraulic support four-bar connecting rod multi-objective optimization[J].Journal of Liaoning Technical University:Natural Science,2015,34(5):628-632.
[14] 冯军发,蒋东杰.综放采场液压支架水平力及稳定性分析[J].煤矿安全,2016,47(10):201-207.
FENG Junfa,JIANG Dongjie.Analysis on horizontal force and stability of hydraulic support at fully mechanized sublevel caving face[J].Safety in Coal Mines,2016,47(10):201-207.
[15] 王国法.高端液压支架及先进制造技术[M].北京:煤炭工业出版社,2010:25-60.
[16] CHENG Jingyi,WAN Zhijun,SYD S Peng,et al.What can the changes in shield resistance tell us during the period of shearer’s cutting and neighboring shields’ advance?[J].International Journal of Mining Science and Technology,2015,25(3):361-367.
[17] 哈尔滨工业大学理论力学教研室.理论力学.I(第7版)[M].北京:高等教育出版社,2009:45-48.
[18] 梁利闯,田嘉劲,郑辉,等.冲击载荷作用下液压支架的力传递分析[J].煤炭学报,2015,40(11):2522-2527.
LIANG Lichuang,TIAN Jiajin,ZHENG Hui,et al.A study on force transmission in a hydraulic support under impact loading on its canopy beam[J].Journal of China Coal Society,2015,40(11):2522-2527.