锚杆支护是巷道支护必不可少的支护手段，随开采强度的加大以及采矿工程向深部的推进，出现了浅部岩体较少出现的围岩大变形现象，围岩大变形主要源于塑性区岩体的塑性变形、扩容变形以及碎胀变形[1]。围岩属于内含大量节理、裂隙等缺陷的非均匀材料，导致各点屈服强度不同，围岩受载后引起内部各点的屈服弱化不同步，围岩屈服强度较低部分先屈服弱化，随后是屈服强度高的，引起围岩发生蠕变现象[2]。围岩塑性区发育程度与蠕变的剧烈程度有密切关系，深入研究围岩蠕变的发展规律、锚固体对围岩蠕变的控制机理显得至关重要[3-4]。
迄今，采用组合基本元件模型可得到许多模型来描述岩体的流变特性，但绝大多数只能描述衰减和稳定蠕变，无法描述加速蠕变[5]。对于加速蠕变阶段的研究，国内外学者做了大量的研究工作，取得了卓有成效的研究成果，总体来说描述加速蠕变的方法大致有两种，一种是采用非线性流变元件代替常规的线性流变元件，建立能描述岩石加速流变阶段的非线性流变模型[6-11];二是采用新的理论，如内时理论、断裂及损伤力学理论等，建立岩石流变本构模型[12-15]。这两种方法建立的流变本构模型均能较好地描述岩石的加速蠕变阶段。
岩体蠕变就是岩体的变形随时间延长逐渐增加，蠕变三阶段发展的过程也是岩体逐渐破坏的过程。围岩的塑性区扩展速率与围岩加速蠕变有密切关系，围岩加速蠕变的触发必将引起塑性区的急速扩张，引起锚杆以及锚固基础受力增大，有可能导致锚杆不同形式的失效。充分发挥锚杆的支护作用需要考虑锚杆与围岩耦合协调作用，锚杆支护允许围岩产生稳定蠕变而限制加速蠕变，即允许其发生适量变形，但不允许超过一定的变形速率。而相关锚固体蠕变本构模型的研究大多是采用岩样室内试验[16-18]，较少结合现场的条件。将锚杆以及加锚围岩体分别视为独立的流变体，研究长期条件下锚固结构间的耦合作用机制具有重要意义。笔者通过分别建立描述锚杆、围岩体弹塑性区的本构模型来研究锚杆对控制围岩蠕变的作用，采用蒲河矿西三采区集中运输大巷的锚杆支护失效实例进行分析验证。
1 改进Burger模型及其蠕变方程
锚杆在正常工作状态下将与围岩发生同步变形，特定锚杆的容许应变量是固定的，当锚固体的应变量超过锚杆的容许应变量后，锚杆会发生破断失效。一般情况下，在高应力软岩巷道中，锚杆破断失效后导致围岩失去约束，其应变量会急剧增加，进入加速蠕变阶段，影响巷道的正常使用。因此，可以采用应变参量来表示岩体是否进入加速蠕变阶段，岩体出现加速蠕变意味着岩体已经出现塑性变形，应力发生卸载后，塑性变形为不可逆的永久变形，传统黏壶在施加反力时应变是可逆的。因此,引入带应变触发的非线性单向运动黏壶来描述岩石进入加速蠕变的阶段[19]，如图1所示，其本构关系为
(1)
式中，ηnl为非线性黏壶的黏滞系数;εa为应变触发临界值，可由试验求得;σ，ε分别为模型受到的应力与整体应变。
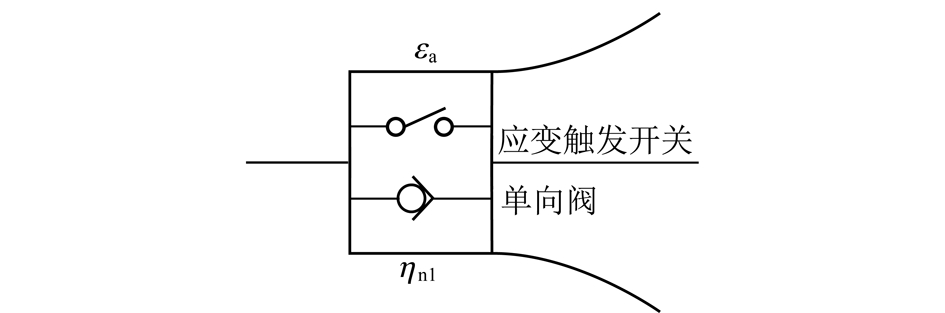
图1 非线性加速蠕变元件
Fig.1 Nonlinear accelerated creep element
非线性单向运动黏壶与能较好描述岩石衰减蠕变及等速蠕变2个阶段的Burger模型进行串联，得到能描述岩石蠕变3阶段的改进Burger模型，如图2所示。
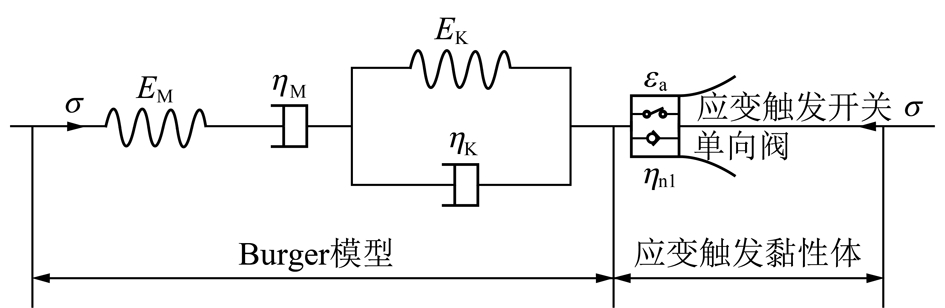
图2 改进Burger模型示意
Fig.2 Schematic diagram of improved Burger model
当ε<εa时，非线性单向黏壶等同于刚体，加速蠕变模型退化为传统的Burger模型，该模型的蠕变方程为
(2)
式中,ε(t)为蠕变应变量;σ为蠕变模型总应力;t为蠕变时间;EM为瞬时弹性模量;EK为黏弹性模量;ηK和ηM均为黏滞系数，表示蠕变趋向稳定的快慢程度。
当ε≥εa时，非线性单向运动黏壶开始触发，岩体进入加速蠕变阶段，总应变表示为
ε=εe+εV+εeV+εnl
(3)
式中，等式右边的4个变量分别为胡克体应变、线黏性体应变、黏弹性体应变、非线性单向运动黏壶应变。
其中，
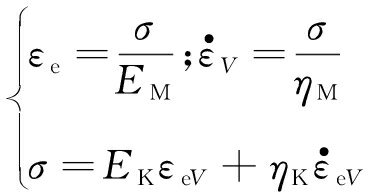
(4)
此时，在t=0时刻，初始条件为
(5)
对式(3)～(5)进行拉普拉斯变换后得出
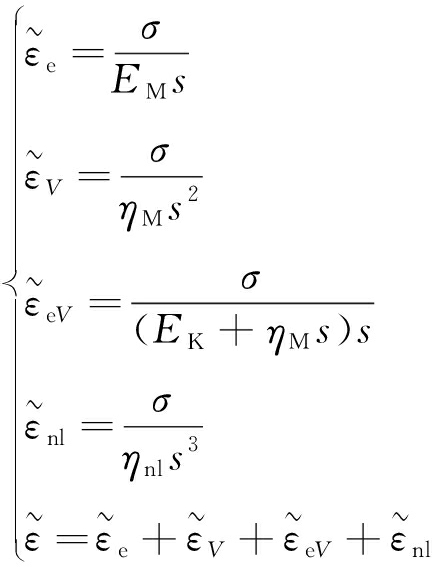
(6)
式中，s为拉氏空间的复变量;
为ε的拉氏变换。
ε的拉普拉斯变换为
(7)
对上式进行拉普拉斯逆变换，得到发生加速蠕变的蠕变方程为
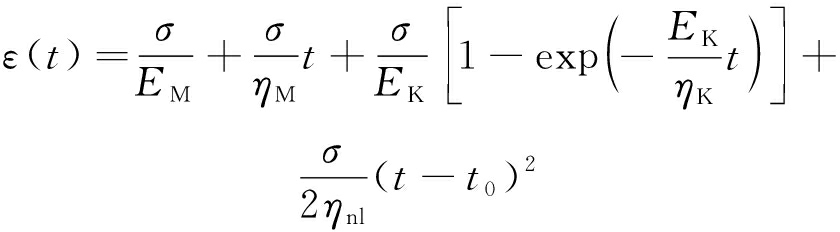
(8)
式中，t0=t|ε=εa,t|ε=εa为岩石进入加速蠕变阶段的时间点。
蠕变速率
(9)
蠕变加速度
(10)
令
得出二阶导数的零点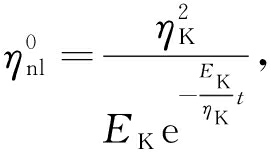
当
时，
当
时，
由此知，ηnl取值不同，应变二阶导数的正负不同，可以相应的表示不同的岩石非线性蠕变特征的衰减蠕变、稳定蠕变、加速蠕变等3个阶段，其中，加速蠕变阶段的应变量随时间延长而迅速增加，蠕变的增长程度由ηnl控制。当时，第3阶段蠕变曲线呈现出急速上升趋势，如图3所示。
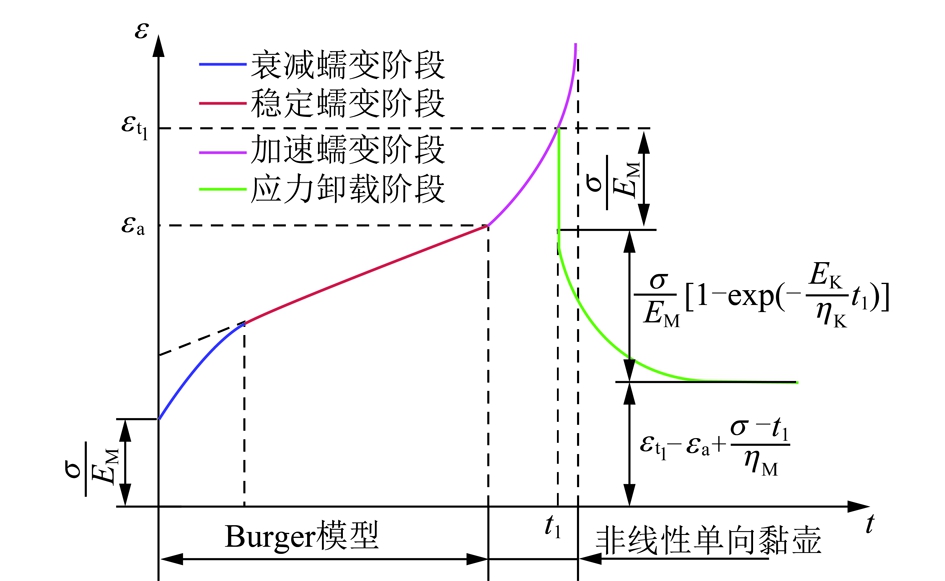
图3 改进Burger模型的蠕变曲线示意
Fig.3 Sketch Map of creep curve of improved Burger model
从图3中看出，改进Burger模型存在蠕变的3个阶段，当在t1时刻发生卸载时，模型中的瞬时应变瞬刻消失，具有弹性后效现象，存在的永久变形主要以非线性单向黏壶产生的塑性变形为主。
2 围岩-锚杆耦合蠕变模型构建
2.1 锚杆对改进Burger模型的蠕变控制作用
根据文献[20]中锚杆的拉伸性能试验曲线知，锚杆的本构模型类似于线性强化弹塑性模型，如图4所示。为研究锚杆对控制围岩加速蠕变的作用，这里假定锚杆属于理想弹性材料，将锚杆考虑成一根与围岩并联的弹簧来模拟实际中锚杆的工作状态来进行分析，如图5所示。
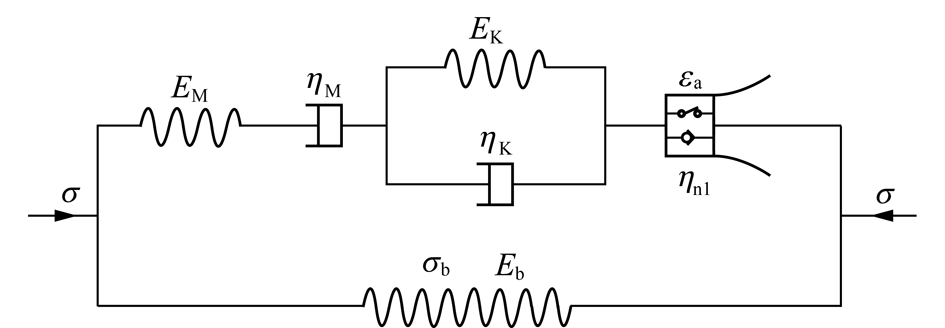
图5 锚固体本构模型
Fig.5 Constitutive model of anchorage body
图4 锚杆本构模型
Fig.4 Constitutive model of bolt
根据流变元件串并联法则及式(8)求得锚固体蠕变方程为
(11)
式中，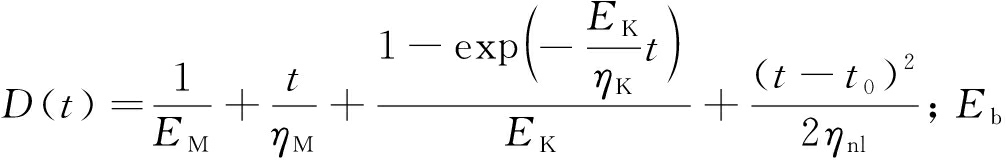
为锚杆的弹性模量;E0为锚杆锚固后的锚固体等效弹性模量。
由式(11)可知，锚杆支护围岩后等效于增加了围岩的弹性模量，提高了围岩抵抗变形的能力，围岩应变量降低，当围岩应变总量不超过εa时，围岩加速蠕变不会触发，围岩处于稳定蠕变状态，塑性区的扩展速率得到有效控制。
锚杆的实际工作状态并非前文假设的理想弹性情况，其具有塑性破坏的特点，亦即锚杆提高锚固体的等效弹性模量是有限的。锚杆的锚固方式根据锚固基础设计长度主要分为全长锚固、加长锚固与端头锚固等 3 种锚固方式[21]。全长锚固、加长锚固均可看作是端头锚固的特殊情况，其中，全长锚固可以认为是端头锚固中自由段长度为0的极限形式，其锚固范围包含塑性区与弹性区。
高应力巷道的塑性区无法得到完全控制，锚杆支护只能限制塑性区的扩张速率，同时，随围岩应变量逐渐增大锚杆自由段与锚固基础上承受的载荷亦逐渐增大，当达到锚固基础的黏结强度及锚杆的极限破断载荷时，锚杆自由段会发生破断，锚固基础则会出现渐进脱黏现象而引起锚固基础有效长度减小以及锚固力逐渐下降。当塑性区向外扩张至锚固基础位置后，锚固基础将部分位于弹性区、部分位于塑性区，因塑性区围岩的刚度特性弱于弹性区围岩，将会削弱锚杆的整体锚固能力。以下对端头锚固形式的锚固基础分别位于塑性区与弹性区时控制围岩变形的效果进行分析。
2.2 围岩弹塑性区蠕变本构模型
锚杆支护的实质是将锚杆与围岩黏结在一起，形成相互作用的工作体系，利用围岩的抗剪强度来传递锚杆的拉力、剪力。从锚杆的工作原理看，围岩蠕变与锚杆变形是一致的，围岩发生蠕变使锚杆内力发生变化，反之，锚杆内力发生变化也会使围岩的蠕变量发生改变，围岩蠕变与锚杆受力变化存在耦合效应。
端锚锚杆由锚固段、自由段和锚头3部分组成，通过分析大量理论研究与工程实践，得出锚固体的破坏失效情况有以下4种形式[22]:锚杆自由段拉断破坏、锚杆体与黏结剂黏结面破坏、黏结剂与围岩黏结面破坏、锚固体与周围围岩整体破坏，其中尤以锚杆自由段拉断破坏、锚杆体与黏结剂黏结面破坏为主。因此，锚杆支护失效主要以锚杆自由段破断及锚固基础失效为主。
(1)锚杆本构模型。
锚固力是衡量锚杆支护的重要指标，锚固基础受力超过锚固基础的屈服极限后，其锚固力的丧失并不是瞬间发生的，随围岩蠕变发展呈现由弹性变形向塑性软化及残余锚固阶段发展，对应的锚固力也逐渐降低。因此，通过引入一个带锚固力损伤系数k的塑性元件来表征锚固基础受力超过其屈服极限后锚固力的渐进损伤过程，端锚锚杆的本构模型如图6所示。
图6 锚杆流变本构模型
Fig.6 Rheological constitutive model of anchor bolt
(12)
式中，k为锚固力损伤系数，0<k<1;σse为锚固基础屈服极限;σs为锚固力。
当σ≤σse时，锚固基础没有出现损伤，锚固基础处于稳定工作状态，与围岩发生同步变形，此时的变形主要是锚杆自由段的拉伸变形，不易触发加速蠕变;反之，锚固基础出现损伤，经历塑性软化、残余锚固阶段后，实际有效锚固长度减小，意味着锚杆自由段的长度逐渐增大。处于残余锚固阶段的锚固基础对弹性岩体控制能力降低，蠕变速率逐渐增大，导致塑性区扩展速率增大，引起锚杆应变量增速变大、应力升高，进一步加剧了锚固基础的损伤失效，形成恶性循环。因此，保证锚固基础不失效是锚杆支护需要重点考虑的问题。
(2)围岩弹塑性区流变模型。
弹性区本构模型采用能够反映弹性区围岩黏弹性性质的Burger模型，认为当弹性区岩体发生加速蠕变后才进入塑性区。
巷道开挖后因围岩应力重新分布引起浅部围岩迅速发生塑性破坏形成塑性区，其自承能力较弱，是巷道支护的主要对象，塑性区外侧的弹性区围岩未发生塑性破坏，自承能力较强。塑性区各处围岩峰后极限强度不同，自塑性区内侧到塑性区外侧弹塑性交界处的围岩峰后极限强度呈非线性增加，此处简化为线性增加，则塑性区的峰后极限强度是与塑性区位置有关的线性函数。
塑性区围岩峰后极限强度为
(13)
式中，a为塑性区的范围;x为塑性区内任一点到塑性区内边界的距离;σep为弹塑性交界处的围岩极限强度。
塑性区本构模型如图7所示。
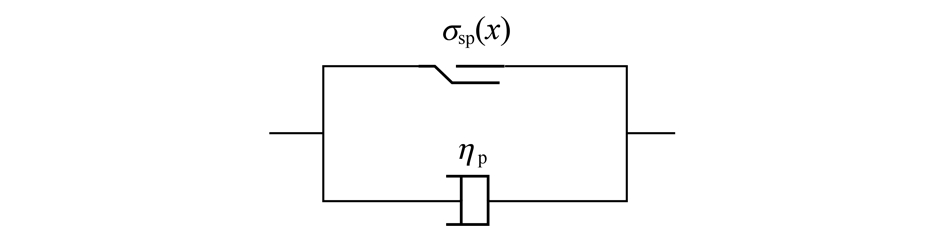
图7 塑性区流变模型
Fig.7 Rheological model of plastic zone
该塑性区流变模型的本质是，当σ<σsp(x)时，该塑性元件不发生作用，塑性区围岩不发生蠕变;反之，塑性区围岩发生蠕变。高应力软岩巷道，塑性区围岩的峰后极限强度降低且持续发生扩容变形，锚固体承受载荷较高，因此，可以认为σ>σsp(x)总是成立的。
塑性区本构方程应变计算公式为
(14)
式中，σr为围岩应力;ηp为塑性区黏壶的黏滞系数;K为塑性区围岩应变速率。
从塑性区的扩展角度来说，在当今科学技术条件下，对于高应力软岩巷道我们所能提供支护阻力不足1 MPa，与开挖巷道后围岩重新分布后的应力相比，远不在同一个数量级，无法完全控制住围岩塑性区的扩展，只能通过一定的支护技术降低塑性区扩展速率的途径来减小围岩变形量，延长两次维护巷道的时间间隔，达到在巷道服务期间内最大程度减小巷道返修次数的目的。塑性区扩展示意如图8所示。
从图8可以看出，随时间发展塑性区范围越来越大，围岩中同一位置处(如x0)受到的应力逐渐降低，因塑性区围岩处于极限平衡状态，围岩受到的应力即是塑性区围岩峰后极限强度，因此，塑性区围岩中某处峰后极限强度随时间发展逐渐降低。在σr不变情况下，式(14)K随时间发展逐渐增大，直至塑性区围岩应变急剧增大引起塑性区围岩完全成为破碎区围岩，塑性区本构模型应变-时间曲线示意如图9所示。从图9可以看出,该塑性区模型随时间发展表现出加速蠕变的特征.
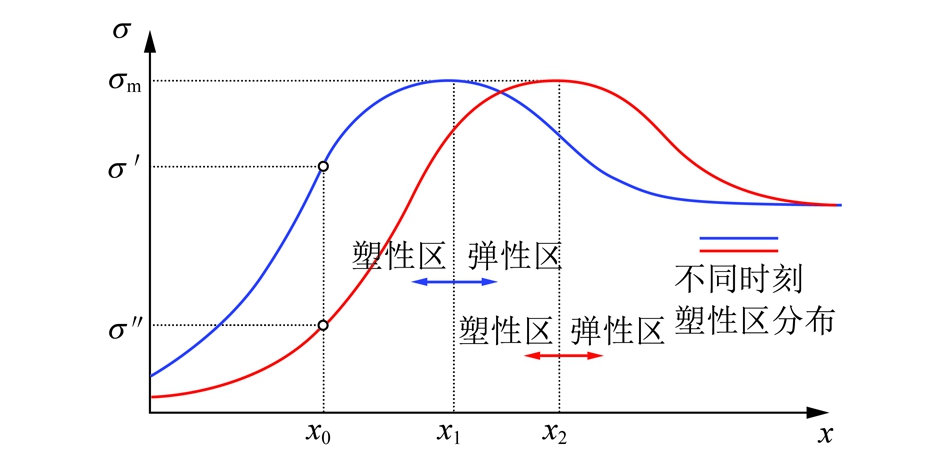
图8 围岩极限强度及塑性区范围示意
Fig.8 Schematic map of ultimate strength and plastic zone of surrounding rock
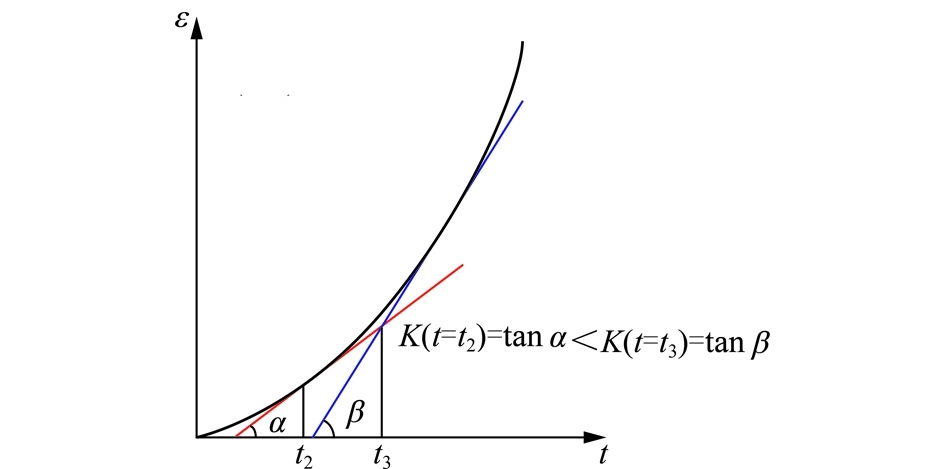
图9 塑性区本构模型应变-时间关系示意
Fig.9 Diagram of strain-time relationship of plastic zone constitutive model
2.3 围岩-锚杆耦合本构模型
锚杆支护对围岩的锚固效果随锚固基础在围岩中的位置不同而不同，锚固基础在围岩中位置分为3种:第1种是完全位于塑性区;第2种是完全位于弹性区;第3种是一部分位于弹性区一部分位于塑性区。锚杆支护是锚杆与围岩耦合的一个过程，因弹塑性区围岩刚度特性差异，锚固基础的位置选择不同最终起到的支护效果不一样。
其中，锚固基础内侧自由端恰好位于弹塑性交界处时的锚固体本构模型如图10所示，此时，锚固基础完全位于弹性区。
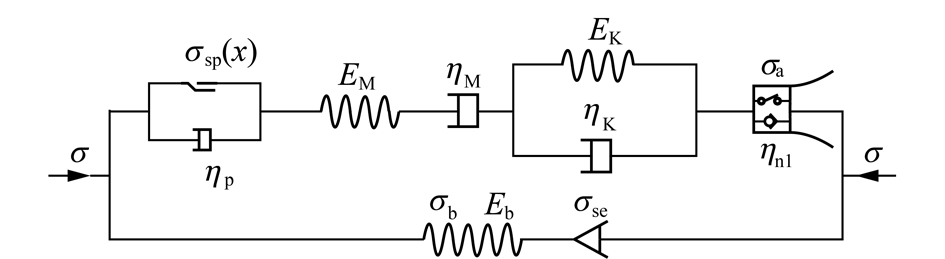
图10 锚固体本构模型
Fig.10 Constitutive model of anchorage body
弹性区围岩应变εe计算公式为
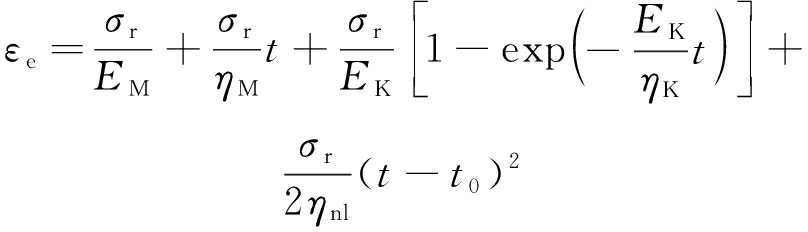
(15)
围岩总应变εr计算公式为
εr=εp+εe
(16)
锚杆模型应变εb计算公式为
(17)
为分析锚固基础位于弹塑性区的区别、作用，假设锚杆处于稳定工作状态，即σb<σse，锚固体的耦合关系为
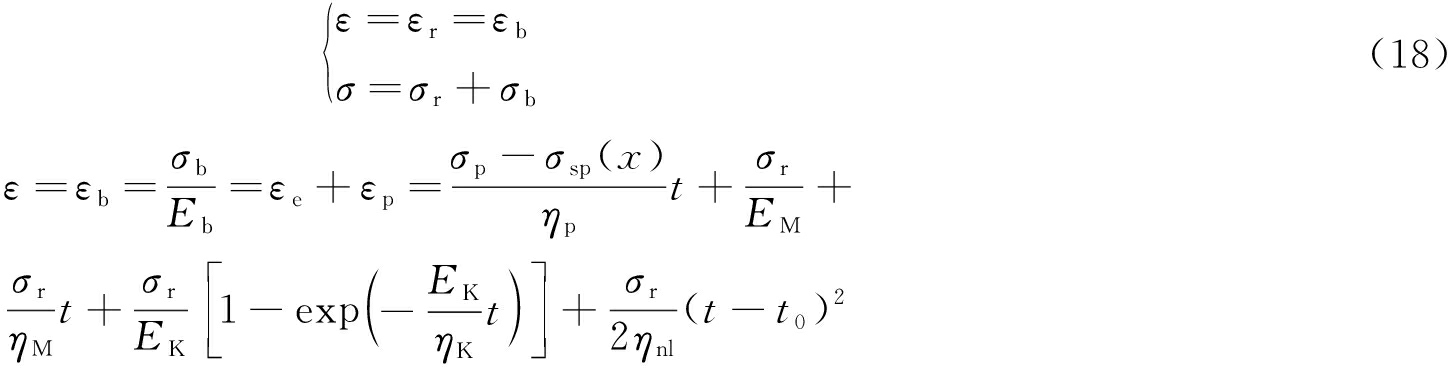
(19)
根据式(17)～(19)可以求出锚固体的蠕变方程为
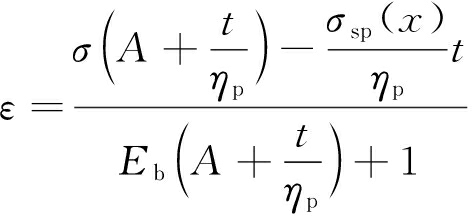
(20)
式中，
由锚固体的耦合关系可知，当锚固基础位于弹性区时，能够增强支护系统的承载能力，分担弹性区围岩承担的围岩载荷。若锚固基础为刚体材料不发生塑性软化，锚杆将与围岩发生同步变形，两者应变相等，随围岩蠕变发展锚杆受力逐渐增大，围岩承担的载荷相对变小，降低了弹性区围岩发生塑性屈服的速率。从式(20)可以得出因锚杆支护围岩应变量降低，从而延缓了围岩发生加速蠕变的时间，遏制了塑性区的扩张速率。因此，锚杆支护对围岩蠕变的控制机理概括为两个方面:一是锚杆支护分担了围岩承受的载荷;二是锚杆支护等效于增大了围岩的刚度，约束了围岩变形。
若锚杆锚头恰位于弹性区、塑性区交界面处，则锚固基础完全位于塑性区内，锚固体本构模型如图11所示，此时，锚固基础完全位于塑性区。
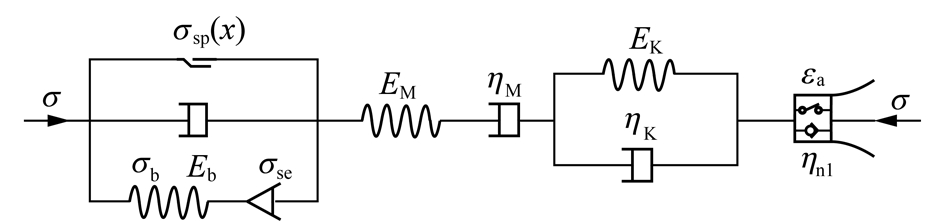
图11 塑性区锚杆支护系统流变本构模型
Fig.11 Rheological constitutive model of bolt support system in plastic zone
支护系统本构模型两端在应力σ的作用下，弹性区的应变计算公式为
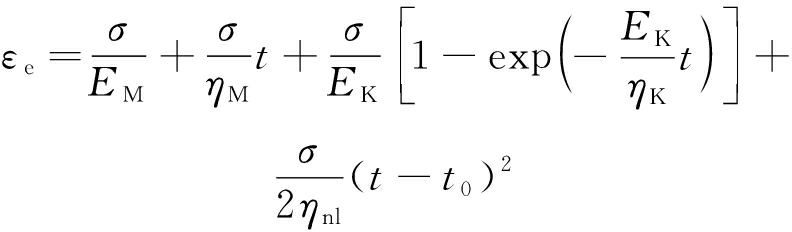
(21)
塑性区围岩与锚杆并联组成新的锚固体，锚杆与围岩的耦合关系式如下：
(22)
根据式(14)，(17)，(22)得出锚固体蠕变方程为
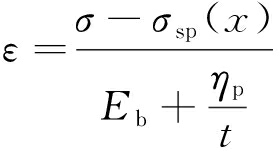
(23)
将锚杆锚固在塑性区内时，由式(23)知锚杆能够降低塑性区岩体的应变，而对弹性区围岩应变没有影响。锚杆的最大锚固力与锚杆的抗拔力、丝扣的抗挤压力、托板承压力、端头的锚固能力有关，取其最小值[23]。前3者与锚杆杆体及其配套构件的性能有关，端头锚固能力不仅与锚杆表面形状、钻孔表面形状、灌浆材料强度特性有关，还与围岩的强度特性有关，且灌浆材料与围岩的黏结面往往是整个锚固系统的薄弱环节。锚杆、钻孔表面形状，灌浆材料强度可以人为控制，而围岩强度特性为不可控因素，只能选择锚固基础位置。
2.4 锚固基础合理布置位置
随塑性区向外扩展，位于塑性区的基础锚固力急剧降低，引起锚固有效长度减小，如图12所示。塑性区围岩残余极限强度明显小于弹性区围岩极限强度，即σsp(x)<σse，因此，若锚固基础位于塑性区，虽能一定程度降低塑性区围岩的应变，但锚固基础锚固力大大降低，对围岩的锚固效果较差，锚杆与围岩容易发生滑脱现象，无法充分发挥锚杆的支护性能，造成一种支护强度不够的假象，易导致巷道过度支护的发生，引起支护的浪费。
图12 锚固基础与塑性区相对位置示意
Fig.12 Sketch map of relative position between anchorage foundation and plastic zone
围岩-锚杆耦合作用过程中，锚杆变形受控于围岩，锚杆受力达到锚固基础屈服极限σse后，即σb≥σse时，锚固基础将出现渐近破坏现象，逐渐由弹性阶段进入塑性软化直至残余锚固阶段，黏锚力峰值逐渐向锚头位置移动，锚固基础的有效锚固长度逐渐减小，如图13所示。锚固基础由内侧到外侧依次承载，锚杆锚固力由黏锚力曲线积分得到，随锚杆受力发展，t1 ～t4时刻部分锚固基础不受力，t5时刻全部受载，并且锚固力下降，最终出现锚杆与围岩之间滑脱现象，锚杆对围岩的支护作用消失。
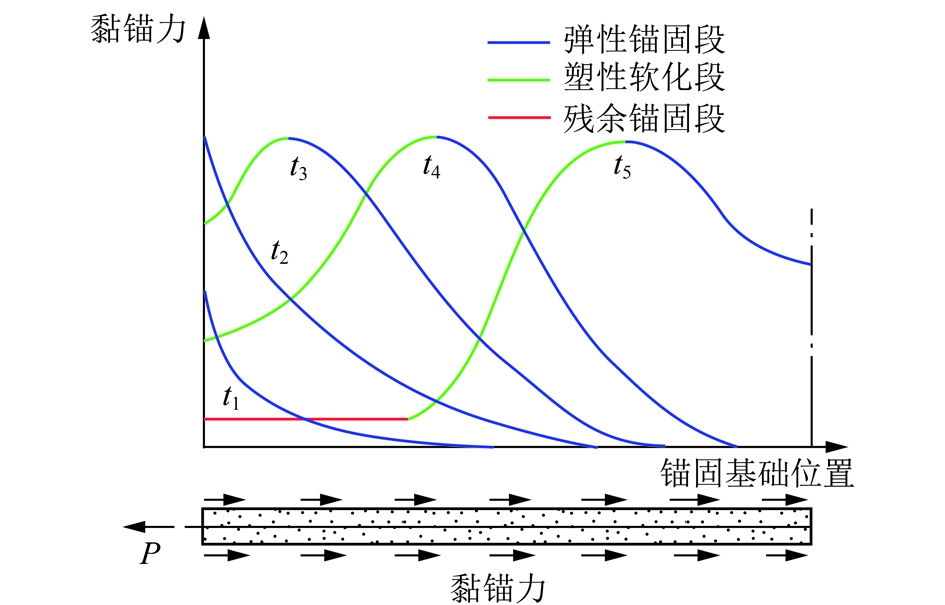
图13 σb≥σse时锚杆黏锚力发展变化示意
Fig.13 Sketch map of change and development of bolt viscous force when σb≥σse
归纳起来，锚固基础失效原因有两种:一是塑性区与锚固基础位置重叠，二是锚固基础受载过高引起自身失效。一般情况下，为充分发挥锚杆的材料性能，锚固基础设计锚固力大于锚杆破断载荷，即锚杆杆体破断先于锚固基础失效发生。当锚固基础位于塑性区时，锚固基础失效就有可能先于锚杆破断发生。因此，锚固基础应位于塑性区之外较稳定的弹性区域。
2.5 锚固时空效应分析
锚固基础长度达到一定值时，继续增加暂不承载的锚固基础长度没有什么意义，锚固力的增加很有限。而全长锚固的锚固基础涵盖了塑性区、弹性区围岩，位于塑性区的锚固基础锚固力较小，塑性区的锚固基础逐渐失效，引起着力基础逐渐转移至位于弹性区的锚固基础处。因此，锚固基础并非越长越好，锚固基础需要一个强度较高的着力基础，并且能够快速发生支护作用，采用将锚固基础布置于弹性区的端锚锚固形式可以快速的起到有效支护作用，同时，锚杆留设一定长度的自由段，有助于锚杆预应力在围岩中扩散，使得有效压应力区面积显著增大，有利于锚杆预应力锚固作用的发挥[24-25]，优于全长锚固形式。
锚固基础处于稳定工作状态，锚杆破断载荷为σsb，随围岩蠕变发展锚杆应变量不断增加，锚杆受载近线性增加，当受载达到锚杆破断载荷后，将引起锚杆发生破断失效。对于高应力软岩巷道尤其如此，防止锚杆发生过载而破断失效是高应力软岩巷道重点解决的问题，需要设置锚杆过载保护来解决锚杆因过载而破断的问题。
综上，将锚固基础布置于弹性区能较好发挥锚杆的支护性能，但随围岩蠕变及塑性区向外扩张，将会引起锚固基础滑脱失效或锚杆破断失效，导致锚杆支护时效变短，不利于巷道围岩稳定控制的同时增加了巷道翻修次数。随掘进工作面向前推进，围岩因巷道空间效应具有一定自稳能力，其变形并不会全部释放，应力重分布也不会迅速完成，应选择合适的时机采用合理的锚杆支护形式将其支护住。而充分发挥锚杆支护性能、延长锚杆支护时效、维持巷道处于稳定工作状态所需的空间需要同时满足两个条件:锚杆受载不超过杆体破断载荷，锚固基础位于塑性区之外。
3 工程实例验证
3.1 工程背景
蒲河煤矿西三采区集中运输大巷为半圆拱形巷道，埋深436 m,布置在可采煤层底板之下，顶板泥质胶结、致密，层理明显。底板赋存有油母页岩等软岩，具有较强的持续变形性和膨胀性，大巷所处位置存在破碎带，巷道开掘后位移量较大，局部存在锚索破断、锚杆拔出等支护失效情况。原支护方案采用锚网索梁喷联合支护形式，锚杆采用φ22 mm×2 200 mm螺纹钢;锚索采用φ17.8 mm×7 000 mm，配用36U钢加工的吊梁，长度为1.6 m;锚固剂选用树脂锚固剂，规格φ23 mm×500 mm;金属网为10号铁丝网，规格为10 m×1.0 m，网孔50 mm×50 mm,喷射混凝土厚度为100 mm,钢筋梯选择圆钢焊接制成，圆钢直径为10 mm，钢筋梯宽为80 mm，支护断面及锚杆锚索间排距如图14所示。
3.2 围岩松动圈及位移实测
通过采用PHD-2型多功能超声波检测仪测试该大巷的松动圈范围，分别在该大巷的3个不同断面的左右帮各设置一个测点进行观测，测点布置以及收集数据如图15所示。
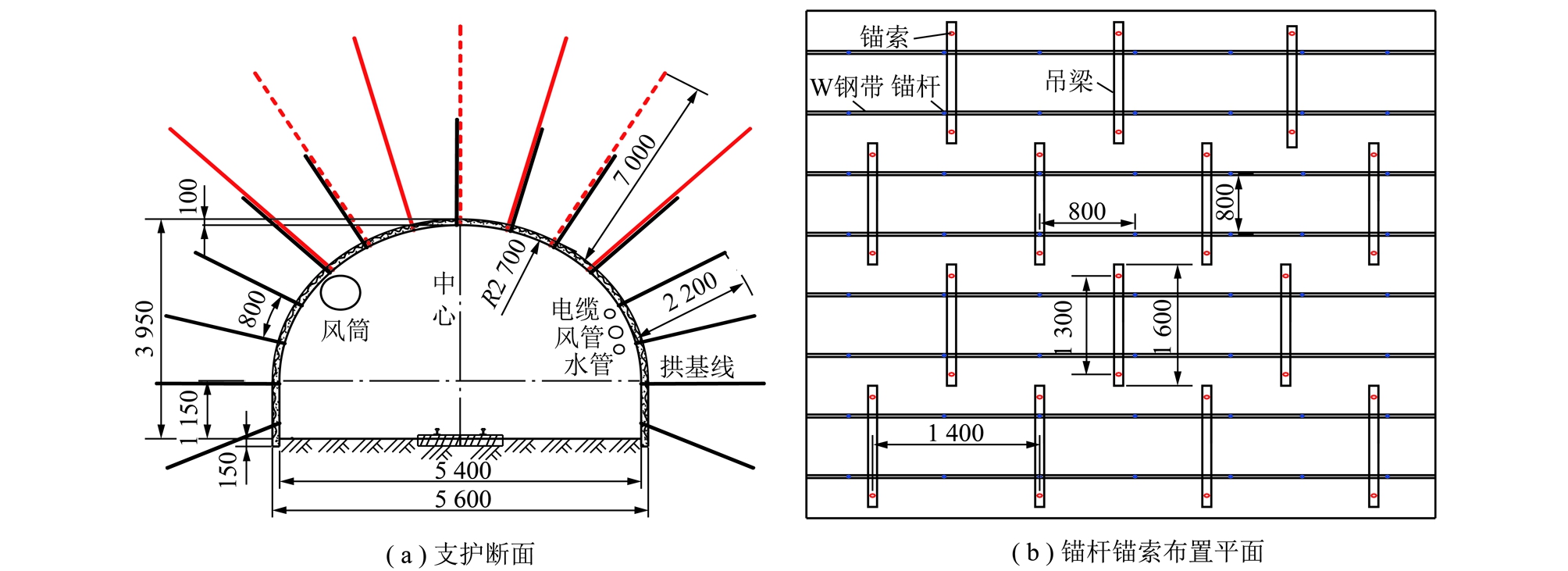
图14 巷道原支护方案
Fig.14 Original support scheme of the roadway
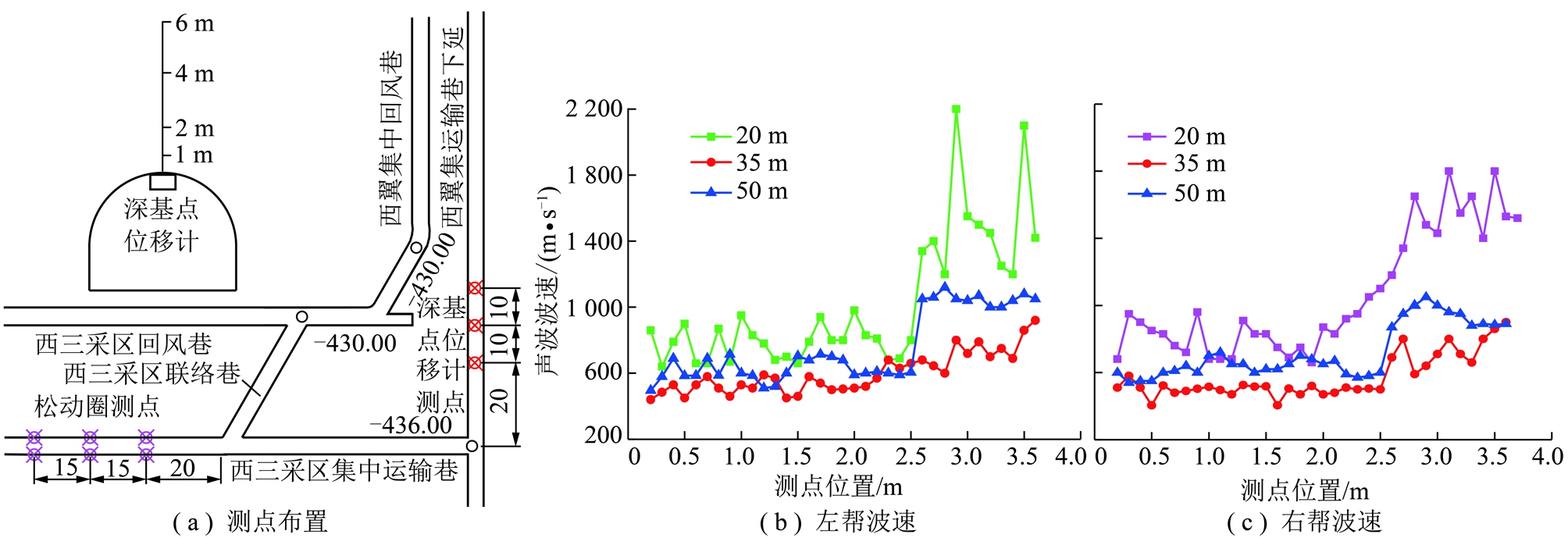
图15 测点布置及收集数据
Fig.15 Layout of measuring points and wave velocity diagrams
通过分析波速图得出，西三采区集中运输大巷松动圈范围大致位于2.3～2.7 m，巷道围岩松动圈与弹塑性理论中的围岩塑性区，均指的是巷道开挖引起围岩应力重新分布后应力超过围岩极限强度的区域，因此，测得的松动圈范围可以认为是围岩塑性区范围，为2.3～2.7 m。而锚杆采用的是长度2.2 m的锚杆，使得锚固基础恰位于塑性区内部，无法提供较高锚固力，从而出现锚杆拔出失效现象。
采用四基点数显深基点位移计，通过在顶板选取3个不同位置观测围岩在不同深度不同时间发生的相对位移量，每个测站测量孔位于顶板中，测点布置图及深基点位移计安设位置如图15(a)所示，监测数据如图16所示。
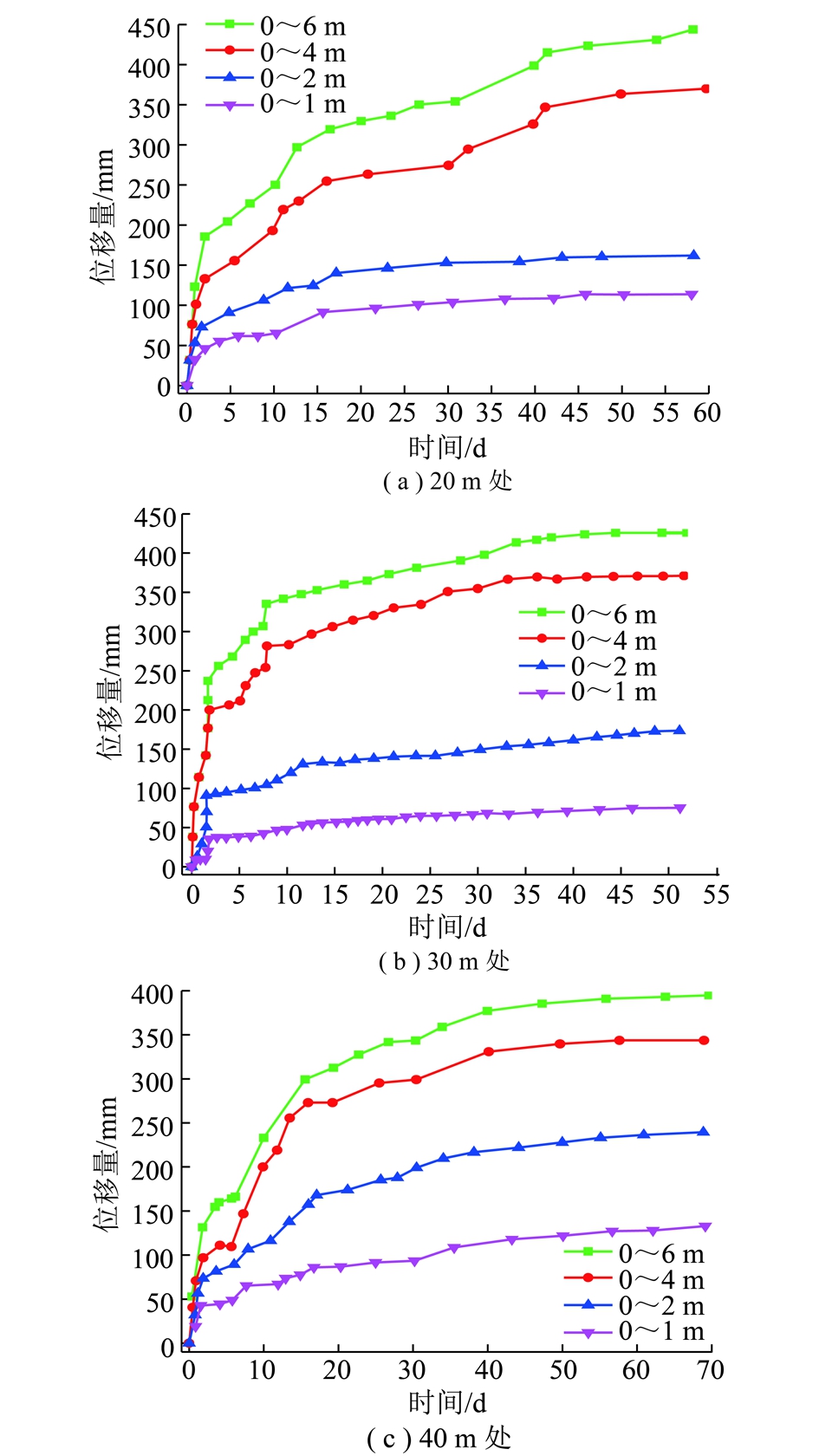
图16 不同深度处深基点位移
Fig.16 Displacement of deep base points of different depth
通过对3个位置的深基点位移监测图可以看出，顶板的位移量约为400 mm，监测范围内的岩层没有发生同步下沉，明显发生了离层现象，2～4 m岩层离层量最大。而锚索延伸率最大为3%，现场应用中锚索的延伸率仅为2%，该巷道所用锚索最大延伸量约为140 mm,顶板位移量已经远超过锚索的最大延伸量，会有大量锚索发生破断失效。
3.3 基于时空效应改进支护方案
马念杰等研制的基于高阻让压的可接长锚杆可以满足以上两个条件[26]，很好的解决深部高应力软岩巷道普通锚杆锚固深度小、锚索延伸率低的问题。该锚杆具有较大延伸率，一般每段2或者2.5 m,能够根据塑性区深度设置锚杆的段数，将锚固基础置于稳定的弹性区内的同时允许围岩发生适量变形。同时，该锚杆具有的高阻让压性能使得锚杆受载达到自设的应力阈值后，能够进行极限强度零损伤延伸，保护杆体及锚固基础免遭塑性屈服破坏，避免了杆体过早破断失效或锚固基础有效锚固长度渐进减小。根据前文测试结果采用可接长锚杆对西三采区集中运输大巷重新设计了支护方案，两帮及拱肩采用由3 000 mm与700 mm长锚杆对接成的长度为3 700 mm的超长锚杆进行支护，规格为φ22 mm×3 700 mm，间排距为800 mm×800 mm,拱顶采用由两段2 500 mm的可接长锚杆组成的超长锚杆进行支护，规格为φ22 mm×5 000 mm，间排距为800 mm×800 mm，均采用采用端头锚固形式，每孔用3个树脂药卷，锚固长度均为1.5 m，支护参数如图17所示。
图17 长锚杆支护方案
Fig.17 Support scheme of long bolt
3.4 支护效果分析
围岩表面位移能够直观的体现支护方案的支护效果，因此通过在巷道表面布置围岩表面位移观测站来分析新支护方案的支护效果。在蒲河矿集中运输巷布置了观测站观测巷道表面位移，在长锚杆试验巷道选取其中3个测站数据进行分析，整理后的监测数据如图18所示。
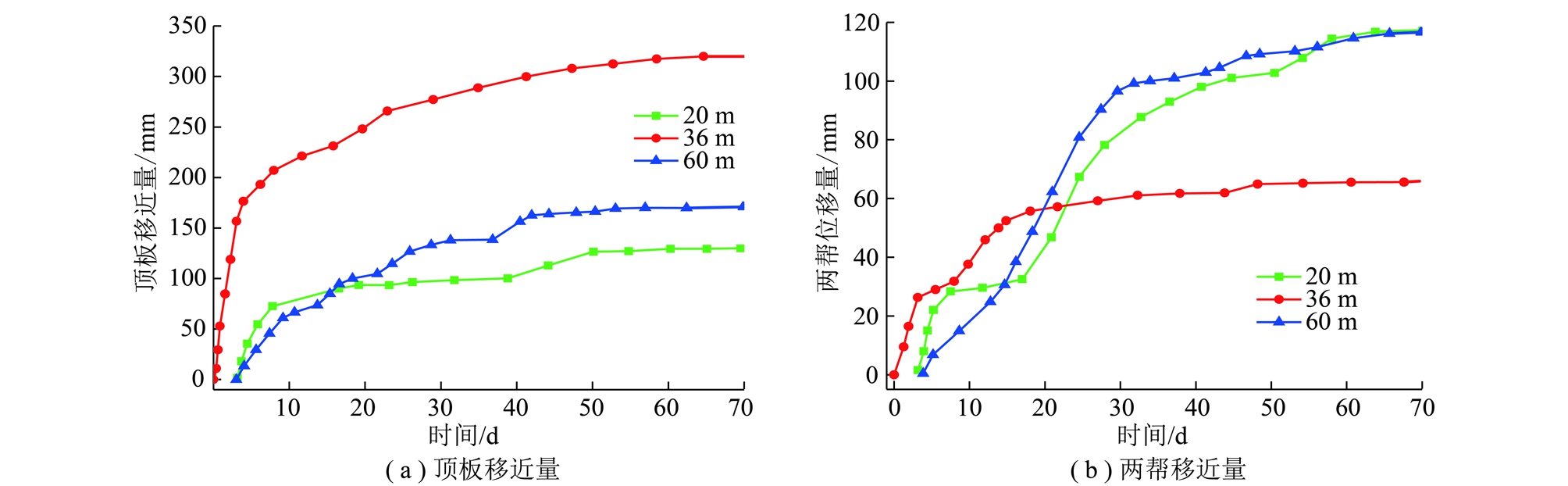
图18 顶板及两帮移近量
Fig.18 Convergence of roof and both sides
通过观测数据看出，巷道在开挖前期25 d左右时，围岩变形速度与变形量均较大，两帮移近量最大90 mm，顶板移近量最大175 mm,之后变形速度降低，监测至80 d时，两帮移近量最大约119 mm,顶板移近量为205 mm，小于可接长锚杆的最大延伸量，可接长锚杆没有发生破断失效、锚固失效现象，很好的控制了围岩变形，避免了重复翻修工作，降低了巷道维护费用，保障了巷道服务期间的正常使用。
4 结 论
(1)通过将带应变触发的非线性单向运动黏壶与Burger模型串联得到可以描述围岩黏弹塑性特征的改进Burger模型。基于应变相等原则将锚杆与改进Burger模型进行并联后，通过分析其蠕变方程得出，锚杆支护围岩后等效于增加了围岩的弹性模量，提高了围岩抵抗变形的能力，将围岩应变控制在εa内，围岩蠕变处于稳定工作状态，塑性区的扩展速率得到有效抑制。
(2)根据围岩变形特性通过变参数塑性元件与黏壶并联得到能够体现塑性区特性的本构模型，然后建立锚固体本构模型。通过分析端锚锚杆的锚固基础位置得出:锚固基础位于弹性区围岩中时能够最大程度发挥支护系统的承载能力，以及分担弹性区围岩承担的围岩载荷;端头锚固优于全长锚固。
(3)锚杆支护对围岩蠕变的控制机理可概括为两个方面:一是锚杆支护分担了围岩承受的一部分载荷;二是锚杆支护等效于增大了围岩的刚度，增强了围岩承担载荷的能力，约束了塑性区的扩张速率。
(4)充分发挥锚杆的支护性能延长锚杆支护的时效、维持巷道处于正常工作状态所需的空间需要满足两个条件:锚杆所受载荷不超过杆体破断载荷，锚固基础处于塑性区之外。蒲河矿西三采区集中运输大巷出现的锚杆滑脱失效、锚索出现破断失效的根本原因在于锚杆锚固基础位于发生破裂损伤的塑性区，以及锚索的延伸率较小。可接长锚杆可根据围岩塑性区的范围灵活选择锚杆长度以及拥有较大的延伸率，可以有效解决该大巷锚固失效的问题。
参考文献(references):
[1] KANG Hongpu.Support technologies for deep and complex roadways in underground coal mines:A review[J].International Journal of Coal Science & Technology,2014,1(3):261-277.
[2] 王清标，张聪，王辉，等.预应力锚索锚固力损失与岩土体蠕变耦合效应研究[J].岩土力学,2014,35(8):2150-2156,2162.
WANG Qingbiao,ZHANG Cong,WANG Hui,et al.Study of coupling effect between anchorage force loss of prestressed anchor cable and rock and soil creep[J].Rock and Soil Mechanics,2014,35(8):2150-2156,2162.
[3] 陈卫忠，谭贤君，吕森鹏，等.深部软岩大型三轴压缩流变试验及本构模型研究[J].岩石力学与工程学报,2009,28(9):1735-1744.
CHEN Weizhong，TAN Xianjun，LÜ Senpeng，et al.Research on large-scale triaxial compressive rheological test of soft rock in depth and its constitutive model[J].Chinese Journal of Rock Mechanics and Engineering，2009,28(9):1735-1744.
[4] 田洪铭，陈卫忠，田田，等.软岩蠕变损伤特性的试验与理论研究[J].岩石力学与工程学报,2012,31(3):610-617.
TIAN Hongming,CHEN Weizhong,TIAN Tian,et al.Experimental and theoretical studies of creep damage behaveior of soft rock[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(3):610-618.
[5] 蒋昱州,张明鸣,李良全.岩石非线性流变模型研究及其参数识别[J].岩石力学与工程学报,2008,27(4):832-839.
JIANG Yuzhou,ZHANG Mingming,LI Liangquan.Study of nonlinear viscoelasto-plastic creep model of rock and its parameter identification[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(4):832-839.
[6] 王来贵，何峰，刘向峰，等.岩石试件非线性蠕变模型及其稳定性分析[J].岩石力学与工程学报,2004,23(10):1640-1642.
WANG Laigui，HE Feng，LIU Xiangfeng，et al.Nonlinear creep model and stability analysis of rock[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(10):1640-1642.
[7] 徐卫亚，周家文，杨圣奇，等.绿片岩蠕变损伤本构关系研究[J].岩石力学与工程学报,2006,25(S1):3093-3097.
XU Weiya,ZHOU Jiawen,YANG Shengqi,et al.Study on creep damage constitutive relation of greenschist specimen[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(S1):3093-3097.
[8] 徐卫亚,杨圣奇,褚为江.岩石非线性黏弹塑性流变模型(河海模型)及其应用[J].岩石力学与工程学报,2006,25(3):433-447.
XU Weiya,YANG Shengqi,CHU Weijiang.Nonlinear visco-elastoplastic rheological model (Hohai model) of rock and its engineering application[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(3):433-447.
[9] 陶波，伍法权，郭改梅，等.西原模型对岩石流变特性的适应性及其参数确定[J].岩石力学与工程学报,2005,24(17):3165-3171.
TAO Bo，WU Faquan,GUO Gaimei,et al.Flexibility of visco-elastoplastic model to rheological char-acteristics of rock and solution of rheological parameter[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(17):3165-3171.
[10] 赵延林，曹平，文有道，等.岩石弹黏塑性流变试验和非线性流变模型研究[J].岩石力学与工程学报,2008,27(3):477-486.
ZHAO Yanlin,CAO Ping,WEN Youdao,et al.Elastovisco-plastic rheological experiment and nonlinear rheological model of rocks[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(3):477-486.
[11] 朱杰兵，汪斌，邬爱清.锦屏水电站绿砂岩三轴卸荷流变试验及非线性损伤蠕变本构模型研究[J].岩石力学与工程学报,2010,29(3):528-534.
ZHU Jiebing,WANG Bin,WU Aiqing.Study of unloading triaxial rheological tests and its nonlinear damage constitutive model of Jinping hydropower station green sandstone[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(3):528-534.
[12] 伍国军，陈卫忠，曹俊杰，等.工程岩体非线性蠕变损伤力学模型及其应用[J].岩石力学与工程学报.2010,29(6):1184-1191.
WU Guojun,CHEN Weizhong,CAO Junjie,et al.Nonlinear creep damage model of engineered rock and its application[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(6):1184-1191.
[13] 曹文贵，袁靖周，王江营，等.考虑加速蠕变的岩石蠕变过程损伤模拟方法[J].湖南大学学报(自然科学版),2013,40(2):15-20.
CAO Wengui,YUAN Jingzhou,WANG Jiangying,et al.A damage simulation technique of the full rock creep process considering accelerated creep[J].Journal of Hunan University(Natural Sciences),2013,40(2):15-20.
[14] 孙金山，陈明，姜清辉，等.锦屏大理岩蠕变损伤演化细观力学特征的数值模拟研究[J].岩土力学,2013,34(12):3601-3608.
SUN Jinshan,CHEN Ming,JIANG Qinghui,et al.Numerical simulation of mesomechanical characteristics of creep demage evolution for Jingping marble[J].Rock and Soil Mechanics.2013,34(12):3601-3608.
[15] 尹光志，何兵，王浩，等.深部采动影响下覆岩蠕变损伤破坏规律[J].煤炭学报,2015,50(6):1390-1395.
YIN Guangzhi,HE Bing,WANG Hao,et al.Damage law of overlying rock induced by mining[J].Journal of China Coal Society,2015,50(6):1390-1394.
[16] 赵同彬，姜耀东，张玉宝，等.黏弹塑性BK-MC锚固模型二次开发及工程应用[J].岩土力学,2014,35(3):881-886.
ZHAO Tongbin,JIANG Yaodong,ZHANG Yubao,et al.Secondary development and engineering application of viscoelasto-plastic BK-MC anchorage model[J].Rock and Soil Mechanics,2014,35(3):881-886.
[17] 付宏渊，蒋中明，李怀玉，等.锚固岩体力学特性试验研究[J].中南大学学报(自然科学版),2011,42(7):2095-2101.
FU Hongyuan,JIANG Zhongming,LI Huaiyu,et al.Mechanics properties of anchored rock[J].Journal of Central South University (Science and Technology),2011,42(7):2095-2101.
[18] 勾攀峰，辛亚军.深井巷道围岩锚固体流变控制力学解析[J].煤炭学报.2013,38(12):2119-2125.
GOU Panfeng,XIN Yajun.Rheological control mechanical analyticity of surrounding rock anchorage body in deep road-way[J].Journal of China Coal Society,2013,38(12):2019-2025.
[19] 齐亚静，姜清辉，王志俭，等.改进西原模型的三维蠕变本构方程及其参数辨识[J].岩石力学与工程学报,2012,31(2):347-355.
QI Yajing,JIANG Qinghui,WANG Zhijian,et al.3D creep constitutive equation of modified Nishihara model and its parameters identification[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(2):347-355.
[20] 刘洪涛，王飞，张胜凯，等.巷帮-支护体本构模型及长螺纹扩帮锚杆研究[J].煤炭学报,2015,40(6):1368-1375.
LIU Hongtao,WANG Fei,ZHANG Shengkai,et al.Research on long-thread lengthened bolt and constitutive model of laneway’s side with support body[J].Journal of China Coal Society,2015,40(6):1368-1375.
[21] 王洪涛，王琦，王富奇，等.不同锚固长度下巷道锚杆力学效应分析及应用[J].煤炭学报,2015,40(3):509-515.
WANG Hongtao,WANG Qi,WANG Fuqi,et al.Mechanical effect analysis of bolts in roadway under different anchoring lengths and its application[J].Journal of China Coal Society,2015,40(3):509-515.
[22] 尤春安，战玉宝.预应力锚索锚固段界面滑移的细观力学分析[J].岩石力学与工程学报,2009,28(10):1976-1985.
YOU Chun’an,ZHAN Yubao.Analysis of interfacial slip mesomechanics in anchorage section of prestressed anchor cable[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(10):1976-1985.
[23] 汤雷，蒋金平.锚杆支护强度[J].地下空间,1997,17(2):65-69.
TANG Lei,JIANG Jinping.Anchoring strength of bolts[J].Underground Space,1997,17(2):65-69.
[24] 王卫军，袁超，余伟健，等.深部大变形巷道围岩稳定性控制方法研究[J].煤炭学报,2016,41(12):2921-2931.
WANG Weijun,YUAN Chao,YU Weijian,et al.Stability control method of surrounding rock in deep roadway with large deformation[J].Journal of China Coal Society,2016,41(12):2921-2931.
[25] 郑西贵，张农，薛飞.预应力锚杆锚固段应力分布规律及分析[J].采矿与安全工程学报,2012,29(3):365-370.
ZHENG Xigui,ZHANG Nong,XUE Fei.Study on stress distribution law in anchoring section of prestressed bolt[J].Journal of Mining & Safety Engineering,2012,29(3):365-370.
[26] 马念杰,赵志强,冯吉成.困难条件下巷道对接长锚杆支护技术[J].煤炭科学技术,2013,41(9):117-121.
MA Nianjie,ZHAO Zhiqiang,FENG Jicheng.Technology of butt long bolt or roadway supporting in difficult conditions[J].Coal Science and Technology,2013,41(9):117-121.
08