深部煤岩体开挖时承载着动力扰动与静载联合作用，动力扰动的主要来源有开采活动、煤岩体对开采活动的动态响应等，具体表现为采煤机割煤、移架、机械震动、爆破、顶底板破断、煤体失稳、瓦斯突出、煤炮、断层滑移等，可统称为矿震[1]。蔡峰等[2]、常未斌等[3]研究证明：矿震产生的动力扰动会以应力波的形式向煤岩体深部传播。
一方面，褚怀保等[4]、HE J等[5]、陈蓥等[6]试验结果表明：动力扰动产生的应力波主要由频次高、相速度快、波数多的各类型高阶纵波组成，传播过程中常常呈现出压应力与拉应力交替出现的现象，能引起煤岩体的强烈振动、损伤甚至破坏;另一方面，许江等[7]的试验结果表明：煤岩体内部裂纹萌生、扩展以及承载结构面的破坏过程均会产生较高幅值声发射(AE)信号，实际上每产生1次AE信号就会产生1次瞬态卸载纵波在煤岩体中传播，也表明煤岩体发生损伤或破坏时会伴随着大量高阶纵波的产生。
同时，在传播过程中由于煤岩体的吸收和弥散效应，高阶纵波会转变成频次低、相速度慢、波数少的低阶纵波。由此可知，煤岩体开挖时高、低阶纵波的传播与作用对煤岩体动态损伤具有重要作用。
现阶段对于动力扰动下煤岩体的动态力学特性与作用机理的研究还处于探索阶段，煤岩体的动态损伤机理、破坏模式及其致灾机制尚不明晰。从应力波的角度切入，基于高、低纵波的传播特征，建立纵波模式下的煤岩体位移、应变、应力、振速与能量动态计算模型，并以此分析煤岩体的动态响应特性与损伤机理，对煤岩动力灾害防治具有借鉴意义。
1 纵波模式下的煤岩体动态力学计算模型的建立
以圆柱煤岩体为研究对象，选用柱坐标r,z,θ分析高、低阶纵波的动态扰动作用。由于纵波是以存在径向和轴向位移分量的轴对称波，且与θ无关[8]。以z与r分别表示沿圆柱煤岩体的轴向与径向方向，为了使分析结果具有代表性，做以下说明：① 圆柱煤岩体是均质的、不考虑裂隙、节理或层理对纵波传播的影响;② 不施加边界条件，即：无围压与轴压;③ 仅在圆柱体的其中一个底面(作用面)施加纵波的扰动作用，即：沿z轴方向有纵波的传播，同时引起径向(r)振动，同样也是纵波的传播;④ 主要研究径向方向的纵波传播与作用，圆柱煤岩体的底面半径为R、相速度为c、纵波波速CL、横波波速CT、波数为k、频率为w。则波动控制方程[8]可表示为
(1)
式中,
为位移;t为时间;λ,μ为拉梅系数;ρ为密度。
令u=v(r,z)T(t)，代入式(1)可得
T″+a2Tw0=0
(2)
2v+w0v=0
(3)
式中，v(r,z)为振速;T(t)为时间;w0为常数。
则式(2)解得
(4)
由式(3)可得
(5)
令v(r,z)=R(r)Z(z)，代入式(5)可得
(6)
式中，k0为常数。
令
代入式(6)变形可得
(7)
因此，由式(6)可得
(8)
则
式(7)为零阶贝塞尔方程，由于R有界(R(0)<+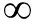
)，因此式(7)的一个特解为
(9)
式中，A0为系数。
因此，式(1)的特解可写成
(10)
式中，A为系数。
为得到控制方程的通解，根据斯托克斯-亥姆霍兹分解定理可得：位移矢量场u可分解为无旋场和无散场2个部分。位移矢量u可由标量势函数φ与矢量势函数ψ写成：
u=φ+×ψ
由于纵波是以轴向、径向的位移分量为特征的轴对称波，结合波动方程特解的形式可知，圆柱形的煤岩体中沿z,r方向传播的高阶纵波的φ与ψ可由以下的函数关系式来表示：
φ=AJ0(pr)ei(kz-wt),ψ=CJ1(qr)ei(kz-wt)
式中，
为系数;CL为纵波波速;CT为横波波速;k为波数;w为频率。
则径向位移ur与轴向位移uz可表示为
(11)
同时，一类0阶与1阶Bessel函数具有以下性质：
则联立式(11)可知径向、轴向位移为
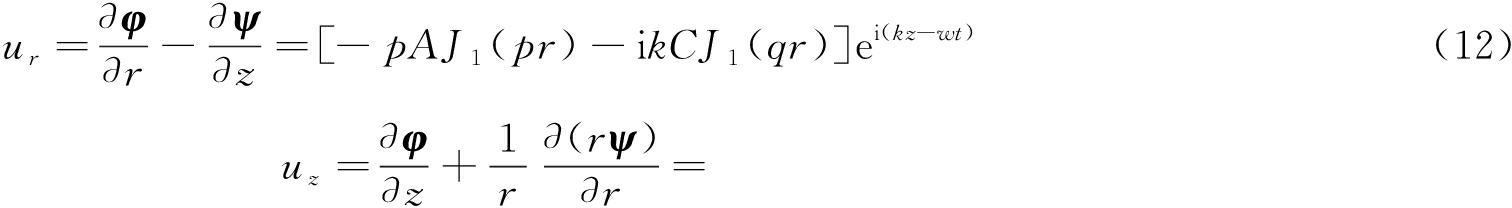
[ikAJ0(pr)+qCJ0(qr)]ei(kz-wt)
(13)
径向、轴向与剪切应变为(省略表达式的指数部分)：
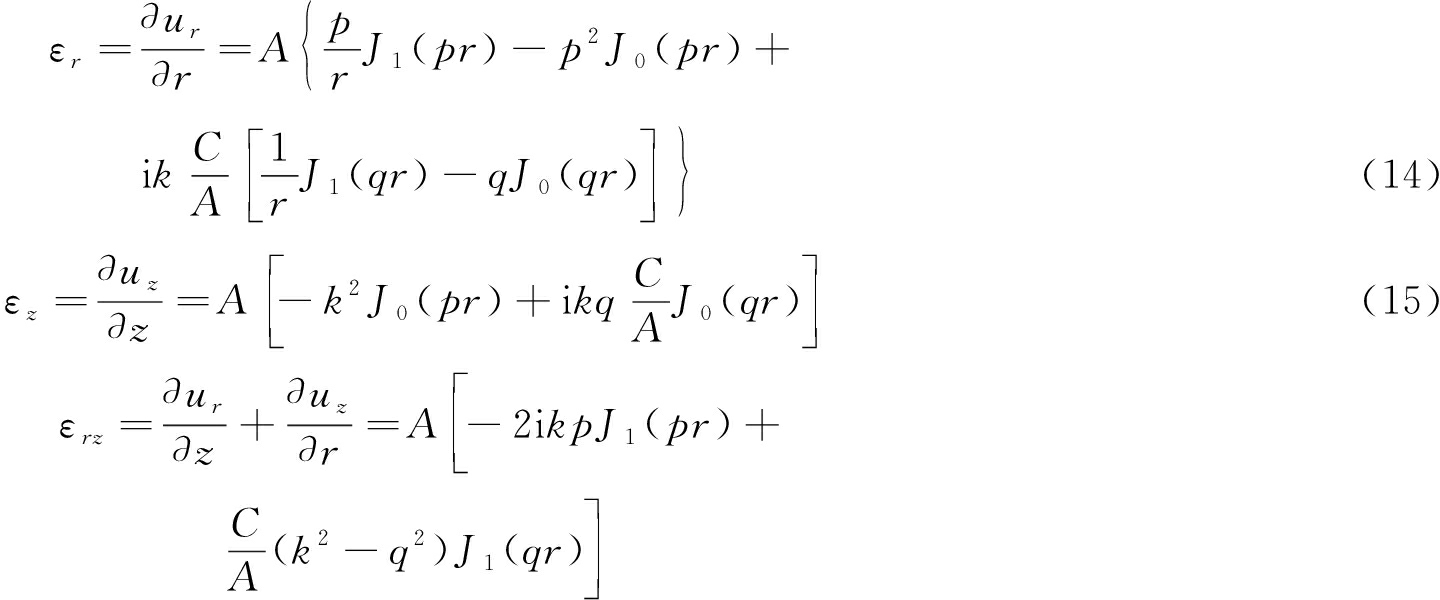
(16)
径向应力、轴向应力与剪切应力为
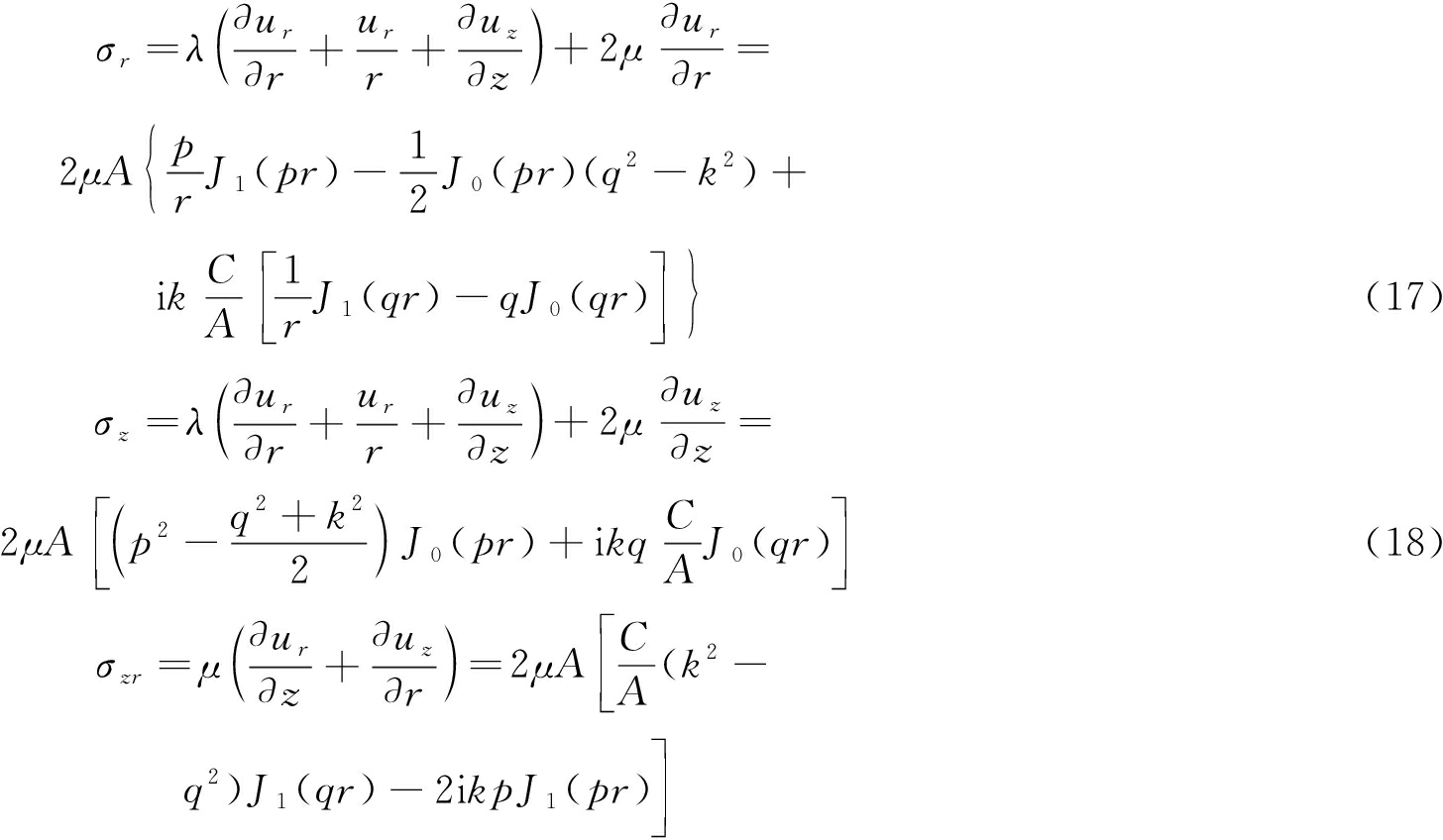
(19)
径向、轴向的振动速度：
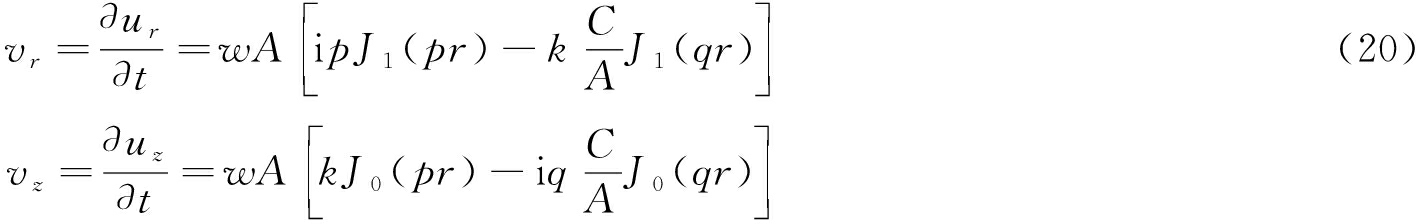
(21)
2 动态力学计算模型的频率方程
2.1 纵波模式下的计算模型的频率方程
为获得上述动态力学计算模型的数值解，首先需要建立频率方程以得到高、低阶纵波传播过程中的相速度、波数、频率等无量纲参数的分布规律。
由于在圆柱煤岩体表面上(r=R)不能承受径向应力与剪切应力，因此两者在表面上的数值大小必定为0，由式(17)和(19)联立可得：
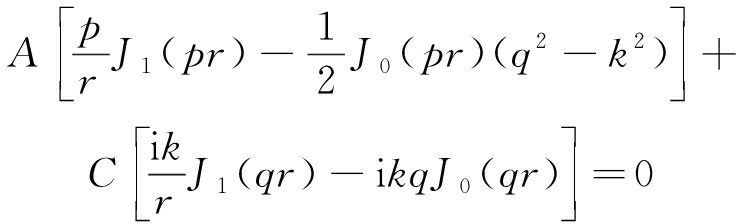
[-2ikpJ1(pr)]A+[(k2-q2)J1(qr)]C=0
若上述两个方程有解，则系数行列式必定为0，可得纵波传播的频率方程为
J0(pr)J1(qr)-4k2pqJ1(pr)J0(qr)=0
(22)
(23)
方程(22),(23)是轴向波数k和频率w的超越方程，对于每一个选定的实波数k，可以找到频率方程的无限个根，这些根代表纵波的频率。由此可绘出频率-波数曲线或频率-相速度曲线。
2.2 低阶纵波模式下频率方程的解
若考虑纵波的相速度c小于纵、横波波速的实根(低阶纵波)，即：c<CT< CL，用相速度和无因次波数u表示具有频率w和波数k的某种波动模式，取：c=w/k，u=kR。令
则低阶纵波作用的频率方程变为
(24)
式中，I0和I1分别为0阶和1阶第一类变形Bessel函数。
2.3 高阶纵波模式下频率方程的解
高阶纵波的相速度c处于纵、横波波速之间，即：CT<c<CL，用相速度和无因次波数u表示具有频率w和波数k的某种波动模式，取c=w/k，u=kR。令：
则高阶纵波作用的频率方程变为
假设，u无限小，化简频率方程[9]可得
(26)
式中，n=1,2,3，…;un为第n种模式时振动位移;
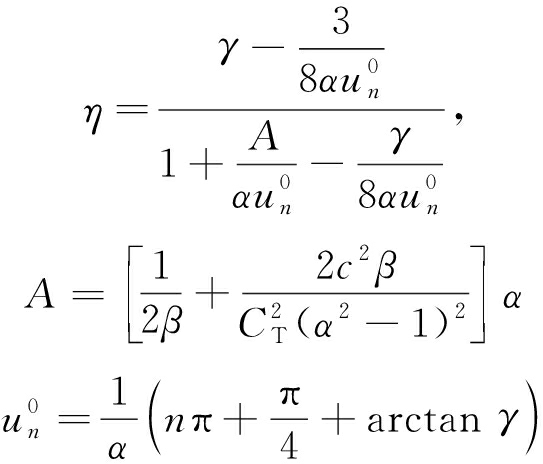
3 频率方程数值解的分布规律
3.1 低阶纵波模式下频率方程解的分布
若取纵波波速为2 500 m/s，泊松比为0.29。由式(24)仿真模拟可得低阶纵波作用中无量纲wR,kR与相速度c的关系如图1所示，可知：kR,wR与c关系曲线存在两条极限值分布曲线，相速度c主要集中在600～1 350 m/s;波数无量纲kR值相对较小，主要集中在12以内，频率无量纲wR值大都集中于1.4×104以内。通过大量的仿真计算表明：低阶纵波模式下，随着纵波波速与泊松比的取值变化所绘制的kR,wR与c关系曲线与图1的曲线分布类似。
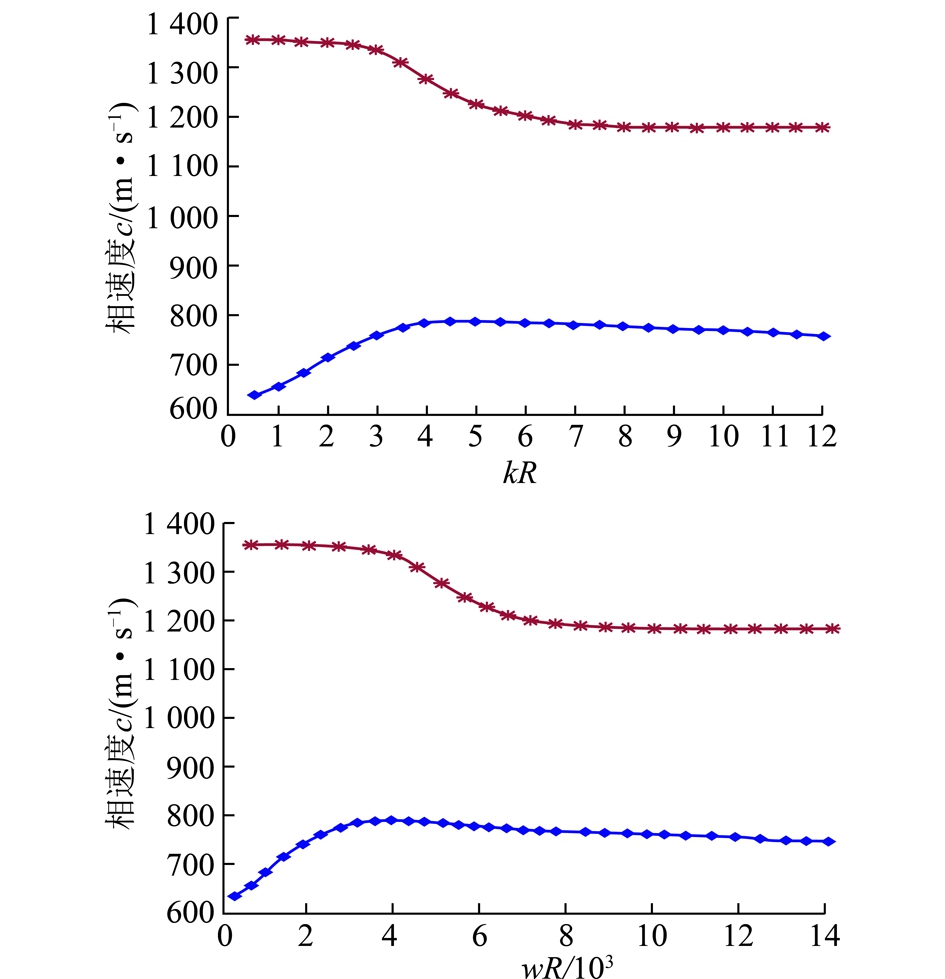
图1 低阶纵波波数、频率无量纲kR,wR与相速度c关系曲线
Fig.1 Relationship between the phase velocity and wR,kR of low order P-waves
3.2 高阶纵波模式下频率方程解的分布
若取煤岩体的纵波波速为2 500 m/s，泊松比为0.2，并取n=8，由式(26)仿真模拟可得，高阶纵波作用中无量纲wR,kR与相速度c的关系如图2所示。由图可知：高阶纵波相速度c与波数、频率无量纲kR,wR均大致呈幂函数递减关系;波数无量纲kR值主要在150以内，频率无量纲wR值大都分布在2×105以内。通过大量的仿真计算表明：高阶纵波模式下，随着纵波波速与泊松比的取值变化所绘制的kR,wR与c关系曲线与图2的曲线分布类似。
4 动态力学计算模型的数值解
4.1 低阶纵波模式下的煤岩体应力动态分布
由式(17),(19)与式(24)联立仿真可得低阶纵波作用过程中，圆柱煤岩体中径向、轴向与剪切应力振动幅值动态分布曲线，如图3所示。由此分析可得：随着波数、频率无量纲kR,wR增加，径向与剪切应力波振动趋势仍然保持相对较平缓，方向始终保持与初始状态一致，无法引起剧烈振动，可以视为准静态作用;剪切应力的振幅相对较大且极值主要分布在r/R>0.7，而径向应力的振幅相对较小且极值主要分布r/R>0.9的区域中。
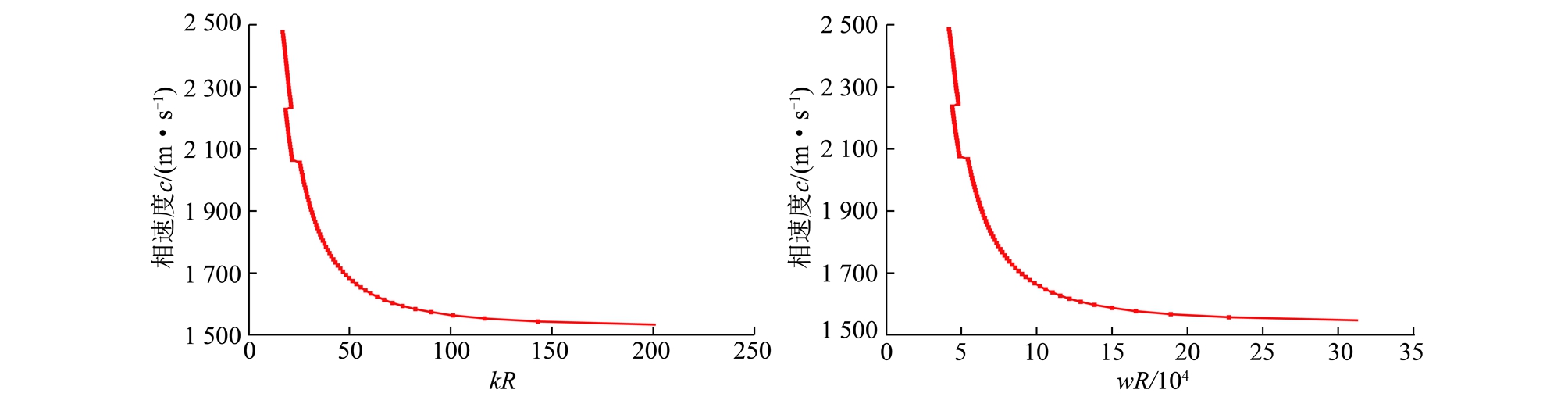
图2 高阶纵波的波数、频率无量纲kR,wR与相速度c关系曲线
Fig.2 Relationships between the phase velocity and kR or wR of high order P-waves
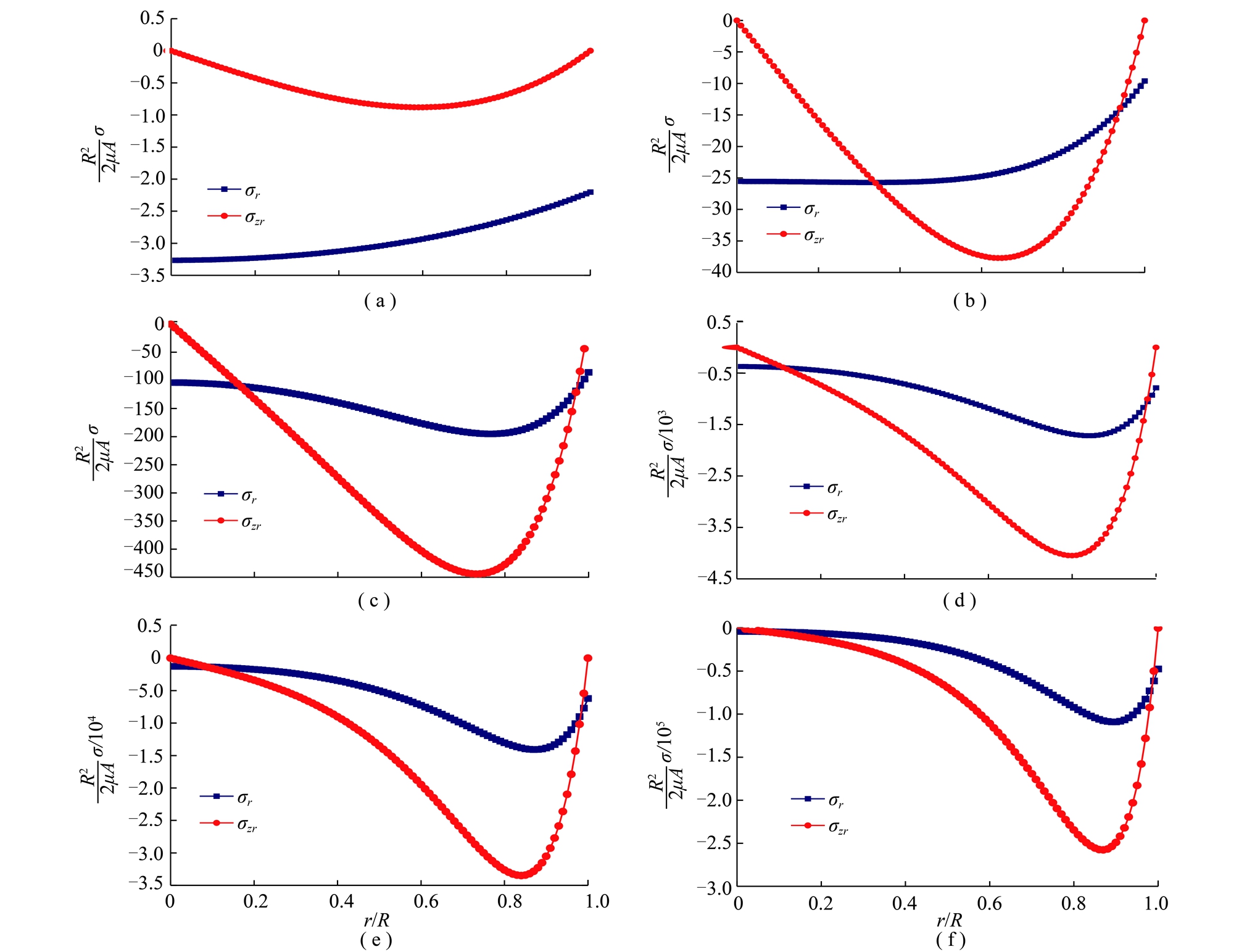
图3 低阶纵波模式下径向与剪切应力的动态分布曲线
Fig.3 Dynamic distribution curves of the radial and shear stresses under the action of low order P-waves
4.2 高阶纵波模式下的煤岩体位移动态分布
由式(12)，(13)与式(26)联立仿真可得高阶纵波作用下圆柱煤岩体截面中径向、轴向位移动振动幅值态分布曲线，如图4所示。由图4可知：沿圆柱煤岩体径向方向，径向、轴向位移大小随着半径无量纲(r/R)增大呈现衰减趋势，大致符合幂函数关系(指数为-0.52～-0.49)。
4.3 高阶纵波模式下的煤岩体应变动态分布
由式(14)，(15)，(16)与式(26)联立仿真可得高阶纵波作用下，圆柱煤岩体截面中径向、轴向与剪切应变振动幅值动态分布曲线，如图5所示。由图5可知：沿圆柱煤岩体径向方向，径向、轴向与剪切应变大小随着半径无量纲(r/R)增大呈现衰减趋势，大致符合幂函数关系;剪切应变最大，同时随着半径增大径向与轴向应变大小逐渐趋于一致，方向趋于相反。
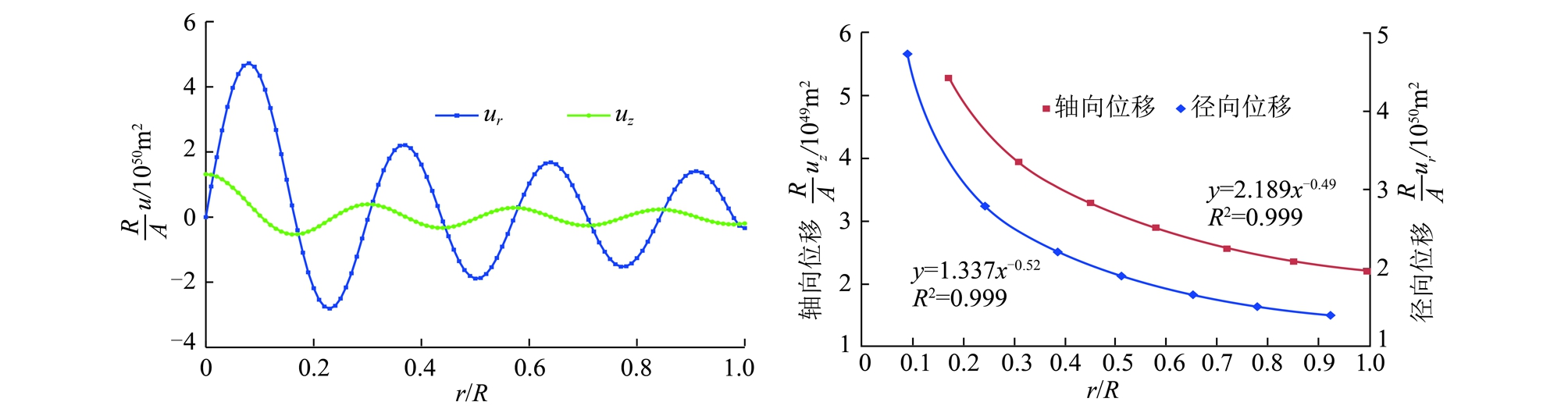
图4 高阶纵波模式下径向与轴向位移动态分布曲线
Fig.4 Dynamic distribution curves of the radial and axial displacement under high order P-waves
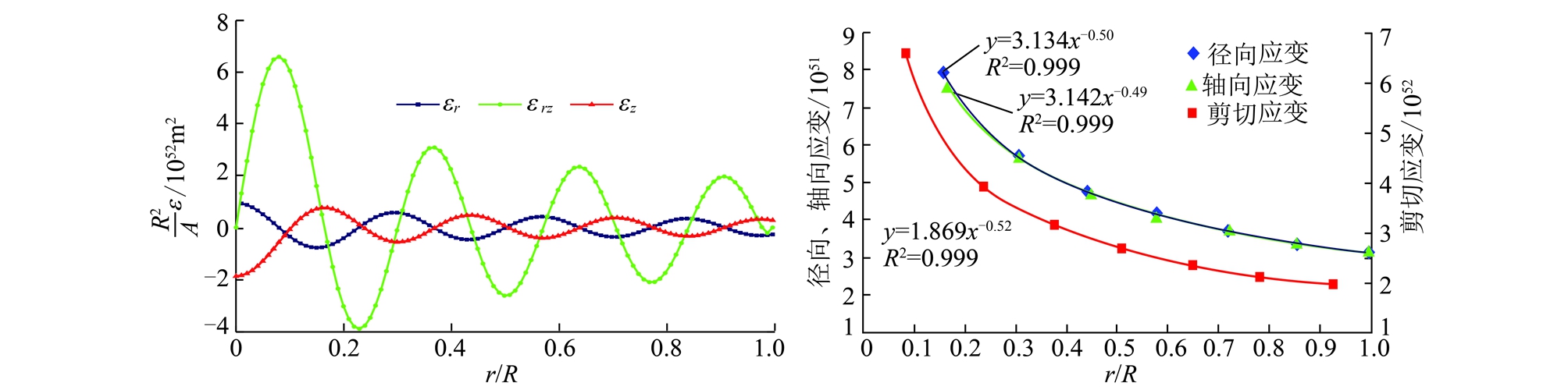
图5 高阶纵波模式下径向、轴向与剪切应变动态分布曲线
Fig.5 Dynamic distribution curves of the radial,axial and shear strain under high order P-waves
4.4 高阶纵波模式下的煤岩体应力动态分布
由式(17)～(19)与式(27)联立仿真可得高阶纵波作用下，圆柱煤岩体截面中径向、轴向与剪切应力振动幅值动态分布曲线，如图6所示。由图6可知：径向、轴向与剪切应力大小随着半径无量纲(r/R)增大呈现衰减趋势，大致符合幂函数关系;剪切应力最大，同时随着半径增大径向与轴向应力大小逐渐趋于一致，方向趋于相反。
4.5 高阶纵波模式下的煤岩体振速动态分布
由式(20),(21)与式(27)联立仿真可得高阶纵波作用下，圆柱煤岩体截面中径向、轴向振速振动幅值动态分布曲线，如图7所示。由图7可知：沿圆柱煤岩体径向方向，径向、轴向振速大小随着半径无量纲(r/R)增大呈现衰减趋势，大致符合幂函数关系。
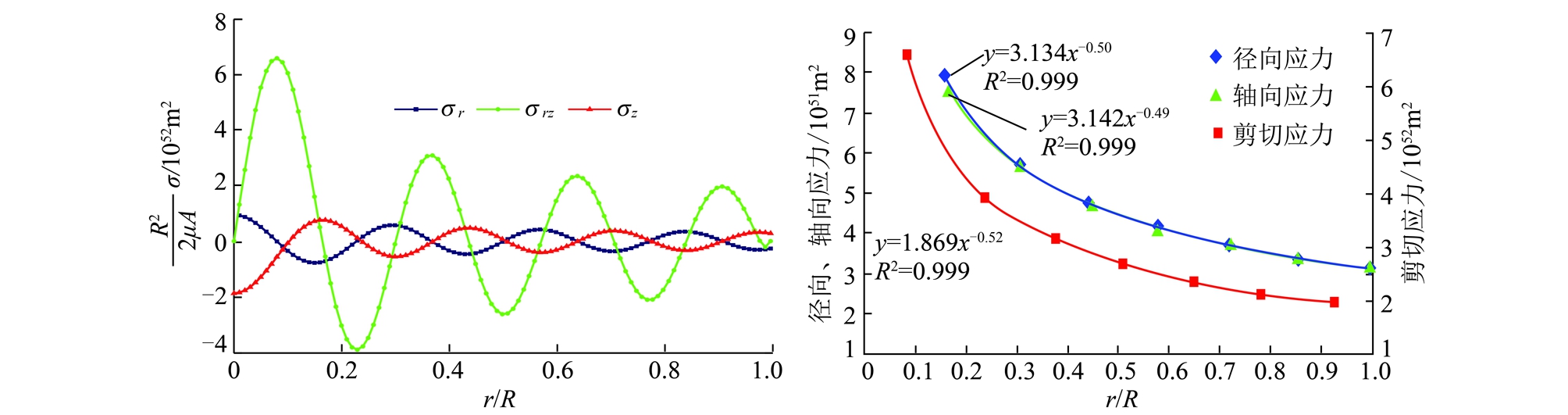
图6 高阶纵波模式下径向、轴向与剪切应力动态分布曲线
Fig.6 Dynamic distribution curves of the radial,axial and shear stress under high order P-waves
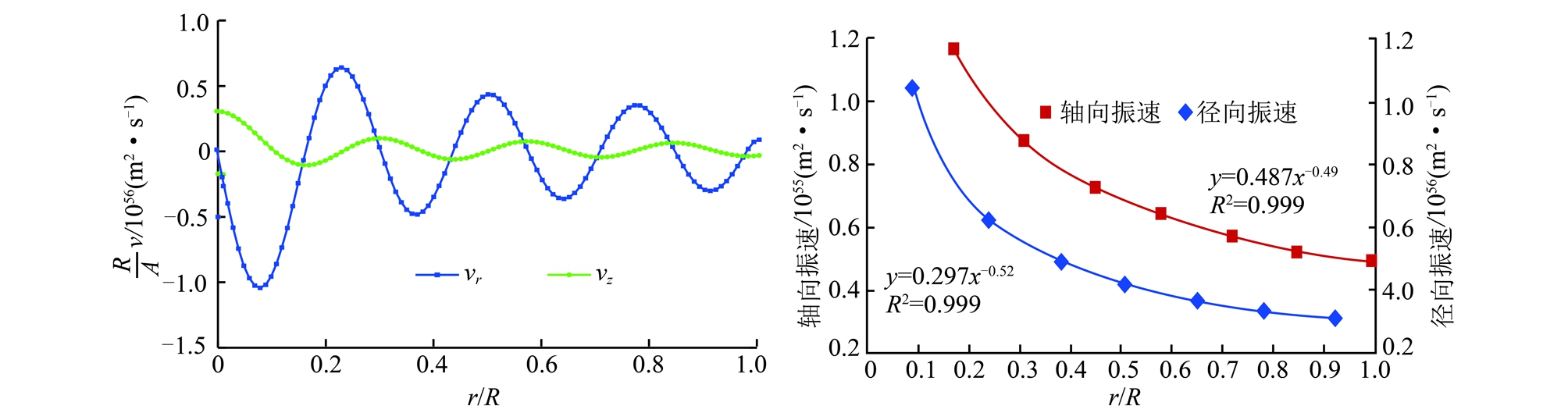
图7 高阶纵波模式下径向与轴向振速动态分布曲线
Fig.7 Dynamic distribution curves of the radial and axial vibration velocity under high order P-waves
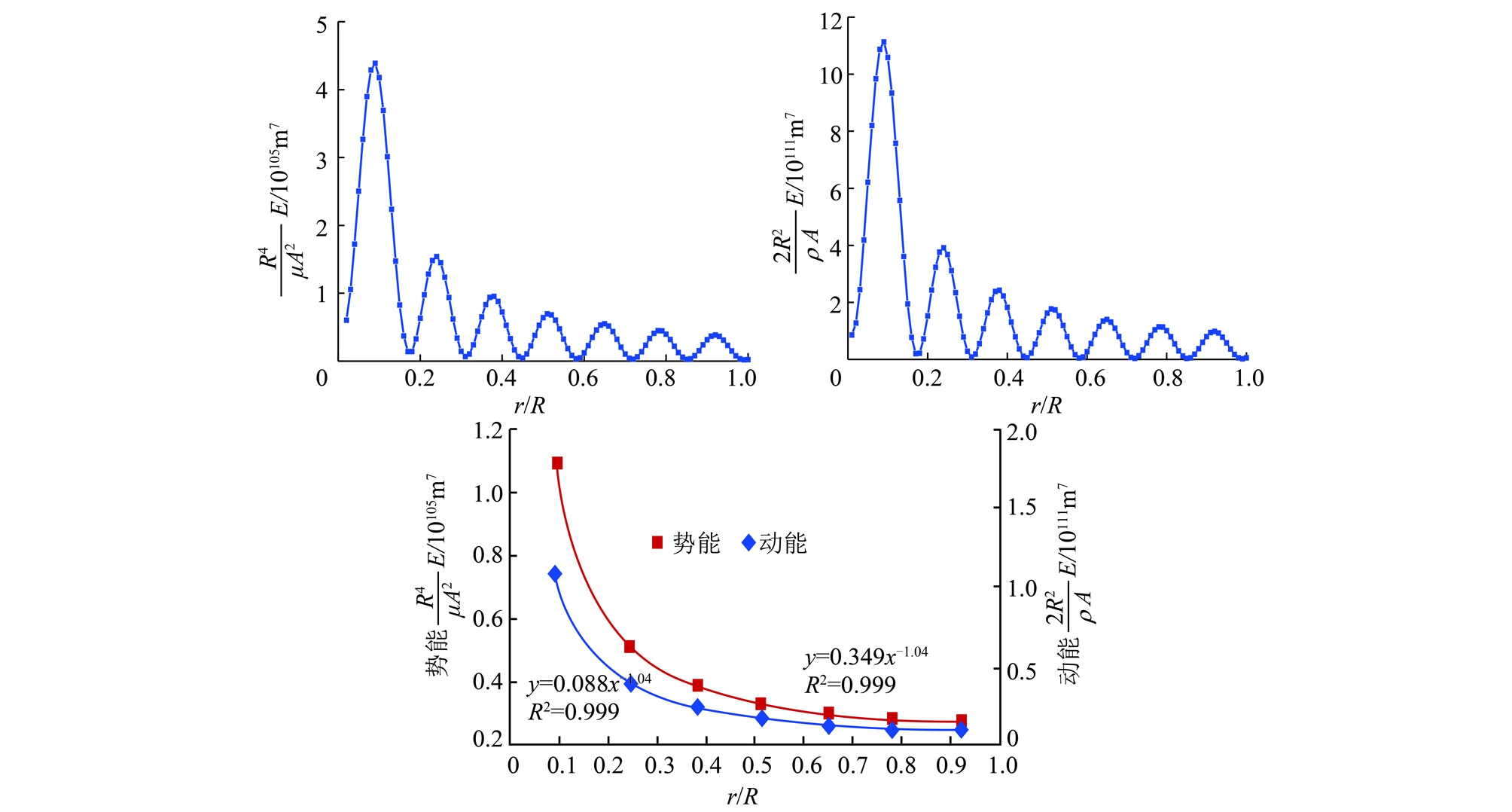
图8 高阶纵波模式下动能、势能幅值动态分布曲线
Fig.8 Dynamic distribution curves of the kinetic and potential energy amplitude
4.6 高阶纵波模式下的煤岩体能量动态分布
由式(13)～(26)联立仿真可得高阶纵波作用下，圆柱煤岩体截面中动能、势能动态振动幅值分布曲线，如图8所示。由图可知：沿圆柱煤岩体径向方向，动能、势能随着半径无量纲(r/R)增大呈现衰减趋势，大致符合幂函数关系(指数为-1.04)。
由图4～8可知：高阶纵波模式下，圆柱煤岩体中各方向位移μ、应变ε、应力σ、振速ν及能量振动幅值E动态分布随着均半径增大均呈现出衰减趋势，而且大致符合幂函数关系。
(u,ε,σ,v,E)=A·(r/R)m
其中，位移、应变、应力、振速动态分布的幂函数指数m=-0.52～-0.49，能量动态分布的幂函数指数m=-1.04。
分析结果表明：① 高阶纵波模式下，沿圆柱煤岩体径向方向，剪切应力、应变振幅的极值最大，能量的衰减速度最快;② 随着r/R增大，径向与轴向应力振幅大小逐渐趋于一致，方向趋于相反。也就是说，当轴向为压应力时，径向为大致同等大小的拉应力;③ 圆柱煤岩体底面圆心处的位移、应变、应力、振速以及能量振动幅值最大。
5 煤岩体动态损伤机理探讨
我国众多学者对煤岩体的常规单轴压缩的破坏特征进行过大量试验研究，唐辉明等[10]对大理岩在单轴压缩条件下的常规破坏特征分析结果如图9所示，试样尺寸φ50 mm×100 mm，轴向加载速率0.005 mm/s，研究结果证明：常规单轴压缩的煤岩体多为剪切破坏。
实际上，煤岩体试样整个实验过程中始终承受着轴向加载作用，而且以一定速率增加，因此，严格来说试样并不处于完全的静态作用而是准静态作用。其加载过程符合低阶纵波的作用模式，其剪切破坏的原因可解释为：① 低阶纵波模式下圆柱煤岩体中剪切应力的振幅相对较大，此时径向应力为压应力且振动幅值相对较小，因此试样主要承载剪切应力的作用;② 圆柱煤岩体底面(作用面)剪切应力振幅的极大值主要分布在临近表面区域(r/R>0.7)，因此试样的初始的破坏位置也应位于此区域，最终形成了图9所示的剪切破坏的形态。
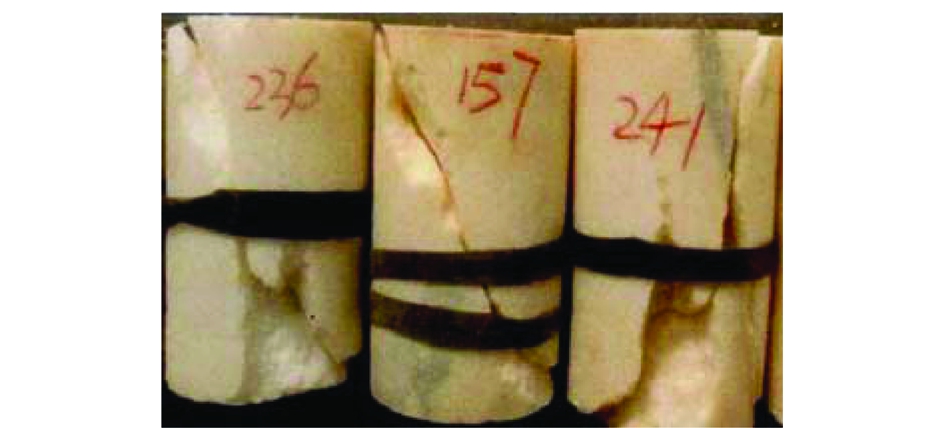
图9 大理岩的常规单轴压缩破坏
Fig.9 Failure of marble under conventional uniaxial compression
赵扬锋等[11]试验研究了大理岩在循环加载作用下单轴压缩的破坏模式如图10所示，加、卸载的速率为1 kN/s，试样尺寸φ75 mm×150 mm，大理岩岩样最终为脆性劈裂破坏，含有1条主要劈裂裂纹，在主要裂纹周围有许多伴生小裂纹。
图10 大理岩循环加载破坏
Fig.10 Failure of marble under cyclic loading
吕鹏飞[12] 、刘晓辉等[13]利用SHPB试验系统对煤样进行冲击破坏如图11所示，试样尺寸φ50 mm×50 mm，冲击速度2.058 m/s，无围压。煤样最终沿轴向出现宏观裂隙，也呈现出明显的劈裂破坏。
图11 煤体的冲击破坏
Fig.11 Failure of coal under impact loading
分析可知：大理岩承受的循环加载作用与煤样承载的动态冲击作用均符合高阶纵波的作用模式，最终煤岩体大都呈现出的劈裂破坏属于拉伸破坏模式，具体原因可解释为：① 高阶纵波模式下，圆柱煤岩体底面随着r/R增大，径向与轴向应力振幅大小逐渐趋于一致，方向趋于相反;也就是说轴向应力为压应力时，径向会产生幅值大致相同的拉应力;② 圆柱煤岩体底面圆心处拉应力振幅最大，而且煤岩体的抗拉强度一般较弱，最初拉伸破坏位置应为底面圆心处，最终形成劈裂破坏。
宫凤强等[14]、李夕兵等[15]、金解放等[16]利用SHPB试验系统对具有三向静载的砂岩进行冲击破坏，如图12所示，试样尺寸φ50 mm×50 mm，轴压125 MPa、围压10 MPa。
图12 具有三向静载的砂岩冲击破坏
Fig.12 Failure of sandstone with three static loading under impact loading
同理，此砂岩试样承载的动态冲击作用符合高阶纵波的作用模式，试验结果表明在循环冲击作用下砂岩破坏形成近似圆锥体，属于拉剪破坏，圆锥表面具有明显的摩擦痕迹，圆锥外的其他部分间为张裂破坏。具体原因可解释为：① 高阶纵波模式下，由于有围压存在而导致不易发生劈裂破坏，同时由于剪切应力振幅的极值最大以及砂岩抗拉强度较低，因此具有三向静载的砂岩冲击破坏中拉应力与剪切应力起主导作用，易发生拉剪破坏;② 由于底面(作用面)圆心处的位移、应变、应力、振速以及能量振动幅值亦最大，因此最初拉剪破坏的位置也应为底面圆心处，最终形成近似圆锥体。
6 结 论
(1)基于纵波传播特征与波动控制方程，得出了纵波传播的频率方程，建立了纵波模式下圆柱煤岩体中位移、应力、应变与振速动态计算模型。
(2)在低阶纵波模式下，圆柱煤岩体中应力波的振动较为平缓，可近似认为是准静力载荷作用，煤岩体以剪切破坏为主，初始破坏位置主要分布在底面(作用面)且临近圆柱煤岩体表面的区域。
(3)高阶纵波模式下，圆柱煤岩体中各方向位移、应变、应力、振速及能量动态分布随着均半径增大均呈现出衰减趋势，大致符合幂函数关系。其中，位移、应变、应力、振速动态分布的幂函数指数m=- 0.52～-0.49，能量动态分布的幂函数指数m=-1.04。
(4)高阶纵波模式下，剪切应力/应变振幅的极值最大，而能量衰减最快;径向、轴向应力/应变随着半径增大径向与轴向应力大小逐渐趋于一致，方向趋于相反。也就是说，当轴向为压应力时，径向为大致同等大小的拉应力。
(5)高阶纵波模式下，煤岩体在无围压条件下易发生脆性劈裂破坏，主要由拉应力导致;在有围压条件下易发生近似圆锥形破坏，主要属于拉剪破坏;圆柱煤岩体端面圆心处的位移、应变、应力、振速及能量动态变化幅值最大，煤岩体损伤破坏的初始位置为底面(作用面)圆心处。
参考文献(References):
[1] 苏国韶，胡李华，冯夏庭，等.低频周期扰动荷载与静载联合作用下岩爆过程的真三轴试验研究[J].岩石力学与工程学报,2016,35(7):1309-1322.
SU Guoshao,HU Lihua,FENG Xiating,et al.True triaxial experimental study of rockburst process under low frequency cyclic disturbance load combined with static load[J].Chinese Journal of Rock Mechanics and Engineering,2016,35(7):1309-1322.
[2] 蔡峰，刘泽功,LOU Yi.爆轰应力波在高瓦斯煤层中的传播和衰减特性[J].煤炭学报,2014,39(1):110-114.
CAI Feng,LIU Zegong,LOU Yi.Propagation and attenuation characteristics of stress waves generated by explosion in high-gas coal-beds[J].Journal of China Coal Society,2014,39(1):110-114.
[3] 常未斌，樊少武，张浪，等.基于爆炸应力波和构造煤带孕育煤与瓦斯突出危险状态的模型[J].煤炭学报,2014,39(11):2226-2231.
CHANG Weibin,FAN Shaowu,ZHANG Lang,et al.A model based on explosive stress wave and tectonic coal zone which gestate dangerous tate of coal and gas outburst[J].Journal of China Coal Society,2014,39(11):2226-2231.
[4] 褚怀保，杨小林，侯爱军，等.煤体中爆炸应力波传播与衰减规律模拟实验研究[J].爆炸与冲击,2012,3(2):185-189.
CHU Huaibao,YANG Xiaolin,HOU Aijun,et al.A simulation-based experimental study on explosion stress wave propagation and attenuation in coal[J].Explosion and Shock Waves,2012,3(2):185-189.
[5] HE J,DOU L M,CAI W,et al.In situ test study of characteristics of coal mining dynamic load[J].Shock & Vibration,2015(1):1-8.
[6] 陈蓥，韩军，宋卫华.爆炸应力波作用煤巷变形破坏模拟试验研究[J].应用基础与工程科学学报,2011,19(6):995-1002.
CHEN Ying,HAN Jun,SONG Weihua.Simulated experiment on the deformation and failure process of coal roadway at blasting Wave[J].Journal of Basic Science and Engineering,2011,19(6):995-1002.
[7] 许江，耿加波，彭守建.煤与瓦斯突出脉动式发展过程的试验研究[J].中国矿业大学学报，2018,47(1):145-154.
XU Jiang,GENG Jiabo,PENG Shoujian,etal.Analysis of the pulsating development process of coal and gas outburst[J].Journal of China University of mining and Technology,2018,47(1):145-154.
[8] 杨桂通，胡海岩.弹塑性动力学基础[M].北京:科学出版社.
[9] AHMAD F.A simple formula for the longitudinal modes in a cylinder[J].Acoustical Society of America,2004,115(2):475-477.
[10] 张利洁.高应力脆性岩石时滞性破坏特性研究[D].武汉：中国地质大学，2016.
ZHANG Lijie.Study on time-lagged fracture chrematistic of brittle rock under high stress condition[D].Wuhan:Chinese university of Geosciences,2016.
[11] 赵扬锋，张超，刘力强，等.循环载荷作用下岩石多参量特征规律研究[J].中国安全科学学报,2016,26(5):105-111.
ZHAO Yangfeng,ZHANG Chao,LIU Liqiang,et al.Experimental research on multi-parameter rules of rock under cyclic loading[J].China Safety Science Journal,2016,26(5):105-111.
[12] 吕鹏飞.聚能爆破煤体增透及裂隙生成机理研究[D].北京：中国矿业大学(北京),2014.
LÜ Pengfei.Research on coal body permeability increase and crack generation mechanism under cumulative blasting[D].Beijing:China University of Mining and Technology(Beijing),2014.
[13] 刘晓辉,张茹,刘建锋.不同应变率下煤岩冲击动力试验研究[J].煤炭学报,2012,37(9):1528-1534.
LIU Xiaohui,ZHANG Ru,LIU Jianfeng.Dynamic test study of coal rock under different strain rates[J].China Coal Society,2012,37(9):1528-1534.
[14] 宫凤强,李夕兵,刘希灵.三维动静组合加载下岩石力学特性试验初探[D].岩石力学与工程学报,2011,30(6):1179-1190.
GONG Fengqiang,LI Xibing,LIU Xiling.Preliminary experimental study of characteristics of rock subjected to 3D coupled static and dynamic loads[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(6):1179-1190.
[15] YE Z Y.LI X B.LIU X L,et al.Testing studies on rock failure modes of statically loads under dynamic loading[J].Transactions of Tianjin University,2008,14(S):530-535.
[16] 金解放,李夕兵,王观石,等.循环冲击载荷作用下砂岩破坏模式及其机理[J].中南大学学报,2012,43(4):1453-1461.
JIN Jiefang,LI Xibing,WANG Guanshi,et al.Failure modes and mechanisms of sandstone under cyclic impact loadings[J].Journal of Central South University,2012,43(4):1453-1461.
03