煤炭自燃是煤炭工业面临的重要灾害之一。褐煤由于变质程度底、挥发分高、易风化破碎，更容易在开采、运输和储存过程中发生自燃。堆积煤体自燃是多因素耦合作用的复杂理化反应，但也具有一定的规律[1]。因此，研究褐煤自燃特性及规律具有十分重要的意义。
众多国内外学者针对煤炭自燃特性进行了研究:FENG[2]综合比较了静态恒温法、可燃性法、绝热法和动态法后，认为静态恒温法是研究煤炭自燃特性的最优方法;仲晓星等[3]基于程序升温实验计算了煤体的自燃临界温度;MOHALIK[4]应用3种不同热分析方法(TG，DTA，DSC)，研究了煤的自燃特性;刘剑等[5]采用活化能理论研究了煤的自燃机理，建立了活化能与采空区自燃关系的理论模型;张瑞新等[6]通过露天煤堆的自然发火实验，分析了煤体内温度场的传播规律。在数值模拟方面，ARISOY等[7]对半绝热状态的长柱形煤体升温过程进行模拟，分析了不同时刻煤体温度和含水量的分布规律;李宗翔等[8]建立采空区非线性渗流-多组分气体-温度场和非均匀耗氧的数值模型;YUAN和SMITH[9]建立大体积煤堆耗氧产热数学模型，模拟了风流量及反应级数对煤堆氧化产热及升温规律的影响;ZHANG等[10]总结了现有煤堆自燃模拟研究，分析了多种边界及初始条件对煤堆自燃的影响。
在上述研究中，煤炭自燃实验忽略了煤体升温过程中各参数间的耦合作用;另外，KAJI等[11]指出，煤体产热速率与时间有密切的关系，而传统数值模拟所用的产热模型不涉及时间效应，与煤炭产热实际不符。传统实验与模拟相结合的研究，主要是通过实验获得煤体特征参数，建立数学模型，并应用于数值模拟，但是未验证数学模型的准确性。针对上述问题，笔者采用开放式恒温法，以不同体积的立方体褐煤为实验对象，探讨其升温规律与临界自燃着火点温度(Tc);基于等效氧化暴露时间(Equivalent Oxidation Exposure Time，EOET)理论[12]，建立均质多孔介质多场耦合仿真数学模型，将实验与模拟相结合，分析堆积煤体升温过程中的温度分布、空气渗流(自然对流)、氧气质量分数分布、水分蒸发作用等多场耦合效应，并依据此模型，对大型煤堆的升温状态进行模拟，验证立方体煤堆临界自燃着火点温度实验式的合理性，为堆积煤炭自燃的预测与防治提供理论依据。
1 开放式恒温实验
1.1 实验方法
实验煤样选取内蒙古白音华矿褐煤,其工业分析及元素分析见表1。
表1 褐煤工业及元素分析
Table 1 Proximate and ultimate analysis of lignite
对采集的煤块进行破碎，筛选出平均粒径为10 mm的煤颗粒，装入4种不同体积的立方体(L=0.05，0.1，0.15，0.25 m)铜网框中，置于DHG-9023A型恒温箱中加热，在L=0.05 m煤样的垂直中心线上布置3个测温点，其余体积煤样布置5个测温点，通过LOGGER GL220多路温度记录仪采集测点温度。煤样外围有无底无盖的铜罩，削弱恒温箱强迫对流作用对其产生影响，气体分析仪辅助温度记录仪判定煤样最终自燃状态。实验测定系统如图1所示。
图1 开放式恒温实验测定系统
Fig.1 Open-ended isothermal experimental system
L为煤样边长，m;H为测点距离煤样底面高度，cm
1.2 实验结果
图2为不同环境温度(Te)下的不同体积煤样中心点升温曲线。临界自燃着火点温度(Tc)为堆积煤体能够发生自燃的最低环境温度，这里采用实验超临界和亚临界环境温度的平均值[13]。4种体积煤样的Tc分别为132.5，112.5，97.5和87.5 ℃。实验结果表明，不同条件下的升温曲线存在共性，依据中心点温度曲线及升温速率可将升温过程划分为4个阶段(图3):快速升温阶段(第Ⅰ阶段)、缓慢升温阶段(第Ⅱ阶段)、温度回升阶段(第Ⅲ阶段)和自热升温阶段(第Ⅳ阶段)，4个阶段分别由不同形式的能量占据主导:热传递、水分蒸发耗热、热传递-氧化产热和氧化产热。
图2 不同尺寸煤样中心点升温曲线
Fig.2 Center temperature profiles of different size samples
图3 升温阶段划分(L=0.1 m，Te=110 ℃)
Fig.3 Division of heating stages(L=0.1 m，Te=110 ℃)
同体积煤样，不同Te下的中心点温度曲线在第Ⅰ阶段及第Ⅱ阶段前期几乎重合，说明在此期间，环境温度对于内部煤体升温状态影响较小。
不同体积煤样，煤样体积越大，Tc越小;根据不同体积煤样超、亚临界温度曲线推算，当Te= Tc时，体积越大，自然发火时间越长(分别约为4.6，19.1，41.8，105 h);第Ⅰ，Ⅱ阶段升温速率均随着体积增加而减小(Ⅰ阶段:44.65，10.81，7.53，3,16 ℃/h;Ⅱ阶段:6.1，0.63，0.34，0.15 ℃/h)。分析图2升温曲线的升温速率可知，第Ⅲ阶段内，超临界温度下的升温速率始终增长，而亚临界温度下的升温速率曲线呈“凸型”变化(图3)，升温速率最高值随着体积增加而减小(分别为75.6，21.6，4.3，2.06 ℃/h)。因此升温速率可作为判定煤样自燃的重要指标。
2 开放式恒温实验的数值模型
2.1 EOET理论
KAJI等[11]通过实验得出，在温度和氧气质量分数恒定条件下，随着时间增加，煤体的热产生率自其暴露于空气始呈现指数减小趋势。等效氧化暴露时间(EOET)理论将此模型与非恒定煤体温度和氧气质量分数相结合，将物理时间转化为EOET，近似计算出煤体在物理时刻t的热产生率:
(2)
式中，qc为单位质量煤体热产生率，kW/kg;t为物理时刻，s;C(t)和T(t)分别为物理时刻t的氧气质量分数(%)和热力学温度(K);A0为指前因子，kW/kg;E为表观活化能，kJ/mol;R为气体常数，8.31 J/(mol·K);γ为衰减系数，0.000 3 s-1;t*为EOET，s;A为t=0时刻煤体的产热速率，kW/kg;∑qiΔti为煤体自暴露开始至物理时刻t产生的累积能量，kJ/kg，Δti，qi分别为时间步长(s)和时间步长内煤体产热速率,kW/kg。
笔者定义EOET与物理时间的比值为相对EOET，相对EOET是表征煤体产热潜能的重要指标:相对EOET越小，产热潜能越大;反之，产热潜能越小。EOET理论是关于产热速率、物理时间、氧气质量分数、温度的耦合公式，弥补了传统经验公式中热产生率与时间无关的缺陷。
2.2 多孔介质渗流基本方程
实验煤样为等粒径褐煤颗粒自然堆积形成，属于各向同性多孔介质，孔隙流体的动量方程[14]为
·(nρvv)=-np+·(nτ)+
(3)
式中，ρ为流场密度，kg/m3;v为渗流速度矢量;n为多孔介质孔隙率;为哈密顿算子;p为流体微元上的压力，Pa;τ为黏性阻力;Bf为重力体积力;μ为动力黏度，N·s/m2;等式最后一项表示多孔介质壁面施加于流体的黏性和惯性张力，K为渗透率，6.8×10-8 m2;C2为惯性阻力系数，9 100 m-1。
煤体升温过程中，煤颗粒裂隙中的水分蒸发吸收热量，水分蒸发耗热速率[15]为
qw=Γβk(φc-φa)
(4)
式中，qw为单位质量煤体水分蒸发耗热速率，kW/kg;Γ为单位质量水分的蒸发潜热，kJ/kg;β为水分蒸发经验常数，0.417 kg/(kg·s);k为干燥参数;φc为煤体的平衡湿度，%;φa为孔隙空气相对湿度，%。Γ,k,φc和φa分别表示[15-16]为
Γ=2.501×106-560T
(5)
(8)
式中，T为热力学温度，K;ω为煤体的含水量，%;Ω为经验常数，0.31;Pv为水蒸气分压，Pa;Psat为饱和水蒸气压力[17]，Pa;Pt为环境大气压力，101 325 Pa。
综上，多孔介质能量守恒方程可以描述为
·(ρfcfvT)=
·[nλf+(1-n)λs]T-qw+qc
(9)
式中，ρf，ρs分别为流体和固体的密度，kg/m3;cf，cs分别为流体和固体的比热容，J/(kg·K);λf，λs分别为流体和固体的导热系数，W/(m·K)。
2.3 热动力学参数的计算
基于Frank-Kamenetskii失稳理论[18]计算实验褐煤的表观活化能，F-K失稳理论认为当热体系中的F-K参数δ大于临界值δc时，热体系便会失稳燃烧，临界F-K参数δc为
(10)
其中，δc为临界F-K参数，m;r0为煤堆1/2边长，m;Q为反应热，J/kg;λ为煤体有效导热系数，W/(m·K)。对式(10)整理可得
(11)
首先将褐煤(平均粒径为10 mm)干燥，消除水分干扰，对不同体积立方体(L=0.05，0.1，0.15 m)干燥煤样进行恒温实验并求得Tc值(分别为122.5，97.5和87.5 ℃)。通过对
与1/Tc直线拟合，求解活化能值为78.9 kJ/mol。
2.4 物理模型构建及相关参数确定
根据实验条件建立三维数值模型(图4)，模型计算区域以恒温箱内部为主体(长×宽×高=0.6 m×0.55 m×0.645 m)，背部两侧各有1个进风口，背部中间设有1个出风口，立方体铜罩边长为0.25 m，测温点位置与实验相同。
边界条件:进风口为速度进口(风速为0.1 m/s，氧气质量分数为23%，水蒸气质量分数为0.02%)，出风口为自由出口，恒温箱壁面为绝热无滑移壁面，铜罩壁面为铜质耦合壁面，多孔与非多孔介质区域重合面为内部界面(Interior)。
图4 三维模型示意
Fig.4 3D model diagram
初始条件:模拟区域温度为实验室环境温度，氧气质量分数为23%，水蒸气质量分数为0.02%，煤样含水量为27.2%。
其他参数:煤体密度为1 291 kg/m3，孔隙率为0.35，比热容为1 210 J/(kg·K)，热传导率为0.3 W/(m·K)，耗氧速率为8.93×10-5 kg/(cm3·s)。
图5 不同Te实验与模拟煤样中心点升温曲线对比
Fig.5 Comparison of center temperature curves of experiment and simulation for different Te
3 模拟结果与实验对比
图5显示了两种尺寸(L=0.15，0.25 m)煤样在不同Te条件下，中心点升温曲线对比。实验与模拟结果吻合度较高，说明数学模型能够客观反映实验煤体升温过程及各种影响因素的耦合作用。
3.1 升温过程特征参数耦合分析
以L=0.15 m煤样为例，分析煤体4个升温阶段各特征参数耦合变化。图6为煤样不同测点(H=3，7.5，9 cm)的升温曲线对比(Te=95 ℃)。图7为煤样垂直中心截面(z=0 m)温度及渗流流线分布的模拟结果，图8为不同测点(H=3，6，7.5，9，12 cm)孔隙氧气质量分数与耗氧速率随时间变化的模拟结果。
图6 模拟与实验温度曲线对比(L=0.15 m，Te=95 ℃)
Fig.6 Temperature profiles of measure points comparison of simulation and experiment (L=0.15 m，Te=95 ℃)
图7 煤样温度场与空气渗流场(L=0.15 m,Te=95 ℃，z=0 m)
Fig.7 Temperature field and air seepage field of coal sample (L=0.15 m，Te=95 ℃，z=0 m)
图8 氧气质量分数与耗氧速率随时间变化(L=
0.15 m，Te=95 ℃)
Fig.8 Oxygen concentration and consumption rate vs.time (L=0.15 m，Te=95 ℃)
第Ⅰ阶段(0～4.25 h):此阶段煤体温度低，氧化产热量及耗氧量小;多孔介质内外空气密度差较大，形成自上而下的自然对流(图7(a))，热传导和对流换热作用强烈;煤体内部水分蒸发强度小。因此，煤体急速升温。如图6及图7(a)所示，热传导和热对流作用分别导致上部及外围煤体率先升温。此阶段煤体焓变主要依托其与环境的热传递实现。
第Ⅱ阶段(4.25～24.4 h):随着煤体温度上升，水分蒸发作用增强。此阶段测点温度及升温速率均不高，氧化产热强度较低，煤样由外界吸收的热量大部分被水分蒸发所消耗。渗流速度缓慢减小(图7(b))，导致氧气供给量逐渐减小，同时，煤温上升致使氧气消耗速率增加，因此，测点氧气质量分数明显减小(图8)。
第Ⅲ阶段(24.4～33.4 h):煤体水分蒸发进入尾声，此时煤体温度较高，氧化产热与热传递占据主导，升温速率及温度逐渐升高。氧气消耗速率增长明显，氧气质量分数显著下降。当上部煤体温度率先达到Te，并在自身氧化产热促使下超过Te时，其孔隙空气渗流方向发生逆转(图7(c))。
第Ⅳ阶段(33.4～48 h):伴随下部煤体温度超越Te，介质空气渗流方向完全逆转(图7(d))。由图8可知，耗氧速率及氧气质量分数增减趋势依旧强势。但是，氧气质量分数也受自然对流方向逆转的影响:尽管下部测点(H=3 cm)的耗氧速率大于上部(H=12 cm)，但是前者的氧气质量分数依然高于后者。当Te<Tc时，测点升温速率不断减小，当其温度升至最大值，热量收支达到动态平衡。随后，煤体产热速率减小，为追求能量平衡状态，其温度不断下降，最终趋于Te。期间，渗流速度和耗氧速率均先增加后减小。当Te>Tc时(图5(a)，Te=100 ℃)，煤体内部温度急剧升高，一直处于焓变持续增长的非平衡状态，最终发生热逃逸。
3.2 相对EOET与产热加速率
相对EOET和产热加速率(产热速率对时间导数)分别表征煤体的产热潜能和产热实际，均为重要的热特征参数。对比L=0.15 m煤样在Te=90，100 ℃条件下中心点的相对EOET及产热加速率变化规律(图9)，发现在相同Te条件下两曲线呈负相关状态，存在耦合关系。
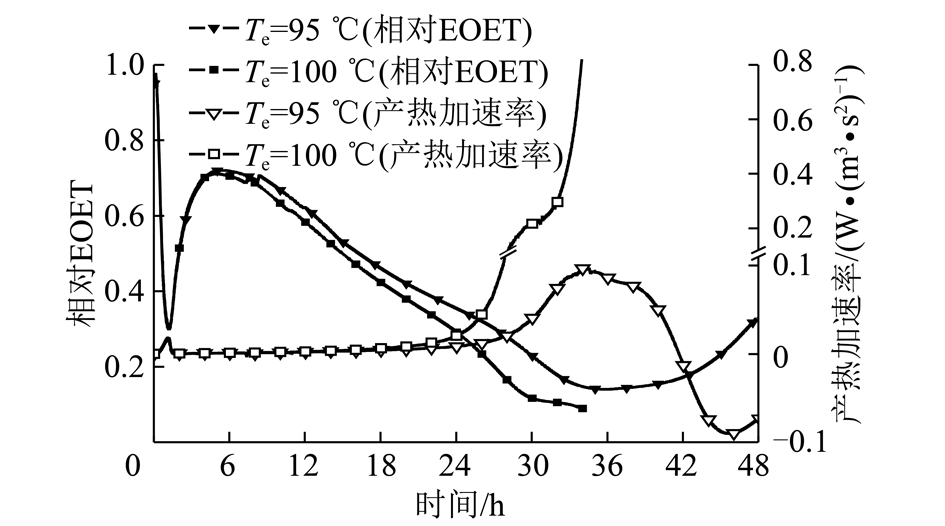
图9 中心点煤体相对EOET与产热加速率变化规律(L=0.15 m)
Fig.9 Relative EOET and heat generation acceleration rate of center coal vs.time (L=0.15 m)
升温过程第Ⅰ阶段，中心点煤体急速升温，相对EOET急剧减小，产热加速率增加。而随着水分蒸发强度增加，煤体升温速率减缓，相对EOET增加，产热加速率减小。第Ⅱ阶段，中心点煤体的相对EOET持续减小，造成产热加速率不断增加。第Ⅲ阶段，相对EOET和产热加速率变化趋势与第Ⅱ阶段相同，然而，变化幅度开始增大。第Ⅳ阶段，当Te>Tc时，相对EOET不断减小，使产热加速率无限增大，煤体自燃;当Te<Tc时，相对EOET下降至一定值后开始增加，煤体产热潜能衰减，产热加速度随之减小。随着时间增加，中心点煤体经历了产热加速率零值(产热速率最大值)和温度最大值后，逐渐下降至Te。因此，实验条件恒定情况下，当第Ⅳ阶段的相对EOET增加时，煤体不再具备自然发火的潜能。
4 表面积体积比与Tc的关系
立方体煤样表面积体积比σ为外表面积与体积之比(1/m)，即σ=6/L。表面积体积比是衡量煤体蓄热能力、吸收热能力和水分散失强度的重要指标。根据实验得到σ-Tc拟合公式:
Tc=37.595e0.266ln σ
(12)
图10 大体积煤堆最高温度随时间变化
Fig.10 Highest temperature vs.time of large coal pile
图11 临界着火点温度随σ变化
Fig.11 Critical self-ignition temperature vs.σ
通过对大型立方体煤堆(L=0.5，1，2，5 m)在不同Te下的升温过程进行模拟，得到其在超临界和亚临界温度条件下最高温度随时间变化曲线(图10)。可以发现:σ越小，煤体吸热能力和水分散失强度越弱，故自热时间越长;同时，其蓄热能力越强，Tc越小，因此煤堆更易自燃。根据数值模拟结果及式(12)求得不同体积煤堆的Tc如图11所示，模拟与经验公式结果基本吻合，说明能够通过式(12)近似计算大型立方体煤堆的Tc值。
5 结 论
(1)针对不同体积堆积褐煤进行开放式恒温实验，根据实验结果，其升温过程可划分为快速升温、缓慢升温、温度回升和自热升温4个阶段。Tc随着体积的增大而减小，第Ⅲ阶段升温速率可作为判定煤样自燃的重要指标。
(2)基于EOET理论的均质多孔介质多场耦合数学模型，高精度再现了实验结果，从而详细描述了煤样升温过程中温度、氧气、水分、空气渗流等特征参数的耦合过程，揭示了相对EOET与产热加速率的负相关关系，若第Ⅳ阶段的相对EOET增加，煤体则不再具备自燃潜能。
(3)根据实验结果建立了σ-Tc关系式，借以预测实验困难的大体积煤堆的临界自燃着火点温度。应用数值模拟验证了上述实验式的合理性，为大型煤堆的自燃预测及防治提供了借鉴。
参考文献(References):
[1] 李青松.褐煤化工技术[M].北京:化学工业出版社.2014:5-26.
[2] FENG K K.Spontaneous combustion of Canadian coals[J].Cim Bulletin,1985,78(877):71-75.
[3] 仲晓星,王德明,尹晓丹.基于程序升温的煤自燃临界温度测试方法[J].煤炭学报,2010,35(S1):128-131.
ZHONG Xiaoxing,WANG Deming,YIN Xiaodan.Test method of critical temperature of coal spontaneous combustion based on the temperature programmed experiment[J].Journal of China Coal Society,2010,35(S1):128-131.
[4] MOHALIK N K,PANIGRAHI D C,SINGH V K.Application of thermal analysis techniques to assess proneness of coal to spontaneous heating[J].Journal of Thermal Analysis and Calorimetry,2009,98(2):507-519.
[5] 刘剑,王继仁,孙宝铮.煤的活化能理论研究[J].煤炭学报,1999,24(3):317-320.
LIU Jian,WANG Jiren,SUN Baozheng.A study on the theory of activation energy of coal[J].Journal of China Coal Society,1999,24(3):317-320.
[6] 张瑞新,谢和平,谢之康.露天煤体自然发火的试验研究[J].中国矿业大学学报,2000,29(3):235-238.
ZHANG Ruixin,XIE Heping,XIE Zhikang.Experimental study on spontaneous combustion of ground coal[J].Journal of China University of Mining & Technology,2000,29(3):235-238.
[7] ARISOY A,BAMISH B B,ÇETEGEN E.Modelling spontaneous combustion of coal[J].Turkish Journal of Engineering & Environmental Sciences,2006,30(3):193-201.
[8] 李宗翔,吴强,王志清.自燃采空区耗氧-升温的区域分布特征[J].煤炭学报,2009,34(5):667-672.
LI Zongxiang,WU Qiang,WANG Zhiqing.Distribution characteristic of remaining coal oxygen consumption and spontaneous combustion heating-up in goaf[J].Journal of China Coal Society,2009,34(5):667-672.
[9] YUAN L,SMITH A C.CFD modeling of spontaneous heating in a large-scale coal chamber[J].Journal of Loss Prevention in the Process Industries,2009,22(4):426-433.
[10] ZHANG J,REN T,LIANG Y,et al.A review on numerical solutions to self-heating of coal stockpile:Mechanism,theoretical basis，and variable study[J].Fuel,2016,182:80-109.
[11] KAJI R,HISHINUMA Y,NAKAMURA Y.Low temperature oxidation of coals-A calorimetric study[J].Fuel,1987,66(2):154-157.
[12] SASAKI K,SUGAI Y.Equivalent oxidation exposure-time for low temperature spontaneous combustion of coal in heat analysis and thermodynamic effects[M].Croatia:In Tech Publisher,2011:235-254.
[13] GARC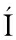
A T J,RAM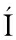REZ G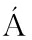 
,QUEROL A E,et al.Determination of the risk of self-ignition of coals and biomass materials[J].Journal of Hazardous Materials,2012,213-214(3):230-235.
[14] 王福军.计算流体动力学分析:CFD软件原理与应用[M].北京:清华大学出版社,2004:7-11.
[15] SASAKI K,MIYAKOSH H,SAITOH A,et al.Water vapor adsorption of coal and numerical simulation related to its effect on spontaneous combustion in a low temperature range[J].Journal of Mining and Materials Processing Institute of Japan,1992,108(6):479-486.
[16] 俞昌铭.多孔材料传热传质及数值分析[M].北京:清华大学出版社,2011:99-100.
[17] BUCK A L.New equations for computing vapor pressure and enhancement factor[J].Journal of Applied Meteorology,1981,20(12):1527-1532.
[18] 岑可法,姚强,骆仲央,等.高等燃烧学[M].杭州:浙江大学出版社,2002:40-47.
08