滇东黔西地区煤层具有多薄层纵向叠置、割理裂隙等结构弱面发育的特殊性[1-2]。在煤层中水力压裂技术是煤层气开发的核心技术[3],该地区的煤层直井压裂时,常采用段内多层组合射孔压裂的分层压裂工艺。压裂过程中存在结构弱面发育、高泊松比、低杨氏模量的多薄煤层中水力压裂裂缝竞争延伸的现象。常规油气多薄层压裂常采用Palmer模型[4]及其修正模型[5-6]来模拟裂缝的纵向穿层[7],但未能刻画天然裂隙等结构弱面对人工裂缝的影响。煤岩割理和裂隙十分发育,人工裂缝在扩展过程中容易发生转向[8],使得裂缝形态多样[9-10]。页岩压裂裂缝延伸模拟研究,考虑了天然裂缝的影响[11-12],但未专门研究纵向多薄层的裂缝竞争延伸。换言之,对结构弱面发育、高泊松比、低杨氏模量的多薄煤层水力压裂裂缝竞争延伸规律缺少系统的理论揭示。因此,笔者针对滇东黔西地区煤层的地质和压裂基本特点,建立专门的松软煤层的人工裂缝竞争延伸模拟方法,以期揭示这一地区压裂人工裂缝延伸的一般特征,为压裂施工设计和评价提供理论参考。
1 模型建立与求解
1.1 物理模型及基本假设
直井多层组合压裂时,压裂液在井筒和纵向多条裂缝中的流动过程如图1(a)所示,压裂液流动过程的井筒摩阻、射孔孔眼摩阻和压裂液缝内摩阻,如图1(b)所示,将裂缝离散为N个矩形单元,并建立全局坐标系与局部坐标系(图2)。

图1 物理模型
Fig.1 Physical model

图2 裂缝单元与坐标系示意
Fig.2 A schematic diagram of fracture elements and coordinate systems
水力压裂裂缝扩展是典型的流-固耦合问题。当人工裂缝扩展时裂缝体积增大,缝内压力降低,进而引起缝口压力的变化。根据管流原理,节点压力的变化会引起流量的变化。换言之,上述图中各裂缝的每一步延伸都可能引井口注入流量在各裂缝间的动态分配。
为刻画这一流固耦合过程,在抓住主要矛盾的同时假设:① 天然裂缝为垂直裂缝;② 在无天然裂缝区域假设地层为均质、各向同性的连续线弹性体;③ 割理、裂隙等分布以蒙特卡洛随机方法生成;④ 煤层活性水压裂液视为牛顿黏性流体,不考虑裂缝端部压裂液滞后现象。
1.2 数学模型
1.2.1 应力场模型
位移不连续法是CROUCH S L[13]于1976年提出的间接边界单元法。该方法将边界单元的上下表面处理为一个理想的位移不连续单元,适合处理裂缝问题。
将裂缝划分为N个矩形单元如图2所示,裂缝单元中心坐标为(xi,yi,zi),i=1,2,…,N。裂缝单元i的不连续位移在任意位置j产生的应力即诱导应力为
![]()
(1)
其中,![]() 为裂缝单元xy向位移不连续量,
为裂缝单元xy向位移不连续量,![]() 为裂缝单元xz向位移不连续量,
为裂缝单元xz向位移不连续量,![]() 为裂缝单元法向位移不连续量,
为裂缝单元法向位移不连续量,![]() 等为边界影响系数,Pa/m;(xi,yi,zi)为裂隙单元j中心在全局坐标系下的坐标位置,m。裂缝宽度可通过下式[14]求得
等为边界影响系数,Pa/m;(xi,yi,zi)为裂隙单元j中心在全局坐标系下的坐标位置,m。裂缝宽度可通过下式[14]求得
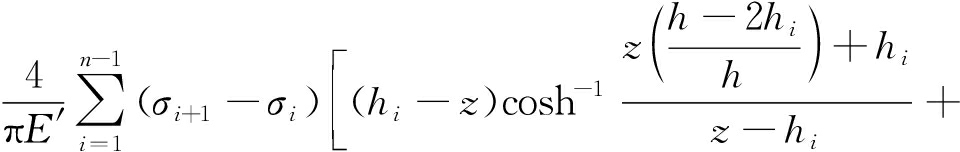
![]()
(2)
式中,E′=E/(1-ν2)为平面应变弹性模量,MPa;ν为泊松比,无量纲;pcp为孔眼高度处裂缝内流体压力,MPa;σn为裂缝单元法向应力,MPa;ρf为压裂液密度,kg/m3;hcp为射孔孔眼高度,m;h为裂缝高度,m;hi为i层高度,m;σi为i层地应力,MPa。
1.2.2 压裂液流动模型
由于裂缝壁面存在摩擦力,裂缝在扩展过程中缝内压力随着裂缝长度的增加会逐渐降低。假设压裂液在平板之间流动,由Navier-Stokes方程可以推出缝内压降方程[15-16]:
(3)
式中,Q为裂缝注入流量,m3/min;w为裂缝宽度,m;n′为流体幂律指数;k′为流体黏度指数,(N·sn′)/m2。
根据伯努利方程可以得到射孔摩阻[17-19],即
(4)
式中,Qi为第i条裂缝的流量,m3/min;ρs为压裂液密度,kg/m3;np,i为第i条裂缝的射孔个数;dp,i为第i条裂缝的射孔孔眼直径,m;cp,i为第i条裂缝的孔眼修正系数。
井筒摩阻与裂缝间距成正比,其中油管内径对摩阻影响极大,作用在筒上的摩阻[16]可表示为
![]()
(5)
其中,xj为裂缝j到井筒末端的距离,m;Qk为进入裂缝翼的流量,m3/min;D为施工管柱内径,m。根据基尔霍夫(Kirchoff)第一、第二定律,在多条裂缝扩展的同时,需满足压力平衡和流体总注入量物质守恒。流量守恒方程与压力平衡方程[20]为
(6)
![]()
(7)
其中,QT和Qi分别为总流体注入量和裂缝i的流体注入量;po为井底流体压力,MPa;pw,i为第i条裂缝入口处流体压力,MPa;ppf,i为第i条裂缝射孔孔眼摩阻,MPa;pcf,i为第i条裂缝井筒摩阻,MPa。根据物质守恒定律,得到总注入流体的守恒方程为
![]()
(8)
式中,CL为滤失系数,m2/min;t为泵注总时间,min;τ为裂缝单元开始滤失时间,min。
1.2.3 断裂与延伸准则
基于应力强度因子的定义,得到缝尖应力强度因子[21]为
![]()
(9)
式中,KI和KII分别为I型和II型应力强度因子,MPa·m1/2;E为杨氏模量,MPa;ν为泊松比,无因次;a为裂缝单元半长,![]() 分别为裂缝尖端单元向、切向位移不连续量,m;C为修正系数,取0.806。
分别为裂缝尖端单元向、切向位移不连续量,m;C为修正系数,取0.806。
对于I-II复合型裂缝,当尖端应力强度因子大于储层岩石的断裂韧性时,则裂缝会发生延伸,尖端应力强度因子为
(10)
其中,β为裂缝延伸角度,(°)。当裂缝尖端应力强度因子大于岩石断裂韧性KIc时,岩石发生断裂。复合型裂缝扩展理论主要包括最大周向应力理论、应变能密度理论和最大能量释放率理论。本文采用最大周向应力理论计算裂缝扩展方向。
1.3 模型的求解
根据上述数值模型,采用Matlab编制计算程序,模拟煤层水力压裂裂缝延伸形态。模型的求解方法以伪代码形式表述如下:
(1)输入:地质参数与施工参数;
(2)假设裂缝宽度wk、各裂缝翼流量Qk、缝内流体压力pk与裂缝高度hk;
(3)For i=1:扩展步数;
(4)For k=1:迭代次数;
(5)将缝内流体压力pk与裂缝高度hk代入方程(1)解得新裂缝宽度wk+1;
(6)将裂缝宽度wk、缝内流体压力pk代入方程(2)解得新裂缝高度hk+1;
(7)将裂缝宽度wk,与裂缝高度hk代入方程(7)解得新缝内压力p'k及各裂缝翼流量Qk+1,新的压力pk+1=αpk+(1-α)p'k,α为松弛因子;
(8)若∣pk+1-pk∣<ε(ε为一个极小值),跳出循环;
(9)计算总物质守恒方程(8),求得时间ti;
(10)若ti大于施工时长返回,跳出循环;
(11)计算尖端因子与裂缝延伸方向;
(12)若K>KIc,裂缝发生扩展,增加裂缝单元;
(13)输出:裂缝水力参数及压裂流体参数。
表2 模拟所需基础参数
Table 2 Basic parameters

以滇东地区的X6井为例,按照上述求解方法,模拟裂缝延伸情况。该井的测井曲线和由此计算的地应力和杨氏模量等如图3所示。

图3 X6井储层地质参数测井曲线
Fig.3 Logging curve of geological parameters of well X6

图4 水力裂缝轨迹
Fig.4 Hydraulic fracture trajectory
模拟得到二维裂缝延伸轨迹与三维裂缝形态。由图4(a)~(d)可见,在天然裂缝影响下,水力裂缝遭遇天然裂缝时会发生明显的弯曲。由于各层天然裂缝分布存在明显差异,因此各层水力裂缝几何形态具有显著的差异。分析图4(e)发现,层1的水力裂缝穿层较为明显,是由于层1与隔层间的应力差较小,而层2、层3的穿层不明显,这是由于隔层间的应力差较大,但在近井筒处,层2裂缝与层3裂缝在水平向具有较小间距,两条裂缝会相互吸引,强化穿层效应。因此,在近井筒处穿层更为明显。
2 多层裂缝竞争延伸特征的影响因素分析
裂缝水力压裂裂缝的裂缝形态受储层地质参数(地应力、杨氏模量、泊松比、天然裂缝参数等)和压裂施工参数(压裂总液量、施工排量、压裂液黏度、
滤失系数等)的共同影响。这里主要分析杨氏模量、泊松比、隔层应力差、施工排量和压裂液黏度等参数对多层合压缝竞争延伸的影响。除讨论的变量外,其余参数取值见表2。
2.1 储层杨氏模量的影响
不同杨氏模量的储层形成的裂缝半长、平均宽度、平均高度以及各层进液量如图5所示。随压杨氏模量增大,裂缝长度明显增大(图5(a)),裂缝平均宽度减小(图5(b)),裂缝平均高度总体变化不大(图5(c))。随杨氏模量的增大,各层间流量差异减小(图5(d))。可见,杨氏模量较小的储层,在多层合压的过程中各层间流量分配差异较小;而杨氏模量较大的储层需要对各层射孔参数进行优化,以调节各层间流量分配情况。

图5 不同杨氏模量下裂缝参数变化曲线
Fig.5 Variation curves of fracture parameters under different Young’s modulus
2.2 储层泊松比的影响
研究发现,随泊松比增大,裂缝的长度增大(图6(a));层1裂缝宽度减小,层2与层3裂缝平均宽度增加(图6(b)),这是由于层1缝宽减小增大缝内摩阻,使得层1进液量减小,层2与层3的进液量增加,进而导致层2与层3缝宽的增加;随泊松比增大,裂缝的高度呈减小的趋势(图6(c))。
2.3 隔层应力差的影响
不同隔层应力差条件下,随隔层应力差下的增大,裂缝的长度增加(图7(a)),裂缝平均宽度减小(图7(b)),裂缝平均高度减小(图7(c))。随隔层应力差下的增大,层1与层3的进液量增加,而层2的进液量会减小(图7(d))。

图6 不同泊松比下裂缝参数变化曲线
Fig.6 Variation curves of fracture parameters under different Poisson ratio

图7 不同隔层应力差下裂缝参数变化曲线
Fig.7 Variation curves of fracture parameters under different vertical stress difference
2.4 压裂液黏度的影响
分析模拟结果,随压裂液黏度的增大,裂缝的长度减小(图8(a)),裂缝平均宽度增加(图8(b)),裂缝平均高度总体呈增加趋势(图8(c))。随压裂液黏度的增大,缝内压降增加,压裂液在井筒中流动阻力也有所增加,进而各层间流量差异减小(图8(d))所示。
2.5 施工排量的影响
随施工排量的增大,裂缝的长度减小(图9(a)),裂缝平均宽度增加(9图(b)),裂缝平均高度总体呈增加趋势(图9(c))。随施工排量的增大,各层间流量分配的差异减小(图9(d))。这是由于缝内压力增加,流量增大的同时射孔孔眼摩阻也有所增加,进而使得各层间流量分配的差异减小。
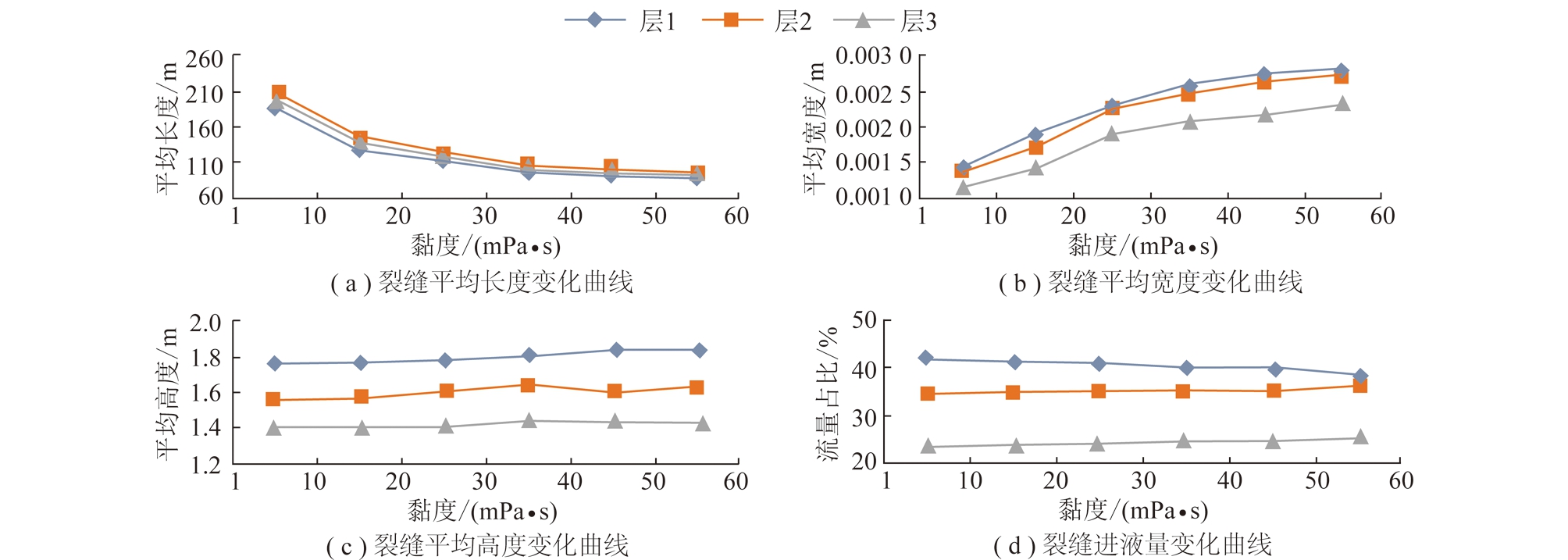
图8 不同压裂液黏度下裂缝参数变化曲线
Fig.8 Variation curves of fracture parameters under different viscosity

图9 不同排量下裂缝参数变化曲线
Fig.9 Variation curves of fracture parameters under different injection rate
3 结 论
(1)水力裂缝在捕获天然裂缝时缝内净压力降低,在该位置处的裂缝宽度以及裂缝高度均有所减小,增加了发生砂堵的风险。
(2)杨氏模量较小的储层,在多层合压的过程中各层间流量分配差异较小,而杨氏模量较大的储层需要对各层射孔参数进行优化,以调节各层间流量分配。
(3)在完井参数无法改变且射孔参数一定的条件下,可增加压裂液黏度,提高施工排量,以降低各层压裂液进液差异。
参考文献(References):
[1] 孟宪武,刘诗荣,石国山,等.滇东黔西地区煤层气开发试验及储层改造效果分析与建议[J].中国煤层气,2006,3(4):31-34.
MENG Xianwu,LIU Shirong,SHI Guoshan,et al.Results of CBM testing and remoulding of reservoir in eastern Yunnan and western Guizhou and related problems & suggestion[J].China Coalbed Methane,2006,3(4):31-34.
[2] 秦勇,申建,沈玉林.叠置含气系统共采兼容性——煤系“三气”及深部煤层气开采中的共性地质问题[J].煤炭学报,2016,41(1):14-23.
QIN Yong,SHEN Jian,SHEN Yulin.Joint mining compatibility of superposed gas-bearing systems:A general geological problem for extraction of three natural gases and deep CBM in coal series[J].Journal of China Coal Society,2016,41(1):14-23.
[3] 李辛子,王运海,姜昭琛,等.深部煤层气勘探开发进展与研究[J].煤炭学报,2016,41(1):24-31.
LI Xinzi,WANG Yunhai,JIANG Zhaochen,et al.Progress and study on exploration and production for deep coalbed methane[J].Journal of China Coal Society,2016,41(1):24-31.
[4] 胡永全,任书泉.压裂裂缝拟三维延伸的数值模拟[J].西南石油大学学报(自然科学版),1992,14(2):54-62.
HU Yongquan,REN Shuquan.Numerical simulation foe peeudo-three-dimensional fracture extension in fracturing[J].Journal of Southwestern Petroleum Institute,1992,14(2):54-62.
[5] 李哲,杨兆中,李小刚.水力压裂模型的改进及其算法更新研究(上)[J].天然气工业,2005,25(1):85-87.
LI Zhe,YANG Zhaozhong,LI Xiaogang.Improved model for hydraulic fracturing and algorithm renewal study(1)[J].Natural Gas Industry,2005,25(1):85-87.
[6] 李哲,杨兆中,李小刚.水力压裂模型的改进及其算法更新研究(下)[J].天然气工业,2005,25(2):100-103.
LI Zhe,YANG Zhaozhong,LI Xiaogang.Improved model for hydraulic fracturing and algorithm renewal study(2)[J].Natural Gas Industry,2005,25(2):100-103.
[7] 杨兆中,刘云锐,张平,等.滇东黔西地区多层叠置煤层压裂分层决策方法研究[J].煤炭科学技术,2017,45(9):7-12.
YANG Zhaozhong,LIU Yunrui,LI Xiaogang.Study on fracturing and slicing decision method of multi layer overlay seam in East Yunnan and West Guizhou[J].Coal Science and Technology,2017,45(9):7-12.
[8] 马耕,张帆,刘晓,等.裂缝性储层中水力裂缝扩展规律的试验研究[J].采矿与安全工程学报,2017,34(5):993-999.
MA Geng,ZHANG Fan,LIU Xiao.Experimental study on hydraulic fracture propagation in fractured reservoir[J].Journal of Mining and Safety Engineering,2017,34(5):993-999.
[9] 高杰,侯冰,谭鹏,等.砂煤互层水力裂缝穿层扩展机理[J].煤炭学报,2017,42(S2):428-433.
GAO Jie,HOU Bing,TAN Peng,et al.Propagation mechanism of hydraulic fracture in sand coal interbedding[J].Journal of China Coal Society,2017,42(S2):428-433.
[10] 路艳军,杨兆中,SHELEPOV V V,等.煤层气储层压裂现状及展望[J].煤炭科学技术,2017,45(6):73-84.
LU Yanjun,YANG Zhaozhong,SHELEPOV V V,et al.Status and prospects of coalbed methane reservoir fracturing[J].Coal Science and Technology,2016,45(6):73-84.
[11] XIE L,MIN K B,SHEN B.Simulation of hydraulic fracturing and its interactions with a pre-existing fracture using displacemen discontinuity method[J].Journal of Natural Gas Science & Engineering,2016.
[12] KRESSE O,WENG X,GU H,et al.Numerical modeling of hydraulic fractures interaction in complex naturally fractured formations[J].Rock Mechanics & Rock Engineering,2013,46(3):555-568.
[13] CROUCH S L.Solution of plane elasticity problems by the displacement discontinuity method I Infinite body solution[J].International Journal for Numerical Methods in Engineering,2010,10(2):301-343.
[14] WENG X,KRESSE O,COHEN C E,et al.Modeling of hydraulic fracture network propagation in a naturally fractured formation[J].SPE Production & Operations,2011,26(4):368-380.
[15] SCHLICTING,HERMANN.Boundary-layer theory(6th ed)[M].McGraw-Hill,1968.
[16] VALKO P,ECONOMIDES M J.Hydraulic fracture mechanics[J].Engineering Structures,1996,12(11):886-887.
[17] CRUMP J B,CONWAY M W.Effects of perforation-entry friction on bottom hole treating analysis[J].Journal of Petroleum Technology,1986,40(8):1041-1048.
[18] BUNGER A P,ZHANG X,JEFFREY R G.Parameters affecting the interaction among closely spaced hydraulic fractures[J].SPE Journal,2012,17(1):292-306.
[19] LECAMPION B,DESROCHES J.Simultaneous initiation of multiple transverse hydraulic fractures from a horizontal well[J].Journal of Asthma Official Journal of the Association for the Care of Asthma,2014,51(4):380-390.
[20] ELBEL J L,PIGGOTT A R,MACK M G.Numerical modeling of multilayer fracture treatments[A].SPE Permian Basin Oil and Gas Recovery Conference[C].1992.
[21] OLSON J E.Fracture aperture,length and pattern geometry development under biaxial loading:A numerical study with applications to natural,cross-jointed systems[J].Geological Society London Special Publications,2007,289(1):123-142.