煤层气、致密气、页岩气(“三气”)合采已成为当前煤系非常规天然气开发的重点研究方向,也引起了学者们的普遍关注[1-3]。在“三气”合采中,率先实现煤层气和致密气的同井筒合采具有较强的可行性,也在鄂尔多斯盆地东缘临兴地区开展了开发试验。煤层气主要以吸附状态储存于煤层,其产出分为解吸、扩散和渗流3个过程,一般采用 “排水降压”的方式[4-9],国内对各地区的煤层气井产能开展了大量研究[10-12],但针对煤层气和致密气合采的产能分析较为薄弱,仅开展了单独煤层气或致密气多层合采的分析和模拟研究[13]。要明确煤系“三气”的开采过程、查明气水流动特征、确定合理排采压差,亟需建立适应于多层合采的气、水流动方程[14]。笔者基于多层合采的等值渗流阻力理论,建立了煤层气和致密气合采过程中,排水期和气水同产期的产能方程,并通过临兴地区合采试验井的验证,分析了该方程的适用性,为后期煤层气和致密气合采,乃至“三气”合理排采制度的确定提供理论支撑。
1 理论分析基础
国内外针对单层气藏压裂井试井开展了很多研究,建立了比较成熟的产能评价模型,与此同时,在多层单一气藏(主要为多层致密气藏)联合开采上也提出了相应的计算方法[15-19]。尽管在单层压裂和多层合采两方面的理论研究都取得了一定的成功,但是关于多层气藏-分层压裂井的产能评价方法的研究,国内外都还处在探索阶段。虽然物理模型已经建立,但是数学模型却还没有突破,更没有可以直接用于多层气藏-分层压裂井产能计算的公式。
1.1 两层气藏分层压裂直井模拟假设条件
如图1所示,假设:① 两层气藏厚度和渗透率不相等,泄流半径相同;② 地层平均压力相等(生产压差相等),不发生层间窜流和倒灌现象;③ 裂缝半长相等,各层裂缝完全穿过地层,裂缝剖面呈矩形,裂缝高度等于各气层厚度;④ 裂缝内流体为单向流动,符合达西定律;⑤ 气藏流体流动为稳态渗流,压力、渗流速度等与时间无关;⑥ 考虑裂缝表皮效应,但是只赋以简单的数值,不考虑其变化。

图1 多层合采示意
Fig.1 Multi-layer co-production diagram
1.2 两层气藏分层压裂直井产能评价模型的建立
引用单层气藏垂直裂缝井产能计算公式,利用等值渗流阻力法,通过并联地层的渗流阻力因子,导出两层气藏分层压裂直井产能计算公式,建立两层气藏分层压裂直井产能评价模型。
对于多层复合线性渗流,利用等值渗流阻力法需要用电学并联电路处理。每一层的厚度分别为hi,渗透率为ki,生产压差为Δp,每一层的产量为qi,供给边界到井筒距离为L,气体体积系数为B,裂缝长度w,流体黏度μ,由单层线性渗流理论,可以得到其每一层的流量公式和渗流阻力因子分别为
(1)
![]()
(2)
由等值渗流阻力法,并联地层总阻力为
(3)
则多层复合气藏的总产量为
(4)
2 排水期产能方程
2.1 单层排水量公式的建立
考虑半径为re、厚度为h的圆形等厚、水平、均质储层发生Darcy径向渗流。如图2所示,供给半径是re,井底流压pwf,表皮因子S,应力敏感系数α,介质渗透率随气藏压力变化(考虑应力敏感效应)。

图2 平面径向渗流及压降漏斗示意
Fig.2 Diagram of radial seepage and pressure drop funnel
若平面径向渗流具有轴对称性,则渗流控制方程为
(5)
直接积分得拟压力分布公式
m(p)=C1+C2lnr
(6)
根据边界条件有
(7)
且m(r=rw)=m(pwf)将式(3)和(4)代入式(2)可得
拟稳态产量公式为
(8)
如果考虑拟稳态渗流和表皮效应,式(5)可以变为
(9)
其中,mi-m(p)=![]() k(p)dp,k(p)为应力敏感渗透率,k(p)=kie-α(pi-p)。将应力敏感渗透率进行积分并变形,按幂级数展开整理可得
k(p)dp,k(p)为应力敏感渗透率,k(p)=kie-α(pi-p)。将应力敏感渗透率进行积分并变形,按幂级数展开整理可得
(10)
其中,![]()
对于垂直裂缝井,进一步修正采水指数[20]有
(11)
其中导流能力影响函数[21]为
(12)
其中,ψ=lncfD。
2.2 煤砂两层合采排水量公式的建立
假设该两层气藏各层的厚度分别为h1,h2;地层渗透率分别为k1,k2;表皮因子分别为sf1,sf2;产量分别为Qf1,Qf2;裂缝半长都为xf;裂缝渗透率表示为kf1,kf2;裂缝宽度为wf1,wf2;泄流半径均为re;裂缝的无量纲穿透比分别为reD1,reD2;无量纲导流能力分别为cfD1,cfD2,生产压差均为Δp。
由单层气藏压裂井产能计算式(11),可以得到两层气藏分层压裂后各层的产量以及其渗流阻力因子分别为
(13)
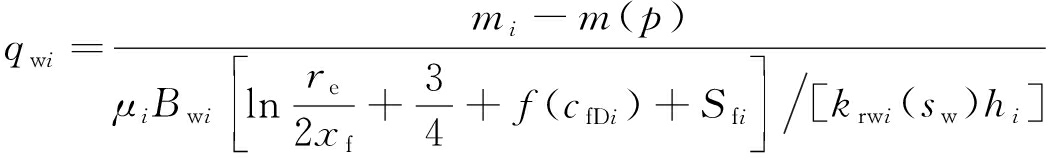
(14)
mi-m(p)=![]() k(p)dp
k(p)dp
(15)
其中
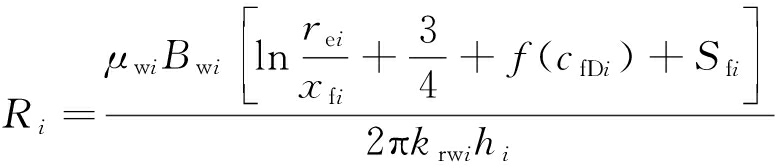
(16)
由等值渗流阻力法,并联两层气藏的阻力因子,得到该两层气藏的总阻力为R=R1R2/(R1+R2)。则有两层气藏分层压裂直井的总产能为
将应力敏感渗透率进行积分并变形,并将e按幂级数展开,代入产量公式变形整理可得
(17)
其中,J=ki/R。
2.3 排水期影响因素分析
影响排水期产水量的参数包括煤层初始渗透率、煤层泄流半径、煤层岩石压缩系数、裂缝半长、裂缝导流能力及表皮因子等因素。分析过程中使用的煤层、砂岩参数可见表1。
对比单层直井、单层裂缝井及双层裂缝井排水量随压差的变化,可见其合理的压差都为5 MPa左右,但排采流量以两层合采最高,为16.05 m3/d,单煤层直井排采时为5.04 m3/d,单层裂缝井排采时为11.26 m3/d(图3(a))。煤层气排水阶段,由于井底压力降低,压差增大,排水量将上升,但随排水量的增加,储层应力敏感效应凸显。达到一定的极限排水量时,随压差继续增加排水量不但不增加,由于渗透率的损害使得排水量逐渐减小,因此排采的合理压差最佳点即曲线的最高点。
表1 产水量分析中使用的参数值
Table 1 Parameters used in the analysis of water production


图3 不同影响因素对排水量的影响
Fig.3 different influencing factors on displacement
图3(b)展示了不同岩石压缩系数cf对排水量的影响,分别取cf=0.20,0.22,0.24,0.26,0.28 MPa-1。可见岩石压缩系数越小,排水量越高,合理的排采压差也越高。选取煤岩初始渗透率ki1=(1×10-15,1.2×10-15,1.4×10-15,1.6×10-15,1.8×10-15m2),由图3(c)可知初始渗透率越小,排水量越小,但初始渗透率的大小对合理排采压差没有影响。设定泄流半径re为500,1 000,1 500,2 000和2 500 m,发现泄流半径越小,排水量越高,但泄流半径的大小对合理排采压差也没有影响(图3(d))。
2.4 实例分析
图4为理论模型与临兴地区LX-26井的实际生产数据拟合结果,通过拟合结果可以计算出合理的压差为1.9 MPa左右,排水期间的生产压差尽量不要高于这个数值,高于这个压差后,储层伤害将增加。
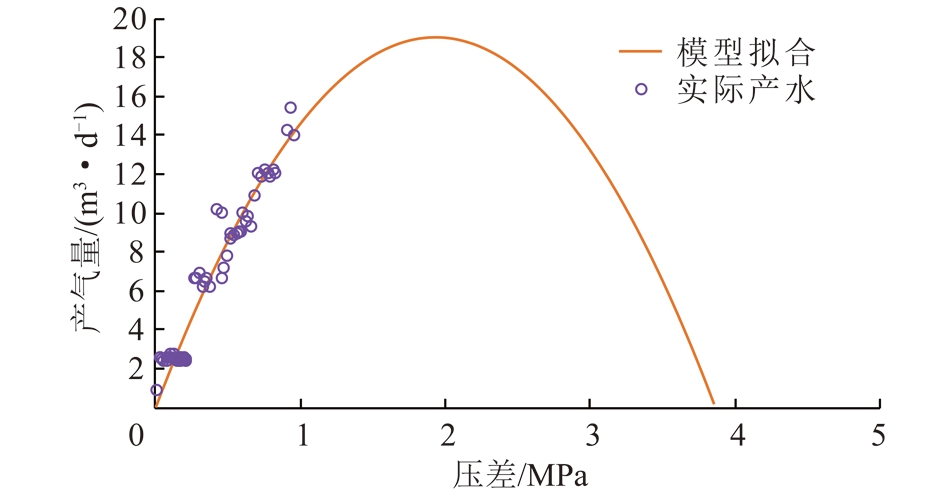
图4 实例拟合
Fig.4 Correlation results with actual case
3 气水同产期产能方程
3.1 单层产气量公式的建立
产水方程在第2节已经建立,要确定气水同产期产水产气量,还需建立产气方程。考虑半径为re,厚度为h的圆形等厚、水平、均质储层发生Darcy径向渗流。如图2所示,若供给半径是re,井底流压是pwf,介质渗透率随气藏压力变化,其控制方程为
(18)
气水同产阶段不仅要建立产水量的产能公式,还要推导产气量的产能公式,两相流动产水量公式就是前面推导的排水量公式,对于直井产气量公式,有
(19)
除了渗流的气体流量外,还应该考虑煤层气吸附解吸量
(20)
因此最终,气体总的产量应该是渗流裂缝中渗流的流量加上基质解吸附的流量综合,即
(21)
其中气体的黏度、体积系数、偏差因子等都是气体平均压力的函数。
3.2 煤砂两层合采产气量公式的建立
由单层气藏压裂井产能计算式(18),可以得到两层气藏分层压裂后各层的产量以及其渗流阻力因子分别为
(22)
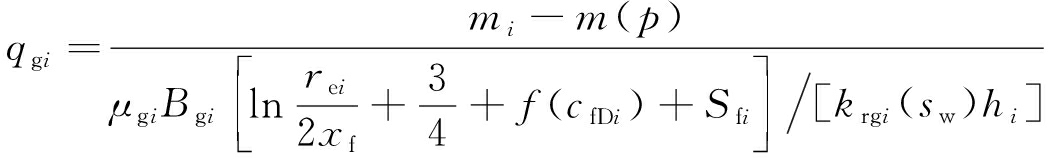
(23)
mi-m(p)=![]() k(p)dp
k(p)dp
(24)
其中
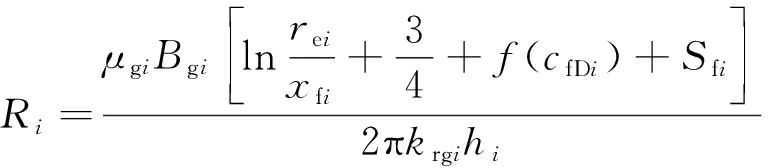
(25)
由等值渗流阻力法,并联两层气藏的阻力因子,得到该两层气藏的总阻力为R=R1R2/(R1+R2),两层气藏分层压裂直井的总产能为qf=[mi-m(p)]/R。
除了渗流的气体流量外,还应该考虑煤层气吸附解吸量
(26)
因此最终,气体总的产量应该是渗流裂缝中渗流的流量加上基质解吸附的流量综合
(27)
其中气体的黏度、体积系数、偏差因子等都是气体平均压力的函数,因此在计算过程中涉及一些重要参数PVT计算。气体产量计算与排水量计算最大不同就是要考虑高压物性的影响。
3.3 产气量影响因素分析
气水同产期影响产气量参数主要包括煤层初始渗透率、煤层岩石压缩系数、裂缝半长、裂缝导流能力、弹性模量、兰氏应变常数、泊松比及弹性模量等。分析过程中使用的煤层、砂岩两层参数列在表2。其中兰氏应变常数指煤储层解吸或吸附时煤基质的最大应变量,其随压力的变化类似于兰氏等温吸附曲线而称之为兰氏应变常数[22]。
表2 产气量分析中使用的参数值
Table 2 Parameters used in the analysis of gas production

初始渗透率分别取ki1=0.01×10-15,0.05×10-15,0.1×10-15m2,由图5(a)可知初始渗透率越大,产气量越高。初始渗透率对合理压差有一定影响,初始渗透率越大,合理压差越小。在实际开采过程中,根据参数取值不同,曲线形态会发生变化,最佳点也会发生变化,要结合生产实际情况具体分析。

图5 不同参数对产气量的影响
Fig.5 Influence of different parameters on gas production
裂缝半长分别取xf=30,50,70 m,由图5(b)中可知裂缝半长越小,产气量越小,然而裂缝半长的大小对合理生产压差几乎没有影响。随兰氏应变常数的增大,产气量也相应增加,同时合理的生产压差也略微增大,曲线变形程度增加(图5(c))。随裂缝导流能力的增加,产气量相应增加,但导流能力对合理生产压差几乎没有影响,不同的导流能力下,合理生产压差是一样的(图5(d))。岩石压缩系数选取cf1=0.25,0.3,0.45 MPa-1,当压差小于2.5 MPa时,不同的岩石压缩系数产气量曲线重合了,几乎没有影响;但当压差大于2.5 MPa时,随岩石压缩系数的增大,产气量减小了,合理的生产压差也相应的减小了(图5(e))。随弹性模量的增加,产气量也对应略微增加,不同的弹性模量下合理的生产压差却几乎不变(图5(f))。除此之外,对比泊松比对产气量的影响,结果发现随泊松比的增加,产气量增加,但增加幅度较小,不同的泊松比下合理的生产压差几乎不发生改变。
4 结 论
(1)运用等值渗流理论,分别推导了排水期及气水同产期,煤层-砂岩合采排水量方程及产气方程,分析了排水过程中影响排水量的主要参数,为煤层气致密气两层合采气藏合理压差确定奠定了基础。
(2)排水期,随井底压力降低,压差增大,排水量将上升。随排水量的增加,储层应力敏感效应凸显,达到一定的极限排水量,由于渗透率损害使得排水量逐渐减小。岩石压缩系数越小,排水量越高,合理的排采压差也越高。泄流半径和初始渗透率对排水量有影响,但对合理排采压差没有影响。实际开发过程中排水量最佳及合理压差最佳点即产量与生产压差曲线上的最高点。
(3)气水同产期,井底压力降低,压差增大,产气量将上升。但随产气量的增加,储层应力敏感效应凸显,在实际开采过程中,根据参数取值不同,曲线形态会发生变化,最佳排采压差点也会发生变化。初始渗透率和岩石压缩系数对合理压差的确定有一定的影响,兰氏应变常数、裂缝导流能力和弹性模量等对产气量有一定的影响,但对合理压差影响较小。
参考文献(References):
[1] 秦勇,申建,沈玉林.叠置含气系统共采兼容性——煤系“三气”及深部煤层气开采中的共性地质问题[J].煤炭学报,2016,41(1):14-23.
QIN Yong,SHEN Jian,SHEN Yulin.Joint mining compatibility of superposed gas-bearing systems:A general geological problem for extraction of three natural gases and deep CBM in coal series[J].Journal of China Coal Society,2016,41(1):14-23.
[2] 孟尚志,李勇,王建中,等.煤系“三气”单井筒合采可行性分析——基于现场试验井的讨论[J].煤炭学报,2018,43(1):168-174.
MENG Shangzhi,LI Yong,WANG Jianzhong,et al.The co-production feasibility of “three gases” in coal measures:Discussion based on field test wells[J].Journal of China Coal Society,2018,43(1):168-174.
[3] LI Y,TANG D,WU P,et al.Continuous unconventional natural gas accumulations of Carboniferous-Permian coal-bearing strata in the Linxing area,northeastern Ordos basin,China[J].Journal of Natural Gas Science & Engineering,2016,36:314-327.
[4] GRAY I.Reservoir engineering in coal seams:Part 1—The physical process of gas storage and process of gas storage and movement in coal seams[J].SPERE,1987,2:28-34.
[5] SAWYER W K,PAUL G M,SCHRAUFNAGEL R A.Development and application of a 3D coalbed simulator[A].The international technical meeting of cim petroleum society and SPE[C].Calgary:SPE,1990.
[6] SEIDLE J P,HUIT L G.Experimental measurement of coal matrix shrinkage due to gas desorption and implications for cleat permeability increases[A].The International Meeting on Petroleum Engineering[C].Beijing:SPE,1995.
[7] MOFAT D H,WEALE K E.Sorption by coal of methane at high pressure[J].Fuel,1955,34:449-462.
[8] RECROFT P J,PATEL H.Gas-induced swelling in coal[J].Fuel,1996,65:816-820.
[9] PALMER I,MANSOORI J.How permeability depends on stress and pore pressure in coalbeds:A new model[A].The SPE annual technical conference and exhibition[C].Denver:SPE,1996.
[10] 陈振宏,王一兵,杨焦生,等.影响煤层气井产量的关键因素分析——以沁水盆地南部樊庄区块为例[J].石油学报,2009,30(3):409-416.
CHEN Zhenhong,WANG Yibing,YANG Jiaosheng,et al.Influencing factors on coal-bed methane production of single well:A case of Fanzhuang Block in the south part of Qinshui Basin[J].Acta Petro-lei Sinica,2009,30(3):409-416.
[11] 陶树,汤达祯,许浩,等.沁南煤层气井产能影响因素分析及开发建议[J].煤炭学报,2011,36(2):194-198.
TAO Shu,TANG Dazhen,XU Hao,et al.Analysis on influence factors of coalbed methane wells productivity and development proposals in southern Qinshui Basin[J].Journal of China Coal Society,2011,36(2):194-198.
[12] 李勇,汤达祯,许浩,等.柳林地区煤层气勘探开发模式研究[J].天然气地球科学,2014,25(9):1462-1469.
LI Yong,TANG Dazhen,XU Hao,et al.Exploration and development model of coalbed methane in Liulin area,China[J].Natural Gas Geoscience,2014,25(9):1462-1469.
[13] 邵长金,邢立坤,李相方,等.煤层气藏多层合采的影响因素分析[J].中国煤层气,2012,9(3):8-12.
SHAO Changjin,XING Likun,LI Xiangfang,et al.Analysis of factors influencing co-production of multi-seam in CBM reservoir[J].China Coalbed Methane,2012,9(3):8-12.
[14] 吕玉民,汤达祯,许浩,等.韩城煤层气田气井合采产能特征及其影响因素探析[A].煤层气学术研讨会[C].杭州,2013.
[15] 何应付,张亚蒲,鲜保安,等.煤层气藏垂直裂缝井压力动态分析[J].石油天然气学报:江汉石油学院学报,2006,28(5):113-117.
HE Yingfu,ZHANG Yapu,XIAN Baoan,et al.Dynamic analysis of vertical fracture well pressure in coalbed methane reservoir[J].Journal of Oil and Gas Technology,2006,28(5):113-117.
[16] 朱维耀,岳明,宋洪庆,等.考虑解吸扩散过程的煤层气压裂直井产能模型研究[J].应用基础与工程科学学报,2013,21(5):953-960.
ZHU Weiyao,YUE Ming,SONG Hongqing,et al.Productivity model of gas flow in cbm fractured reservoirs considering desorption and diffusion[J].Journal of Basic Science and Engineering,2013,21(5):953-960.
[17] 同登科,刘文超,薛莉莉.变形三重介质低渗透油藏三渗模型流动特征[J].力学季刊,2010,31(3):334-341.
TONG Dengke,LIU Wenchao,XUE Lili.Flow characteristics of three-permeability model of low-permeability reservoir in deformed triple-medium[J].Chinese Quarterly of Mechanics,2010,31(3):334-341.
[18] 张先敏,冯其红,陈东,等.阜新盆地煤层气渗流规律实验[J].重庆大学学报,2011,34(4):58-61.
ZHANG Xianmin,FENG Qihong,CHEN Dong,et al.Experiment on seepage of coalbed methane in Fuxin basin[J].Journal of Chongqing University,2011,34(4):58-61.
[19] 马天然,刘卫群,陈兴.基于图像识别的裂隙煤层气非Darcy渗流模拟[J].力学季刊,2013,34(3):494-500.
MA Tianran,LIU Weiqun,CHEN Xing.Simulation of non-Darcey seepage of fractured coalbed methane based on image recognition[J].Chinese Quarterly of Mechanics,2013,34(3):494-500.
[20] 王晓冬,张义堂,刘慈群.垂直裂缝井产能及导流能力优化研究[J].石油勘探与开发,2004,31(6):78-81.
WANG Xiaodong,ZHANG Yitang,LIU Ciqun.Productivity evaluation and conductivity optimization for vertically fractured wells[J].Petroleum Exploration and Development,2004,31(6):78-81.
[21] WANG Lei,WANG Xiaodong,DING Xumin,et al.Rate decline analysis of a vertical fractured well with fracture face damage[J].Journal of Energy Resources Technology-transactions of the Asme,2012,134(2):032803.
[22] CUI Xiaojun,BUSTIN R M.Volumetric strain associated with methane desorption and its impact on coalbed gas production from deep coal seams.AAPG Bulletin,2005,89(9):1181-1202.