软岩巷道以“围岩软，强度低，强膨胀性”等显著性特点，困扰着煤矿的正常生产，尤其是煤矿软岩处在富水条件下，巷道围岩的蠕变速率快，变形量大，如果软岩巷道支护不得当，会造成工程的返修量，不仅造成经济的损失，而且会使整个矿井陷入困境，甚至关闭。因此，开展对具有时间效应的富水软岩蠕变特性研究，不仅可以对含水条件下岩体流变规律有更清晰地认识，而且能为富水软岩巷道的支护理论和支护技术方面提供更可靠、更全面的资料。
为了解决岩石力学的实际问题及其深入认识岩石本身的流变特性，目前大量的岩石力学研究者基于蠕变特性和损伤理论，致力于建立恰当的本构模型[1-6]。SINGH和MICTHELL[7]总结前人关于剪应力作用下应力应变的时间特性的成果，认为D(偏应力水平)固定时ln
和lnt，时间固定时ln和D都成直线关系(其中
是偏态蠕变速率，t偏态蠕变作用时间)，得到偏态蠕变规律，WU Xijia等[8]建立了一种识别变形机制的应力-应变蠕变模型。该模型提供了一种基于物理的对整个蠕变变形过程、断裂应变和寿命的描述，与实验结果吻合较好。ZHAO Y R等[9]在物理模型中，预测改进的9cr-1mo钢的长期蠕变强度和寿命，指出应力指数的变化不是由于蠕变机理的变化，而是由于在不同的蠕变荷载作用下的微观结构变化。尹光志等[10]采用Burgers体模型对采动影响下的岩石蠕变损伤破坏机理分析，建立反映岩体蠕变损伤破坏特征的煤岩蠕变损伤模型。陶波等[11]用三轴压缩蠕变试验结果，分别利用伯格斯模型及西原模型，运用最小二乘法对赵各庄煤矿断层破碎带灰黄色糜棱岩的流变曲线进行了拟合，并求取了流变参数。拟合结果表明西原模型更适合描述岩石蠕变特性。巨能攀等[12]研究了红层泥岩蠕变的非线性特征，提出一个黏弹性模量，并建立一个改进的伯格斯模型。沈明荣等[13]通过对锦屏II级水电站引水隧洞中含有绿片岩软弱结构面的灰白色大理岩进行分级加载剪切流变试验，结果显示结构面的剪切蠕变试验曲线表现出明显的3个阶段，在此基础上选用改进的Burgers模型，探讨了绿片岩软弱结构面的蠕变特性。李鹏等[14]通过开展不同含水率条件下砂岩软弱结构面剪切蠕变试验，得到了不同含水率条件下剪切蠕变曲线，并考虑加载历史对试验曲线进行了修正。齐亚静等[15]通过在西原模型上串联一个带应变触发的非线性黏壶，提出改进的西原模型，推导岩石在恒应力情况下的三维蠕变本构方程，并采用该流变模型对三峡库区万州红层砂岩流变试验全过程曲线进行辨识，获得模型各参数值。舒志乐等[16]在分析应力水平、孔隙水压力对蠕变特性影响的基础上，提出了一个非线性黏滞系数牛顿元件，其黏滞系数是所加应力水平、孔隙水压力和蠕变时间的函数，将非线性黏性模型与西原模型串联，得到一个软岩非线性黏弹塑性蠕变模型，推导了不同恒定荷载情况下的蠕变方程，并分析了模型的非线性特征和参数的敏感性，初步表明复合流变模型的适用性和正确性。杨圣奇等[17]通过岩石非线性流变变形是时间的Weibull分布函数的假定，提出了一个新的非线性流变元件(NRC模型)，将NRC模型与西原模型的串联，建立一个新的岩石非线性流变模型;利用盐岩单轴压缩流变试验曲线对所建立的模型进行辨识，获得了岩石非线性流变参数。
综上所述，软岩蠕变特性的研究具有十分重要的理论价值和工程意义，若能够深入了解，将可以完全掌握在复杂应力状态下软岩蠕变特性和破坏机理，可以为软岩体工程的长期稳定性与安全性提供参考依据，丰富和完善岩石流变力学的研究。由于软岩的主要矿物成分是黏土矿物，它具有亲水性、不连续面、活性大、力学性质灵敏等性质，遇水后对其蠕变应力有效值的分布、蠕变变形量都会产生影响。另外，已知的西原模型仅能描述线性阶段(初始蠕变和稳态蠕变)，而无法描述非线性阶段(加速蠕变)。当前对研究含水率问题的蠕变模型也不太多，假设有一种本构模型，既能考虑含水率对软岩力学参数的影响，又能顾及软岩蠕变力学参数的时间效应，它才能够准确无误地描述富水软岩的蠕变特性。因此笔者针对含水软岩蠕变特性，提出一种反映含水率影响的非线性剪切加速蠕变启动模型用来描述含水软岩蠕变全过程，并通过实验结果对该模型进行验证。
1 考虑含水率的蠕变试验特性分析
1.1 剪切蠕变试验
选取某矿软岩巷道的岩石进行室内天然直剪试验，富水软岩的含水率w分别是5%，12%，24%，试件的直径是50 mm，高为100 mm的圆柱体，采用分级加载的方法，分为4个荷载等级:32，40，48，64 kPa。根据试验数据整理出各级剪应力作用下的蠕变曲线(图1)和等时应力-应变曲线(图2)。
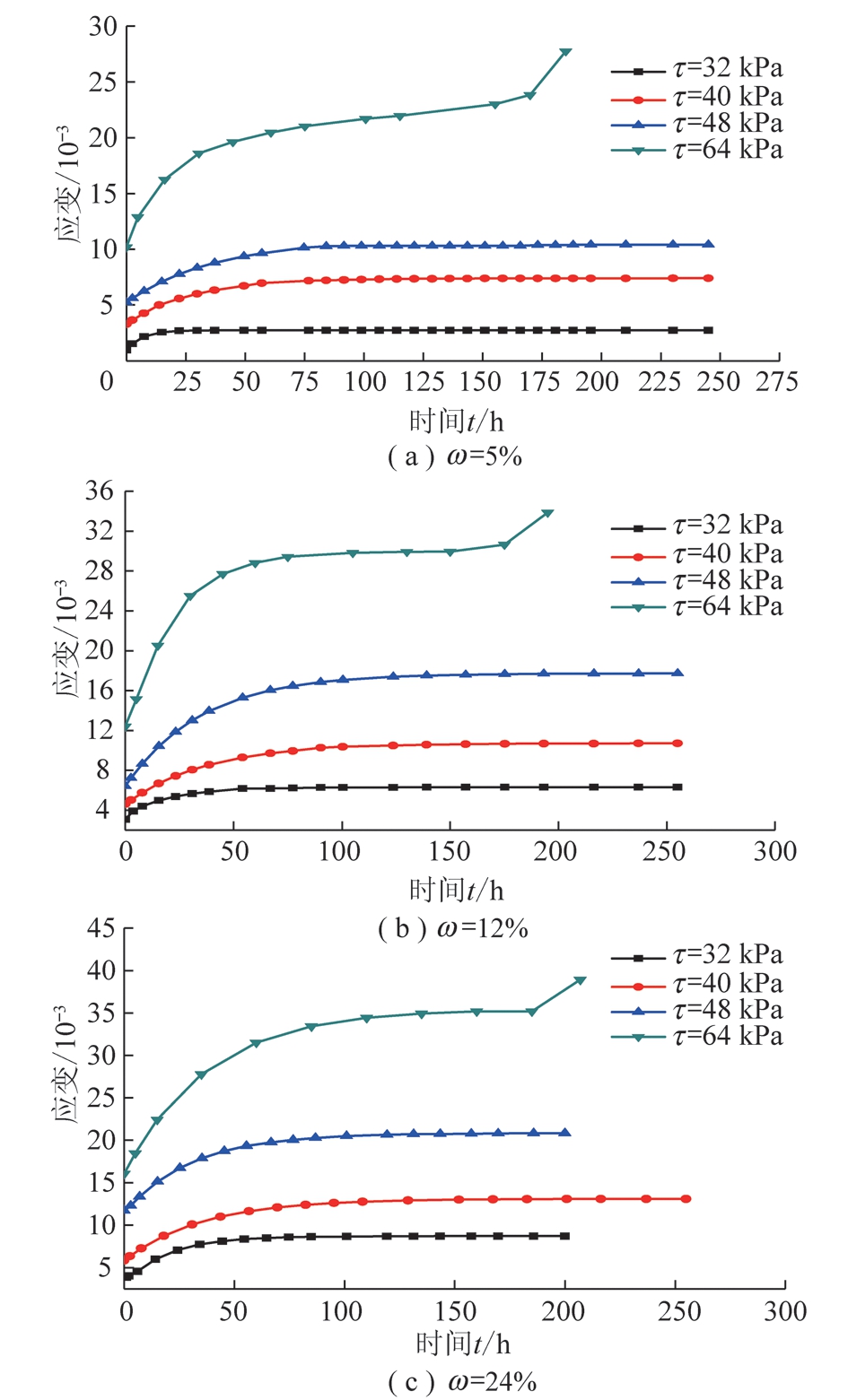
图1 分级加载蠕变曲线
Fig.1 Hierarchical loading creep curves
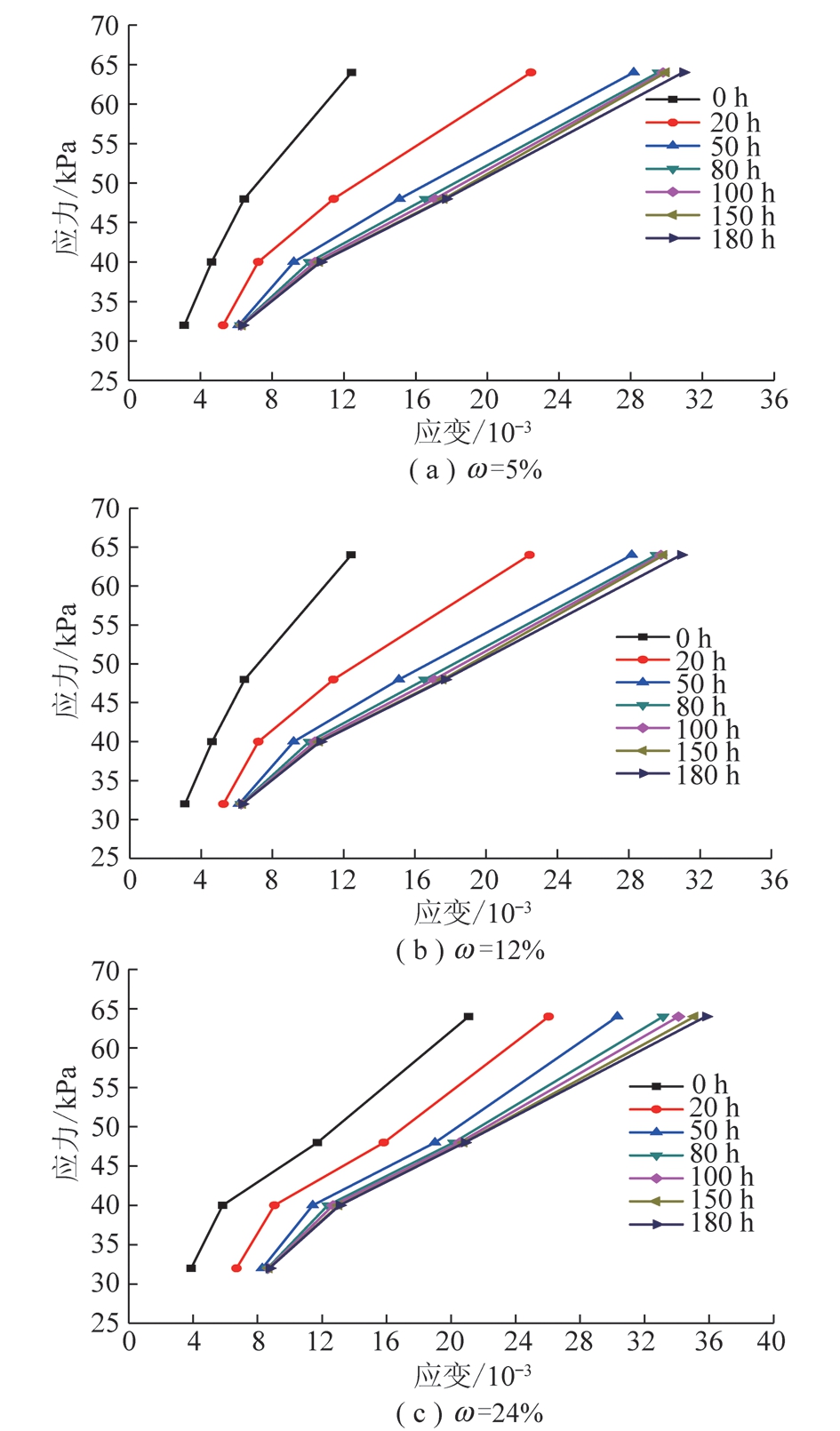
图2 等时应力-应变曲线
Fig.2 Isochronous stress-strain curves
1.2 含水率的影响
表1为不同含水岩样蠕变的瞬时弹性模量E0值，可知随着软岩含水率的增加，其瞬时弹性模量E0越来越小。所谓的瞬时弹性模量就是岩样所施加的应力跟刚加载时的瞬时应变的比值，其大小决定了岩样抵抗瞬时弹性变形的能力。这是由于水能够影响岩石的物理和化学作用，从而改变岩石的成分和结构。当含水率较低时,孔隙中的主要成分是空气，压缩孔隙时没有太大的阻碍，所以弹性模量随着含水率的增加而降低;当孔隙中的含水率达到一定程度时，由于水和空气的压缩系数差距非常大，导致水分子还没有来得及向四周挤出，因而瞬时弹性模量会出现一定量的回弹现象，所以随着含水率的越来越大，其瞬时弹性模量的下降程度会越来越小。从图3所示的各级剪应力不同含水状态蠕变曲线可以看出，在同一应力条件下，随着含水率的增加岩石的极限蠕变应变也跟着增加，由表2可知，含水率的增加会使得极限蠕变变形模量E1明显降低，说明含水率对软岩蠕变有极大地影响。
表1 不同含水岩样蠕变的E0值
Table 1 E0value of creep of different water-bearing rock samples
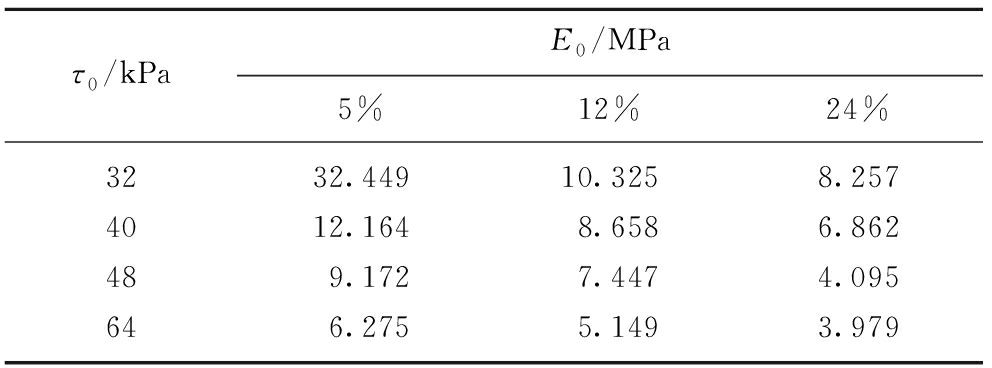
水能够改变软岩的时效性，因此对软岩的蠕变性状有了本质上的改变。因为水改变了岩石的力学性质，其承载能力和弹性模量都会随着含水率的增加而越来越小。液体(水)和气体统称为流体，水具有流动性，在外力的作用下内部发生相对运动，使得岩体内部孔隙增多，岩体的强度降低，故而岩石的极限蠕变变形量增大，极限蠕变变形模量则减小。
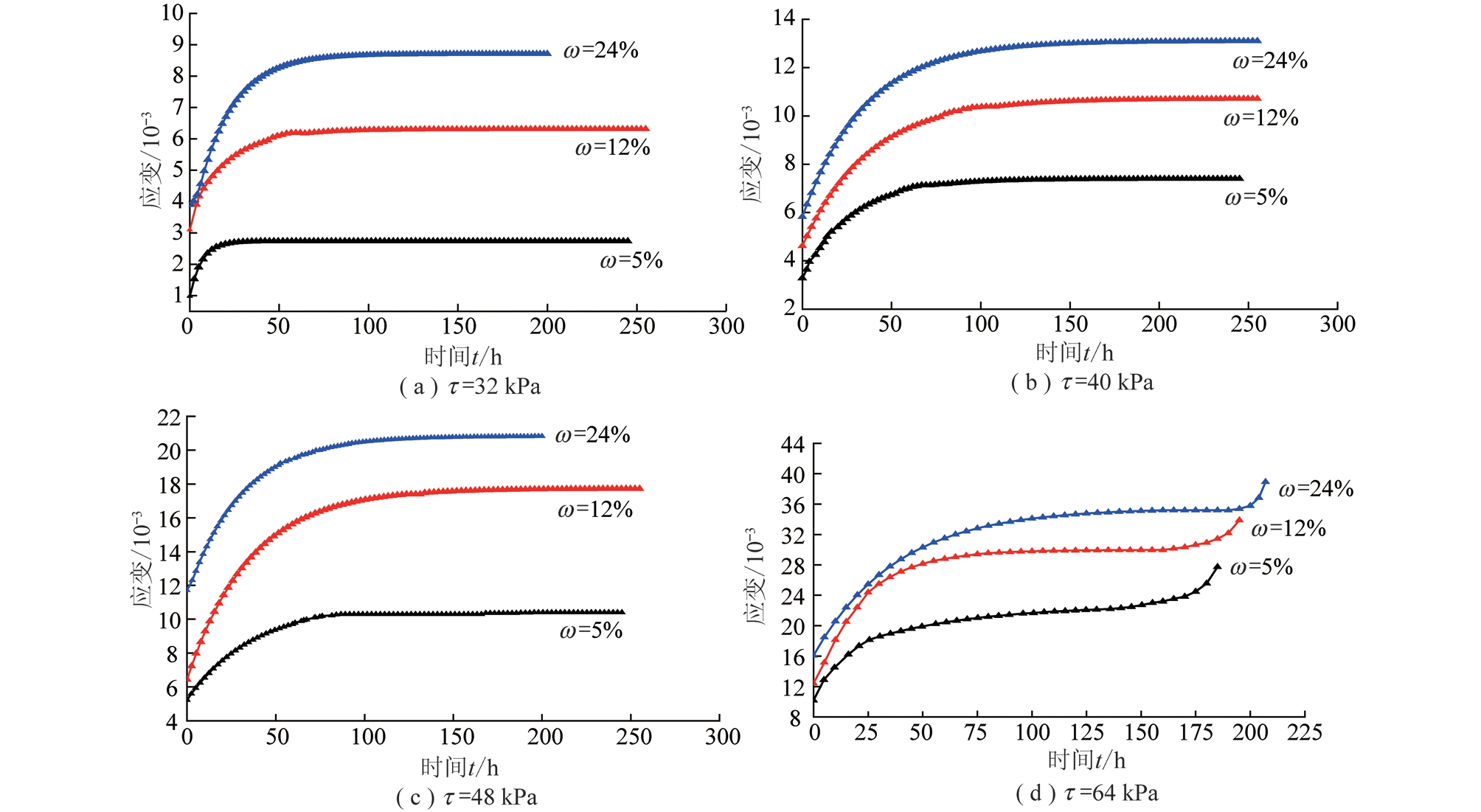
图3 各级剪应力不同含水状态的蠕变曲线
Fig.3 Creep curve of different shear stress at different levels
表2 不同含水岩样蠕变的E1值
Table 2 E1 value of creep of different water-bearing rock samples
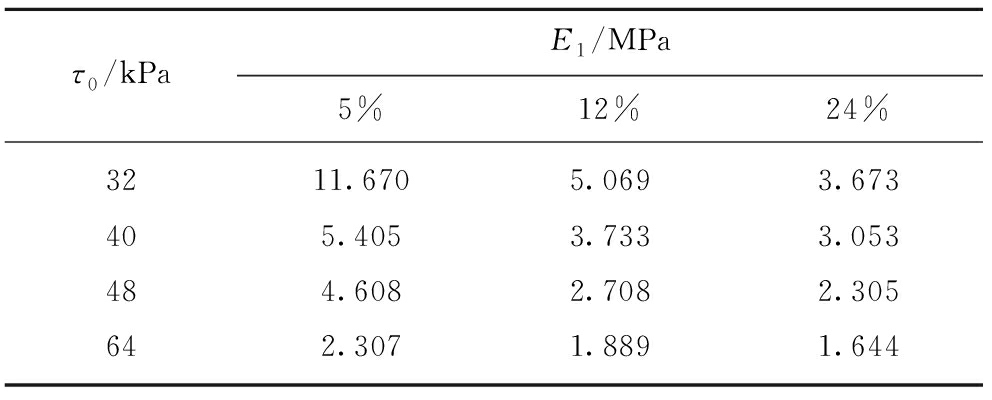
岩石的蠕变应变速率v跟模型参数η(黏滞系数)是密切相关的，由图4所示的各级剪应力不同含水状态的蠕变速率曲线可知，岩石的含水率和蠕变应变速率成正比例关系，因而岩石的模型参数η会随着含水率的增加变得越来越小，是由于有水侵入时，可溶岩溶解，胶体水解，使原有的连接变成水胶连接，极大的阻碍了矿物颗粒间的连接作用，则其摩擦力也会降低，这就是所谓水的润滑作用。当含水率相同时，随着应力水平的增加黏滞系数η的降低的程度不会很大，说明黏滞系数η是岩石蠕变性能的综合体现。在应力达到64 kPa时，蠕变速率曲线呈马蹄形(图4(d))，左侧代表的衰减蠕变阶段，右侧则是加速蠕变阶段，且左侧蠕变速度小于右侧蠕变速度，因而在应力水平相对较大且发生加速蠕变时，含水率越大，其加速破坏速率就越快。
由图4可以看出，伴随着含水率的上升，软岩蠕变进入稳定阶段的时间就会延长，由于岩石在水、应力及其蠕变等的作用下会产生新的孔隙，这样会使得岩石的孔隙数目增多。此外，水的流动需要一个时间过程，所以水的流速就会降低，进入稳态蠕变的时间就会增加。
岩石是由矿物颗粒连接在一块的，水的侵入会使其强度大大降低，含水率越大说明岩石的强度就越小，这样就会使得岩石的破坏时间就会缩短。加速蠕变阶段，岩石的蠕变速率大，作用在岩石上的应力也大，强度越低就破坏的越快。故而随着含水率的增加岩石的破坏时间就越短(图3，4)。
通过以上的分析，含水率对蠕变的瞬时弹性模量E0、极限弹性模量E1、进入稳态阶段的时间、蠕变速率及其黏滞系数η都有至关重要的影响，并且它也满足非线性流变理论，说明模型参数里面考虑含水率是有必要的。
1.3 剪切应力水平的影响
由图1所示的分级加载蠕变曲线可以看出，含水率恒定的情况下，随着每一级剪切应力的加载，都会发生明显的瞬时变形，且其随着剪切应力的增大而增大。当剪切应力τ小于64 kPa时，蠕变的变形会随着时间的变化越来越小，最后趋近于一个稳定的值，不再变化。然而，当剪切应力τ大于64 kPa时，稳态蠕变随着时间的增加就会发生加速蠕变，变形速率大，直至岩石被破坏。在蠕变曲线中衰减阶段的形态变化与剪应力水平的大小有关，当剪应力水平增大时，衰减蠕变曲线的曲率半径也会随之增大，意味着达到稳态的时间就会延长。因此在非线性剪切流变模型里考虑剪切应力τ是非常有价值的。
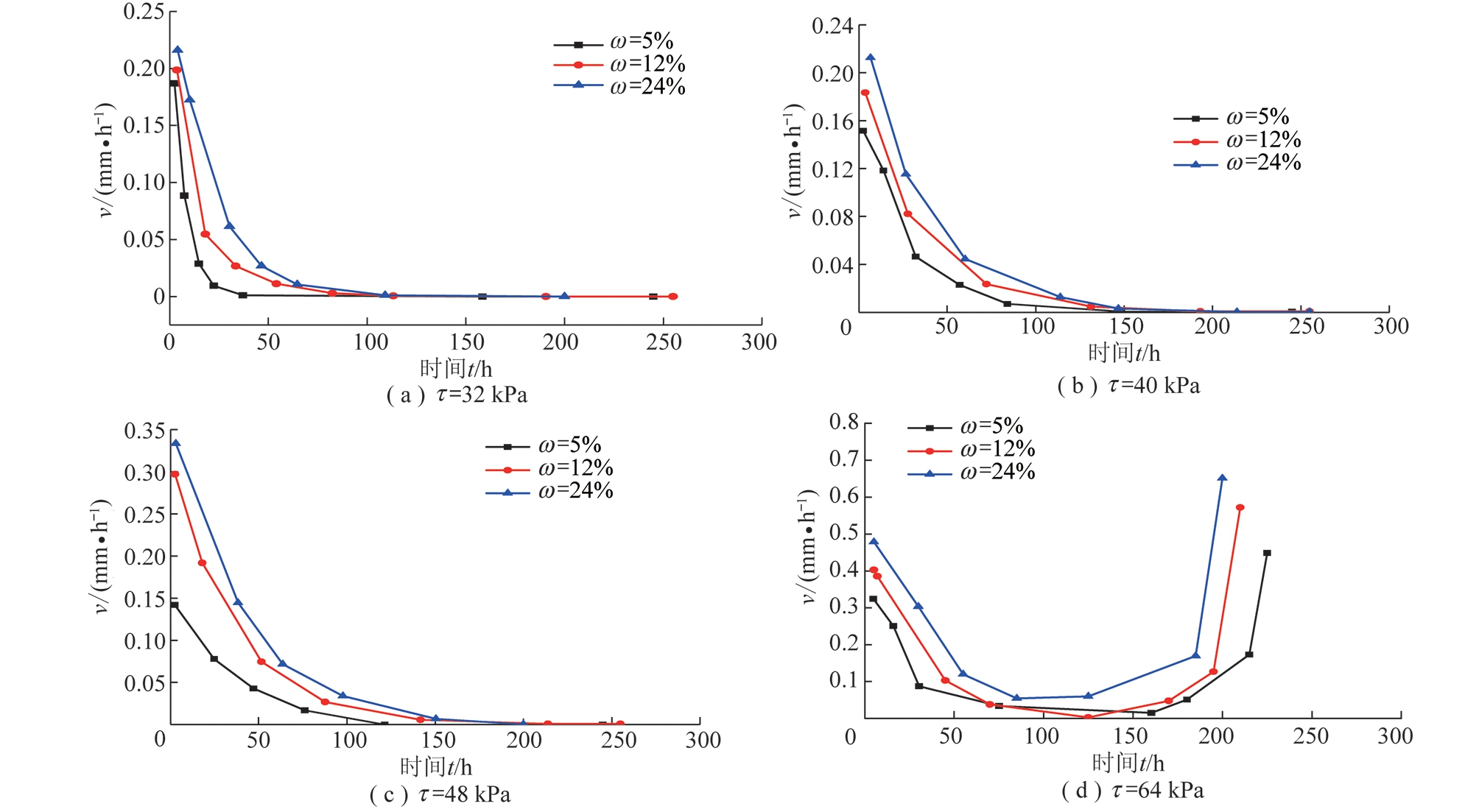
图4 各级剪应力不同含水状态的蠕变速率曲线
Fig.4 Creep rate curve of different shear stress at different levels
2 改进的NRC模型
由图2可以看出，软岩蠕变的非线性特征逐渐体现出来，在未达到屈服强度前，软岩蠕变主要表现为黏弹性变形，黏弹性就是等时应力应变曲线途中近线性，应此将它的斜率定义为黏弹性模量G。
杨圣奇等[18]为了能充分反映岩石加速流变变形，通过对龙滩水电站泥板岩剪切流变力学特性的研究，提出一个描述加速流变的非线性流变元件，简称NRC模型。NRC模型在剪应力恒定的条件下，剪切位移与黏弹性模量G、时间t变化有关。
考虑到含水率对岩石蠕变的影响，笔者通过软岩等时应力应变曲线，得到黏弹性模量G跟含水率ω的曲线关系图5。因而将NRC模型中的流变参数G建立为一个与含水率ω有关的函数，实质是一个改进的NRC模型。
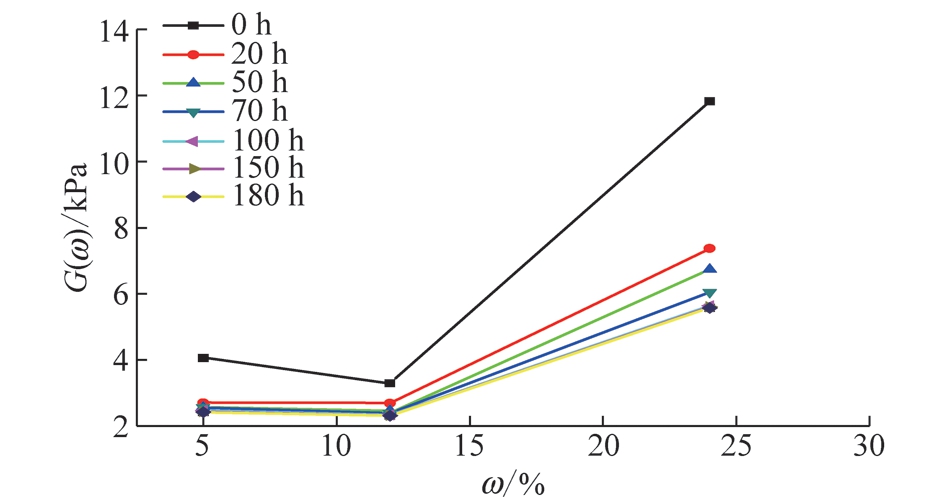
图5 黏弹性模量与含水率关系
Fig.5 Relationship between viscoelastic modulusand moisture content
由图5可以看出，此曲线是非线性的，用多项式方程
G(ω)=B0+B1ω+B2ω2
(1)
进行回归，得B0,B1,B2，见表3。式中，B0为反映剪应力水平对黏滞系数影响的特征参数;B1为与含水率有关的加速蠕变因子;B2为与含水率有关的稳态蠕变因子。
表3 G(ω)的多项式回归结果
Table 3 Polynomial regression results of G(ω)
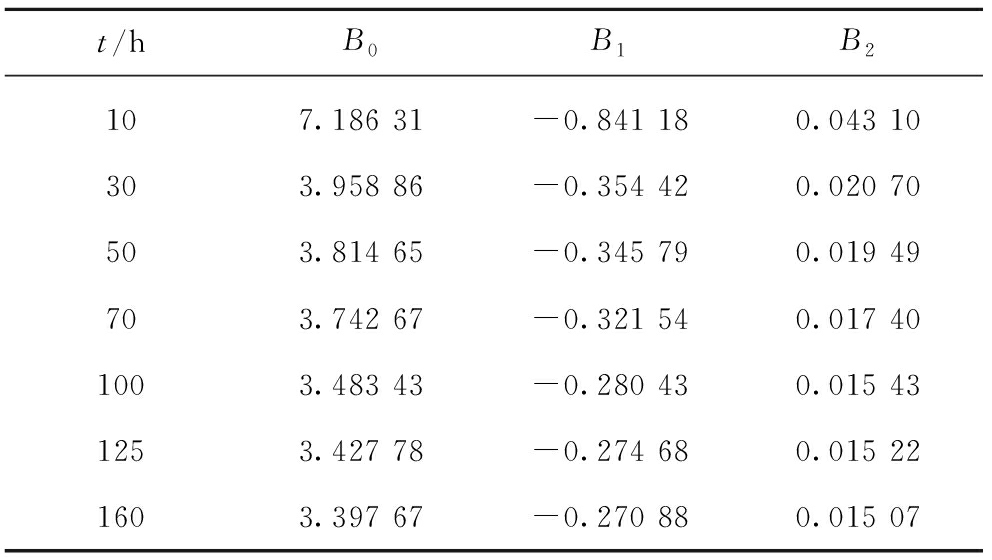
由表3可知B0，B1，B2随着时间t的变化而变化，用关系式B=aexp(-t/b)+c进行非线性拟合，得出
G(ω,t)=a0exp(-t/b0)+c0+[a1exp(-t/b1)+
c1]ω+[a2exp(-t/b2)+c2]ω2
(2)
即表示了黏弹性模量G与时间t及含水率ω之间的关系。通过式(2)可以建立软岩蠕变受含水率和时间影响的水岩作用时效力学响应过程。
3 非线性剪切蠕变模型及参数敏感性分析
3.1 含水率有关的非线性剪切蠕变模型
岩石流变过程往往是弹性、黏性、塑性、黏弹性和黏塑性等多种变形共存的一个复杂过程，因而需要采用多种原件(线性和非线性元件)的复合来对其进行模拟。传统的西原模型只能模拟初始蠕变和稳态蠕变，而对于非线性加速蠕变难以描述，因此，给传统的西原模型串联一个改进的NRC模型，组合成一个考虑含水率的岩石非线性黏弹塑性剪切流变模型(图6)来进行模拟。该非线性剪切蠕变模型的状态及蠕变方程分为如下:
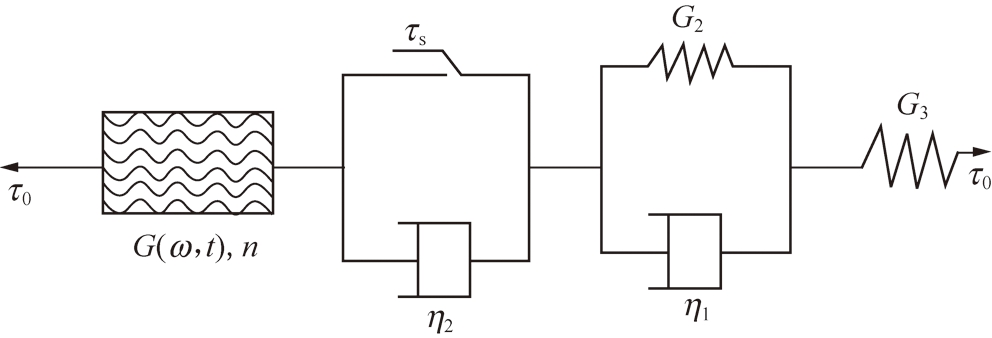
图6 软岩非线性剪切蠕变模型
Fig.6 Nonlinear shear creep model of soft rock
(1)当τ0≤τs时，非线性黏塑性体失效，成为三元件广义Kelvin流变模型，相应的状态方程为
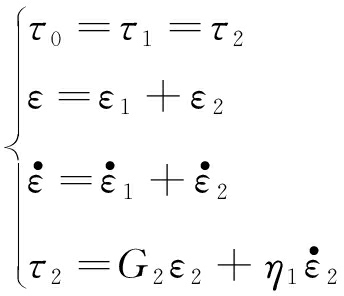
(3)
式中，τ为剪切应力;ε为剪切位移;
为蠕变速率;G2为黏弹性剪切模量;η为黏滞系数;τs为屈服强度。
相应的蠕变方程为
(4)
式中,G1为瞬时剪切模量;u为岩石总的剪切位移。
(2)当τ0>τs且t≤tp时，是传统的西原流变模型，相应的状态方程为
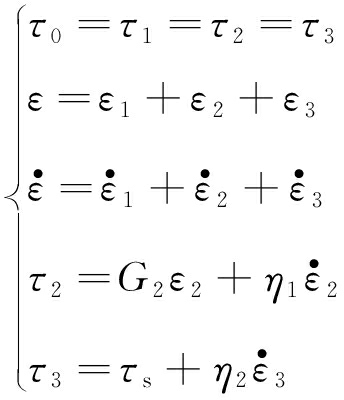
(5)
式中，tp为岩石发生加速蠕变的时间。
相应的蠕变方程为
(6)
(3)当τ0>τs且t>tp时，改进的NRC模型发挥作用，相应的状态方程为
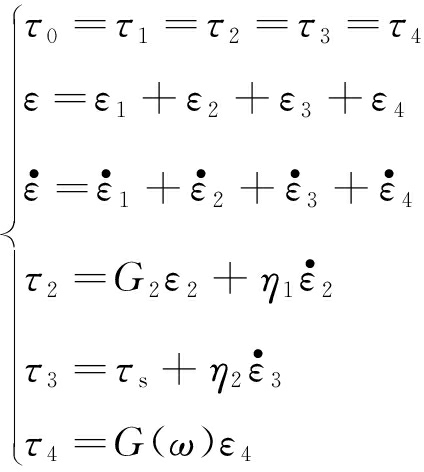
(7)
相应的蠕变方程为
(8)
式中，tFR为岩石破坏的瞬间时刻;G3与n为NRC模型中的蠕变参数;τ为剪切应力;
为ε与时间t的一阶导数;η为黏滞系数。
其中，H(τ0-τs)为正值函数:
(9)
3.2 参数B0，B1，B2的敏感性分析
(1)当应力、含水率及其余参数都相同时参数B0取不同的值(B0=0.25,0.30,0.45)，利用式(8)得到蠕变曲线，如图7所示。
(2)当应力、含水率及其余参数都相同时参数B1取不同的值(B1=0.25,0.30,0.45)，利用式(8)得到蠕变曲线，如图8所示。
(3)当应力、含水率及其余参数都相同时参数B2取不同的值(B2=0.25,0.30,0.45)，利用式(8)得到蠕变曲线，如图9所示。
由图7，8，9可知，蠕变参数B1，B2一定时，随着参数B0的增加，蠕变变形量变化不大，蠕变速率几乎为0，岩石完全处于黏弹性阶段，然而当蠕变参数B1
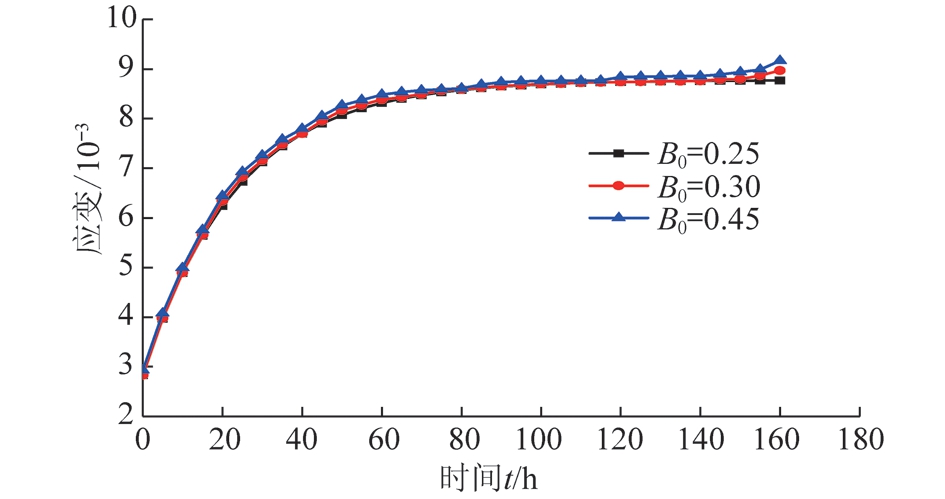
图7 参数B0不同取值时非线性剪切流变模型蠕变曲线
Fig.7 Parameters of B0of different values of nonlinear creep shear rheological model curves
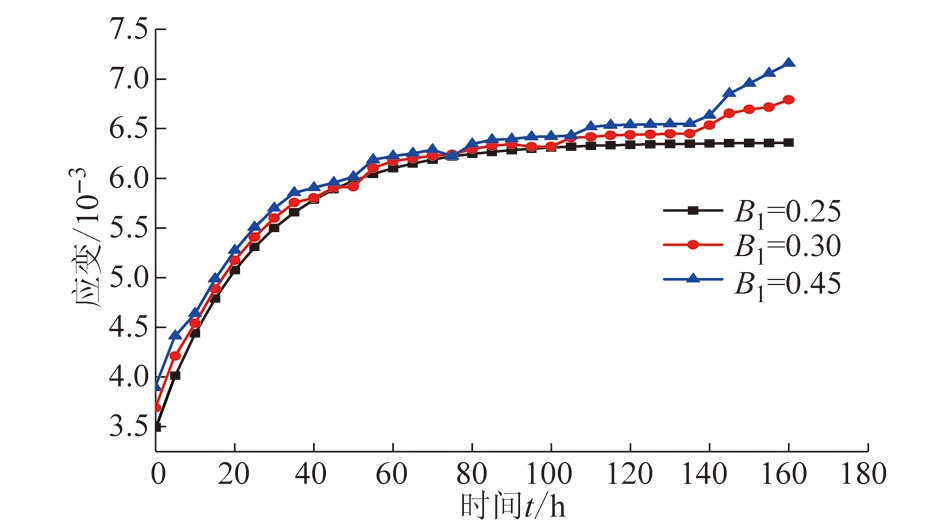
图8 参数B1不同取值时非线性剪切流变模型蠕变曲线
Fig.8 Parameters of B1of different values of nonlinear creep shear rheological model curves
的值逐渐增大时，蠕变变形量也逐渐增大，变化速率直线上升，表明软岩蠕变全程曲线逐渐由黏弹性向黏弹塑性过渡，充分反映水对软岩软化的蠕变特性。蠕变参数B2的增大，致使蠕变变形和蠕变速率先增大后减小，是破坏后的一种回弹现象。综上所述，与含水率有关的加速蠕变因子B1敏感性最强，与含水率有关的稳态蠕变因子B2次之，特征参数B0敏感性最差。
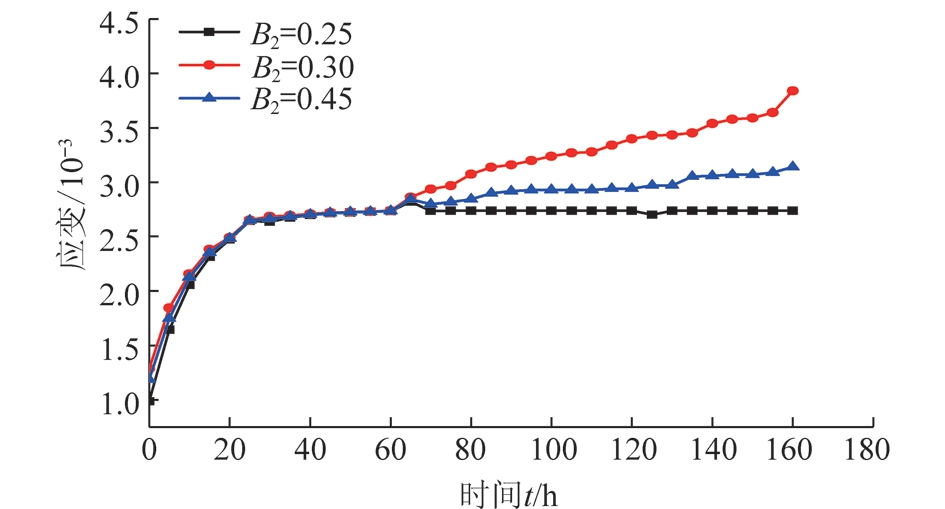
图9 参数B2不同取值时非线性剪切流变模型蠕变曲线
Fig.9 Parameters of B2of different values of nonlinear creep shear rheological model curves
4 流变模型参数的确定及验证
基于蠕变试验结果，采用精确可靠的技术方法，对蠕变模型中的参数进行识别，使模型拟合曲线能与实验曲线更好的吻合，这是蠕变模型研究中必不可少的一部分。本文基于BFGS算法和通用全局优化法的数学优化软件1st Opt对图1曲线进行辨识，得出相关参数见表4和5。由于软岩的水理性质和力学性质，即使在正应力相等条件下，各试样的蠕变参数值的大小会反映出含水率和剪应力对软岩蠕变特性的影响。图10为剪应力64 kPa条件下的剪切蠕变变实验值与所建立的非线性剪切蠕变模型的对比，图11为含水率为24%条件下的剪切蠕变实验值与建立的蠕变模型的对比。由图10和11可以看出，软岩非线性剪切蠕变模型拟合曲线与直剪实验结果吻合良好，通过表4，5及图10，11得到的瞬时弹性模量E0、极限蠕变变形模量E1、蠕变应变速率v、黏滞系数η、进入稳态的时间及其加速蠕变的破坏时间，与1.2节和1.3节的蠕变特性分析完全符合，这表明本节所建立的剪切流变理论模型的正确性与合理性。
表4 富水软岩非线性剪切流变模型参数
Table 4 Parameters of nonlinear shear rheological model of rich soft rock
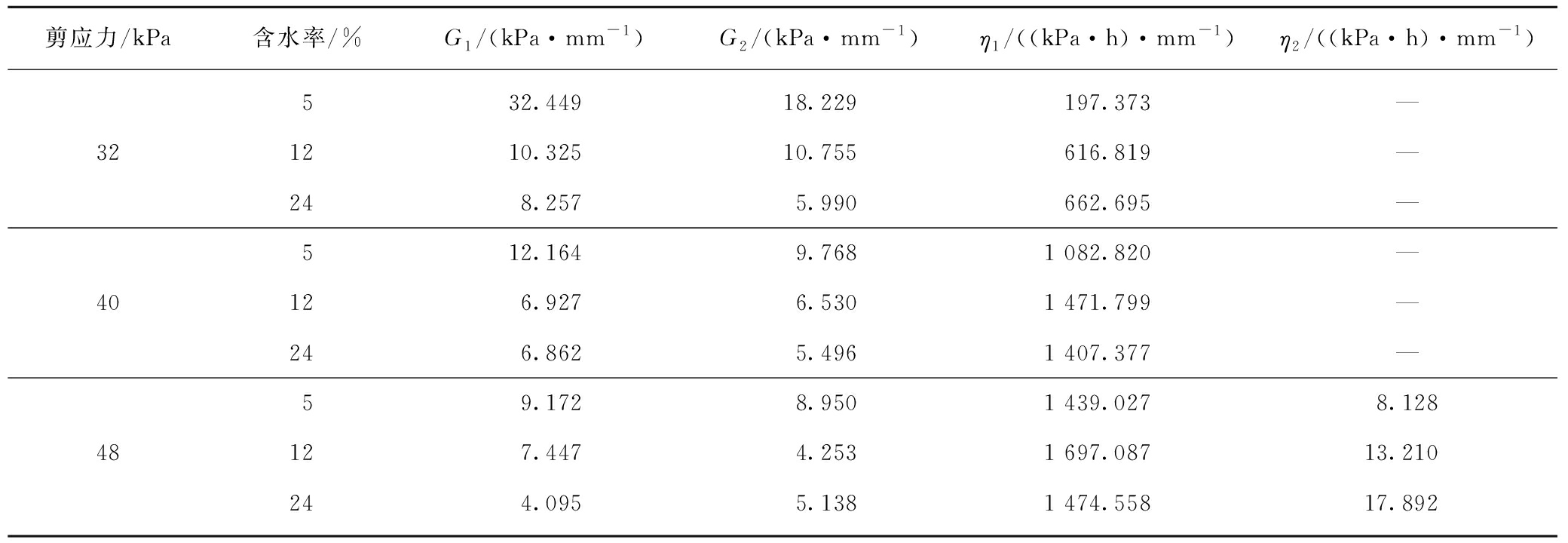
表5 富水软岩线性剪切流变模型参数
Table 5 Parameters of linear shear rheological model of rich soft rock
注：G1,G2单位为kPa/mm;η1,η2单位为(kPa·h)/mm;B0,B1,B2单位为kPa/mm。
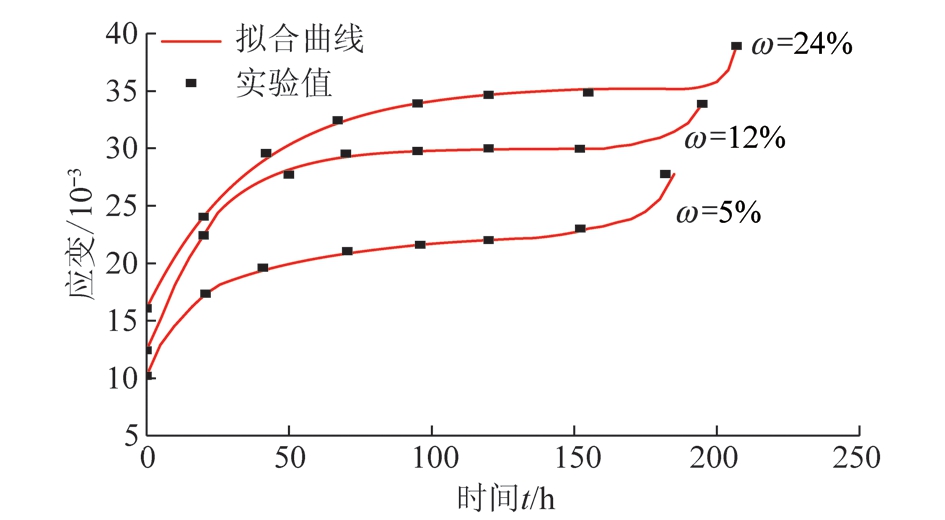
图10 τ=64 kPa非线性剪切流变模型和实验值对比
Fig.10 Comparison of τ=64 kPa linear shear rheological model and experimental value
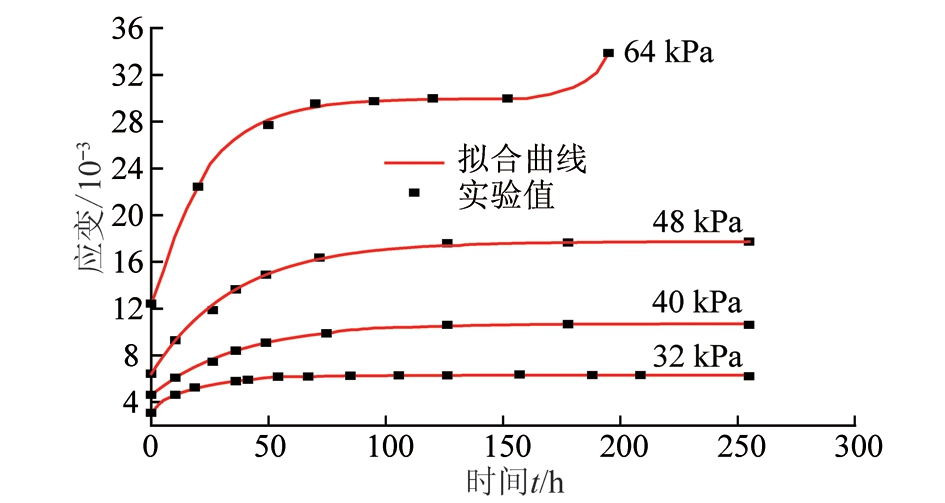
图11 ω=24%非线性剪切流变模型和实验值对比
Fig.11 Comparison of ω=24% linear shear rheological model and experimental value
5 结 论
(1)通过对某矿软岩进行蠕变试验表明:软岩在剪切应力水平恒等时，含水率的逐渐增大，使得瞬时弹性模量E0、极限蠕变变形模量E1和黏滞系数η呈递减趋势;蠕变速率v先减小后增大呈马蹄形，且左边蠕变速率小于右边蠕变速率;岩石的破坏时间就会减少。
(2)软岩在同一含水率条件下，随着剪切应力的增加，跟时间变化有关的剪切应变逐渐增加 。在每一级加载时，会出现瞬时剪切应变，其变化随着剪应力的增大而增大。另外，剪应力的大小跟蠕变曲线中衰减阶段的曲率半径呈正比例函数，剪应力越大曲线进入稳态蠕变的时间就会延迟。当达到一定的剪切应力水平时，软岩蠕变速率迅增，直至破坏。
(3)建立了一个有关含水率变化的软岩非线性剪切蠕变模型，并且经过蠕变方程分析了改进的NRC模型参数的敏感性，认为该模型能够较为准确的描述软岩在不同含水率条件下随时间变化的非线性蠕变特性。
(4)通过直剪实验获得的数据验证考虑含水率变化的非线性剪切蠕变模型，结果表明试验曲线与模型曲线吻合良好，证明了该复合流变模型的适用性和正确性。
参考文献(References):
[1] 徐平,杨挺青.岩石流变试验与本构模型辨识[J].岩石力学与工程学报,2001,20(S1):1739-1744.
XU Ping,YANG Tingqing.Current research on the rheological test and model identification of rock[J].Chinese Journal of Rock Mechanics and Engineering,2001,20(S1):1739-1744.
[2] 刘江,杨春和,吴文,等.盐岩蠕变特性和本构关系研究[J].岩土力学,2006,27(8):1267-1271.
LIU Jiang,YANG Chunhe,WU Wen,et al.Study on creep characteristics and constitutive relation of rock salt[J].Rock and Soil Mechanics,2006,27(8):1267-1271.
[3] 陈卫忠,王者超,伍国军,等.盐岩非线性蠕变损伤本构模型及其工程应用[J].岩石力学与工程学报,2007,26(3):467-472.
CHEN Weizhong,WANG Zhechao,WU Guojun,et al.Nonlinear creep damage constitutive model of rock salt and its application to engineering[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(3):467-472.
[4] 王军保,刘新荣,郭建强,等.盐岩蠕变特性及其非线性本构模型[J].煤炭学报,2014,39(3):445-451.
WANG Junbao,LIU Xinrong,GUO Jianqiang,et al.Creep properties of salt rock and its nonlinear con-stitutive model[J].Journal of China Coal Society,2014,39(3):445-451.
[5] 王来贵,何峰,刘向峰,等.岩石试件非线性蠕变模型及其稳定性分析[J].岩石力学与工程学报,2004,23(10):1640-1642.
WANG Laigui,HE Feng,LIU Xiangfeng,et al.Nonlinear creep model and stability analysis of rock[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(10):1640-1642.
[6] 韦立德,杨春和,徐卫亚.基于细观力学的盐岩变损伤本构模型研究[J].岩石力学与工程学报,2005,24(23):4253-4258.
WEI Lide,YANG Chunhe,XU Weiya.Study on the constitutive model of saline rock damage based on detailed mechanics[J].Journal of Rock Mechanics and Engineering,2005,24(23):4253-4258.
[7] SINGH A,MICTHELL J K.General stress-straln-time functions for soils[J].Soil Mech.Found.Div,Asce,1968,94(1):21-46.
[8] WU Xijia,STEVE Williams,GONG Diguang.A true-stress creep model based on deformation mechanisms for polycrystalline materials[J].Journal of Materials Engineering and Performance,2012,21(11):2255-2262.
[9] ZHAO Y R,YAO H P,SONG X L,et al.On the physical models for predicting the long-term creep strengths and lifetimes of modified 9Cr-1Mo steel[J].Journal of Alloys and Compounds,2017,726:1246-1256.
[10] 尹光志,何兵,王浩,等.深部采动影响下覆岩蠕变损伤破坏规律[J].煤炭学报,2015,40(6):1390-1395.
YIN Guangzhi,HE Bing,WANG Hao,et al.The damage of overburden creep damage under the influence of deep mining[J].Journal of China Coal Society,2015,40(6):1390-1395.
[11] 陶波,伍法权,郭改梅,等.西原模型对岩石流变特性的适应性及其参数确定[J].岩石力学与工程报,2005,24(17):3165-3171.
TAO Bo,WU Faquan,GUO Gaimei,et al.The adaptability and parameters of the rheological properties of the rocks in the western model[J].Journal of Rock Mechanics and Engineering,2005,24(17):3165-3171.
[12] 巨能攀,黄海峰,郑达,等.考虑含水率的红层泥岩蠕变特性及改进伯格斯模型[J].岩土力学,2016,37(S2):67-74.
JU Nengpan,HUANG Haifeng,ZHENG Da,et al.Considering the creep properties of red layer mudstone with moisture content and improving the boggs model[J].Geotechnical Mechanics,2016,37(S2):67-74.
[13] 沈明荣,张清照.绿片岩软弱结构面的剪切蠕变特性研究[J].岩石力学与工程学报,2010,29(6):1149-1155.
SHEN Mingrong,ZHANG Qingzhao.Study on shear creep characteristics of weak structure of green schist[J].Journal of Rock Mechanics and Engineering,2010,29(6):1149-1155.
[14] 李 鹏,刘建,朱杰兵.软弱结构面剪切蠕变特性与含水率关系研究[J].岩土力学,2008(7):1875-1872.
LI Peng,LIU Jian,ZHU Jiebing.Research on effects of water content on shear creep behaviorof weak structural plane of sandstone[J].Rock and Soil Mechanics,2008(7):1875-1872.
[15] 齐亚静,姜清辉,王志俭,等.改进西原模型的三维蠕变本构方程及其参数辨识[J].岩石力学与工程学报,2012,31(2):347-355.
QI Yajing,JIANG Qinghui,WANG Zhijian,et al.Improving the three-dimensional creep constitutive equation of the western model and its parameter identification[J].Journal of Rock Mechanics and Engineering,2013,31(2):347-355.
[16] 舒志乐,刘保县,黄山,等.软岩非线性黏弹塑性蠕变模型及参数识别[J].采矿与安全工程学报2017,34(4):803-809.
SHU Zhile,LIU Baoxian,HUANG Shan,et al.Non-linear viscoelastic plastic creep model and parameter identification of soft rock[J].Journal of Mining and Safety Engineering,2013,34(4):803-809.
[17] 杨圣奇,倪红梅,于世海.一种岩石非线性流变模型[J].河海大学学报(自然科学版),2007,35(4):388-392.
YANG Shengqi,NI Hongmei,YU Shihai.A nonlinear rheological model of rocks[J].Journal of Hehai University(Natural Science Edition),2007,35(4):388-392.
[18] 杨圣奇,徐卫亚,杨松林.龙滩水电站泥板岩剪切流变力学特性研究[J].岩土力学,2007,28(5):895-902.
YANG Shengqi,XU Weiya,YANG Songlin.Research on shear rheological properties of mudstone in longtan hydropower station[J].Geotechnical Mechanics,2007,28(5):895-902.