沿空留巷无煤柱开采技术是在相邻工作面开采后，沿着采空区边缘将相邻工作面巷道保留下来供本工作面开采使用。沿空留巷具有提高煤炭采出率、减少巷道掘进量、缓解采掘接替紧张、改善工作面通风环境等优点[1-3]。近年来，我国学者对沿空留巷围岩控制机理及技术方面进行了有益探索。张农，韩昌良等基于采场上覆岩层运动特征，对沿空留巷围岩稳定性和支护机理进行了分析[4]。陈勇、柏建彪等运用数值模拟对巷内支护与围岩变形、应力分布的关系进行了探析，提出了沿空留巷巷内支护机理[5]。康红普、牛多龙等通过对深井沿空留巷围岩变形与应力分布特征进行分析，提出了深井留巷支护设计方法[6]。李化敏探析了沿空留巷巷旁充填体与顶板相互作用关系，提出了充填体支护力确定原则[7]。

同时根据塑性力学可知，围岩应力是球应力和偏应力的叠加，偏应力是围岩发生畸变的根本原因，其对塑性变形的发生和发展起主要决定作用。我国学者对巷道围岩偏应力和塑性区分布规律进行了探索和实践。余伟健，吴根水等运用数值模拟分析了不同应力状态下巷道围岩和塑性区演化过程，提出了在不同侧压系数下巷道失稳分为典型正对称失稳模式和典型角对称失稳模式[8]。马念杰，李季等通过对圆形围岩偏应力场和塑性区分布规律的研究，提出了蝶形塑性区理论[9]。许磊，魏海霞等模拟了煤层残余煤柱底板偏应力场分布特征，得到不同煤柱宽度下底板偏应力分布规律，确定了下位煤层巷道合理位置的选取[10]。

以上成果为研究沿空留巷围岩控制技术和巷道围岩偏应力场分布规律提供了很好的借鉴，但对深部充填开采沿空留巷围岩偏应力分布规律及其控制技术没有针对性的研究。为此，笔者选用邢东矿1126充填开采工作面的沿空留巷为工程背景，数值模拟研究工作面推进全过程中留巷围岩偏应力的时空演化及塑性区分布规律，得到了留巷围岩偏应力和塑性区非对称分布特征，提出了深部充填开采沿空留巷分区非对称围岩控制技术，可为类似深部矿井进行充填开采沿空留巷围岩控制提供参考。

1 工程概况

邢东矿1126工作面是该矿首个高水材料充填工作面，位于一水平(-760)的一采区，在-760轨道大巷东北方向，工作面地面标高+56.5～+58.0 m，煤层标高-740～-825 m，以2号煤层为主采煤层，煤层倾角平均为9°，煤层厚度为4.43～4.8 m，平均厚度4.7 m，煤层结构简单且厚度较稳定，受断裂构造影响，煤层局部变薄、破碎、松软。沿空巷道为1126工作面运料巷，巷道沿2号煤层顶板掘进，巷道为矩形巷道，巷道高度为3.6 m，宽度为4.5 m。

2 深部充填开采留巷数值模拟分析

2.1 应变软化模型

岩石在应力达到峰值后，随着变形的继续增加，其强度迅速降到一个较低的水平，这种现象称为“应变软化”[11]。应变软化模型认为岩石材料的属性随着塑性变化而发生变化，塑性屈服开始后，岩石的黏聚力、内摩擦角、剪胀角等均会随着塑性应变而发生衰减，当到达残余阶段时保持不变。

在FLAC3D中为了实现岩石材料强度参数随着塑性变化而发生衰减的特点，在岩石材料达到屈服后，用户可以利用FLAC3D中内置的FISH语言来编写其抗剪强度参数为塑性应变的功能函数，通过计算材料屈服后的每个时步上的塑性应变，将其代入用户设置的功能函数来弱化材料的抗剪强度参数，且材料的本构关系仍遵从Mohr-Coulomb模型。同时，应变软化模型的屈服函数、流动法则、应力修正均与Mohr-Coulomb模型的一样[12]。

应变软化模型中单元的应力应变关系，在弹性阶段，即屈服前呈线性分布，单元的应变只有弹性应变(εe)，即

ε=εe

(1)

式中,ε为单元的总应变。

屈服后，单元的应力-应变关系成非线性分布，单元的应变由弹性应变(εe)和塑性应变(εp)构成。此时单元总应变为

ε=εe+εp

(2)

本文以塑性剪切应变参量εps来描述单元在非线性阶段的塑性变形。在不考虑中间主应力σ2的情况下，εps可写[13]为

(3)

(4)

其中，均为塑性主应变分量。通过对岩石材料做常规三轴试验，根据试验所获得的数据，绘制出在不同围压下主应力差(σ1-σ3)与轴向应变ε1和侧向应变ε3的曲线，从而由试验获得岩石材料的塑性主应变分量。

在FLAC3D里内置的应变软化模型是基于Mohr-Coulomb屈服准则建立起来的[13]，岩石材料在峰后应变软化阶段任意一点的应力状态满足如下Mohr-Coulomb强度准则:

(5)

其中，σ1为最大主应力，MPa;σ3为最小主应力，MPa;φ(εps)，c(εps)是用户在岩石材料达到屈服后，设置的抗剪强度参数与塑性应变之间的功能函数，功能函数的表现形式是分段函数，用来表示岩石材料塑性屈服后，对单元的内摩擦角φ和黏聚力c逐渐弱化处理。设自定义功能函数为

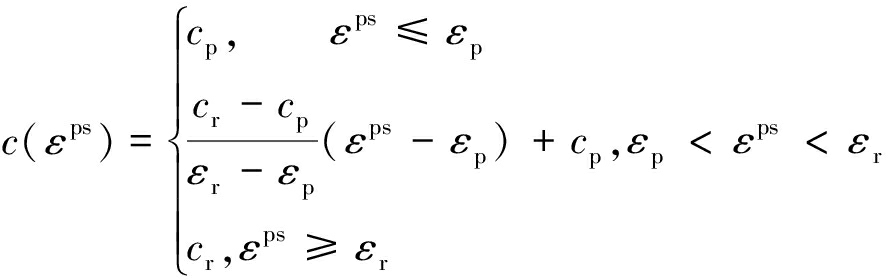
(6)

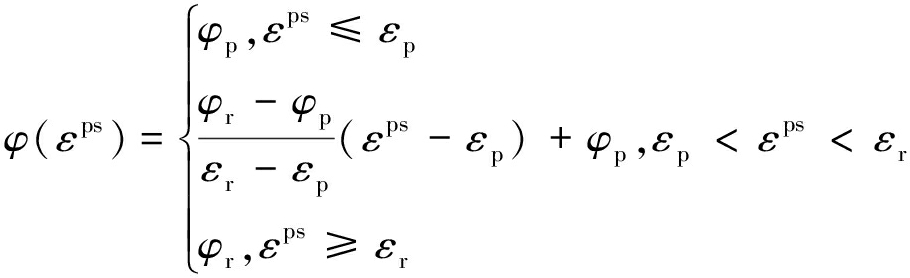
(7)

式中,εp为峰值处的塑性应变;εr为残余强度开始处的塑性应变;cp为峰值处的黏聚力，MPa;φp为峰值处的内摩擦角;cr为残余强度开始处的黏聚力，MPa;φr为残余强度开始处的内摩擦角。

据此，在数值模拟计算中，应变软化模型能够真实反映出围岩破坏情况，进而可为巷道合理支护提供可靠的支护方案。鉴于此，以下采用应变软化模型对深部充填开采留巷围岩进行数值模拟分析。

2.2 偏应力分析指标

物体内的任意一点应力状态可以由9个应力分量来描述，这些应力分量包括3个正应力分量和6个剪应力分量，将这9个应力分量按照服从一定坐标变换式排列而定义的量叫做应力张量。在弹塑性力学中，通常将应力张量分为球应力张量(静水应力张量)和偏应力张量两部分。当一点应力状态以主应力表示时，则应力张量可以分解为:设σi(i=1,2,3)为相互垂直的主应力，σ1≥σ2≥σ3，MPa。

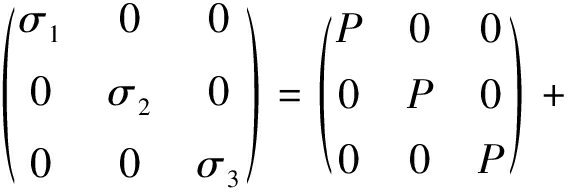
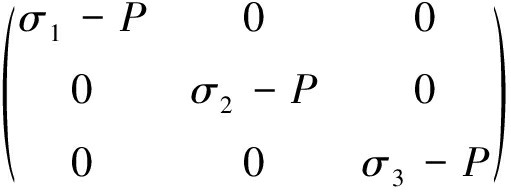
(8)

其中,右边第1项是球应力张量，P为球应力张量分量(球应力，MPa)，其只引起岩体单元体积改变，不引起岩体单元形状改变，球应力表达式为

(9)

右边第2项是偏应力张量，σi-P为主偏应力(偏应力，MPa)，其只引起岩体单元畸变，即只引起岩体单元形状变化，不引起岩体单元体积变化，偏应力是导致围岩的变形和破坏本质原因。

式(8)中,σ1-P为最大主偏应力在应力张量中起主导作用，本文以最大主偏应力为分析围岩稳定性的指标。最大主偏应力的表达式为

(10)

2.3 计算模型建立

为了探讨深部充填开采留巷围岩变形和破坏规律，进而为留巷围岩支护方案作出指导。采用FLAC3D软件对留巷围岩偏应力与塑性区演化规律进行分析。根据研究问题需要，建立模型尺寸为220 m×150 m×100 m(长×宽×高)，模型上部施加载荷γh=25 kN/m3×799.5 m=19.99 MPa，左右边界水平方向位移约束，底部边界垂直方向位移约束，采用应变软化模型进行研究，岩层力学参数见表1。

邢东矿在实际充填开采过程中，顶板有一定下沉，经现场对实际充填高度的测量，得到实际充填高度低于采高0.2 m。因此，为了更好的符合现场工作面推进和充填开采，模拟中在充填体与顶板之间留0.2 m，采用分步开挖。工作面开挖步距为2 m，共模拟开挖160 m，同时紧随工作面开挖对采空区进行充填，即开挖2 m，充填2 m，采用“一挖一充”直至工作面开挖完。

监测方案:在1126运料巷中布置7个测面，其中测面1到测面7距工作面开切眼的距离分别为32,48,64,80,96,112及128 m。在每个测面中，分别沿顶板、底板、实体煤帮和回采帮/充填体帮中线处各布置1条垂直于巷道轴向的测线，并在测线上布置若干个测点。从工作面回采开始到工作面回采结束的整个过程对围岩偏应力进行监测(160 m全部开采)，具体如下:工作面每推进8 m，对7个测面中的每条测线分别进行1次监测，并提取在此次推进步距下每条测线中测点的监测值;到工作面回采结束时(工作面推进160 m)，对7个测面中的每条测线分别进行了20次监测，并对每条测线中测点的监测值进行提取，以此绘制出在不同工作面推进步距下，顶底板和两帮偏应力分布规律曲线。

通过对7个测面监测数据分析，认为测面4(距开切眼80 m)能够较完整的反映出留巷围岩偏应力和塑性区演化进程的全过程。因此，限于篇幅限制，下文针对测面4(距开切眼80 m)进行详细分析。

2.4 留巷围岩偏应力和塑性区演化规律

2.4.1 沿巷道轴向顶底板和两帮偏应力分布规律

如图1所示为工作面推进80 m时(即工作面推进到测面4)沿巷道轴向偏应力分布云图。

(1)顶板偏应力分布规律。由图1(a)可知，超前采动影响较明显区约32 m，留巷采动影响较明显区约32 m。滞后工作面约32 m以后，顶板受留巷采动影响逐渐趋于稳定。滞后工作面段，顶板偏应力峰值大幅度向深部稳定岩层中转移，顶板破坏深度增加。

(2)底板偏应力分布规律。由图1(a)可知，超前采动影响较明显区约16 m，留巷采动影响较明显区约24 m。滞后工作面约24 m以后，底板受留巷采动影响逐渐趋于稳定。滞后工作面段，底板偏应力峰值大幅度向深部稳定岩层中转移，底板破坏深度增加。

(3)两帮偏应力分布规律。由图1(b)可知，超前采动影响较明显区约16 m。滞后工作面段，充填体先呈较低应力状态，之后充填体呈逐渐承载变化趋势;实体煤帮始终受留巷采动影响，且偏应力峰值向深部方向转移，其围岩破坏深度增加。

上述可知:超前工作面段，超前采动影响较明显区顶板约为32 m，底板和两帮均约为16 m;滞后工作面段，留巷采动影响较明显区顶板约为32 m，对底板约为24 m，实体煤帮和充填体帮始终受留巷采动影响。

据此，要实现留巷围岩稳定，应在受到较明显超前采动影响之前(超前工作面距离大于32 m)，完成巷道围岩加强支护，即巷道支设单体液压支柱和实体煤帮补打帮锚索。滞后工作面段，要实现充填体侧顶板围岩稳定，需增加巷旁支护，同时对充填体留巷侧表面采用护表构件，以提高充填体帮承载能力。鉴于此，研究采动影响较明显区巷道围岩偏应力和塑性区演化规律，对巷道支护方案选取具有重要指导意义，所以下文以测面4(距开切眼80 m)对留巷围岩偏应力和塑性区演化规律进行详细分析。

2.4.2 留巷围岩偏应力和塑性区分布规律

2.4.2.1 留巷围岩偏应力和塑性区分布形态

如图2所示为不同工作面推进步距下留巷围岩偏应力分布云图，如图3所示为不同工作面推进步距下围岩塑性区分布形态。

由图2可知，① 工作面推进64 m之前，偏应力分布以瘦高椭圆状进行演化分布，偏应力峰值带位于顶底板。② 工作面从推进64 m到推进112 m，偏应力分布以近似圆状→小半圆拱→大半圆拱进行演化分布，偏应力峰值带由顶底板转移到顶底帮角(实体煤侧)和实体煤帮。③ 工作面推进大于112 m，偏应力分布以扇形拱进行演化分布。偏应力峰值带位于顶底帮角(实体煤侧)和实体煤帮。

由图3可知，当工作面逐渐接近测面时，塑性区以近似椭圆状→近似圆状进行演化分布;当工作面逐渐远离测面时，塑性区以半球状演化分布，顶底板塑性区范围大幅度增长，其范围均大于实体煤帮塑性区范围，且顶板塑性区呈非对称分布特征。

2.4.2.2 留巷围岩偏应力分布曲线

如图4所示为不同工作面推进步距下围岩偏应力分布曲线。

(1)顶底板偏应力分布曲线。由图4(a),(b)可知，随工作面推进，顶底板偏应力分布曲线形态基本一致。① 工作面推进64 m之前，顶底板偏应力在围岩浅部呈类“线性”关系快速增长至峰值，峰值后向围岩深部呈类“负指数”关系逐渐降低并最终趋于稳定，整体呈现“线性”到“负指数”的分布形态。顶底板偏应力峰值在逐渐降低。② 工作面从推进64 m到推进112 m，其中逐渐接近测面时，顶底板偏应力整体也呈现“线性”到“负指数”的分布形态;逐渐远离测面时，顶底板偏应力呈类“对数”关系增长至峰值，峰值后呈类“负指数”关系逐渐降低并最终趋于稳定。③ 工作面推进112 m以后，顶底板偏应力呈类“对数”关系增长至峰值，峰值后呈类“负指数”关系逐渐降低并最终趋于稳定。顶板偏应力峰值逐渐增长，底板偏应力峰值逐渐降低。

(2)实体煤帮偏应力分布曲线。由图4(c)可知，从工作面回采开始到工作面回采结束，实体煤帮偏应力均是在围岩浅部呈类“线性”关系快速增长至峰值，峰值后向围岩深部呈类“负指数”关系逐渐降低并最终趋于稳定，整体呈现“线性”到“负指数”的分布形态，偏应力峰值在逐渐增长。

(3)回采帮/充填体帮偏应力分布曲线。在图4(d)中，当工作面逐渐接近测面时，“回采帮/充填体帮”是实体煤，当工作面逐渐远离测面时，“回采帮/充填体帮”是充填体，并用负值表示距底板表面距离。

由图4(d)可知，① 工作面推进64 m之前，回采帮偏应力在围岩浅部呈类“线性”关系快速增长至峰值，峰值后向围岩深部呈类“负指数”关系逐渐降低并最终趋于稳定，整体呈现“线性”到“负指数”的分布形态，偏应力峰值在逐渐增长。② 工作面从推进64 m到推进112 m，其中逐渐接近测面时，回采帮偏应力整体也呈现“线性”到“负指数”的分布形态;逐渐远离测面时，充填体帮偏应力整体呈类“对数”关系增长并趋于稳定。③ 工作面推进112 m以后，充填体帮偏应力整体呈类“对数”关系增长并趋于稳定。充填体帮偏应力逐渐增长，此时充填体呈逐渐承载变化趋势。

2.4.2.3 留巷围岩偏应力峰值和塑性区范围变化规律

如图5所示为不同工作面推进步距下偏应力峰值变化规律，如图6所示为不同工作面推进步距下塑性区范围变化规律。由图5，6可知:

(1)随工作面推进，顶板偏应力峰值和塑性区范围变化规律为:① 偏应力峰值缓慢降低(推进8～64 m)→缓慢增长(推进64～80 m)→快速降低(推进80～112 m)→缓慢增长(推进112 m以后)。② 偏应力峰值距顶板表面由恒定→快速增长→恒定。③ 顶板塑性区范围先恒定后快速增长最后保持恒定，塑性区破坏深度由3 m增长至13.5 m。

顶板偏应力峰值位置距顶板表面距离达15.5 m，顶板塑性区破坏深度达13.5 m。可见，顶板围岩破坏范围较大。由顶板偏应力分布曲线(图4)可知，距顶板表面6～13.5 m，顶板偏应力为9.5～13.83 MPa，是浅部围岩(3～5 MPa)的1.9～4.6倍。据此，虽然顶板在该区域内进入了塑性区，但该区域不是破碎区，其仍具有相对较高的整体性和承载能力。由文献[14]可知，深部岩体所处的复杂力学环境，使适合锚索锚固的稳定区域很难找到，但可以找到相对承载能力较高的区域，以实现锚索有效承载。同时，根据顶板偏应力峰值带向顶帮角转移和回采帮偏应力快速降低的特点，为保证顶板围岩稳定，对顶板进行高强度高预应力锚杆索支护(锚索采用φ21.8 mm×8 500 mm的高强高延伸率预应力锚索)，并将靠近实体煤帮锚索采取倾斜方式布置，使其越过顶帮角偏应力峰值带且锚固在稳定岩层中。同时，采用高预应力桁架锚索，将桁架锚索中靠近实体煤帮的锚索越过顶帮角偏应力峰值带且锚固在稳定岩层中，用桁架锚索使顶板围岩形成整体结构，实现顶板围岩稳定。现场实践表明锚索锚固性能较好。据此，虽然顶板塑性区深度较大，但在一定区域内仍具有相对较高的整体性和承载能力，可以使锚索发挥较好的支护性能。

(2)随工作面推进，底板偏应力峰值和塑性区变化规律为:① 偏应力峰值缓慢降低(推进8～64 m)→缓慢增长(推进64～80 m)→快速降低(推进80～112 m)→缓慢降低(推进112 m以后)。② 偏应力峰值距底板表面呈恒定→快速增长→恒定的转移趋势。③ 底板塑性区范围先恒定后快速增长最后保持恒定，塑性区破坏深度由3 m增长至10 m。

(3)随工作面的推进，实体煤帮偏应力峰值和塑性区变化规律:① 偏应力峰值逐渐增长。② 偏应力峰值距实体煤帮表面逐渐增长，最终为4 m。③ 实体煤帮塑性区范围逐渐增长，最终为3.8 m。

实体煤帮破坏范围大于3 m，已超过常规的锚杆支护作用范围。为保证围岩稳定性，实体煤帮需采用帮锚索支护形式，使帮锚索穿过偏应力峰值带，并锚固在稳定煤体中，与帮锚杆支护结构共同形成较大范围高稳定性围岩承载结构。

(4)随工作面推进，回采帮/充填体帮偏应力峰值变化规律:① 偏应力峰值缓慢增长(推进0～80 m)→快速降低(推进80～88 m)→快速增长(推进88～112 m)→缓慢增长(推进112 m以后)。② 偏应力峰值距回采帮/充填体帮表面缓慢增长(推进8～64 m)→快速增长(推进64～88 m)→快速降低(推进88～104 m)→恒定(推进104 m以后)。

回采帮由实体煤变成充填体过程中，偏应力峰值出现快速下降，且快速向深部转移。由于充填体帮承载能力低，致使采空区充填体留巷侧顶板下沉量较大。因此，对充填体留巷侧表面采用护表构件，使充填体浅部围岩由二向受压状态调整为三向受压状态，以提高充填体帮承载能力，同时对充填体侧采用巷旁支护，以防止充填体侧顶板严重下沉。

由以上分析得到，顶底板和实体煤帮的偏应力峰值位置与塑性区范围相距不超过2 m。据此可知，偏应力峰值带位于弹塑性交界面区域。偏应力峰值带以里岩体处于稳定和不稳定过渡状态，所以要实现留巷围岩稳定需控制偏应力峰值带以里不稳定岩体的稳定。

3 深部充填开采留巷围岩非对称控制技术

3.1 留巷围岩非对称控制原理

工作面开挖并及时充填采空区后，围岩在偏应力的作用下而产生剪切破坏，加之深部巷道处于高地应力环境，会导致留巷围岩稳定性进一步恶化，其围岩强度降低，体积增大，进而产生膨胀变形并向巷道自由面挤出，以致产生顶板冒落、垮帮、底臌等现象，严重影响巷道的整体稳定。可见要实现对留巷围岩稳定性控制，就要采取合理的支护方案和参数，以减少偏应力及其产生的剪切破坏对留巷围岩的破坏作用。

根据数值模拟结果、邢东矿生产地质条件及工程实践认为1126运料巷受采动影响时，其维护难点如下:① 回采帮由实体煤变成充填体，其围岩偏应力峰值从实体煤时13 MPa快速下降到充填体时0.41 MPa，下降达12.59 MPa，偏应力出现快速下降。② 随工作面推进，偏应力峰值带逐渐转移至顶底帮角(实体煤侧)和实体煤帮，巷道顶板岩层(从充填体侧到实体煤侧)偏应力呈非对称分布。由于充填体强度低，充填体不能及时对顶板产生有效支撑，且实体煤帮自身的力学性能及对顶板的约束作用都要优于充填体，所以充填体侧顶板下沉量比实体煤帮顶板下沉量大。③ 顶板和实体煤帮塑性区范围较大，以及顶板塑性区呈非对称分布，所以很难找到适合锚杆索锚固的稳定区，受本工作面回采影响，巷道变形破坏将会加剧[15]。

基于以上分析，要实现深部充填开采沿空留巷围岩在偏应力非对称、塑性区非对称条件下的稳定性控制，首先需要控制偏应力峰值带以里不稳定岩体的稳定，其次对顶板及充填体侧重点加固，并实现在留巷过程中围岩稳定，鉴于此，提出了分区非对称围岩控制技术，其控制原理如图7所示。

对留巷围岩分成3个区域，分别是充填体侧(A区)，顶板(B区)和偏应力峰值带(C区，即顶底帮角和实体煤帮)。控制技术主要包括:

(1)充填体侧钢管混凝土支架支护(A区)。由数值模拟可知，充填体侧中偏应力相对处于较低值，使得留巷围岩在高地应力的作用下，顶板将会向充填体侧发生弯曲下沉变形，进而影响留巷整体稳定性。鉴于此，提出沿充填体侧布置双排钢管混凝土支架强力支护，钢管混凝土支架是由向钢管中浇筑混凝土而形成的构件，通过混凝土来保障钢管材料性能的充分发挥，同时利用钢管的约束作用使混凝土处于三维受压状态，使其具有更高的抗压强度和抗变形能力，以适应深部充填开采留巷充填体侧围岩的支护要求。同时，对充填体临空侧采用π型钢梁压经纬网护表结构，使充填体浅部围岩由二向受压状态调整为三向受压状态，以提高充填体帮承载能力。

(2)顶板高强度高预应力锚杆索、高预应力桁架锚索、双排钢管混凝土支架和单体液压支柱联合支护(B区)。针对顶板破坏范围较大，采用锚杆索和桁架锚索联合支护，用桁架锚索使围岩形成整体结构，以使单体锚索形成的“点支护”、桁架锚索形成的“整体支护”及浅部围岩形成的锚杆承载结构，共同构成预应力更高、范围更广的承载结构。通过现场实践可知，锚索能够满足留巷支护要求。此外，顶板锚杆采用φ22 mm×2 400 mm高强左旋螺纹钢锚杆，现场表明锚杆锚固性能较好，说明顶板采用单体锚索和桁架锚索支护后，为锚杆能够锚固在较稳定区域创造了条件。针对顶板塑性区非对称分布，防止充填体侧顶板严重下沉，沿充填体侧布置双排钢管混凝土支架强力支护。同时，为防止局部顶板围岩劣化而发生冒顶垮塌事故，采取在运料巷中部附近支设单体液压支柱进行加强支护。

(3)顶底帮角、实体煤帮高强度高预应力锚杆索支护(C区)。随工作面推进，偏应力峰值带逐渐转移至顶底帮角和实体煤帮。若要保持巷道围岩稳定，应实现偏应力峰值带以里不稳定岩体的稳定，故靠近实体煤帮的顶锚索要采取倾斜方式布置，使其越过偏应力峰值带及塑性区1.5 m，锚固在肩角稳定压缩区内，且靠近肩角的顶锚杆和帮锚杆也用倾斜方式布置。对底帮角和实体煤帮采用帮锚索整体偏向底帮角侧布置方式，并使帮锚索也越过偏应力峰值带且锚固在稳定压缩区内，同时靠近底板处帮锚杆向下倾斜布置。

3.2 非对称支护参数

通过以上研究，确定深部充填开采留巷联合支护方案如图8所示。

(1)顶板选用φ22 mm×2 400 mm高强左旋螺纹钢锚杆，每排布置7根锚杆，锚杆间排距700 mm×800 mm，顶锚杆间采用钢筋梯子梁连接。顶锚索选用φ21.8 mm×8 500 mm高强度高延伸率预应力锚索，延伸率为7%，每排布置3根锚索，锚索间排距1 250 mm×1 600 mm，通过14号槽钢沿巷道轴向方向两两连接起来，呈迈步方式布置，中间单体锚索垂直于顶板单独布置。桁架锚索选用φ17.8 mm×8 500 mm高强度高延伸率预应力锚索，延伸率为7%，桁架锚索排距4 800 mm，底部跨度为2 100 mm。此外，巷道中部附近架设单体液压支柱，其排距为1 200 mm。

(2)实体煤帮选用φ20 mm×2 100 mm高强左旋螺纹钢锚杆，每排布置6根锚杆，锚杆间排距700 mm×800 mm，锚杆间钢筋梯子梁连接。帮锚索选用φ17.8 mm×4 500 mm高强度高延伸率预应力锚索，其延伸率为7%，呈三花布置，其间排距1 050 mm×1 600 mm，沿走向方向上用钢筋梯子梁连接。

(3)充填体侧采用双排6寸钢管混凝土支架，间排距500 mm×700 mm，呈三花布置。布置钢管混凝土支架是在高水材料充填采空区后，先对靠近充填体侧巷道底煤进行清理，同时对充填体临空侧采用π型钢梁+金属网进行护表。π型钢梁上部通过钢管混凝土支架顶部布置的木垫板和十字铰接顶梁进行固定，下部通过钢管混凝土支架与π型钢梁之间的底支点木块进行固定。

3.3 留巷围岩控制效果

对深部充填开采沿空留巷进行联合支护后，为了验证支护方案和参数的效果，对巷道中部顶底板移近量、实体煤侧顶底板移近量、充填体侧顶底板移近量、两帮移近量进行了连续观测。通过观测可知，工作面推进70 m以后留巷围岩移近量基本趋于稳定。其中巷道中部顶底板、实体煤侧顶底板、充填体侧顶底板以及两帮的最大移近量分别是443,391,490,305 mm，顶底板移近量大于两帮移近量，充填体侧移近量大于实体煤侧移近量。1126工作面开采留巷过程中，未出现钢管混凝土支架和单体液压支柱压弯损毁及锚杆索支护失效等现象，说明对深部充填开采沿空留巷所提出的支护方案能够满足留巷围岩稳定性控制。

4 结 论

(1)根据数值模拟分析得到，超前采动影响较明显区顶板约为32 m，底板和两帮均约为16 m;留巷采动影响较明显区顶板约为32 m，底板约为24 m，实体煤帮和充填体帮始终受留巷采动影响。

(2)留巷围岩偏应力以瘦高椭圆状→近似圆状→小半圆拱→大半圆拱→扇形拱进行时空演化。偏应力峰值带以顶底板→顶底帮角(实体煤侧)和实体煤帮进行转移，偏应力峰值带位于弹塑性交界面区域。塑性区以近似椭圆状→近似圆状→半球状进行演化，且塑性区呈非对称分布。据此，得到了采空区充填体侧需进行重点加固、顶板需进行非对称加固以及顶底帮角、实体煤帮需控制偏应力峰值带以里不稳定岩体的稳定。

(3)基于深部充填开采留巷围岩偏应力和塑性区非对称分布特征，提出了高强度高预应力锚杆索、高预应力桁架锚索、双排钢管混凝土支架和单体液压支柱联合支护的分区非对称围岩控制技术，现场实践表明，留巷围岩控制效果良好。

参考文献(References):

[1] 孙恒虎,赵炳利.沿空留巷的理论与实践[M].北京:煤炭工业出版社,1993:1-3.

[2] 华心祝.我国沿空留巷支护技术发展现状及改进建议[J].煤炭科学技术,2006,34(12):78-81.

HUA Xinzhu.Development status and improved proposals on gob-side entry retaining support technology in China[J].Coal Science and Technology,2006,34(12):78-81.

[3] HUA Xinzhu.Study on gob-side entry retaining technique with roadside packing in longwall top-coal caving technology[J].Journal of Coal Science &Engineering (China),2004,10(1):9-12.

[4] 张农,韩昌良,阚甲广,等.沿空留巷围岩控制理论与实践[J].煤炭学报,2014,39(8):1635-1641.

ZHANG Nong,HAN Changliang,KAN Jiaguang,et al.Theory and practice of surrounding rock control for pillarless gob-side entry retaining[J].Journal of China Coal Society,2014,23(18): 3059-3065.

[5] 陈勇,柏建彪,王襄禹,等.沿空留巷巷内支护技术研究与应用[J].煤炭学报,2012,37(6):903-910.

CHEN Yong,BAI Jianbiao,WANG Xiangyu,et al.Support technology research and application inside roadway of gob-side entry retaining[J].Journal of China Coal Society,2012,37(6):903-910.

[6] 康红普,牛多龙,张镇,等.深部沿空留巷围岩变形特征与支护技术[J].岩石力学与工程学报,2010,29(10):1977-1987.

KANG Hongpu,NIU Duolong,ZHANG Zhen,et al.Deformation characteristics of surrounding rock and supporting technology of gob-side entry retaining in deep coal mine[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(10):1977-1987.

[7] 李化敏.沿空留巷顶板岩层控制设计[J].岩石力学与工程学报,2000,19(5):651-654.

LI Huamin.Control design of roof rocks for gob-side entry[J].Chinese Journal of Rock Mechanics and Engineering,2000,19(5):651-654.

[8] 余伟健,吴根水,袁超,等.基于偏应力场的巷道围岩破坏特征及工程稳定性控制[J].煤炭学报,2017,42(6):1408-1419.

YU Weijian,WU Genshui,YUAN Chao,et al.Failure characteristics and engineering stability control of roadway[J].Journal of China Coal Society,2017,42(6):1408-1419.

[9] 马念杰,李季,赵志强.圆形巷道围岩偏应力场及塑性区分布规律研究[J].中国矿业大学学报,2015,44(2):206-213.

MA Nianjie,LI Ji,ZHAO Zhiqiang.Distribution of the deviatoric stress field and plastic zone in circular roadway surrounding rock[J].Journal of China University of Mining &Technology,2015,44(2):206-213.

[10] 许磊,魏海霞,肖祯雁,等.煤柱下底板偏应力区域特征及案例[J].岩土力学,2015,36(2):561-568

XU Lei,WEI Haixia,XIAO Zhenyan,et al.Engineering cases and characteristics of deviatoric stress under coal pillar in regional floor[J].Rock and Soil Mechanics,2015,36(2):561-568.

[11] 陆银龙,王连国,杨峰,等.软弱岩石峰后应变软化力学特性研究[J].岩石力学与工程学报,2010,29(3):640-647.

LU Yinlong,WANG Lianguo,YANG Feng,et al.Post-peak strain softening mechanical properties of weak rock[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(3):640-647.

[12] 曹日红,曹平,张科,等.考虑应变软化的巷道交叉段稳定性分析[J].岩土力学,2013,34(6):1760-1821.

CAO Rihong,CAO Ping,ZHANG Ke,et al.Stability analysis of roadway intersection considering strain softening[J].Rock and Soil Mechanics,2013,34(6):1760-1821.

[13] ITASCA Consulting Group Inc.FLAC3D (Version 2.1) users manual[R].Itasca Consulting Group Inc.，2003.

[14] 张俊文.深部大规模松软围岩巷道破坏分区理论分析[J].中国矿业大学学报,2017,46(2):292-298.

ZHANG Junwen.Theoretical analysis on failure zone of surrounding rock in deep large-scale soft rock roadway[J].Journal of China University of Mining &Technology,2017,46(2):292-298.

[15] QIAO Jianyong.On the preimages of parabolic points[J].Nonlinearity,2000(13):813-818.