微震技术作为一种先进的动力灾害监测手段，在国内外已得到了广泛应用[1-3]。微震监测利用传感器接收岩体破裂等诱发的振动，然而接收到的信号通常含有大量背景噪声，这对P,S波初至拾取、震源定位和震源机制分析等后续工作影响较大，需要探究微震信号降噪的有效方法。
目前，主要借助小波和经验模态分解对微震信号降噪。小波阈值降噪研究较多:徐宏斌等[4]、李学龙等[5]和金晶晶等[6]分别结合小波和全局阈值、分层阈值和改进阈值对微震信号进行降噪，而曹思远、陈香朋[7]和MOUSAVI等[8]分别借助二代小波变换、同步压缩小波变换和阈值对微震信号降噪，取得了一定的降噪效果。此外，李稳等[9]借助小波重构系数稀疏特征降噪，BEENAMOL等[10]结合小波和Shannon熵、Tsallis熵对微震信号降噪，ZHANG等[11]借助小波重构系数降低了噪音对微震震相拾取的影响。然而，小波降噪需选取合适的小波基才能达到较好的降噪效果[12]。HUANG等[13]提出的经验模态分解能较好地处理随机非平稳信号，且其无需预先设定基函数就能自适应地将信号分解至本征模态分量。有鉴于此，EMD分解在微震信号中的应用越来越广泛。贾瑞生等[14]采用EMD分解微震信号，并根据信号频谱特征，筛选低频IMF分量重构微震信号。贾瑞生等[15]使用独立成分分析(Independent Component Analysis,ICA)对IMF分量进行盲源分离，提取有效微震信号。梁喆等[16]利用互信息熵筛选得到主要IMF分量，进而重构微震信号。
然而，EMD在分解过程中会产生模态混叠现象，即多个时间尺度的特征出现在同一个IMF中，降低了去噪效果[17]。为降低模态混叠的影响，WU和HUANG[17]提出了基于噪声辅助的集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)，在一定程度上抑制了模态混叠的问题，但尚不能完全消除模态混叠的影响。为此，HAN等[18]采用EEMD阈值对微震信号降噪。笔者提出了一种基于EEMD_Hankel_SVD的微震信号降噪方法。该方法采用EEMD获得多层模态分量，并用模态分量与原信号相关系数差值剔除噪音特别大的模态分量，再对剩余各模态分量采用Hankel_SVD法降噪，进而将降噪的模态分量相加得到重构信号，以期得到一种较好的微震信号降噪方法。
1 降噪方法
1.1 EEMD
WU和HUANG[17]提出的EEMD是一种非线性非平稳的自适应信号分解方法，是对经验模态分解的改进。EMD将信号x分解为多个IMF分量ci(i=1,2,…,n)和一个残余分量rn[13]，即
(1)
该方法适用于非线性非平稳信号的分析，然而当信号存在跳跃性变化时，会出现模态混叠现象，降低了降噪效果。而EEMD能降低模态混叠的影响，其主要思想如下:将均匀的白噪声序列添加到原信号中，再用EMD对加入白噪声的信号分解得到本征模态分量，加入不同的白噪声序列重复上述步骤，直到设定的加入噪声次数，借助白噪声在求平均时相互抵消的思想，对本征模态分量集合求平均，便得到真实分量。然而有限次的平均不能使白噪声完全消除[19]，为此有必要使用Hankel_SVD对模态分量进一步降噪。
1.2 Hankel_SVD降噪
微震信号通常由真实信号s(t)和噪音信号n(t)两部分组成，即
x(t)=[x(1),x(2),…,x(N)]=s(t)+n(t)
(2)
其中N为微震信号长度。
对x(t)构造p×q阶Hankel矩阵H，见式(3)。同理可得到s(t)和n(t)构造的p×q阶Hankel矩阵Hs和Hn。
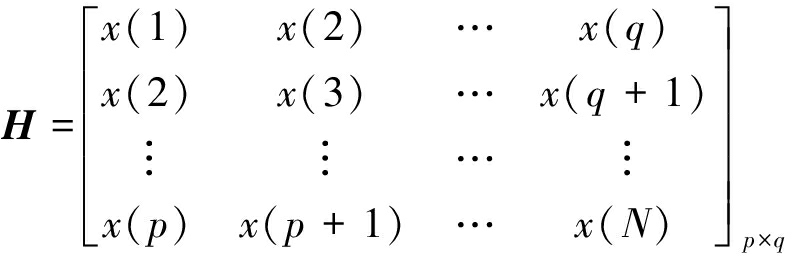
(3)
其中，H(i,j)=x(i+j-1)，Hs(i,j)=s(i+j-1)，Hn(i,j)=n(i+j-1)，p+q-1=N，p≥q。
由此，可先求出Hs(i,j)=s(i+j-1)，进而得到重构微震信号
借助真实信号s(t)与噪音信号n(t)互不相关，且真实信号能量比较集中，而噪音信号能量比较分散的特点，可认为SVD将Hankel矩阵H分成两个互不相关的空间，即较大奇异值对应真实信号重构，而较小奇异值对应噪音信号重构[20]。对H进行SVD分解得到:
(4)
其中，U∈Rp×p,Us∈Rp×rs,Un∈Rp×rn,V∈Rq×q,Vs∈Rq×rs，Vn∈Rq×rn,∑∈Rp×q,∑s∈Rrs×rs,∑n∈Rrn×rn,σi为奇异值，σl为信号与噪音分界对应的奇异值。
由此，找到分界奇异值σl即可重构信号
和CAKAR[21]建议采用奇异值曲线确定σl，若σi/σ1≥σl，则σi用于重构微震信号
反之则舍弃σi。σl计算方法如下[21]:
(5)
其中，η为噪音标准差。
1.3 EEMD_Hankel_SVD降噪方法
通常EEMD分解得到的前几个模态分量对应高频噪声，本文在使用Hankel_SVD降噪前，利用IMF分量与原信号相关系数差值剔除高频IMF分量，再用Hankel_SVD对剩余模态分量分别降噪，进而将降噪模态分量相加得到重构微震信号
相关系数定义如下:
(i=1,2,…,n)
(6)
其中,
分别为原信号和IMF分量的均值。
基于EEMD_Hankel_SVD的降噪方法具体步骤如下:
(1)采用EEMD分解原信号x(t)，得到n个IMF分量ci(t)和1个残余分量rn(t);
(2)利用式(6)计算ci与x(t)的相关系数R(i)，再计算相关系数的差值R(i)-R(i-1);
(3)寻找R(i)-R(i-1)的第一个局部极大值对应的下标j，则j对应高频噪音与真实信号的分界，去除前j-1个IMF分量;
(4)对剩余的每个IMF分量ci(t)和残余分量rn(t)分别用式(3)构造Hankel矩阵H，采用SVD分解H，并用式(5)确定奇异值分界值σl，再采用式(4)得到重构IMF分量
和残余分量
(5)将重构的IMF分量
和残余分量
相加便得到降噪后信号
即
2 仿真结果
2.1 仿真测试
为测试提出的降噪方法效果，选取Matlab中ECG信号作为计算案例(图1中(a)(1))。取信号长度T=1 024，噪声n(t)=0.2×randn(1,102 4)，即噪声为标准正态分布的0.2倍，含噪信号x(t)如图1(a)中(2)所示。采用EEMD分解x(t)得到9个IMF分量c1(t)～c9(t)和1个残余分量r9(t)，图1(a)中(3)～(12)。由图1(a)可知，随着EEMD的分解，IMF分量的整体频率降低，前三个IMF分量的高频噪音非常大。采用式(6)计算各IMF分量与x(t)相关系数，并计算相邻相关系数差值，得到图2。由图2可知，第4个IMF分量对应的相关系数差值最大。因此，重构时前3个IMF分量直接剔除。
以c4(t)为Hankel_SVD降噪实例。首先以c4(t)构造600×425阶Hankel矩阵H，并用SVD计算H的奇异值，再用式(5)计算得到σl=0.169 7，σi/σ1，σl与奇异值编号关系如图3所示。利用σi/σ1≥0.169 7的奇异值σi重构得到
如图1(b)中(6)所示。同理采用Hankel_SVD对每一IMF分量ci(t)(i=1,2,…,9)和残余分量r9(t)进行降噪，得到图1(b)中(3)～(12)。由图1(b)可见，前三个IMF分量噪音降低，但仍基本为噪音信号。Hankel_SVD降噪后的
增强了T=300～450段的局部特征，且对其他段的振幅进行了压制;其他分量降噪大多也有类似效果，可见Hankel_SVD降噪是有效的。采用式
重构降噪信号，得到图1(b)中(2)，可知降噪后信号较好的保留原信号特征。为定量的评价降噪效果，引入信噪比(Signal to Noise Ratio,SNR)，其定义见式(7)。由表1知降噪前和降噪后的SNR分别为0.63和9.68，降噪效果明显。
(7)
式中，si为真实信号的幅值;ni为噪音信号的幅值。
此外，笔者还对Matlab中“Blocks”，“Bumps”,“Doppler”和“Heavy sine”信号进行了测试。为便于比较，首先采用公式x=2(x-xmin)/(xmax-xmin)-1将上述4个信号转化到[-1，1]区间(图4(a)～(d)中(1))，再加入噪声n(t)=0.2randn(1,1 024)，得到含噪信号，如图4(a)～(d)中(2)所示。EEMD_Hankel_SVD降噪效果如图4(a)～(d)中(3)所示。由图4和表1知降噪后微震信号信噪比得到了明显提升。
图1 EEMD分解和EEMD_Hankel_SVD降噪IMF分量
Fig.1 EEMD decomposition and EEMD_Hankel_SVD denoised IMFs
图2 相邻相关系数差值
Fig.2 Difference between neighboring correlation coefficients
图3 σi/σ1与奇异值编号曲线
Fig.3 Curve between singular value number and σi/σ1
图4 4种典型测试信号(标准化至[-1,1])、含噪信号和EEMD_Hankel_SVD降噪信号
Fig.4 Four typical testing signals (normalized to[-1,1]),noisy signals and EEMD_Hankel_SVD denoised signals
2.2 降噪方法比较
为测试EEMD_Hankel_SVD降噪方法的优越性，选取小波重构、EMD重构和Hankel_SVD降噪作为比较。其中，小波重构采用db5分解，去除相关系数差值第一个局部最大值前的系数重构得到;EMD重构去除相关系数差值第一个局部最大值前的IMF分量重构得到;Hankel_SVD降噪指对所有模态分量采用Hankel_SVD降噪，再重构得到。上述4种方法对图1中含噪音的ECG信号降噪效果如图5所示，且2.1节中5个信号降噪后的信噪比见表1。
表1 不同降噪方法的信噪比
Table 1 SNRs of different denoising methods
图5 ECG信号不同方法降噪效果
Fig.5 Denoising results of the ECG signal using different methods
由图5和表1可知:① 不同降噪方法均对信噪比有一定的提升;② Hankel_SVD降噪较其他方法降噪效果最差，这是由于最初的几个IMF分量含噪音很大，Hankel_SVD降噪后IMF分量仍含大量噪音(例如图1(b)中(3)～(5));③ 小波重构和EMD重构降噪效果较好，且EMD重构降噪效果略优于小波重构，这是由于小波按照频带进行分解，且小波分解需要选取小波基，而EMD是基于经验的分解，其与信号本身相关，因而能更好地分离真实信号与噪音信号;④ 小波重构和EMD重构降噪在一些细节地方逊于本文方法(图5):一方面，EEMD分解能降低模态混叠;另一方面，Hankel_SVD对剩余模态分量具有一定的降噪作用。由此可见，EEMD_Hankel_SVD具有较好的降噪效果。
3 微震信号降噪
以某矿微震信号作为降噪数据，微震信号采样频率6 000 Hz。采用长短时窗均值比法(STA/LTA法)、峰度法(PAI-K法)和池赤回归准则法(AIC法)拾取微震信号P波初至[22]，进而评价降噪效果。
从微震监测系统中随机抽取500个微震信号，并对原始信号和EEMD_Hankel_SVD降噪信号进行STA/LTA，PAI-K和AIC法拾取，其中3个典型微震信号及其降噪信号拾取如图6所示(左侧为原始信号及其拾取、右侧为降噪信号及其拾取)。
图6 3个典型微震信号降噪前后P波初至拾取结果
Fig.6 P-wave arrival picking results for three typical original and denoised microseismic signals
由图6可知，原微震信号信噪比较低，含有高频噪音及尖刺噪音等，EEMD_Hankel_SVD能有效去除上述噪音，增强P波初至信息。降噪后微震信号的STA/LTA，Kurtosis和AIC值具有更好的尖锐性，验证了信噪比的增强。低信噪比下，原信号STA/LTA法可能未触发，而降噪后STA/LTA法触发(图6(b))。PAI-K法和AIC法可能受尾部振荡拾取误差较大(图6(c))，而降噪后信号可消除上述影响。
对上述500个微震信号拾取误差进行统计得到图7。为便于图形观察，拾取误差大于210个点的记为210点，采用LI等[23]提出的一种定量方法评价P波初至拾取统计效果。该方法认为信号拾取误差越小，则权重越小，并对所有信号的拾取权重求和，权重和越小对应方法越优。
对所有微震信号拾取权重Ci求和，得到总惩罚值TCF，亦列于图7中。由图7知，3种方法降噪后拾取误差均整体低于原始信号拾取误差，且拾取误差大于180个点或无拾取的微震信号数目降低，可见降噪后信号增强了拾取的稳定性。定量分析显示降噪后信号拾取的TCF值明显小于原始信号拾取的TCF值，验证了定性分析的合理性。降噪后信号AIC法拾取效果优于其他拾取结果，可考虑将EEMD_Hankel_SVD与AIC法结合用于P波初至拾取。此外，对2.2节中不同降噪方法STA/LTA拾取误差进行统计，得到表2。
表2 不同降噪方法STA/LTA拾取误差统计及其总惩罚值
Table 2 Statistical results of the STA/LTA picking errors for different denoising methods and their total costs
图7 3种方法拾取误差统计
Fig.7 Picking residual statistics for the three methods
由表2知，4种降噪方法均对STA/LTA拾取有提升，且Hankel_SVD降噪拾取效果明显差于其他3种降噪方法。小波重构和EMD重构信号STA/LTA拾取效果差别不大，且EEMD_Hankel_SVD降噪信号拾取效果最优。
4 结 论
(1)借助相关系数能有效剔除含噪特别大的模态分量，Hankel_SVD对剩余模态分量降噪是必要的，且EEMD_Hankel_SVD法能有效提高信噪比，同时保留了信号局部特征。
(2)利用EEMD能降低模态混叠的特性和Hankel_SVD对剩余模态分量的降噪作用，EEMD_Hankel_SVD提高了降噪效果，并与3种降噪方法比较，验证了其优越性。
(3)EEMD_Hankel_SVD法微震信号降噪，有效地提高了STA/LTA，PAI-K和AIC法P波初至拾取效果，且降噪后信号与AIC法结合拾取效果最优。综上知，EEMD_Hankel_SVD降噪方法为矿山微震信号降噪提供了一种可靠途径。
参考文献(References):
[1] 姜福兴,尹永明,朱权洁,等.基于微震监测的千米深井厚煤层综放面支架围岩关系研究[J].采矿与安全工程学报,2014,31(2):167-174.
JIANG Fuxing,YIN Yongming,ZHU Quanjie,et al.Relationship between support and surrounding rock of fully mechanized caving face in thick coal seam of kilometer deep mine based on microseismic monitoring technology[J].Journal of Mining &Safety Engineering,2014,31(2):167-174.
[2] 李伟.基于LMD和模式识别的矿山微震信号特征提取及分类方法[J].煤炭学报,2017,42(5):1156-1164.
LI Wei.Feature extraction and classification method of mine microseismic signals based on LMD and pattern recognition[J].Journal of China Coal Society,2017,42(5):1156-1164.
[3] PYTEL 
A.The effect of mining face’s direction on the observed seismic activity[J].International Journal of Coal Science &Technology,2016,3(3):322-329.
[4] 徐宏斌,李庶林,陈际经.基于小波变换的大尺度岩体结构微震监测信号去噪方法研究[J].地震学报,2012,34(1):85-96.
XU Hongbin,LI Shulin,CHEN Jijing.A study on method of signal denoising based on wavelet transform for micro-seismicity monitoring in large-scale rockmass structures[J].Acta Seismologica Sinica,2012,34(1):85-96.
[5] 李学龙,李忠辉,王恩元,等.矿山微震信号干扰特征及去噪方法研究[J].中国矿业大学学报,2015,44(5):788-792.
LI Xuelong,LI Zhonghui,WANG Enyuan,et al.Study of mine microseismic signals interference characteristic and its de-noising method[J].Journal of China University of Mining &Technology,2015,44(5):788-792.
[6] 金晶晶,王旭,吴雪,等.基于改进阈值函数的体震信号平移不变去噪[J].东北大学学报(自然科学版),2009,30(3):333-336.
JIN Jingjing,WANG Xu,WU Xue,et al.Translation-invariant de-noising of body fluttering signal based on improved threshold function[J].Journal of Northeastern University (Natural Science),2009,30(3):333-336.
[7] 曹思远,陈香朋.第二代小波变换及其在地震信号去噪中的应用[J].应用地球物理(英文版),2005,43(2):547-550.
CAO Siyuan,CHEN Xiangpeng.The second-generation wavelet transform and its application in denoising of seismic data[J].Applied Geophysics (English Version),2005,43(2):547-550.
[8] MOUSAVI S M,LANGSTON C A,HORTON S P.Automatic microseismic denoising and onset detection using the synchrosqueezed continuous wavelet transform[J].Geophysics,2016,81(4):V341-V355.
[9] 李稳,刘伊克,刘保金.基于稀疏分布特征的井下微地震信号识别与提取方法[J].地球物理学报,2016,59(10):3869-3882.
LI Wen,LIU Yike,LIU Baojin.Downhole microseismic signal recognition and extraction based on sparse distribution features[J].Chinese Journal of Geophysics,2016,59(10):3869-3882.
[10] BEENAMOL M,PRABAVATHY S,MOHANALIN J.Wavelet based seismic signal de-noising using Shannon and Tsallis entropy[J].Computers &Mathematics with Applications,2012,64(11):3580-3593.
[11] ZHANG H.Automatic P-wave arrival detection and picking with multiscale wavelet analysis for single-component recordings[J].Bulletin of the Seismological Society of America,2003,93(5):1904-1912.
[12] OMITAOMU O A,PROTOPOPESCU V A,GANGULY A R.Empirical mode decomposition technique with conditional mutual information for denoising operational sensor data[J].IEEE Sensors Journal,2011,11(10):2565-2575.
[13] HUANG N E,SHEN Z,LONG S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society of London,Series A,1998,454:903-995.
[14] 贾瑞生,谭云亮,孙红梅,等.低信噪比微震P波震相初至自动拾取方法[J].煤炭学报,2015,40(8):1845-1852.
JIA Ruisheng,TAN Yunliang,SUN Hongmei,et al.Method of automatic detection on micro-seismic P-arrival time under low signal-to-noise ratio[J].Journal of China Coal Society,2015,40(8):1845-1852.
[15] 贾瑞生,赵同彬,孙红梅,等.基于经验模态分解及独立成分分析的微震信号降噪方法[J].地球物理学报,2015,58(3):1013-1023.
JIA Ruisheng,ZHAO Tongbin,SUN Hongmei,et al.Micro-seismic signal denoising method based on empirical mode decomposition and independent component analysis[J].Chinese Journal of Geophysics,2015,58(3):1013-1023.
[16] 梁喆,彭苏萍,郑晶.基于EMD和互信息熵的微震信号自适应去噪[J].计算机工程与应用,2014,50(4):7-11.
LIANG Zhe,PENG Suping,ZHENG Jing.Self-adaptive denoising for microseismic signal based on EMD and mutual information entropy[J].Computer Engineering and Applications,2014,50(4):7-11.
[17] WU Z H,HUANG N E.Ensemble empirical mode decomposition:A noise-assisted data analysis method[J].Advances in Adaptive Data Analysis,2009,1(1):1-41.
[18] HAN J,MIRKO V D B.Microseismic and seismic denoising via ensemble empirical mode decomposition and adaptive thresholding[J].Geophysics,2015,80(6):KS69-KS80.
[19] TORRES M E,COLOMINAS M A,SCHLOTTHAUER G,et al.A complete ensemble empirical mode decomposition with adaptive noise[A].IEEE International Conference on Acoustics,Speech and Signal Processing[C].IEEE,2011:4144-4147.
[20] ZHAO X,YE B.Similarity of signal processing effect between Hankel matrix-based SVD and wavelet transform and its mechanism analysis[J].Mechanical Systems &Signal Processing,2009,23(4):1062-1075.
[21] SANLITURK K Y,CAKAR O.Noise elimination from measured frequency response functions[J].Mechanical Systems &Signal Processing,2005,19(3):615-631.
[22] 田优平,赵爱华.基于小波包和峰度赤池信息量准则的P波震相自动识别方法[J].地震学报,2016,38(1):71-85.
TIAN Youping,ZHAO Aihua.Automatic identification of P-phase based on wavelet packet and Kurtosis-AIC method[J].Acta Seismologica Sinica,2016,38(1):71-85.
[23] LI X B,SHANG X Y,MORALES-ESTEBAN A,et al.Identifying P phase arrival of weak events:The Akaike information criterion picking application based on the empirical mode decomposition[J].Computers &Geosciences,2017,100:57-66.