构造应力较大或埋深较大的软岩巷道掘进后,常表现出短时间变形大且持续时间久,普通支护结构支护强度不足且返修频繁的现象。其根本原因是高应力区在开挖后,形成一定的围岩扰动区,当普通支护结构不足以抵抗时,围岩扰动区会向内进一步扩大,围岩只剩残余强度[1]。一些学者指出,提升围压对提升破碎围岩强度效果显著[2-3]。
钢管混凝土支架是由4个圆弧拱通过套管拼接而成的封闭结构,如图1所示,具有比U型钢支架更强的支护力,且韧性良好。中国矿业大学(北京)高延法教授成功地把钢管混凝土技术应用于巷道支护中,已有20余条巷道成功应用[4-5],钢管混凝土支架支护一般是由4个四分之一钢管混凝土圆弧拱通过套管拼接而成,属于被动支护方式。

图1 钢管混凝土支架示意
Fig.1 Sketch map of concrete filled steel tube support
井巷工程的钢管混凝土圆弧拱结构与实腹式拱桥和空腹式拱桥所受竖向荷载不同且不考虑平面外失稳[6-8],巷道工程中,理想情况下钢管混凝土圆弧拱受静水压力作用。但在实际施工过程中,由于特殊的地应力构造,每个圆弧拱受围岩压力存在较大差异,人工安装的钢管混凝土支架不能与围岩完全贴合,钢管混凝土支架会出现应力集中现象。图2,3给出了邢东煤矿二水平胶带下山巷道中钢管混凝土支架局部和整体失稳破坏情况。钢管混凝土支架局部失稳一般发生在套管附近或拱顶处。所以本文以四分之一圆弧拱受六分点集中径向荷载为研究对象,与实际工程具有较好的一致性。

图2 套管附近发生弯折
Fig.2 Bushing-nearby bucking

图3 整体破坏
Fig.3 Wholesale destruction
目前关于钢管混凝土拱桥的研究已经成熟,但隧道用钢管混凝土支架受径向荷载作用,与拱桥受竖向荷载不同,组成钢管混凝土支架构建的四分之一圆弧拱的跨度、截面尺寸远小于拱桥设计参数[9],所以钢管混凝土拱桥设计规范不适用于隧道用钢管混凝土支架承载力的计算。目前,隧道用钢管混凝土理论多把外界受力形式简化为静水压力,并将钢管混凝土支架承载力计算方法折算成钢管混凝土短柱极限承载力计算方法[10],准确性较差。
本文选取钢管混凝土支架中单拱构件,拱底为单拱套管处,拱顶为单拱中点,单拱整体失稳意味着钢管混凝土支架局部失稳。通过分析六分点等值集中荷载下四分之一钢管混凝土圆弧拱截面应力分布、截面强度,研究局部破坏原因。并给出适用于隧道的钢管混凝单拱整体失稳,即钢管混凝土支架局部失稳的承载力计算公式,为防止钢管混凝土支架整体失稳破坏、局部返修、钢管混凝土支架设计提供理论依据。
1 试验研究
1.1 圆弧拱试件的设计制作
圆弧拱试件主体钢管选用φ140 mm×6 mm无缝钢管热煨弯制,核心混凝土强度等级按C40配制,制作150 mm3的不同钢纤维掺量混凝土试块,其强度如图4所示。说明混凝土掺入钢纤维有助于提高其抗压强度。

图4 混凝土立方体抗压强度随钢纤维掺量变化
Fig.4 Compressive strength of concrete cube varies with steel fiber content
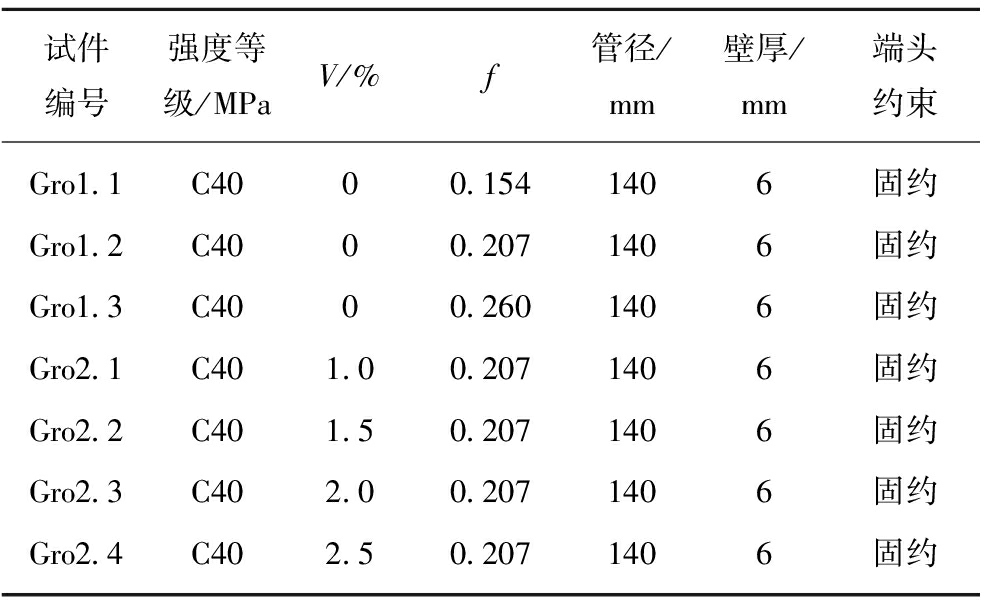
测试2组共7根不同矢跨比f和钢纤维体积掺量V的圆弧拱试件,钢管混凝土支架套管处强度最高,所以采用长200 mm,宽200 mm,厚160 mm钢板焊接于圆弧拱试件端头,作为固定端。试件具体参数见表1。
表1 不同矢跨比、钢纤维体积掺量圆弧拱试件参数
Table 1 Circular arch parameters with steel fiber parameter and steel fiber volume
1.2 试验设备与加载
课题组将实验进行于山东建筑大学土木工程学院结构实验室,采用大型反力架试验台、3个独立控制的千斤顶和3个分配梁共同组建六分点集中径向荷载加载装置。对圆弧拱试件四等分点处施加侧向约束。实验装置如图5所示。拱顶进行位移监测[11]。

图5 实验台与加载方案
Fig.5 Experiment rig and loading scheme
1.3 实验结果
施加分级荷载后,两组圆弧拱试件跨中的千斤顶试验荷载—位移关系绘制成曲线如图6,7所示。

图6 不同矢跨比圆弧拱荷载-位移曲线
Fig.6 Load-displacement curve of circular arch with different rise-span ratio
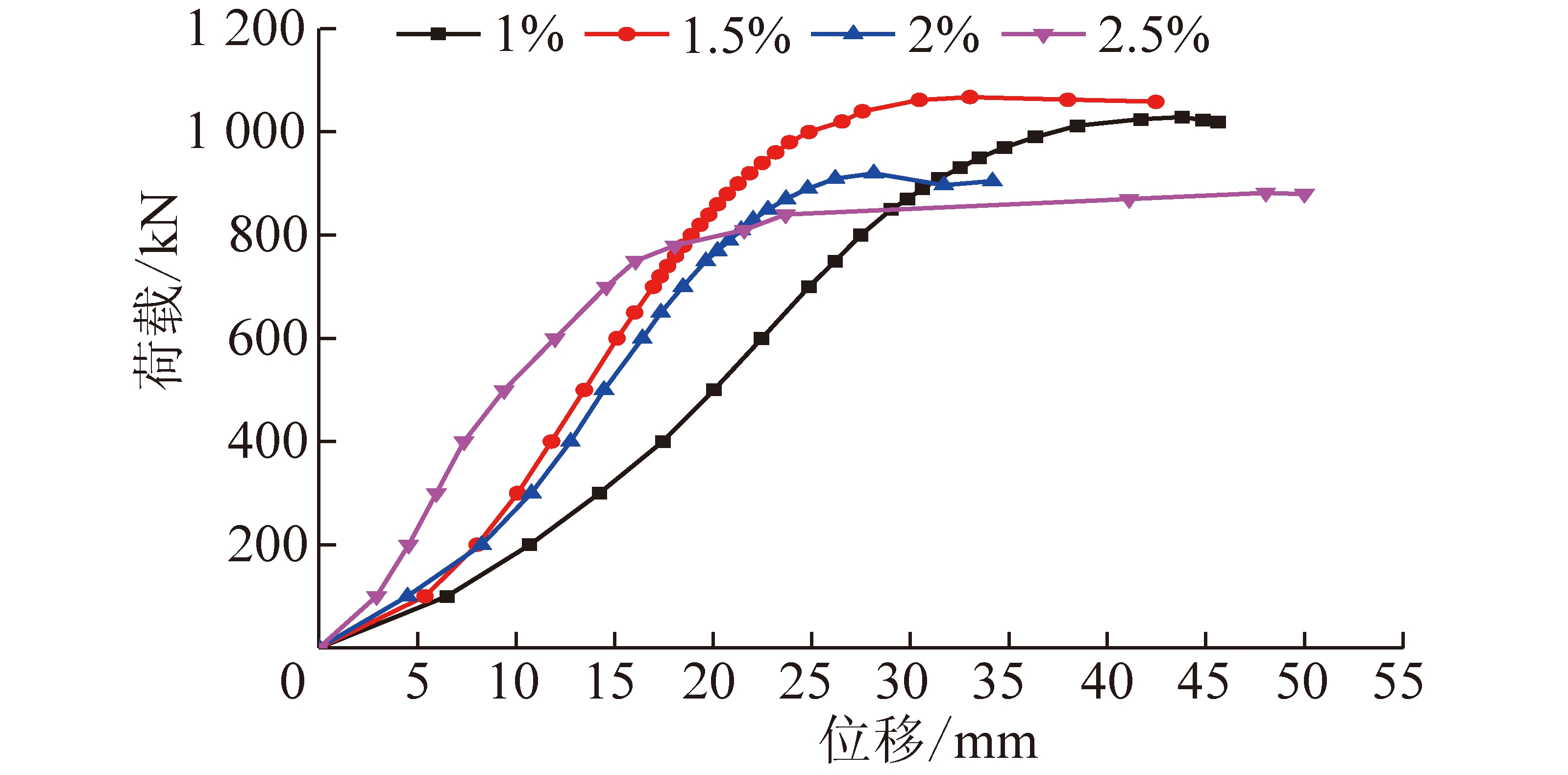
图7 不同钢纤维掺量圆弧拱荷载-位移曲线
Fig.7 Load-displacement curve of circular arch with different steel fiber dosage
两点间斜率首次并持续减小时的荷载认为是屈服荷载,荷载最大值认为是极限荷载,试验荷载的屈服荷载、极限荷载及各自对应位移见表2。
1.4 试件破坏特征
图8为典型拱底破坏形态,与图2中现场钢管混凝土支架近套管处破坏形态一致,具有弯曲和剪切破坏特征。
表2 试件屈服荷载,极限荷载和位移
Table 2 Yield load,ultimate load and displacement of specimens


图8 试件拱底破坏情况
Fig.8 Disruption situation of arch bottom
将试件用气割切开半跨钢管。不同矢跨比,钢纤维含量1%~2%的6根圆弧拱试件拱底、拱顶核心混凝土破坏形态如图9所示。

图9 拱顶、拱底核心混凝土破坏形式
Fig.9 Destruction form of apex and bottom of arch
由图9可知:
(1)不同矢跨比的圆弧拱试件拱底处破坏形态均为三角状碎裂,只有钢纤维含量为1%的圆弧拱试件拱底处破坏形态为整体上移,所有含钢纤维体积率的圆弧拱试件,拱底处破碎程度都比不添加钢纤维试件严重。
(2)只有矢跨比为0.260的圆弧拱试件拱顶产生斜裂纹。钢纤维含量为2%的圆弧拱试件拱顶的破坏形态为压制破碎。
实验表明,圆弧拱试件在受力过程中,拱顶处主要受轴向应力影响,拱底受力较复杂。拱顶、拱底都是圆弧拱最可能发生破坏的危险位置。
2 数值模拟
本文使用Abaqus有限元分析软件,由于掺有钢纤维的核心混凝土模型的参数定义非常复杂,所以只对不同矢跨比的圆弧拱试件进行数值模拟,以研究圆弧拱试件的整体应力分布及拱底、拱顶的截面应力分布规律,为截面强度的理论计算提供理论依据。
考虑到试件几何、材料的双非线性因素,钢管、混凝土分别采用Mises模型、损伤塑性模型。混凝土损伤参数见表3。边界条件非线性主要考虑钢管与核心混凝土接触面之间的作用关系,通过定义切向摩擦接触和径向受压接触得以实现。
数值模拟效果与实验保持较好的吻合,矢跨比0.154,0.207和0.260的模型千斤顶试验极限承载力为750,1 030和1 280 kN,与实验值的最大误差小于5%,模拟效果较为理想。
取半跨圆弧拱,从拱顶截面至拱底截面,依次平均选取15个监测点,对模型轴力、弯矩进行监测。不同矢跨比模型在弹性阶段(以500 kN为例)和达到极限承载力后的轴力与弯矩数值大小监测曲线如图10所示。
由图10可知,轴力下凹段是试件加载垫块处。进入塑性阶段后,不同矢跨比的轴力趋于相等,最大弯矩向四分之一跨过度,最大弯矩处距拱底的距离约是半跨的40%。这说明钢管混凝土局部失稳后,局部失稳区域仍存在一定的残余强度,试件各截面应力发生变化,继续承受荷载直至某一截面发生屈服,试件整体失稳。
表3 混凝土本构模型参数
Table 3 Constitutive model parameters of concrete


图10 不同矢跨比半跨模型轴力和圆弧拱弯矩监测
Fig.10 Axial force and bending moment diagram of half models with different rise-span ratios
图11为0.260矢跨比试件在弹性范围内(以300 kN为例)拱底、拱顶截面轴向应力分布云图,可看出拱底内拱轴力最大,越向外轴力越小,且钢管轴向应力分布要大于核心混凝土轴向应力分布。拱顶处、核心混凝土应力分布较为均匀,钢管外拱的轴向应力明显大于内拱;拱顶轴向应力要大于拱底。

图11 弹性阶段拱底、拱底轴向应力分布
Fig.11 Axial stress distribution of apex and bottom of arch in elastic stage
随荷载的增加,试件进入塑性阶段(以800 kN为例),拱底、拱顶处轴向应力分布如图12所示,拱底核心混凝土轴向应力分布趋于均匀,且中心位置轴向应力略大于两边,这是因为此处的钢管承受了更多的轴向应力。拱顶处的核心混凝土外拱处的核心混凝土轴向应力略大于其他位置。

图12 塑性阶段拱顶、拱底轴向应力分布
Fig.12 Axial stress distribution of apex and bottom of arch in plastic stage
数值模拟得到的不同矢跨比试件极限强度、局部失稳形态与试验结果一致。各截面钢管的应力要大于核心混凝土,且轴向应力云图随数值模拟中y轴变化均匀。
此外对不同壁厚,不同截面尺寸单一影响因素的四分之一圆弧拱极限承载力进行数值模拟计算,结合不同矢跨比的试件极限承载力结果见表4。
表4 不同影响因子的极限承载力
Table 4 Ultimate bearing capacity of different influence factors

绘制钢体积量-承载力曲线如图13所示。

图13 含钢量-承载力曲线
Fig.13 Steel content-bearing capacity curve
数值模拟结果表明三种影响因素中,截面尺寸影响比重最大,矢跨比次之,壁厚最小。可以说明在巷道设计时,应尽量增加钢管混凝土支架的截面尺寸;应在围岩应力较大侧,使用矢跨比较大的钢管混凝土圆弧拱构件。
3 理论分析
拱结构内力分析通过一维采用弹性中心法,找出圆弧拱结构在六分点均布径向加载下内力分布规律。截面强度分析是依据数值模拟模型截面应力分布规律,建立三维截面应力分布模型,计算出截面强度;并分析局部失稳和破坏形态的原因。整体失稳分析是研究试件整体屈服时,最大承载力的计算方法。
3.1 拱结构内力分析
笔者采用结构力学中弹性中心法对拱结构进行内力分析,考虑了压力线与拱轴线偏移和弹性压缩对内力的影响。
均布径向荷载是巷道工程中钢管混凝土圆弧拱最理想受力形式。这种状态下,压力线与拱轴线重合。可理解为轴向应力方向受均布径向荷载影响,合力方向始终沿着该点的切线方向。本文研究遵循如下原则:试件受六分点等值荷载的压力线Lp1,p5如图14所示,其中Lpi,pi+1的斜率同点Pi、原点间连线与圆弧线的交点切线斜率相同,且xpi近似地作为该交点的横坐标。通过几何方法易求得:
f=H/L
(1)
α4-α0=arcsin(L/2R)
(2)
![]()
(3)
式中,H,L,R分别为四分之一圆弧拱跨高、跨宽、圆弧半径;α为各加载点与水平向夹角。
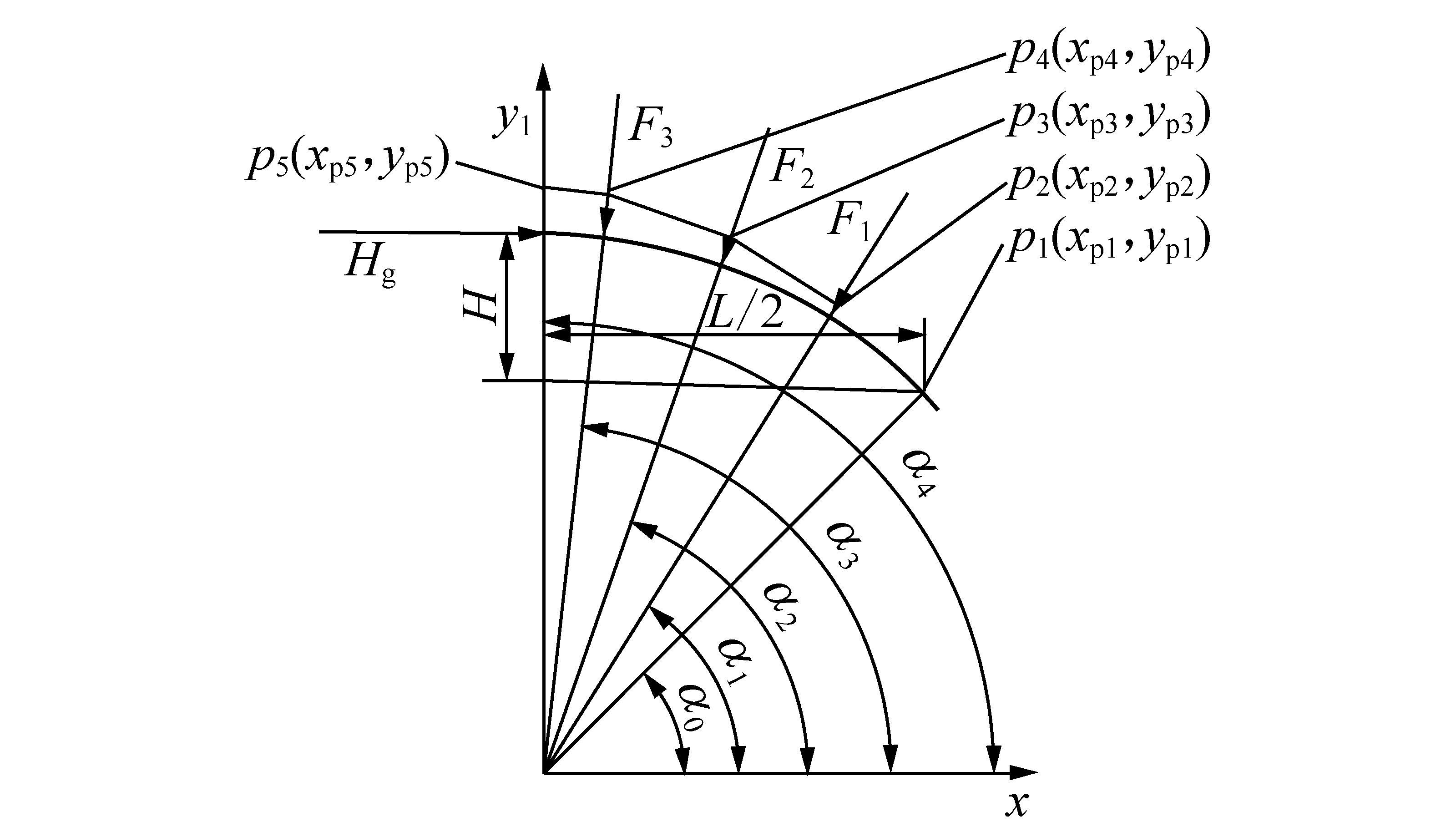
图14 压力线示意
Fig.14 Sketch map of permanent-loaded compression line
求解压力线节点Pi坐标有:
当i=1时,
yp1=Rsin α0
(4)
当1<i<5时,
(5)
当i=5时,
(6)
xpi=Rcos(αi-1)
(7)
当考虑压力线与拱轴线偏移和弹性压缩的影响,采用弹性中心法对圆弧拱试件进行力学分析,表达式如下:
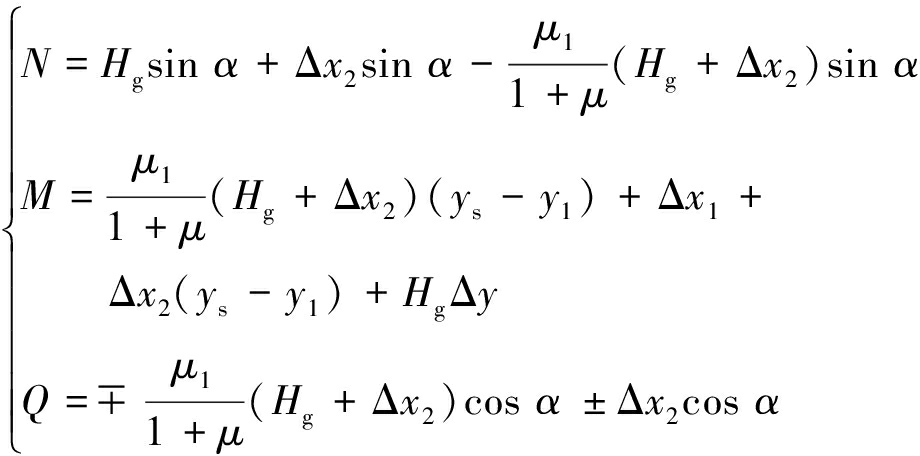
(8)
式中,N,M,Q分别为截面轴向力、弯矩、剪切力;Hg为拱的恒载推力;ΔHg为弹性压缩引起的在弹性中心处的水平推力;Δx1,Δx2为当考虑压力线与拱轴线偏移引起的偏离弯矩时,引起次定弯矩、次定轴力;y1表示以圆心为原点(向上为正)的拱轴坐标;y表示以弹性中心为原点(向上为正)的拱轴坐标,y=y1-ys。
根据弹性中心法计算式(8)中未知量有
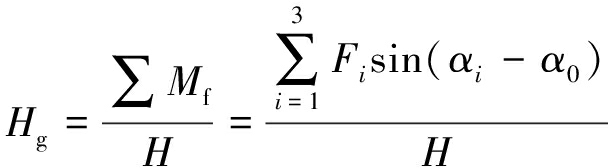
(9)
![]()
(10)
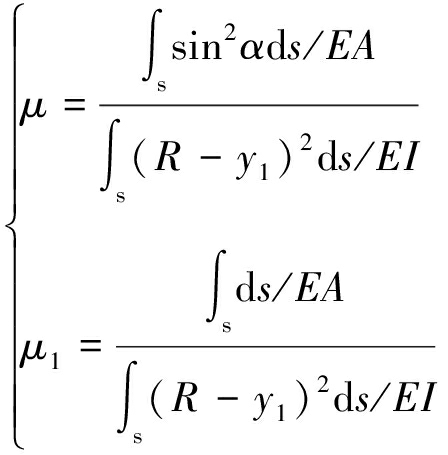
(11)
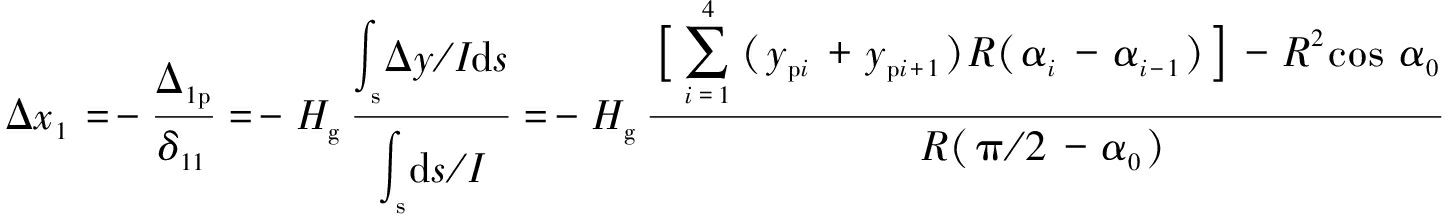
(12)
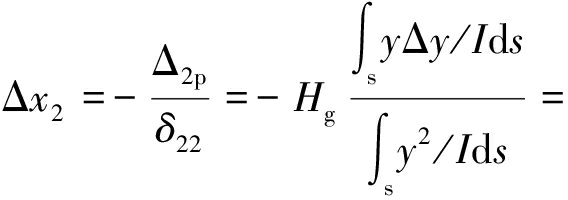

(13)
式中,Δip表示基本结构因外因导致Xi方向的广义荷载位移。
由式(8)可知,N,M,Q与Fi一次相关,所以当六分点等值荷载为单位1时,相关计算参数见表4。
表4 相关计算参数
Table 4 Related calculation parameters

注:G=μ1/(1+μ)。
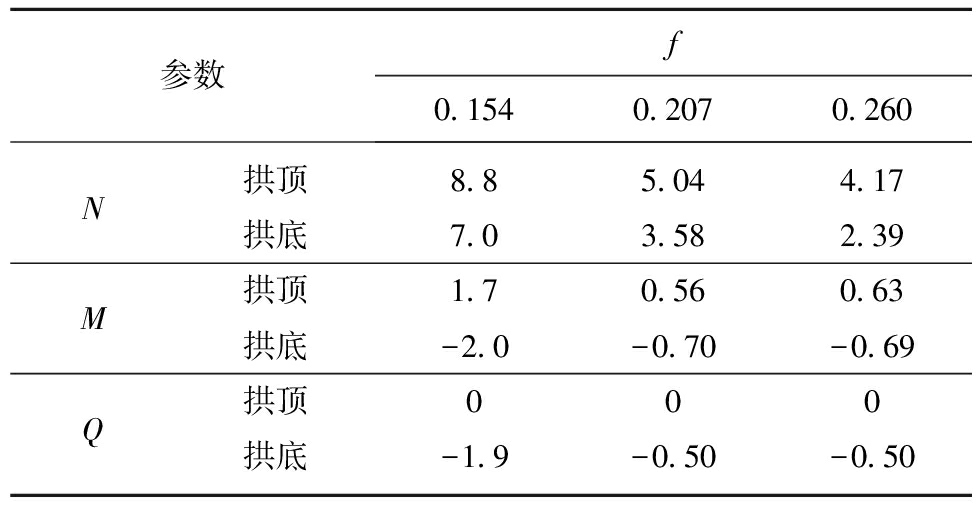
根据表4可计算出在单位力Fi下四分之一圆弧拱内力系数N,M,Q随α的变化如图15所示,可知,相同矢跨比拱顶轴力始终大于拱底,且变化不大;最大弯矩出现在拱顶和拱底处,方向相反;拱底剪力最大,拱顶和拱底是最有可能发生破坏的位置。
矢跨比越小,拱顶和拱底的轴力,弯矩,剪力越大。且矢跨比为0.154的浅拱与其他两种矢跨比相比,各内力相差很大,所以其承受荷载的能力最弱。

图15 不同矢跨比轴力、弯矩、剪力与角度关系曲线
Fig.15 Axial force,bending moment,shear defmation-angle curves with different rations
图15中拱顶、拱底处各内力参数见表5。
表5 不同矢跨比拱顶,拱底内力系数
Table 5 Internal forces of apex and bottom of arch and zero bending moment with different rations
3.2 截面强度分析
一维模型中发现拱顶和拱底是危险点,拱顶和拱底的弯矩方向相反。根据数值模拟截面应力云图,发现轴向应力分布随数值模拟中y轴变化均匀,且钢管轴向应力远大于核心混凝土的轴向应力。所以构建拱顶和拱底二维截面和三维截面应力分布遵循如下假设。
以拱底为例,截面轴向应变与x线性相关,如图16所示。
ε(x)=kx
(14)
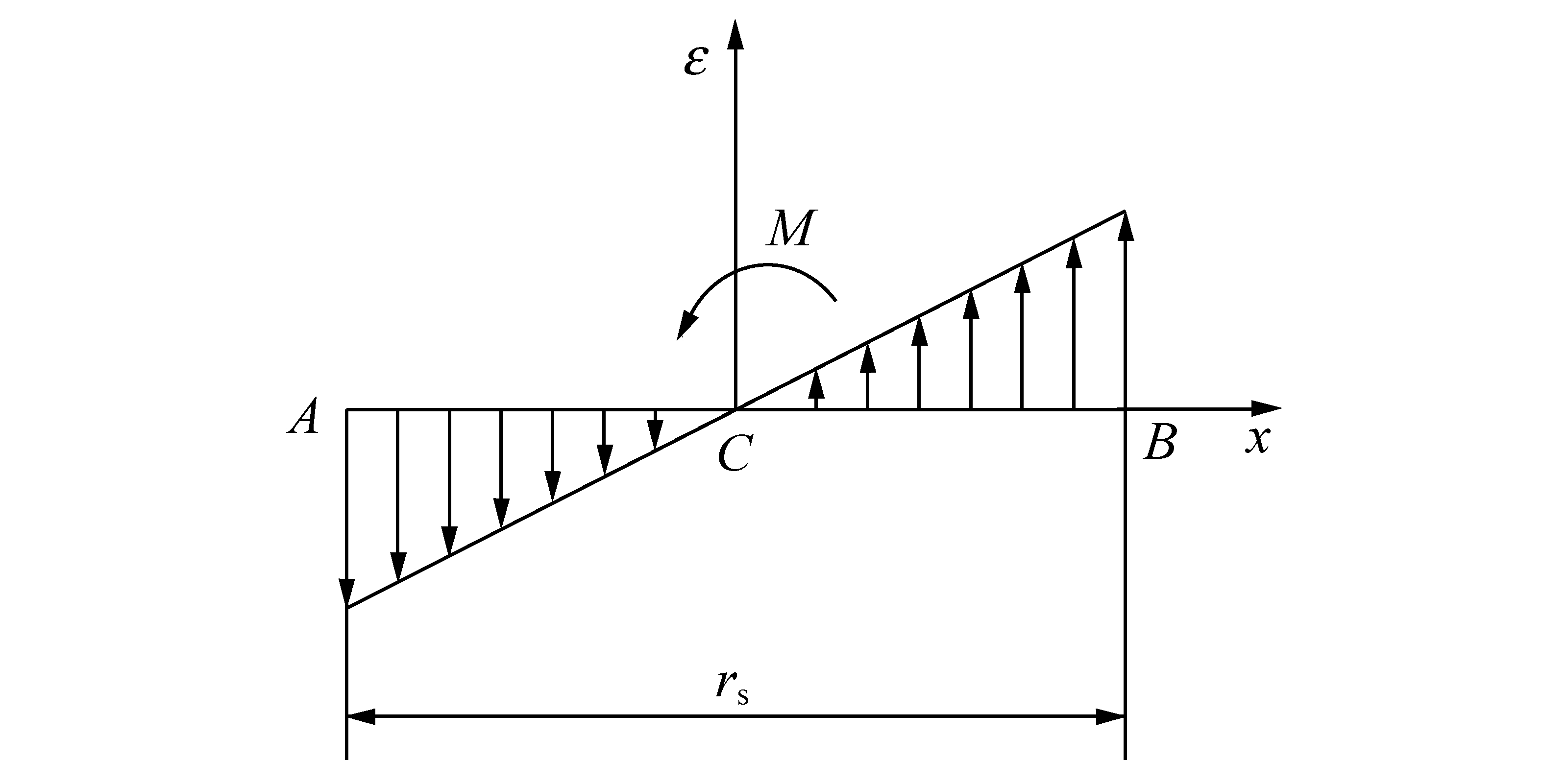
图16 仅弯矩影响拱底轴力正视图
Fig.16 Elevation view of axial force bottom arch with bending moment effect only
则弯矩和轴力共同影响的轴向应力分布正视图如图17所示;建立拱底截面坐标系如图18所示。
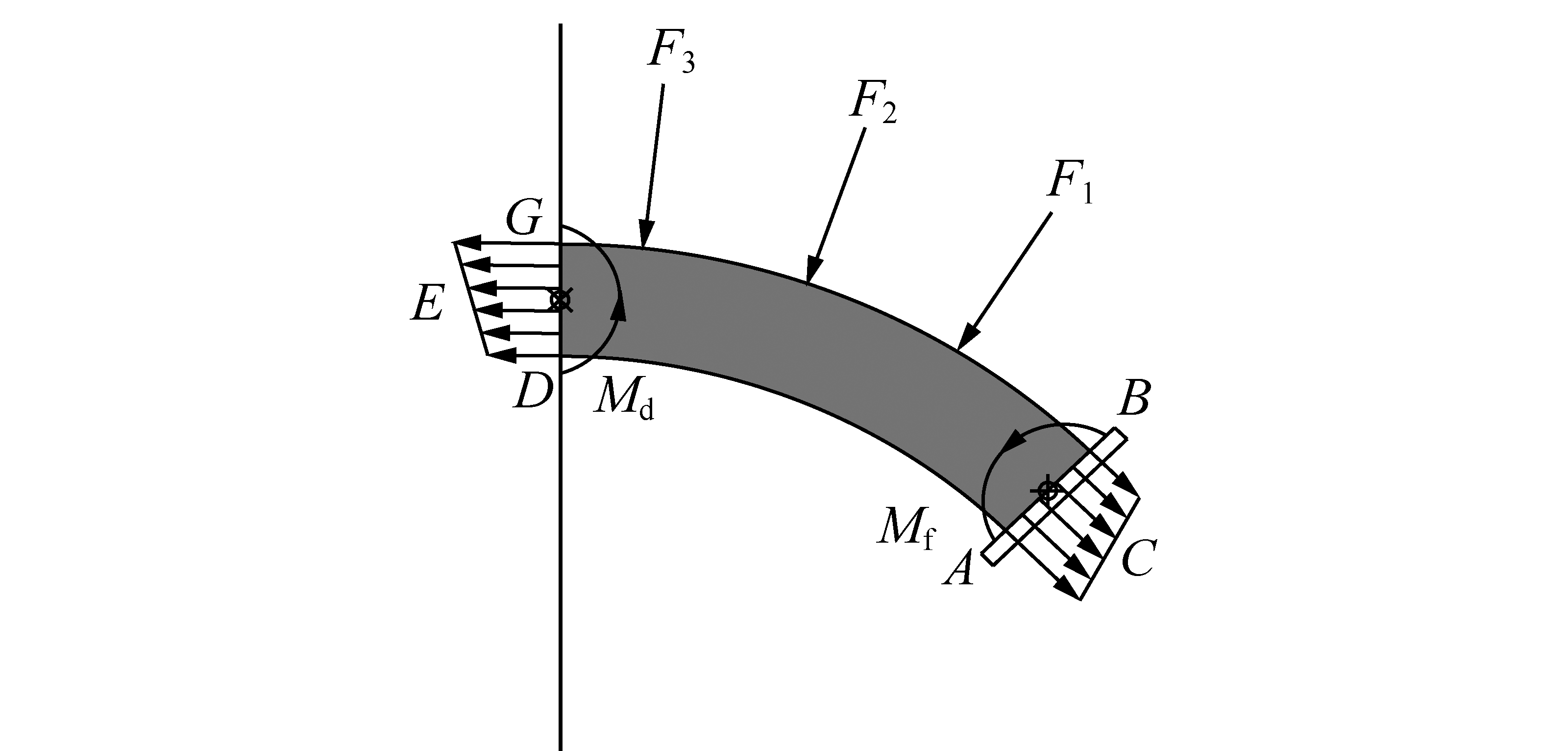
图17 拱顶和拱底轴力
Fig.17 Sketch of axial force at vault and arch feet

图18 拱底三维示意
Fig.18 Schematic digram of bottom arch
根据假设对y轴取矩:
![]()
(15)
式中,L表示单位力Fi倍数;rs,rc表示钢管半径、核心混凝土,mm;Es,Ec表示钢、核心混凝土的弹性模量分别取2.06×105 MPa,3.3×104 MPa。
钢管、混凝土应力分布qs/c(x):
(16)
同理得到拱顶轴向应力分布,容易看出,拱底处内拱轴向荷载大于外拱轴向荷载,拱顶处外拱轴向荷载大于内拱轴向荷载,且钢管轴向应力大于混凝土。
通过钢管混凝土短柱弹性作用机理可得[12]:
(17)

(18)
σ1=V/Uσ3=Wσ3
(19)
![]()
(20)
其中,σ1表示钢管截面正应力,MPa;σ2表示钢管环向应力,MPa;σ3表示核心混凝土作用于钢管内壁径向应力,MPa;D表示轴向横截面的直径,mm;t表示钢管壁厚,mm;μs,μc表示钢、核心混凝土的泊松比,分别取0.3,0.2。截面剪应力为
τ=QL/A
(21)
式中,A表示截面面积,mm2。
截面钢管处最大压应力σ1-c为
(22)
截面钢管处最大拉应力σ1-t为
(23)
截面钢管轴向应力分布受弯矩影响,截面核心混凝土径向应力σ3是截面钢管的径向反作用力,所以应计算截面钢管平均正应力,即式(16)中x取零,再通过式(19)计算σ3为
(24)
式(20)~(23)代入Mises准则,求得各截面能承受的最大外力Fi(α)做为该截面强度。截面强度物理意义是,当外力达到Fi(α)时,与图8中x轴成角度为α的截面发生屈服。
![]()
(25)
式中,fs取Q235钢的屈服强度235 MPa;σ1取式(22)中σ1-c值计算得出的Fi(α)作为截面受压强度Fc;取式(23)中σ1-t值计算得出的Fi(α)作为截面受拉强度Ft。
3.3 局部失稳研究
通过计算各截面受压、受拉强度,取不同矢跨比拱顶、拱底截面应力系数和截面受压、受拉截面强度见表6。
表6 拱顶和拱底应力系数和截面强度
Table 6 Stress coefficient of apex and bottom of arch and section strength
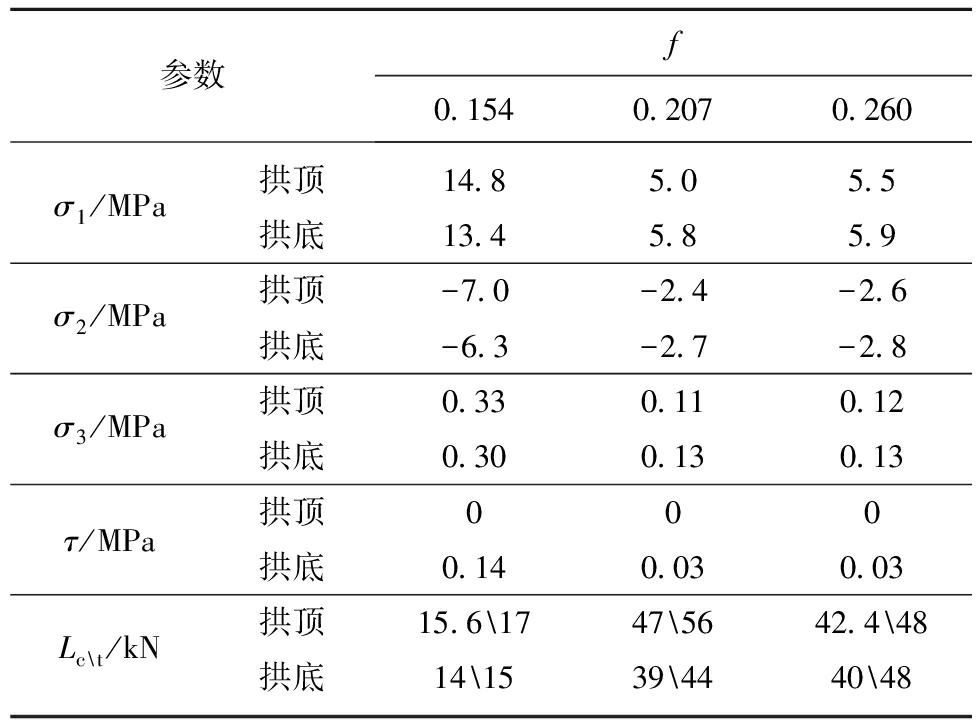
由表6可知,六分点集中荷载下试件拱底、拱顶更容易发生受压破坏,其中拱底最容易发生受压破坏,这是因为截面因弯矩影响,受拉区被截面轴向压应力部分抵消,而受压区轴向压力部分叠加,这解释了图9中拱底的破坏形态。矢跨比0.260的试件与矢跨比0.207的试件相比,拱顶更容易发生破坏,解释了图9中,只有矢跨比0.260的试件拱顶处核心混凝土破坏的原因。
不同矢跨比L(α)-α变化曲线如图19所示。

图19 矢跨比0.154 Fi(α),0.207 Fi(α),0.260Fi(α)与α关系曲线
Fig.19 Fi(α)-α curve of ratio of rise to span 0.154,0.207,0.260
由图19可知,
(1)不同截面抗压强度始终小于截面抗拉强度,这说明构建更容易发生受压破坏,这解释了拱底处出现压致裂纹的原因。
(2)截面抗压强度在四分之一跨出现峰值,说明试件在该部位截面抗压强度最高,难发生破坏,当试件拱底、拱顶局部失稳后,仍有残余应力,拱内截面应力向四分之一跨集中,这解释了数值模拟中塑性范围内,四分之一跨弯矩急剧增加的原因。
(3)拱顶和拱底截面抗压强度和抗拉强度接近,越接近四分之一跨,截面抗压强度与抗拉强度差值越大,所以更容易在受压侧破坏,四分之一跨至拱底截面容易发生逆时针转动,四分之一跨至拱顶容易发生顺时针转动,不仅解释了发生对称跃越失稳的原因[13],如图20所示,也解释了图3中圆弧拱整体破坏的形态。
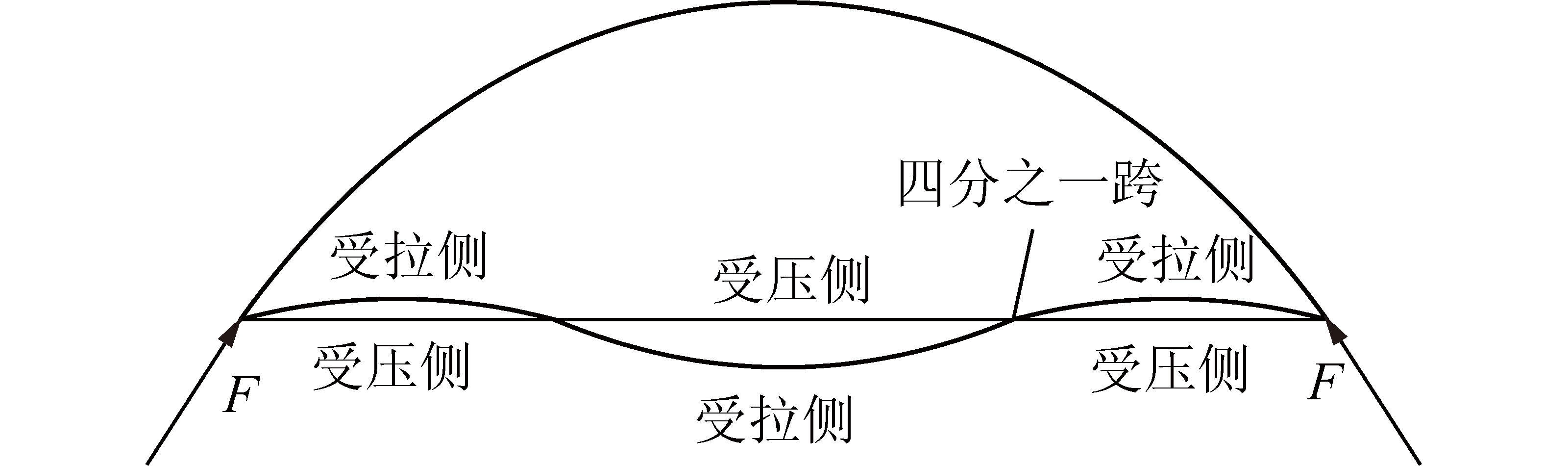
图20 对称跃越失稳
Fig.20 Symmetrical jump instability
结合表6、图9,15表明:
(1)拱底弯矩转化为不均匀轴向应力,钢管中轴向应力大于混凝土的轴向应力,拱底处截面内拱侧核心混凝土破坏形态均为三角破碎,钢管向外凸出。拱底破坏形式为压弯剪破坏,拱顶为轴向受压破坏。
(2)钢的泊松比,弹性模量,强度远大于核心混凝土,钢纤维的形状细小。混凝土单轴实验中,混凝土试块破坏形式属于压制拉裂,掺入钢纤维是提高了混凝土的抗拉性进而提高抗压性。钢管混凝土圆弧拱混凝土受钢管套箍作用,限制了核心混凝土侧向膨胀,掺入钢纤维以提高混凝土的抗压性能效果大幅降低,抗弯性能有所增强。例如,含1%钢纤维体积量的试件拱顶处核心混凝土较完整,拱底处没有呈三角破碎,而是整体破坏且发生相对上移,含1%钢纤维体积量增加了拱底核心混凝土抗弯剪强度。含2%钢纤维体积量的试件拱顶处核心混凝土产生压制碎裂现象,强度不升反降。拱底呈大面积三角破坏。这说明继续增加钢纤维含量,因拱底所受弯矩转化成不均匀轴向应力,轴力影响显著,所以核心混凝土抗压强度降低,使得拱底的内拱侧呈大面积三角破碎。所以钢纤维体积掺量在一定范围内可增加试件的抗弯剪强度,但降低抗压强度。
3.4 四分之一圆弧拱整体失稳极限承载力估算
钢管混凝土圆弧拱是整体结构,局部失稳仍存在残余强度,并与试件整体变形协调。六分点等值集中荷载主要以受压破坏为主,所以以截面抗压强度作为整体失稳承载力的依据,不同矢跨比Fc(α)-α如图21所示。
因为试验荷载是六分点等值集中荷载的6倍,则:
F(α)=pu/6
(26)
式中,pu为试验荷载的极限荷载,kN。

图21 不同矢跨比F(α)-α曲线
Fig.21 F(α)-α curve with different Rise span ratio
将式(25)代入式(24)求得α的数值,表示该截面发生屈服,则整体失稳,计算结果见表7。
表7 钢管混凝土圆弧拱屈服强度计算值
Table 7 Calculation value of yield strength of steel tube concrete arch
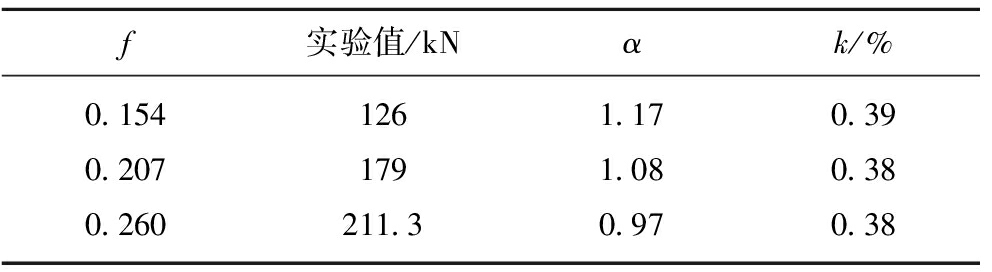
注:k为屈服截面距拱底的距离占半跨长的百分比。
由表7可知,距拱底的距离占半跨长约38%的截面发生屈服就代表试件整体失稳,这一现象在数值模拟也有体现。为验证此结果的准确性,取课题组试验的不同管径相同壁厚、不同壁厚相同管径试件的实验结果[11,13]及本文计算结果比较情况见表8。
表8 计算结果比较
Table 8 Comparison of calculation results
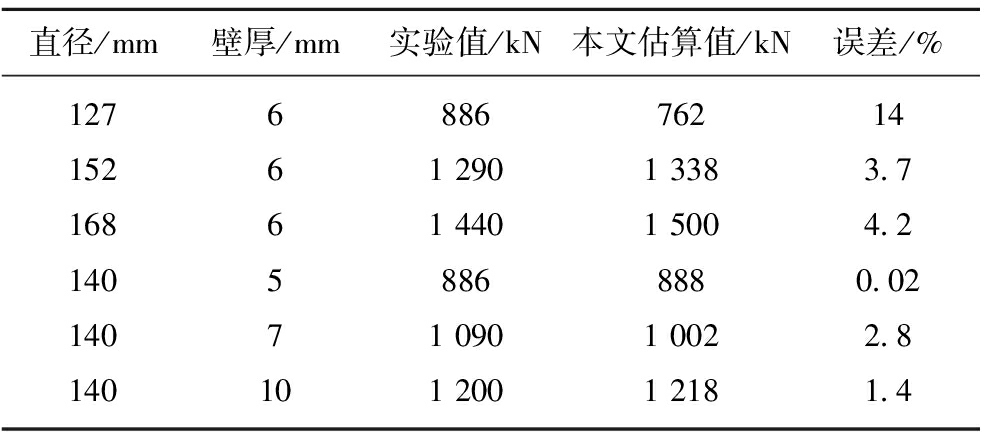
考虑钢管混凝土圆弧拱试验误差,本文的计算值与实际值较为相符。
4 算 例
根据课题组全国20多个深井软岩巷道支护经验,结合山东某巷道深部胶带下山围岩地质条件,初步估计巷道围岩作用在支护体上的荷载为1.15~1.45 MPa。钢管混凝土支架结构设计前需确定支架设计尺寸,以巷道净断面(净宽×净高)尺寸作为钢管混凝土支架净断面的控制点,净宽≤4 000 mm,地坪宽2 600 mm,净高≤3 500 mm,通风面积≥11 m2,得钢管混凝土支架结构尺寸如图22所示。
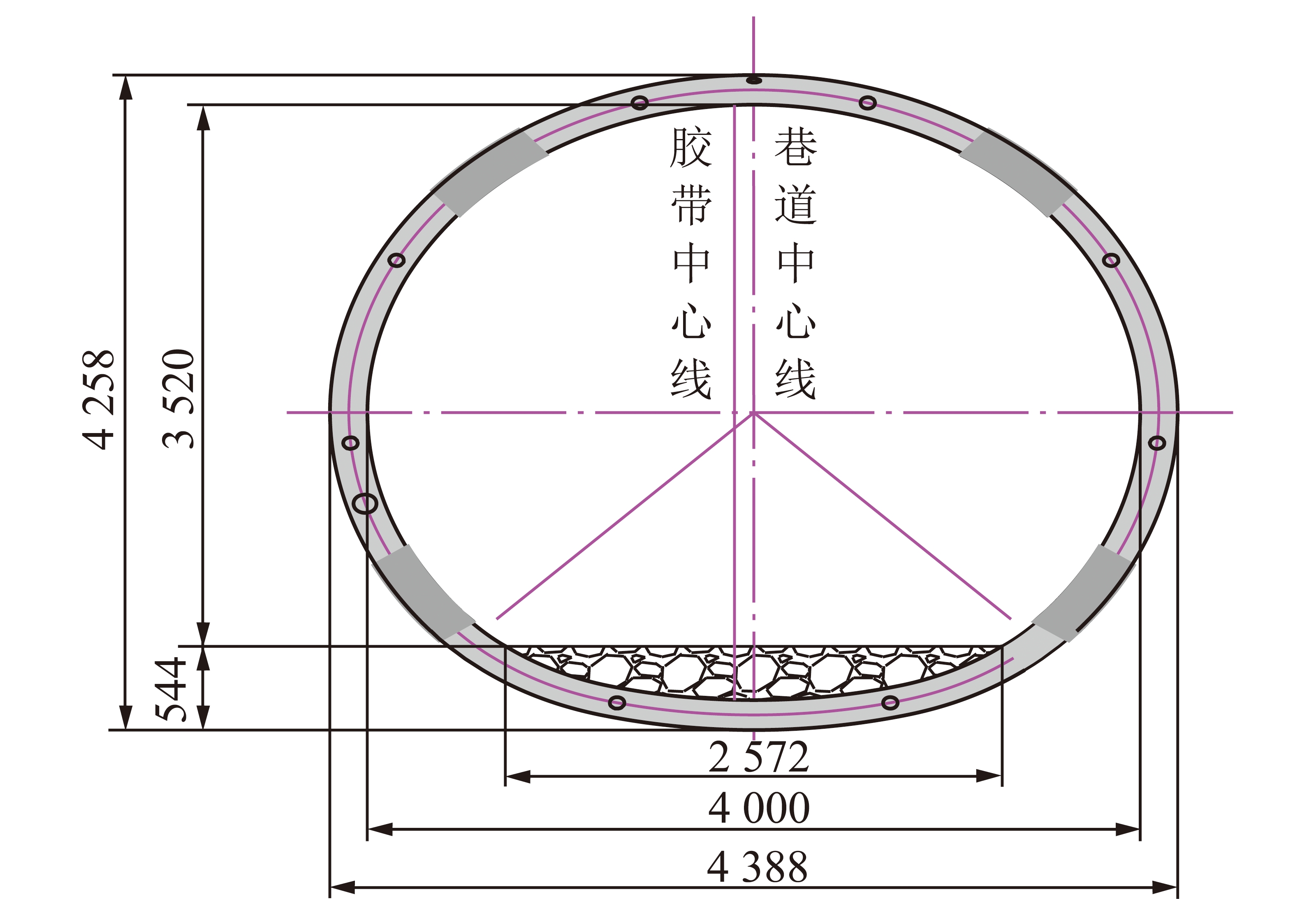
图22 钢管混凝土支架结构尺寸
Fig.22 Dimension diagram of concrete filled steel tubular supports structure
支架钢管型号为φ194 mm×10 mm,钢管选用20号钢,钢材的屈服极限fs=245 MPa,钢管的横截面积As=5 777.6 mm2。设计混凝土型号C40,核心混凝土抗压强度设计值为fc=19.1 MPa,钢管内填混凝土横截面的净面积Ac=23 766.6 mm2。
巷道截面是正圆形,矢跨比为0.207,直径为2 000 mm。取本文矢跨比为0.207,直径2 000 mm的四分之一圆弧拱内力系数。通过式(15),(16)计算出各截面轴向应力分布;通过式(21)~(23)计算出截面环向应力,径向应力以及剪切应力分布,再通过式(25)求得截面抗压强度,最后取距拱底的距离占半跨长约38%的截面抗压强度作为钢管混凝土支架中四分一圆弧拱在均布荷载下的极限承载力,此时钢管混凝土支架局部失稳,计算值约为2 544 kN。
根据力学模型计算支架支护反力为
σ0=6L(α)/(sl)
(27)
式中,s表示支架间距,mm;l表示四分之一圆弧拱的弧长,mm;σ0表示支架的支护反应力,MPa。
根据巷道设计规范,锚网喷支护阻力为(0.1~0.2)MPa。所以由式(27)得出锚网喷钢管混凝土支护阻力:
(1)间距为600 mm时,锚网喷钢管混凝土支架提供支护阻力为(1.45~1.55)MPa,大于1.45 MPa,完全满足支护条件。
(2)间距为800 mm时,钢管混凝土支架支护阻力为1.01 MPa。锚网喷钢管混凝土支架支护阻力为(1.11~1.21)MPa,略大于1.15 MPa,适当增加锚网喷强度也满足支护条件。
5 结 论
(1)为增加钢管混凝土支架准许变形量,添加1%~1.5%钢纤维体积含量为宜。在巷道围压较大的部位应使用较大矢跨比钢管混凝土圆弧拱,以增加支护强度。
(2)圆弧拱试件拱顶承受最大轴向压力作用,拱底受压弯剪复合作用力。试件拱底内拱成三角形破碎是因为拱底截面所受弯矩转化为不均匀轴力。
(3)计算巷道中钢管混凝土支架受力时,先拆解为四分之一圆弧拱并用弹性中线法求出拱底、拱顶的各内力系数,再计算出各截面抗压强度,取距拱底的距离约占半跨的38%的截面抗压强度作为钢管混凝土支架中四分之一圆弧拱的极限强度,此时钢管混凝土支架局部失稳。
参考文献(Reference):
[1] 袁亮,薛俊华,刘泉生,等.煤矿深部岩巷围岩控制理论与支护技术[J].煤炭学报,2011,36(4):535-543.
YUAN Liang,XUE Junhua,LIU Quansheng,et al.Surrounding rock stability control theory and support technique in deep rock roadway for coal mine[J].Journal of China Coal Society,2011,36(4):535-543.
[2] 杨超,陆士良,姜耀东.支护阻力对不同岩性围岩变形的控制作用[J].中国矿业大学学报,2000,29(2):170-173.
YANG Chao,LU Shiliang,JIANG Yaodong.Controlling effects of support resistance on roadway deformation under different rock conditions[J].Journal of China University of Mining and Technology,2009,29(2):170-173.
[3] 侯公羽.围岩-支护作用机制评述及其流变变形机制概念模型的建立与分析[J].岩石力学与工程学报,2008,27(2):3618-3629.
HOU Gongyu.Review of interaction mechanism between surrounding rock and support and analysis of conceptual model of rheological deformation mechanism[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(2):3618-3629.
[4] 高延法,何晓升,陈冰慧,等.特厚富水软岩巷道钢管混凝土支架支护技术研究[J].煤炭科学技术,2016,44(1):84-89.
GAO Yanfa,HE Xiaosheng,CHEN Binghui,et al.Study on support technology of concrete filled steel tubular in roadway with huge thick and rich water soft rock[J].Coal Science and Technology,2016,44(1):84-89.
[5] 高延法,王波,王军,等.深井软岩巷道钢管混凝土支护结构性能试验及应用[J].岩石力学与工程学报,2010,29(S1):2604-2609.
GAO Yanfa,WANG Bo,WANG Jun,et al.Test on structural property and application of concrete-filled steel tube support of deep mine and softrock roadway[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(S1):2604-2609.
[6] 蒋启平.三次样条插值确定拱桥合理拱轴线的方法探讨[J].武汉理工大学学报(交通科学与工程版),2001,25(1):101-104.
JIANG Qiping.A Study of method of determining rational arch axis using three order splin interpolation[J].Journal of Wuhan University of Technology(Transportation Science &Engineering),2001,25(1):101-104.
[7] 孙文波,郑佳丽.轴向可压缩两铰圆弧拱静水压力屈曲荷载研究[J].建筑结构学报,2016,37(S1):426-433.
SUN Wenbo,ZHENG Jiali.Research on buckling loads of compressible hinged-circular archunder uniform hydrostatic pressure[J].Journal of Building Structures,2016,37(S1):426-433.
[8] 邢万里,郁银泉,蒋航军,等.石家庄站大跨度钢拱试验研究[J].建筑结构学报,2016(19):21-25.
XING Wanli,YU Yinquan,JIANG Hangjun,et al.Experimental study on large-span steel arch in Shijiazhuang railway station[J].Building Structure,2016(19):21-25.
[9] JJG/T D65-06—2015.公路钢管混凝土拱桥设计规范[S].
[10] GB 50936—2014.钢管混凝土结构技术规范[S].
[11] 刘珂铭.钢管混凝土圆弧拱压弯性能实验与支护应用[D].北京:中国矿业大学(北京),2016.
[12] 单仁亮,肖禹航,何晓生.钢管混凝土短柱作用机理与塑性极限承载力研究[J].矿业科学学报,2017,2(6):519-528.
SHAN Renliang,XIAO Yuhang,HE Xiaosheng.The mechanism and plasticity ultimate bearing capacity of concrete-filled steel tubular short columns under axial compression[J].Journal of Mining Science and Technology,2017,2(6):519-528.
[13] 何晓升.压弯状态下钢管混凝土圆弧拱的工作机理与应用研究[D].北京:中国矿业大学(北京),2016:55-60.