煤层开采过程中,受采空区形成和应力强扰动的影响,工作面前方煤体在3个方向的应力和应变都在产生变化[1-2]。垂直方向的支承压力升高而水平方向持续出现卸压膨胀过程,煤体经历采动应力路径。与此同时,开采扰动引起煤体内部孔裂隙结构的扩展和贯通,打破煤体内瓦斯原有的吸附平衡状态,造成煤体内瓦斯解吸、增透、运移[3-4]。三向应力条件控制下煤体渗透率的变化是影响瓦斯解吸渗透过程的关键因素。因此,针对三向应力条件下煤体渗透率演化过程的研究具有非常重要的意义。
在室内试验方面,大量学者[5-9]采用三轴加载渗流试验对含瓦斯煤体的渗透特性进行了研究,但以上研究大多集中在瓦斯渗透规律的分析上,较少提出可适用于三向应力条件下的煤体渗透率模型。
目前,关于煤体渗透率模型的研究成果大多集中于煤储层及煤层气开采方面。GRAY[10]从弹性理论出发,假设水平应力增量相同、垂直应力不变,建立了水平应力与煤层等效吸附压力的关系,最先搭建了煤储层渗透率与有效应力的关系。SEIDLE[11]利用“火柴棍”几何模型,建立了煤体渗透率与应力的负指数型关系式。PALMER和MANSOORI[12]基于单轴应变、上覆压力不变的条件,将吸附变形等效为基质热膨胀作用,从孔隙变化角度建立了煤储层渗透率与孔隙度的立方关系式(P-M模型)。SHI和DURUCAN[13-14]以“火柴棍”几何模型为基础,基于热弹性理论,考虑煤体有效应力及吸附变形的影响,建立了单轴应变及恒定上覆荷载条件下煤储层渗透率的动态演化模型(S-D模型)。CUI和BUSTIN[15]假设煤体孔隙率主要由割理结构决定,建立了考虑吸附应变影响的煤体渗透率模型(C-B模型)且证明了该模型在单轴应变条件下可变换为与P-M模型、S-D模型相似的形式。LIU[16]通过理论推导,修正了S-D模型中吸附应变项的系数,提高了吸附应变对煤体渗透率的影响效果。除了单轴应变条件之外,HARPALANI和CHEN[17-18]、MA等[19]、LIU等[20]分别建立了常体积条件下考虑气体压力和基质膨胀变化的煤体渗透率模型。
煤体渗透率的理论模型较多从孔隙度变化和应力状态变化的两个角度建立,前者以P-M模型为代表,后者则以S-D模型为代表。但是,上述模型[10-16]较多建立在单轴应变(即水平方向应变为0)、上覆荷载恒定的假设条件之上。此外,也有少量煤体渗透率模型是基于常体积的假设条件建立的[17-20]。这些模型可以较好的反映煤层气抽采过程中煤体的渗透率变化,但是不能较好的反映出煤层开采过程中煤体三向应力和应变同时改变下煤体的渗透率变化规律。
PERERA等[21]根据弹性理论推导出了三轴应力无侧限条件下煤体的割理渗透率模型,该模型以注气压力、围压、轴压和气体吸附量为控制变量。LU等[22]从基质和裂隙应变的角度计算孔隙度变化,进而建立了有效应力与吸附变形共同作用下的煤体渗透率模型,并且给出了5种不同边界条件下煤体的渗透率模型。可以看出,三向应力条件下煤体渗透率演化模型方面的研究成果还较少。
笔者通过分析室内三轴试验条件下煤体的空间应力状态,以捆绑的火柴棍模型为几何原型,将煤体看作是裂隙和基质的组合体,建立了两种三向应力条件下的煤体渗透率动态演化模型——指数型和立方型,并将两种模型与室内试验结果进行了对比分析,确定了不同试验条件下煤体的渗透规律及两种模型的适用性。
1 三向应力煤体渗透率模型建立
国内外广泛采用室内三轴加载渗流实验对煤体渗流特性进行分析[5-9,23],因而本文以室内三轴加载渗透实验过程为背景建立三向应力条件下煤体渗透率模型。
1.1 模型假设
煤体可分为煤基质和割理两种结构,根据方向上的差异性,割理结构又可分为面割理和端割理(图1(a))。割理结构垂直于煤层的平面,两种割理结构相互正交。因此,在以往研究中煤体分别被简化为球形模型、毛细管模型、火柴棍模型、立方体模型等[22],将煤体假设为火柴棍模型进行分析(图1(b))。此外,基于以下假设对三向应力条件下的煤体渗透率模型进行推导:① 气体仅沿着竖直(z轴)方向进行渗透;② 气体渗透过程在等温条件下进行;③ 将煤体内的孔隙均视为导通的裂隙进行渗透;④ 仅考虑吸附饱和状态下煤体的渗透过程。

图1 煤体割理结构及火柴棍模型
Fig.1 Coal cleat structure and match-stick model
1.2 煤体应力状态分析
三轴压缩试验过程中,煤体试件内的应力状态对称于通过z轴的任一平面,故将三轴压缩试验过程中的圆柱煤体简化为平面问题[24]进行分析(图2(a),(b)),可以得出
σρ=σθ=σc
(1)
因此,三轴应力条件下煤体内部的应力分量在柱坐标系统内的表达式[σC]如下
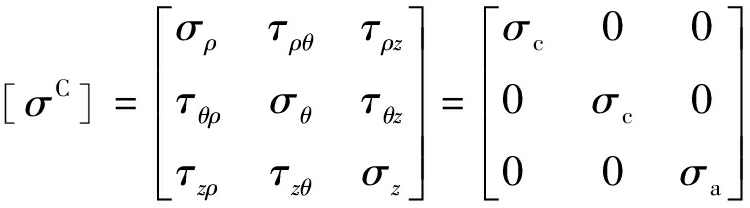
(2)
将煤体假设为捆绑的火柴棍模型,且捆绑的火柴棍沿z轴对称分布,煤体内的应力分量均采用柱坐标表示。此时,沿z轴任意截取角度为dθ的扇形柱体(图2(b))。由于dθ角度微小,这里将取出的扇形体看作是沿径向空间分布的薄板来分析,同时建立直角坐标系(图2(c)),薄板的宽度为r、高度为l、厚度为dθ。

图2 煤体平面模型及薄板煤体示意
Fig.2 Plane model and plate element of coal
图2中可以看出,对煤体圆柱进行分析采用的柱坐标系与对煤体薄板进行分析的直角坐标系在z轴方向重合,进而利用坐标转换公式[T]对两坐标系下的应力分量进行转换,可以得出直角坐标系下煤体薄板的应力分量[σD]如下
[σD]=[T][σC][T]-1
(3)
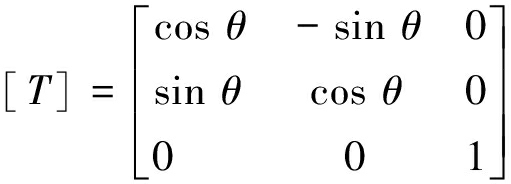
(4)
煤体薄板沿煤体圆柱的径向进行截取,因此,取θ=0,柱坐标系的ρ轴与直角坐标系的x轴重合,将式(4)代入式(3)进行转换可以得出直角坐标应力分量[σD]如下:

(5)
1.3 煤体裂隙孔径变形
煤体渗透率的变化由煤体裂隙孔径变形决定,因而求出裂隙孔径的变化量可以定量描述煤体渗透率的变化。由捆绑的火柴棍模型出发,将取出的薄板煤体(图2(c))看作是由大量煤体基质单元和裂隙单元组成,每个煤体基质单元与裂隙单元组成1个煤体单元。将煤体基质单元和裂隙单元看作是各向同性的弹性体,则煤体薄板可视为大量煤体基质单元和裂隙单元串联而成的弹性系统(图3)。

图3 煤体弹性系统示意
Fig.3 Sketch of coal elastic system
在整个弹性系统中,整个煤体的变形量可认为是由煤体基质变形与裂隙变形之和组成。因此裂隙的变形量可表示为
uf=ub-us
(6)
式中,uf,ub,us分别为裂隙变形量、煤体变形量和煤体基质变形量,m。
煤体由大量煤体基质单元和裂隙单元组成,则将煤体变形、煤体基质变形和裂隙变形采用各自单元变形量求和的形式表示为
(7)
式中,ufi,ubi,usi分别为裂隙单元变形量、煤体单元变形量和煤体基质单元变形量,m。
采用裂隙孔径和基质宽度(图2(c))的几何尺寸变化量来表示煤体弹性系统各部分的变形量为
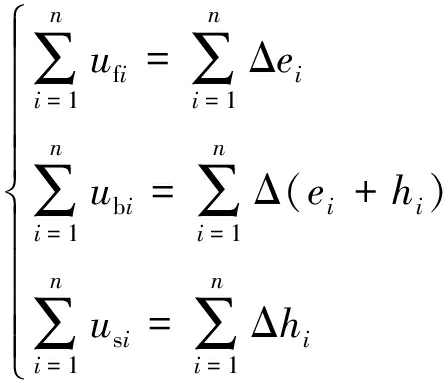
(8)
式中,ei为每个裂隙单元的孔径,m;hi为每个基质单元的宽度,m。
考虑到煤体赋存初始应力状态的差异,采用增量形式体现不同应力路径下煤体应变的改变量。结合工程应变的定义,式(7)可以转换为应变表示的增量形式:
(9)
式中,Δεb,Δεs分别表示煤体和煤体基质在直角坐标x轴方向的应变。
根据广义胡克定律,在x轴方向上,煤体应变、煤体基质应变与有效应力增量的关系为
(10)
![]()
(11)
式中,Eb,Es分别为煤体和煤体基质的弹性模量,GPa;νb,νs分别为煤体和煤体基质的泊松比;![]() 分别表示直角坐标下x,y,z轴方向的有效应力增量,MPa。
分别表示直角坐标下x,y,z轴方向的有效应力增量,MPa。
将式(10),(11)代入式(9),同时认为νb=νs,可得
![]()
(12)
以压缩为正,与材料力学中规定拉伸为正相反,故而在式(12)等号右端添加负号。由串联的弹簧系统可知各弹簧元件的拉压刚度值存在如下关系
(13)
式中,Kb,Ks,Kf分别为煤体、煤体基质、裂隙的刚度值。
由于弹性体的拉压刚度K=EA,A为弹性体横截面,则式(13)变换如下
(14)
将式(14)代入式(12)可得
![]()
(15)
将式(15)两端同时除以![]() 可得
可得
![]()
(16)
根据孔隙度的定义(图3),可以得出煤体薄板沿x轴方向的初始孔隙度![]() 如下
如下
(17)
则
(18)
将式(18)代入式(16)得到裂隙孔径应变为
![]()
(19)
此外,根据Biot固结原理有
Δσe=Δσ-αbΔp
(20)
式中,Δσe为煤体的有效应力增量,MPa;Δσ为煤体的总应力增量,MPa;Δp为煤体内气体压力增量,MPa;αb为Biot系数。
将式(5),(20)代入式(19),得到三向应力条件下煤体圆柱试件中x方向裂隙孔径应变的表达式为
Δσc-νbΔσa+(2νb-1)αbΔp]
(21)
类比上述方法,可以得到室内三轴加载过程中y轴方向的裂隙变形量为
νb)Δσc-νbΔσa+(2νb-1)αbΔp]
(22)
捆绑的火柴棍模型中(图1(b)),x轴和y轴方向的每根火柴棍(煤体基质单元)及裂隙单元均为各向同性体,即在空间上具有相同的物理力学特征。沿x轴和y轴分别截出的煤体薄板单元和煤体具有同样的孔隙度,即
(23)
式中,φ0表示煤体圆柱试件的初始孔隙度;上标pl表示截取出的煤体薄板单元;下标x,y表示薄板截取的方向。
1.4 渗透率模型表达式
1.4.1 指数型
煤体渗透率与煤体基质宽度及裂隙孔径的关系式[25]可表示为
(24)
式中,ki是煤体单元的渗透率,m2。
对式(24)进行推导可以得出煤体割理渗透率与裂隙孔径变形量之间的关系[21]为
(25)
式中,k0为煤体的初始渗透率,m2。
对式(25)进行变形,可以得到同时考虑x和y两个方向裂隙变形影响的煤体在z方向的渗透率表达式为
(26)
由式(21),(22)可以看出,每根煤体基质单元在x和y方向同时发生变形且变形量相等。将式(21)~(23)代入式(26)可得三向应力条件下煤体渗透率的指数型表达式
![]()
(27)
1.4.2 立方型
根据ZHANG等的研究成果[26-27],煤体在x和y两个水平方向裂隙变形影响下,z方向的渗透率可表示为
(28)
将式(21)~(23)代入式(28)可得三向应力条件下煤体渗透率的立方型表达式为
![]()
(29)
2 渗透率模型对比验证分析
为了对比分析以上所建立的两种渗透率模型的正确性和适用性,利用室内三轴加载渗透试验数据进行对比验证分析。
2.1 渗透率测定试验
渗透率测试采用法国TOP高温高压流变仪(图4(a))进行,该仪器主要由加压系统、三轴压力室、计算机控制系统、数据采集系统及气压控制系统等装置组成。最大轴向压力200 kN,最大围压100 MPa。测试煤样取自平煤十二矿己15-31030工作面。根据《GB/T 23561.9—2009煤和岩石物理力学性质测定方法》的规定将煤体加工成直径50 mm、高度100 mm的圆柱体试件(图4(b))进行渗透率测试。

图4 渗透率测试仪器及试验样品
Fig.4 Permeability test instruments and test samples
测试方法采用瞬态压力脉冲法进行,测试所用气体为高纯氮气,对不同围压和轴压下深部煤体的渗透率进行测试。渗透率测试的过程中,首先施加静水压力并通入渗透气体待试件吸附至饱和状态,依次改变围压和轴压的组合值,每一级载荷下保持其瞬态脉冲压力差的初始值不变,进行每一级载荷下的渗透率测试,具体的试验条件见表1和2。煤体渗透率根据式(30)和(31)进行计算[28]。
(30)
![]()
(31)
式中,k为煤样的渗透率,m2;μ为气体动力黏度,Pa·s;η为气体压缩系数,MPa-1;L为煤样的高度,m;A为煤样的横截面积,m2;V1,V2为上、下游气体缓冲容器体积,m3;Pf为系统平衡后压强,MPa;ΔPg为初始时刻上游和下游气体缓冲容器内的压力差,MPa。
表1 试件编号及气体压力
Table 1 Specimen number and gas pressure

表2 渗透率测试载荷水平
Table 2 Load level of permeability test

在岩石渗透率低于10-16 m2的条件下,气体分子的自由程接近岩石的孔隙尺寸时会出现滑脱现象,导致所测得的岩样气体渗透率大于其绝对渗透率。KLINKENBERG对此现象进行了研究[29],并提出利用式(32)和(33)对气测岩石渗透率进行修正,以此得到岩石内的绝对渗透率。
kg=k
![]()
(32)
![]()
(33)
式中,kg为煤样的气测渗透率,m2;k 为煤样的绝对渗透率,m2;b为滑脱因子,MPa,Pm为平均气体压力,MPa;c为比例因子,通常取0.9;rp为煤样孔隙半径,m;λ为气体分子平均自由程,m。
为煤样的绝对渗透率,m2;b为滑脱因子,MPa,Pm为平均气体压力,MPa;c为比例因子,通常取0.9;rp为煤样孔隙半径,m;λ为气体分子平均自由程,m。
气体平均自由程可由式(34)计算[30]:
(34)
式中,R为气体常数,取8.314 J/(K·mol);Tabs为绝对温度,K;M为气体摩尔质量,kg/mol。
2.2 改变轴压和围压条件
结合上文推导出的指数型和立方型的渗透率计算公式,即式(27)和(29),将试验结果和理论值进行对比分析。考虑到煤体试样渗透率存在的差异性,为了便于验证煤体渗透率与应力的关系,故将渗透率进行归一化处理后分析。理论值计算所需参数见表3,煤体初始渗透率k0为静水压力为5 MPa下的煤体渗透率。
表3 煤体基本参数
Table 3 Basic parameters of coal

由图5可以看出,保持每个试样气体渗透压力差不变,在载荷水平增量由0向15 MPa逐级增加的过程中,指数型和立方型的煤体渗透率计算结果变化规律较为一致,均呈现出随着载荷应力水平的增高而降低的变化趋势,渗透率降低的速率越来越慢且立方型的渗透率下降速率大于指数型。

图5 不同载荷水平下渗透率结果
Fig.5 Results of permeability at different loading levels
在气体压力保持不变的前提下,随着载荷水平的增加,环向和轴向受到更大的压应力,煤体有效应力增大,产生压缩变形。煤体内部孔隙和裂隙结构出现不同程度的闭合现象,造成煤体内孔隙度降低、裂隙开度减小,气体流动通道变窄,煤体试样对气体的渗透性能下降。
指数型、立方型渗透率模型理论值与实测值对比的拟合优度见表4,可见在仅改变围压和轴压组合值的条件下,指数型煤体渗透率表达式与实测值的拟合优度更高,可以更好的表达渗透率演化过程。
表4 改变载荷水平条件的拟合优度
Table 4 Goodness of fit under different load level

2.3 改变气体压力条件
所建立的两种煤体渗透率模型均为吸附饱和状态下(不考虑吸附影响)煤体随压力变化的渗透率模型。因此,后文使用氦气作为渗透气体,基于恒定围压和轴压条件下仅改变气体压力条件的实测数据[31-32],对不同气体压力条件下煤体的渗透率进行了拟合分析。
图6可以看出,在保持围压和轴压不变的条件下,两种形式的煤体渗透率均随着气体压力的升高而增大。在氦气压力不断增大的过程中,煤体渗透率的增长速率越来越快且指数型的渗透率增幅大于立方型。

图6 不同气体压力下渗透率
Fig.6 Permeability under different gas pressures
当煤体外部载荷恒定,随着气体压力的不断增加,煤体产生整体的膨胀变形,煤体内所受的有效应力减小,内部裂隙扩张、孔隙率增大,气体通道产生扩展贯通现象,造成煤体渗透率增大。
两种形式煤体渗透率理论值与实测值的拟合优度见表5,指数型的结果与实测值贴合较好,所以指数型较立方型能够更好的体现气体压力改变下煤体渗透率的演化过程。
表5 改变气体压力条件的拟合优度
Table 5 Goodness of fit under different gas pressure

对比分析改变轴压围压、改变气体压力条件下指数型和立方型的拟合结果可知,两者表现的规律较为一致:渗透率均随着载荷水平的增高而减小、而随着气体压力的增高而增大。在改变载荷水平或气压的过程中,指数型的结果较立方型更接近试验结果,且立方型的渗透率计算结果始终小于指数型结果的变化幅度。此外,结合式(27),(29)可以看出,在实际试验过程中,对于任意的加卸载条件和外部应力组合值下,立方型的渗透率计算结果可能因为Δσc,Δσa,Δp取值相差较大而出现负值的情况,而指数型的计算结果能够保证煤体渗透率恒为正值。综上所述,指数型的渗透率模型更适合描述三向应力条件下煤体的渗透率演化过程。
3 结 论
(1)以弹性理论为基础,对室内三轴试验加载过程中煤体的空间应力状态进行了理论分析,得出三向应力条件下受载煤体的空间应力分量。
(2)以捆绑的火柴棍模型为几何原型,将煤体看作是基质和裂隙组成的单元体,突破以往单轴应变假设,考虑三向应力的作用建立了指数型和立方型的煤体渗透率演化模型。
(3)分别改变煤体所受的轴压和围压、气体压力条件,通过试验结果和理论结果进行对比分析得出:煤体渗透率随着载荷水平的增大而降低、随着气体压力的增大而升高。两种条件下指数型均比立方型更符合三向应力条件下煤体渗透率的变化过程。
参考文献(References):
[1] 谢和平,周宏伟,刘建锋,等.不同开采条件下采动力学行为研究[J].煤炭学报,2011,36(7):1067-1074.
XIE Heping,ZHOU Hongwei,LIU Jianfeng,et al.Mining-induced mechanical behavior in coal seams under different mining layouts[J].Journal of China Coal Society,2011,36(7):1067-1074.
[2] WANG G F,PANG Y H.Surrounding rock control theory and longwall mining technology innovation.International Journal of Coal Science &Technology 2017,4(4):301-309.
[3] 谢和平,高峰,周宏伟,等.煤与瓦斯共采中煤层增透率理论与模型研究[J].煤炭学报,2013,38(7):1101-1108.
XIE Heping,GAO Feng,ZHOU Hongwei,et al.On theoretical and modeling approach to mining-enhanced permeability for simultaneous exploitation of coal and gas[J].Journal of China Coal Society,2013,38(7):1101-1108.
[4] 薛东杰,周宏伟,孔琳,等.采动条件下被保护层瓦斯卸压增透机理研究[J].岩土工程学报,2012,34(10):1910-1916.
XUE Dongjie,ZHOU Hongwei,KONG Lin,et al.Mechanism of unloading-induced permeability increment of protected coal seam under mining[J].Chinese Journal of Geotechnical Engineering,2012,34(10):1910-1916.
[5] 刘见中,张东明,袁地镜.含瓦斯煤在不同围压下的渗流特性试验[J].煤炭科学技术,2009,37(7):70-72,89.
LIU Jianzhong,ZHANG Dongming,YUAN Dijing,et al.Vadose features test of gas content coal under different surrounding pressures[J].Coal Science and Technology,2009,37(7):70-72,89.
[6] 王广荣,薛东杰,郜海莲,等.煤岩全应力-应变过程中渗透特性的研究[J].煤炭学报,2012,37(1):107-112.
WANG Guangrong,XUE Dongjie,GAO Hailian,et al.Study on permeability characteristics of coal rock in complete stress-strain process[J].Journal of China Coal Society,2012,37(1):107-112.
[7] 魏建平,李明助,王登科,等.煤样渗透率围压敏感性试验研究[J].煤炭科学技术,2014,42(6):76-80.
WEI Jianping,LI Mingzhu,WANG Dengke,et al.Experimental research on sensibility of coal samples permeability under confining pressure[J].Coal Science and Technology,2014,42(6):76-80.
[8] 孙光中,荆永滨,张瑞林,等.轴向应力循环加卸载作用下含瓦斯煤渗透性研究[J].岩石力学与工程学报,2016,35(5):928-938.
SUN Guangzhong,JING Yongbin,ZHANG Ruilin,et al.Permeability of coal samples containing methane under cyclic loading-unloading of axial stresses[J].Chinese Journal of Rock Mechanics and Engineering,2016,35(5):928-938.
[9] 宫伟东,张瑞林,郭晓洁,等.构造煤原煤样制作及渗透性试验研究[J].煤炭科学技术,2017,45(3):89-93,122.
GONG Weidong,ZHANG Ruilin,GUO Xiaojie,et al.Experiment study on raw coal sample preparation and permeability of structure coal[J].Coal Science and Technology,2017,45(3):89-93,122.
[10] GRAY I.Reservoir engineering in coal seams:Part 1-The physical process of gas storage and movement in coal seams[J].SPE Reservoir Engineering,1987,2(1):28-34.
[11] SEIDLE J P,JEANSONNE M W,ERICKSON D J.Application of matchstick geometry to stress dependent permeability in coals[A].SPE Rocky Mountain Regional Meeting[C].Society of Petroleum Engineers,1992:433-444.
[12] PALMER I,MANSOORI J.How permeability depends on stress and pore pressure in coalbeds:A new model[J].SPE Reservoir Evaluation &Engineering,1998,1(6):539-544.
[13] SHI J Q,DURUCAN S.Drawdown induced changes in permeability of coalbeds:A new interpretation of the reservoir response to primary recovery[J].Transport in Porous Media,2004,56(1):1-16.
[14] SHI J Q,DURUCAN S.A model for changes in coalbed permeability during primary and enhanced methane recovery[J].SPE Reservoir Evaluation &Engineering,2005,8(4):291-299.
[15] CUI X J,BUSTIN R M.Volumetric strain associated with methane desorption and its impact on coalbed gas production from deep coal seams[J].AAPG Bulletin,2005,89(9):1181-1202.
[16] LIU S M,HARPALANI S,PILLALAMARRY M.Laboratory measurement and modeling of coal permeability with continued methane production:Part 2-Modeling results[J].Fuel,2012,94(1):117-124.
[17] HARPALANI S,CHEN G L.Estimation of changes in fracture porosity of coal with gas emission[J].Fuel,1995,74(10):1491-1498.
[18] HARPALANI S,CHEN G L.Influence of gas production induced volumetric strain on permeability of coal[J].Geotechnical &Geological Engineering,1997,15(4):303-325.
[19] MA Q,HARPALANI S,LIU S M.A simplified permeability model for coalbed methane reservoirs based on matchstick strain and constant volume theory[J].International Journal of Coal Geology,2011,85(1):43-48.
[20] LIU J S,CHEN Z W,ELSWORTH D,et al.Evolution of coal permeability from stress-controlled to displacement-controlled swelling conditions[J].Fuel,2011,90(10):2987-2997.
[21] PERERA M S A,RANJITH P G,CHOI S K.Coal cleat permeability for gas movement under triaxial,non-zero lateral strain condition:A theoretical and experimental study[J].Fuel,2013,109:389-399.
[22] LU S Q,CHENG Y P,LI W.Model development and analysis of the evolution of coal permeability under different boundary conditions[J].Journal of Natural Gas Science and Engineering,2016,31:129-138.
[23] PAN Z J,CONNELL L D.Modelling permeability for coal reservoirs:A review of analytical models and testing data[J].International Journal of Coal Geology,2012,92:1-44.
[24] 徐秉业,刘信声,沈新普.应用弹塑性力学(第2版)[M].北京:清华大学出版社,2017:138-141.
[25] GU F G,CHALATURNYK R.Permeability and porosity models considering anisotropy and discontinuity of coalbeds and application in coupled simulation[J].Journal of Petroleum Science and Engineering,2010,74(3-4):113-131.
[26] ZHANG J C,ROEGIERS J C,SPETZLER H A.Influence of stress on permeability around a borehole in fractured porous media[J].International Journal of Rock Mechanics and Mining Sciences,2004,41(3):496-501.
[27] LIU J S,ELSWORTH D.Three-dimensional effects of hydraulic conductivity enhancement and desaturation around mined panels[J].International Journal of Rock Mechanics and Mining Sciences,1997,34(8):1139-1152.
[28] BRACE W F,WALSH J B,FRANGOS W T.Permeability of granite under high pressure[J].Journal of Geophysical Research,1968,73(6):2225-2236.
[29] KLINKENBERG L J.The permeability of porous media to liquids and gases[J].API Drilling and Production Practices,1941(2):200-213.
[30] CIVAN F.Effective correlation of apparent gas permeability in tight porous media[J].Transport in Porous Media,2010,82(2):375-384.
[31] WANG Y,LIU S M,ELSWORTH D.Laboratory investigations of gas flow behaviors in tight anthracite and evaluation of different pulse-decay methods on permeability estimation[J].International Journal of Coal Geology,2015,149:118-128.
[32] QIU Y K,LI Z P,HAO S Y.Comparison between steady state method and pulse transient method for coal permeability measurement[A].IOP Conference Series:Earth and Environmental Science[C].Bristol:IOP Publishing,2017,64(1):012013.