岩溶陷落柱广泛分布于我国华北地区的20多个煤田中，其引发的突水事故均具有隐蔽性、滞后性和突发性特点，给煤矿安全生产带来了极大的威胁[1-2]。据统计，历史上我国华北煤田发生了一系列严重的陷落柱突水事故，造成了大量的人员伤亡和经济损失[3]。近年来，随我国煤矿开采向深部延伸，陷落柱引发的突水灾害愈加严重[4]。因此深入研究陷落柱突水机理并为其突水灾害防治提供理论依据具有重要实践意义。
目前，围绕煤矿陷落柱突水模式、发展过程、渗流特性等科学问题，有关学者通过理论分析、数值模拟和室内实验等手段开展了大量的研究工作，建立了以“圆形厚壁筒”[5]、“椭圆形截面”[6]、“塞子模型”[7]等为代表的陷落柱突水力学模型，分析了陷落柱渗流突变机制[8]及采动条件下的陷落柱突水过程[9]，模拟了陷落柱突水过程中的渗流场分布规律[10-11]。此外，文献[12-14]对采动破碎岩体渗流规律进行了大量的试验分析研究;文献[15-19]探讨了水-力耦合作用下岩体的渗透特性演化问题。上述研究成果对于了解陷落柱渗流特性、揭示其突水机理具有重要意义。但是，相关分析较少涉及充填物流失对陷落柱渗透特性的影响，在陷落柱充填物颗粒和流体的运移以及岩体的变形之间的耦合作用方面亦未开展系统的研究。
因此，在上述相关研究的基础上，笔者综合考虑了陷落柱渗流过程岩块骨架变形-水渗流-充填物颗粒迁移的耦合作用，建立了多场耦合的陷落柱突水变形-渗流-冲蚀力学模型。在此基础上，结合研究矿区地质条件，借助相应数值模拟软件将力学模型数值化，模拟研究了煤矿底板承压陷落柱突水发展的全过程，从充填物颗粒流失引发多场耦合系统运动失稳的角度揭示陷落柱突水机制。
1 陷落柱突水力学模型的建立
陷落柱内部结构主要由岩块骨架、裂隙充填物以及流体3部分组成，如图1(a)所示，且可以看作是一种双重孔隙介质:其中，岩块为基质块，岩块间裂隙为流体渗流的主要通道，充填物位于裂隙侧壁，其几何模型可用Warren-Root模型[20]表示，如图1(b)所示。
图1 陷落柱双重孔隙模型及特征微元
Fig.1 Dual-porosity model for KCP and representative elemental volume
1.1 基本假设
为建立陷落柱突水的变形-渗流-冲蚀耦合力学模型，做以下假设:① 陷落柱可看作双重孔隙结构;② 陷落柱内流体运动符合非达西渗流;③ 颗粒为不可压缩性固体;④ 颗粒运移速度和流体渗流速度近似相等;⑤ 流体中冲蚀颗粒均匀分布;⑥ 忽略冲蚀颗粒对流体流动特性的影响。
1.2 应力场方程
基于上述陷落柱双重孔隙模型，取模型特征微元体，如图1(c)所示，设基质块边长为a，裂隙宽度为b，且b≪a，则微元体体积为V=(a+b)3≅a3。设基质块的孔隙率为φm，裂隙率为φf，则微元体的空隙度φ为
≅
(1)
根据李传亮等[21-22]提出的有效应力原理，利用线弹性本构模型，得到模型的应力场控制方程为
(λ+G)εV,i-G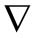
2ui+φpi=0
(2)
式中，(i=1,2,3)表示3个方向，λ，G为模型的等效Lame常数;u为固体骨架位移;εV为体积应变;p为饱和孔隙水压力。
1.3 渗流场方程
研究表明[23]，陷落柱等破碎构造渗流非线性特征明显，因此笔者采用布里克曼方程来表征其流体运动控制方程
(3)
式中，q为流体渗流速度，m/s;k为微元体的渗透率，m2;η为流体的动力黏度，Pa·s。
研究表明，孔隙的渗透率km与孔隙率、裂隙的渗透率kf与裂隙率之间均满足3次方关系，则微元体的渗透率可表示为
(4)
式中，φm0为微元体的初始孔隙率。
1.4 质量守恒方程
微元体内冲蚀颗粒在对流和扩散的共同作用下迁移，在xi(i=1,2,3)方向上，单位时间内进入微元体的颗粒质量为
(5)
式中，C为颗粒的体积浓度;ρs为颗粒密度;D为扩散系数。
根据微元体颗粒质量守恒可得
(6)
由于颗粒不可压缩，整理得
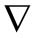(Cq)-·
(7)
若忽略颗粒的扩散作用，则颗粒的质量守恒方程可简化为
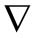
(8)
同理，可以得到流体的质量守恒方程为
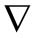·[(1-C)q]=0
(9)
1.5 孔隙率演化方程
微元体基质孔隙的变化主要受应力控制。设Vs为基质块固体体积，Vp为孔隙体积，则基质块总体积为V=Vs+Vp，孔隙率为φm=Vp/V，则基质块体应变以及孔隙体应变可表示为
(10)
其中，
为平均应力;α=1-Km/Ks，β=1-Kp/Ks分别为基质块和孔隙的Biot系数;Ks,Km,Kp分别为骨架、基质块和孔隙的体积模量，其中Km=E/3(1-2μ)，E,μ分别为微元体弹性模量和泊松比。根据Betti-Maxwell互易定理[24]，可以得到
(11)
由式(10)和式(11)可得
(12)
将式(12)对时间t求导，得孔隙率动态演化方程:
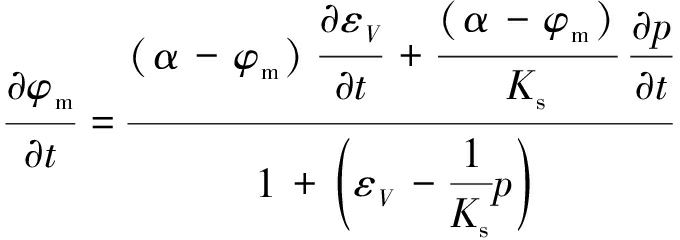
(13)
1.6 裂隙率演化方程
微元体裂隙率主要受应力和冲蚀作用控制。其中有效应力引起的裂隙开度变化为
(14)
式中，Δσet为有效应力;Em为微元体基质弹性模量，可表示[25]为
(15)
式中，kn为裂隙法向刚度系数，kn=(λ+2G)/b[26]。
由式(14)可知，在有效应力作用下裂隙开度变化为微元体变形与基质块变形之差。定义弹性模量衰减率Rm=1-E/Em，有效应变Δεet=Δσet/E=ΔεV/3，结合式(14)，单位宽度裂隙开度变化可表示为
(16)
由于裂隙率Δφf≈3Δb/a，则有效应力作用下裂隙率φf1变化控制方程可表示为
Δφf1=φf1-φf0=(1-Rm)ΔεV
(17)
将式(17)对时间t求导可得
(18)
参考I.VARDOULAKIS[17]关于介质溶蚀问题方面的研究成果，得到单独考虑冲蚀下的微元体裂隙演化控制方程为
(19)
式(19)表明冲蚀引起的裂隙变化与颗粒浓度和流体渗流速度均呈正比，其中，λ1为常数，
为流体的渗流速度。
由于φf=3b/a，根据式(18)和式(19)可得到微元体在应力和冲蚀共同作用下的裂隙演化控制方程:
(20)
综上，式(2)，(8)，(9)，(13)和(20)共同构成了陷落柱突水的固体变形-流体渗流-充填物颗粒迁移多场耦合力学模型，图2给出了模型方程之间耦合关系。
图2 模型的多物理场耦合关系
Fig.2 Coupling relationship for mechanical model
2 陷落柱突水数值模型的建立
2.1 工程背景
某矿19号煤轨道下山掘进工作面发生陷落柱突水事故，最初巷道两帮裂隙出现涌水，其水量为9 m3/h，8.5 h后涌水量猛增到1 398 m3/h，最终造成全矿井被淹。不同时刻的涌水量见表1。据事故调查，确定本次事故水源为奥灰岩溶水，后经采取三段式注浆治理控制确定通道为隐伏陷落柱。
表1 不同时刻的陷落柱涌水量
Table 1 KCP water flow at different time
2.2 数值计算模型建立
根据该突水陷落柱区域地质资料，得到其物理模型如图3(a)所示，陷落柱近似为圆台型，顶部直径为14 m，底部直径为28 m，高为34 m，与其相连通的是厚度为4 m的承压含水层。基于陷落柱突水物理模型，运用多物理场耦合软件COMSOL Multiphysics将力学模型数值化，并考虑模型的轴对称性，建立如图3(b)所示的数值计算模型。对于模型的变形场，左边界为轴对称，陷落柱右边界为应力边界，围压为1.0 MPa，其余为位移边界;对于模型的渗流场，模型右边界和上边界均为压力边界，压力值分别为含水层压力2.5 MPa和大气压力0.1 MPa，其余边界为无流出边界。表2给出了数值模型的参数取值。
图3 陷落柱突水物理模型及数值计算模型
Fig.3 Physical and numerical model for KCP water outburst
通过查看钻探取芯和冲入巷道堆积物发现陷落柱内部充填物大部分为软岩且已风化变软。为深入分析陷落柱导水通道演化规律，笔者考虑了陷落柱内初始裂隙分布的非均质性，并用Weibull概率密度函数表示:
(21)
式中，b0为初始裂隙开度;s为均匀性指数，值越大表明均匀性越好。
表2 数值模拟参数
Table 2 Parameters for numerical simulation
3 数值模拟结果及分析
通过数值模拟，得到了陷落柱裂隙开度、颗粒体积浓度、涌水量等渗流特性变化规律，并再现了煤矿底板承压陷落柱突水发展的全过程。
图4和图5分别为模拟得到的不同时刻陷落柱裂隙开度和渗流速度的分布云图，图6为模型y=20 m水平测线上的渗流速度在不同时刻的分布曲线。由图4～6可知，在渗流初始阶段，模型各处裂隙开度和渗流速度差异性均较小，在变形-渗流-冲蚀耦合作用下，模型各处裂隙开度和渗流速度随时间逐渐分化:部分区域裂隙开度和渗流速度增加越来越快，而其它区域则变化缓慢，最终渗流优势区域的裂隙逐步扩展、贯通，形成数条导水通道并导致了突水事故的发生。
图4 不同时刻模型裂隙开度分布云图
Fig.4 Fracture aperture at different time
图5 不同时刻模型渗流速度变化云图
Fig.5 Seepage velocity at different time
图6 不同时刻模型z=24 m测线速度分布曲线
Fig.6 Seepage velocity along z=24 m at different time
图7为陷落柱内平均裂隙开度和颗粒体积浓度随时间变化曲线，可知在两者变化趋势基本保持一致，表明陷落柱在骨架变形-水渗流-充填物颗粒冲蚀耦合作用下，充填物颗粒不断液化运移、流失，导致陷落柱部分裂隙发生扩展连通，最终形成优势的导水通道，其中流体的冲蚀作用是造成陷落柱突水发生的主导因素。
图7 模型裂隙开度和颗粒体积浓度随时间变化曲线
Fig.7 Fracture aperture and particle concentration with time
图8为模拟的陷落柱涌水量及现场实测曲线，可知两者变化趋势基本一致，证明了本文所建立的陷落柱突水的变形-渗流-冲蚀力学模型的正确性。还可知，模型涌水量初始增加缓慢，从初始时刻的9 m3/h增加到5.5 h时刻的65 m3/h，0～5.5 h时间段内涌水量的变化速度仅为10.2 m3/h2;而5.5 h后涌水量变化速度明显加快，5.5～8.5 h时间段内涌水量的变化速度高达444.4 m3/h2，后者为前者的43.6倍。可见，5.5 h时后陷落柱涌水量会徒然增加，发生突水事故，该时刻即为陷落柱“突水临界点”，若在此时刻之前对陷落柱采取注浆加固等措施，可有效防止突水事故发生。
图8 现场-模拟条件下陷落柱涌水量变化曲线
Fig.8 KCP water flow for numerical simulation and field test
4 结 论
(1)在研究矿区相关水文地质条件和涌水量等数据基础上，将所建立力学模型数值化，模拟研究了陷落柱内裂隙开度、颗粒体积浓度、涌水量等随时间的变化规律，数值再现了煤矿底板承压陷落柱突水发展的全过程。模拟得出的陷落柱涌水量时变曲线和现场数据基本一致，验证了本文建立的陷落柱突水力学模型的正确性。
(2)计算结果显示，模型涌水量初始阶段增加缓慢，在骨架变形-水渗流-充填物颗粒冲蚀迁移耦合作用下，裂隙/孔隙不断增大，渗透性增加，渗透性增加后进一步加速了颗粒的运移以及渗流通道的贯通，涌水量增加速度越来越快，这样一个相互加速的过程最终导致了陷落柱渗透性发生突变，并造成突水事故的发生。因此，对于导水陷落柱，一旦揭露，应尽快采取注浆等措施预防发生煤层底板陷落柱突水。
笔者所建力学模型对于研究煤矿陷落柱的渗透特性演化规律、指导突水防治具有较强的理论指导意义。但模型没有深入考虑围岩与陷落柱的相互作用以及工作面开采的动态过程，因此，在后续的工作中需进一步考虑开采等因素，深入揭示陷落柱突水机理。
参考文献(References):
[1] 朱万成,魏晨慧,张福壮,等.流固耦合模型用于陷落柱突水的数值模拟研究[J].地下空间与工程学报,2009,5(5):928-933.
ZHU Wancheng,WEI Chenhui,ZHANG Fuzhuang,et al.Investigation of water inrush from karst subsidence column by using a coupled hydro-mechanical[J].Chinese Journal of Underground Space and Engineering Model,2009,5(5):928-933.
[2] 张凯,姚邦华,吴松刚,等.陷落柱的变质量渗流特性及其突水危险性数值模拟[J].采矿与安全工程学报,2013,30(6):892-896.
ZHANG Kai,YAO Banghua,WU Songgang,et al.Study on the characteristics of variable mass seepage and water inrush mechanism of collapse column[J].Journal of Mining and Safety Engineering,2013,30(6):892-896.
[3] 赵铁锤.全国煤矿典型水害案例与防治技术[M].徐州:中国矿业大学出版社,2007:17-23.
[4] 焦阳,白海波.煤层底板含隐伏溶洞滞后突水机理[J].煤炭学报,2013,38(S2):377-382.
JIAO Yang,BAI Haibo.Mechanism of delayed groundwater inrush from covered karst cave in coal seam floor[J].Journal of China Coal Society,2013,38(S2):377-382.
[5] 尹尚先,王尚旭,武强.陷落柱突水模式及理论判据[J].岩石力学与工程学报,2004,23(6):964-968.
YIN Shangxian,WANG Shangxu,WU Qiang.Water inrush patterns and theoretic criteria of Karstic collapse columns[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(6):964-968.
[6] 宋彦琦,王兴雨,程鹏,等.椭圆形陷落柱厚壁筒突水模式力学判据及数值模拟[J].煤炭学报,2011,36(3):452-455.
SONG Yanqi,WANG Xingyu,CHENG Peng,et al.The mechanical criterion and numerical simulation of thick-walled elliptical cylinder collapse column model under water inrush[J].Journal of China Coal Society,2011,36(3):452-455.
[7] BAI H,MA D,CHEN Z.Mechanical behavior of groundwater seepage in karst collapse pillars[J].Engineering Geology,2013,164:101-106.
[8] 张勃阳,白海波,张凯.类陷落柱介质渗流突变机制试验研究[J].岩土力学,2016,37(3):745-812.
ZHANG Boyang,BAI Haibo,ZHANG Kai.Experimental research on seepage mutation mechanism of collapse column medium[J].Rock and Soil Mechanics,2016,37(3):745-812.
[9] 王家臣,李见波,徐高明.导水陷落柱突水模拟试验台研制及应用[J].采矿与安全工程学报,2010,27(3):305-309.
WANG Jiachen,LI Jianbo,XU Gaoming.Development and application of simulation test system for water inrush form the Water-conducting collapse column[J].Journal of Mining and Safety Engineering,2010,27(3):305-309.
[10] 杨天鸿,陈仕阔,朱万成,等.矿井岩体破坏突水机制及非线性渗流模型初探[J].岩石力学与工程学报,2008,27(7):1411-1416.
YANG Tianhong,CHEN Shikuo,ZHU Wancheng,et al.Water inrush mechanism in mines and nonlinear flow model for fractured rocks[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(7):1411-1416.
[11] 杨天鸿,师文豪,刘洪磊,等.基于流态转捩的非线性渗流模型及在陷落柱突水机理分析中的应用[J].煤炭学报,2017,42(2):315-321.
YANG Tianhong,SHI Wenhao,LIU Honglei,et al.A non-linear flow model based on flow translation and its application in the mechanism analysis of water inrush through collapse pillar[J].Journal of China Coal Society,2017,42(2):315-321.
[12] 缪协兴,刘卫群,陈占清.采动岩体渗流理论[M].北京:科学出版社,2004.
[13] 马占国,缪协兴,陈占清,等.破碎煤体渗透特性的试验研究[J].岩土力学,2009,30(4):985-988.
MA Zhanguo,MIAO Xiexing,CHEN Zhanqing,et al.Experimental study of permeability of broken coal[J].Rock and Soil Mechanics,2009,30(4):985-988.
[14] 李顺才,缪协兴,陈占清,等.破碎岩体非等温渗流的非线性动力学研究[J].力学学报,2010,42(4):652-659.
LI Shuncai,MIAO Xiexing,CHEN Zhanqing,et al.Study on nonlinear dynamics of non-isothermal flow in broken rock[J].Chinese Journal of Theoretical and Applied Mechanics,2010,42(4):652-659.
[15] HABIB M A,BADR H M,BEN-MANSOUR R,et al.Erosion rate correlations of a pipe protruded in an abrupt pipe contraction[J].International Journal of Impact Engineering,2007,34(8):1350-1369.
[16] ORTOLEVA P J,CHADAM J,MERINO E,et al.Geochemical self-organization II:The reactive-infiltration instability[J].American Journal of Science,1987,287(10):1008-1040.
[17] VARDOULAKIS I,STAVROPOULOU M,PAPANASTASIOU P.Hydro-mechanical aspects of the sand production problem[J].Transport in Porous Media,1996,22(2):225-244.
[18] 申林方,冯夏庭,潘鹏志,等.单裂隙花岗岩在应力-渗流-化学耦合作用下的试验研究[J].岩石力学与工程学报,2010,29(7):1379-1388.
SHEN Linfang,FENG Xiating,PAN Pengzhi,et al.Experimental research on mechano-hydro-chemical coupling of granite with single fracture[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(7):1379-1388.
[19] 姚邦华.破碎岩体变质量流固耦合动力学理论及应用研究[D].徐州:中国矿业大学,2012:62-78.
[20] WARREN J E,ROOT P J.The behavior of naturally fractured reservoirs[J].Society of Petroleum Engineers Journal,1963,3(3):245-255.
[21] 李传亮,孔祥言,徐献芝,等.多孔介质的双重有效应力[J].自然杂志,1999,21(5):288-292.
LI Chuanliang,KONG Xiangyan,XU Xianzhi,et al.Double effective stresses of porous media[J].Chinese Journal of Nature,1999,21(5):288-292.
[22] 徐献芝,李培超,李传亮.多孔介质有效应力原理研究[J].力学与实践,2001,23(4):42-45.
XU Xianzhi,LI Peichao,LI Chuanliang.Principle of effective stress based on porous medium[J].Mechanics in Engineering,2001,23(4):42-45.
[23] 杨天鸿,师文豪,李顺才,等.破碎岩体非线性渗流突水机理研究现状及发展趋势[J].煤炭学报,2016，41(7):1598-1609.
YANG Tianhong,SHI Wenhao,LI Shuncai,et al.State of the art and trends of water-inrush mechanism of nonlinear flow in fractured rock mass[J].Journal of China Coal Society,2016,41(7):1598-1609.
[24] 张凤婕,吴宇,茅献彪,等.煤层气注热开采的热-流-固耦合作用分析[J].采矿与安全工程学报,2012,29(4):505-510.
ZHANG Fengjie,WU Yu,MAO Xianbiao,et al.Coupled thermal-hydrological mechanical analysis of exploiting coal methane by heat injection[J].Journal of Mining and Safety Engineering,2012,29(4):505-510.
[25] 欧阳治华,姚高辉.基于应变耦合渗流模型的裂隙岩体弹性模量研究[J].金属矿山,2008(3):65-67.
OUYANG Zhihua,YAO Gaohui.Study on elastic modulus for fractured rock mass based on strain coupled hydraulic model[J].Metal Mine,2008(3):65-67.
[26] 殷德胜,汪卫明,陈胜宏.随机裂隙岩体渗流-应力耦合分析的块体单元法[J].岩土力学,2011,32(9):2861-2866.
YIN Desheng,WANG Weiming,CHEN Shenghong.Block element method for seepage-stress coupling in random fractured rock[J].Rock and Soil Mechanics,2011,32(9):2861-2866.