深部煤炭开采面临着诸多时间相关性问题[1],如围岩流变引起巷道变形速度快、变形量大而难以维护,瓦斯抽采钻孔因流变特性而出现塌孔堵孔现象,煤与瓦斯延迟突出等问题。因此,研究煤体流变本构关系和变化规律对于深部煤炭开采具有重大的理论和工程实际意义。
岩石流变本构模型研究主要有3类:经验模型、组合元件模型和基于损伤机理分析的流变模型。经验模型以实验为基础,多数采用对数、幂函数、指数函数建立应变-时间的函数关系[2-5],具有拟合参数少、针对性强的优势,但是经验模型存在实验时间长、物理意义不明确、实验室研究成果难以外推应用的问题[6]。元件组合模型采用虎克弹性体(H)、牛顿黏性体(N)和圣维南塑性体(St.V)3种基本元件组合来建立岩石流变力学本构模型,从而对岩石流变规律进行描述,具有物理意义明确的优势。如冯夏庭等[7]利用Burgers模型建立了包含体积蠕变的流变模型,用于描述孔隙砂岩的流变行为。徐卫亚等[8]在黏性与塑性元件并联组合基础上增加了流变指数,提出了一种非线性黏塑性体(NVPB),并与五元件蠕变模型串联,得到了反映岩石加速蠕变特性的七元件模型。周福宝等[9]在已有元件模型基础上提出了一种包含黏弹塑性行为和损伤特征的蠕变本构模型,用于分析软煤中抽采钻孔的蠕变规律。夏才初等[10]提出了同时包含黏弹性、黏塑性、黏性、黏弹塑性4种基本流变力学形态的统一流变力学模型。然而元件组合模型存在本构关系复杂、参数多且难以确定的问题。在基于机理分析的流变模型方面,SHAO等[11-12]提出了可以描述岩石材料的塑性变形、损伤、体积膨胀、率相关性及蠕变等主要特征的本构模型;OKUI等[13]考虑岩石细微观尺度上裂纹演化和损伤积累,建立了描述花岗岩流变特性的本构模型,并基于此模型分析了水、温度及应力状态对岩石长期强度的影响;ZHOU等[14-15]在经验和组合模型基础上,考虑盐岩在变形破坏时的损伤积累,建立了基于分数阶导数的流变本构模型,能很好地反映盐岩三阶段,特别是加速流变阶段。
已有的流变模型能很好地描述单轴应力状态下的岩石流变特征,但地下岩体通常处于复杂的三维应力状态下,那么研究三维应力条件下的流变模型对于岩石流变学的发展更有理论和工程意义。目前,三维应力状态下的流变本构模型研究多是基于已有的元件模型从一维模型推导得出[16],且未考虑体积蠕变应变。尹光志等[17]运用自制的含瓦斯煤三轴蠕变试验系统进行了煤体卸围压蠕变试验,通过改进Chaboche黏塑性本构模型以描述含瓦斯煤的卸压短期蠕变破坏。李宁等[18]在文献[15]的基础上假设岩体环向应变是轴向应变的函数,推导了岩石分数阶体积变形模型,并通过实验进行了验证。
笔者基于周宏伟[14-15]提出的分数阶导数流变模型,推导出深部煤体非线性三维蠕变本构方程,并利用相似的模型得出了体积蠕变方程,然后通过三维应力条件下煤体卸围压蠕变试验进行参数分析。
1 深部煤体非线性三维蠕变本构方程
1.1 分数阶导数蠕变本构方程
将Nishihara模型中2个线性黏壶用Abel黏壶代替,并考虑变黏性系数Abel黏壶,得出分数阶导数蠕变本构方程一维表达式[14],模型如图1所示。

(2)
式中,ε为轴向应变;σ为轴向应力;σs为屈服应力;E0为弹性模量;E1为黏弹性体的弹性模量;γ为分数阶导数;η1,η2为黏滞性系数;α为黏性系数参数。

图1 分数阶蠕变模型
Fig.1 Fractional creep constitutive model
1.2 分数阶蠕变本构三维模型
在三维应力条件下,分数阶导数蠕变模型的总应变可以表示为
(3)

图2 煤体分数阶蠕变模型示意
Fig.2 Schematic representation of the fractional derivative model of coal
按照图2(a)求解偏应力条件下煤体蠕变应变。
根据广义Hook定律,弹性体三维本构关系为
(4)
式中,eij为应变偏张量;sij为应力偏张量;G0为剪切模量。
黏弹性体三维本构关系为
(5)
式中,G1为黏弹性剪切模量;![]() 为黏弹性黏滞系数。
为黏弹性黏滞系数。
黏塑性体的三维本构关系与岩石屈服函数F和塑性势函数相关,采用关联流动法则,黏塑性体变形本构关系可以表示为
〉![]() tγE1,1+γ(αt)
tγE1,1+γ(αt)
(6)
其中,

(7)
式中,F为岩石屈服函数;F0为岩石屈服函数初始参考值;φ(·)为幂函数形式,通常n=1[19]。
假设煤体为各向同性材料,煤体体积蠕变可忽略,泊松比不随蠕变过程而变化,那么三维蠕变方程表达式为

(8)
当屈服函数形式表示为
(9)
式中,![]() 为应力偏量第二不变量。
为应力偏量第二不变量。
在等围压卸载蠕变试验条件下有σ2=σ3,则

(10)
将式(9),(10)代入式(8),令初始屈服函数F0=1,得到非线性轴向蠕变方程为
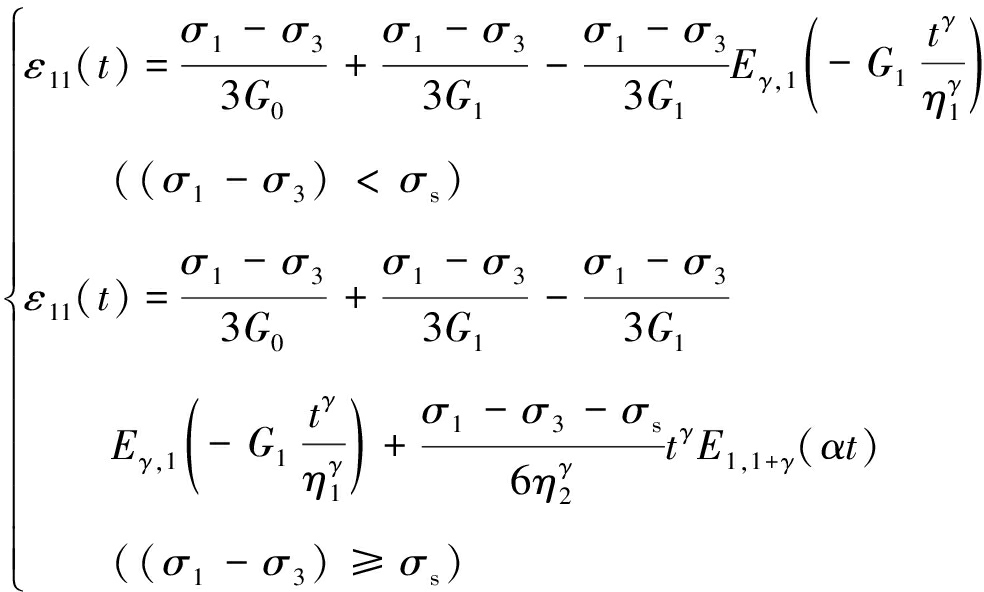
(11)
同理,按照图2(b)可以得到在球应力状态下煤体蠕变方程

(12)
式中,K0,K1为体积模量;k为体积蠕变的分数阶导数;![]() 为体积蠕变的黏滞系数;αV为体积蠕变的黏滞系数参数。
为体积蠕变的黏滞系数;αV为体积蠕变的黏滞系数参数。
1.3 考虑体积蠕变的分数阶蠕变本构方程
结合1.2节中式(11)~(12)可得,考虑体积蠕变的煤体三维蠕变表达式。

(13)
那么,当考虑体积应变时,轴向应变表达式为

(14)
2 深部煤体三向应力下卸围压蠕变实验
2.1 实验过程
煤体试样取自平煤集团十二矿己15-31030采煤工作面,取样深度为1 100 m。首先将煤样加工成φ50 mm×100 mm(高度)的标准试样。
本次实验在四川大学进行,设备为Rock Triaxial V4流变试验系统,围压:0~100 MPa,轴力0~200 t,温度最高200 ℃,测试精度0.3%RO,如图3所示。实验过程采用轴压恒定、围压分级卸载的方式,实验初始围压设定为25 MPa,每级按5 MPa进行卸载。

图3 岩石三轴流变实验系统
Fig.3 Experimental set-up of triaxial rheology test of rock
实验分为3个阶段:① 根据煤体实际赋存条件,将围压和轴压按照2.0 MPa/min速率加至静水压力25 MPa;② 当轴压和围压达到25 MPa 且变形稳定后,保持围压σ3=25 MPa,继续施加轴压至预定数值(30,40,50 MPa),保持轴向应力不变,记录煤样轴向及环向应变随时间的变化关系,直至该级应力水平下煤样变形趋于稳定;③ 保持轴向应力恒定(如σ1=40 MPa),以每级5 MPa差值卸除围压进行蠕变变形,直到试样发生流变破坏,结束试验。卸载速率为2 MPa/min。
2.2 三向应力下蠕变结果分析
选取轴压σ1=40 MPa条件下三轴卸围压蠕变实验,轴向和环向应变的蠕变曲线如图4所示。在分级卸围压蠕变实验中,煤样试件的轴向和环向应变随时间变化规律相似,然而每一级卸围压蠕变条件下两者应变值则不相同。蠕变实验差应力起始值为15 MPa,每一级荷载下,轴向和环向先发生瞬时应变,然后蠕变应变,并且随差应力增加而增大。当轴压σ1=40 MPa,围压σ3=25 MPa时,环向应变为正值,表示煤样试件环向仍为压缩状态;当围压卸载至5 MPa,差应力为35 MPa时,试件轴向应变为0.23%,环向应变为-0.25%,环向应变大于轴向应变直至试件破坏。

图4 分级卸围压蠕变曲线
Fig.4 Creep curves under step unloading confining pressure
2.3 相同围压条件下煤体蠕变规律
从煤体分级卸围压实验中,提取围压为σ3=10 MPa,差应力Δσ=20,30,40 MPa条件下蠕变数据,绘制轴向应变和环向应变曲线如图5所示。轴向应变在相同围压、不同差应力条件下表现为初始蠕变和稳态蠕变,差应力分别取20,30,40 MPa时,轴向应变最大值分别为0.115 58%,0.161 42%,0.160 94%,即εa-30>εa-40>εa-20,且应变值均很小。当差应力分别取20,30,40 MPa时,径向应变大小排序为εs-30>εs-20>εs-40。由此可知,在相同围压,不同轴压条件下,轴向应变和环向应变变化规律不一致。

图5 围压σ3=10 MPa时,不同差应力下蠕变曲线
Fig.5 Creep curves under different differential stress while confining pressure σ3=10 MPa
2.4 相同差应力条件下煤体蠕变规律
从煤体分级卸围压实验中,提取围压为σ3=5,15,25 MPa,差应力Δσ=25 MPa条件下蠕变数据,绘制轴向应变和环向应变曲线如图6所示。在差应力Δσ=25 MPa条件下,当围压分别为5,15,25 MPa时,轴向应变εa-5>εa-15>εa-25,环向应变εs-5>εs-15>εs-25,即随着围压的增加,轴向应变和环向应变而减小。

图6 Δσ=25 MPa时,不同围压下蠕变曲线
Fig.6 Creep curves under different confining pressure while differential stress Δσ=25 MPa
3 深部煤体三维蠕变模型参数分析
3.1 深部煤体蠕变模型参数拟合
根据煤体三轴流变实验确定式(11),(14)中参数。采用Levenberg-Marquardt方法进行参数拟合。模型拟合曲线如图7所示,参数拟合结果见表1。对比实验数据和模型拟合曲线可以发现,利用分数阶流变模型所推导的三维流变公式可以很好地描述深部煤体三轴流变实验结果,而且该模型能很好地描述煤体流变过程中体积应变规律。

图7 煤体三轴流变实验结果及非线性流变模型拟合分析
Fig.7 Experimental data and the fitting curves by non-linear creep model on coal
表1 基于深部煤体流变实验的参数拟合结果
Table 1 Parameters determined by fitting analysis based on creep tests of coal at depth

3.2 应力水平的影响
参照3.1节煤体流变实验条件和表1拟合分析结果,将参数![]() 代入式(13),改变轴向应力使得差应力水平不同,即取Δσ=36,38,40,42和44 MPa,得到一组在不同差应力条件下流变曲线(图8)。可见,在同一时刻,差应力越大,轴向应变值越大,稳态蠕变阶段越短,越快进入加速蠕变阶段。
代入式(13),改变轴向应力使得差应力水平不同,即取Δσ=36,38,40,42和44 MPa,得到一组在不同差应力条件下流变曲线(图8)。可见,在同一时刻,差应力越大,轴向应变值越大,稳态蠕变阶段越短,越快进入加速蠕变阶段。

图8 不同差应力条件下蠕变曲线
Fig.8 Sensitivity of the creep strain to the differential stress level in the case
3.3 分数阶导数γ的影响
在其他参数保持不变的条件下,改变γ值,得到不同分数阶导数阶数下蠕变曲线(图9)。可见,蠕变速率及大小依赖于模型中分数阶导数阶次,分数阶次越高,蠕变速率及加速蠕变阶段应变值越大,反映了分数阶导数在描述蠕变模型上适用性强。
3.4 参数α的影响
在其他参数不变的前提下,仅改变反映加速蠕变阶段的参数α,可得煤体蠕变曲线随α的变化规律(图10)。可见,当α=0时,煤体蠕变过程并未出现明显的非稳定阶段即加速阶段,只有当α>0时,蠕变曲线才会出现加速阶段,且随α的增加,越快出现加速阶段。
由此可见,对深部煤体蠕变曲线影响较大的参数主要有应力水平、分数阶求导阶次和黏性系数参数。应力水平主要影响煤体蠕变量的大小和稳定蠕变阶段的长短;分数阶导数阶次主要影响蠕变速率的大小;而黏性系数参数的大小直接影响了煤体蠕变曲线的形态,当α>0时加速蠕变阶段才会出现。

图9 不同求导阶数的蠕变曲线
Fig.9 Sensitivity of the creep strain to the fractional derivative order in the case

图10 不同α下的蠕变曲线
Fig.10 Sensitivity of the creep strain to the α in the case
4 结 论
(1)针对深部煤体蠕变特征描述,基于分数阶导数一维蠕变本构模型,推导并建立了分数阶导数三维蠕变本构模型,同时在该模型中考虑了体积蠕变特性。
(2)在分析深部煤体所赋存应力场的实际情况下,通过室内实验模拟了深部煤体在三轴应力卸围压条件下蠕变特征。煤样试件的轴向和环向应变随时间变化规律相似,然而每一级卸围压蠕变条件下两者应变值不尽相同;在同围压条件下,轴向和环向应变随轴压的变化规律不一致;在差应力相等条件下,随着围压的增加,轴向应变和环向应变随时间而减小。
(3)利用蠕变实验结果,拟合了煤体非线性三维本构方程中力学参数,并在此基础上对差应力水平、分数阶导数阶数、加速蠕变参数进行了敏感性分析。随着差应力水平、导数阶数、加速蠕变参数的增加,煤体蠕变曲线的稳态阶段逐渐缩短,加速阶段则更容易出现。
参考文献(References):
[1] 谢和平,林柏泉,周宏伟,等.深部煤与瓦斯共采理论与技术[M].北京:科学出版社,2017.
XIE Heping,LIN Baiquan,ZHOU Hongwei,et al.Theory and technology of coal and gas simultaneous mining in depth[M].Beijing:Science Press,2017.
[2] YANG Chunhe,DAEMENA J J K,YIN Jianhua.Experimental investigation of creep behavior of salt rock[J].International Journal of Rock Mechanics and Mining Sciences,1999,36(2):233-242.
[3] 徐平,夏熙伦.三峡枢纽岩体结构面蠕变模型初步研究[J].长江科学院院报,1992,9(1):42-46.
XU Ping,XIA Xilun.A study on the creep model of rock mass discontinuity of the Three Gorges project[J].Journal of Yangtze River Scientific Research Institute,1992,9(1):42-46.
[4] 张向东,李永靖,张树光,等.软岩蠕变理论及其工程应用[J].岩石力学与工程学报,2004,23(10):1635-1639.
ZHANG Xiangdong,LI Yongjing,ZHANG Shuguang,et al.Creep study of soft rock and its engineering application[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(10):1635-1639.
[5] 张学忠,王龙,张代钧,等.攀钢朱矿东山头边坡辉长岩流变特性试验研究[J].重庆大学学报:自然科学版,1999,22(5):99-103.
ZHANG Xuezhong,WANG Long,ZHANG Daijun,et al.An experimental study on rheological characteristics of gabbro in East Mountain Slope of Zhujiabao Mine[J].Journal of Chongqing University:Natural Science,1999,22(5):99-103.
[6] HOU Zhengmeng.Mechanical and hydraulic behaviour of salt in the excavation disturbedzone around underground facilities[J].International Journal of Rock Mechanics & Mining Sciences,2003,40(5):725-738.
[7] ZHENG Hong,FENG Xiating,HAO Xianjie.A creep model for weakly consolidated porous sandstone including volumetric creep[J].International Journal of Rock Mechanics & Mining Sciences,2015,78:99-107.
[8] 徐卫亚,杨圣奇,褚卫江.岩石非线性黏弹塑性流变模型(河海模型)及其应用[J].岩石力学与工程学报,2006,25(3):433-447.
XU Weiya,YANG Shengqi,CHU Weijiang.Nonlinear viscoelasto-plastic rheological model (Hohai model) of rock and its engineering application[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(3):433-447.
[9] LIU Chun,ZHOU Fubao,KANG Jianhong,et al.Application of a non-linear viscoelastic-plastic rheological model of soft coal on borehole stability[J].Journal of Natural Gas Science & Engineering,2016,36:1303-1311.
[10] 夏才初,王晓东,许崇帮,等.用统一流变力学模型理论辨识流变模型的方法和实例[J].岩石力学与工程学报,2008,27(8):1594-1600.
XIA Caichu,WANG Xiaodong,XU Chongbang,et al.Method to identify rheological model by unified rheological model theory and case study[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(8):1594-1 600.
[11] SHAO J F,ZHU Q Z,SU K.Modeling of creep in rock materials in terms of material degradation[J].Computers and Geotechnics,2003,30(7):549-555.
[12] SHAO J F,CHAU K T,FENG X T.Modeling of anisotropic damage and creep deformation in brittle rocks[J].International Journal of Rock Mechanics and Mining Sciences,2006,43(4):582-592.
[13] MIURA K,OKUI Y,HORII H.Micromechanics-based prediction of creep failure of hard rock for long-term safety of high-level radioactive waste disposal system[J].Mechanics of Materials,2003,35(3):587-601.
[14] ZHOU H W,WANG C P,HAN B B,et al.A creep constitutive model for salt rock based on fractional derivatives[J].International Journal of Rock Mechanics and Mining Sciences,2011,48(1):116-121.
[15] 周宏伟,王春萍,段志强,等.基于分数阶导数的盐岩流变本构模型[J].中国科学:物理学 力学 天文学,2012,42:310-318.
ZHOU Hongwei,WANG Chuanping,DUAN Zhiqiang,et al.Time-based fractional derivative approach to creep constitutive model of salt rock (in Chinese)[J].Sci Sin-Phys Mech Astron,2012,42:310-318.
[16] 齐亚静,姜清辉,王志俭,等.改进西原模型的三维蠕变本构方程及其参数辨识[J].岩石力学与工程学报,2012,31(2):347-355.
QI Yajing,JIANG Qinghui,WANG Zhijian,et al.3D creep constitutive equation of modified NISHIHARAmodel and its parameters identification[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(2):347-355.
[17] 尹光志,王浩,张东明.含瓦斯煤卸围压蠕变试验及其理论模型研究[J].煤炭学报,2011,36(12):1963-1967.
YIN Guangzhi,WANG Hao,ZHANG Dongming.Creep experimental and theory model on coal containing gas under the condition of unloading confining pressure[J].Journal of China Coal Society,2011,36(12):1963-1967.
[18] 何明明,李宁,朱才辉,等.岩石分数阶体积变形模型及其试验研究[J].岩土力学,2016,37(11):3137-3144.
HE Mingming,LI Ning,ZHU Caihui,et al.The volume deformation behavior of rock based on fractional calculus and its experimental study[J].Rock and Soil Mechanics,2016,37(11):3137-3144.
[19] ZIENKIEWICZ O C,CORMEAU I C.Visco-plasticity and creep in elastic solids-a unified numerical solution approach[J].International Journal for Numerical Method in Engineering,1974,8(4):821-845.