岩石作为自然形成的天然材料，具有复杂的物理特性。关于岩石材料本构模型建立和模型参数确定的研究一直是热点和难点问题。HOLMQUIST等[1]提出的HJC模型能够较好地描述材料在大变形、高静水压力和高应变率下的动态力学行为，在混凝土侵彻、贯穿问题的数值分析中得到广泛应用[2-5]。
目前，对混凝土HJC模型参数的研究较多。张凤国和李恩征[6]基于美国混凝土协会(ACI)提出的混凝土强度经验计算公式，给出了通过单轴抗压强度推导确定模型中其他基本力学参数的简易方法，但该方法未涉及极限面中重要参数。陈建林等[7]以单轴压缩、循环压缩和SHPB冲击实验数据为基础，确定了素混凝土的HJC模型参数。熊益波等[8]根据屈服面理论建立了黏聚强度与Mohr-Coulomb准则参数的关系，提出了一种通过三轴围压实验获取极限面参数的方法，随后又通过总结相关文献数据，对三段式经验状态方程进行统计分析并确定了方程的相关参数[9]。孙其然等[10]对HJC模型关键字参数中的失效类型参数(FS)进行了分析，研究其对混凝土压实破坏的影响并确定了取值范围。美国陆军实验室[11]将HJC模型推广到砌体砖、砂浆中，通过实验确定了模型所有参数，并应用于侵彻的数值模拟中，取得了较好的效果。
在应用HJC模型研究岩石类材料动态响应问题方面，已有论著报道了岩石材料冲击爆炸数值模拟[12-15]，相关学者一般采用文献[1]所给出的混凝土HJC模型参数，或结合室内实验和数值模拟试算得到了一些岩石材料的HJC模型参数，但关于岩石类材料HJC模型参数的确定却鲜有人涉及。笔者通过对HJC模型的理论分析，提出了一套比较系统的实验方法来测定岩石的HJC模型参数。利用该实验方法，对砂岩HJC模型参数进行了测定，依据确定的参数对砂岩SHPB冲击实验进行数值模拟，从而验证模型参数的合理性和有效性。
1 HJC模型理论
HJC模型综合考虑了混凝土在爆炸与冲击作用下的压缩效应、应变率效应及损伤对失效强度的影响。该模型分为失效面方程、状态方程和损伤演化方程3部分。
1.1 强度模型
如图1(a)所示，HJC强度模型以归一化等效应力描述，其表达式为
(1)
式中，σ*为归一化等效应力，σ*=σ/fc，σ为实际等效应力，fc为材料的准静态单轴抗压强度;
为归一化应变率，
为加载应变率，
为参考应变率，取为1.0 s-1;D为损伤因子，取值由损伤方程决定;p*为归一化压力，p*=p/fc，p为静水压力;A，B，C，N为材料模型参数，分别代表归一化内聚力强度、归一化压力硬化系数、应变率硬化指数、压力硬化指数;SMAX为归一化等效应力的最大值。
图1 HJC混凝土模型
Fig.1 HJC concrete model
1.2 损伤模型
HJC模型中损伤由塑性应变累积而成，塑性应变包括剪切变形塑性应变(等效塑性应变)和体积压缩塑性应变两部分，如图1(b)所示。损伤模型的表达式为
(3)
式中，Δεp和Δμp分别为一个计算循环内单元的等效塑性应变增量和等效塑性体积应变增量;
和
分别为当前积分步下的等效塑性应变和等效塑性体积应变;T*为归一化抗拉强度，T*=T/fc，T为材料的抗拉强度;D1，D2为材料损伤参数;EFMIN为材料破坏时的最小塑性应变，用以抑制拉伸应力波导致的混凝土脆性开裂。
1.3 状态方程
HJC模型中，状态方程为体积应变与静水压力的函数，如图1(c)所示，方程分为3部分。第1部分为线弹性区，当P≤Pcrush时，材料处于线弹性状态，此时
P=Kμ
(4)
式中，μ为体积应变;K为体积模量，K=Pcrush/μcrush，Pcrush，μcrush分别为弹性极限静水压力和对应的体积应变。
第2部分为塑性过渡区，Pcrush<P<Plock时，材料处于塑性状态，此阶段材料内部的空隙被逐渐排出，产生塑性体积损伤。
第3部分为高压缩区，当P≥Plock，材料处于高压状态，在这个区间内压力与体积的关系为
(5)
式中，K1，K2，K3为压力常数；
为等效体积应变，
为对应体积应变;Plock为压实静水压力。
2 砂岩HJC模型参数的确定方法
本文选用的砂岩取自四川省威远县小河镇，该砂岩材质均匀、颗粒组成细腻、致密性好。试件直径为50 mm，长度分为3种，长度为100 mm的试件用于单轴压缩和三轴压缩实验，长度为40 mm的试件用于SHPB动态冲击实验，长度为20 mm的试件用于劈裂拉伸实验。实验前试件两端均精细打磨，不平行度在0.02 mm以内。
2.1 基本物理力学参数测定
HJC模型中基本物理力学参数包括密度ρ、单轴抗压强度fc、弹性模量E、泊松比υ、剪切模量G、体积模量K。砂岩密度采用蜡封法进行测量。采用万能压力机配合引伸计对砂岩试件进行静力学实验，求得单轴静态抗压强度、最大拉伸静水压力及相应的应变，并通过式(6)～(10)求出其他基本力学参数。测定砂岩的物理力学参数见表1。
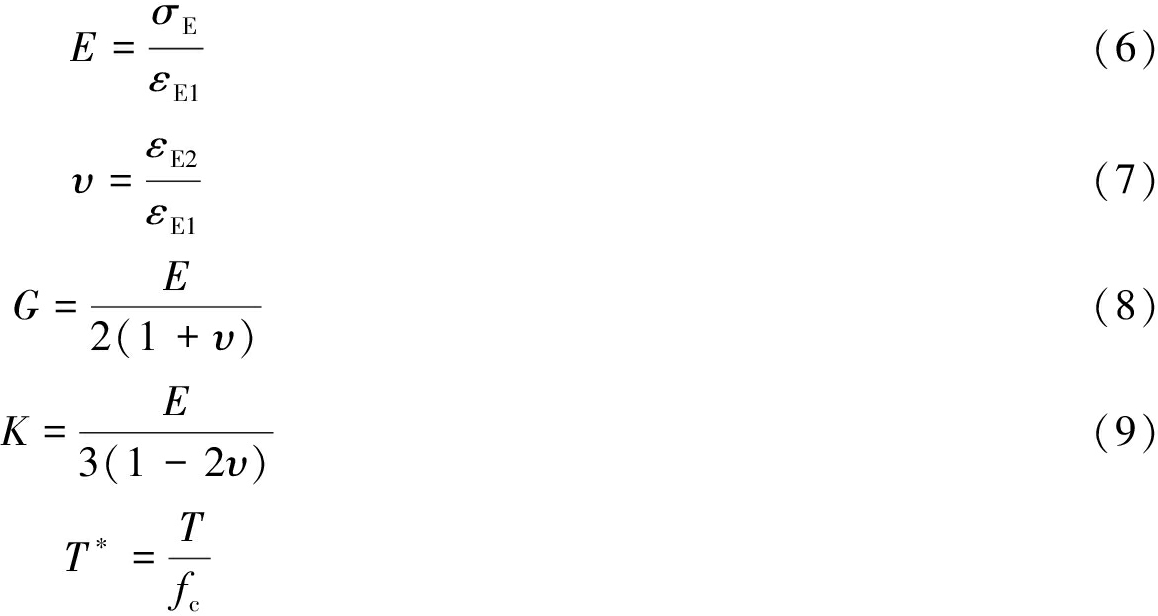
(10)
式中，σE为砂岩弹性极限强度;εE1为砂岩弹性极限强度对应的轴向应变;εE2为砂岩弹性极限强度对应的径向应变;G，K分别为剪切模量和体积模量;T*为归一化最大拉伸静水压力，T为最大拉伸静水压力，其值由劈裂实验获得。
表1 砂岩基本物理力学参数取值
Table 1 Determination of basic physical and mechanical parameters of sandstone
2.2 应变率效应参数测定
利用SHPB实验系统测定不同应变率条件下砂岩单轴动态强度，结合已测得的准静态单轴压缩强度，得到砂岩试件在不同应变率下的无量纲等效强度σ*，如图2所示。
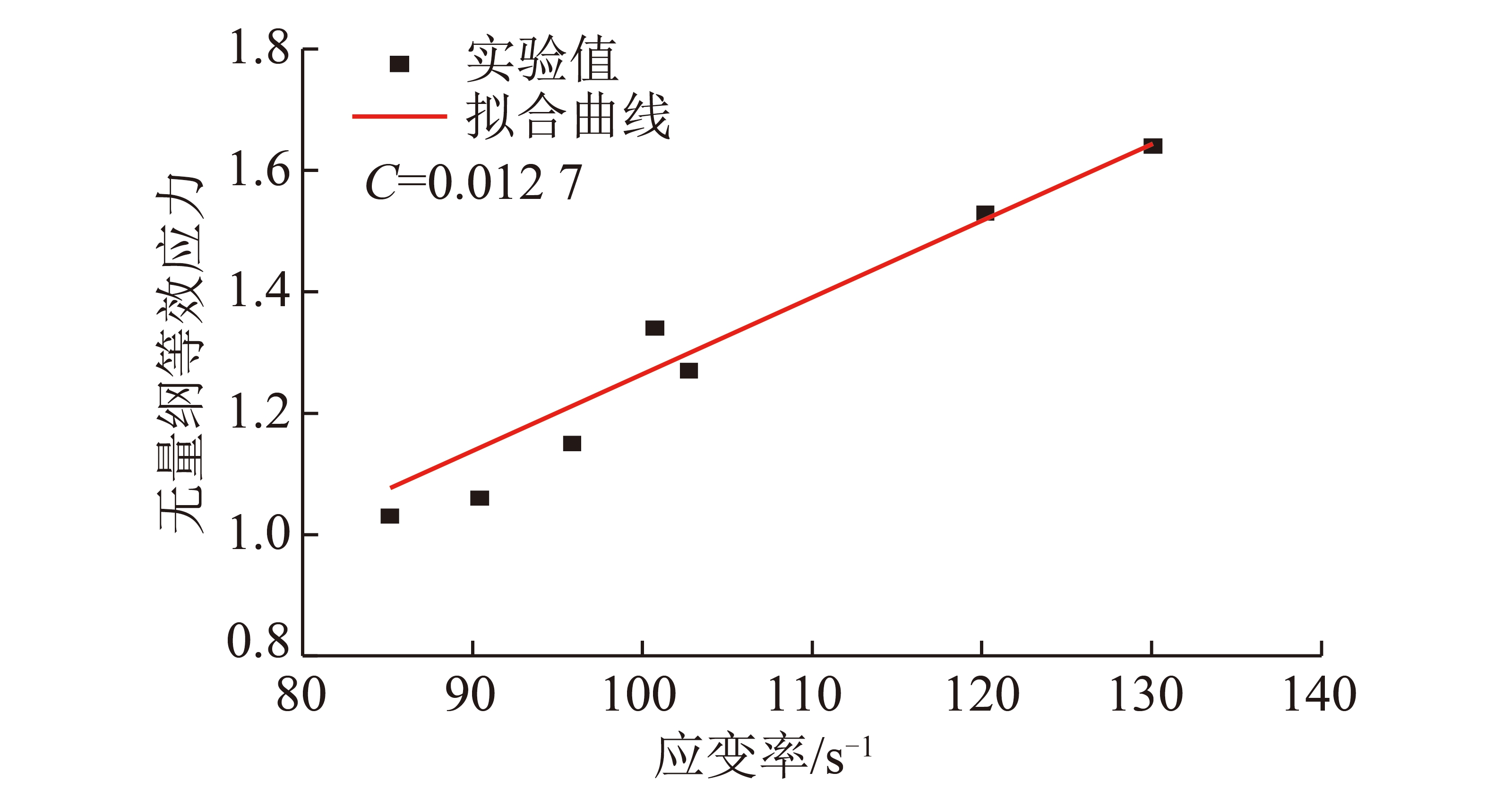
图2 获取C值的数据处理方法
Fig.2 Description of the data processing method for C value
由图2可以看出，无量纲等效应力随应变率的提高而逐渐增大。采用直线方程对实验数据进行拟合，由HJC模型理论可知，该直线方程的斜率即为应变率硬化指数C的值，即C=0.012 7。
2.3 极限面参数测定
(1)参数A的实验测定方法
若不考虑损伤和应变率效应的影响，HJC极限面方程转化为
σ*=A+BP*N
(11)
由于式(11)未考虑罗德角的影响，极限面在偏平面上的投影即为Mises圆。由塑性理论可知，罗德角θ=60°时，Mises准则在偏平面上的压缩子午线与M-C准则压缩子午线相接，如图3所示。M-C准则的表达式为
σ=c+Ptan φ
(12)
其中，c为黏聚力，φ为内摩擦角。根据不同围压下三轴实验数据绘制莫尔圆，并做该组莫尔圆的包络线，得到c值为22.20 MPa。
图3 HJC极限面与M-C包络线关系
Fig.3 Relationship between HJC limit surface and enveloping line of M-C
通过以上分析可知，若M-C准则满足线性关系，则当P=0时，有A=c/fc，此时可得到准静态时
黏聚力强度，即A=0.292。将其归一化到
时，得到A=0.292/(1+Cln10-4)=0.32。
(2)参数B，N的测定
利用万能实验机进行三轴压缩实验。在不同围压条件下，按照式(13)和(14)测得不同静水压力p及对应的最大差压Δσ值，将获得的数据按式(15)进行归一化处理，得到一系列点(P*，σ*)，最后利用式(16)对数据点进行拟合，从而得到B，N的值。
(13)
Δσ=σ1-σ3
(14)
(15)
σ*=0.32+BP*N
(16)
实验数据及拟合结果如图4所示。由拟合数据得到该砂岩的模型参数值为B=1.76，N=0.79。
图4 获取参数B和N的数据处理方法
Fig.4 Description of data processing method for B and N value
2.4 状态方程参数测定
根据文献[1]，Pcrush=fc/3=25.38 MPa，μcrush=Pcrush/K=0.001 67，μlock=ρg/ρ0，其中，ρg和ρ0分别为颗粒密度和试件密度。根据实验结果得到μlock=0.008。
K1，K2，K3的值可通过材料的Hugoniot实验数据获得，但实验成本较高。在缺少相关实验数据时，可借鉴Los Alamos 国家实验室所做的各类岩石材料Hugoniot实验数据或经验公式[16]。采用的砂岩与文献[17]实验所用砂岩在密度、抗压强度及孔隙率方面更为接近，因此，采用文献[17]的实验数据，对砂岩密实阶段的压力参数进行拟合，如图5所示。根据拟合结果得到K1=81 GPa，K2=-91 GPa，K3=89 GPa。Plock的数值根据计算效果最佳的原则确定。最终确定的压力参数列于表2。
图5 获取参数K1，K2，K3的数据处理方法
Fig.5 Description of data processing method for K1,K2 and K3 value
表2 状态方程相关参数取值
Table 2 Values of relevant parameters of state equation
2.5 损伤参数测定
在SHPB实验系统中对砂岩试件进行循环冲击加载实验，得到重复冲击荷载作用下该砂岩的应力-应变关系，利用该曲线簇可做出假定破坏面并得到失效应变为0.004 65，如图6所示。在低速冲击状态下，试件的体积应变近似等于0，因此由式(3)可得到
图6 获取参数EFMIN的数据处理方法
Fig.6 Description of data processing method for EFMIN value
文献[18-19]在研究HJC模型参数时均发现损伤参数D2对数值结果的影响极小。因此，在没有足够实验数据的情况下，本文沿用文献[1]中的方法，首先假定D2=1.0，然后根据式(3)确定D1的值。式(3)中P*由冲击应力波幅值决定，取值为0.27，T*取值为0.100 2。计算得到D1取值为0.013。
3 砂岩HJC模型参数的应用
3.1 SHPB数值计算模型
与SHPB实验相对应，在ANSYS/LS-DYNA中建立SHPB冲击实验数值计算模型，如图7所示。其中，冲击杆长度为400 mm，入射杆长度2 000 mm，透射杆长度2 000 mm，试件直径50 mm，长度40 mm。杆件的材质定义为弹性材料，参数选取铝镁合金的属性值:密度为2 800 kg/m3、弹性模量为77 GPa、泊松比为0.27。
图7 SHPB数值计算模型
Fig.7 Numerical model of SHPB
3.2 模拟结果对比
根据前文确定的数值计算模型和模型参数，分别对冲击速度为7.5和9.5 m/s的SHPB实验进行数值模拟。按SHPB两波法对模拟数据进行处理，得到试件的应力-应变曲线，并与对应的实验结果进行对比，如图8所示。
图8 数值模拟与实验结果对比
Fig.8 Comparison of numerical simulation with experimental results
由于在SHPB冲击实验的压力范围内混凝土仅能达到过渡段，状态方程第3阶段对模拟结果影响较小，SHPB实验得到的应力-应变曲线无法明显地体现出状态方程的控制作用。但由图8中可以看出，随着冲击速度的增大，动态峰值强度也随之增大，符合应变率强化效应的特性。在相同冲击速度下，以动态峰值强度和峰值应变为特征值进行误差分析，误差均未超过10%。应力-应变曲线中屈服段和软化段的形态与实验结果均吻合地较好。因此，由上述方法确定的模型参数能够准确地描述砂岩材料受冲击荷载作用的屈服过程，充分反映了高应变率下损伤的演化规律，说明提供的砂岩HJC模型参数确定方法合理有效，取值可靠。
4 结 论
(1)以物理实验和静力学实验为基础，测定了威远砂岩的基本物理力学参数，并根据HJC模型定义和现有Hugoniot实验数据，分析得到了压力参数的取值。
(2)应用SHPB实验测得了砂岩在不同应变率下的动态强度和循环冲击下的失效应变，从而确定了砂岩的应变率硬化指数和损伤参数。
(3)根据极限面理论，建立HJC模型极限面参数A与M-C准则中黏聚强度的关系，通过常规三轴压缩实验数据获取了极限面参数。
(4)利用确定的HJC模型参数，采用有限元软件LS-DYNA模拟了SHPB砂岩动态冲击过程，结果显示，应力-应变曲线与实验结果吻合较好，峰值应力及峰值应变与实验结果的误差均未超过10%，说明提出的实验方法能够获得可靠的HJC模型参数，也能为其他岩石动载数值模拟计算提供参考和帮助。
参考文献(Reference):
[1] HOLMQUIST T J,JOHNSON G R.A computational constitutive model for concrete subjected to large strains,high strain rates,and high pressures[A].14th International Symposium on Ballistic[C].Quebec City,Canada,1993:593-600.
[2] 纪冲，龙源，万文乾.弹丸侵彻钢纤维混凝土数值模拟[J].解放军理工大学学报(自然科学版),2005,6(5):459-463.
JI Chong,LONG Yuan,WAN Wenqian.Numerical simulation of projectile penetrating into steel fiber reinforced concrete[J].Journal of PLA University of Science and Technology,2005,6(5):459-463.
[3] 韩丽，高世桥，李明辉，等.弹丸垂直贯穿混凝土靶的数值研究[J].北京理工大学学报,2006,26(11):953-956.
HAN Li,GAO Shiqiao,LI Minghui,et al.Numerical studies on a projectile perforating concrete targets[J].Transactions of Beijing Institute and Technology,2006,26(11):953-956.
[4] 姜华，王君杰.弹体侵彻混凝土数值模拟失效指标研究[J].振动与冲击,2009,28(8):30-34.
JIANG Hua,WANG Junjie.Investigation on failure index of concrete in the projectile perforation simulation[J].Journal of Vibration and Shock,2009,28(8):30-34.
[5] 孟阳，文鹤鸣.钢筋混凝土靶板在弹丸冲击及爆炸载荷下响应的数值模拟[J].高压物理学报,2011,25(4):370-378.
MENG Yang,WEN Heming.Numerical simulation of the response of reinforced concrete slabs to projectile impact or explosive loading[J].Chinese Journal of High Pressure Physics,2011,25(4):370-378.
[6] 张凤国，李恩征.混凝土撞击损伤模型参数的确定方法[J].弹道学报,2001,13(4):12-16.
ZHANG Fengguo,LI Enzheng.A method to determine the parameters of the model for concrete impact and damage[J].Journal of Ballistics,2001,13(4):12-16.
[7] 陈建林，李旭东，刘凯欣.素混凝土本构模型参数的实验研究[J].北京大学学报(自然科学版),2008,44(5):689-694.
CHEN Jianlin,LI Xudong,LIU Kaixin.Experimental research on parameters of constitutive model for a cement mortar[J].Acta Scientiarum Naturalium Universitatis Pekinensis,2008,44(5):689-694.
[8] 熊益波，胡永乐，徐进，等.混凝土Johnson-Holmquist模型极限面参数确定[J].兵工学报,2010,31(6):746-751.
XIONG Yibo,HU Yongle,XU Jin,et al.Determining failure surface parameters of the Johnson-Holmquist concrete constitutive model[J].Acta Armamentarii,2010,31(6):746-751.
[9] 熊益波，陈剑杰，胡永乐，等.混凝土Johnson-Holmquist本构模型关键参数研究[J].工程力学,2012,29(1):121-127.
XIONG Yibo,CHEN Jianjie,HU Yongle,et al.Study on the key parameters of the Johnson-Holmquist constitutive model for concrete[J].Engineering Mechanics,2012,29(1):121-127.
[10] 孙其然，李芮宇，赵亚运，等.HJC模型模拟钢筋混凝土侵彻实验的参数研究[J].工程力学,2016,33(8):248-256.
SUN Qiran,LI Ruiyu,ZHAO Yayun,et al.Investigation on parameters of HJC model applied to Simulate perforation experiments of reinforced concrete[J].Engineering Mechanics,2016,33(8):248-256.
[11] CHRISTOPHER S Meyer.Development of geomaterial parameters for numerical simulations using the Holmquist-Johnson-Cook constitutive model for concrete[R].ARL-TR-5556,U.S.Army Research Laboratory,2011.
[12] 闻磊，李夕兵，吴秋红，等.花岗斑岩Holmquis-Johnson-Cook本构模型参数研究[J].计算力学学报,2016,33(5):725-731.
WEN Lei,LI Xibing,WU Qiuhong,et al.Study on parameters of Holmquist-Johnson-Cook model for granite porphyry[J].Chinese Journal of Computational Mechanics,2016,33(5):725-731.
[13] 闻磊，李夕兵，吴秋红，等.冻融循环作用下花岗斑岩动载强度研究[J].岩石力学与工程学报,2015,34(7):1297-1306.
WEN Lei,LI Xibing,WU Qiuhong,et al.Study on dynamic strength of granite porphyry under freeze-thaw cycles[J].Chinese Journal of Rock Mechanics and Engineering,2015,34(7):1297-1306.
[14] 王政，楼建锋，勇珩，等.岩石、混凝土和土抗侵彻能力数值计算与分析[J].高压物理学报,2010,24(3):175-180.
WANG Zheng,LOU Jianfeng,YONG Heng,et al.Numerical computation and analysis on anti-penetration capability of rock,concrete and soil[J].Chinese Journal of High Pressure Physics,2010,24(3):175-180.
[15] 李成武，王金贵，解北京，等.基于HJC本构模型的煤岩SHPB实验数值模拟[J].采矿与安全工程学报,2016,33(1):158-164.
LI Chengwu,WANG Jingui,XIE Beijing,et al.Numerical simulation of SHPB tests for coal by using HJC model[J].Journal of Mining & Safety Engineering,2016,33(1):158-164.
[16] MARSH S P.LASL shock Hugoniot data[M].California:University of California Press,1980:365-411.
[17] 苏绍曾，张效飞.砂岩在2×103～10×103MPa情况下冲击压缩特性[J].防护工程,1996(3):13-26.
[18] 巫绪涛，李耀，李和平.混凝土HJC本构模型参数的研究[J].应用力学学报,2010,27(2):340-345.
WU Xutao,LI Yao,LI Heping.Research on the material constants of the HJC dynamic constitutive model for concrete[J].Chinese Journal of Applied Mechanics,2010,27(2):340-345.
[19] 熊益波，陈剑杰，胡永乐.混凝土Johnson-Holmquist本构模型灵敏参数的初步确认[J].兵工学报,2009,30(S2):145-148.
XIONG Yibo,CHEN Jianjie,HU Yongle.Preliminary identification of sensitive parameters in Johnson-Holmquist concrete constitutive model[J].Acta Armamentarii,2009,30(S2):145-148.