金属和非金属地下矿山开采形成的采空区是影响矿山安全生产的灾源之一,空区突然垮塌引发的高速气浪和冲击波极易造成人员伤亡和设备破坏。因此,在矿山安全生产管理中常常将采空区与地压作为重要监测内容[1]。
目前对采空区的勘测技术主要有工程钻探、地球物理勘探、激光扫描探测等技术[2-3]。其中,激光扫描探测技术在准确获取采空区三维形态方面具有明显优势。三角网模型使用三角形面片来表达三维实体模型,具有许多良好的几何特性,能够用多个面片逼近复杂形体的表面,而且容易处理,因此在测绘工程、地质工程、采矿工程、三维动画、CAD/CAM、虚拟现实、正/逆向工程等领域得到广泛地运用[4-5]。借助激光三维探测数据及三维建模软件可构建采空区的三角网模型。采空区三角网模型及其剖面是采空区基础形态的重要表征,为矿山开采设计和采空区安全性分析等提供了依据[6-7]。对于三维剖面生成算法,国内外相关学者进行了大量研究,沈敬伟等[8]研究形成了基于四面体网格模型的地质体剖面生成算法。赵龙等[9]对传统八叉树剖面算法进行了改进,通过画廊看守算法成功构建了地质体三维剖面。KRIANGCHAIPORN N等[10]研究形成了TRIGA三维几何体中多剖面高效生成算法。WOON K J等[11]采用非负散射截面生成方法得到了三维地质体剖面。当前剖面生成算法的研究大多集中在基于水平方向或者垂直水平方向上,对于任意方向剖面生成算法的研究相对较少。
由于岩体节理裂隙、爆破冲击、失稳破坏等因素的影响,使得采空区实际形态复杂多变,如何沿任意方向精确生成其剖面轮廓线并对模型断面有效封闭,成为复杂采空区三角网模型任意方向剖面生成技术研究的关键。
1 研究技术路线
以空区激光探测系统(CMS)获得的采空区边界点云数据构建的采空区三角网模型为基础[12-13],开展复杂采空区三角网模型任意方向剖面生成算法研究,其技术路线如图1所示。其中,CMS设备每抬升一次旋转360°采集到的点云标记为一圈,最终采集到的全部点云按照圈层分布在整个空间。采空区三维模型是在点云三角剖分的基础上,形成的表面闭合的实体模型。

图1 技术路线
Fig.1 Technical route
2 任意方向剖切平面确定
根据解析几何相关知识,空间中任意平面都可表示为点法式方程,见式(1),其中点M(x0,y0,z0)为平面上已知点,向量n=(A,B,C)为平面的法向量。
A(x-x0)+B(y-y0)+C(z-z0)=0
(1)
实际交互操作一般不直接输入已知点坐标和法向量坐标参数,而是通过在三维视景视口中选点拉出一根线段或者将一初始平面旋转和平移到目标位置来确定剖切平面。
2.1 拉线方式
采用拉线方式时,首先在视口中人工选择两点P1,P2,默认选择视口另一点Q,获取3点对应点![]() 的实际坐标,然后根据3点坐标求出
的实际坐标,然后根据3点坐标求出![]() 指向Q′的垂线段的法向量,即为剖切平面的法向量n,进而求出剖切平面的点法式方程,方法如图2所示。
指向Q′的垂线段的法向量,即为剖切平面的法向量n,进而求出剖切平面的点法式方程,方法如图2所示。

图2 拉线方式确定剖切平面示意
Fig.2 Line to determine section plane
2.2 旋转和平移方式
首先生成一个初始平面,然后将平面以初始中心点为原点,围绕X,Y,Z轴分别旋转角度α,β,γ。假设初始法向量n0(x0,y0,z0)变换为旋转后法向量n1(x1,y1,z1),当平面绕X轴旋转α角时,其坐标变换见式(2)[14]:
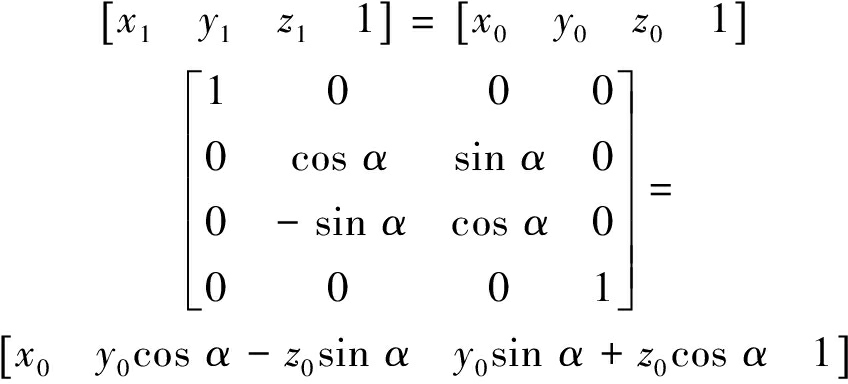
(2)
同理,绕y轴旋转β角坐标变换见式(3),绕Z轴旋转γ角坐标变换见式(4),通过三维交互操作确定剖切平面的点法式方程。

(4)
3 相交判断及交线提取
3.1 相交判断
根据空间平面的一般式方程Ax+By+Cz+D=0,对于空间中任何一点P(X,Y,Z),判断点与平面位置有如下关系:① 当AX+BY+CZ+D=0,则P点在平面上;② 当AX+BY+CZ+D>0,则P点在平面正半空间(正区);③ 当AX+BY+CZ+D<0,则P点在平面负半空间(负区)。
根据上述判据,三角形与剖切平面的空间位置关系主要有9种情况,如图3所示。由于编程存在浮点误差,判据(1)计算值不会刚好等于0,需要对判据进行简化:当AX+BY+CZ+D>ε时,则认为点在平面的正区,当AX+BY+CZ+D≤ε时,则认为点在负区,忽略在点平面上的情况,ε取值为10-6。通过简化判据推导出三角形与剖切平面相交判断表,见表1,表中“正”表示位于正区,“负”表示位于负区,“平”表示位于平面。

图3 三角形与平面的空间关系
Fig.3 Relationship between triangle and plane
3.2 提取交线
联立直线参数方程和平面点法式方程来求取交点。设线段两点P1(x1,y1,z1)和P2(x2,y2,z2),交点为I(xi,yi,zi),由线性比例关系,可得参数t的表达式。
表1 三角形与剖切平面相交判断表
Table 1 Intersection judgment between triangle and plane

(5)
用参数方式来表示交点的坐标值为
(6)
将式(6)代入式(1),计算求出参数t的值。
(7)
式(7)中F1,F2分别为过点(x1,y1,z1)和(x2,y2,z2)的平面点法式方程。当F1=0时,说明P1(x1,y1,z1)点在平面上,当F2=0时,说明P2(x2,y2,z2)点在平面上。将计算的t值代入式(6)可求出交点I(xi,yi,zi)点坐标值。
如果剖切平面与三角形相交则交点数为2,2个交点组成1条交线,将交线按照交线结构(表2)进行存储。遍历三角网中的三角形,获得所有交线,存入交线容器中,用于生成剖面轮廓线。
3.3 三角形重构
与剖切平面相交的三角形被切开为两个部分,如图4(a)所示。需要对切开的三角形重新生成三角形,三角形重构算法步骤如下:
Step1:利用简化判据判断剖切平面Π和ΔP1P2P3三角形的相交关系;
Step2:当判断相交存在交点时,则运用3.2节方法求出交线,设两个交点为I1和I2;
Step3:计算线段P1I2和P2I1长度,当长度<10-6时则将线段视为共点,四边形作为一个三角形输出;
Step4:如果上述两线段长度均大于10-6时,分别计算四边形P1P2I1I2的两条对角线P1I1和P2I2剖分的一对三角形中最小角,取最小角较大的对角线情况作为三角形重构方案;
Step5:输出三角形1、三角形2和三角形3,如图4(b)所示。
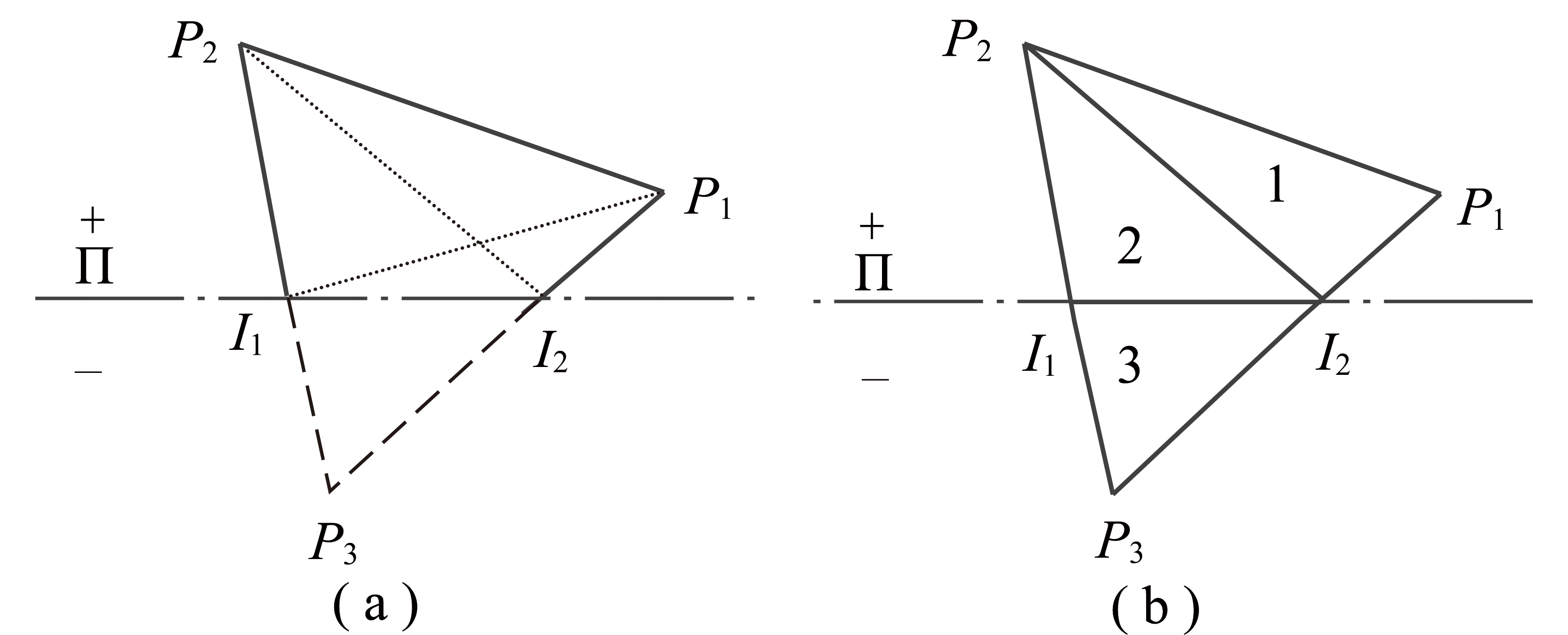
图4 切开的三角形重构算法示意
Fig.4 Reconstruction algorithm of cut-through triangle
4 剖面轮廓线生成及模型断面封闭
4.1 剖面轮廓线生成
交线容器中的交线存储是无序的,从中准确提取剖面轮廓线的关键在于寻找交线的首尾相邻关系[15-16]。剖面轮廓线生成算法步骤如下:
Step1:从交线容器中任取一条交线作为初始轮廓线,定义其首尾点,并删除该交线;
Step2:遍历交线容器中所有交线并计算交线的两点与轮廓线尾点P点的距离,当距离小于ε(10-6)则确定相邻关系;
Step3:将存在相邻关系的交线的较远点压入到轮廓线容器作为新的尾点,从交线容器删除该交线;
Step4:重复Step2和Step3直到轮廓线的首点和尾点距离小于ε(10-6),则说明生成一条闭合的轮廓线;
Step5:如果交线容器为空,则说明所有的轮廓线全部生成。否则回到Step1开始生成新的轮廓线。
4.2 模型断面封闭
剖面切三角网可生成正区三角网和负区三角网两部分,需要对生成的模型断面进行封闭以确保新三角网模型的完整性。模型断面可能为一个或多个不规则的多边形,封闭的实质是对平面上不规则多边形进行内部三角剖分,目前采用较多的方法为切耳法和插中心点的方法,上述方法易生成狭长或自相交三角形。为了生成较优三角形,提出了切耳法、插值和线圈间三角剖分相结合的模型断面封闭方法。
(1)切耳法。
根据耳朵理论[17]:多边形上3个连续的顶点a,b,c如果ac是一条内部对角线,b为外凸的顶点,则Δabc为多边形的一个耳朵。切耳法三角剖分算法基本思维为,首先初始化每个顶点的耳朵尖状态,当顶点数n>3时,定位一个耳朵尖v2,输出对角线v1v3和耳朵尖v2组成的三角形,然后切除耳朵E2,更新顶点v1和v3的状态。
如果没有耳朵的控制条件,断面轮廓线会被全部三角剖分,容易生成非常狭长的三角形。通过设定耳朵外凸角度控制条件,可将带尖角多边形切成较规整的多边形,便于后续插值。
(2)内部插值及生成正三角形网格。
切耳法步骤完毕后,对多边形进行内部插值,按照正三角形排列方式进行内部插值最为合理,内部插值步骤如下,如图5所示。

图5 正三角形排列的内部插值示意
Fig.5 Internal interpolation based on equilateral triangle arrangement
Step1:以多边形边长平均值的1~5倍作为插值间距;
Step2:取多边形上距离最大的两点连线作为插值主线,图中线段AB。参照主线逆时针旋转60°得到一系列直线,即为辅线系,辅线与辅线之间距离为插值间距,如图l-2,l-1,l0,l1,l2,l3线等;
Step3:判断辅线和轮廓线多边形是否相交,求出交点,交点数为0,2,4等偶数;
Step4:在相邻的2个交点之间,等插值间距插入新点;
Step5:根据辅线系上插值点的正三角形排列的拓扑关系,对插值点进行三角剖分生成正三角形网格。
(3)线圈间三角剖分。
生成正三角形网格后,通过依次顺时针查找的方法可提取正三角形网格的边界。正三角形网格边界和轮廓线多边形可视为两个独立不交叉的线圈,如图6(a)所示。可采用最大张角三角剖分算法实现线圈与线圈之间的三角剖分[18],在2个线圈的邻点中寻找相对已知边张角最大的点作为三角形的第3点,上述已知边是连接在两线圈间的一条逐步推进的边。
模型断面封闭方法在不丢失剖面轮廓线细节前提下,通过插值避免产生狭长三角形,能够生成优质三角形并完美封闭模型断面,如图6(b)所示。

图6 模型断面封闭算法示意
Fig.6 Algorithm of closing model’s fracture surface
5 算法实现与实例应用
5.1 主要数据结构
算法在VS 2010的VC++编程环境中实现,其主要的数据结构包括点、线、三角形、三角网、交线和点位等结构,主要数据结构见表2,存储链表采用标准模板库STL的序列容器vector。
5.2 实例应用
将研究的算法成功应用到某金属矿山多个复杂采空区,实例验证表明该算法效率高,能生成精确的剖面轮廓线,能很好地封闭模型断面并输出完整封闭的新采空区三角网模型。图7为算法生成剖面轮廓线效果,可见运用算法生成的轮廓线精准且没有丢失细节,1个剖面可切出1个或者多个轮廓线。图8为模型断面封闭算法效果对比,可见利用研究的断面封闭算法的生成的三角网较为均匀规整,而单一采用切耳法封闭断面则产生较多的狭长三角形。图9为封闭断面的三角网局部效果。
表2 主要数据结构表
Table 2 Main data structure


图8 断面封闭算法对比效果
Fig.8 Contrast effect of fracture surface closing algorithm

图7 算法生成剖面轮廓线效果
Fig.7 Effect diagram of section outline generated by algorithm

图9 封闭断面的三角网局部效果
Fig.9 Triangulation local effects of closing fracture surface
6 结 论
(1)研究形成了一种新的复杂采空区三角网模型的任意方向剖面生成算法,实现了三维交互操作选定剖切平面、基于简化判据的剖切平面与三角形相交判断、对切开的三角形进行重构、提取交点和交线。
(2)通过判断交线首尾相邻关系精确提取剖面轮廓线,以及采用切耳法、插值和线圈间三角剖分相结合的方法对模型断面进行封闭等多种功能。
(3)实际应用表明:算法剖面生成具有很高的效率,能使用多种操作交互,生成的剖面轮廓线精度高,对模型断面封闭效果好,具有较高的工程应用价值。
参考文献(References):
[1] CAI Yue,JIANG Yujing,LIU Baoguo,et al.Computational implementation of a GIS developed tool for prediction of dynamic ground movement and deformation due to underground extraction sequence[J].International Journal of Coal Science & Technology,2016,3(4):379-398.
[2] 过江,古德生,罗周全.金属矿山采空区3D激光探测新技术[J].矿冶工程,2006,26(5):16-20.
GUO Jiang,GU Desheng,LUO Zhouquan.A new technique of 3D laser survey of finished stopes in metal mines[J].Mining and Metallurgical Engineering,2006,26(5):16-20.
[3] LUO Zhouquan,LIU Xiaoming,ZHANG Bao,et al.Cavity 3d modeling and correlative techniques based on cavity monitoring[J].Journal of Central South University of Technology,2008,15(5):639-644.
[4] 张尧,樊红,黄旺,等.基于Delaunay三角网的等高线树生成方法[J].测绘学报,2012,41(3):461-467,474.
ZHANG Yao,FAN Hong,HUANG Wang,et al.The method of generating contour tree based on contour delaunay triangulation[J].Acta Geodaetica et Cartographica Sinica,2012,41(3):461-467,474.
[5] 张尧,樊红,李玉娥,等.一种基于等高线的地形特征线提取方法[J].测绘学报,2013,42(4):574-580.
ZHANG Yao,FAN Hong,LI Yu’e,et al.A method of terrain feature extraction based on contour[J].Acta Geodaetica et Cartographica Sinica,2013,42(4):574-580.
[6] XU Jialin,XUAN Dayang,HE Changchun.Innovative backfilling longwall panel layout for better subsidence control effect—separating adjacent subcritical panels with pillars[J].International Journal of Coal Science & Technology 2014,1(3):297-305.
[7] 罗周全,杨彪,刘晓明,等.采用CMS辅助矿柱回采爆破设计研究[J].金属矿山,2007(3):15-17.
LUO Zhouquan,YANG Biao,LIU Xiaoming,et al.Research on cms-aided blast design for ore pillar extraction[J].Metal Mine,2007(3):15-17.
[8] HEJMANOWSKI Ryszard.Modeling of time dependent subsidence for coal and ore deposits[J].International Journal of Coal Science & Technology 2015,2(4):287-292.
[9] 赵龙,闵世平,代强玲.基于八叉树的三维地质剖面生成算法[J].计算机工程,2014,40(2):250-255.
ZHAO Long,MIN Shiping,DAI Qiangling.3D geological section generating algorithm based on octree[J].Computer Engineering,2014,40(2):250-255.
[10] KRIANGCHAIPORN N,IVANOV K,HAGHIGHAT A,et al.Transport model based on three-dimensional cross-section generation for TRIGA core analysis[J].Annals of Nuclear Energy,2010,37(9):1254-1260.
[11] WOON K J,HONG S G,YOUNG-OUK L,et al.An extension of the non-negative scattering cross section generation method for a three dimensional geometry with unstructured tetrahedral mesh[J].Journal of Korean Physical Society,2011,59(23):2079-2083.
[12] 王建华,徐强勋,张锐.任意形状三维物体的Delaunay网格生成算法[J].岩石力学与工程学报,2003,22(5):71-77.
WANG Jianhua,XU Qiangxun,ZHANG Rui.Delaunay algorithm and related procedure to generate the tetrahedron mesh for an object with arbitrary boundary[J].Chinese Journal of Rock Mechanics and Engineering,2003,22(5):71-77.
[13] ITO Y,SHIH A M,ERUKALA A K.Parallel unstructured mesh generation by an advancing front method[J].Mathematics & Computers in Simulation,2007,75(5):200-209.
[14] 陈斐,周晓光.平面分割的线/线相接、交叉类型判断[J].测绘学报,2014,43(2):186-192.
CHEN Fei,ZHOU Xiaoguang.An algorithm for determining the touching and crossing relations between a pair of lines based on one line splitting plane to two parts[J].Acta Geodaetica Et Cartographica Sinica,2014,43(2):186-192.
[15] 张小青,吴坤华,黄鹤,等.基于三角网格模型的剖面轮廓信息提取[J].测绘通报,2012,(9):26-28.
ZHANG Xiaoqing,WU Kunhua,HUANG He,et al.Extraction of section contour information based on triangular meshes[J].Bulletin of Surveying and Mapping,2012,(9):26-28.
[16] 李衷怡,赵新方.三角网格剖切算法的研究[J].计算机与数字工程,2007,35(3):4-5.
LI Zhongyi,ZHAO Xinfang.Cutting of triangular meshes method[J].Computer and Digital Engineering,2007,35(3):4-5.
[17] JOSEPH O Rourke.Computational geometry in c (second edition)[M].Cambridge:Cambridge University Press,1997:11-35.
[18] 罗贞焱.基于CMS探测的采空区三维可视化系统研究[D].长沙:中南大学,2010:25-35.
LUO Zhenyan.The research of goaf’s 3d visual system based on cms detection[D].Changsha:Central South University,2010:25-35.