
刘 勇1,2,3,陈长江1,2,魏建平1,2,3,张 娟1,2
(1.河南理工大学 河南省瓦斯地质与瓦斯治理重点实验室(省部共建国家重点实验室培育基地),河南 焦作 454000; 2.河南理工大学 安全科学与工程学院,河南 焦作 454000; 3.煤炭安全生产河南省协同创新中心,河南 焦作 454000)
摘 要:为验证磨料气体射流破岩可行性,对比分析磨料水射流和磨料气体射流破岩效果。理论分析了磨料水射流和磨料气体射流中磨料加速机理,得出磨料动能与磨料水射流和磨料气体射流入口压力之间的数值关系。基于统一强度理论,建立了适用于磨料射流破岩的能量准则,得出了岩石破坏时所需的临界能量。根据磨料加速理论和岩石破坏临界能量计算了岩石破坏临界磨料速度以及所需入口压力。基于理论计算结果,试验验证了磨料水射流和磨料气体射流冲蚀灰岩的破碎效果。结果表明:当磨料速度达到270 m/s时,所需气体射流压力的理论值为15 MPa,水射流压力的理论值为45 MPa;两种磨料射流冲蚀坑形状相同,均呈现 “V”型,磨料水射流的冲蚀坑形状相较于磨料气体射流具有“口小”,“坑深”的特征,磨料气体射流破灰岩形成的冲蚀坑体积要大于磨料水射流。
关键词:磨料水射流;磨料气体射流;能量屈服准则;破岩;冲蚀坑体积
中图分类号:TD421.59
文献标志码:A
文章编号:0253-9993(2018)09-2510-08

移动阅读
刘勇,陈长江,魏建平,等.磨料水射流与磨料气体射流破岩压力对比分析[J].煤炭学报,2018,43(9):2510-2517.doi:10.13225/j.cnki.jccs.2017.1770
LIU Yong,CHEN Changjiang,WEI Jianping,et al.Comparison analysis on the rock breakage pressure induced by abrasive water jets and abrasive gas jets[J].Journal of China Coal Society,2018,43(9):2510-2517.doi:10.13225/j.cnki.jccs.2017.1770
收稿日期:2017-12-13
修回日期:2018-05-19
责任编辑:许书阁
基金项目:国家自然科学基金资助项目(51704096);河南理工大学自然科学基金资助项目(J2018-4);河南省瓦斯地质与瓦斯治理重点实验室开放基金资助项目(WS2017A02)
作者简介:刘 勇(1984—),男,山东临沂人,副教授,博士研究生。E-mail:yoonliu@hpu.edu.cn
LIU Yong1,2,3,CHEN Changjiang1,2,WEI Jianping1,2,3,ZHANG Juan1,2
(1.State Key Laboratory Cultivation Base for Gas Geology and Gas Control,Henan Polytechnic University,Jiaozuo 454000,China; 2.School of Safety Science and Engineering,Henan Polytechnic University,Jiaozuo 454000,China; 3.Coal Production Safety Collaborative Innovation Center in Henan Province,Jiaozuo 454000,China)
Abstract:In order to verify the feasibility of rock breaking by abrasive gas jet,the effect of abrasive water jet and abrasive gas jet on rock breaking is compared and analyzed.In this paper,the mechanism of abrasive acceleration in abrasive water jet and abrasive gas jet is theoretically analyzed.The numerical relationship between the abrasive kinetic energy and inlet pressure of abrasive water jet and abrasive gas jet is obtained.Based on the unified strength theory,the energy criterion for rock breaking by abrasive jet is established,and the critical energy required for rock failure is obtained.Based on the accelerated theory of abrasive and the critical energy of rock failure,the critical rock velocity and the required inlet pressure of rock are calculated.Based on the theoretical calculation results,the crushing effect of abrasive water jet and abrasive gas jet on limestone erosion is experimentally studied.The results show that when the abrasive speed reaches 270 m/s,the required gas jet pressure theoretical value is 15 MPa,the water jet pressure theoretical value is 45 MPa.Two kinds of abrasive jet erosion pits are shaped with “V” type.Compared with the abrasive gas jet,the shape of the crater of abrasive water jet has the characteristics of “small mouth” and “deep pit”.The size of the erosion crater formed by the abrasive gas jet is larger than that of the abrasive water jet.
Key words:abrasive water jet;abrasive gas jet;energy yield criterion;rock breaking;erosion pit volume
磨料水射流被广泛应用于煤层气、油气开采等破岩作业中[1]。但磨料水射流在辅助钻进煤层气井时,由于水的侵入,容易导致塌井,降低煤层气开采效率。无水化钻井是解决该问题的重要手段。磨料气体射流作为一种典型的无水射流,已被广泛应用于金属钻孔等领域。研究表明高压磨料气体射流也可进行破岩作业[2],且以气体作为动力,可有效降低射流成本,节约资源。但目前尚无法确定磨料气体射流的破岩效率是否优于磨料水射流。磨料射流是通过高速流体加速磨料粒子,进而利用磨料粒子的冲击动能实现材料的去除加工和冲蚀破坏[3]。因此,为对比磨料水射流和磨料气体射流的破岩效果,需对水射流和气体射流中磨料加速规律进行分析,并明确磨料射流破岩机理。
磨料的冲击速度决定于磨料在喷嘴及射流核心段的加速过程[4]。磨料冲击速度可通过PIV等非接触或间接测量方法测得[5],虽能够间接观察到磨料运动轨迹,但试验结果只能反应试验条件下磨料粒子的运动,不能揭示一般规律。通过分析单颗磨料粒子受力情况,建立磨料运动方程,利用迭代算法进行求解[6-7],得到的磨料冲击速度具有普遍适用性。
目前对磨料射流破岩的研究均是在破坏强度理论以及试验基础上提出的各种射流破岩假说[8]。基于强度准则,认为磨料射流破岩为准静态加载过程,当刚性流体的滞止动压超过岩石的门限压力时,岩石发生变形甚至破坏[9]。但磨料射流过程是一个涉及诸多因素的非线性冲击动力学问题,具有瞬时强值动载荷、大变形及高应变率等特点[10]。因此,从应力-应变角度建立的描述岩石在准静态条件下的破坏的各种假说,并不能较准确的反映磨料射流破岩的实质。
因此,为明确磨料气体射流破岩效果,笔者对比分析磨料水射流和磨料气体射流的破岩效率,在理论分析磨料加速规律的基础上,确定磨料冲击速度和射流压力的关系,计算磨料冲击动能;并建立适合磨料射流破煤岩的破坏准则,得出磨料射流冲击破坏岩石的临界压力,并开展磨料水射流和磨料气体射流破岩试验,对比分析高压磨料水射流和高压磨料气体射流破岩效果,验证高压气体射流破岩的可行性。
本文建立的磨料加速理论模型,是基于流体为连续相,磨料粒子为稀疏相。磨料粒子的加速是依靠于液固或气固之间的速度差和加速度差,即流体对磨料粒子产生曳力作用[11]。磨料粒子加速过程主要分为喷嘴内及喷嘴出口与靶体材料之间的远场段[12]。因此,本文分别在理论分析磨料水射流和磨料气体射流磨料在喷嘴内及射流段加速过程的基础上,明确磨料与流体之间的速度关系,得出磨料速度、流量与射流压力之间关系。
前混合磨料水射流喷嘴广泛采用圆锥收敛型喷嘴[13],结构如图1所示。
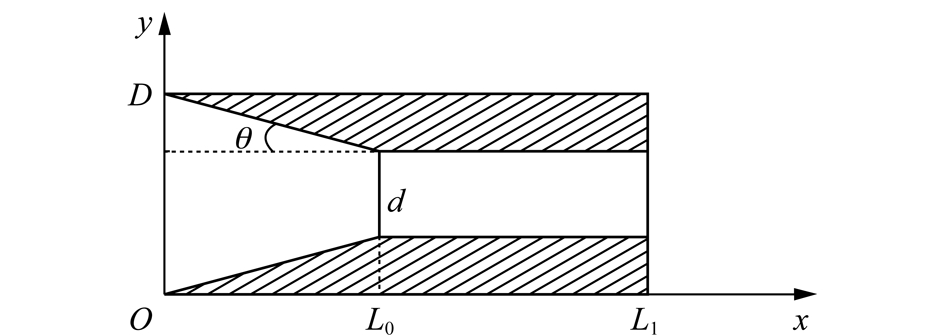
图1 圆锥收敛喷嘴结构
Fig.1 Structure of conical convergent nozzle
图1中,D为喷嘴入口直径;θ为喷嘴的收缩半角;d为喷嘴出口直径;OL0为收敛段长度,L0L1为圆柱段长度。
假设沿喷嘴径向水流及磨料速度分布均匀,且喷嘴内磨料与水流运动属于一维定常流动[14],只分析x方向加速度。
(1)
![]()
(2)
式中,a为水流加速度;as为磨料加速度;v为流体轴向速度;vs为磨料轴向速度。
磨料水射流中水是连续介质,对收缩段O~L0内应用连续性方程,可得任意位置x处的水流速度:
(3)
式中,![]() ;
;![]() ;v0为喷嘴入口处水流速度。
;v0为喷嘴入口处水流速度。
在喷嘴收缩段内,磨料粒子在两相速度差以及加速度差的共同作用下做加速运动,其运动方程为
as=h(v-vs)2+ka
(4)
式中,![]() ;
;![]() ,其中,ρ为流体密度,ρs为磨料密度,ds为单颗磨料粒子直径,cD为阻力系数,取0.44。
,其中,ρ为流体密度,ρs为磨料密度,ds为单颗磨料粒子直径,cD为阻力系数,取0.44。
磨料在高压管道内充分加速,喷嘴入口处磨料与水流有共同的初始速度。联立式(1)~(4)可得喷嘴收敛段任意位置处磨料与入口处速度以及位置x之间的方程;
(5)
联立式(3),(5)可求出喷嘴收敛段L0处磨料速度与水流速度的数值关系,设满足下式:
vs1=n1v1
(6)
式中,vs1为磨料粒子在L0处速度,即圆柱段入口处速度;v1为水流在L0处速度;n1为常数,且n1<1。
喷嘴圆柱段内,忽略磨料与边界层对水流速度的影响,为均匀定常流,流体速度近似等于收敛段L0处的速度v1,磨料粒子的运动方程由(4)可简化为
as=h(v1-vs)2
(7)
联立式(6),(7)可得圆柱段内磨料粒子轴向速度与轴线位置x关系为
![]()
(8)
对喷嘴出口截面上应用伯努利方程,可得
v1=44.![]()
(9)
式中,p为水射流压力,MPa。
联立式(8),(9)可得喷嘴出口处磨料粒子速度与射流压力数值解,设满足
(10)
式中,vs2为喷嘴出口处磨料速度;n2为常数。
对喷嘴圆柱段内再应用连续性方程,可得喷嘴出口水的体积流量qV,即
qV=2.![]()
(11)
认为喷嘴出口处磨料是均匀分布,设磨料体积分数为n3,磨料流量qVs满足
qVs=2.![]()
(12)
水射流离开喷嘴后受静止流体的掺混,流体速度从边缘至射流中心依次降低。流场结构划分为受静止流体影响的混合层以及未受影响的等速核区。处于等速核内的磨料粒子会持续加速,加速过程满足上式(8),等速核段长度[15]满足:
Lc=6.2d
(13)
本文选取磨料为120目的石榴石,磨料密度为ρs=3.5 g/cm3。选取的喷嘴具体参数见表1。
表1 圆锥收敛型喷嘴参数
Table 1 Parameters of cone convergent nozzle

将喷嘴和磨料参数代入式(3),(5)可求得n1=0.57,即可得喷嘴收敛段出口速度:
vs1=0.57v1
(14)
再联立式(8),(9)可求得n2=40.3,即喷嘴出口处磨料粒子速度与射流压力关系:
vs2=40.![]()
(15)
试验时选取磨料体积分数n3=5%,代入式(12)得
qVs=0.![]()
(16)
根据式(13),求得等速核长度Lc=12.4 mm,设定为试验靶距。由于喷嘴出口处磨料速度已接近于水流速度的90%,等速核内气流速度对磨料轴向速度影响较小,即认为磨料粒子接触靶体时的轴向速度与流量仍满足式(15),(16)。
气体具有可压缩性,通过缩放型喷嘴能够获得超音速[16]。为提高磨料加速性能,笔者选用缩放型喷嘴结构如图2所示。
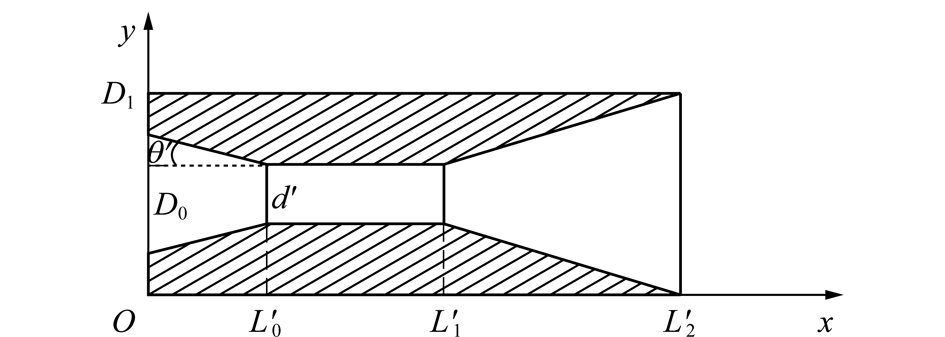
图2 缩放型喷嘴结构
Fig.2 Structure of laval nozzle
图2中,D0为喷嘴收缩管段入口直径;θ′为喷嘴收缩半角;d′为喷嘴喉管段直径;![]() 为喷嘴收缩段长度;
为喷嘴收缩段长度;![]() 为喷嘴喉管段长度;
为喷嘴喉管段长度;![]() 为喷嘴扩张段长度;D1为喷嘴出口直径。
为喷嘴扩张段长度;D1为喷嘴出口直径。
缩放型喷嘴内气体的加速过程分为收缩段亚音速流动、喉管内音速流动和扩张段超音速流动。根据空气动力学知识[17],可知喷嘴收缩段以及喉管内气流状态参数满足:
(17)
![]()
(18)
pg=ρRT
(19)
式中,ρ0为滞止密度;ρg为气体密度;p0为滞止压力;pg为气体压力;Ma为马赫数;K=1.44为绝热指数;R=287 J/(mol·K)为空气的气体常数;T为气体热力学温度。
喉管内达到音速时,其速度满足:
(20)
式中,ρ*为临界密度;c为当地音速。
亚音速气流在收缩段内主要依靠压力推动增加速度,最终在喉管入口处气体密度减小到临界密度,速度达到音速。若气体密度取临界密度,收缩段内气体速度变化可由式(3)近似表示;磨料在收缩段以及喉管内的加速过程分别满足式(5),(8)中的运动方程。其中,v1=c为当地音速,可由式(20)确定;气流密度ρg为临界密度,即当Ma=1时由式(17),(19)确定的密度,即
ρ*=0.![]()
(21)
联立式(5),(8),(18),(20),(21)可得磨料粒子在扩张段入口处速度与气体速度满足:
(22)
式中,![]() 为磨料粒子在L1处速度;i1为比例系数。
为磨料粒子在L1处速度;i1为比例系数。
在扩张段中超音速气流主要是依靠气体膨胀加速,认为密度变化是引起气体加速的主要原因。磨料加速同样满足式(4)的加速方程:
(23)
式中,![]() 为磨料粒子速度;vx为气体速度。
为磨料粒子速度;vx为气体速度。
缩放型喷嘴内的气体状态参数满足:
(24)
![]()
(25)
![]()
(26)
联立式(22)~(25)可得任意位置处磨料速度与气体密度之间的关系:
![]()
(27)
式中,pg1为喷嘴出口气体压力;ds为磨料粒子直径。
且A为喷嘴扩张段的截面积,满足:
(28)
气体在喷嘴出口处的速度与流量满足:
(29)
![]()
(30)
式中,v2为喷嘴出口气体平均速度;qgm为喷嘴出口气体流量;A1为喉管截面积。
又根据连续方程可得:
(31)
式中,ρg1为喷嘴出口截面密度;A2为喷嘴出口截面积。
联立式(22),(24),(27),(28),(30),(31)可得喷嘴出口处磨料粒子速度与气体速度的关系为
(32)
式中,i2为喷嘴出口处磨料粒子与气体速度之间比例系数。
将式(29)代入式(32)即可求得喷嘴出口处磨料粒子速度与入口压力之间关系。
等速射流区内气体会维持喷嘴出口速度,继续对磨料粒子加速。磨料粒子的加速过程可用式(8)求解。
高压磨料气体射流磨料同样为120目石榴石,选取缩放型喷嘴具体参数见表2。
表2 缩放型喷嘴参数
Table 2 Parameters of Laval nozzle

试验中管路内气体与磨料速度小,可忽略沿程损失压力,即认为滞止压力p0等于管路的初始压力p。认为气体在喷嘴出口压力为大气压力P1=0.1 MPa,喷嘴入口热力学滞止温度为室温T1=300 K。将磨料与喷嘴参数代入,可求解出靶距L=12.4 mm处磨料速度与不同入口压力之间的数值关系满足表3。
表3 入口压力与磨料速度关系
Table 3 Relationship between inlet pressure and abrasive speed

为对比研究磨料水和气体射流破岩效果,在保证磨料具有相同冲击动能的同时,还需要采用合适的破坏准则作为岩石破坏判据。
岩石破坏准则的建立可以分别从应力或能量角度出发[18]。由于磨料冲蚀是涉及多种因素的非线性冲击,从应力角度出发建立岩石破坏准则时,会出现理论分析与岩石实际破坏偏差较大。磨料射流破岩是能量传递与转化的过程,初始流体具有的静压能经过加速运动转化为磨料与流体的动能,岩石变形破坏的实质是在外载能量的驱动下,岩石内部积聚的能量突然耗散与释放的宏观表现[19]。因此,笔者选择从能量角度出发建立岩石的屈服准则。
岩石受外力作用产生弹性变形时,会在其内部积蓄有弹性应变能。由于岩石是典型的摩阻材料,其破坏过程中应考虑到摩擦应力的影响。因此,本文将从考虑内摩擦力的3个滑动面的剪切应变比能来建立描述岩石变形破坏过程中的能量准则[20]。
岩石剪切破坏是岩石内一点积聚的剪切应变能大于颗粒间的胶接能量时,出现的裂隙或剪切面滑动。剪切应变能本质是岩石在剪应力破坏时沿滑动面滑动克服内摩擦力做的功。岩石是一种内摩擦型材料,具有压硬性,其内摩擦力与静水压力影响。岩石材料在静水压力作用下,可以画出3个莫尔圆,表示3个滑动面应力情况。如图3所示。
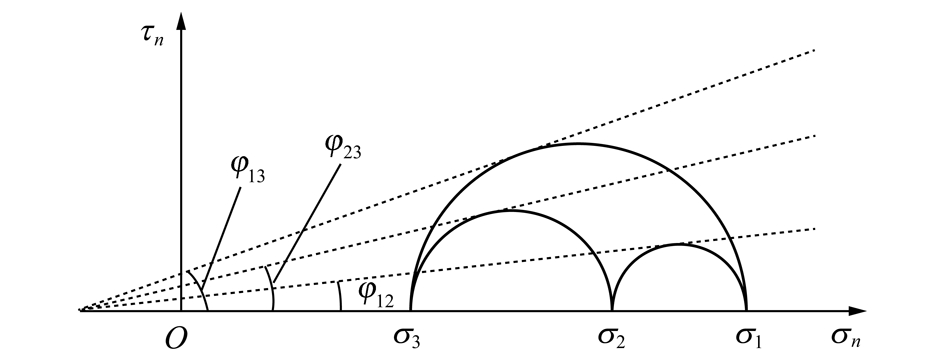
图3 莫尔应力圆表示的复合滑动面
Fig.3 Slip surface of rock represented by Mohr stress circle
由几何关系可以求得3个复合滑动面的法向应力和剪切应力分别为
φ12
(33)
![]() φ12
φ12
(34)
![]() φ23
φ23
(35)
![]() φ23
φ23
(36)
![]() φ13
φ13
(37)
![]() φ13
φ13
(38)
式中,σ12,σ23,σ13分别为3个滑动面的法向应力;τ12,τ23,τ13分别为3个滑动面的切向应力;σ1,σ2,σ3分别为岩石所受到3个主应力;φ12,φ23,φ13分别为3个复合滑动面的内摩擦角。
由于岩石是典型的摩阻材料,其破坏时克服的胶结能量是关于黏聚力的函数。则岩石屈服时3个滑动面的弹性剪切应变能分别为
×
![]()
(39)
![]() ×
×
![]()
(40)
![]() ×
×
![]()
(41)
式中,Ws12,Ws23,Ws13,为3个复合滑动面的弹性剪切应变能;G为剪切模量。
磨料射流冲蚀岩石过程中,岩石破坏可处理为剪切破坏,耗散的弹性比能表示为
Ws=Ws12+Ws23+Ws13
(42)
本试验选取典型硬岩(硅质灰岩)制作φ50 mm×100 mm标准试样。在岩石力学测试系统MTS-815试验机上测定的试样力学参数见表4。
表4 灰岩岩样力学参数
Table 4 Mechanical parameters of rock samples

表4数据代入式(38)~(41)可得:灰岩破坏时所需要的能量为Ws=30.4 kJ。
磨料冲蚀岩石过程中遵循能量守恒定律,初始能量是磨料动能Eks。当用于破岩的能量高于由式(42)得出的临界能量时,岩石内部急聚的弹性应变能会以剪切应变能Ws的形式迅速耗散与释放。根据HUTCHING等[21]的研究,认为经冲击后,垂直入射的磨料粒子有超过90%的能量损失在靶体上。即:
Ws≤0.9Eks
(43)
控制冲蚀时间为5 s,将上述灰岩试样临界能量Ws=30.4 kJ代入式(15),(16),(43)可得磨料水射流破岩临界压力为45 MPa,相应的磨料流量为0.16 kg/s,速度为270 m/s,再根据表3可选取磨料气体射流入口压力为15 MPa,见表5。
表5 磨料射流破岩压力参数
Table 5 Rock breaking pressure parameters of abrasive jet

磨料水射流破岩试验选用喷嘴结构见表1,磨料为120目石榴石,靶距选取为12.4 mm,入口压力分别选为40,45,50 MPa;高压磨料气体射流选用自主研制的磨料气体射流冲蚀岩石试验系统[2],喷嘴参数为表2,磨料为120目石榴石,靶距同样选为12.4 mm,入口压力分别选为10,15,20 MPa。试验过程是沿岩样轴心冲蚀5 s,结果如图4所示。

图4 磨料射流冲击灰岩破坏形态
Fig.4 Damage form of abrasive jet impact limestone
如图4所示,当水压力为40 MPa、气体压力为10 MPa,磨料动能低于灰岩破坏临界能量时,灰岩表面仅存在磨损,未形成明显冲蚀坑破坏。当水压力高于45 MPa、气体压力高于15 MPa,岩石能量发生突变,岩石形成冲蚀坑破坏。磨料粒子撞击过程中,加载的局部压力产生拉应力,促使岩石表面及内部产生微裂纹,岩石发生磨损,粒子动能以弹性势能释放;如图4所示,在水压力为40 MPa、气体压力为10 MPa时,岩石发生表面磨损。磨料粒子动能高于岩石破坏临界能量,岩石形成以射流轴线为圆心的大变形塑性区,区域内微裂纹扩展;又由于射流断面上粒子动能沿径向逐渐减小,岩石塑性区周围存在环形弹性区,当磨料粒子撞击过程中沿轴向动能减小,局部压力卸载时,弹性区域内岩石恢复形变,在塑性与弹性过渡区域内产生剪应力,导致塑性区的扩展裂纹贯穿,岩石发生剪切破坏,形成冲蚀坑,储蓄能量以剪切应变能释放。如图4所示,当水压力大于45 MPa、气体压力大于15 MPa,岩石在高频磨料粒子的冲蚀作用下,呈现为“v”型冲蚀坑破坏。
图4(a)为灰岩在磨料水射流作用下的破坏形式。相较于图4(b)中气体磨料射流,冲蚀坑具有“口小”,“坑深”的特征。根据普朗特边界层理论知,射流沿轴向速度间断面不稳定,会产生波动形成涡旋,对射流场周围静止流体产生卷吸作用,阻碍磨料运动。由于水动力黏度系数远大于空气,边界层内磨料动能会迅速衰减到不足以提供岩石破坏所需的能量,所以冲蚀坑相较于磨料气体射流呈现“口小”特征。射流核心区域水流速度远低于空气速度,易于磨料粒子混入;边界层对射流核心区内流体速度影响小,粒子动能耗散低,磨料水射流破岩呈现“坑深”特征。
如图4所示,灰岩在入口压力为45 MPa磨料水射流和入口压力为15 MPa磨料气体射流冲蚀下的平均冲蚀坑体积分别为2.2 mm3和4.2 mm3。即磨料粒子具有相同能量时,磨料气体射流冲蚀坑体积大于磨料水射流。水为不可压缩流体,密度变化小,磨料粒子冲击动能主要转移为岩石内能及以热能形式耗散于岩石表面,高速气流为可压缩流体,动能易受内能影响,磨料气体射流冲击岩石过程中,耗散于岩石表面的磨料粒子动能会以热能形式被气体重新吸收,气体温度升高、密度增大,导致磨料粒子动能增加,用于破岩能量效率高;受流场结构影响,轴心区域内气体射流中的磨料粒子数量低于水射流;但在整个射流作用区域内,具有破岩能力的磨料粒子数量气体射流要远大于水射流;气体射流为非连续性射流,脉动压力要高于水流,高脉动有利于破坏磨料射流过程中岩石表面形成的“砂垫”效应,降低耗散于反射粒子与入射粒子碰撞的能量,有利于提高破岩效率。
通过上述试验可以得出,入口压力为15 MPa的磨料气体射流破岩效果要优于入口压力为45 MPa磨料水射流。又根据理论计算结果,磨料粒子具有相同动能时,气体压力要远小于水压力。即进行破岩作业时,高压磨料气体射流要优于磨料水射流。
(1)通过理论分析高压磨料水射流和高压磨料气体射流磨料加速机理,分别建立了两种形式磨料射流磨料冲击速度计算模型,结合建立的岩石破坏能量屈服准则,得出了高压磨料气体射流破岩临界压力较高压磨料水射流低,具有更高的破岩效率,证明了磨料气体射流破煤岩的可行性。
(2)基于单颗磨料受力情况研究了水和气体中磨料加速过程,建立了适用于前混合条件下的水加速磨料及气体加速磨料的计算模型。并在此基础上,得出了磨料速度与射流入口压力之间的理论值。
(3)考虑到岩石破坏是剪应力克服内摩擦力做功的宏观变现,本文基于统一强度理论,建立了岩体破坏时剪切应变能的计算模型,并通过对灰岩力学参数测试,计算了试验岩样破坏的临界能量。
(4)结合试验条件和参数,计算了试验岩样破坏时对应的气体射流和水射流入口临界压力分别为15 MPa和45 MPa。基于计算结果,试验对比研究了磨料水射流和磨料气体射流破灰岩效果。灰岩冲蚀坑破坏形态均成“V”型,磨料水射流相较于磨料气体射流冲蚀坑具有“口小”、“坑深”的特征,但磨料气体射流冲蚀体积大于磨料水射流。
参考文献(References) :
[1] 李晓红,孙家骏.准直管磨料射流在岩石上切割深槽的研究[J].煤炭学报,1999,24(4):395-398.
LI Xiaohong,SUN Jiajun.Study on cutting deep slots on rock by quasi straight pipe abrasive jet[J].Journal of China Coal Society,1999,24(4):395-398.
[2] 温志辉,梁博臣,刘笑天.磨料特性对磨料气体射流破煤影响的实验研究[J].中国安全生产科学技术,2017,13(5):103-107.
WEN Zhihui,LIANG Bochen,LIU Xiaotian.Experimental study on the effect of abrasive characteristics on coal breaking of abrasive gas jet[J].Journal of Safety Science and Technology,2017,13(5):103-107.
[3] 郭楚文,徐晓东.空化磨料水射流粉碎技术[M].北京:中国科学文化出版社,2002.
[4] BAHRAMI H,REZAEE R,CLENNELL B.Water blocking damage in hydraulically fractured tight sand gas reservoirs:An example from PERTH Basin,Western Australia[J].Journal of Petroleum Science and Engineering,2012,88/89:100-106.
[5] 章文峰,卢义玉,汤积仁,等.基于PIV技术的磨料水射流中固体磨料粒子速度分布实验研究[J].振动与冲击,2016,35(8):159-165.
ZHANG Wenfeng,LU Yiyu,TANG Jiren,et al.Experimental study on velocity distribution of solid abrasive particles in abrasive water jet based on PIV Technology[J].Journal of Vibration and Shock,2016,35(8):159-165.
[6] 陆国胜,龚烈航,王强,等.前混合磨料水射流磨料颗粒加速机理分析[J].解放军理工大学(自然科学版),2006,7(3):275-280.
LU Guosheng,GONG Liehang,WANG Qiang,et al.Research on acceleration mechanism of abrasive in pre-mixed abrasive water jet[J].PLA University of Science and Technology(Natural Science Edition),2006,7(3):275-280.
[7] 左伟芹,王晓川,郝富昌,等.基于迭代算法的磨料颗粒加速机制研究[J].中国石油大学学报(自然科学版),2016,40(4):104-109.
ZUO Weiqin,WANG Xiaochuan,HAO Fuchang,et al.Research on acceleration mechanism of abrasive in pre-mixed abrasive water-jet based on iterative algorithm[J].Journal of China University of Petroleum(Edition of Natural Science),2016,40(4):104-109.
[8] 王瑞和,倪红坚.高压水射流破岩机理研究[J].中国石油大学学报(自然科学版),2002,26(4):118-122.
WANG Ruihe,NI Hongjian.Study on rock breaking mechanism under high pressure jet[J].Journal of China University of Petroleum(Edition of Natural Science),2002,26(4):118-122.
[9] 廖华林,李根生,易灿.水射流作用下岩石破碎理论研究进展[J].金属矿山,2005(7):1-5.
LIAO Hualin,LI Gensheng,YI Can.Advance in study on theory of rock breaking under water jet impact[J].Journal of Metal Mine,2005(7):1-5.
[10] 汤积仁,卢义玉,孙惠娟,等.基于CT方法的磨料射流冲蚀损伤岩石特性研究[J].岩石力学与工程学报,2016,35(2):297-302.
TANG Jiren,LU Yiyu,SUN Huijuan,et al.Study of erosion and damage characteristics of rock by abrasive water jet using CT[J].Chinese Journal of Rock Mechanics and Engineering,2016,35(2):297-302.
[11] 李宝玉,郭楚文,林柏泉.用于安全切割的磨料水射流喷嘴设计理论和方法[J].煤炭学报,2005,30(2):251-254.
LI Baoyu,GUO Chuwen,LIN Baiquan.Theory and method of designing abrasive water-jet nozzle in safety cutting[J].Journal of China Coal Society,2005,30(2):251-254.
[12] 林晓东,卢义玉,汤积仁,等.前混合式磨料水射流磨料粒子加速过程数值模拟[J].振动与冲击,2015,34(16):19-24.
LIN Xiaodong,LU Yiyu,TANG Jiren,et al.Numerical simulation of abrasive particles acceleration process in pre-mixed abrasive water jet[J].Journal of Vibration and Shock,2015,34(16):19-24.
[13] 王晓川,卢义玉,康勇,等.磨料水射流切割煤岩体实验研究[J].中国矿业大学学报,2011,40(2):246-251.
WANG Xiaochuan,Lu Yiyu,KANG Yong,et al.Experimental study of abrasive water jet cutting coal rock mass[J].Journal of China University of Mining and Technology,2011,40(2):246-251.
[14] 董星.前混合式磨料水射流磨料颗粒运动的理论分析[J].黑龙江科技大学学报,2001,11(3):4-6.
DONG Xing.Theoretical analysis of particle motion of abrasive water jet abrasive with pre mixed abrasive water[J].Journal of Heilongjiang University of Science and Technology,2001,11(3):4-6.
[15] 董志勇.射流力学[M].北京:科学出版社,2005.
[16] 康勇.超音速低温旋流分离器拉瓦尔喷管流场数值分析[J].西北大学学报(自然科学版),2011,41(4):593-597.
KANG Yong.The numerical analysis on laval-nozzle flow field of the supersonic low-temperature swirling separator[J].Journal of Northwest University(Natural Science Edition),2011,41(4):593-597.
[17] 潘锦珊.气体动力学基础(修订版)[M].北京:国防工业出版社,1989:56-60.
[18] 高红,郑颖人,冯夏庭.岩土材料能量屈服准则研究[J].岩石力学与工程学报,2007,26(12):2437-2443.
GAO Hong,ZHENG Yingren,FENG Xiating.Study on energy yield criterion of geomaterials[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(12):2437-2443.
[19] 谢和平,鞠杨,黎立云,等.岩体变形破坏过程的能量机制[J].岩石力学与工程学报,2008,27(9):1729-1740.
XIE Heping,JU Yang,LI Liyun,et al.Energy mechanism of de-formation and failure of rock masses[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(9):1729-1740.
[20] 周辉,李震,杨艳霜,等.岩石统一能量屈服准则[J].岩石力学与工程学报,2013,32(11):2170-2184.
ZHOU Hui,LI Zhen,YANG Yanshuang,et al.Unified energy yield criterion of rock[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(11):2170-2184.
[21] HUTCHINGS I M.Energy absorbed by elastic waves during plastic impact[J].Journal of Physics D Applied Physics,1979,12(11):1819.