煤层气主要储集在煤层裂隙中，煤层中裂隙的存在使煤储层表现为方位各向异性和双相介质特征[1-3]，这些特征为利用地震技术预测煤层气奠定了基础。在地震数据采集过程中，由于地表环境复杂性和仪器性能限制，采集到的地震数据中常常出现坏道、空白道，如果不对这些缺失的地震数据进行处理，势必会影响后续的数据处理，进而影响到对煤层中裂隙走向的判断，不利于揭示复杂构造带下的地层结构特征，因此有必要采取措施对缺失的地震数据进行恢复重建。

近年来，压缩感知理论在信号处理领域得到快速发展，它能以远低于传统Nyquist采样率实现不完整地震数据重建。该理论表明，可以通过设计一个与稀疏变换基不相关的测量矩阵对信号进行观测，得到少量的观测数据，利用稀疏促进重建算法就可以重建出满足一定精度要求的信号[4]。由于大部分信号是不满足稀疏性要求的，因此在压缩感知框架下需要先将数据进行某种稀疏变换以达到稀疏性要求。常用的稀疏变换方法包括傅里叶变换、小波变换和Curvelet变换等。其中，Curvelet变换在地震数据稀疏表示方面具有较大优势，很多学者利用Curvelet变换结合压缩感知理论进行了缺失地震数据重建方法研究[5]。2004年CANDS等的研究中发现了在数据不满足Nyquist-Shannon采样定理时重构数据所需要的最小个数[6]，带动了稀疏促进算法方面的研究。DAUBECHIES等[7]在文中阐述了基于该理论的阈值迭代法，这种方法简单易用、计算复杂度低因而得到了广泛的研究;后来研究人员在阈值迭代法的基础上又进一步提出了新的阈值迭代法。如2008年HERRMAN等将CRSI(Curvelet Recovery by Sparsity-promoting Inversion，CRSI)方法[3]应用于不完整地震数据重建中，通过冷却阈值不断迭代得到了较好的重建结果，验证了CRSI方法在地震勘探领域的可行性，但是该方法需要进行多次的迭代，收敛速度慢;随后BREGMAN对CRSI方法进行了改进[8-9]，提出了快速迭代法，即在每次迭代阈值处理之前先“吸收”阈值之前的所有恢复量，仅仅需要若干次迭代就能恢复出有效的信号，加快了算法的收敛速度，但该方法在迭代后期，阈值逐渐减少的过程中，将小于阈值的非有效信息也吸收到了重建结果中，从而导致重建结果变差。

针对传统算法中存在的收敛速度与重建结果不能同时兼顾的问题，笔者提出了一种基于改进Curvelet变换的地震数据重建方法，该方法将指数阈值引入到CRSI方法中，既保证了地震数据重建结果具有高信噪比的优点，同时提高了重建算法的收敛速度。最后利用合成地震数据进行数值实验，验证本文所提方法的有效性。

1 相关理论基础

1.1 压缩感知理论

压缩感知理论体系中，主要包括3个方面:信号的稀疏表示、观测矩阵的设计以及数据重建算法的选择。其本身所关注的问题可以表述为通过对信号的高度不完备测量，从较少的测量数据中精确地重建原始信号[4,10]。具体过程为:设原始稀疏信号 f=(f1,f2,…,fN)∈RN为N维离散实值信号且稀疏度为k(k≤N)，然后通过一组稀疏变换基Ψ={ψ1,ψ2,…,ψN}∈RM×N对其进行稀疏变换，可表示为

f=Ψα

(1)

其中，α为稀疏系数，不完整地震数据的重建问题可以通过模型y=Φf=ΦΨα=Θα来表示，其中，N维向量f表示向量化后的原始地震数据;Φ是一个M×N的采样矩阵，采集点处的元素值为1，未采集点处元素值为0;N维向量y表示向量化后的不完整地震数据;Θ是一个M×N矩阵，称为测量矩阵。

在压缩感知理论中，测量过程是非自适应性的，即Φ无需根据信号f变化而变化，其服从“有限等距性质(Restricted Isometry Property，RIP)”[11]，即对任意k-稀疏信号α及常数βk∈(0,1)，Θ满足≤‖Θα≤的关系。RIP为不完整地震数据重建提供了理论保证。但是RIP为一个组合复杂度问题，很难计算。BARANIUK给出了RIP的等价条件[12]:如果测量矩阵与稀疏变换基不相关，则感知矩阵在高概率的条件下满足RIP。数据的重建过程可重新表述为

min‖α‖0,s.t.y=ΦΨα

(2)

从式(2)可知，这是一个典型的非凸优化问题，不易求解，通常通过不断求逼近解来解决该类问题[13]。常采用的方法有最小l1范数法、匹配追踪法和迭代阈值法等[7,14-15]。

1.2 Curvelet变换

Curvelet变换现在已经发展到了第2代，第1代变换是在Ridgelet变换的基础上提出的[16]，实现起来比较复杂，需要经过子带分解、平滑分块、正规化和脊波分析等一系列步骤，并且由于其采用的是金字塔式的分解结构，数据冗余量很大。为了克服第1代变换的缺陷，CANDS和DONOHO提出了基于第2代Curvelet变换理论的快速离散Curvelet变换方法[6]。第2代Curvelet变化理论是在连续域内进行定义的，与第1代相比，该理论简单易用，数据冗余量大大减少，因此具有更广泛的应用前景。笔者采用的是第2代Curvelet变换作为稀疏变换基，第2代Curvelet变换公式为

c(j,l,k)=〈f,

(3)

其中，j表示尺度;l表示角度;k表示位置;函数f∈L2(R2)是目标函数;φj,l,k是Curvelet函数，其在频率域是一种楔形函数;c(j,l,k)是Curvelet系数由目标函数与基函数φ做内积得到的。其中基函数频率表达式可以表示为

φj,l,k(x)=2πxj,l(ω)uj,k(Rj,l(ω))

(4)

式中，ω=(ω1,ω2)T， k=(k1,k2)T，k1,k2∈z，ω为频率变量。

在式(4)的基础上，得到式(3)在频率域上的表示，有

c(j,l,k)ωω=

ω)Uj(Rθlωω

(5)

其中，ω)是f(ω)的频率域表示;ω)是φj,l,k(ω)的傅里叶变换;Uj(Rθlω)是频率域极坐标下与尺度，角度有关的扇形窗函数。在频域内的表示可以用楔形图[6]表示，如图1所示。

图1中由内向外的每一个同心圆代表一个尺度，尺度控制Curvelet窗函数的大小，角度控制Curvelet窗函数的旋转，位置控制Curvelet窗函数的平移，Curvelet窗函数覆盖整个频率域。完整的Curvelet变换是由无方向的粗糙尺度和带方向的精细尺度共同构成的。

定义粗尺度上的低通窗口W0，并满足

(6)

定义粗尺度下的Curvelet基为

(7)

其中，j0为最内尺度参数;k为位置参数。由式(6)和(7)可知，Curvelet变换的粗糙尺度是不具有方向性的，而精细尺度是由带方向的曲波(Ψj,l,k)j>j0,l,k构成的。基于这些特性，只要地震数据可以表示成二次可微的曲线奇异函数，Curvelet就可以探测到地震波同相轴并且可以稀疏表达此类有效信号。

2 地震数据重建算法设计

2.1 重建模型构建

缺失地震数据的重建，需要首先求解出最优稀系数α，然后通过设计稀疏促进算法[17-18]，求解出完整的地震数据。稀疏促进问题可以表示为

pε:

(8)

式(8)约束优化问题pε可转化成下面的非约束优化问题:

pλ: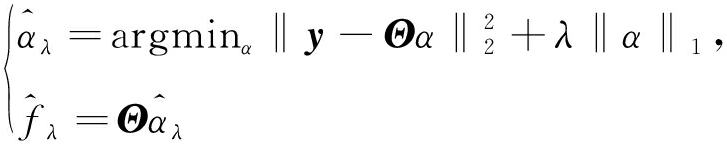

(9)

其中，拉格朗日因子λ决定了l1项和l2之间的权重。pλ的求解过程就是通过不断调解λ直到满足:

λz=supλ{λ:‖y-Θ2≤ε}

(10)

在上述问题的求解过程中，通常是先选取较大的λ值求取稀疏逼近解，再增加l2项的相对权重，通过不断的迭代得到真实的逼近解。根据理论模型，研究者在Landweber下降法[19]基础上发展的冷却阈值迭代方法[5,20]，以及改良的Bregman迭代阈值法[8-9]等。

笔者在重建地震数据时使用的是一种冷却阈值迭代法，即CRSI方法，该方法最终的重建结果具有高信噪比的优点，但是收敛速度要慢于Bregman迭代阈值方法。Bregman方法仅仅是加快了收敛的速度，但是最后重建出的地震数据信噪比要低于CRSI方法。为了解决CRSI收敛速度慢的缺点，笔者引入指数阈值法来加快收敛速度。

2.2 阈值函数

根据压缩感知理论可知，数据的采样重建问题可以转化为简单的降噪问题[21]，而降噪的问题在于阈值的选取，不同的阈值参数λi将会影响数据的重建结果，合适的阈值参数将会在保证CRSI方法收敛速度变快的同时保证数据的高信噪比。在CRSI算法迭代过程中，阈值参数一般的变化趋势为从大到小，大部分的Curvelet系数在前面的迭代过程中进行处理，剩下的则是能量较强的同相轴需要进行细微处理，由此可得出阈值参数λi满足:

‖Ψy‖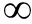=λ1>λ2>…>λi>ε

(11)

其中，ε为接近0的值，从式(11)中可知，随迭代次数的增加，阈值参数开始不断接近ε。Gao等根据(0≤x≤1)衰减规律设计了指数型阈值参数[22]，并且在其论文中基于傅里叶变换POCS算法下对指数型阈值进行了验证，验证结果表明指数型阈值参数重建效果要优于线性阈值参数重建的结果。根据Gao等在其论文中的研究[22]，该阈值参数的表达式为

(12)

式中，λmax为阈值参数中的最大值;N为算法迭代次数;i为当前迭代次数。

综上所述，指数型阈值参数的衰减规律，适合处理Curvelet系数，尤其是在后期处理能量较强的同相轴更加的细微，同时提高了迭代收敛的速度。

2.3 地震数据重建算法

综合考虑了传统重建方法的优缺点后，笔者结合上述的指数阈值，提出了一种改进Curvelet变换的地震数据重建方法，基本思路是:对于不完整的地震数据f，设计采样矩阵Φ，初始化迭代次数N，阈值参数λ，以及相关参数u和v。将要重建的地震数据在Curvelet域不断的进行迭代修正，将最终修正后的Curvelet域恢复结果vi+1进行Curvelet逆变换，得到重建后的信号其重建流程图如图2所示。

由图2可知，本文所使用的方法是在原始CRSI的方法上进行改进，利用了CRSI方法重建后的结果具有高信噪比的优点，同时引入了指数阈值模型，来解决CRSI收敛速度慢的缺陷。具体算法:

输入:不完整的地震数据f，设计的采样矩阵Φ，迭代次数N;

输出:输出为重建后信号，即Ψvi+1。

Step1:输入不完整的地震数据f，初始化阈值λ0，迭代次数N，以及初始化进行记录Curvelet域恢复结果的临时变量u和v;

Step2:使用本文指数阈值更新阈值参数，得到第i次迭代的阈值，使得λ=λi;

Step3:使用第i次得到的Curvelet域恢复结果vi，加上第i次迭代的恢复量,得到第i+1次未经修正的Curvelet域恢复结果，其表达式为:ui+1=vi+ΨTΦT(f-ΦΨvi)，其中ΨT是Curvelet变换,Ψ是Curvelet逆变换;

Step4:使用软阈值函数Tλ(ui+1)=:sgn(x)·max(0,|ui+1|-λ)更新未经修正的Curvelet域恢复结果ui+1，得到第i+1次的Curvelet域恢复结果vi+1;

Step5:判断是否满足迭代结束条件，即i+1为否大于设定的迭代次数N，如果满足迭代终止条件，使用Curvelet逆变换Ψ，将满足条件的第i+1次的Curvelet域恢复结果vi+1，转换为重建后的地震数据,不满足则跳转Step2。

3 实验及性能分析

为了验证算法的可行性及有效性，对地震数据进行数值实验。重建效果的衡量指标为峰值信噪比(PSNR)和信噪比(SNR)，即

(13)

(14)

式中，f0为原始地震数据;f为重建后地震数据;MSE为原始地震数据与重建数据的均方根误差[23]。

笔者采用有限差分方法模拟了一个简单的4层水平均匀介质，采用点震源，中间放炮两端接收，使用了35 Hz的Ricker子波进行模拟，时间采样间隔为1 ms，道距为2 m，总共500道地震记录，图3(a)为4层水平均匀介质的模型，采样点500，第1层介质模型的速度为2 000 m/s，第2层介质模型的速度为3 000 m/s，第3层介质模型的速度为4 000 m/s，第4层介质模型的速度为5 000 m/s，密度为常数，震源设置在第1层介质中。图3(b)为合成单炮地震记录，图3(c)为相应的f-k谱图。由图3(c)中可知波谱特征明显，能量较强，频率分布范围为10～60 Hz。图4分别为随机缺失30%的地震记录及使用CRSI方法重建结果、使用Bregman方法进行重建的结果和使用本文方法重建的结果，同时使用f-k谱图进行分析，图5为随机缺失50%的地震数据以及各算法的恢复对比结果。由图4(e)和5(e)中看出f-k谱图中有很多随机噪声干扰，这是由于地震道的随机缺失所引起的。利用本文所提及的方法，可以有效压制噪声的干扰。

由表1以及图4和5的重建图的数据分析可得，与其他方法重建效果相比，本文所提方法的重建效果更好，同相轴更加连续、光滑，在消除噪声的同时获取精确的重建结果。本文方法的恢复效果优于CRSI方法与Bregman方法，PSNR总体被提高了1到1.5 dB。验证了本文重建方法的可行性、有效性。

为了进一步的验证本文方法的正确性，选取Marmousi速度模型模拟了地震数据用于分析。Marmousi模型,如图6(a)所示，采用中间放炮两边接收模型进行正演，在中心点放置单炮，接收道为800，道间隔为10 m，采样间隔为10 m，采样时间为9.6 s，采样间隔为16 ms，采用10 Hz的Ricker子波作为震源，使用产生的单炮模拟数据进行数值实验，如图6(b)所示。随后随机缺失30%，50%的地震道，图7为随机缺失30%的地震记录、使用CRSI方法、使用Bregman方法和使用本文方法重建的结果。图8对应的是随机缺失50%的地震道数据以及各算法的重建结果。

由图6～8可知，本文所提的方法在缺失30%和50%地震道的情况下都可以重建出结果，各缺失道均得到了很好的恢复，地震同相轴光滑、连续。由表1可知，本文的重建结果的PSNR要优于其他两种方法，总体被提高了2～3 dB。

图9为在4层水平均匀介质模型的合成地震数据的基础上进行统计的，其中图9(a)中3条曲线分别代表Bregman方法、CRSI方法和本文方法在随机缺失30%的地震数据情况下，以不同的迭代次数进行重建后的地震数据的信噪比的情况。由图9(a)中的曲线可知，本文的方法在10次迭代就可以基本接近最好的信噪比，说明本文方法收敛速度较快;而Bregman方法在20次左右才开始收敛，并且信噪比要低于本文的方法;而传统的CRSI方法，在40次左右才开始收敛，收敛速度较慢。图9(b)以固定迭代40次为例，比较指数阈值与线性阈值的变化趋势，阈值的最大值设置为2，最小值设置为0.001;由阈值变化趋势可知，指数阈值可以快速下降，在下降到一定程度之后开始变缓，这对于Curvelet系数的细节部分有更好的处理，综上所述指数阈值更有利于Curvelet阈值处理。

4 结 语

本文所提出的方法框架综合了CRSI方法和指数阈值的优点，通过利用指数阈值的变化特性，使得CRSI方法在迭代的中后期更加细致处理待重建地震数据在Curvelet域的小系数，使得细节处理更加到位，本文方法在保持高信噪比的同时，加快了收敛速度。最后利用4层水平均匀介质层状模型合成的地震数据和Marmousi模型正演的地震数据分别进行数值实验，详细比较了本文方法、原有的CRSI方法和Bregman方法。实验结果验证了本文方法的准确性与有效性，表明本文的方法具有收敛快，信噪比高等特点。

参考文献(References) :

[1] 王绪本,陈进超,郭全仕,等.沁水盆地北部煤层气富集区CSAMT勘探试验研究[J].地球物理学报,2013,56(12):4310-4323.

WANG Xuben,CHEN Jinchao,GUO Quanshi,et al.Research of the CSAMT exploration mode and experiment for the coalbed enrichment region in the north Qinshui basin[J].Geophysics Journal,2013,56(12):4310-4323.

[2] WANG Jiachen,WU Renlun,ZHANG Peng.Characteristics and applications of gas desorption with excavation disturbances in coal mining[J].International Journal of Coal Science & Technology,2015,2(1):30-37.

[3] LIU Yu,ZHU Yanming.Comparison of pore characteristics in the coal and shale reservoirs of Taiyuan Formation,Qinshui Basin,China[J].International Journal of Coal Science & Technology,2016,3(3):330-338.

[4] DONOHO D L.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.

[5] HERRMANN F J,HENNENFENT G.Non-parametric seismic data recovery with curvelet frames[J].Geophysical Journal of the Royal Astronomical Society,2010,173(1):233-248.

[6] CANDS E J,DONOHO D L.New tight frames of curvelets and optimal representations of objects with piecewise C2 singularities[J].Communications on Pure & Applied Mathematics,2004,57(2):219-266.

[7] DAUBECHIES I,DEFRISE M,DE MOL C.An iterative thresholding algorithm for linear inverse problems with a sparsity constraint[J].Communications on Pure & Applied Mathematics,2003,57(11):1413-1457.

[8] MA J,PLONKA G.The curvelet transform[J].Signal Processing Magazine IEEE,2010,27(2):118-133.

[9] YIN W.Analysis and generalizations of the linearized bregman method[J].Siam Journal on Imaging Sciences,2010,3(4):856-877.

[10] CANDS E J,ROMBERG J,TAO T.Robust uncertainty principles:Exact signal reconstruction from highly incomplete frequency information[J].IEEE Transactions on Information Theory,2004,52(2):489-509.

[11] BARANIUK R.Compressive sensing[A].Information Sciences and Systems,2008[C].2008.

[12] CANDS E J.The restricted isometry property and its implications for compressed sensing[J].Comptes Rendus Mathematique,2008,346(9-10):589-592.

[13] 白兰淑,刘伊克,卢回忆,等.基于压缩感知的Curvelet域联合迭代地震数据重建[J].地球物理学报,2014,57(9):2937-2945.

BAI Lanshu,LIU Yinke,LU Huiyi,et al.Curvelet-domain joint iterative seismic data reconstruction based on compressed sensing[J].Chinese Journal of Geophysics,2014,57(9):2937-2945.

[14] CHEN S S,DONOHO D L,SAUNDERS M A.Atomic decomposition by basis Pursuit[J].SIAM Rev.,2001,43(1):129-159.

[15] MALLAT S G,ZHANG Z.Matching pursuits with time-frequency dictionaries[J].IEEE Trans on Signal Processing,1993,41(12):3397-3415.

[16] 唐刚.基于压缩感知和稀疏表示的地震数据重建与去噪[D].北京:清华大学,2010:42.

TANG Gang.Seismic data reconstruction and denoising based on compressed sensing and sparse representation[D].Beijing:Tsinghua University,2010:42.

[17] HERRMANN F J,WANG D,HENNENFENT G.Multiple prediction from incomplete data with the focused curvelet transform[J].Society of Exploration Geophysicists,2007(1):2505.

[18] BREGMAN L M.The relaxation method of finding the common point of convex sets and its application to the solution of problems in convex programming[J].Ussr Computational Mathematics & Mathematical Physics,1967,7(3):200-217.

[19] LANDWEBER L.An iteration formula for fredholm integral equations of the first kind[J].American Journal of Mathematics,1951,73(3):615-624.

[20] PATI Y C,REZAIIFAR R,KRISHNAPRASAD P S.Orthogonal matching pursuit:Recursive function approximation with applications to wavelet decomposition[A].Signals,Systems and Computers,1993,Conference Record of The Twenty-Seventh Asilomar Conference on[C].IEEE,2002:40-44.

[21] 张华,陈小宏.基于jitter采样和曲波变换的三维地震数据重建[J].地球物理学报,2013,56(5):1637-1649.

ZHANG Hua,CHEN Xiaohong.Seismic data reconstruction based on jittered sampling and curvelet transform[J].Geophysics,2013,56(5):1637-1649.

[22] GAO J J,CHEN X H,LI J Y,et al.Irregular seismic data reconstruction based on exponential threshold model of POCS method[J].Applied Geophysics,2010,7(3):229-238.

[23] 周亚同,王丽莉,蒲青山.压缩感知框架下基于K-奇异值分解字典学习的地震数据重建[J].石油地球物理勘探,2014,49(4):652-660.

ZHOU Yatong,WANG Lili,PU Qingshan.Based on K-singular value decomposition dictionary learning based seismic data reconstruction[J].Petroleum Geophysical Exploration,2014,49(4):652-660.