 移动阅读
移动阅读汤伏全,董龙凯,王宗良,黄景偲
(西安科技大学 测绘科学与技术学院,陕西 西安 710054)
摘 要:利用合成孔径雷达干涉测量(InSAR)技术进行煤矿开采沉陷监测时,所获得的雷达视线方向(LOS)位移是地表点垂直向、南北向、东西向三维位移的矢量叠加。将LOS向位移分解为地表下沉及沿工作面走向和倾向水平位移,是研究开采沉陷规律和获取地表移动参数的基础。目前,基于 InSAR LOS位移反演开采沉陷三维位移的主要方法有:利用不同轨道卫星的三幅SAR影像建立LOS位移方程组来求解三维位移分量;根据开采沉陷预计模型将地表水平位移视为下沉的关联函数,由单幅SAR影像来解算下沉及水平位移;或者直接忽略水平位移的影响,将 LOS向位移投影为下沉分量。本文在分析上述方法局限性的基础上,根据近水平煤层开采地表下沉和水平位移关于移动盆地主断面对称的基本特征,建立地表移动盆地对称点上多期InSAR LOS向叠加位移的几何方程组,并对该方程组进行叠加和差分处理,导出LOS向位移反演开采沉陷三维位移的函数模型。在工作面推进过程中,由于地表移动具有滞后性,使得动态沉陷盆地中心偏向开切眼一侧,本文依据移动盆地中央地表下沉达到最大且水平位移趋近为零的特征,基于相邻像元LOS向位移进行叠加和差分,自动搜索出地表移动盆地的动态中心位置,从而实现工作面推进过程中地表动态三维位移的分解。基于Matlab平台对上述三维位移反演模型进行了算法实现,并利用多期InSAR 实测数据进行了模型验证,其下沉和水平位移反演结果与实测资料较为一致,明显优于忽略水平位移而直接分解地表下沉的方法。上述模型能够用于近水平煤层开采地表移动稳定后和动态移动过程中InSAR监测的三维位移分解,具有较好的普适性。
关键词:InSAR;形变监测;开采沉陷;对称性;三维位移反演
中图分类号:TD173
文献标志码:A
文章编号:0253-9993(2019)01-0210-11
汤伏全,董龙凯,王宗良,等.基于沉陷对称特征的近水平煤层开采InSAR三维位移反演模型[J].煤炭学报,2019,44(1):210-220.doi:10.13225/j.cnki.jccs.2018.0698
TANG Fuquan,DONG Longkai,WANG Zongliang,et al.A 3-D inversion model for InSAR detected displacements based on ground subsidence symmetry induced by horizontal coal mining[J].Journal of China Coal Society,2019,44(1):210-220.doi:10.13225/j.cnki.jccs.2018.0698
收稿日期:2018![]() 05
05![]() 24
24
修回日期:2018![]() 11
11![]() 19
19
责任编辑:常 琛
基金项目:国家自然科学基金资助项目(51674195);陕西省自然科学基金资助项目(2016JM5048)
作者简介:汤伏全(1966—),男,湖南湘潭人,教授,博士。E-mail:2504557922@qq.com
通讯作者:董龙凯(1995—),男,山西运城人,硕士研究生。E-mail:731648282@qq.com
TANG Fuquan,DONG Longkai,WANG Zongliang,HUANG Jingcai
(College of Geomatics,Xi’an University of Science and Technology,Xi’an 710054,China)
Abstract:When using synthetic aperture radar interferometry (InSAR) technology to monitor coal mining sub-sidence,the displacement of radar line of sight (LOS) obtained is the vector superposition of three-dimensional displacement of surface points in vertical,north-south,east-west directions.Decomposing the LOS displacement into the surface subsidence and the horizontal displacement along the strike and incline of the working face is the basis for studying the law of mining subsidence and obtaining the parameters of surface movement.At present,the main method of inverting mining subsidence three-dimensional displacement based on InSAR LOS displacement is using three SAR images of different orbiting satellites to establish LOS displacement equations for solving three-dimensional displacement components.According to the prediction model of mining subsidence,the horizontal displacement of surface is regarded as the correlation function of subsidence,and the subsidence and horizontal displacement are calculated from a single SAR image.The LOS displacement is projected into the sub-sidence component through directly ignoring the influence of horizontal displacement.Based on the analysis of the limitations of the above methods and the basic characteristics of the surface subsidence and horizontal displacement of the near-horizontal coal seam mining on the main section of the mobile basin,the geometric equations of the multi-period InSAR LOS superposition displacement on the symmetry point of the surface moving basin was established.The equations are superimposed and differentially processed to derive the function model for LOS displacement inversion three-dimensional mining displacement.During the advancement of the working surface,because of the hysteresis of the surface movement,the center of the dynamic subsidence basin deviates to the side of the open hole.According to the characteristics of the central surface subsidence of the moving basin reaching the maximum and the horizontal displacement approaching zero,the dynamic center position of the surface moving basin is automatically searched based on the superposition and difference of the LOS displacement of adjacent pixels.Thereby,the decomposition of the dynamic three-dimensional displacement of the surface during the advancement of the working surface is realized.In this paper,the above three-dimensional displacement inversion model is implemented based on the platform of Matlab,and the model was validated by multi-phase InSAR data.The inversion results of subsidence and horizontal displacement are in a good agreement with the measured data,which is obviously superior to the method of directly decomposing surface subsidence without considering horizontal displacement.This model can be used to decompose the three-dimensional displacement monitored by InSAR in the process of surface movement stability and dynamic movement in near-horizontal coal seam mining.
Key words:InSAR;deformation monitoring;mining subsidence;symmetry;three-dimensional displacements inversion
InSAR技术已成为煤矿开采沉陷变形监测的重要手段[1]。煤矿开采沉陷引起的地表三维位移包括垂直下沉、沿地表移动盆地走向主断面及倾向主断面的水平位移(或转换为南北向及东西向水平位移),而InSAR影像的干涉处理多采用一种SAR数据,如升轨数据或降轨数据,主要获得地表点在雷达视线方向(LOS)的一维位移量,这种InSAR LOS向位移是煤矿地表点下沉和水平向位移沿雷达视线方向投影后的叠加结果[2-4]。其中,下沉方向始终垂直向下,水平位移方向指向采空区中央,移动盆地内地表点的移动方向随位置而变化,因而在InSAR监测结果中通过单个的LOS 向一维位移,并不能直接分解出地表点在垂直与水平方向上的三维位移值。为此,本文根据InSAR LOS向位移分解的几何模型及近水平煤层开采地表移动的基本特征[5],提出一种基于开采沉陷对称原理将InSAR LOS向位移分解地表三维位移的新方法。
地表点沿雷达视线方向的位移(LOS向位移)由该点在东西向、南北向和垂直向三维位移在视线方向上的投影叠加而成,它们之间的几何关系如图1所示[6]。
图1中θ为卫星入射方位角;αh为卫星飞行方向与北方向的夹角(顺时针方向为正)[7]。由图1的空间几何关系可得地表点沿雷达视线方向的(LOS)位移dLOS与三维位移的关系式
dLOS=Wcos θ-sin θ[UNcos(αh-
3π/2)+UEsin(αh-3π/2)](1)
式中,W,UN,UE分别是地面点在垂直、南北、东西3个方向上的位移。LOS位移因地表点真实的三维位移引起并由InSAR处理得到,其方向指向卫星为正[7]。
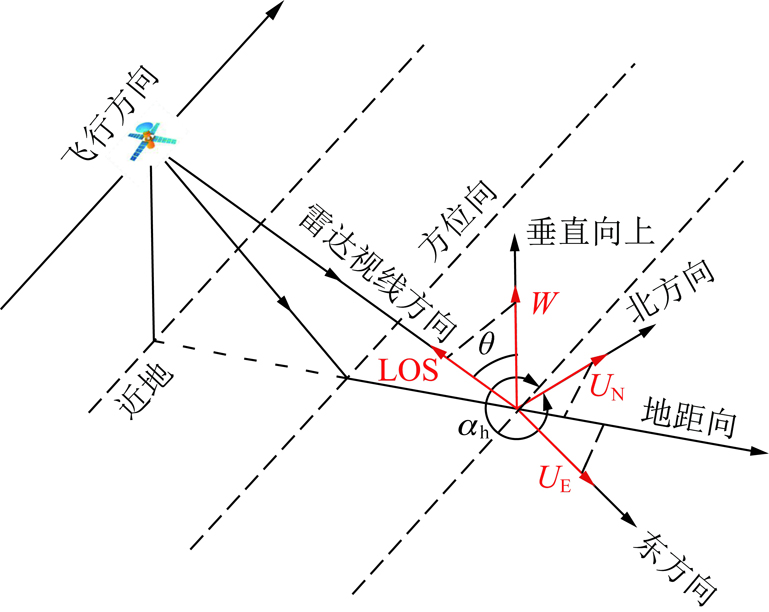
图1 LOS向位移与地面点三维位移的几何关系
Fig.1 Geometric relationships between LOS displacement and 3D displacement of ground points
由式(1)可知,当地表点的三维位移均为未知量时,由单个LOS 位移方程无法确定3个未知量。一些学者在利用InSAR位移数据提取矿区地表下沉值W时,直接将式(1)中的水平向位移分量UN,UE忽略不计,计算出下沉值W的近似公式:
(2)
由于地下开采引起的地表移动特征与常规的区域沉降不同,矿区移动盆地内的地表点均发生显著的水平位移量,一般相当于下沉量的0.3~0.5倍,尤其在移动盆地边缘地带,其水平位移量甚至会大于下沉量。这种将LOS位移简单地换算成垂直下沉的方法,不仅无法获得对开采沉陷有重要影响的水平向位移,而且所得到的下沉量及其分布可能与实际情况相差甚远。
一些文献利用3幅具有显著不同几何形状成像的SAR影像,分别提取3个雷达视线方向的一维位移,通过3个不同的LOS位移观测方程联合解算未知的三维位移量,即
dLOS1=Wcos θ1-sin θ1[UNcos(αh1-3π/2)+
UEsin(αh1-3π/2)]
dLOS2=Wcosθ2-sinθ2[UNcos(αh2-3π/2)+
UEsin(αh2-3π/2)]
dLOS3=Wcosθ3-sinθ3[UNcos(αh3-3π/2)+
UEsin(αh3-3π/2)](3)
式中,θi为第i组同步卫星入射方位角;αhi为第i组卫星飞行方向与北方向的夹角,i=1,2,3,分别是地面点在垂直、南北、东西3个方向上的位移。由于该方法需要至少3个不同几何形状成像的干涉像对,利用不同轨道参数处理得到的三组LOS位移值之间相互独立,它们本身存在较大的系统性误差。因此,利用式(3)解算出的地表点三维位移量不可避免地存在显著误差。
近年来,有学者依据现有的开采沉陷概率积分法预计模型,利用地表移动稳定后的下沉与水平位移之间存在的概率积分函数关系,将地表点水平位移变量表达为下沉变量的函数式,实现一维LOS向位移的反演[9]。根据概率积分法模型,开采引起的地表水平位移与垂直下沉梯度(即地表倾斜值)成正比,其数学关系如式(4)所示
UN=BΔWN
UE=BΔWE(4)
式中,ΔWN,ΔWE分别为下沉W沿东西、南北向的下沉梯度(即倾斜值);B为概率积分法中描述水平移动与下沉关系的参数,由地质采矿条件或经验值确定[2]。将约束条件方程(4)与式(1)联合求解可得三维位移值。上述模型曾在国际知名期刊Journal of Geodesy上发表[2],为矿区InSAR三维形变场的求解提供了一种新方法。
上述模型假定开采沉陷中地表任意点的下沉变化和水平向位移分量之间均存在相同的(函数)比例关系,因此地表三维位移量中只有下沉量为未知变量,水平位移则视为下沉的关联变量[10]。但大量的地表移动实测资料表明,地表移动盆地中下沉与水平位移之间的关系很复杂,且难以用概率积分法函数模型来描述。因此,这种反演方法基于下沉和水平位移之间存在确定的函数关系,因而存在较大的局限性。同时,在开采过程中的地表动态变形中,垂直位移和水平位移的动态分布特征十分复杂,现有的开采沉陷理论尚未建立动态垂直位移和水平位移的函数模型。
根据现有的开采沉陷理论,在常规的单一长壁工作面近水平煤层开采条件下,由于煤层倾角接近为零,上覆岩层和地表的几何特征与物理性质均表现为各向同性,开采引起的覆岩与地表沉陷盆地则呈现对称分布特征,其对称轴为过采空区中央且平行(或垂直)于工作面推进方向的走向主断面和倾向主断面,地表移动盆地内任意点的下沉和水平位移均关于走向主断面和倾向主断面呈对称分布[11-13]。因此,在煤矿布设地表移动观测站时,常常利用上述开采沉陷的对称性,仅在工作面开切眼或终采线一侧设置半条观测线,利用所得到的半个移动盆地主断面上的观测值,来描述整个地表移动盆地的特征[14]。
根据水平煤层开采沉陷的基本规律,在不同开采充分程度下地表主断面上的下沉与水平位移分布如图2所示。图2表明,无论在非充分开采和超充分开采条件下,地表下沉和水平位移均以盆地中心o(采空区中心正上方最大下沉点)为对称分布[5]。表移动盆地内任意点的水平位移矢量分布如图3所示,所有点的水平位移方向均指向盆地中心o。其中,走向主断面Z1Z2和倾向主断面Q1Q2相交于o点,将地表移动盆地划分为I,II,III,IV四个区域,对称区I和III内任意两个对称点P1和P3的下沉量相等,水平位移则大小相等而方向相反,对称区II和IV内的两个对称点P2和P4也是如此。根据这一特征可以建立地表任意2个对称点上的LOS向位移与三维形变之间的函数模型,并进行叠加和差分处理,从而解算出三维形变分量。
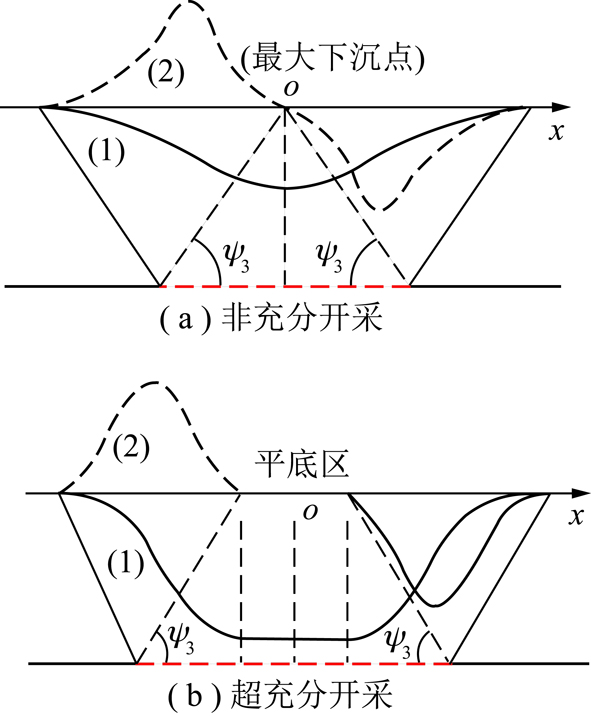
图2 近水平煤层开采地表移动主断面上的下沉与水平位移特征曲线
Fig.2 Surface movement curve of main section of near horizontal seam mining
如图3所示,对于近水平煤层开采地表移动盆地的对称区I和III中任意一组对称点P1,P3,两者的LOS向位移与地表水平位移的几何关系如图4所示。P1和P3水平位移方向与北方向的夹角分别为ω1,ω3,两者相差180°。
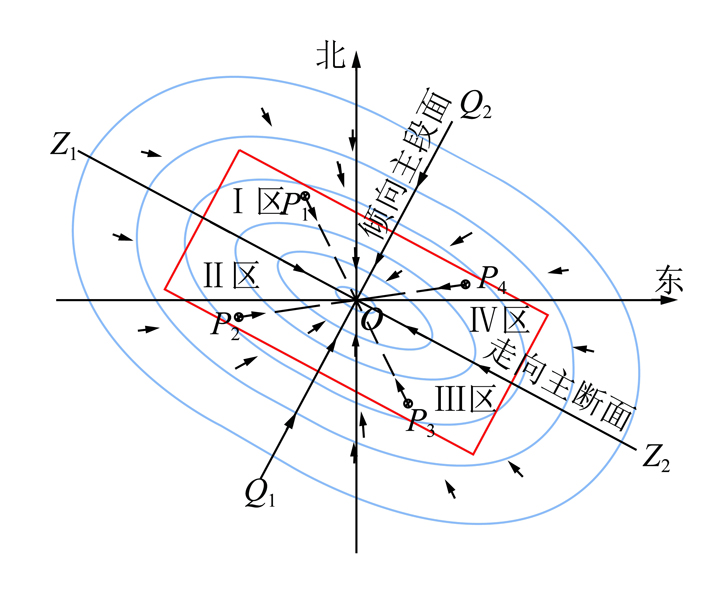
图3 地表移动盆地对称区域的下沉和水平位移矢量图
Fig.3 Vector map of subsidence and horizontal displa-cement in the basin symmetry area ofsurface movement

图4 采空区地表移动平面示意
Fig.4 Sketch map of the surface movement of the goaf
图4中,地表移动对称点P1与P3的LOS位移dLOS1 ,dLOS3与垂直向、南北向、东西向位移的关系由式(1)可得:
dLOS1=cos θW1-sin θcos(αh-3π/2)UN1-
sin θsin(αh-3π/2)UE1
dLOS3=cos θW3-sin θcos(αh-3π/2)UN3-
sin θsin(αh-3π/2)UE3(5)
式(5)中,各符号的意义与式(1)相同。对称点P1和P3的水平位移的大小相等,设为SP,在南北、东西方向的投影UN1,UN3,UE1,UE3由式(6)确定:
UN1=Spcos ω1,UE1=Spsin ω1
UN3=Spcos ω3,UE3=Spsin ω3(6)
式中,ω1,ω3分别为P1,P3与移动盆地中心o点之连线与北方向的夹角,由于ω1与ω3相差180°,所以无论在南北方向还是东西方向上,对称点P1和P3的水平位移分量都是大小相等而方向相反,且其下沉量相等,则由式(6)可得:
UN3=-UN1
UE3=-UE1
W3=W1(7)
将式(6),(7)代入式(5)可得:
dLOS1=cos θW1-sin θcos(αh-3π/2)Spcos ω1-
sin θsin(αh-3π/2)Spsin ω1(8)
dLOS3=cos θW1+sin θcos(αh-3π/2)Spcos ω1+
sin θsin(αh-3π/2)Spsin ω1(9)
将式(8)与式(9)相加后可得到对称点P1,P3的下沉值为
(10)
将式(8)与式(9)相减后可得到对称点P1,P3的水平位移值:
Sp=(dLOS1-dLOS3)/{-2sin θ[(cos(αh-
3π/2)cos ω1+sin(αh-3π/2)sin ω1]}(11)
将式(11)代入式(6)可以得到对称点P1,P3在南北,东西方向的水平位移分量:
UN1=(dLOS1-dLOS3)cos ω1{-2sin θ[cos(αh-
3π/2)cos ω1+sin(αh-3π/2)sin ω1]}=-UN3(12)
UE1=(dLOS1-dLOS3)sin ω1{-2sin θ[cos(αh-
3π/2)cos ω1+sin(αh-3π/2)sin ω1]}=-UN3(13)
依据单个InSAR干涉对获取得LOS位移值,由式(10)~(13)可解算出矿区地表移动盆地内任意点的三维位移量。
地表开采沉陷是一个持续时间达1~2 a的动态过程,地表稳定后的三维位移值是多期监测的沉陷叠加的结果。在InSAR矿区形变监测中,目前常采用差分干涉处理方法获得不同时段的LOS位移,然后进行叠加得到最终的地表形变量。进行InSAR处理时要求两幅SAR影像之间的时间基线不能太长,以免引起影像的失相干。目前现有的SAR卫星影像的重复周期一般为15~45 d[13]。因此,矿区地表移动盆地内的三维位移是通过多景SAR进行数据处理后并叠加得到的,地表任意点的LOS位移,相当于将每个时间段内的LOS位移叠加进行矢量求和。如果将同一SAR卫星在不同时段的卫星入射方位角和飞行方向视为常量,则LOS位移的叠加计算公式如下:
∑LOS=cos θ∑wi-sin θcos(αh-3π/2)
∑uNi-sin θsin(αh-3π/2)∑uEi(14)
式中,i=1~n(n为总时段数)Wi,UNi,UEi为第i时段内地表点垂直下沉、水平南北向、水平东西向的三维位移增量。式(14)中右边第1项为地表点各时段下沉增量Wi之和在LOS向的投影值。由于下沉方向始终为垂直向下,则该项与式(1)中右边第1项Wcos θ完全相同。式(14)的后2项为地表点各时段的南北向、东西向水平位移矢量之和在LOS向的投影值。
在工作面推进过程中,地表移动盆地中央任意点P的水平位移经历着复杂变化,其位移轨迹如图5所示。当工作面由远处推进到位置1时,开采影响波及到地表点P,该点发生下沉伴随着指向工作面推进边界的水平位移,其方向与工作面推进方向相反;当工作推进过P点下方后,该点下沉速度达到最大值,而水平位移方向则发生逆转,与工作面推进方向相同[5]。当工作面远离P点后,回采工作面的影响逐渐减小,直至地表移动稳定。在常规地质采矿条件下,盆地中央地表点P在经历下沉和动态水平位移后,基本稳定在其初始位置的正下方,总的水平位移值趋于零。对于移动盆地的其它点,无论处于开切眼一侧还是终采线一侧,移动过程中始终保持方向不变[5],其大小由零增加至稳定后的水平位移分量UN,UE,式(14)实质上与式(1)相同。因此,利用多时段InSAR处理的LOS位移相叠加后,所得到的地表稳定后的移动变形仍可以按照式(10)~(13)的反演模型进行三维位移分解。
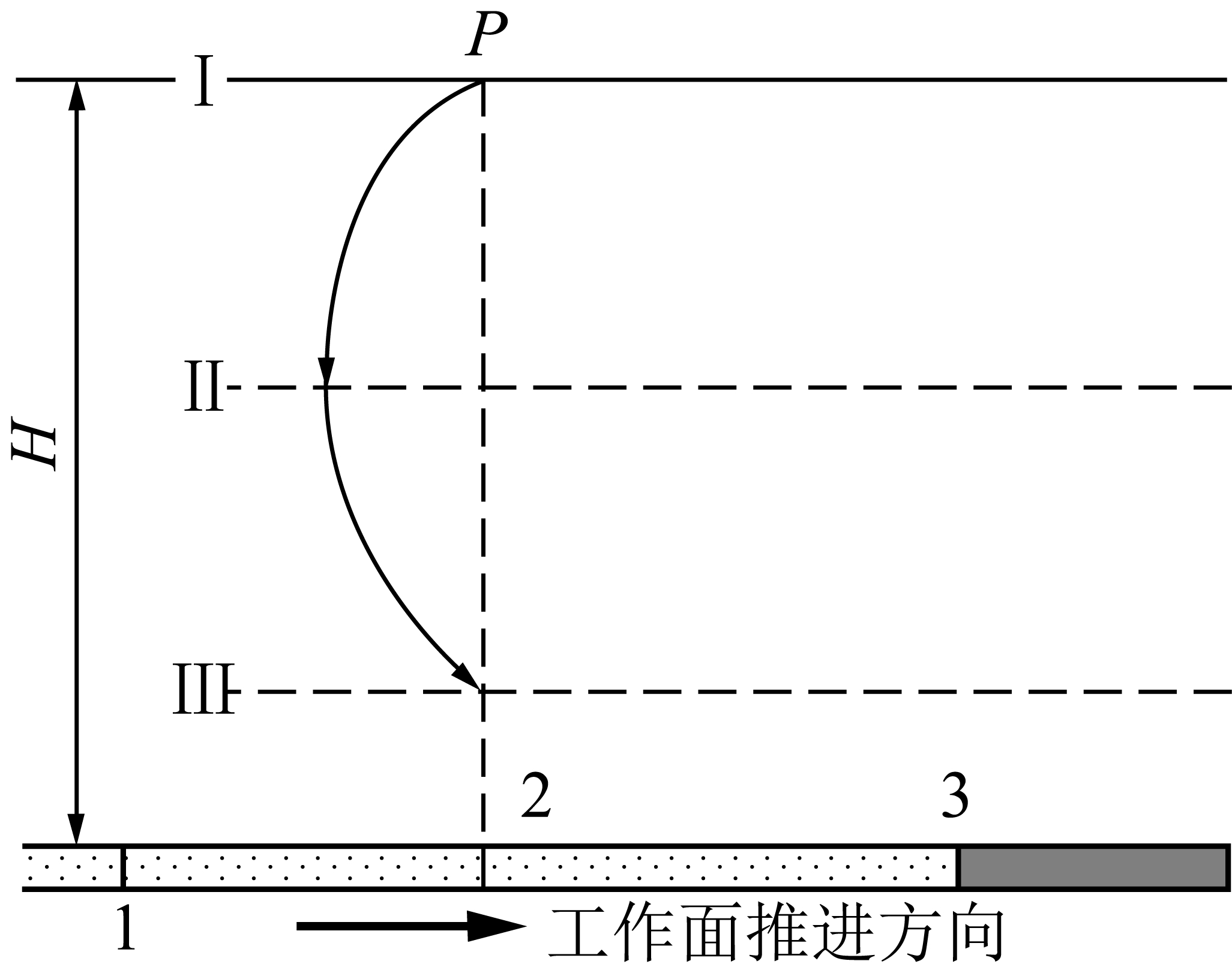
图5 盆地中中央地表点移动轨迹
Fig.5 Central surface movement trajectory in the basin
3.4.1 反演函数模型
在工作面推进过程中,地表动态沉陷盆地中开切眼一侧和推进边界一侧对应点的下沉和水平位移不再具备对称特征,上述关于稳定后的地表三维位移反演公式(10)~(13)不适用于动态三维位移反演。但是,由于近水平煤层的倾角接近为零,开采沉陷动态过程中的下沉和水平位移始终是关于走向主断面对称的。如图6所示,工作面推进过程中地表点的移动变形始终以走向主断面Z1Z2为对称轴线。对称点P1,P2的下沉值、沿走向方向的水平位移值均相等,沿倾向的水平位移值大小相等而方向相反。图6中P1点水平位移方向指向动态的地表移动盆地中心o′,该方向与北方向的夹角为ω1。由于地表沉陷具有一定的滞后性,上述动态的移动盆地中心o′并不位于动态的采空区中央位置,一般会偏向开切眼一侧。设工作面推进方向与北方向的夹角为α,则对称点P1,P2的水平位移方向与Z1Z2的夹角均为(ω1-α)。
设走向、倾向的水平位移分别为UT,UI,沿南北、东西向的水平位移分量UN,UE,则两位移分量之间的转换关系为:
UT=UEsin α+UNcos α
UI=UEcos α-UNsin α
UN=UIsin α+UTcos α
UE=UIcos α-UTsin α(15)
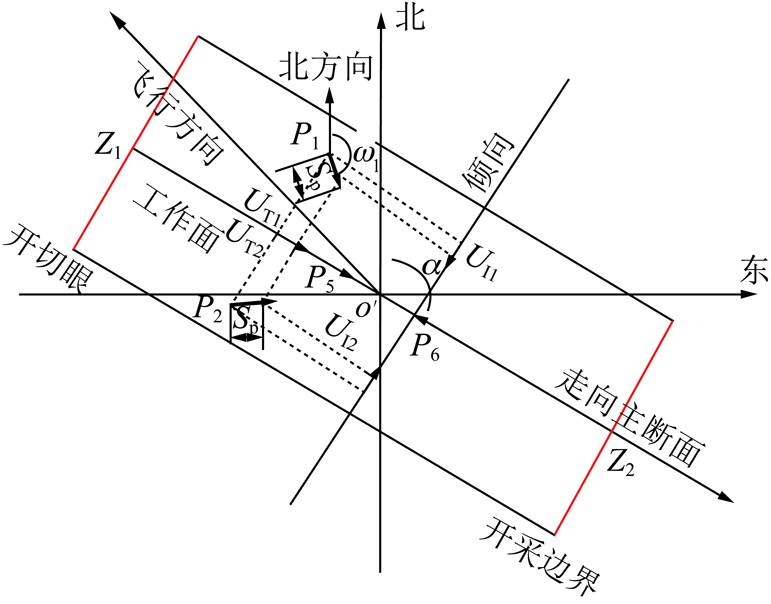
图6 开采过程中地表水平移动示意
Fig.6 Horizontal movement of the surface in the mining
式(15)中α为工作面推进方向与北方向的夹角,即工作面推进方向的方位角。设图6中对称点P1与P2的LOS位移为dLOS1,dLOS2,参照式(1)可得LOS位移与垂直向、南北向、东西向位移W1,W2,UN1,UN2,UE1,UE2的关系式:
dLOS1=cos θW1-sin θcos(αh-3π/2)
UN1-sin θsin(αh-3π/2)UE1
dLOS2=cos θW2-sin θcos(αh-3π/2)
UN2-sin θsin(αh-3π/2)UE2(16)
根据近水平煤层开采地表动态移动的对称特征,可得如下关系式:
UT1=UT2
UI1=-UI2
W1=W2(17)
将式(15),(17)代入式(16)并整理得:
dLOS1=cos θW1+(Bsin α+Ccos α)UI1+
(Bcos α-Csin α)UT1
dLOS2=cos θW1-(Bsin α+Ccos α)UI1+
(Bcos α-Csin α)UT1(18)
式中B=-sin θcos(αh-3/2π),C=-sin θ sin(αh-3/2π)。将式(18)中的两式进行求差得到倾向水平位移分量UI1,UI2为
(19)
由图6和式(19)可得走向水平位移分量UT1,UT2为
![]() (20)
(20)
式中,水平位移的方位角ω1为P1点与动态地表移动盆地中心o′之连线的方位角,将式(18)中的两个等式相加得到:
dLOS1+dLOS2=2cos θW1+2(Bcos α-Csin α)UT1(21)
将式(20)代入式(21)即的下沉分量W1,W2为
UN1=(dLOS1-dLOS2)[sin αtan(α-ω1)+
cos α]/2tan(α-ω1)(Bsin α+Ccos α)
UN2=(dLOS1-dLOS2)[-sin αtan(α-ω1)+
cos α]/2tan(α-ω1)(Bsin α+Ccos α)
UE1=(dLOS1-dLOS2)[cos αtan(α-ω1)-
sin α]/2tan(α-ω1)(Bsin α+Ccos α)
UE2=(dLOS1-dLOS2)[-cos αtan(α-ω1)-
sin α]/2tan(α-ω1)(Bsin α+Ccos α)(22)
将式(19),(20)代入式(15)得
UN1=(dLOS1-dLOS2)[sin αtan(α-ω1)+
cos α]/2tan(α-ω1)(Bsin α+Ccos α)
UN2=(dLOS1-dLOS2)[-sin αtan(α-ω1)+
cos α]/2tan(α-ω1)(Bsin α+Ccos α)
UE1=(dLOS1-dLOS2)[cos αtan(α-ω1)-
sin α]/2tan(α-ω1)(Bsin α+Ccos α)
UE2=(dLOS1-dLOS2)[-cos αtan(α-ω1)-
sin α]/2tan(α-ω1)(Bsin α+Ccos α)(23)
式(22),(23)即为工作面推进过程中地表三维位移的分解模型。式中的中间变量B,C 与式(18)相同。
3.4.2 动态地表移动盆地中心o′的确定
为了求取地表移动过程中的水平位移方向角ω1,必须确定动态的地表移动盆地中心o′。由于地下开采影响向上传播至地表是一个时间过程,使得动态的地表移动盆地中心o′滞后于对应的采空区中央位置,但滞后的具体位置因地质采矿条件不同而难以确定。根据开采沉陷的基本规律,近水平煤层开采地表移动过程中的动态移动盆地中心o′点在平行于推进方向并通过采空区中间的走向主断面上,且具备以下特征:
(1) 在整个走向主断上动态盆地中心o′点的下沉值应为最大值;
(2) 动态盆地中心o′点处的水平位移绝对值应趋近于零。
依据上述特征,基于走向主断面线Z1Z2上InSAR-LOS位移的叠加计算,来搜索动态移动盆地中心o′。在式(18)雷达视线(LOS)方向与下沉、倾向水平位移、走向水平位移的几何关系式中,由于垂直于走向主断面上的横向(即倾向)水平位移为零,则由式(18)可得走向主断上任一点的三维位移分解公式:
dLOS=cos θW+(Bcos α-Csin α)UT(24)
由于盆地中心o′两侧对称点的下沉值相等,水平位移则大小相等而方向相反(均指向中心o′),则将中心点o′两侧对称点(可以选点o′两侧的相邻像元)的LOS位移进行叠加并取均值可得下沉值Wm,进行求差后可得水平位移值Um。由于该点处于动态盆地中心o′,则下沉值Wm应为整个走向主断面上的最大下沉值,水平位移值Um应趋近为零。因此,在整个走向主断面上针对任意两个相邻像元或一定窗口区域的LOS位移值或位移均值,进行上述叠加和求差计算,搜索出满足下沉值达到最大且水平位移趋于零的像元对,取其中间位置即为动态盆地中心o′。具体步骤如下:
(1)将LOS位移图中走向主断面上的像元位移进行编号(LOS1,LOS2,LOS3,LOS4,…,LOSn-2,LOSn-1,LOSn),由于盆地中心不可能偏到采空区以外,搜索起始点可以从开切眼正上方的地表位置开始。
(2)选取1,2号像元的位移值,用dLOSA,dLOSB表示,分别代入式(24)得:
dLOSA=cos θWA+(Bcos α-Csin α)UTA
dLOSB=cos θWB+(Bcos α-Csin α)UTB
WA=WB
UTA=-UTB(25)
将式(25)中的dLOSA与dLOSB分别进行叠加和差分,计算出像元1,2的下沉与水平位移值,记录为第1组移动值(W1,UT1)。
(3)选取2,3号像元的位移值,分别赋值为dLOSA,dLOSB,由式(25)计算出像元2,3的下沉与水平位移值,记录为第2组数据(W2,UT2)。
(4)以此类推,直至计算出第n-1,n号像元的下沉和水平位移值,记录为第n-1组数据,形成位移值数组(W1,UT1),(W2,UT2),…,(Wn-1,UTn-1)。计算流程如图7所示。
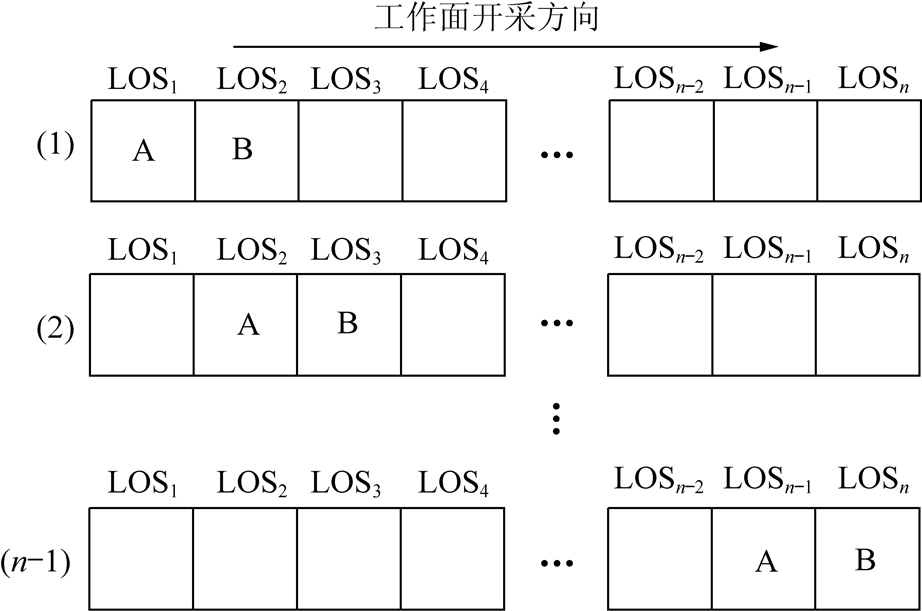
图7 移动盆地中心搜索计算流程
Fig.7 Flow diagram of mobile basin center search
(5)将上述全部(n-1)数组进行比较,分别搜索出下沉值最大的像元组合,以及水平位移绝对值最小的像元组合。当两者位置一致时,该像元组的中间位置即为动态移动盆地的中心o′。当2个条件发生冲突时,优先将下沉值最大的位置选为盆地中心。
应该指出,当地表沉陷达到超充分采动后,动态移动盆地中央会出现“平底”现象,按照上述搜索方法将得到多组满足条件的像元区域。此种情况下开切眼一侧的半盆地内水平位移指向第一组满足条件的像元位置,而推进边界一侧半盆地内水平位移指向最后一组满足条件的像元位置。
开采沉陷三维反演模型式(10)~(13)中涉及的参数包括:
(1)卫星入射方位角θ,可从雷达遥感数据的头文件中获取;
(2)卫星飞行方向与北方向的夹角αh,顺时针方向为正。该参数可在雷达遥感数据的头文件中获取。
(3)地表点P1的水平位移方向与北方向的夹角ω1。在InSAR形变图所处的坐标系统中,获取任意地表P1及采空区中心O的平面坐标P1(N1,E1),O(NO,EO),通过坐标反算得到两点之间的距离Lp及两点连线与北方向的夹角(即方位角)ω1。先用公式(15)求出P1O的象限角λ,再根据相应的象限条件将λ转换为方位角ω1。
λ=arctan[(N0-N1)/(EO-E1)](26)
(4)地表点P1在移动盆地内的对称点P3的坐标(N3,E3)根据对称几何关系由下式计算:
N3=NO+LPcos ω1
E3=EO+LPsin ω1(27)
地表任意点P1及其对称点P3的LOS向位移dLOS1,dLOS3,可根据其坐标为索引,利用InSAR形变数据文件或LOS形变图进行内插得到。因此,利用数学模型式(10)~(13)反演地表点的三维位移的算法流程如图8所示。

图8 稳定后的三维位移反演算法流程
Fig.8 Algorithm flow of 3-D displacement inversion of Insar
根据上述算法在MATLAB中进行编程实现,将L向位移数据分解为下沉、水平南北向、东西向的三维位移数据,并绘制出开采沉陷三维位移分布图。
动态的地表三维位移反演模型中的卫星入射方位角θ、卫星飞行方向与北方向的夹角αh、地表点的水平位移方位角ω1、工作面推进方向的方位角α等参数含义与稳态的模型相同。此外,还要获取对称点P1,P2的坐标(N1,E1),(N2,E2),并按照上述搜索算法确定动态的地表移动盆地中心O′的坐标(NO′,EO′)。其反演计算流程与图8基本相同,不再赘述。应注意的是,对称点P2坐标是利用与P1关于走向主断面Z1Z2对称的条件来求取的,与稳态情况下对称点P3坐标的计算公式有所不同。
4.3.1 地表移动稳定后的三维位移反演模型验证
某矿开采近水平煤层,地表较为平缓。采用长壁工作面开采方式,工作面由正南向北推进。开采宽度L1=250 m,走向长度L3=500 m,开采厚度m=2 m,地表为平地,平均采深H=500 m;煤层倾角α=0°。工作面回采时间为2014-10-16—2015-04-18,平均每月推进83 m。在工作面正中央地表布设了走向和倾向观测线。根据2015-12-03号最后一次实测数据绘制出地表稳定后的下沉与水平位移曲线,如图9所示。
在2014-09-26—2015-12-10的时间段内,利用15景sentinel SAR影像做差分干涉处理并将LOS向位移进行叠加,绘出地表稳定后的LOS向位移等值线,经过平滑简化后如图10所示。LOS位移的最大值明显偏离采空区中心位置。
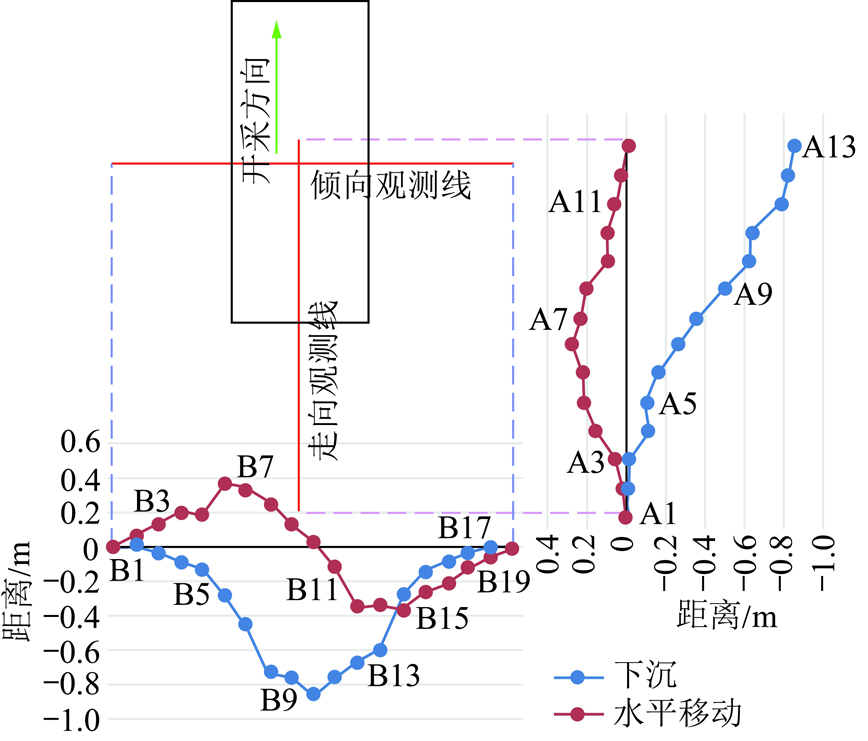
图9 实测数据绘制的下沉与水平位移曲线
Fig.9 Subsidence and horizontal displacement curve

图10 LOS向位移
Fig.10 LOS displacement

图11 忽略水平位移的下沉
Fig.11 Subsidence diagram that neglected the horizontal displacement
首先采用常规忽略水平位移的方法,直接将图10中的LOS位移投影为垂直下沉值。SAR影像的卫星入射角θ=30°,卫星飞行方向与北方向的夹角αh=345°,按式(2)计算下沉量,绘出下沉等值线分布如图11所示。所得到的最大下沉值明显偏离采空区中央上方,与图9的实测数据相差较大。
按照图8的计算流程对图10的LOS位移进行三维分解。应用专门的MATLAB 程序计算地表格网点的下沉、南北和东西水平位移值,并生成对应的等值线图,如图12所示。图12(a)中,最大下沉值位于采空区中心附近,地表下沉、南北(走向)水平位移、东西(倾向)向水平位移基本呈现以采空区中心(走向和倾向主断面线)为对称的分布特征。

图12 LOS向位移三维分解
Fig.12 LOS displacement to 3-D decomposition
4.3.2 动态地表三维位移反演模型验证
选取2014-09-26—2015-02-20的前5 h段LOS向叠加位移,进行动态的三维位移分解。此时间段工作面推进距离为340 m,地表沉陷处在动态过程中。绘出叠加至2015-02-20的地表LOS向位移等值线图,经过简化和平滑处理后如图13所示。地表LOS向位移明显偏离动态的采空区中央。按照上述搜索计算方法确定地表动态的移动盆地中心位置,偏离采空区中心43 m。
按照动态的三维位移分解模型式(22),(23)对图13的LOS向位移进行三维分解,生成地表下沉、南北向水平位移、东西向水平位移的等值线图,如图14所示。可以看出,工作面推进到340 m时,地表动态下沉、南北(即走向)、东西(即倾向)位移在走向主段面线的两侧都基本呈现对称特征,而在开切眼和推进边界上方地表的下沉和水平位移分布均为不对称状态。应该指出,本例中工作面走向为正南北向,倾向为东西向。如果工作面推进方向与北方向斜交,则应将计算出的南北向、东西向水平位移按照式(15)转换为沿工作面走向和倾向的水平位移后,再绘制走向和倾向水平位移等值线图。
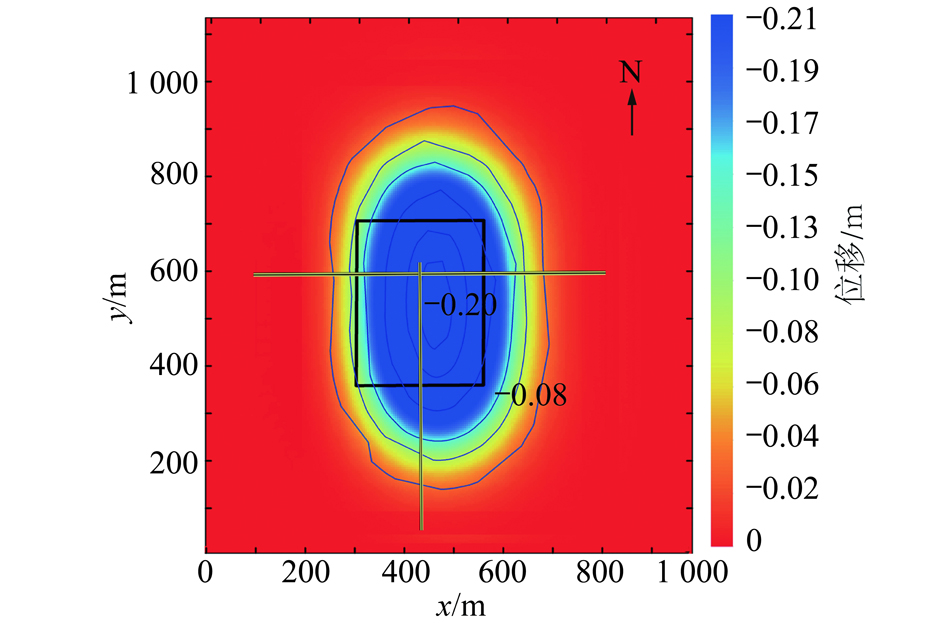
图13 动态的地表LOS向位移
Fig.13 Dynamic surface LOS displacement

图14 动态的地表三维位移
Fig.14 Dynamic 3-D surface displacement
4.3.3 反演模型的精度验证
以倾向线实测数据来验证本文模型反演得到的下沉、水平位移值,对比曲线如图15所示。统计表明,静态模型反演的下沉值(图15(a)曲线2)与实测值(图15(a)曲线1)相比的均方根误差为±20.1 mm,倾向水平位移(图15(b)曲线2)与实测值(图15(b)曲线1)相比的均方根误差为±22.8 mm。
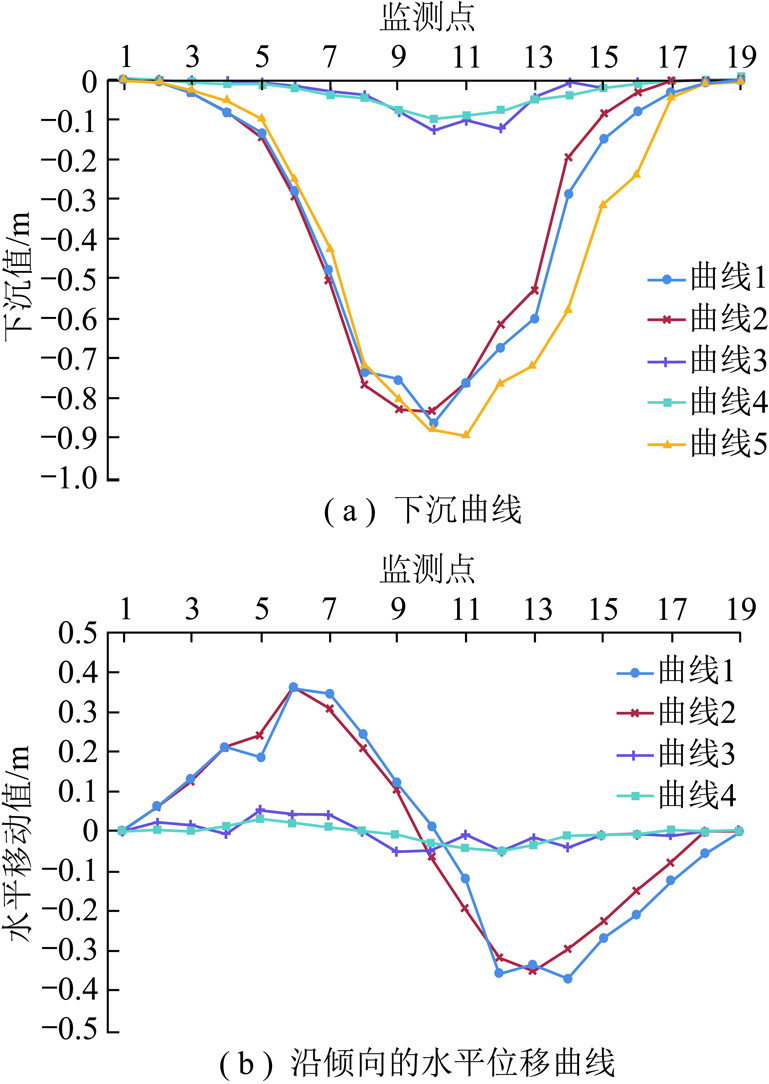
图15 倾向线上反演曲线与实测曲线对比
Fig.15 Comparison of displacement inversion curve on dip line with measured curve on dip line1—稳态实测曲线;2—稳态模型反演的曲线;3—推进至340 m时的实测曲线;4—动态模型反演曲线;5—直接忽略水平位移反演的稳态下沉曲线
如果忽略水平位移直接用LOS向位移来计算地表下沉值(图15(a)曲线5),则与实测下沉值相比的均方根误差达±104 mm。工作推进至340 m时,基于动态模型反演的下沉值(图15(a)曲线4)与实测值(图15(a)曲线3)相比的均方根误差为±17.5 mm,倾向水平位移(图15(b)曲线4)与实测值(图15(b)曲线3)相比的均方根误差为±19.2 mm。考虑到InSAR监测本身的误差影响,上述稳态和动态的模型反演三维位移的精度本身是可靠的。
(1)本文根据近水平煤层开采地表移动盆地中的下沉和水平位移所具备的对称特征,建立了一种基于InSAR监测数据反演三维位移的新模型。现有的开采沉陷研究及大量实测资料已经证实,在近水平煤层长壁工作面开采及地形起伏较小的情况下,地表移动盆地在形态上确实存在明显的对称特征。在工作面推进中,地表动态下沉和水平位移也同样存在以走向主断面为轴线的对称特征。因此,本文所建立的稳态和动态三维位移反演模型遵循了近水平煤层开采沉陷的基本原理。模型验证表明,本文模型反演的结果符合实际情况,明显优于忽略水平位移而直接分解地表下沉的方法。
(2)由于矿区地表下沉和水平向位移本身属于独立的形变分量,其相互关系难以用确定的函数模型来描述。因此,相对于现有在概率积分法基础上推导的InSAR三维位移反演模型来说,本文方法具有更好的普适性和实用性。
(3)在稳定后的地表移动三维分解中,可以利用地表移动关于倾向和走向都存在对称的特征(图3中I,II,III,IV区均为对称区),将地表点的三维位移作为3个独立未知量,列出四个区域对称点的4个LOS向位移方程式,按照最小二乘原理进行三维位移解算。所以,在地表移动稳定后的三维位移反演中,也可以将动态的位移方程式(16)并入稳态反演模型中,求出三维位移的最小二乘解。
应该指出,由于矿区开采沉陷规律受多种复杂的地质采矿因素影响,在倾斜煤层、山区地形及不规则工作面开采条件下,地表移动变形可能丧失对称性特征,笔者正在进一步研究非对称沉陷情况下的InSAR三维位移反演模型。
参考文献
[1] 廖明生,林兴华.合成孔径雷达干涉测量.原理和信号处理[M].北京:测绘出版社,2003.
[2] LI Zhiwei,YANG Zefa,HU Jun.Retrieving three-dimensional displacement fields of mining areas from a single InSAR pair[J].Journal of Geodesy,2015,89(1):17-32.
[3] WRIGHT T J.使用InSAR技术对三维地表变形进行映射[J].地理研究通讯,2004,31(1):69-76.
WRIGHT T J.Toward mapping surface deformation in three dimensions using InSAR[J].Geophyical Research Letters,2004,31(1):69-76.
[4] LUO Yi.An improved influence function method for predicting subsidence caused by longwall mining operations in inclined coal seams[J].International Journal of Coal Science & Technology,2015,2(3):163-169.
[5] 何国清,杨伦,凌赓娣,等.矿山开采沉陷学[M].徐州:矿业大学出版社,1991.
[6] HU Zhenqi,CHEN Chao,XIAO Wu,et al.Surface movement and deformation characteristics due to high-intensive coal mining in the windy and sandy region[J].International Journal of Coal Science & Technology,2016,3(3):339-348.
[7] YANG Zefa,LI Zhewei,ZHU Jianjun.An extension of the InSAR-based probability integral method and its application for predicting 3-D mining-induced displacements under different extraction conditions[J].IEEE Transactions on Geoscience and Remote Sensing,2017:3835-3845.
[8] YANG Zefa,LI Zhewei,ZHU Jianjun.Deriving dynamic subsidence of coal mining areas using InSAR and logistic model[J].Remote Sensing,2017,9(2):125.
[9] 刘晓菲,邓喀中,范洪冬,等.D-InSAR监测老采空区残余变形的试验[J].煤炭学报,2014,39(3):467-472.
LIU Xiaofei,DENG Kazhong,FAN Hongdong,et al.D-InSAR monitoring of residual deformation in old goafs[J].Journal of China Coal Society,2014,39(3):467-472.
[10] 张学东,葛大庆,吴立新.基于相干目标短基线InSAR的矿业城市地面沉降监测研究[J].煤炭学报,2012,37(10):1606-1611.
ZHANG Xuedong,GE Daqing,WU Lixin.Study on ground subsidence monitoring of mining cities based on short baseline InSAR of coherent targets[J].Journal of China Coal Society,2012,37(10):1606-1611.
[11] LI Peixian,TAN Zhixiang,DENG Kazhong.Study of probability integration method parameter inversion by the genetic algorithm[J].International Journal of Mining Science and Technology,2017,27(6):1073-1079.
[12] 李培现,谭志祥,闫丽丽,等.基于支持向量机的概率积分法参数计算方法[J].煤炭学报,2010,35(8):1247-1251.
LI Peixian,TAN Zhixiang,YAN Lili,et al.Parameter calculation method of probability integral method based on support vector machine[J].Journal of China Coal Society,2010,35(8):1247-1251.
[13] CAI Yue,JIANG Yujing,LIU Baoguo,et al.Computational implementation of a GIS developed tool for prediction of dynamic ground movement and deformation due to underground extraction sequence[J].International Journal of Coal Science & Technology,2016,3(4):379-398.
[14] 祝传广,邓喀中,张继贤,等.基于多源SAR影像矿区三维形变场的监测[J].煤炭学报,2014,39(4):673-678.
ZHU Chuanguang,DENG Kazhong,ZHANG Jixian,et al.Monitoring of three-dimensional deformation field in multi-source SAR image mining area[J].Journal of China Coal Society,2014,39(4):673-678.