 移动阅读
移动阅读程久龙1,黄少华2,温来福1,董 毅1,王浩宇1
(1.中国矿业大学(北京) 地球科学与测绘工程学院,北京 100083; 2.中国石油化工股份有限公司石油物探技术研究院,江苏 南京 211103)
摘 要:研究瞬变电磁场中的电性各向异性问题,可以为各向异性条件下的地下全空间瞬变电磁法资料处理解释工作提供理论指导,对提高瞬变电磁法探测精度具有重要意义。为了研究矿井全空间条件下主轴各向异性介质的瞬变电磁场响应特征,采用改进的交错网格有限差分方法实现了主轴各向异性介质的瞬变电磁场三维正演。将电导率张量加入麦克斯韦方程组,对Yee氏交错网格进行了改进以便于对主轴各向异性介质中的瞬变电磁场进行差分离散处理,形成了全空间三维主轴各向异性有限差分正演算法。在均匀全空间模型中对比各向异性有限差分数值解及均匀全空间解析解,验证了算法的正确性。建立了不同各向异性类型和不同各向异性对称主轴姿态模型,分别计算了其瞬变电磁场响应,最后结合工程探测实例,通过正演模拟分析了不同主轴各向异性介质对瞬变电磁场的影响特征,解释了探测结果存在偏差的原因。研究表明:在矿井超前探测模式下,对于HTI-X介质,各向异性系数的变化对瞬变电磁场的影响不明显,不同各向异性系数条件下的感应电动势曲线差异较小;对于HTI-Y介质和VTI介质,各向异性系数的变化对瞬变电磁场有明显的影响,随着介质各向异性系数增大,介质瞬变电磁场响应不断变小;随着各向异性介质对称主轴方向与探测方向之间夹角的增大,各向异性介质产生的瞬变电磁场响应不断增大,当对称主轴方向与探测方向一致时(HTI-X介质),各向异性介质产生的感应电动势最弱,而对称主轴方向与探测方向垂直时(VTI介质),各向异性介质产生的感应电动势最强;不同类型的主轴各向异性介质具有明显的各向异性瞬变电磁场响应特征。
关键词:主轴各向异性;响应特征;矿井全空间;瞬变电磁场;三维数值模拟
中图分类号:P631.3
文献标志码:A
文章编号:0253-9993(2019)01-0278-09
程久龙,黄少华,温来福,等.矿井全空间三维主轴各向异性介质瞬变电磁场响应特征研究[J].煤炭学报,2019,44(1):278-286.doi:10.13225/j.cnki.jccs.2018.1667
CHENG Jiulong,HUANG Shaohua,WEN Laifu,et al.Response characteristics of three-dimensional axial anisotropic media for transient electromagnetic method in underground whole-space[J].Journal of China Coal Society,2019,44(1):278-286.doi:10.13225/j.cnki.jccs.2018.1667
收稿日期:2018![]() 11
11![]() 02
02
修回日期:2018![]() 12
12![]() 20
20
责任编辑:韩晋平
基金项目:国家自然科学基金资助项目(51574250)
作者简介:程久龙(1965—),男,安徽安庆人,教授,博士生导师。E-mail:jlcheng@126.com
CHENG Jiulong1,HUANG Shaohua2,WEN Laifu1,DONG Yi1,WANG Haoyu1
(1.College of Geoscience and Surveying Engineering,China University of Mining and Technology (Beijing),Beijing 100083,China; 2.SINOPEC Geophysical Research Institute,Nanjing 211103,China)
Abstract:The study of the electrical anisotropy in the transient electromagnetic field could provide theoretical guidance for the data processing and interpretation of the underground full-space transient electromagnetic method under the condition of anisotropy,and it has important guiding significance to improve the detection accuracy of transient electromagnetic method.In order to study the transient electromagnetic field response characteristics of axial anisotropic media in underground whole-space,an improved staggered mesh finite difference method was used to realize a 3D forward modeling of the transient electromagnetic field of axial anisotropic media.The conductivity tensor was added to Maxwell’s equations.Yee’s staggered grid was improved to facilitate the differential discretization of axial anisotropic media’s transient electromagnetic fields.The whole-space finite difference forward algorithm for axial anisotropic media was developed.The correctness of the algorithm was verified by comparing the anisotropic finite difference numerical solution and the uniform whole-space analytical solution in a uniform whole-space model.Finally,combined with actual engineering detection,the influence characteristics of different axial anisotropic media on transient electromagnetic field were analyzed by forward modeling,and the reasons for the deviation of the detection results were explained.The results show that in the advanced detection mode,the change of anisotropy coefficient of HTI-X medium has no obvious influence on the transient electromagnetic field,the difference of induced electromotive force curves under different anisotropic coefficients is very small.For HTI-Y media and VTI media,the change of anisotropy coefficient has a significant impact on the transient electromagnetic field,as the anisotropy coefficient of the medium increases,the transient electromagnetic field response of the medium decreases continuously.With the increase of the angle between the symmetric axis of anisotropic media and the direction of detection,the transient electromagnetic field response generated by anisotropic media increases continuously.When the symmetric axis of anisotropic medium is consistent with the detection direction (HTI-X medium),the induced electromotive force generated by anisotropic medium is the weakest.When the symmetric axis is perpendicular to the detection direction (VTI medium),the induced electromotive force generated by anisotropic medium is the strongest.Different types of axial anisotropic media have obvious anisotropic transient electromagnetic field response characteristics.
Key words:axial anisotropy;response characteristic;underground whole-space;transient electromagnetic field;3D Numerical simulation
在矿井和地下隧道进行瞬变电磁探测的过程中,忽略各向异性介质的存在,按照各向同性介质假设进行资料处理及地质解释,将会得出不符合实际情况的结论,研究瞬变电磁场中的电性各向异性问题,可以为各向异性条件下的地下全空间瞬变电磁法资料处理解释工作提供理论指导,对提高瞬变电磁法探测精度具有重要的指导意义,对矿井地球物理勘探[1]的发展有积极作用。
国内外学者对于电性各向异性的研究在大地电磁法[2-5]、海洋可控源电磁法[6-7]、可控源音频大地电磁法[8]等频率域方法上取得了丰富的成果,但对瞬变电磁法在各向异性介质中的研究主要集中在以下领域:FRID N等[9]研究了瞬态电磁波在分层的、各向异性、色散介质中的传播,解决了直接散射问题;FERNANDO等[10]提出了在柱坐标系下用于复杂(各向异性、色散、传导性)和无界介质瞬变电磁数值模拟的三维时域有限差分方法,该方法将完全匹配层(PML)吸收边界条件(ABC)扩展到了三维柱坐标,应用分段线性递归卷积(PLRC)算法对模型进行离散,对不同模型进行了数值模拟并对结果进行了分析;COLLINS等[11]在对德克萨斯州的风化变质岩的瞬变电磁探测过程中发现了近地表的水平各向异性现象,并且采用了直流电法及地震勘探方法对瞬变电磁法的探测进行了补充,最后通过正演模拟与观测数据进行对比分析,探讨了近地表水平各向异性现象的产生原因;HOBBS[12]提出了在各向异性介质中的应用多道瞬变电磁法,研究电阻率各向异性对瞬变电磁场响应的影响,并指出在反演方法中应包括各向异性,最后提出了一种求取各向异性的实用方法;HAGIWARA[13]研究了在两层地层中的三轴瞬变电磁感应测量,通过代数方法从三轴瞬变电磁测量中得到了时间相关的视倾角及视各向异性,并由此计算出真倾角及各向异性用以描述真实地层;严良俊等[14]对储层电各向异性模型的瞬变电磁场响应进行了研究,通过数字滤波算法实现了数值模拟,对薄互层下的各向异性模型的瞬变电磁场响应进行了分析;周建美等[15]研究了一维层状地层的电阻率各向异性对瞬变电磁场响应的影响,采用正余弦数字滤波算法得到一维各向异性地层中海洋瞬变电磁场响应;周建美等[16]采用模拟离散的有限体积法实现了双轴各向异性地层回线源瞬变电磁三维正演,对于不同的各向异性地层模型进行了数值模拟,分析了不同方向上电导率变化对瞬变电磁场响应的影响。以上国内外学者主要研究了近地表、地下半空间介质的电性各向异性,包括电磁场在各向异性介质中的传播情况、各向异性介质中瞬变电磁场响应的计算与分析、不同因素对各向异性介质中瞬变电磁响应的影响等方面的内容。
N等[9]研究了瞬态电磁波在分层的、各向异性、色散介质中的传播,解决了直接散射问题;FERNANDO等[10]提出了在柱坐标系下用于复杂(各向异性、色散、传导性)和无界介质瞬变电磁数值模拟的三维时域有限差分方法,该方法将完全匹配层(PML)吸收边界条件(ABC)扩展到了三维柱坐标,应用分段线性递归卷积(PLRC)算法对模型进行离散,对不同模型进行了数值模拟并对结果进行了分析;COLLINS等[11]在对德克萨斯州的风化变质岩的瞬变电磁探测过程中发现了近地表的水平各向异性现象,并且采用了直流电法及地震勘探方法对瞬变电磁法的探测进行了补充,最后通过正演模拟与观测数据进行对比分析,探讨了近地表水平各向异性现象的产生原因;HOBBS[12]提出了在各向异性介质中的应用多道瞬变电磁法,研究电阻率各向异性对瞬变电磁场响应的影响,并指出在反演方法中应包括各向异性,最后提出了一种求取各向异性的实用方法;HAGIWARA[13]研究了在两层地层中的三轴瞬变电磁感应测量,通过代数方法从三轴瞬变电磁测量中得到了时间相关的视倾角及视各向异性,并由此计算出真倾角及各向异性用以描述真实地层;严良俊等[14]对储层电各向异性模型的瞬变电磁场响应进行了研究,通过数字滤波算法实现了数值模拟,对薄互层下的各向异性模型的瞬变电磁场响应进行了分析;周建美等[15]研究了一维层状地层的电阻率各向异性对瞬变电磁场响应的影响,采用正余弦数字滤波算法得到一维各向异性地层中海洋瞬变电磁场响应;周建美等[16]采用模拟离散的有限体积法实现了双轴各向异性地层回线源瞬变电磁三维正演,对于不同的各向异性地层模型进行了数值模拟,分析了不同方向上电导率变化对瞬变电磁场响应的影响。以上国内外学者主要研究了近地表、地下半空间介质的电性各向异性,包括电磁场在各向异性介质中的传播情况、各向异性介质中瞬变电磁场响应的计算与分析、不同因素对各向异性介质中瞬变电磁响应的影响等方面的内容。
目前对于地下各向异性介质的全空间瞬变电磁场响应的研究才刚刚起步,笔者将电性各向异性理论引入矿井地下全空间瞬变电磁法的研究,采用Yee氏交错网格有限差分方法,从三维正演来研究电性各向异性介质的瞬变电磁场响应特征。
瞬变电磁法勘探中所利用的电磁波频率较低,通常情况下将会忽略位移电流,但同时为了构成FDTD计算所需要的时间步进格式,根据WANG T和HOHMANN G.W.(1993)所使用的Dufort-Frankel方法[17],加入一项虚拟位移电流,此时无源情况下的时间域Maxwell方程组为
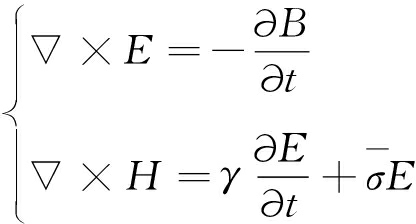
式中,E为电场强度;B为磁感应强度;H为磁场强度;![]() 为电导率;γ具有介电常数的量纲,本文称其为虚拟介电常数,包含γ的项具有电流的量纲,称为虚拟位移电流。
为电导率;γ具有介电常数的量纲,本文称其为虚拟介电常数,包含γ的项具有电流的量纲,称为虚拟位移电流。
在电性各向异性介质中,电导率为完全张量电导率![]() 笔者将任意各向异性简化为主轴各向异性,并对主轴各向异性介质的瞬变电磁场响应进行分析,因此将完全张量电导率
笔者将任意各向异性简化为主轴各向异性,并对主轴各向异性介质的瞬变电磁场响应进行分析,因此将完全张量电导率![]() 简化为
简化为
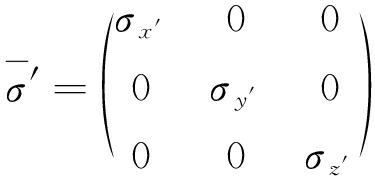
采用小回线源作为场源,并将A.A.考夫曼和 G.V.凯勒[18]推导的均匀全空间中垂直磁偶极子阶跃电流断开时的时间域电磁场表达式代入初始时间求得初始电磁场值并加入到差分迭代中,采用四阶的修正廖氏吸收边界及超吸收边界条件对截断边界进行处理,通过CFL稳定性条件控制模拟的时间步长、空间步长及人工项虚拟介电常数。
采用均匀网格剖分对连续的空间离散化处理,由于研究区域内存在电性各向异性的情况,在使用Yee氏网格对主轴各向异性立方体单元中的电磁场进行离散时,主轴各向异性立方体单元在不同方向上的电导率是不一样的,图1为主轴各向异性介质中的Yee氏交错网格,X,Y,Z方向上的电场进行计算的时候分别代入相应方向上的电导率σx′,σy′,σz′。此外,由于电导率是对整个立方体单元进行定义的,对于立方体单元棱边上的电导率则需要特殊定义,由于是均匀剖分,这里通过棱边周围4个立方体单元电导率的算术平均值对其定义。
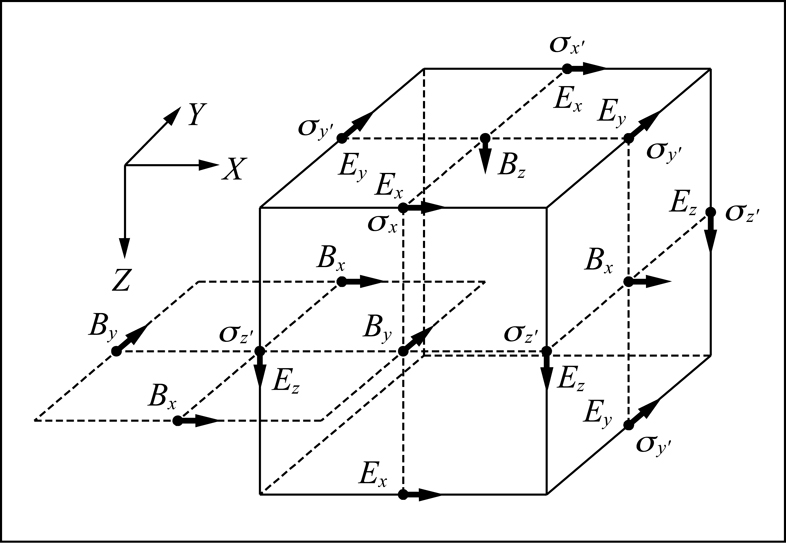
图1 主轴各向异性介质中Yee氏交错网格示意
Fig.1 Yee’s staggered grids in axial anisotropic media
以上为在Yee氏交错网格中主轴各向异性介质的电场和磁场空间采样方式,电场和磁场交替出现。对于电磁场在时间上的采样,同一个时刻仅对于电场或磁场的其中一个进行采样,在时间轴上,电场和磁场的采样交替进行,采样间隔为半个时间步长,在一个完整的电场采样时间步长中存在一个磁场采样,同样,在一个完整的磁场采样时间步长中存在一个电场采样。
采用各向同性均匀全空间模型,对比各向异性正演算法计算所得数值解与均匀全空间解析解可验证算法的有效性。将均匀全空间模型电阻率设置为100 Ω·m,给定模拟空间为2 000 m×2 000 m×2 000 m,接收回线与发射回线重合,均位于模型中心位置。发射线圈尺寸为2 m×2 m,匝数为40匝,发射电流为2 A,接收回线面积归一化为1 m2,接收信号为dBz/dt,即单位接收面积的感应电动势值。图2为对比结果。
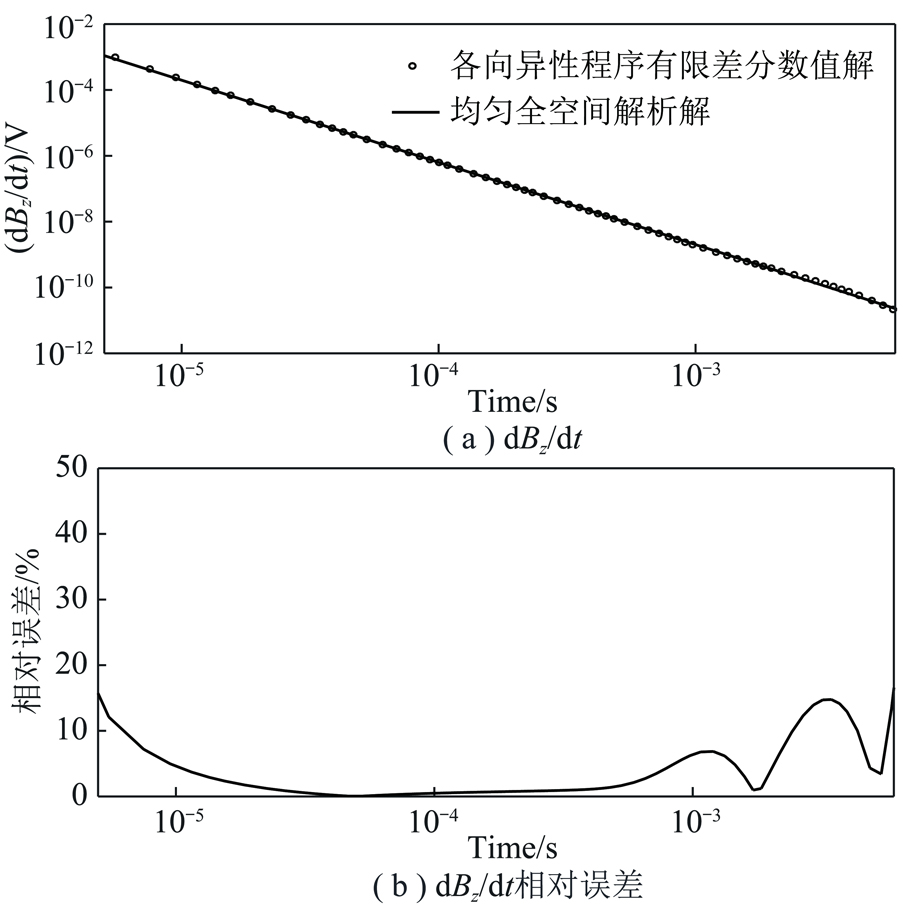
图2 均匀全空间感应电动势解析解及各向异性计算程序数值解对比
Fig.2 Analytical solution and anisotropic FDTD solution of dBz/dt in uniform whole space
由图2可以看出,dBz/dt解析解及数值解的误差在研究时段(5.0×10-6~1.0×10-2 s)的相对误差总体在10%以下,在2.0×10-5~1.0×10-3 s时段内相对误差在5%以内,早期和晚期也在15%以下,说明本文各向异性三维正演算法计算得到的数值解与均匀全空间解析解基本吻合,验证了各向异性三维正演算法的正确性。
采用全空间巷道超前探测模型,研究不同各向异性介质类型的瞬变电磁场响应。模型如图3所示,在巷道掌子面正前方50 m处设置各向异性立方含水体模型,各向异性含水异常体尺寸设置为100 m×100 m×100 m,全空间中围岩电阻率设置为100 Ω·m,巷道掌子面位于整个模型空间中心位置,巷道走向沿着X轴方向延伸,巷道截面尺寸为10 m×10 m,巷道长度1 000 m,巷道中的空腔电阻率值给定为10 000 Ω·m,模型采用10 m×10 m×10 m的均匀网格剖分,模拟的空间大小为2 000 m×2 000 m×2 000 m;接收线圈与发射线圈重迭,均位于巷道掌子面,尺寸为2 m×2 m,匝数为40匝,发射电流为2 A,探测方向垂直于掘进工作面(沿巷道掘进方向),接收回线面积归一化为1 m2,由于探测方向为X方向,接收信号为dBx/dt。
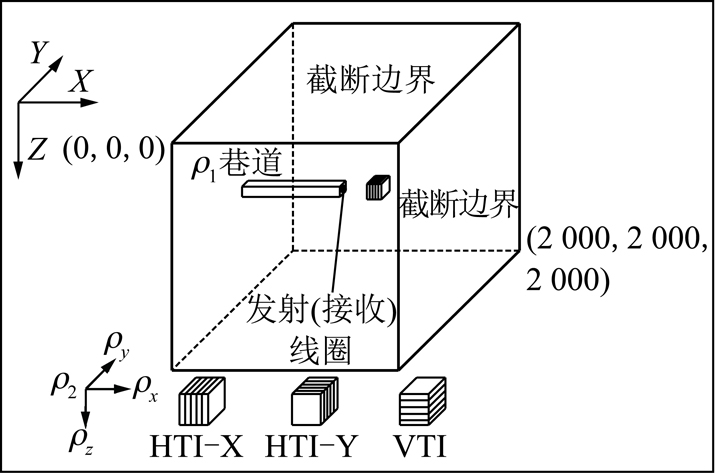
图3 不同各向异性异常体全空间超前探测模型
Fig.3 Whole space advanced detection model of different anisotropic anomalous body
将巷道正前方的含水异常体分别设置为HTI-X,HTI-Y,VTI介质,其电阻率张量表达式分别为
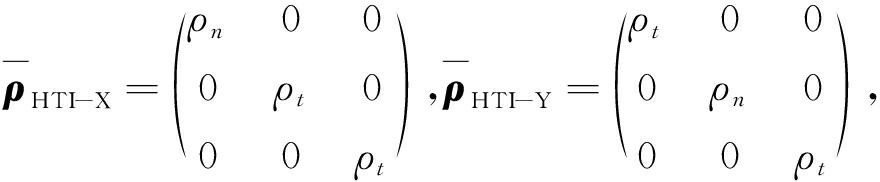
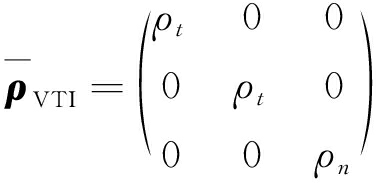
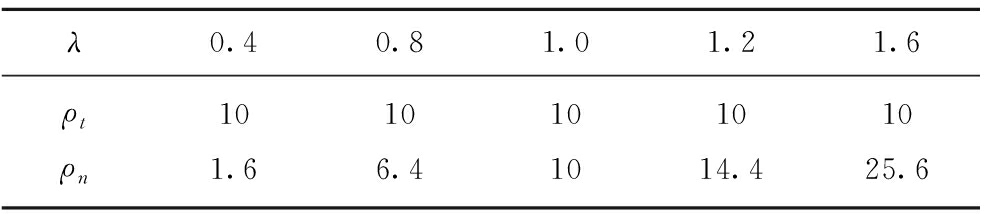
根据各向异性系数λ的定义,![]() 将以上3种不同的各向异性介质分别设定不同的各向异性系数λ,横向电阻率ρt及纵向电阻率ρn取值见表1,横向电阻率全部取值为10 Ω·m。
将以上3种不同的各向异性介质分别设定不同的各向异性系数λ,横向电阻率ρt及纵向电阻率ρn取值见表1,横向电阻率全部取值为10 Ω·m。
表1 各向异性介质电阻率
Table 1 Resistivity of anisotropic mediaΩ·m
HTI-X,HTI-Y,VTI介质含水异常体取不同各向异性系数时,数值模拟计算得到的感应电动势衰减曲线及感应电动势比值曲线分别如图4~6所示。图4(a)、图5(a)、图6(a)分别为HTI-X,HTI-Y,VTI介质含水异常体取不同各向异性系数时的感应电动势衰减曲线,图中最下方的黑色曲线为仅含巷道的感应电动势衰减曲线;图4(b)、图5(b)、图6(b)分别为含不同各向异性异常体的巷道全空间瞬变电磁感应电动势与纯巷道全空间瞬变电磁感应电动势的比值随时间变化的曲线。

图4 HTI-X异常体不同各向异性系数瞬变电磁场响应
Fig.4 TEM response of HTI-X anomalous bodies with different anisotropic coefficients
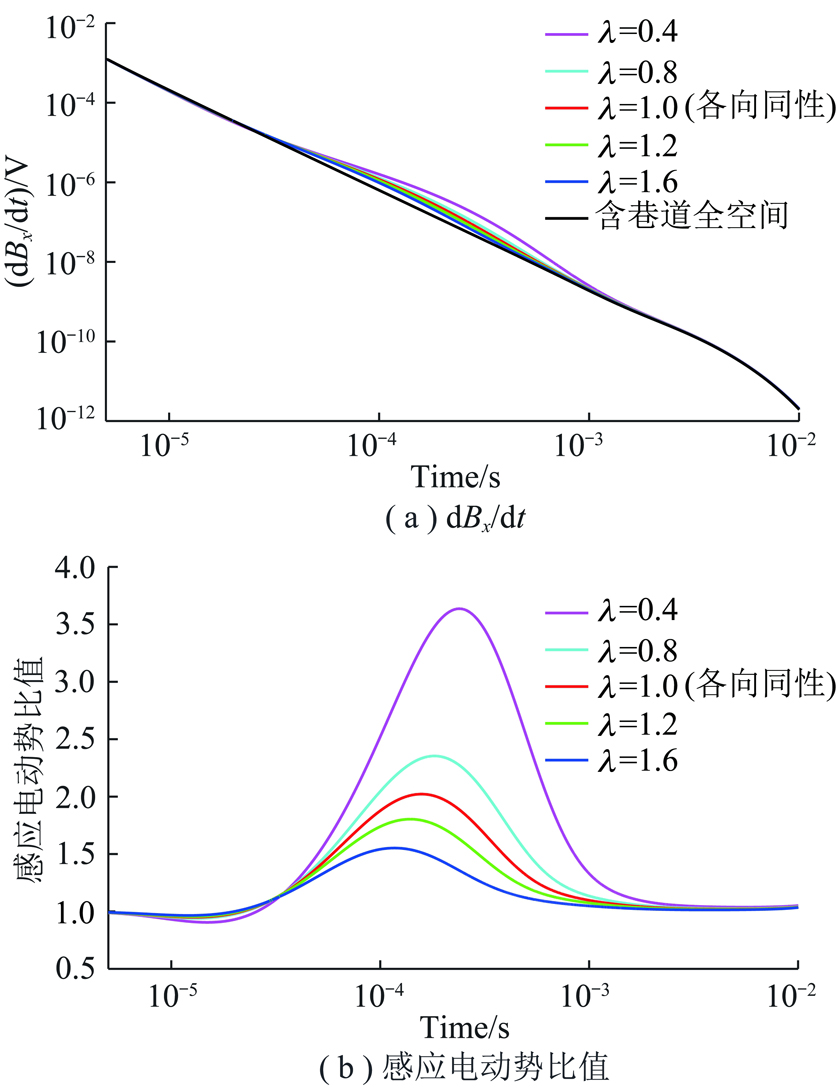
图5 HTI-Y异常体不同各向异性系数瞬变电磁场响应
Fig.5 TEM response of HTI-Y anomalous bodies with different anisotropic coefficients

图6 VTI异常体不同各向异性系数瞬变电磁场响应
Fig.6 TEM response of VTI anomalous bodies with different anisotropic coefficients
由图4(a)可以看出,当HTI-X异常体取不同各向异性系数时,感应电动势曲线没有出现明显的变化,因此图4(b)的曲线也同样基本重合;在图5(a)中HTI-Y异常体取不同各向异性系数时,感应电动势曲线明显分离,在图5(b)中可以明显看出随着各向异性系数的增大,异常体部分产生的感应电动势在减小;在图6(a)中VTI异常体取不同各向异性系数时,感应电动势曲线明显分离,在图6(b)中同样可以看出随着各向异性系数的增大,异常体部分产生的感应电动势在减小。
为研究各向异性介质在不同各向异性对称主轴姿态时的瞬变电场磁响应,首先将全空间超前探测模型中含水异常体设置为HTI-X介质(各向异性对称主轴为X轴),随后旋转各向异性对称主轴方向,使之与X轴方向夹角变为30°,45°,60°及90°,当夹角为30°,45°及60°时异常体为TTI介质,当夹角为90°时异常体为VTI介质,模型如图7所示。

图7 不同各向异性对称主轴姿态瞬变电磁场响应
Fig.7 Anisotropic media with different symmetrical axis in whole-space advanced detection model
各向异性介质在不同各向异性对称主轴姿态时计算得到的感应电动势衰减曲线及感应电动势比值曲线如图8所示。图8(a)为含水异常体在不同各向异性对称主轴姿态时的感应电动势衰减曲线,图中最下方的黑色曲线为仅含巷道的感应电动势衰减曲线。图8(b)为含各向异性异常体的巷道全空间瞬变电磁感应电动势与纯巷道全空间瞬变电磁感应电动势的比值随时间变化的曲线。

图8 不同各向异性对称主轴姿态瞬变电磁场响应
Fig.8 TEM response of anisotropic media with different symmetrical principal axis posture
随着各向异性对称主轴姿态的变化,含水异常体从对称主轴为X轴的HTI-X介质转变成对称主轴为Z轴的VTI介质,由图8可以看出,由于探测方向为X轴方向,在此过程中各向异性对称主轴与探测方向夹角不断增大,异常体部分产生的感应电动势也在不断增大,并且当各向异性对称主轴与探测方向一致时,各向异性介质产生的感应电动势最弱,而对称主轴与探测方向垂直时,各向异性介质产生的感应电动势最强。
在山东某矿应用地下全空间瞬变电磁法进行工作面出水点超前探测工作中发现,实测数据处理结果与钻探结果存在一定的偏差,实测数据处理结果中低阻异常区域偏小且低阻不明显,且在超前探测平面图及剖面图中低阻异常区域形态不能较好的对应,使基于各向同性的地质解释工作不能达到精细探测的要求,针对这种现象,根据巷道周围地质资料和水文地质情况,考虑到是由地层各向异性引起了这种偏差,因此通过数值模拟对该问题进行分析研究。
将顺层方向超前探测成果图叠加在巷道平面图上,将竖直方向超前探测成果图叠加在巷道剖面图上,得到图9所示实测视电阻率平面及剖面分布情况图。其中巷道平面图中标有三维地震勘探圈定的构造异常区,巷道剖面图中标有根据钻探资料分析推断的断层。

图9 实测视电阻率(Ω·m)平面及剖面分布情况
Fig.9 Distribution diagram of the measured apparent resistivity in plane and profile
由图9(a)可以看出① 号异常区位于构造异常区边界,由图9(b)可以看出② 号异常区位于断层所在位置。实际上① 号异常区及② 号异常区在空间上是重合的,由于断层等构造的存在,在此区域内发育有破碎裂隙,这些含水破碎裂隙构成了一定范围的低阻区域,根据裂隙方向性集中体积模型[19],不同裂隙分布情况对应于不同类型的电性各向异性介质。
首先根据工程实例建立全空间超前探测模型,如图10所示,巷道掌子面位于整个模型空间中心位置,巷道走向沿着X轴方向延伸,巷道截面尺寸为10 m×10 m,巷道长度1 000 m,巷道中的空腔电阻率值给定为10 000 Ω·m,模型采用10 m×10 m×10 m的均匀网格剖分,模拟的空间大小为2 000 m×2 000 m×2 000 m;发射线圈位于巷道掌子面,尺寸为2 m×2 m,匝数为40匝,发射电流为2 A,接收线圈与发射线圈重合。由于该矿区为典型的华北型石炭二叠系煤田,将全空间地层的各层电阻率及厚度设置如下:第1层电阻率设为50 Ω·m,厚度500 m;第2层电阻率设为100 Ω·m,厚度490 m;煤层电阻率设为500 Ω·m,厚度10 m;第4层电阻率设为100 Ω·m,厚度300 m;第5层电阻率设为50 Ω·m,厚度700 m。
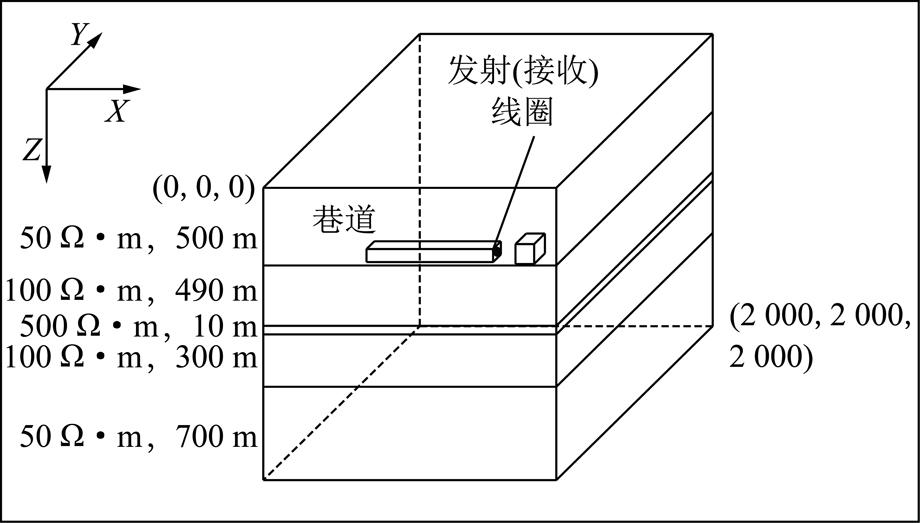
图10 工程实例超前探测模型示意
Fig.10 Schematic map of advance detection model in engineering example
由于异常区域主要位于断层、裂隙密集带等位置,将该区域设置为含水异常区域,在模型中用立方体表示该区域。将该含水异常体设置在巷道正前方40 m处,异常体尺寸为40 m×40 m×40 m。
在该含水异常区域内部的裂隙分布情况存在多种可能,如图11所示为几种典型的裂隙分布情况,分别对应于相应的电性各向异性模型,其中图11(a)为无裂隙分布的情况,对应于各向同性介质模型,设置该模型是为了与其他各向异性介质模型进行对比;图11(b)为主裂隙法向为Z方向时的情况,对应于VTI介质模型;图11(c)为主裂隙走向为Y方向的情况,对应于HTI-X介质模型;由于在工程实例中异常体位置处存在倾角为50°的逆断层,因此设置了如图11(d)中所示主裂隙法向与水平方向夹角为50°时的情况,对应于TTI介质模型。分别将这几种异常体模型加入超前探测模型中进行正演模拟。

图11 异常区域不同裂隙模型
Fig.11 Different fracture models of abnormal regions
其中各向同性介质电阻率设为10 Ω·m,由于是含水区域,将VTI,HTI-X,TTI介质的各向异性系数λ均设置为0.4。
根据实际超前探测方案,在巷道掌子面处沿顺层方向设置11个方向的测点,实现对巷道掌子面前方以及左右侧帮的探测,在竖直方向上设置9个方向的测点实现对巷道掌子面前方及顶底板的探测。将不同电性各向异性异常体的正演模拟结果进行处理,首先通过感应电动势计算得到视电阻率,然后运用时深转换计算公式将时间-视电阻率数据转换为深度-视电阻率数据,根据测点布置,按照每个测点的实际探测方向绘制扇形视电阻率断面图。
图12为顺层方向11个测点的视电阻率断面图,图中纵坐标表示沿巷道工作面前进方向距离,横坐标表示垂直于巷道方向上的距离,负半轴表示巷道左侧帮方向,正半轴表示巷道右侧帮方向。

图12 顺层方向超前探测视电阻率断面
Fig.12 Apparent resistivity sectional drawing of advanced detection in bedding direction
图12中正方形框指示异常体所在位置。图12(a)中低阻异常区域并不明显,不能较好的指示出各向同性异常体的位置;图12(b)中蓝色及深蓝色低阻异常区域更大,说明VTI介质的整体视电阻率低于各向同性介质,并且低阻异常区域较好的反映出了VTI异常体的大小及所在的位置;图12(c)中HTI-X异常体的视电阻率分布规律与前两种并不一致,在横坐标方向上视电阻率分布较稀疏,纵坐标方向上视电阻率分布较密集,这是HTI-X异常体的电性结构导致的,HTI-X介质在X方向上的电阻率低于Y,Z方向上的电阻率;图12(d)中TTI异常体的视电阻率分布规律与图12(a)及图12(b)基本一致,而TTI异常体对应的低阻异常区域视电阻率值介于VTI介质和HTI-X介质低阻异常区域的视电阻率值之间。
图13分别为对各向同性异常体、VTI异常体、HTI-X异常体及TTI异常体在竖直方向探测时的视电阻率断面图,图中正方形指示异常体所在位置,横坐标表示沿巷道工作面前进方向距离,纵坐标正半轴表示顶板方向,负半轴表示底板方向。图13(a)中低阻区域仍不明显,对比图13(a)及图12(a),可以发现各向同性介质在顺层及竖直方向视电阻率断面图中的视电阻率分布规律基本一致,说明在竖直方向及顺层方向探测中各向同性介质的瞬变电磁场响应特征是一致的;对比图13(b)及图12(b),可以发现VTI介质在顺层及竖直方向视电阻率断面图上的视电阻率分布规律并不一致,在竖直方向视电阻率断面图中,横轴方向上的视电阻率分布较稀疏,纵轴方向上的视电阻率分布较密集,这是由于VTI介质电性结构导致的,VTI介质在Z方向上的电阻率低于X,Y方向上的电阻率;对比图13(c)及图12(c),两图中视电阻率分布规律基本一致,在竖直方向视电阻率断面图中,横轴方向上的视电阻率分布较密集,纵轴方向上的视电阻率分布较稀疏,这是由于HTI-X介质电性结构导致的;对比图13(d)及图12(d),可以发现TTI介质在顺层及竖直方向视电阻率断面图上的低阻异常区域形态不一致,在竖直方向视电阻率断面图中,横轴方向上的视电阻率分布较稀疏,纵轴方向上的视电阻率分布较密集。

图13 竖直方向超前探测视电阻率断面
Fig.13 Apparent resistivity sectional drawing of advanced detection in vertical direction
以上模拟结果可对上文中提及的偏差问题做出合理解释。在工程实例中异常区域处存在倾角为50°的逆断层,因此设置了TTI介质模型与其对应,TTI介质主裂隙法向与水平方向夹角为50°。
在顺层方向及竖直方向视电阻率断面图中,TTI介质相对于各向同性介质,低阻异常区域更明显,这是介质电阻率结构差异导致的。因此,对于低阻异常区域偏小且低阻不明显这一问题,主要是现有探测技术无法对各向异性进行有效探测导致,发展电磁多分量方位观测及张量观测技术有利于各向异性探测。
TTI介质模型在顺层方向及竖直方向视电阻率断面图中,低阻异常区域的形态存在一定差异,表现出了TTI介质的电阻率结构特征,这一模拟结果为在地质解释工作中应用各向异性理论提供了有力佐证,也合理解释了工程实例超前探测平面图及剖面图中低阻异常区域形态不能较好的对应同一低阻异常体模型(各向同性模型)的问题。
(1)对于不同类型的各向异性介质,均表现出各向异性介质产生的瞬变电磁场响应与各向异性系数变化呈负相关的规律。随着各向异性系数的增大,HTI-Y介质及VTI介质的瞬变电磁场响应明显减小,HTI-X介质的瞬变电磁场响应也有所减小,但变化不明显,这是由于研究模型设置的探测方向为X轴方向,由回线源产生的感应电流主要在YZ平面方向上,瞬变电磁场响应主要受到Y,Z方向上的电阻率变化影响,而受X方向上的电阻率变化影响较小。
(2)各向异性介质对称主轴方向与探测方向之间夹角对各向异性介质产生的瞬变电磁场响应具有较大影响,当对称主轴方向与探测方向一致,均为X轴方向时,各向异性介质产生的感应电动势最弱,而对称主轴方向与探测方向垂直,对称主轴方向为Z轴方向时,各向异性介质产生的感应电动势最强,对称主轴方向由平行于探测方向旋转至垂直于探测方向时,电阻率变化的主要方向由X方向朝Z方向变化,增强了对YZ平面上感应电流的影响,因此各向异性介质产生的感应电动势不断增大。
(3)各向异性介质与各向同性介质具有不同的瞬变电磁场响应特征,不同各向异性介质之间的瞬变电磁场响应特征也不一致,不同的介质电阻率结构导致了瞬变电磁响应特征之间的差异,介质的瞬变电磁场响应特征与介质的电阻率结构表现出较强的相关性。
参考文献
[1] DU Wenfeng,PENG Suping,ZHU Guowei,et al.Time-lapse geophysical technology-based study on overburden strata changes induced by modern coal mining[J].International Journal of Coal Science & Technology,2014,1(2):184-191.
[2] O’BRIEN DOUGLAS P,MORRIS H-F.Electromagnetic fields in an n-layer anisotropic half-space[J].Geophysics,1967,32(4):668-677.
[3] LI Xiaobo,PEDERS Laust B.The electromagnetic response of an azimuthally anisotropic half-space[J].Geophysics,1991(56):1462-1473.
[4] WANG T,FANG S,3-D electromagnetic anisotropy modeling using finite differences[J].Geophysics,2001,66:1386-1398.
[5] 胡祥云,霍光谱,高锐.大地电磁各向异性二维模拟及实例分析[J].地球物理学报,2013,56(12):4268-4277.
HU Xiangyun,HUO Guangpu,GAO Rui,et al.The magnetotelluric anisotropic two-dimensional simulation and case analysis[J].Chinese Journal of Geophysics,2013,56(12):4268-4277.
[6] 罗鸣,李予国.一维电阻率各向异性对海洋可控源电磁响应的影响研究[J].地球物理学报,2015,58(8):2851-2861.
LUO Ming,LI Yuguo.Effects of the electric anisotropy on marine controlled-source electromagnetic responses[J].Chinese Journal of Geophysics,2015,58(8):2851-2861.
[7] 殷长春,贲放,刘云鹤,等.三维任意各向异性介质中海洋可控源电磁法正演研究[J].地球物理学报,2014,57(12):4110-4122.
YIN Chancun,BEN Fang,LIU Yunhe,et al.MCSEM 3D modeling for arbitrarily anisotropic media[J].Chinese Journal of Geophysics,2014,57(12):4110-4122.
[8] WANG T,WANG K P,TAN H D.Forward modeling and inversion of tensor CSAMT in 3D anisotropic media[J].Applied Geophysics,2017,14(4):590-605.
[9] FRID N J,KRISTENSSON G,STEWART R D.Transient electromagnetic wave propagation in anisotropic dispersive media[J].Journal of the Optical Society of America,1993,10(12):2618-2627.
N J,KRISTENSSON G,STEWART R D.Transient electromagnetic wave propagation in anisotropic dispersive media[J].Journal of the Optical Society of America,1993,10(12):2618-2627.
[10] FERNANDO L Teixeira,WENG CHO Chew.Finite-difference computation of transient electromagnetic waves for cylindrical geometries[J].IEEE Transactions on Geoscience and Remote Sensing,2000,38(4):1530-1543.
[11] JAMIE L Collins,MARK E Everett,BRANN Johnson.Detection of near-surface horizontal anisotropy in a weathered metamorphic schist at Llano Uplift(Texas) by transient electromagnetic induction[J].Physics of the Earth and Planetary Interiors,2006,158(26):158-173.
[12] HOBBS B,WERTHMÜLLER D,ENGELMARK F.The effect of resistivity anisotropy on transient electromagnetic earth responses[J].ASEG Extended Abstracts,2009.
[13] TERUHIKO Hagiwara.Determination of dip and anisotropy from transient[J].Geophysics,2012,77(4):105-112.
[14] 严良俊,周磊,谢兴兵,等.储层电各向异性模型的瞬变电磁响应[J].工程地球物理学报,2014,11(3):346-350.
YAN Liangjun,ZHOU Lei,XIE Xingbing,et al.The transient electromagnetic response of electrical anisotropic reservoir model[J].Chinese Journal of Engineering Geophysics,2014,11(3):346-350.
[15] 周建美,李貅,戚志鹏.浅水域各向异性地层中的瞬变电磁响应分析[J].石油地球物理勘探,2016,51(4):821-830.
ZHOU Jianmei,LI Xiu,QI Zhipeng.Transient electromagnetic response analysis for anisotropic media in shallow water[J].Oil Geophysical Prospecting,2016,51(4):821-830.
[16] 周建美,刘文韬,李貅,等.双轴各向异性介质中回线源瞬变电磁三维拟态有限体积正演算法[J].地球物理学报,2018,61(1):368-378.
ZHOU J M,LIU W T,LI X,et al.Research on the 3D mimetic finite volume method for loop-source TEM response in biaxial anisotropic formation[J].Chinese Journal of Geophysics,2018,61(1):368-378.
[17] WANG T,HOHMANN G W.A finite-difference time-domain solution for three-dimensional electromagnetic modeling[J].Geophysics,1993,58(6):797-809.
[18] 考夫曼A A,凯勒G V.频率域和时间域电磁测深[M].王建谋,译.北京:地质出版社,1987:25-57.
[19] 阮爱国.地壳介质弹性、电性各向异性理论及对地震过程的联合解释[D].北京:中国地震局地球物理研究所,2000.