锚杆支护作为巷道支护的一种主动支护方式因其支护强度高、成本低等特点而被广泛使用。随着我国煤矿采深的不断增加,最大开采深度已达到1 500 m[1-2],巷道周边围岩变形及条件日益复杂,锚杆单体承载能力不断加强,但由于全长锚固锚杆在支护过程中受力复杂,使得锚固技术理论分析和设计发展较缓慢[3],锚固支护技术缺乏理论依据,而锚杆杆体受力特征理论分析是锚固支护技术中的重要内容。
许多学者通过数值模拟、拉拔试验和现场实测等方法[4-5]对全长锚固锚杆杆体受力形式及特征展开了大量的研究工作。FREEMAN T J[6]通过拉拔试验及现场实测对全长锚固锚杆杆体应力分布进行研究,并提出中性点理论、锚固段和拉拔段的概念,在中性点位置处,杆体所受剪应力为零,轴力达到最大值,杆体拉拔段所受剪应力方向指向孔口,而锚固段剪应力方向与其相反。然而基于拉拔试验及现场实测获得的经验及数据建立的模型并不能从本质上说明全长锚固锚杆的实际作用机制。FARMER[7]通过理论分析围岩及锚固体微元体得到了锚固界面轴向位移解析式并比较了在不同围岩条件下受较小张拉荷载作用的全长锚固锚杆杆体剪应力分布,得出在软弱围岩中锚杆杆体会发生明显的脱粘现象的结论;HYETT 等[8]基于杆体表面剪应力和围岩-杆体的相对剪切位移的线性关系得到了在围岩存在裂隙的情况下的锚杆的轴力分布;TAO[9]给出了确定全长锚固锚杆中性点位置的公式;尤春安[3]基于Mindlin问题的位移,得到全长锚固锚杆沿杆体所受的剪切力分布的弹性解,并分析了全长黏结式锚杆的受力特征及其影响因素;姚显春[10]结合了尤春安的理论分析方法将全长锚固锚杆穿过的围岩依次分为3个部分,并根据各个部分剪应力特点确定中性点位置,再由半无限体受集中力作用的Mindlin得到杆体剪应力、轴力分布规律;杨更社等[11]分析了托盘对全长锚固锚杆杆体应力分布的影响并给出带托盘的全长锚固锚杆中性点位置的解析式;CAI等[12-13]在已有理论研究基础上提出了一种全长锚固锚杆应力分布理论分析模型,描述了锚杆与围岩相互作用机理,探讨了锚杆长度对支护效果的影响。但上述理论研究成果在分析过程中大多都简化了全长锚固锚杆的锚固效果且较少考虑实际围岩变形对全长锚固锚杆锚固效果的影响,得到的结论具有一定的局限性。
因此,笔者基于实际围岩变形及杆体受力平衡关系得到全长锚固锚杆在正常支护过程及临界失效时的轴力、剪应力解析表达式,考虑了锚杆及锚固剂弹性模量、锚杆及锚固剂横截面面积等锚固参数的影响对其进行修正,得到了全长锚固锚杆杆体应力分布规律,并着重分析了围岩条件、锚杆长度、托锚力对杆体应力分布的影响,为锚杆支护技术及设计提供了一定的理论依据。为了便于分析,本文先假定:① 巷道无限长,断面为圆形,变形属于平面变形问题;② 围岩具有各向同性,属于均质、连续体,未经采动影响的岩体处于静水压力的状态;③ 锚杆属于线弹性体,并沿巷道径向布置。
1 巷道表面岩体和深部岩体变形规律
在锚杆对围岩进行支护时,其杆体必须插入岩体才能达到支护目的,所以要深入的分析锚杆的受力特征,必须要理解锚杆支护过程中岩体深部变形和巷道周边岩体变形的关系。在这一问题上大部分学者取得了许多重要的研究成果,其中陆士良提出了深表比这个重要指标,其表示岩体深部位移和巷道周边位移的比值[14](图1),即
μr=Ur/U0
(1)
式中,μr为深表比;Ur为距巷道中心r处的岩体位移,m;U0为巷道的周边位移,m。

图1 巷道周边位移与岩体深部位移关系示意
Fig.1 Relationship between the displacement around the
roadway and the deep displacement of the rock mass
而深表比在巷道周边为最大值,从巷道周边至围岩深处按负指数曲线衰减,曲线方程为
μr=e-b(r-a0)
(2)
式中,b为与岩性有关的系数;r为巷道中心到岩体中某一点的距离,m;a0为巷道半径,m。
将式(2)代入式(1)中得
Ur=U0e-b(r-a0)
(3)
假定无锚杆条件下岩体位移Ur与有锚杆条件下岩体的实际位移Us(r)之差为
Fr=Ur-Us(r)
(4)
并假定杆体与围岩之间没有相对位移,即
Ub=Us(r)
(5)
则
Ub=Ur-Fr
(6)
式中,Ub为锚杆杆体的位移量。
进一步将Fr取成幂级数形式,即
Fr=m1+m2r+m3r2+m4r3
(7)
则
Ub=Ur-m1-m2r-m3r2-m4r3
(8)
2 杆体应力分布计算及规律分析
2.1 杆体受力解析计算公式的推导
取锚杆杆体微单元如图2所示,可得其轴力与杆体表面剪力关系为
dN=Tdr
(9)
式中,T为单元体表面所受剪力;N为杆体轴力。

图2 杆体微单元示意
Fig.2 A small element of the bolt
根据胡克定律可得杆体轴力为
N=AbEbb=AbEbdUb/dr
(10)
其中,Ab为锚杆杆体折算横截面面积:
Ab=As+AcEb/Ec
(11)
式中,As,Eb分别为锚杆横截面面积及弹性模量;Ac,Ec为锚固剂横截面面积及弹性模量。
由式(9),(10)可得
![]()
(12)
将剪切力T平均分布至锚杆上得到剪应力为
![]()
(13)
其中,d为锚杆杆体的直径,m。并由杆体表面所受剪切力T与托板反力Q平衡关系可得
![]() Tdr+Q=0
Tdr+Q=0
(14)
式中,L为杆体长度,m。
同时,由式(8),(10),(12)可得
T=AbEb[-U0e-b(r-a0)-m2-2m3r-3m4r2]
(15)
N=AbEb[b2U0e-b(r-a0)-2m3-6m4r]
(16)
在全长锚固锚杆安装过程中,对杆体尾部螺母人为的施加扭矩而产生预紧力,此时杆体应力分布与拉拔实验中锚杆应力分布一致。
之后在锚杆正常支护过程中,由于巷道周边不同深处围岩变形量不同,杆体各部分剪力方向不完全相同,一部分剪力与托盘反力方向相同并同时指向孔口方向且两者之和与指向锚固段端部的剪力平衡,使得杆体上存在中性点[7],即有中性点全长锚固锚杆(图3(a)),在中性点位置剪应力为零,轴力达到最大值。
随着围岩变形量不断增大,支护强度不可有效抑制围岩变形时,锚杆与围岩即将发生相对滑动,即支护临界失效时,杆体所受剪力方向均指向其端部并与托盘反力Q平衡,在孔口处和杆端剪应力为零,即无中性点全长锚固锚杆(图3(b))。

图3 全长锚固锚杆杆体受力情况
Fig.3 Forces acting on a fully anchored bolt
因此,下面先讨论图3(a)中杆体的受力情况,其边界条件为

(17)
式中,rx为孔口到中性点的距离,即中性点半径。
将边界条件式(17)代入式(15),(16)可得
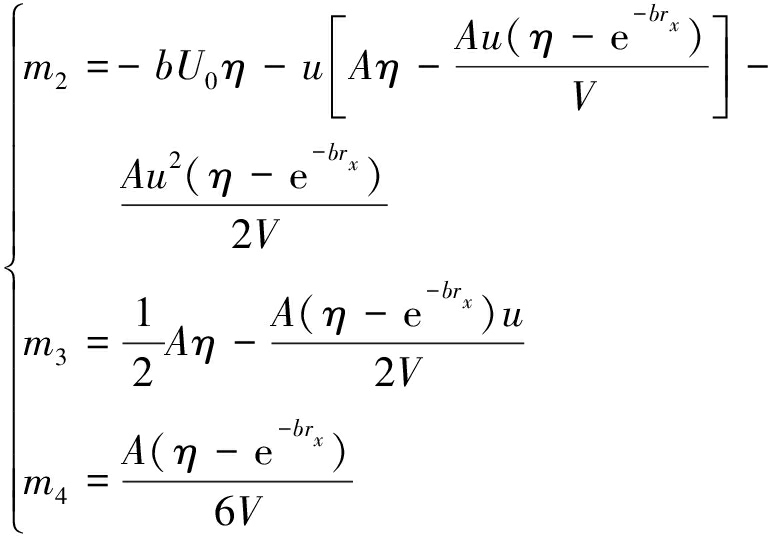
其中,η=e-bL;A=b2U0;u=a0+L;V=L-rx。
将m2,m3,m4代入式(15),(16)并联立式(13)得到剪应力和轴力表达式,有
![]()
(18)
N=AbEb(W-Ir-Kr2)
(19)
其中,![]()
将上述锚杆第1种受力情况中剪应力表达式及式(13)代入式(14)可得托板反力Q和中性点半径rx的关系,则
Q=H1+H2
(20)
式中,H1为第1个计算解析式;H2为第2个计算解析式,分别如下:
![]()
(21)
H2={-AbEbU0be-b(rx+L)[2Leb(rx+L)+
(bL+1)ebrx+ebL(bL2-4L)+2ebrx+bLebrx]}/2V
(22)
对于图3(b)中锚杆的受力情况,其边界条件为

(23)
将式(23)代入式(15),(16),则可求得系数m2,m3,m4。

同理,将m2,m3,m4的值代入式(15),(16)中并联立式(13)可分别得到锚杆剪应力及轴力解析式:
![]()
(24)
N={-AbEb{A(r-u)(-r+ηr+u+ηu)-
2Aη(-r+u)a0-2bL[eb(-r+a0)-η]U0}}/2L
(25)
2.2 有中性点的全长锚固锚杆受力算例分析
从式(18)~(20)看出有中性点的全长锚固锚杆锚固界面应力分布与相关锚固参数及围岩性质有关。现分别进行分析:
2.2.1 不同围岩条件对有中性点全长锚固锚杆应力分布影响
作为算例,假设巷道半径为2.7 m,锚杆长度为3.0 m,弹性模量为200 GPa,横截面面积450 mm2,锚固剂横截面面积550 mm2,弹性模量16 GPa,而当锚杆分别对极软岩、软岩、中硬及以上岩体中进行支护时,岩体的稳定性系数b和围岩表面位移量U0并不相同,文献[14]对不同围岩条件下的相关参数进行赋值,见表1。
表1 岩体相关参数
Table 1 Parameters of the surrounding rock

相关参数极软岩软岩中硬及以上稳定性相关系数b0.450.65>0.9表面位移量U0/m0.80.60.3
由表1可知,当锚杆在中硬及以上岩体中时,稳定性系数b取值应大于0.9,本文取值0.95。将上述参数代入式(20)中,可得到当锚杆在极软岩、软岩和中硬及以上岩体中时托盘反力与中性点半径关系曲线(图4)。

图4 不同围岩条件下托盘反力与中性点半径关系曲线
Fig.4 Relation curves of tray reaction force and the radius of neutral point under different surrounding rock conditions
由图4可以看出,托盘反力与中性点半径成反比,即随着托盘反力的增大,中性点向孔口方向移动,且岩体越坚硬,中性点移动范围越大且托盘反力整体变大,所以为了分析在不同围岩条件下有中性点全长锚固锚杆应力分布,以托盘反力为110 kN为例,得到杆体应力分布曲线(图5)。

图5 不同围岩条件下锚杆应力分布曲线
Fig.5 Distribution law of shear stress under different surro-
unding rock conditions
由图5可以看出,围岩越松软,中性点越向孔口移近。锚杆对极软岩及软岩支护时中性点至孔口这段范围内所受剪应力均小于在中硬及以上岩体中所受剪应力,而在中性点至杆端所受剪应力均大于在中硬及以上岩体中所受剪应力,在中性点处轴力均达到峰值,在极软岩中锚杆轴力峰值为137 kN,明显大于当锚杆在软岩及中硬岩中时所受轴力峰值,同时锚杆在极软岩中所受轴力均大于在软岩及中硬岩中所受轴力。说明锚杆在正常支护过程中,随着围岩变软,杆体中性点前移且轴力、剪应力增大。
2.2.2 不同托锚力对有中性点全长锚固锚杆应力分布影响
在锚杆支护过程中,托盘对围岩施加托锚力阻止围岩向巷道内位移,所以托锚力与托盘反力大小相等、方向相反,而托锚力根据锚杆支护过程不同分为初始托锚力、工作托锚力及残余托锚力[15],初始托锚力的形成主要依靠扭矩产生,在螺母拧紧后达到初始托锚力的最大值。之后在锚杆正常支护过程中,演化形成工作托锚力,最后支护逐渐失效形成残余托锚力[16]。从式(20)可以看出托盘反力会直接影响杆体应力分布,为了探究托锚力对锚杆杆体应力分布的影响,分别在不同托盘反力的条件下对全长锚固锚杆应力分布进行分析。

图6 托盘反力与中性点半径关系曲线
Fig.6 Relation curve of tray reaction force and the radius of neutral point with different support anchor forces
现假设巷道半径为2.7 m,围岩条件为软岩,锚杆及锚固剂参数与上述算例一致,则可得到托盘反力与中性点半径的变化曲线如图6所示,中性点移动范围为距孔口0.86 m处至孔口这一部分,在距孔口0.86 m处托盘反力有最小值72.8 kN。随着托盘反力的不断增大,中性点向孔口方向不断移动,当中性点位于孔口处时,托板反力达到峰值即托锚力有最大值146.3 kN。设置托锚力分别为80,90,100,110 kN,经计算得到了锚杆应力分布曲线(图7)。

图7 不同托盘反力条件下锚杆应力分布
Fig.7 Distribution law of shear stress with different tray reaction forces
从图7可看出,托锚力的变化影响杆体应力分布。从图7(a)可看出,锚杆所受剪应力沿杆体呈不均匀分布,在锚杆与围岩接触的孔口处,剪应力较大,方向指向孔口,在中性点位置处,剪应力减小至0,之后随着距中性点距离增大,剪应力快速增大到最大值且方向指向杆体端部,在峰值以后以较快速率衰减直至到杆体末端为0。而随着托锚力增大,中性点前移,剪应力分布越平缓,在孔口处剪应力减小,但其峰值变大。从图7(b)看出,在孔口处轴力较大,随着距孔口距离的不断增大,轴力先逐渐增大到峰值再迅速减小,轴力增大速率明显小于减小速率,并且峰值出现在中性点位置处。而随着托锚力不断增大,轴力分布越不均匀,中性点向孔口方向移动,杆体所受轴力也明显增大。
所以全长锚固锚杆在正常支护过程中,托锚力是影响全长锚固锚杆应力分布的重要因素。在锚杆实际支护过程中可实时监测锚杆托锚力,依据本文提出方法即可实时得到锚固界面应力分布曲线,可进一步深入揭示支护过程中锚杆受力特征。
2.2.3 不同锚杆长度对有中性点全长锚固锚杆应力分布影响
为了探究锚杆长度对支护过程中锚杆杆体应力分布的影响,保持除锚杆长度外其他相关参数与上述算例一致计算得到当锚杆长度分别为2.0,2.2,2.4,2.6 m时托盘反力与中性点半径的关系曲线(图8)。

图8 不同锚杆长度下托盘反力与中性点半径关系曲线
Fig.8 Relation curve of tray reaction force and the radius of neutral point with different bolt lengths
从图8可以看出,随着锚杆长度的增加,中性点移动范围变大,托盘反力整体增大,现设置托盘反力为55 kN,得到在不同锚杆长度条件下杆体的应力分布曲线(图9)。从图9看出,在锚杆正常支护过程中,不管锚杆长度多长,杆体所受剪应力及轴力分布均符合中性点理论,中性点始终位于锚杆长度的1/4处至孔口范围内,并随着锚杆长度的增加,孔口处锚杆所受剪应力增大,但其峰值减小;锚杆的最大轴力值减小,而自轴力峰值以后,锚杆所受轴力随着长度的增加而增大,所以在锚杆正常支护过程中,锚杆长度超过一定范围后再增大锚杆长度并不能显著提升锚杆的锚固效果。

图9 不同锚杆长度条件下锚杆剪应力分布曲线
Fig.9 Distribution law of shear stress under different bolt lengths
2.3 无中性点全长锚固锚杆受力算例分析
对于无中性点全长锚固锚杆的应力分布,可从其剪应力及轴力解析式看出两者大小与岩性及锚固参数有关。现分别在不同围岩、不同锚杆长度条件下对锚固界面应力分布进行模拟分析。
2.3.1 不同围岩条件对无中性点全长锚固锚杆应力分布的影响
巷道半径、锚杆及锚固剂参数与在不同围岩条件下的有中性点全长锚固锚杆各参数选取一致,以此得到了锚杆在不同围岩条件下支护临界失效时杆体的应力分布曲线,如图10所示。

图10 不同围岩条件下锚杆应力分布曲线
Fig.10 Distribution law of shear stress under different surrounding rock condition
从图10(a)可看出:无论锚杆对何种岩体支护,当锚杆不能有效抑制围岩变形时,剪应力均呈现不均匀分布,且在孔口处和杆端剪应力均为零,随着距孔口距离的增大,剪应力不断上升到峰值再快速衰减至零。当锚杆对中硬及以上岩体支护时,剪应力增大速率明显最大,并且在距孔口1.20 m处剪应力达到峰值1.6 MPa;当锚杆对软岩进行支护时,在距孔口1.30 m处剪应力达到峰值0.98 MPa;当锚杆对极软岩进行支护时,锚固界面各处的剪应力明显较小,在距孔口1.37 m处剪应力达到峰值0.4 MPa。说明在支护临界失效时,随着岩体稳定性系数减小,即岩体越松软,杆体所受剪应力减小且分布更均匀,最为明显的是岩体从软岩变为极软岩时锚杆所受剪应力最大值减小约2.5倍,且剪应力峰值位置向杆端方向移动。对于锚杆所受轴力分布,从图10(b)可以看出:当锚杆对中硬及以上岩体支护时,在孔口处轴力达到最大值236.0 kN,之后沿孔口指向杆端的方向快速减小直至衰减至零。而当锚杆分别对软岩和极软岩支护时,轴力分布与锚杆对中硬及以上岩体支护时相似,轴力峰值分别为146.2,57.6 kN,且轴力衰减速率明显小于锚杆对中硬及以上岩体支护时的衰减速率。说明在支护临界失效时,若岩体稳定性系数增大,即岩体越坚硬,岩体的弹模越大,会使得锚杆所受轴力增大,轴力作用相对更加集中。
2.3.2 不同锚杆长度对无中性点全长锚固锚杆应力分布的影响
为了探究锚杆长度对支护临界失效时锚杆杆体应力分布的影响,现假设巷道半径为2.7 m,围岩条件为软岩,锚杆、锚固剂横截面面积、弹性模量与上述算例一致,得到当锚杆长度分别为1.8,2.0,2.2,2.6,3.0 m时杆体的应力分布曲线,如图11所示。由图11可以看出,在全长锚固锚杆支护临界失效时,锚杆长度的增加,会使得杆体各处轴力及剪应力不断增大,说明当锚杆不能有效抑制围岩变形时,若增加锚杆长度能够提高锚杆锚固效果。

图11 不同长度条件下锚杆剪应力分布曲线
Fig.11 Distribution law of shear stress under different bolt lengths
3 结 论
(1)以围岩变形为基础,建立了锚杆-围岩相互作用模型,推导出全长锚固锚杆在正常支护及临界失效时杆体的轴力及剪应力解析表达式,并得到了影响锚杆应力分布的因素有围岩条件、锚杆及锚固剂参数、托锚力。
(2)在全长锚固锚杆正常支护过程中,杆体应力分布符合中性点理论。托锚力直接影响中性点位置,托锚力越大,中性点半径越小,导致中性点前移,孔口到中性点位置处剪应力减小,中性点到杆端剪应力增大。
(3)在全长锚固锚杆正常支护过程中,不同围岩条件下的有中性点全长锚固锚杆应力分布规律表现为围岩越松软,中性点越向孔口移近。在孔口至中性点范围内,锚杆在软岩中时杆体所受剪应力明显小于在中硬及以上岩体中所受剪应力;而在中性点至杆端范围内,锚杆所受剪应力均大于在中硬及以上岩体中所受剪应力,在中性点处轴力均达到峰值。在软岩中锚杆所受轴力处处大于在中硬岩中所受轴力,同时在软岩中时杆体所受轴力峰值大于在中硬岩中所受轴力峰值,表明锚杆在正常支护过程中,随着围岩变软,杆体中性点将前移且轴力、剪应力增大。
(4)在全长锚固锚杆支护临界失效时,不同围岩条件下的无中性点全长锚固锚杆应力分布规律表现为围岩越坚硬,杆体所受剪应力及轴力越大,表明锚杆在支护临界失效时,岩体稳定性系数越大,锚杆所受剪应力、轴力越大,应力分布更加集中。
(5)锚杆长度影响全长锚固锚杆的支护效果,但由于锚杆与围岩之间长期作用的时效性,当锚杆长度在合理的范围内时,增大锚杆长度可改善锚杆的支护性能,而在锚杆长度超过一定范围后再增大长度并不能显著提升锚杆的锚固效果。
[1] 谢和平,高峰,鞠杨,等.深部开采的定量界定与分析[J].煤炭学报,2015,40(1):1-10.
XIE Heping,GAO Feng,JU Yang,et al.Quantitative definition and Investigation of deep mining[J].Journal of China Coal Society,2015,40(1):1-10.
[2] 康红普.我国煤炭巷道锚杆支护技术发展60年及展望[J].中国矿业大学学报,2016,45(6):1072-1081.
KANG Hongpu.Sixty years development and prospects of rock bolting technology for underground coal roadways in China[J].Journal of China University of Mining & Technology,2016,45(6):1072-1081.
[3] 尤春安.全长粘结式锚杆的受力分析[J].岩石力学与工程学报,2000,19(3):339-341.
YOU Chun’an.Analysis of the force of full-length bond bolt[J].Chinese Journal of Rock Mechanics and Engineering,2000,19(3):339-341.
[4] BALLIVY G,BENMOKRANE B,IAHOUD A.Integral method for the design of grouted rock anchors[A].Ir IProc.6th ISRM Congr[C].Montreal:McGmwHill,1987.
[5] STILLE H,HOLMBERY M,Nord G Support of weak rock with ground bolts and shotcrete[J].Rock Mechanics & Rock Engineering,1989,22(3):73-78.
[6] FREEMAN T J.The behavior of fully-bonded rock bolts in the Kielder experimental tunnel[J].Tunnels and Tunnelling,1978,10(5):37-40.
[7] FARMER I W.Stress distribution along a resin grouted rock anchor[J].International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts,1975,12(11):347-351.
[8] HYETT A J,MOOSAVI M,BAWDEN W F.Load distribution along fully grouted bolts,with emphasis on cable bolt reinforcement[J].International Journal for Numerical and Analytical Methods in Geomechanics,2015,20(7):517-544.
[9] TAO Z,CHEN J X.Behavior of rock bolting as tunneling support[A].Stephansson O ed.Proceedings of the International Symposium on Rock Bolting[C].Rotterdam:Balkema,1984:87-92.
[10] 姚显春,李宁,陈蕴生.隧洞中全长粘结式锚杆的受力分析[J].岩石力学与工程学报,2005,24(13):2272-2276.
YAO Xianchun,LI Ning,CHEN Yunsheng.Theoretical solution for shear stresses on interface of fully grouted bolt in tunnels[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(13):2272-2276.
[11] 杨更社,何唐镛.全长锚固锚杆的托板效应[J].岩石力学与工程学报,1991,10(3):236-245.
YANG Gengshe,HE Tangyong.Effects of the backing plate of a wholly grouted rock bolt[J].Chinese Journal of Rock Mechanics and Engineering,1991,10(3):236-245.
[12] CAI Y,ESAKI T,JIANG Y J.An analytical model to predict axial load in grouted rock bolt for soft rock tunnelling[J].Tunnelling and Underground Space Technology Incorporating Trenchless Technology Research,2004,19(6):607-618.
[13] CAI Y,ESAKI T,JIANG Y J.An analytical model to predict axial load in grouted rock bolt for soft rock tunneling[J].Tunnelling and Underground Space Technology,2004,19(6):607-618.
[14] 陆士良,付国彬,汤雷.采动巷道岩体变形与锚杆锚固力变化规律[J].中国矿业大学学报,1999,28(3):201-203.
LU Shiliang,FU Guobin,TANG Lei.Regularity of deformation of rocks around roadway under mining influence and change of rockbolt resistance[J].Journal of China University of Mining & Technology,1999,28(3):201-203.
[15] 陆士良,汤雷,杨新安.锚杆锚固力与锚固技术[M].北京:煤炭工业出版社,1998.
[16] 郑西贵.煤矿巷道锚杆锚索托锚力演化机理及围岩控制技术[D].徐州:中国矿业大学,2013.
ZHENG Xigui.Evolution mechanism of coalmine roadway supporting anchoring force of bolt and cable and surrounding rock control technology[D].Xuzhou:China University of Mining and Technology,2013.
