煤岩变形破坏是内部裂纹萌生、扩展、汇聚的动态演化过程,利用声发射设备监测、采集裂纹发育所释放的弹性能在煤岩介质中传播的应力波振幅、频率特征可间接反映其内部裂纹演化规律。深入研究声发射信号时-频域特征与裂纹表征参量间的力学联动机制对提高基于声发射监测方法的冲击地压预警准确性具有重要的科学意义和工程价值。
关于煤、岩石材料破坏过程的声发射特征众多学者已经开展了大量研究。在声发射信号时域特征研究方面,LOCKNER D[1]利用实验方法研究了岩石破裂中裂隙发育与声发射特征信号间的关系;左建平等[2]对岩石、煤和煤岩组合体开展了单轴压缩过程声发射监测试验,探讨了不同材料声发射时空演化机制;ZHAO和JIANG[3],舒龙勇等[4]分别对冲击倾向性煤岩、突出煤岩受载变形过程声发射行为演化特征进行了试验研究,对其前兆信息规律进行了探讨;肖晓春等[5-6],苏承东等[7]采用试验方法对不同应力路径下的煤岩破坏过程声发射规律进行了分析和研究;赵兴东等[8-9]基于声发射定位技术对岩石裂纹动态破坏过程开展了试验研究;李德行等[10]探讨了裂纹倾角影响下的声发射响应、煤样峰值强度和裂纹扩展方式;BACKERS T等[11]利用实验方法对不同加载速率下岩石破坏过程的声发射活跃度进行研究。但现有研究多以声发射为监测手段对煤、岩体内部裂纹发育过程反演,鲜有对裂纹扩展影响的声发射信号特征与机制的相关报道。
在煤岩材料破坏声发射信号频域特征方面,何满潮等[12-14]分别对真三向应力状态下煤岩及花岗岩岩爆过程声发射频谱特征进行探讨;CAI M等[15],王恩元等[16],肖晓春等[17]分别利用傅里叶变换方法探讨了原煤、型煤、不同冲击倾向性和大尺度下煤岩破裂过程频域演化规律;苏国韶等[18],康玉梅等[19]利用小波变换方法建立了新的声发射定位延时估计;彭冠英等[20]根据岩石破坏的声发射信号波形特征构造了新的小波基函数并用于频域分析;赵奎等[21]基于小波分析手段对岩石破裂的Kaiser点信号开展了规律研究;杨永杰等[22]利用离散小波分析方法开展了灰岩压缩破坏声发射信号预测研究;高保彬等[23]基于小波变换方法对煤岩声发射信号开展了试验研究和信号降噪计算,有效提高了试验的准确性。现有的煤岩声发射信号频谱分析主要采用傅里叶变换方法对信号整体情况进行反映;而小波变换能实现对细节信息采集,目前该方法主要集中于岩石破坏声发射信号分析,关于煤岩的声发射信号小波频域研究甚少。
综合以上,笔者以物理试验结果为基础,引入数字信号分析相关理论与方法,开展基于小波包变换方法的煤岩破裂声发射信号时-频域规律研究,以岩石力学、断裂力学相关理论为基础,深入探讨煤岩裂隙扩展过程的应力波幅、频特性的力学机制,以期为煤岩失稳声发射前兆信息识别提供理论和试验指导。
1 试验系统
试验系统包括岩石力学测试系统和声发射监测系统:利用TAW-2000型刚性电液伺服压力机开展单轴压缩试验,试验机最大负荷2 000 kN,试验精度为示值的0.5%,设置加载速率为0.025 mm/s;声发射信号监测利用声华科技公司SAEU2S多通道声发射监测仪,传感器频率10~1 000 kHz,灵敏度峰值>75 db,采样频率1 000 kHz,参数和波形门槛值均为40 db,主放增益20 db,采样点1 024个。试验所用煤岩采集自辽宁阜新某矿,按国际岩石力学测试标准切割成尺寸为φ50 mm×100 mm的标准煤岩试样。试验中,将试样置于屏蔽缸内的上、下压头之间,并将声发射探头固定在煤岩表面,传感器接收面与煤岩表面涂耦合剂充分保证接触良好,试验结果由数据线穿过传输孔传输至采集仪并存,利用MATLAB软件进行后处理,试验系统如图1所示。

图1 试验系统
Fig.1 Test system
2 单轴压缩过程的煤岩力学性质及声发射变化规律
2.1 煤岩受载过程力学性质变化规律
图2为完整性较高、含有弱夹矸或裂隙、弱夹矸与裂隙共存3种煤岩典型应力应变曲线。

图2 3种类型煤岩典型应力-应变曲线
Fig.2 Typical stress-strain curves of three types of coal
根据图2中3种类型煤样的应力-应变曲线,取自同一开采层的煤岩试样受其内部弱夹矸或孔裂隙影响煤岩强度具有显著差异,应力-应变曲线仍具有岩石典型的压密、弹性、强化和峰后阶段,但煤样完整性越好即无弱夹矸无明显表面裂隙情况,其强度越高、弹性阶段较长、峰后阶段应力跌落越明显、破坏时间缩短,反之则峰后应力软化特征越显著。根据弹性阶段应力-应变关系计算平均弹性模量![]() 统计获得了试验所用煤岩试样受软弱夹矸和裂隙影响的弹性模量变化范围,见表1,统计结果表明,弹性模量随着煤岩的完整性提高而增加。
统计获得了试验所用煤岩试样受软弱夹矸和裂隙影响的弹性模量变化范围,见表1,统计结果表明,弹性模量随着煤岩的完整性提高而增加。
表1 3种类型煤岩平均弹性模量![]() 范围
范围
Table 1 Average elastic ![]() range of three types of coalGPa
range of three types of coalGPa

裂隙弱夹矸共存煤样裂隙或弱夹矸煤样较完整煤样0.41~0.920.95~1.461.52~2.87
2.2 不同强度煤岩声发射信号时域特征
选择声发射能量(Q)和累积能量(∑Q)为特征参量分析具有不同强度煤样变形破坏过程的声发射信号演化规律,在所有试验结果中选取3组受夹矸及孔裂隙影响呈高、中、低3种强度的煤岩试样典型受载破坏过程力、声发射能量、声发射能量累积量随时间变化关系曲线,如图3所示。

图3 3种类型煤样应力、声发射能量、声发射累积量-时间曲线
Fig.3 Stress,AE energy,AE energy accumulation-time curves of three types of coal
结果表明,单轴压缩过程煤岩力学性质与监测获得的声发射能量变化具有明显的规律性。在加载初期的压密阶段均有零星微弱的声发射能量信号产生,弹性阶段存在声发射信号激增点,该时刻声发射能量信号幅值明显升高,同时能量累积曲线的斜率也在该点后逐渐变大。在图3(a)中的压密阶段就有高幅值信号出现,但较为离散,而在弹性阶段为多个高幅值信号连续出现因而确定该点为信号激增点。声发射激增点的存在表明监测到裂纹扩展释放的弹性能显著增加,可以推断该点前后煤岩内部裂纹的尺寸和扩展速率发生了显著变化;在随载荷继续上升达峰值前阶段,高幅值信号密集、连续产生,累积曲线斜率继续增长,但在两相继产生的高幅值信号间常伴随有一段信号小幅值震荡,能量累积曲线增长斜率也略有减小趋势,这表明该阶段内有宏观裂纹形成并扩展,且前后两次扩展的时间间隙为驱动力的集聚过程,这侧面反映了大尺度裂纹形成、扩展是一个发育-蓄能的渐进过程[24];载荷继续升高达峰值后具有应力跌落现象,同时伴随有显著的能量高值信号出现,声发射累积曲线具有陡增现象;峰后软化阶段高幅值信号密集产生,能量累积曲线增长速率为整个受载过程最大,这表明峰值时刻及峰后阶段煤岩中宏观主破裂形成、贯通过程连续释放大量能量。
以3个典型试验结果为例,随煤岩强度增加声发射激增点所对应的应力值越大,从裂纹发育角度分析,将信号激增点处应力值定义为煤岩内部细观微裂隙向宏观大裂隙转化的临界应力,煤样强度越高结构完整性越好,应力强度因子K越大,裂纹起裂临界应力越高,则扩展过程对外界释放的盈余能越多,声发射监测到的能量信号幅值越大、累积量越多。对于较完整的高强度煤样,激增点后声发射能量累积量曲线斜率远高于其他两组应力较低的煤岩,累积的声发射能量达60.516 mV·s,如图3(a)中实线所示,裂隙或弱夹矸存在的中强度煤样声发射累积能量为39.21 mV·s,裂隙弱夹矸共存的低强度煤样声发射累积能量最小为28.132 mV·s,如图3(b)和(c)所示。
根据声发射能量计算方法,单位时间内所监测到的全部事件能量总和与波形幅值的平方成正比。为深入了解激增点和峰值点声发射信号所携带的特征信息,分别选取了3种强度煤岩受载过程中两特征点的声发射原始时域波形,如图4所示。由图4中的试验结果表明,声发射时域信号波形幅值随激增点应力降低逐渐减小,强度较高煤样的波形信号两相邻峰值的间隔时间较长,而中等强度和软弱煤样信号相邻波峰间隔时间缩短,同时在每个大波形中夹杂的小幅震荡信号逐渐增多。
由图5中试验结果,在峰值点处声发射信号的波形变化规律与激增点相同且规律性更加明显,煤岩强度越高其声发射相邻两波峰间隔时间越长、信号幅值越大,随强度降低间隔时间变短,信号中夹杂的小震荡波形越多。

图4 3种类型煤岩试样信号激增点的声发射时域波形
Fig.4 Acoustic emission time domain waveform of the signal surge point of three types of coal samples
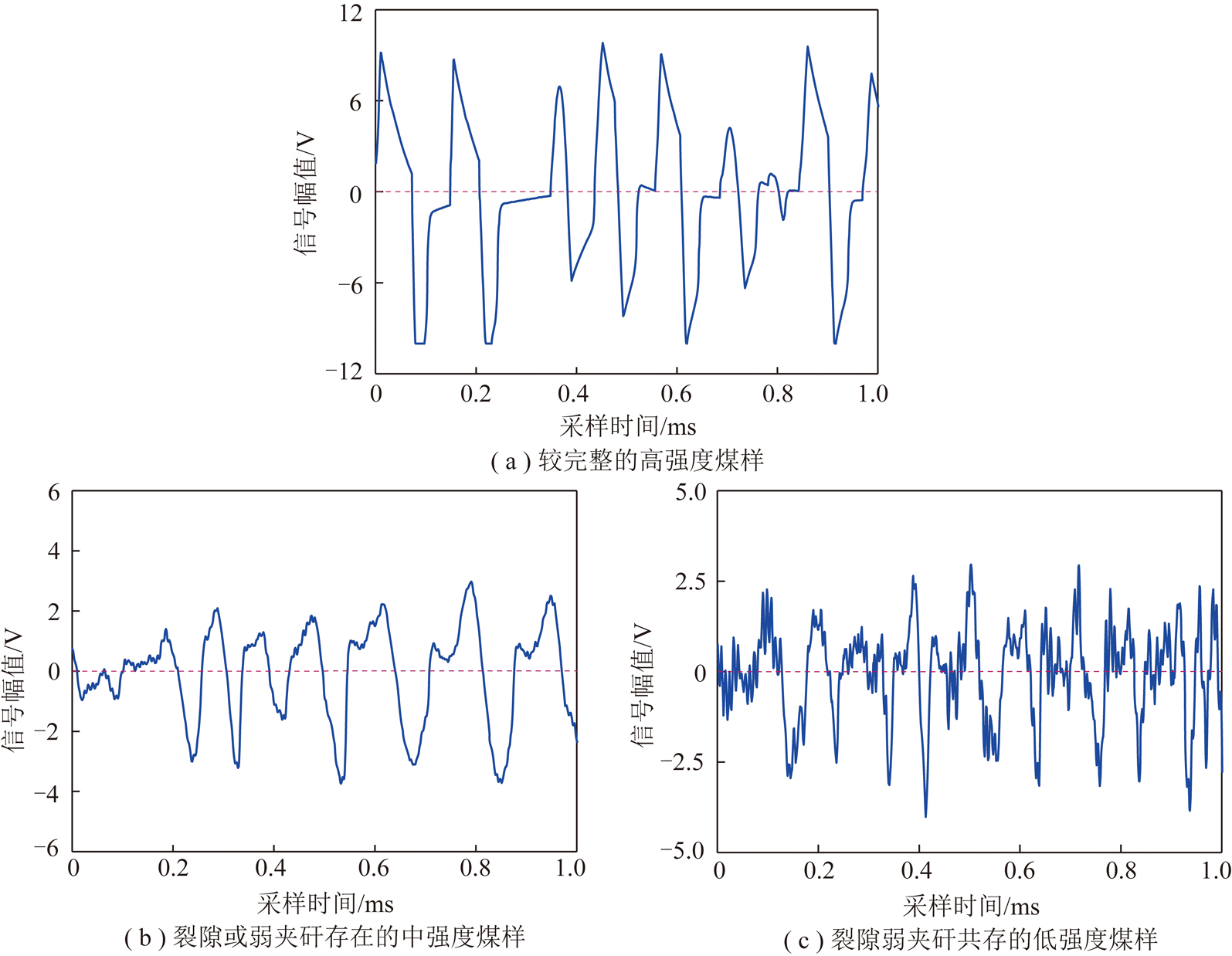
图5 3种类型煤岩试样信号应力峰值点的声发射时域波形
Fig.5 Acoustic emission time domain waveform of the peak stress point of three types of coal samples
根据声发射采样基本原理[25],数字信号是多个具有不同频率的波形信号叠加组成,仅对时域波形探讨无法将信号中蕴含的特征信息完全反映,因而还需要在频域对信号特征进一步研究。
3 基于小波分析的煤岩破裂过程声发射频域信号特征
小波变换是将特定函数作基,在时域和频域同时对数据信号开展多尺度分析,与傅里叶变换相比,该方法在对信号细节特征反映的同时不会因一点的突变而影响整个频域规律优势明显,其原理如图6所示。

图6 信号小波分析原理
Fig.6 Signal wavelet analysis principle
3.1 小波分析基本原理与最优小波基选取
对一组数字信号可表述为ψ(t)∈L2(R),其傅里叶变换![]() 为
为

(1)
小波变换基本原理是将小波基函数作位移τ,在不同尺度a下与待分析信号作内积运算,即

(2)
尺度控制小波函数的伸缩对应于频率,平移量控制小波函数的平移对应于时间。
小波基函数按单位尺度和平移量从信号始端逐次与信号相乘至尾端后获得一系列小波,不同小波展现了原始信号中不同频率下的信号细节信息即小波系数,小波系数就是小波基函数在每一次变换后与原信号的相似程度,再利用小波重构函数式(3),对不同尺度下的小波系数还原获得不同频率的特征时域信号,小波基函数与原信号的在整体相似度越大结果越精确。
本节中选择haar,morl,mexh,dbN等11个常用小波基函数,逐次与各试验结果的激增点和峰值点处声发射波形信号对比,以获得相关性最高的最优小波基函数。图7为各特征点与小波基函数的相似度。
![]()
(3)

图7 小波基函数与声发射波形相似度
Fig.7 Similarity between AE waveforms and wavelet basis function
图7中散点为各基函数比较相似度结果散点,框图中“★”代表平均值,与框图中横线上、下位置反映平均值与总体分布范围关系。结果表明,激增点波形与db5函数平均相似度最高,峰值点波形与sym2函数平均相似度最高,如图8所示,分别选择相似度最高的基函数开展小波变换能获得最准确的声发射信号时-频特性。

图8 最优小波基函数
Fig.8 Best wavelet basis function
dbN小波基函数没有明确的形式,但其传递函数的模的平方具有显式表达,小波函数Ψ(t)和尺度函数φ(t)中的支撑区为2N-1,Ψ(t)的消失矩为N,具有较好的正则性;symN小波基函数也无明确的显式表达,是对dbN小波基函数的改进,具有支撑范围为2N-1,消失矩为N,也具备较好的正则性。利用小波Besttree分析结果,确定试验结果的最佳分析层数均为3层。
3.2 煤岩信号激增点和峰值点声发射信号时域-频域规律
通过对所有的试验结果开展小波变换获得了试验所用煤样的声发射信号时-频域变化特征,选择3种类型煤岩信号激增点声发射时-频域信号色谱图进行探讨,如图9所示。

图9 3种类型煤岩试样信号激增点的声发射时-频域特征
Fig.9 Time-frequency characters of the signal surge point of three types of coal samples
根据图9中时-频域关系曲线结果,将频率范围分成3个频带,第1频带0~70 kHz,第2频带70~225 kHz,第3频带225~500 kHz。随信号激增点应力值差异,高强度和中等强度煤岩声发射频率分量均集中在第1和第2频带内,且前者在第1频带内的分量少于后者;与高、中强度煤岩相比,低强度煤岩试样声发射频域覆盖范围较宽泛,在3个主频带内均有分布。3种类型煤岩声发射信号的高值(颜色较深部分)都集中在第1主频带内,且在该频带的分量信号幅值随应力水平提高而增加,表明第1频带为声发射信号的主频,信号激增点应力越低,信号中夹杂的高频信号分量越多,反之应力越高信号频域组成越单一。
图10为3种类型煤岩峰值点声发射时-频域信号色谱图。图10峰值点处的声发射信号主频仍然集中在第1频率带(0~70 kHz)、少量信号分量频率在第2频带,且信号在第1频域内的分量幅值随强度升高具有明显的增加特征,将图10与图5相结合,随着煤岩强度减小信号中夹杂的小振幅波的增多,其频域覆盖范围明显增加,特别是较软弱煤岩,信号频率在第1,2,3频带内均有分布。结果表明,随着煤岩强度降低其声发射信号频域覆盖范围越宽泛,信号的组成频率分量越多。

图10 3种类型煤岩试样信号峰值点的声发射时-频域特征
Fig.10 Time-frequency characters of the peak stress point of three types of coal samples
为量化分析不同应力时信号激增点和峰值点声发射特征,分别利用db5和sym2小波基函数对声发射信号开展3层小波包分析处理并根据式(4)~(6)获得了各频带的能量比例。
![]()
(4)
![]()
(5)
![]()
(6)
其中,Q0为信号总能量;Qn,j为n层小波包能量分量;j为节点;η为信号能量分量百分比。
图11结果更直观的反映了随应力水平提高,声发射信号的频带组成由多频率向单一频率过渡。具体表现为,随应力值升高,0~125 kHz频带信号能量所占百分比增加。结合前文试验结果,认为文献[16,18]中“随加载临近峰值声发射信号主频前移”现象的根本原因是煤岩的主破裂频带范围固定,随受载升高宏观主破裂形成,主频带范围内的信号分量比重逐渐增加,高频分量逐渐减小。

图11 3种类型煤岩试样声发射频带能量特征
Fig.11 Acoustic emission frequency band energy charac-
teristics of three types of coal samples
4 煤岩裂纹扩展过程应力波传递力学机制与声发射影响因素
煤岩作为一种脆性材料,声发射仪主要监测裂纹尖端扩展所释放的弹性能在煤岩内形成的应力波,释放的能量大小直接影响应力波传递特征,进而引起声发射信号变化。取单一裂纹为研究对象,并作如下假设:① 裂纹受载-扩展过程遵循能量守恒定律同时体系内能保持不变;② 伴随裂纹扩展产生的弹性能在煤体中主要以纵波形式传递;③ 裂隙至表面部分煤岩视为均质体,不考虑应力波衰减。图12为示意图,裂纹长度为2c,宽度为B,张开角度为θ,其所在平面的截面积为A,E为弹性模量,σA为裂纹受到的应力,扩展释放的弹性能向除去裂纹张开截面以外的球面的空间均匀释放。在以裂纹中心为球心、半径为r的球面内存在近似矩形的微小面元S,应力波在面元S上的分量产生平均激振力P0,εr为径向应变,u为应力波传递长度。
根据能量守恒定律煤岩内部单一裂纹系统总能量(U)与应变能(UM)、表面能(US)和惯性动能(UK)间的关系为
U=UM+US+UK
(7)

图12 应力波传递
Fig.12 Stress wave transmission
裂纹所受应力超过临界扩展应力(σc)则裂纹发生扩展。当应力达临界扩展应力时表面能US=0,系统中惯性动能UK=0,在 “固定边界”恒位移加载方式下裂纹系统所具有的总能量(U)为系统的应变能:
![]()
(8)
US=4cγ
(9)
其中,γ为表面能释放率。裂纹完成扩展后应力迅速降低而停止扩展,由式(7)可知,其内部的应变能降低,应力再次逐渐升高至应力峰值发生二次扩展前裂纹系统的表面能保持稳定,如图13所示。

图13 裂纹驱动力,表面能与长度关系[24]
Fig.13 Relationship of creak force and interface energy with creak length[24]
在裂纹扩展结束的短暂稳定时间内,外力对系统做功为0,则裂纹扩展瞬间系统所具有的总能量就是系统的应变能,扩展前后系统能量转化关系为
![]()
(10)
则应力波所具有的动能数值上就为伴随裂纹扩展过程的惯性能:
![]()
(11)
由式(11)可知,当裂纹单位表面能与裂纹长度固定,伴随裂纹扩展释放的惯性能随裂纹扩展临界应力与跌落后的应力差值正相关变化。另一方面在常位移加载方式下,煤岩内部裂纹体系始终具有恒定的轴向应变(εA),将Mott动能方程与裂纹扩展柔度变换方程相结合[25],在常位移加载过程中以速率描述的惯性能(UK)表述为
![]()
(12)
![]()
(13)
式中,k′为数值常数;ρ为煤岩试样的密度;v为裂纹扩展速率;α为量纲参量表示裂纹尺寸相对于样品尺寸的大小;c0为裂纹未发生扩展的临界尺寸。
由于所取的球面半径微小,将裂纹尾部张开面积近似看成矩形,根据几何关系其面积S1为
![]()
(14)
剩余均匀受载部分面积表述为空间球面面积与尾部张开面积的差值:
![]()
(15)
面积为S的微元受到的能量分量(U′S)与总能量间的关系可表述为

(16)
根据受迫振动激振力的功能关系,应力波产生的激振力在一个周期内做功为
U′S=W=πAPP0sin φ
(17)
其中,AP为振幅。在振动过程中引起煤岩微元体径向应变与应力波振幅、平均激振力间的关系分别为
AP=εru
(18)
P0=SEεr
(19)
将式(16),(18),(19)代入式(17),则煤岩内部单一裂隙扩展释放弹性能引起的纵波振动幅值表述为

(20)
在纵波传递过程中,vP为波速,f为频率与振幅三者间分别存在关系式:
vp=2πfAp
(21)
vP={E(1-μ)/[ρ(1+μ)(1-2μ)]}1/2
(22)
其中,μ为泊松比。将式(20)~(22)联立,则煤岩破裂过程单一裂纹扩展过程释放弹性能引起的纵波振动频率表述为
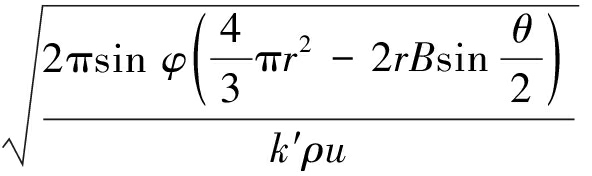
(23)
式(20)和式(23)分别为煤岩裂纹扩展过程释放弹性能在煤岩体内部产生应力波的振幅、频率力学表达,在固定位移加载条件下煤岩具有恒定的轴向应变,其弹性模量和密度一定时,在煤岩表面监测到的应力波振幅与裂纹尺寸、扩展速率呈正相关变化,与弹性模量呈负相关变化;而应力波频率与裂纹尺寸、扩展速率呈负相关变化,与弹性模量呈正相关变化。
为进一步明确裂纹尺寸、扩展速率和弹性模量对应力波幅值、频率的影响,根据文献[24]选择了典型裂纹扩展速率、长度,具体见表2。结合试验结果,选择弹性模量E=1.5 GPa代入式(20)和式(23)分别获得了裂纹扩展速率影响的应力波振幅与频率关系曲线,如图14所示。
表2 试验参数
Table 2 Experimental parameters

裂纹尺寸比c/c0裂纹扩展速率v/(m·s-1)弹性模量E/GPa密度ρ/(kg·m-3)1,3,5,7,9,110~5 0000.41~2.871 460

图14 裂纹扩展速率与振幅、频率关系
Fig.14 Relationship between creak growth rate and amplitude,frequency
由图14(a)中应力波振幅与裂纹扩展速率呈正比例函数关系增长,裂纹扩展速率在0~1 500 m/s时振幅增长了0.1 mm,而扩展速率在1 500~5 000 m/s振幅幅值变化量均在1个数量级内;在同一扩展速率下随着裂纹尺寸逐渐增加,振幅呈增大趋势但增长量逐渐减小,认为裂纹尺寸对振幅的影响会逐渐趋于某一固定值,裂纹扩展速率是决定振幅大小的主要参数。由图14(b)中应力波频率与裂纹扩展速率间呈非线性负相关变化,扩展速率在0~1 km/s的阶段频率降低十分明显,从108数量级迅速降低到105数量级,而1~5 km/s频率降低趋势逐渐减小;当扩展速率相同,随裂纹尺寸增加应力波频率呈减小趋势并且影响程度逐渐降低。

图15 弹性模量与振幅、频率关系
Fig.15 Relationship between elastic module and amplitude,frequency
设定裂纹扩展速率v=2 km/s获得了弹性模量影响下的应力波振幅与频率间关系(图15)。由图15(a)中振幅与弹性模量监测呈非线性负相关变化,在0.4~1.2 GPa,振幅降低趋势明显,在1.2~3.2 GPa振幅变化趋于平缓,在同一弹性模量下随着裂纹尺度增加振幅逐渐增大但振幅增量逐渐减小,总体看来弹性模量对振幅的影响在1个数量级内。由图15(b)中振动频率与弹性模量呈线性正相关变化,相同长度裂纹产生的应力波振动频率随弹性模量增加而提高,变化量均在1个数量级内,在相同弹性模量下随裂纹长度增加振动频率逐渐降低,降幅随长度增加逐渐减小。
理论分析表明裂纹扩展速率和弹性模量影响下应力波振幅均在0.01~0.1 mm,随裂纹长度增加呈增高趋势,因而弹性模量和裂纹扩展速率共同确定了振幅的范围,裂纹尺寸决定了振幅的变化趋势;对振动频率的影响裂纹扩展速率较弹性模量明显,特别是在0~1 km/s的低速扩展阶段近似达3个数量级,在1~5 km/s的中高速扩展阶段频率逐渐降低,逐渐接近弹性模量影响范围,因而裂纹扩展速率是决定应力波频率的关键参量。试验中信号激增点应力较低,裂纹尺寸较小,不同强度煤岩弹性模量虽然具有明显差异,但在受载初期裂纹扩展速率较低,二者共同决定了应力波幅值大小;另一方面低强度煤岩信号激增点处应力较低,裂纹扩展越缓慢,则应力波幅值越小,声发射时域信号幅值随应力水平降低而减小,而应力波振幅主要受裂纹扩展速率影响,速率越低应力波频率越高,声发射频域覆盖范围宽泛;同样的在峰值点处,应力越高其宏观裂纹扩展速度越快、应力波幅值越大并逐渐向低频过渡,声发射时域信号振幅随应力增高而增大,频域覆盖范围减小向主频带移动。
分别在试验结果各选取激增点和峰值点所对应的声发射信号实测结果,参数理论结果见表3。将振动实测频率代入式(23)获得裂纹空间传播特征计算结果,进而再将结果代入式(20)获得振幅理论值。
结果表明理论计算值大于实测值,存在相当的误差但数量级基本相同,这主要是由于裂纹尺寸和扩展速率无准确实测结果所致。从定性角度看,理论结果对前文中试验规律能较好的吻合,但后续还需继续开展定量化分析研究与验证。
表3 实测结果与参数设定
Table 3 Measured results and parameter setting

信号点幅值/V频率/kHz波速实测结果/(m·s-1)裂纹尺寸/m裂纹扩展速率/(km·s-1)波速理论结果/(m·s-1)激增点0.27154.8×10-54×10-415.6×10-5峰值点8.99151.5×10-32×10-356.8×10-3
注:由于裂纹尺寸和扩展速率无法测量,验证计算中相应数值结合相关资料[24]人为设定。
5 结 论
(1)受夹矸和原生裂隙影响同一采煤工作面煤岩力学性质具有显著离散性,随所含夹矸或裂隙增加而强度、弹性模量降低,峰后软化特征明显,受载过程声发射存在由低幅振荡向高幅脉冲转化的信号激增点,统计表明随煤岩强度升高,激增点和峰值点的特征信号波形幅值越大,相邻波峰间隔增加,夹杂的小震荡波形越少,整个受载过程总能量越多。
(2)选取信号激增点和峰值点声发射特征信号与小波基函数相似性对比表明db5和sym2小波基函数分别与激增点和峰值点相似度最高,最佳分解层数为3,db5和sym2小波基函数对煤岩声发射信号时-频域变换更加适用,为后续开展相关研究提供了借鉴,煤岩受载、破坏过程声发射信号主频带为0~70 kHz,但煤岩强度越低信号频率分布越宽泛,随受载应力提高信号频带分布范围逐渐向主频移动、信号主频带分量幅值越低。
(3)声发射主要监测伴随着裂纹发育释放盈余应变能在煤岩中形成的应力波,基于断裂力学、振动力学相关理论构建了裂纹扩展释放弹性能引起应力波的振幅、频率力学表达,理论分析表明弹性模量和裂纹扩展速率共同确定了振幅的范围,裂纹尺寸越大应力波振幅越大、频率越低,裂纹扩展速率是决定应力波频率的关键参量,煤岩受载过程的应力大小影响了裂纹扩展速率和尺寸造成了应力波参量变化,进而产生了声发射信号的特征性规律,结合实测结果初步验证了理论结果的准确性。
[1] LOCKNER D.The role of acoustic emission in the study of rock fracture[J].International Journal of Rock Mechanics,Mining Science & Geomechanics.1993,30(7):88-899.
[2] 左建平,斐建良,刘建锋,等.煤岩体破裂过程中声发射行为及时空演化机制[J].岩石力学与工程学报,2011,30(8):1564-1570.
ZUO Jianping,FEI Jianliang,LIU Jianfeng,et al.Investigation on acoustic emission behavior and its time-space evolution mechanism in failure process of coal-rock combined body[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(8):1564-1570.
[3] ZHAO Yixin,JIANG Yaodong.Acoustic emission and thermal infrared precursors associated with bump-prone coal failure[J].International Journal of Coal Geology,2010,83:11-20.
[4] 舒龙勇,王凯,张浪,等.突出煤体受载变形破坏声发射行为演化特征[J].采矿与安全工程学报,2018,35(3):589-597.
SHU Longyong,WANG Kai,ZHANG Lang,et al.Investigation on acoustic emission behavior evolution characteristics of outburst coal under uniaxial compression[J].Journal of Mining & Safety Engineering,2018,35(3):589-597.
[5] 肖晓春,丁鑫,潘一山,等.颗粒煤岩破裂过程声发射与电荷感应试验[J].煤炭学报,2015,40(8):1796-1804.
XIAO Xiaochun,DING Xin,PAN Yishan,et al.Experiment of acoustic emission and charge induction in granular coal rock failure[J].Journal of China Coal Society,2015,40(8):1796-1804.
[6] 丁鑫,肖晓春,吴迪,等.不同加载路径煤岩破裂过程声-电荷复合信号特性[J].煤炭学报,2016,41(S2):359-368.
DING Xin,XIAO Xiaochun,WU Di,et al.Study on compound signal characteristics of acoustic emission and charge induction in coal rock failure under different loading paths[J].Journal of China Coal Society,2016,41(S2):359-368.
[7] 苏承东,高保彬,南华,等.不同应力路径下煤样变形破坏过程声发射特征的试验研究[J].岩石力学与工程学报,2009,28(4):757-766.
SU Chengdong,GAO Baobin,NAN Hua,et al.Experimental study on acoustic emission characteristics during deformation and failure processes of coal sample under different stress paths[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(4):757-766.
[8] 赵兴东,李元辉,袁瑞甫,等.基于声发射定位的岩石裂纹动态演化过程研究[J].岩石力学与工程学报,2007,26(5):944-950.
ZHAO Xingdong,LI Yuanhui,YUAN Ruifu,et al.Study on crack dynamic propagation process of rock samples based on acoustic emission location[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(5):944-950.
[9] 赵兴东,李元辉,刘建坡,等.基于声发射及定位技术的岩石破解过程研究[J].岩石力学与工程学报,2008,27(5):990-995.
ZHAO Xingdong,LI Yuanhui,LIU Jianpo,et al.Study on rock failure process based on acoustic emission and its location technique[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(5):990-995.
[10] 李德行,王恩元,李楠,等.单轴压缩下宏观裂纹倾角对煤体特性影响研究[J].岩石力学与工程学报,2017,36(S1):3206-3213.
LI Dexing,WANG Enyuan,LI Nan,et al.Research on the coal characteristics of macro-crack dip angles under uniaxial compression[J].Chinese Journal of Rock Mechanics and Engineering,2017,36(S1):3206-3213.
[11] BACKERS T,STANCHITS S,DRESEN G.Tensile fracture propagation and acoustic emission activity in sand stone:the effect of loading rate[J].International Journal of Rock Mechanics & Mining Sciences,2005,42:1094-101.
[12] HE M C,MIAO J L,FENG J L.Rock burst process of limestone and its acoustic emission characteristics under true-triaxial unloading conditions[J].International Journal of Rock Mechanics & Mining Sciences,2010,47:286-298.
[13] 苗金丽,何满潮,李建德,等.花岗岩岩爆声发射特征及微观断裂机制[J].岩石力学与工程学报,2009,28(8):1593-1603.
MIAO Jinli,HE Manchao,LI Jiande,et al.Acoustic emission characteristics of granite under strain rock burst test and its micro-fracture mechanism[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(8):1593-1603.
[14] 宫宇新,何满潮,汪政红,等.岩石破坏声发射时频分析算法与瞬时频率前兆研究[J].岩石力学与工程学报,2013,32(4):787-799.
GONG Yuxin,HE Manchan,WANG Zhenghong,et al.Research on time-frequency analysis algorithm and instantaneous frequency precursors for acoustic emission data from rock failure experiment[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(4):787-799.
[15] CAI M,KAISER P K,MORIOKA H,et al.FLAC/PFC coupled numerical simulation of AE in large-scale underground excavation[J].International Journal of Rock Mechanics and Mining Science,2007,44(4):550-564.
[16] 王恩元,何学秋,刘贞堂,等.煤体破裂声发射的频谱特征研究[J].煤炭学报,2004,29(3):289-292.
WANG Enyuan,HE Xueqiu,LIU Zhentang,et al.Study on frequency spectrum characteristics of acoustic emission in coal or rock deformation and fracture[J].Journal of China Coal Society,2004,29(3):289-292.
[17] 肖晓春,金晨,丁鑫,等.基于声发射时频特征的不同含水煤样冲击倾向试验研究[J].煤炭学报,2018,43(4):931-938.
XIAO Chunxiao,JIN Chen,DING Xin,et al.Experimental study on rock burst tendency of coal with different moisture content based on acoustic emission time-frequency signals[J].Journal of China Coal Society,2018,43(4):931-938.
[18] 苏国韶,石焱炯,冯夏庭,等.岩爆过程中声音信号特征研究[J].岩石力学与工程学报,2016,35(6):1190-1201.
SU Guoshao,SHI Yanjiong,FENG Xiating,et al.Acoustic signal characteristics in rock-burst process[J].Chinese Journal of Rock Mechanics and Engineering,2016,35(6):1190-1201.
[19] 康玉梅,白泉,朱万成,等.基于小波变换时频能量分析技术的岩石声发射信号时延估计[J].岩石力学与工程学报,2010,29(5):1010-1016.
KANG Yumei,BAI Quan,ZHU Wancheng,et al.Time-delay estimation of acoustic emission signals of rock using time-frequency energy analysis based on wavelet transform[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(5):1010-1016.
[20] 彭冠英,许明,谢强,等.基于岩石声发射信号的指数衰减型小波基构造[J].岩土力学,2016,36(7):1868-1876,1894.
PENG Guanying,XU Ming,XIE Qiang,et al.Construction of exponential attenuation wavelet basis by characteristics of rock acoustic emission[J].Rock and Soil Mechanics,2016,36(7):1868-1876,1894.
[21] 赵奎,邓飞,金解放,等.岩石声发射Kaiser点信号的小波分析及其应用初步研究[J].岩石力学与工程学报,2006,25(S2):3854-3858.
ZHAO Kui,DENG Fei,JIN Jiefang,et al.Wavelet analysis of Kaiser signal of rock acoustic emission and its application[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(S2):3854-3858.
[22] 杨永杰,王德超,陈绍杰,等.基于离散小波分析的灰岩压缩破坏声发射预测研究[J].煤炭学报,2010,35(2):2013-2017.
YANG Yongjie,WANG Dechao,CHEN Shaojie,et al.AE predicting study on compression and fracture of limestone sample based on discrete wavelet analysis[J].Journal of China Coal Society,2010,35(2):2013-2017.
[23] 高保彬,李回贵,王晓蕾,等.基于小波包变换的不同强度煤样的声发射特性[J].煤田地质与勘探,2013,41(6):53-57.
GAO Baobin,LI Huigui,WANG Xiaolei,et al.Acoustic emission characteristics of coal samples with different strength based on wavelet packet transform[J].Coal Geology & Exploration,2013,41(6):53-57.
[24] BRIAN Lawn.Fracture of Brittle Solids:2nd edition[M].London:Cambridge University Press,2009.
[25] 程佩青.数字信号处理教程(第四版)[M].北京:清华大学出版社,2015.06.
