裂隙岩体的渗透特性在空间上存在客观的各向异性取决于岩体中不同产状、迹长、隙宽、密度等几何特征[1]。目前多采用双重介质模型、等效连续介质模型、混合模型、离散裂隙网络等渗流模型来研究裂隙岩体的渗流[2]。等效连续介质模型凭借其计算量小、操作简单等优势,在大型岩体工程的渗流分析中应用最为广泛,而且可以清楚地描述裂隙水在岩体中的宏观渗流特点[3],但对于裂隙局部渗流无法清楚描述。
在理论研究方面,探讨裂隙岩体渗透性过程中,SNOW[4]根据优势节理组特点,推导出裂隙岩体渗透张量计算公式,但是忽略了节理连通状态以及空间分布,无法应用于确定裂隙岩体渗透REV值;BUDHI SAGAR[5]的二阶统计分析方法则考虑了裂隙几何特征参数对渗透系数的影响;MASANOBU Oda[6-7]充分考虑裂隙的空间分布规律,巧妙地采用统计理论计算渗透张量,并探讨了应力作用对岩体渗透性的影响;在数值模拟方面,ZHANG,SANDERSON[8]借鉴多孔介质和离散裂隙网络模型,考虑裂隙几何特征,通过数值模拟计算应力条件下裂隙岩体的二维渗透张量;CHEN等[9]提出的复合单元法,在蒙特卡罗方法生成裂隙网络的基础上,直接将裂隙置于网格单元中,根据裂隙的产状对单元网格信息进行拓扑计算,计算得到各子单元流量,通过统计计算不同尺寸岩体试件不同方向上的等效渗透系数,但计算过程中完全忽略裂隙的连通性,计算结果偏高;GUAN等[10]凭借自主研发的节理网络模拟技术,将渗流能量进行叠加,推导出节理岩体渗透张量公式,并讨论了裂隙几何特征对岩体渗透特性的影响,但公式中涉及的参数多数取决于工程概况及工程经验,计算公式不具有普适性;王培涛等[11]提出的平面渗流分析法,充分利用VC++6.0软件平台,构建离散裂隙网络模型,计算节理岩体渗透张量,为定量分析岩体渗流的定向特征,自定义渗流定向性系数。但迭代计算过程中未剔除孤死裂隙(模型中未连通裂隙、与边界未连通裂隙);车富强等[3]先用裂隙样本法来计算出裂隙岩体的初始渗透张量,进而再结合现场压水试验测试法来进一步修正渗透张量,得到最终渗透张量。
在利用蒙特卡罗随机方法过程中,即使所取参数和分布规律完全一致,生成的多组随机裂隙也会有区别,特别是结合工程勘察数据生成随机裂隙过程中,多数研究者往往忽略这一点。笔者结合蒙特卡罗方法,针对同一分布规律下,生成多组随机裂隙模型,导入RFPA2D-Flow渗流计算模块进行渗流计算分析,方便之处在于只需要设置边界条件,对裂隙、岩块赋值水力传导系数。特别地,模拟计算过程中对同一分布规律下多组模型迭代计算,取多组模型边界流量的平均值,已消除随机裂隙带来的误差,求解出等效渗透系数。
1 表征单元体基本原理的确定
本文计算裂隙岩体渗流表征单元体主要依据张宜虎[12]提出的类常量与类张量特性。一般流程[13]为:对区域中的节理进行实测,获得相关几何参数,构建二维裂隙网络生成域,从生成域中选取一系列不等尺寸、不同方位的正方形作为REV试算域(从裂隙网格生成域中选取的一系列不等尺寸、不同方位的正方形计算域,通过模拟计算确定渗流表征单元体尺寸(REV)的计算模型)。一般情况下,取裂隙平均迹长的3~4倍作为REV的尺寸[14]。为了使计算有意义,裂隙网络模型生成域需要大于2倍分析域尺寸,而且分析域的尺寸必须大于REV尺寸(图1)。

图1 分析模型
Fig.1 Analysis model
1.1 裂隙岩体的平面渗流模型
二维裂隙网络模型中,节理相互交错贯通,呈短直线状。根据裂隙几何特征的几何分布规律,生成裂隙网络进行渗流计算,如图2所示。

图2 REV分析模型和渗流矢量图
Fig.2 Analysis model for REV and flow vectors
图2中定义水头边界是MM′,NN′,不透水边界是MN,M′N′。MM′,NN′间渗透系数为
![]()
(1)
式中,Δq为流经区域的总流量,m3/s;ΔH为MN方向上的水头差,m;K为等效渗透系数,m/s;模型边长(m)也就是MN,MM′,二者等长,在模型上下边界上施加水头条件,根据达西定律,通过计算流量来计算等效渗透系数。
1.2 二维稳定渗流数学模型及渗透特性计算
图3中整体坐标系xoy和局部坐标系x′oy′通过逆时针旋转形成,方向余弦分别记作:lx′x=cos θ,lx′y=sin θ,ly′x=-sin θ,ly′y=cos θ。

图3 坐标系相对位置与椭圆关系曲线
Fig.3 Relative position and elliptic curves
则局部坐标系下渗透系数ki′j′与整体坐标系下kij之间满足转换关系:
ki′j′=kijli′ilj′j
(2)
假定主渗透系数的方向沿着整体坐标系下x轴和y轴,通过坐标转换,逆时针旋转θ角度,可得局部渗透系数:
Kθ=K1cos2θ+K2sin2θ
(3)
椭圆方程在极坐标系(l,θ)下可以表示为
cos2θ/a2+sin2θ/b2=1/l2
(4)
若令1/a2=K1,1/b2=K2,1/l2=Kθ,联立公式(3),(4),即θ与Kθ满足图3渗透椭圆曲线。
模拟步骤:① 利用节理裂隙的几何特征参数及其分布规律,生成裂隙网络生成域;② 选取模型中心,以2 m为起点截取正方形研究域,每增加2~28 m,每个尺寸下每隔30°旋转1次构成12个方向,获得不同尺度不同方位模型中裂隙的位置参数;③ 在RFPA中建立同尺度的分析模型,划分网格,将节理裂隙导入RFPA,即获得等效裂隙岩体渗透计算模型;④ 给定同一渗流边界条件,根据立方定律、网格尺寸计算裂隙的等效水力传导系数,(优先假定工程中裂隙隙宽为0.15 mm),通过统计边界流量求得裂隙岩体等效渗透系数;⑤ 给定满足类常量与类张量特性的误差限,当不超过误差限时,即可确定渗透特性表征单元体REV。此处利用裂隙网络对称性,仅对0°~150°上6个方向进行模拟计算,故对应6个局部坐标系,i取值1~6算。
将得到的等效渗透系数矩阵平均,得到与整体坐标系方向一致的平均渗透系数矩阵:
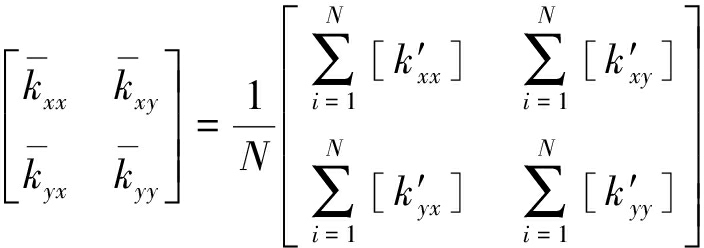
(5)
将各个[k′i]中的k′xiyj组成一个数据样本,得到变异系数:
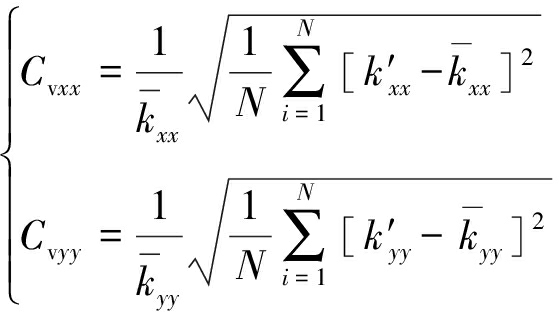
(6)
1.3 类张量与类常量特性
裂隙岩体渗透REV即在宏观方面能等效的表现岩体渗透性的最小值。在误差限制内,岩体的渗透性参数即符合类张量特性,也符合类常量特性,对应研究域尺寸即渗透REV。
将裂隙岩体等效为连续介质,但它的渗透性参数不一定完全具备张量特性和常量特性,为了深化研究,在此引入类张量和类常量特性[12]。
张量特性指不同方向上的渗透系数具有坐标转换特性,常量特性指连续介质的水力学参数不具备尺度效应,不随研究域尺度的变化而变化。所谓的类张量特性与类常量特性就是指在一定程度上(达到一定尺度后)近似的满足张量特性与常量特性。
2 裂隙岩体渗透特性分析
2.1 裂隙密度对渗透特性的影响
主要讨论裂隙密度对裂隙岩体渗透特性的影响,只改变密度大小,其他几何参数保持不变。首先生成最小密度裂隙网络模型,此基础上逐渐增大裂隙密度(条数)。表1给出2个工况下的初始参数,迹长服从对数正态分布,方向角服从正态分布,张开度为定值,密度分别取0.14,0.16,0.18,0.20和0.24条/m2。
表1 不同密度某岩体裂隙的初始几何参数
Table 1 Initial geometric parameters of a fractured rock mass with different densities
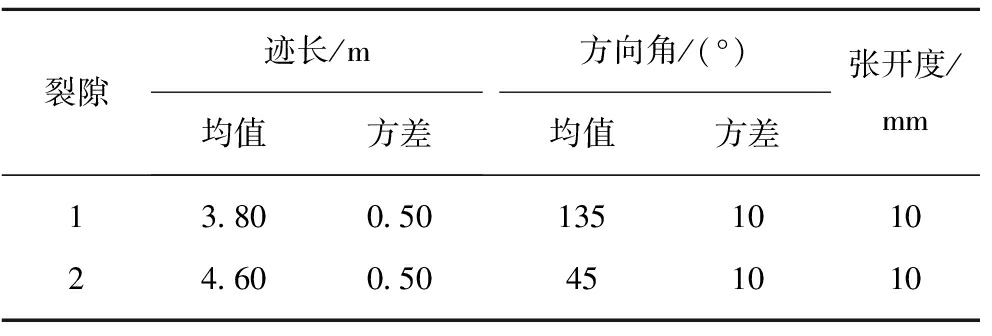
裂隙迹长/m均值方差方向角/(°)均值方差张开度/mm13.800.50135101024.600.50451010
2.1.1 裂隙密度对渗透表征单元体的影响
根据表1相关参数,生成随机裂隙网络,通过图1所示分析模型,进行渗流数值模拟计算,得到各个方向上的渗透系数,利用渗透椭圆方法对数据进行拟合,得到渗透张量和变异系数随分析尺寸的变化规律,如图4所示。
给定误差限15%,从图4(a)看出当尺寸达到16 m时,kxx,kyy,kxy满足类常量特性;当尺寸达到15 m时,Cvxx,Cvyy小于0.15,满足类张量特性。裂隙密度为0.14条/m2时渗流表征单元体为16 m。
从图4(b)可以看出当尺寸达到15 m时,kxx,kyy,kxy满足类常量特性;当尺寸达到10 m时,Cvxx,Cvyy小于0.15,满足类张量特性。裂隙密度为0.16条/m2时对应的二维渗流表征单元体为15 m。
从图4(c)可以看出当尺寸达到14 m时,kxx,kyy,kxy满足类常量特性;Cvxx,Cvyy小于0.15,满足类张量特性。裂隙密度为0.18条/m2时对应的二维渗流表征单元体为14 m。
从图4(d)可以看出当尺寸达到13 m时,kxx,kyy,kxy满足类常量特性;Cvxx,Cvyy小于0.15,满足类张量特性。裂隙密度为0.20条/m2时对应的二维渗流表征单元体为13 m。
从图4(e)可以看出当尺寸达到11 m时,kxx,kyy,kxy满足类常量特性,Cvxx,Cvyy小于0.15,满足类张量特性。裂隙密度为0.24条/m2时对应的二维渗流表征单元体为11 m。
由图5可见,裂隙密度随着密度的增大,渗透表征单元体尺寸逐渐减小。在一定密度范围内,随着密度的增大,裂隙密度与表征单元体尺寸处于负相关的线性关系。近似的满足:当密度增加50%,渗透主值增加100%的趋势。
2.1.2 裂隙密度对渗透张量的影响
从2.1.1节可知,表征单元体不超过18 m,此处模型尺寸选取18 m×18 m来计算渗透系数张量。
为研究裂隙几何特征对岩体渗透张量及各向异性的影响,自定义各向异性系数r=kmax/kmin(kmax,kmin为渗透主值最大值与最小值),r越大,渗透各向异性越强,裂隙岩体渗流定向性越明显。
图6描述不同密度情况下裂隙岩体的渗透张量的分布:纵坐标轴取值为渗透椭圆的半径,通过在Origin软件中绘制而成渗透椭圆。密度增大,渗透椭圆半径减小,即渗透系数越来越大;由于只改变密度大小,渗透主方向并没有随着密度的增大而变化(或者变化很小),渗透主方向在45°~60°方向上。这说明密度一定程度上对渗透主值大小有直接影响,对渗透主方向影响较小。
图7分析不同裂隙密度情况下各向异性系数r随旋转角度θ的变化。当裂隙密度最小(d=0.14条/m2)时,各向异性系数r达到最大值,渗透各向异性性特征最强。随着裂隙密度增大,连通性增强,各向异性系数r值逐渐减小;同一密度条件下,各向异性系数r值随旋转角度θ增大,呈现出正弦函数变化规律;不同密度条件下,在旋转角度θ为30°与120°时,各向异性系数r达到峰值,说明此渗流各向异性较强。
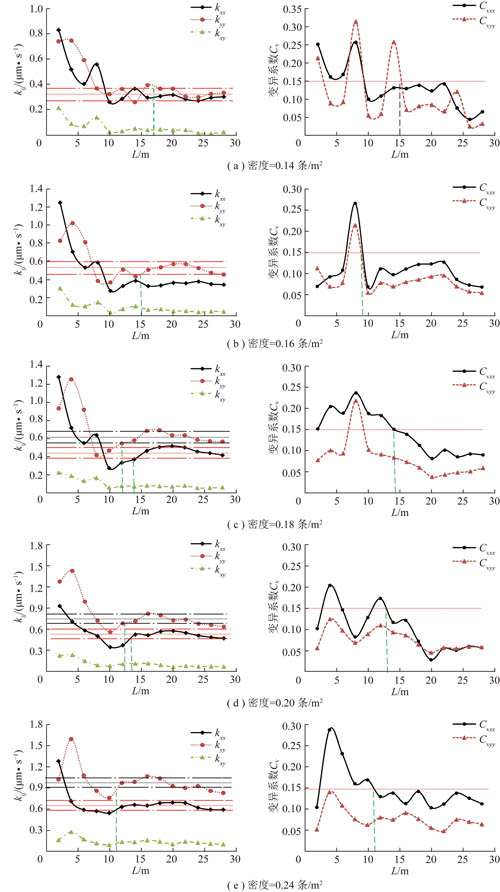
图4 渗透系数(左)与变异系数(右)随密度变化规律
Fig.4 Coefficient of permeability (left) and variation (right) varies with concentration

图5 REV随裂隙密度变化关系
Fig.5 Variation of REV with fracture density

图6 渗透张量随裂隙密度分布
Fig.6 Permeability tensor with different fracture densities

图7 各向异性系数与旋转角度θ关系
Fig.7 Relations between anisotropic coefficient and rotation
2.2 裂隙迹长对渗透特性的影响
本节主要讨论裂隙迹长对裂隙岩体渗透特性的影响,只改变裂隙迹长的大小,其他几何参数保持不变。表2具体给出了2个工况下不同迹长的裂隙初始参数。其中,方向角服从正态分布,密度和张开度均取定值。
表2 不同迹长某岩体裂隙的初始几何参数
Table 2 Initial geometric parameters of a fractured rock mass with different traces
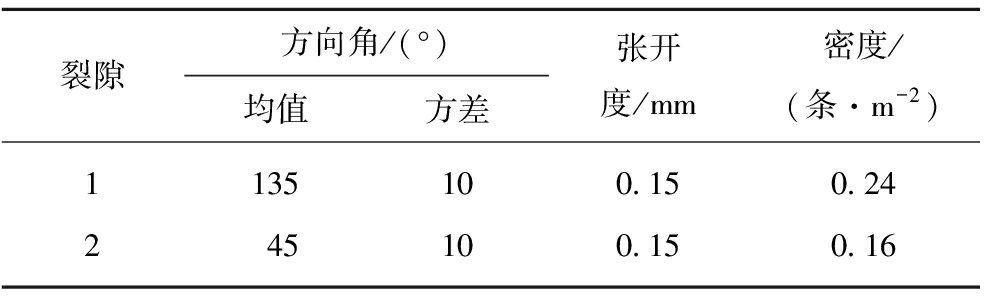
裂隙方向角/(°)均值方差张开度/mm密度/(条·m-2)1135100.150.24245 100.150.16
2.2.1 裂隙迹长对渗透表征单元体的影响
在随机生成的裂隙网络模型中,裂隙的迹长越长,则连通性相对越好,渗透性就越大。通过数值模拟计算,得到渗透张量和变异系数随分析尺寸变化规律,如图8所示。
图8(a)表明当尺寸满足24 m≥L≥15 m时,kxx,kyy,kxy满足类常量特性;当尺寸满足25 m≥L≥15 m时,Cvxx,Cvyy小于0.15,满足类张量特性。裂隙迹长为3.6 m和4.4 m时,渗流REV为15 m。
从图8(b)看当尺寸满足22 m≥L≥13 m时,kxx,kyy,kxy满足类常量特性;当尺寸满足25 m≥L≥11 m时,Cvxx,Cvyy小于0.15,满足类张量特性。裂隙迹长为3.8 m和4.6 m时,渗流REV为13 m。
从图8(c)可看出当尺寸满足20 m≥L≥8 m时,kxx,kyy,kxy满足类常量特性;当尺寸满足25 m≥L≥7 m时,Cvxx,Cvyy小于0.15,满足类张量特性。裂隙迹长为4.0 m和4.8 m时,渗流REV为8 m。
从图8(d)看当尺寸满足22 m≥L≥8 m时,kxx,kyy,kxy满足类常量特性;当尺寸满足L≥7 m时,Cvxx,Cvyy小于0.15,满足类张量特性。裂隙迹长为4.2 m和5.0 m时,渗流表征单元体为8 m。
从图8(e)看出当尺寸满足22 m≥L≥8 m时,kxx,kyy,kxy满足类常量特性;当尺寸满足L≥7 m时,Cvxx,Cvyy小于0.15,满足类张量特性。裂隙迹长为4.4 m和5.2 m,岩体渗流表征单元体为8 m。
裂隙迹长在一定范围内,随着迹长增大,渗透特性表征单元体尺寸逐渐减小,当迹长达到一定尺寸后,对表征单元体尺寸基本没影响;而且随着尺寸的继续增大,渗透性又趋于不稳定,说明迹长对渗透性影响较大。
2.2.2 裂隙迹长对渗透张量的影响
本节在计算渗透系数张量同样选取模型尺寸为18 m×18 m。
图10描述不同裂隙迹长情况下裂隙岩体渗透张量的分布:随着裂隙迹长的增大,渗透椭圆半径越来越小,即渗透系数越来越大;迹长在一定范围内,随着裂隙迹长的增大,渗透主方向并没有变化(或者变化很小),所以裂隙迹长一定程度上对渗透主值的大小有直接影响,而对渗透主方向影响较小。
图11分析了不同裂隙迹长情况下各向异性系数r随旋转角度θ关系。当迹长均值为最大值![]() 时,各向异性系数r达到峰值,此时渗透各向异性性特征最强;随着裂隙迹长的增大,各向异性系数r值呈现出先减小后增大规律,当迹长均值为4.4 m时,各向异性系数r取得最小值;同一迹长条件下,各向异性系数r值呈现余弦函数变化规律;不同迹长条件下,渗流各向异性系数r均在旋转角度θ为60°与150°时达到峰值,说明此渗流各向异性较强。
时,各向异性系数r达到峰值,此时渗透各向异性性特征最强;随着裂隙迹长的增大,各向异性系数r值呈现出先减小后增大规律,当迹长均值为4.4 m时,各向异性系数r取得最小值;同一迹长条件下,各向异性系数r值呈现余弦函数变化规律;不同迹长条件下,渗流各向异性系数r均在旋转角度θ为60°与150°时达到峰值,说明此渗流各向异性较强。
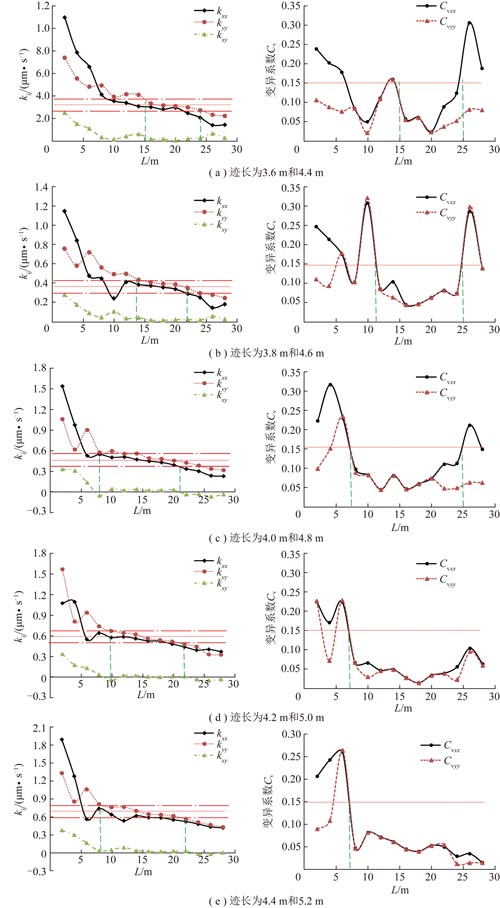
图8 渗透系数(左)与变异系数(右)随迹长变化规律
Fig.8 Coefficient of permeability (left) and variation (right) varies with fracture trace

图9 REV随裂隙迹长变化关系
Fig.9 Variation of REV with fracture trace

图10 渗透张量随迹长分布
Fig.10 Permeability tensor with different fracture traces
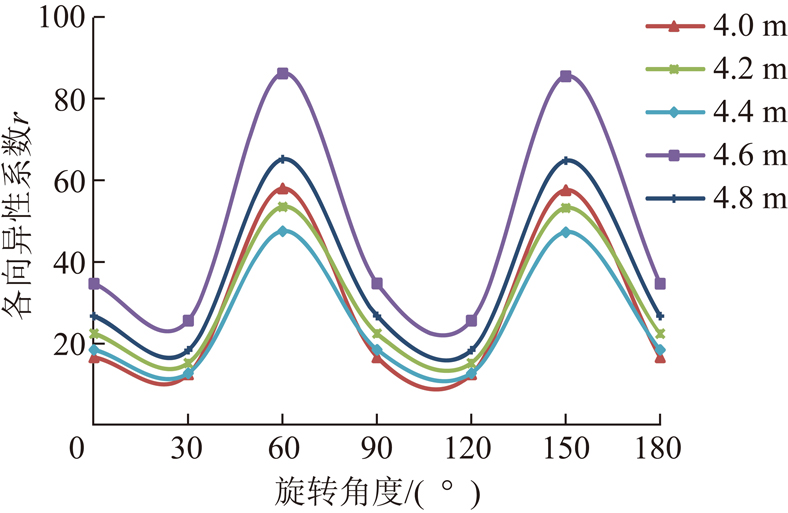
图11 各向异性系数与旋转角度θ关系
Fig.11 Relations between anisotropic coefficient and rotation
3 工程实例
锦屏一级左岸岩层的倾向在285°~295°内,倾角在35°~45°内。整个区域中岩体结构面明显,同时受地质构造作用的影响强大[15]。裂隙网络模型生成参数见表3。
3.1 渗透REV的计算
给定误差限15%,从图12可以看出,当尺寸达到12 m×12 m以上,kxx,kyy,kxy满足类常量特性;当尺寸达到11 m×11 m,Cv在允许误差范围内;因此可以取岩体的REV为12 m×12 m,尺寸大小约为最大裂隙迹长的4倍,这与参考文献[16]的研究结果相一致,进一步说明本文研究方法的可靠性。
表3 岩体结构面几何参数[17]
Table 3 Geometrical parameters of joints[17]

组号结构面产状/(°)倾向倾角统计名称概率分布均值标准差1258~33024~65倾角对数43.227.61迹长对数0.900.412120~16244~82倾角对数61.268.11迹长正态2.500.33380~11945~74倾角正态59.055.99迹长正态2.490.37416~7647~90倾角均匀70.0111.30迹长正态3.071.625170~22052~90倾角正态80.7613.00346~36065~90迹长对数2.491.19

图12 渗透张量与变异系数随尺寸变化规律
Fig.12 Variation of permeability tensor and variation coefficient with different sizes
3.2 渗透张量的计算与修正
分析域尺寸为12 m×12 m,数值模拟计算各研究域初始渗透张量(表4),为更能准确的代表工程岩体的平均渗透性,需对数值模拟得到的初始渗透张量进行修正,此处取几何平均值[18-20]进行修正:
表4 初步确定渗透张量
Table 4 Preliminary determine permeability characteristics m/s

区域渗透张量kij渗透主值综合渗透系数强卸荷8.23×10-59.76×10-69.76×10-66.65×10-6éëêêùûúú8.35×10-55.41×10-6éëêêùûúú2.13×10-5弱卸荷5.74×10-66.85×10-76.85×10-74.87×10-7éëêêùûúú5.83×10-63.96×10-7éëêêùûúú1.52×10-6微卸荷3.40×10-74.05×10-84.05×10-82.85×10-8éëêêùûúú3.45×10-72.33×10-8éëêêùûúú8.97×10-8新鲜岩体1.38×10-71.65×10-81.65×10-81.16×10-8éëêêùûúú1.40×10-79.49×10-9éëêêùûúú3.65×10-8
![]()
(5)
式中,Kω为修正后的渗透系数;Ki(i=1,2,…,n)为渗透主值。
m=K0/Kω
(6)
式中,m为修正系数;K0为现场压水试验得到的渗透系数。
结合现场试验数据求取各岩层的平均值(表5)对初始渗透张量进行修正,修正后渗透张量(表6)。
表5 各岩层水压试验得到的水力传导系数[21]
Table 5 Hydraulic conductivity of the rock stratum from pressure test[21]m/s

岩层强卸荷弱卸荷微卸荷新鲜岩体平均值1.49×10-41.04×10-56.15×10-72.50×10-7
表6 修正后的渗透张量
Table 6 Revised permeability characteristics

区域渗透张量kij/(m·s-1)渗透主值/(m·s-1)综合渗透系数/(m·s-1)修正系数强卸荷5.77×10-4 6.84×10-56.84×10-5 4.66×10-5éëêêùûúú5.86×10-43.79×10-5éëêêùûúú1.49×10-47.01弱卸荷3.92×10-54.68×10-64.68×10-63.30×10-6éëêêùûúú4.09×10-52.77×10-6éëêêùûúú1.06×10-56.84微卸荷2.33×10-62.77×10-72.77×10-71.95×10-7éëêêùûúú2.42×10-61.63×10-7éëêêùûúú6.29×10-76.86新鲜岩体9.47×10-71.13×10-71.13×10-77.95×10-8éëêêùûúú9.82×10-76.65×10-8éëêêùûúú2.56×10-76.85
4 结 论
(1)裂隙密度和裂隙迹长对渗透主值有影响,但对渗透主方向几乎无影响,随密度或者迹长的增大,渗透主值增大。
(2)在一定范围内,随着裂隙密度、迹长的增大,渗透表征单元体尺寸逐渐减小。
(3)各向异性系数r随密度增大逐渐减小,且随旋转角θ变化呈正弦函数规律;各向异性系数r值随裂隙迹长的增大先减小后增大,随旋转角度θ呈现余弦函数规律。
(4)以锦屏一级水电站坝区左岸岩体为例,利用现场压水试验结果对数值模拟结果进行修正,修正系数在一个数量级之内,说明本文模拟计算结果可行有效,并且得到工程岩体的REV尺寸为最大迹长的4倍,这与张贵科,徐卫亚[14]的研究结果也相吻合。
(5)本文研究考虑了节理的实际分布及连通情况、不同岩层及岩体等级对渗透特性的影响,通过渗透张量计算方法确定表征单元体,模拟结果同许多学者研究具有一致性,具有计算方便、易于理解的优势。
[1] 荣冠,周创兵,王恩志.裂隙岩体渗透张量计算及其表征单元体积初步研究[J].岩石力学与工程学报,2007,26(4):740-746.
RONG Guan,ZHOU Chuangbing,WANG Enzhi.Preliminary study on permeability tensor calculation of fractured rock mass and its representative elementary volume[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(4):740-746.
[2] HSIEH P,NEUMANN S P,SIMPSON E S,et al.Field determination of the three dimensional hydraulic conductivity tensor of anisotropic media,2,Methodology with application to fractured rocks[J].Water Resources Research,1985,21(11):1667-1676.
[3] 车富强,陈益峰,李益,等.基于等效连续介质坝区裂隙岩体渗控效应分析[J].中南大学学报,2014,45(6):1967-1974.
CHE Fuqiang,CHEN Yifeng,LI Yi,et al.Seepage analysis of fractured rock mass in a dam foundation based on equivalent continuum model[J].Journal of Central South University,2014,45(6):1967-1974.
[4] SNOW D T.Anisotropic permeability of fractured media[J].Water Resources Research,1969,5(6):1273-1289.
[5] BUDHI Sagar,AKSHAI Runchal.Permeability of fractured rock:Effect of fracture size and data uncertainties[J].Water Resources Research,1982,18(2):266-274.
[6] MASANOBU Oda.Permeability tensor for discontinuous rock masses[J].Geo-technique,1985,35(4):483-495.
[7] MASANOBU Oda.An equivalent continuum model for coupled stress and fluid flow analysis in jointed rock masses[J].Water Resources Research,1986,22(13):1845-1856.
[8] ZHANG X,SANDERSON D J,HARKNESS R M.Evaluation of the 2-D permeability tensor for fractured rock masses[J].International Journal of Rock Mechanics & Mining Science & Geomechanics Abstracts,1996,33(1):17-37.
[9] CHEN S H,FENG X M S Isam.Numerical estimation of REV and permeability tensor for fractured rock mass by composite element method[J].International Journal for Numerical and Analytical Methods in Geomechanics,2008,32(12):1459-1477.
[10] RONG Guan,PENG Jun,WANG Xiaojiang,et al.Permeability tensor and representative elementary volume of fractured rock masses[J].Hydrogeology Journal,2013,21:1655-1671.
[11] 王培涛,杨天鸿,于庆磊,等.基于离散裂隙网络模型节理岩体渗透张量及特性分析[J].岩土工程,2013,34(2):448-455.
WANG Peitao,YANG Tianhong,YU Qinglei,et al.Permeability tensor and seepage properties for jointed rock masses based ondiscrete fracture network model[J].Rock and Soil Mechanics,2013,34(2):448-455.
[12] 张宜虎.岩体等效水力学参数研究[D].武汉:中国地质大学,2006.
ZHANG Yihu.Research on the equivalent hydro-mechanical parameters of rock mass[D].Wuhan:China University of Geosciences,2006.
[13] 宋晓晨.裂隙岩体渗流非连续介质数值模型研究及工程应用[D].南京:河海大学,2004.
SONG Xiaochen.Study on discontinuous numerical models for flow in fractured rock and its engineering applications[D].Nanjing:Hehai University,2004.
[14] 张贵科,徐卫亚.裂隙网络模拟和REV尺度研究[J].岩土力学,2008,29(6):1675-1670.
ZHANG Guike,XU Weiya.Analysis of joint network simulation method and REV scale[J].Rock and Soil Mechanics,2008,29(6):1675-1670.
[15] 田洪圆,张亮,李宏.锦屏一级左岸岩体渗透特性的数值模拟研究[J].水利与建筑工程学报,2017,15(3):67-71.
TIAN Hongyuan,ZHANG Liang,LI Hong.Numerical simulation of permeability of rock mass on the left bank of jinping-I[J].Journal of Water Resources and Architectural Engineering,2017,15(3):67-71.
[16] 安玉华,王清.基于三维裂隙网络的裂隙岩体表征单元体研究[J].岩土工程,2012,33(12):3775-3780.
AN Yuhua,WANG Qing.Analysis of representative element volume size based on 3D fracture network[J].Rock and Soil Mechanics,2012,33(12):3775-3780.
[17] 汪小刚,贾志欣,张发明.岩体结构面网络模拟原理及其工程应用[M].北京:中国水利水电出版社,2010.
[18] LEE C H,DENG B W,CHANG J L.A continuum approach for estimating permeability in naturally fractured rocks[J].Engineering Geology,1995,39(1/2):71-85.
[19] 黄义,张引科.张量及其在连续介质力学中的应用[M].北京:冶金工业出版社,2002:115-124.
[20] 王鹏,蔡美峰,周汝弟.裂隙岩体渗透张量的确定和修正[J].金属矿山,2003(8):5-7.
WANG Peng,CAI Meifeng,ZHOU Rudi.Estimation and modification of permeability tensor of fractured rock mass[J].Metal Mine,2003(8):5-7.
[21] 荔强.锦屏一级左岸高边坡雾化渗流稳定性问题研究[D].北京:清华大学,2010.
LI Qiang.Research on the stability of Jinpin I slope in the condition of atomization[D].Beijing:Tsinghua University,2010.
