层状复合岩体是工程施工中常见的岩体结构,边坡稳定性、隧道施工、煤矿开采、层状盐岩储积库的密闭性及页岩气开采等工程均涉及到与沉积岩层有关的层状岩体力学问题[1-2]。因此,揭示层状岩体的裂纹破裂机理对实际工程施工设计及能源高效、安全开发利用具有重要指导意义。
层理面将直接影响岩体的破裂模式,揭示层理对岩体破裂模式的机理尤为重要。周扬一等[3]利用薄层灰岩,研究了层厚对岩层抗弯性能的影响,并且分析了裂纹在层理岩石中的扩展路径,提出裂纹的3种破裂模式。许多等[4]分析了层状煤岩在拉伸状态下的破裂机理及层理对声发射特征的影响。王洪建等[5]进行了含预制切槽的红砂岩三点弯曲试验,分析了不同破裂模式下的声发射特征。黄明利等[6]模拟了动态条件下含偏置裂纹的三点弯试样破裂过程,揭示了偏置裂纹的位置影响裂纹扩展时间和裂纹破坏模式。彭瑞东等[7]通过微观层状岩盐三点弯曲试验,从裂纹在微观层面上的扩展路径,揭示了界面处失效破坏的内在原因。以上研究均表明层理主要影响了岩体的破裂模式,而不同的破裂模式表现出不同的声发射特征。
也有学者提出层理两侧的材料属性将影响裂纹的破裂模式。张桂民等[8]研究了盐岩界面抗剪强度特征,提出两种由不同界面组成的强度模型,根据该模型得到界面产生破损是由于盐岩和夹层的力学属性不同导致变形不协调从而产生的附加作用力的结果。代树红等[9]利用数字散斑实验和数值模拟,研究了界面层两侧岩石强度差异对裂纹在层状岩石中扩展的影响规律,得到界面层具有止裂作用,止裂效果随不含裂纹一侧岩石强度的增高而提高,裂纹在层状岩石中的扩展呈非连续性扩展特征。在页岩气开采中岩体的破裂模式将直接影响采气率。李芷等[10]利用室内真三轴水力压裂试验,研究了水力裂纹与天然层理面的相互作用机理,得到层理面可以为水力裂纹提供较好的导流通道。衡帅等[11]采用室内圆柱形三点弯曲试验,通过改变切槽与层理面的角度,解释了断裂韧度的各向异性,并在此理论基础上开展了水力压裂试验,探讨了层理对水力裂纹的影响。许丹等[12]采用混凝土试样,进行了室内真三轴水力压裂试验,研究了层理角度、层理厚度和间距对水力裂纹的影响。层理面决定了裂纹破裂模式,直接影响裂纹形态,决定压裂效果。
层状岩体层理各向异性明显,而岩体性质随不同层理角度表现出较大差异。在层理面与载荷处于垂直和平行两个方向上时,刘恺德等[13]通过煤岩的巴西劈裂和单轴压缩试验,分析了两个层理方向的力学特性及破裂机制。发现不同层理方向力学特征差异较明显,两个层理方向单轴抗压强度均远大于抗拉强度。邓博知等[14]研究了不同应力条件下含层理煤样在垂直和平行层理方向的裂隙度及渗流特性,得到层理对裂隙度及渗透性均有较大影响。赵子江等[15]发现层理方向导致断裂韧度值表现不同的分布范围,表明层理对工程稳定性具有较大影响。而对于其他层理面角度已有学者通过室内试验及数值模拟进行了相关研究。张桂民等[2]利用盐岩模拟材料,研究了不同层面倾角的强度变化规律,发现不同层理倾角表现出不同的破裂模式,岩石抗压强度曲线呈U型变化,并通过理论分析验证了试验结果的可靠性。梁正召等[16]研究了不同层理面角度对单轴压缩试样的影响,随着层理面角度的增加,岩体强度呈现“肩型破坏”。层面角度为0°和90°时,强度较高,发生脆性剪切破坏,层面倾角处于中间角度时,表现为顺层剪切破坏。以上两名学者均得到岩体强度随层理面角度呈现U型变化。张树文等[17]结合室内巴西劈裂试验与离散元数值模拟,研究了不同层理角度对页岩力学特征和破裂模式的影响,得到层理角度决定了页岩的破裂模式。
目前对于层理面的研究主要集中在层理角度、层厚及层间距方面,而层理面的强度性质(胶结程度)也是影响工程施工的重要参数,且学者对于这方面研究较少。因此,笔者通过Python编程语言对ABAQUS进行二次开发,建立了岩石层理各向异性与矿物颗粒非均质性数值模型。通过控制层理面的强度参数,研究了在三点弯曲条件下,层理面强度性质对裂纹扩展过程的影响。提取模拟结果,结合MATLAB编程实现了声发射(AE)模拟,为精细化研究裂纹扩展过程提供了有效手段。
1 数值计算原理
黏聚力模型(Cohesive Zone Model)首先由DUGDALE D S[18]和BARENBLATT G I[19]提出,该模型解决了裂纹尖端奇异性带来的研究难点,被广泛应用于复合材料的界面分层研究[20]。STROM J L等[21]利用Cohesive模型,基于应力能量方法解释了裂纹在经过层理面时的穿透和偏转行为,验证了该模型的适用性。
1.1 Cohesive单元本构方程
Cohesive单元基于牵引分离规律的线弹性本构模型,Cohesive单元在损伤前,应力与应变满足线弹性关系,即
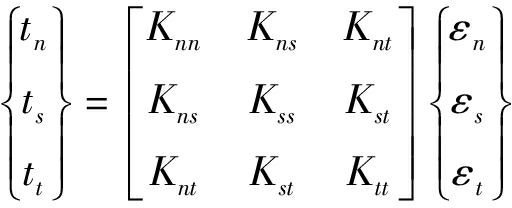
其中,t为应力;ε为应变;下标n为法向;下标s和t为两个切向方向;K为黏性单元的刚度。对于非耦合本构关系,只需定义Knn,Kss,Ktt。
1.2 破裂准则
1.2.1 损伤起始准则
模拟中采用最大主应力控制准则,即法向拉应力或切向应力达到相应强度时即破坏:
其中,σn为法向应力;σs,σt为两个方向的剪切应力;Nmax为抗拉强度;Smax和Tmax为2个方向的抗剪强度;〈σn〉表示为
即Cohesive单元在纯压缩状态下不会产生起始损伤。
1.2.2 损伤演化准则
本文采用基于有效位移的损伤演化准则,定义损伤变量D为
式中,![]() 为失效时的有效位移,该模型中定义为
为失效时的有效位移,该模型中定义为![]() 为损伤起始演化时的有效位移;
为损伤起始演化时的有效位移;![]() 为加载过程中的有效位移最大值。
为加载过程中的有效位移最大值。
1.3 声发射模拟实现原理
利用Python语言编程提取了ABAQUS模拟结果,对结果参数进行MATLAB编程处理,实现了加载过程中的声发射模拟,通过声发射定位图与声发射特征参数,进一步描绘了裂纹破裂情况,为深入分析裂纹扩展过程提供了有效手段。
声发射事件数:将损伤单元数作为声发射事件数,每损伤一个单元看做是一次声发射事件。
声发射定位方法:提取损伤单元的节点坐标,根据节点坐标计算出损伤单元中心点位置坐标,作为声发射事件定位坐标点。
声发射能量:提取损伤单元单位体积总能量耗散能作为声发射能量。
破裂类型判别准则:根据参数MMIXDME判断破裂类型,参数定义为
式中,GT为破裂单元的总断裂能;Gn为I型拉张断裂能;Gs为II型滑移断裂能;Gt为 III型撕裂断裂能。
MMIXDME取值为0~1,MMIXDME为0时表示拉张破裂,数值为1时表示剪切破裂,数值在两者之间时表示为拉剪混合破裂。
2 数值模型
建立二维三点弯曲数值模型如图1所示,模型尺寸为100 mm×400 mm,设置单层厚度为10 mm,在岩体下部中轴线右侧28 mm处预制一个3 mm的初始裂纹。同时建立3个半圆形刚体作为承压轴,下部两个承压轴间的距离为300 mm,模拟时,将下部两个承压轴作为支座完全固定,对上部承压轴施加总位移为1 mm的位移载荷,所有承压轴均与试样之间设置通用接触。

图1 模型设计
Fig.1 Model design diagram
考虑到页岩矿物的非均质性,对ABAQUS软件进行二次开发,根据XRD矿物成份分析结果,确定单个矿物所占比例,将矿物所占比例转化成单元个数所占比,利用random随机分布函数进行矿物单元的随机分布,并建立相应集合,赋予参数(表1)。
表1 矿物成分及参数
Table 1 Mineral composition and parameters

矿物(页岩)百分比/%弹性模量/GPa泊松比石英49400.20斜长石11210.24微斜长石4200.25方解石6270.23云母17180.27高岭石4220.23白云石5210.23黄铁矿4350.22
对模型全局嵌入0厚度Cohesive单元,建立层理面Cohesive单元集合与实体单元间Cohesive单元集合,分别赋予不同材料属性,从而实现了岩石的层理各向异性与矿物非均质性(图2)。

图2 各向异性网络模型
Fig.2 Anisotropic network model
设置层理面处的Cohesive单元强度小于实体单元间的Cohesive单元,本文通过将层理面处的Cohesive单元设置成不同的强度参数,进行了4种强度工况下的数值模拟试验,从工况a到工况d层理面强度越来越强,参数见表2。
表2 Cohesive单元参数
Table 2 Cohesive unit parameters

参数层理面Cohesive单元工况a工况b工况c工况d实体单元间Cohesive单元Knn1012151617Kss1012151617Ktt1012151617抗拉强度/MPa12346抗剪强度/MPa48121620
模型总单元数为35 679个,其中实体单元(CPE4四节点平面应变单元)11 977个。Cohesive单元(COH2D4四节点二维黏结单元)23 702个。采用Static,General分析步,总分析步时间为1 s,初始增量步为0.01,最小增量步为10-10,最大增量步为0.1。
3 模拟结果
3.1 位移-载荷及声发射能量
提取4种工况下的位移载荷曲线及整个加载过程中的声发射能量如图3所示。4种工况下,声发射能量与位移载荷曲线均表现出相似变化趋势。声发射能量均开始产生于峰值载荷前的塑性阶段,此时裂纹起裂,有少量声发射能量释放。随着加载的进行,裂纹持续扩展,声发射能量呈簇状大量集中在峰后,且能量值较大。在峰后破裂阶段(图3中浅灰色区域),4种工况下最大声发射能量聚集区(图3中灰色区域)出现位置发生转移:工况a条件下,最大声发射能量聚集区出现在峰后破裂阶段的2/5位置,工况b,c出现在峰后破裂阶段的3/5位置,工况d出现在峰后破裂阶段的4/5位置处,表明层理面强度越大,岩体整体贯通时间出现的更晚。载荷达到峰后破裂阶段之后(图3中浅灰色区域之后),4种工况中的载荷均不再发生明显变化,基本维持在一个稳定值,可以理解为此时进入峰后残余强度阶段[22]。层理面强度较弱时,残余强度较大,岩石在层面处破裂剥离,导致应力释放及再次集中,有零散声发射事件出现。

图3 位移载荷曲线与声发射能量
Fig.3 Displacement-load curves and acoustic emission energy
提取4种工况下的峰值载荷大小(图4),由峰值载荷曲线可知,从工况a到工况d峰值载荷越来越小,即层理面强度越弱峰值载荷越大,由于层理面越弱对裂纹的止裂行为越明显,载荷除需提供沿着最大主应力方向的拉张破裂外,还需另外克服顺层理面的剪切破裂,因此破裂所需载荷越大。

图4 峰值载荷
Fig.4 Peak load
3.2 应力云图
根据图3位移载荷曲线与声发射能量,可知裂纹在接近峰值载荷时,开始起裂,达到峰值载荷后开始失稳破坏,峰后破裂阶段可观测到裂纹的破裂过程。因此,分别提取峰值载荷阶段、峰后80%阶段、峰后残余阶段3个时间点的水平方向应力云图,分析裂纹起裂、扩展、贯通过程中的应力变化情况(图5)。
在峰值载荷阶段,试样底部拉应力集中,上部加载点处压应力集中。工况a条件下层理面胶结强度较小,在层理面处,应力集中程度很高,应力首先达到层理面的抗剪强度[10],因此在层理处较先出现横向裂纹,表现为非连续扩展。工况a下,峰值载荷阶段,预制裂纹处小范围应力集中程度要大于其他3种工况,是由于层理面处先产生的横向裂纹阻隔了应力波的传递,导致应力集中发生在小厚度范围内,应力场波及的范围更小导致应力集中程度更强。
裂纹起裂之后,在峰后80%阶段,工况a条件下应力集中程度要小于峰值阶段,而其他3种工况下此时应力集中程度均增强。裂纹尖端上部拉应力集中,随着裂纹的扩展,拉应力集中区也转移到新的裂纹尖端上部,表现出应力不连续现象,从而导致裂纹断续扩展[23],峰后残余阶段裂纹完全贯通,应力骤降。

图5 水平方向应力云图
Fig.5 Horizontal stress nephogram
3.3 裂纹扩展路径及声发射定位
3.3.1 裂纹扩展路径
分别提取4种工况下的裂纹路径信息(图6),裂纹均从预制裂纹处起裂,整体扩展方向为沿着最大主应力方向,趋近上部集中载荷点处。从工况a到工况d裂纹路径越来越单一,受层理的影响越来越小。层理面阻碍裂纹沿最大主应力方向扩展,导致裂纹沿层理面水平迁移。层理面较弱时,裂纹路径主要表现为顺层破裂与穿层破裂交互发生,产生较多分叉、转折复杂形态的裂纹。且层理面越弱,顺层破裂现象越明显,随着层理面的增强,裂纹扩展方式由顺层破裂与穿层破裂交互发生复合破裂,转变为单一的穿层破裂。由于弱层理面的存在,导致应力首先达到弱层理面处的强度值,发生超前破裂,出现断续雁裂状扩展,这一现象与崔振东在微观试验中观测到的裂纹形态相吻合[24-25]。

图6 裂纹扩展路径
Fig.6 Crack propagation path
3.3.2 声发射定位图及破裂类型
利用Python语言提取声发射参数,通过Matlab软件实现声发射定位图绘制(图7)。图中使用声发射事件点的大小表示声发射能量大小,MMIXDME作为声发射事件点的破裂类型,并用不同的颜色表示,其中红色为拉张破裂,紫色为剪切破裂,介于两者之间的为拉剪混合型破裂。从定位图中可发现:拉张破裂为主要破裂类型,且主要表现在穿层破裂上,穿层破裂能量要远大于顺层破裂能量,层理面较弱时,裂纹呈断续位错式扩展。从工况a到工况d,裂纹位错越来越不明显,裂纹扩展过程中所波及的损伤区(声发射事件分布范围)越来越小。由于预制裂纹尖端处于I-II型复合应力状态[26],因此4种工况下裂纹尖端起裂处均表现为拉剪破裂类型。

图7 声发射定位
Fig.7 Acoustic emission location map
3.4 裂纹长度及声发射事件数
分别提取4种工况下的总裂纹长度及顺层、穿层裂纹长度(图8),从工况a到工况d,总裂纹长度与顺层裂纹长度越来越小,表明层理面强度越弱,裂纹受层理面的影响越大,层理面的止裂效果越好,裂纹顺层水平扩展长度越大。而4种工况穿层裂纹长度差异较小,均在100 mm左右,结合图7声发射定位图可知4种工况下裂纹整体扩展趋势均为沿着最大主应力方向,直到贯通,因此穿层裂纹长度均较接近试样高度。

图8 裂纹长度
Fig.8 Crack length
本文定义MMIXDME在0~0.5为拉张破裂,0.5~1.0为剪切破裂。利用Matlab提取4种工况下的声发射事件数(图9)。4种工况下拉张破裂类型AE事件数要明显大于剪切破裂类型AE事件数,拉张破裂占主导地位。从工况a到工况d,总AE事件数、拉张破裂AE事件数、剪切破裂AE事件数均呈逐渐减小的趋势,即随着层理面强度的增大,破裂事件数逐渐减小。剪切破裂多产生在顺层部位,而层理面越弱,顺层破裂现象越明显,因此剪切破裂越多。

图9 声发射事件数
Fig.9 Number of acoustic emission events
4 结 论
(1)层理面的存在会抑制裂纹沿着最大主应力方向扩展,产生顺层水平迁移裂纹,且层理面强度越弱,顺层裂纹长度越长,层理面对已有穿层裂纹沿着其延长线方向继续扩展的抑制效果越明显,裂纹的破裂路径与层理面强度密切相关。
(2)不同层理面强度下,裂纹扩展方式均有穿层破裂与顺层破裂交替出现现象,呈现断续位错式的破裂特征,且层理面越弱,该破裂特征越明显。
(3)裂纹在接近峰值载荷时开始起裂,层理面强度较弱时,层理界面处要早于预制裂纹处起裂;较先产生的横向裂纹会阻隔应力波的传递,导致应力场波及范围变小应力集中程度更强。
(4)由于层理面的存在,裂纹扩展除了需要克服岩石的拉张强度之外,还需要提供裂纹顺层破裂所需能量,层理面强度越弱所需外界提供的总能量越多,峰值载荷越大。
(5)破裂过程中穿层破裂占主导优势,主要表现为拉张破裂类型,顺层破裂主要为剪切破裂类型,随着层理面强度的增加,顺层破裂长度、总声发射事件数、剪切破裂、拉张破裂声发射事件数均逐渐减小。
[1] 贾蓬,唐春安,王述红.巷道层状岩层顶板破坏机理[J].煤炭学报,2006,31(1):11-15.
JIA Peng,TANG Chun’an,WANG Shuhong.Destroy mechanism of tunnel with stratified roof[J].Journal of China Coal Society,2006,31(1):11-15
[2] 张桂民,李银平,杨长来,等.软硬互层盐岩变形破损物理模拟试验研究[J].岩石力学与工程学报,2012,31(9):1813-1820.
ZHANG Guimin,LI Yinping,YANG Changlai,et al.Physical simulation of deformation and failure mechanism of soft and hard interbedded salt rocks[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(9):1813-1820.
[3] 周扬一,冯夏庭,徐鼎平,等.受弯条件下薄层灰岩的力学响应行为试验研究[J].岩土力学,2016,37(7):1895-1902.
ZHOU Yangyi,FENG Xiating,XU Dingping,et al.Experimental study of mechanical response of thin-bedded limestone under bending conditions[J].Rock and Soil Mechanics,2016,37(7):1895-1902.
[4] 许多,张茹,高明忠,等.基于间接拉伸试验的煤岩层理效应研究[J].煤炭学报,2017,42(12):3133-3141.
XU Duo,ZHANG Ru,GAO Mingzhong,et al.Research on coal bedding effect based on indirect tensile test[J].Journal of China Coal Society,2017,42(12):3133-3141.
[5] WANG H,LIU D,CUI Z,et al.Investigation of the fracture modes of red sandstone using XFEM and acoustic emissions[J].Theoretical & Applied Fracture Mechanics,2016,85:283-293.
[6] 黄明利,朱万成,逄铭彰.动载荷作用下含偏置裂纹三点弯曲梁破坏过程的数值模拟[J].岩石力学与工程学报,2007,26(S1):3384-3389.
HUANG Mingli,ZHU Wancheng,PANG Mingzhang.Numerical simulation of dynamic failure processes of three-point bending beam with offset notch[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(S1):3384-3389.
[7] 彭瑞东,武志德,周宏伟,等.层状盐岩中裂纹扩展规律的细观实验研究[J].岩石力学与工程学报,2011,30(S2):3953-3959.
PENG Ruidong,WU Zhide,ZHOU Hongwei,et al.Meso-experimental investigation on crack evolution in bedded salt rock[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(S2):3953-3959.
[8] 张桂民,李银平,刘伟,等.基于沉积特征的层状盐岩界面抗剪强度特性研究[J].岩石力学与工程学报,2014,33(S2):3631-3638.
ZHANG Guimin,LI Yinping,LIU Wei,et al.Study of shear strength properties of interfaces in bedded salt formations based on sedimentary characteristics[J].Chinese Journal of Rock Mechanics and Engineering,2014,33(S2):3631-3638.
[9] 代树红,王召,马胜利,等.裂纹在层状岩石中扩展特征的研究[J].煤炭学报,2014,39(2):315-321.
DAI Shuhong,WANG Zhao,MA Shengli,et al.Study on characteristics of crack propagation in stratified rock[J].Journal of China Coal Society,2014,39(2):315-321.
[10] 李芷,贾长贵,杨春和,等.页岩水力压裂水力裂缝与层理面扩展规律研究[J].岩石力学与工程学报,2015,34(1):12-20.
LI Zhi,JIA Changgui,YANG Chunhe,et al.Propagation of hydraulic fissures and bedding planes in hydraulic fracturing of shale[J].Chinese Journal of Rock Mechanics and Engineering,2015,34(1):12-20.
[11] 衡帅,杨春和,郭印同,等.层理对页岩水力裂缝扩展的影响研究[J].岩石力学与工程学报,2015,34(2):228-237.
HENG Shuai,YANG Chunhe,GUO Yintong,et al.Influence of bedding planes on hydraulic fracture propagation in shale formations[J].Chinese Journal of Rock Mechanics and Engineering,2015,34(2):228-237.
[12] 许丹,胡瑞林,高玮,等.页岩纹层结构对水力裂缝扩展规律的影响[J].石油勘探与开发,2015,42(4):523-528.
XU Dan,HU Ruilin,GAO Wei,et al.Effects of laminated structure on hydraulic fracture propagation in shale[J].Petroleum Exploration and Development,2015,42(4):523-528.
[13] 刘恺德,刘泉声,朱元广,等.考虑层理方向效应煤岩巴西劈裂及单轴压缩试验研究[J].岩石力学与工程学报,2013,32(2):308-316.
LIU Kaide,LIU Quansheng,ZHU Yuanguang,et al.Experimental study of coal considering directivity effect of bedding plane under brazilian splitting and uniaxial compression[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(2):308-316.
[14] 邓博知,康向涛,李星,等.不同层理方向对原煤变形及渗流特性的影响[J].煤炭学报,2015,40(4):888-894.
DENG Bozhi,KANG Xiangtao,LI Xing,et al.Effect of different bedding directions on coal deformation and permeability characteristics[J].Journal of China Coal Society,2015,40(4):888-894.
[15] 赵子江,刘大安,崔振东,等.半圆盘三点弯曲法测定页岩断裂韧度(KIC)的实验研究[J].岩土力学,2018,39(S1):258-266.
ZHAO Zijiang,LIU Da’an,CUI Zhendong,et al.Experimental study of determining fracture toughness KIC of shale by semi-disk three-point bending[J].Rock and Soil Mechanics,2018,39(S1):258-266.
[16] 梁正召,唐春安,李厚祥,等.单轴压缩下横观各向同性岩石破裂过程的数值模拟[J].岩土力学,2005,26(1):57-62.
LIANG Zhengzhao,TANG Chun’an,LI Houxiang,et al.A numerical study on failure process of transversely isotropic rock subjected to uniaxial compression[J].Rock and Soil Mechanics,2005,26(1):57-62.
[17] 张树文,鲜学福,周军平,等.基于巴西劈裂试验的页岩声发射与能量分布特征研究[J].煤炭学报,2017,42(S2):346-353.
ZHANG Shuwen,XIAN Xuefu,ZHOU Junping,et al.Acoustic emission characteristics and the energy distribution of the shale in Brazilian splitting testing[J].Journal of China Coal Society,2017,42(S2):346-353.
[18] DUGDALE D S.Yielding of steel sheets containing slits[J].Journal of the Mechanics & Physics of Solids,1960,8(2):100-104.
[19] BARENBLATT G I.The mathematical theory of equilibrium cracks in brittle fracture[J].Advances in Applied Mechanics,1962,7:55-129.
[20] 沈珉,刘赫,于济菘.材料断裂内聚力区牵引-分离曲线的测量方法研究[J].实验力学,2018,33(3):395-409.
SHEN Min,LIU He,YU Jisong.Measurement of traction separation curve in cohesive zone of material fracture[J].Journal of Experimental Mechanics,2018,33(3):395-409.
[21] STROM J L,PARMIGIANI J P.Transition of crack path at bi-material interfaces[J].Engineering Fracture Mechanics,2014,115(1):13-21.
[22] 彭俊,荣冠,蔡明,等.基于一种脆性指标确定岩石残余强度[J].岩土力学,2015,36(2):403-408.
PENG Jun,RONG Guan,CAI Ming,et al.Determination of residual strength of rocks by a brittle index[J].Rock and Soil Mechanics,2015,36(2):403-408.
[23] 崔振东,李晓,刘大安,等.页岩微纳观尺度雁列式断续裂纹的原位观测[J].工程地质学报,2018,26(1):85-90.
CUI Zhendong,LI Xiao,LIU Daan,et al.In-situ observation of en echelon intermittent cracks of shale in micro-nano scale[J].Journal of Engineering Geology,2018,26(1):85-90.
[24] CUI Z,HAN W.In situ scanning electron microscope (SEM) observations of damage and crack growth of shale[J].Microscopy & Microanalysis,2018,24(2):107-115.
[25] 崔振东,刘大安,李晓,等.页岩微纳观断裂的原位观测[J].地下空间与工程学报,2017,13(1):117-123.
CUI Zhendong,LIU Daan,LI Xiao,et al.In-situ observation on the micro-nano cracks of shale[J].Chinese Journal of Underground Space and Engineering,2017,13(1):117-123.
[26] 姚学锋,熊春阳,方竞.含偏置裂纹三点弯曲梁的动态断裂行为研究[J].力学学报,1996,28(6):22-30.
YAO Xuefeng,XIONG Chunyang,FANG Jing.Study of dynamic fracture behaviour on three point bend beam with off center edge crack[J].Chinese Journal of Theoretical and Applied Mechanics,1996,28(6):22-30.
