随着国家经济的高速发展,岩体光面爆破技术在地下工程、水利水电、矿山等领域均得到了广泛应用[1-2]。但在隧道等地下工程爆破施工中,超欠挖现象仍然十分突出,不仅使施工成本大大增加,同时威胁隧道施工期的安全性。通过现场调研,当结构面与隧道轮廓线斜交时,超欠挖现象尤为明显。因此,研究炮孔间含倾斜裂隙条件下的爆生裂纹扩展规律,具有重要的理论和实际意义。
在双孔同时起爆条件下,爆生主裂纹及缺陷介质尖端产生的衍生裂纹的扩展过程十分复杂。近些年来,学者们通过不同手段对双孔同时爆破作用下裂纹的动态扩展过程进行了研究,得出了相应的结论。HOLLOWAY D C[3]利用动态全息干涉法,研究了双孔同时起爆时裂纹扩展位移的特征条纹,对裂纹扩展位移峰值区域进行了分析。BHANDARI S[4]对爆炸荷载下,含多炮孔岩体的破坏模型进行试验研究。张志呈[5-6]以大理石为研究对象,通过动光弹试验方法,研究双孔同时起爆条件下,裂纹的起裂、扩展及交汇过程,并认为爆生气体是岩石破碎后裂纹扩展的主要动力,而之前的以应力波为主的碎岩理论值得商榷。黄涛等[7]运用流变元数值分析方法,对双孔爆破下岩石破裂过程进行数值模拟,得到冲击荷载作用下,裂纹的扩展形式及块体破碎、爆破漏斗形成的全过程。FENDER等[8]研究了两条相向运动裂纹相互贯通机制。YANG R S[9-12],YUE Z W[13]等对有机玻璃板进行试验,采用3种不同切槽的模型进行双孔同时爆破的裂纹动态扩展过程研究,得到裂纹尖端扩展速度、加速度、应力强度因子和能量释放率等变化规律。王雁冰[14-15]通过动态焦散线试验系统,在预制水平缺陷和垂直缺陷模型下,分别进行了双孔同时爆破试验,得到裂纹的扩展路径、扩展速度、角度、加速度及应力强度因子的变化趋势。李清[16]在不同药量的切缝药包双孔同时起爆条件下,获得了爆生主裂纹和双垂直预制裂隙尖端衍生裂纹的扩展规律。沈世伟等[17]在不同节理间距,双孔同时爆破条件下,对裂纹扩展的动态行为进行了分析。上述学者的研究及发现,对于双孔同时爆破条件下,无缺陷、含水平缺陷、含垂直缺陷等模型的裂纹动态响应问题提供了相应的理论基础及试验思路,为之后的研究奠定了基础,然而对含倾斜缺陷模型裂纹的动态扩展问题的深入研究较为欠缺。笔者利用动态焦散线试验,在双孔同时爆破条件下,研究分析了不同角度预制裂隙对裂纹动态扩展的影响,得到预制裂隙尖端衍生裂纹及爆生主裂纹扩展的路径、破坏形态,裂纹扩展速度、应力强度因子和能量释放率等试验参数的变化规律,更加贴近工程实际,对隧道等地下工程施工中的爆破效果控制具有重要的指导意义。
1 试验系统与模型
1.1 试验系统
本次试验采用焦散线方法[18],该方法运用光测力学试验原理,系统操作简单,试验现象易于观察且试验结果的精准度较高,成功率较大。新型数字激光动焦散线试验系统,由激光器、扩束镜、加载架、场镜组合、高速相机、同步开关与计算机组成,如图1所示。扩束镜和场镜Ⅰ将激光器持续稳定发出的高亮光波处理成平行光入射到试件表面,处于破坏阶段中的试件使平行光发生偏转,偏转后的光束经场镜Ⅱ聚合进入高速摄影机镜头内,摄影机便可拍摄到某时刻的动焦散线图像照片,光路如图2所示。调节摄影机的曝光速度,便可实现裂纹扩展过程的全部记录。

图1 新型数字激光动焦散线试验系统
Fig.1 New digital laser caustics rest system

图2 透射式焦散线试验系统光路
Fig.2 Optical path of transmission caustics test system
1.2 试验模型及参数
本次试验在中国矿业大学深部岩土力学与地下工程国家重点实验室进行,采用有机玻璃板作为试件。根据KUTTER H K等的研究结论,有机玻璃板在爆炸荷载作用下,其裂纹扩展机制与岩石材料裂纹的动态扩展机制相似,可以近似反映岩石动态断裂特性[19-21],且其光学透光性较强,力学具有各向同性,能较好的适应于动态焦散线试验系统,因此成为近些年来人们研究岩石动态裂纹扩展规律的一种重要替代材料。其动态力学参数见表1,ct为材料的应力光学常数。
表1 有机玻璃动态力学参数
Table 1 Dynamic mechanical parameters of PMMA
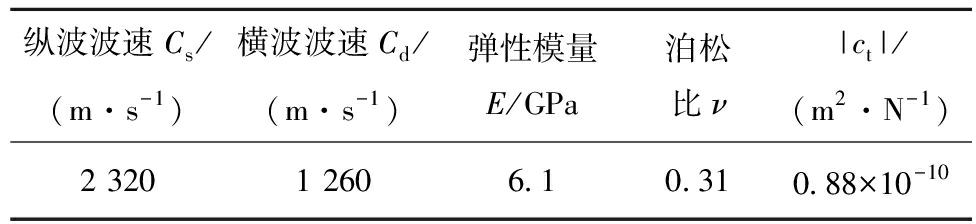
纵波波速Cs/(m·s-1)横波波速Cd/(m·s-1)弹性模量E/GPa泊松比ν|ct|/(m2·N-1)2 3201 2606.10.310.88×10-10
有机玻璃板规格为长×宽×厚=300 mm×300 mm×5 mm,在试件中央预制两炮孔,间距150 mm,炮孔直径10 mm,在炮孔间几何中心位置切割70 mm×1 mm的预制裂隙,试件尺寸如图3,4所示。设计两种预制裂隙试件,预制裂隙倾斜角度分别为30°,45°。试件边界无约束,炮孔均采用不耦合装药[22],不耦合系数1.67,炸药采用叠氮化铅单质炸药,装药量120 mg,起爆方式为双孔同时起爆。
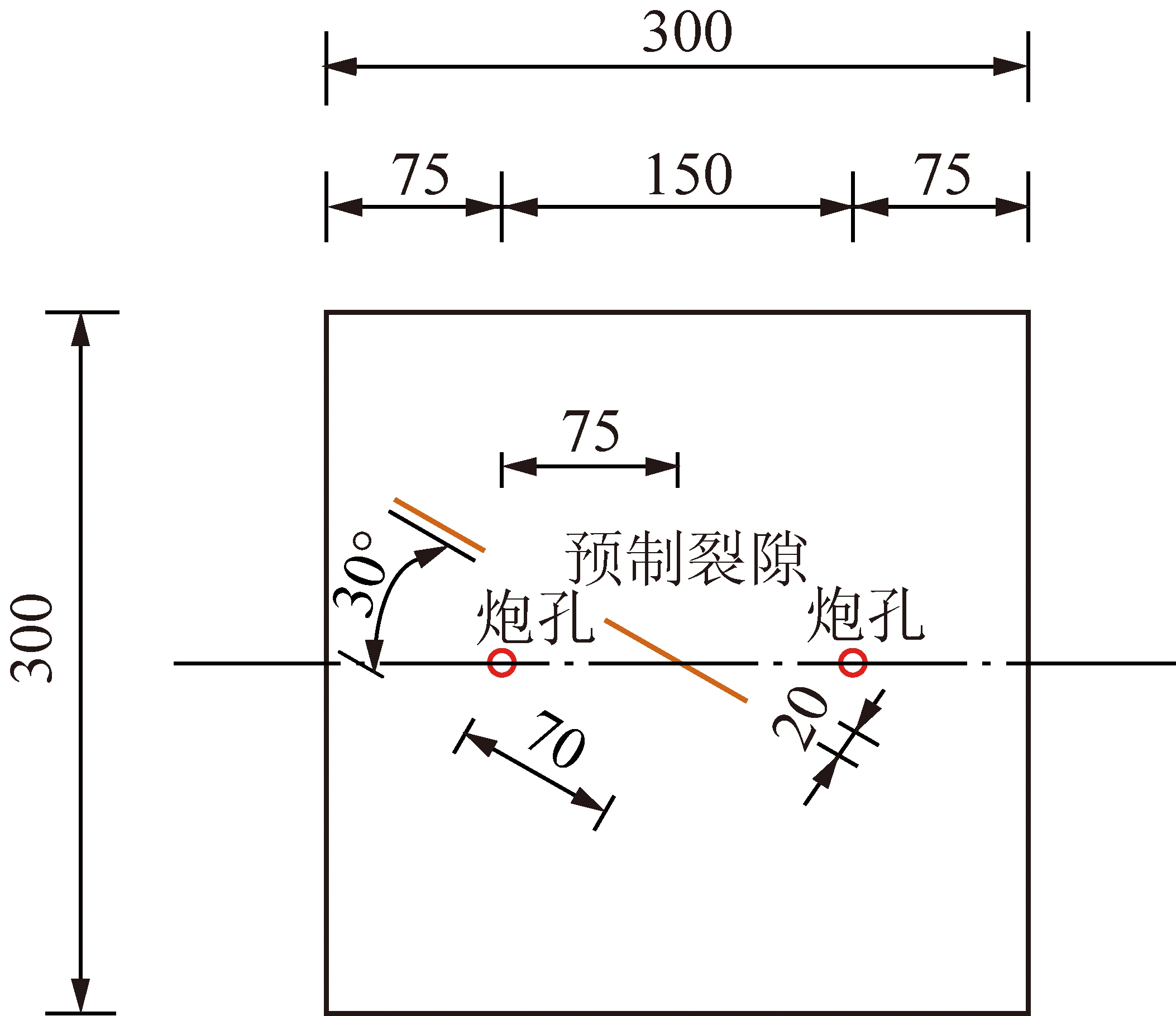
图3 30°预制裂隙模型
Fig.3 30° pefabricated fissure model

图4 45°预制裂隙模型
Fig.4 45° prefabricated fissure model
1.3 计算原理
(1)裂纹扩展速度
根据TAKAHASHI K和ARAKAWAK[23]在1987年提出的数据拟合方法,裂纹扩展长度可拟合成时间的9次多项式,即
![]()
(1)
其中,L(t)为裂纹扩展长度;t为时间;系数Li可用最小二乘法得出。将裂纹扩展长度对时间求一阶导数即可得到裂纹扩展速度。
(2)裂纹尖端应力强度因子
应力强度因子是表征裂纹尖端应力场特征的唯一需要确定的物理量,其大小代表裂纹尖端应力的强弱[24-25]。其中,KI为I型(张开型)裂纹尖端应力强度因子,裂纹尖端主要受拉伸作用;KII为II型(剪切型)裂纹尖端应力强度因子,裂纹尖端主要受剪切作用。爆炸荷载下,裂纹尖端的复合应力强度因子[23,26]为
![]()
(2)
KII=μKI
(3)
式中,Dmax为复合型裂纹尖端焦散斑最大直径;z0为参考平面到物体平面的距离;c为材料的应力光学常数;d为试件的有效厚度;μ为应力强度因子比例系数;η为入射光的收敛因子;F(v)为动载作用下裂纹扩展速度的调节因子;v为裂纹扩展速度;δmax为关于沿着动焦散线最大横向直径的校正因子。
(3)裂纹尖端动态能量释放率
裂纹尖端的能量释放率代表着裂纹扩展单位面积时整个系统能量的下降率[19],反映驱动裂纹向前扩展的能力。当其超过材料本身的裂纹扩展阻力时,裂纹开始扩展。且根据最大能量释放率理论,裂纹扩展的偏转将沿着能量释放率一阶导数为0的方向,这些都对研究裂纹的动态扩展具有重要意义。FREUND[27]总结在平面应力情况下,动态能量释放率G为
![]()
(4)
式中,AI(v),AII(v)为裂纹扩展速度函数。
当v=0时,AI(v)=AII(v)=1;当v≠0时,
式中,E为弹性模量;Cs,Cd为压缩波波速和剪切波波速;ν为泊松比;αd,αs,D为公式的过度系数。
将上述各系数公式代入到动态能量释放率公式中,即可得到速度不为0时复合型裂纹动态能量释放率:
![]()
(5)
由于E,Cs,ν,z0,d,c,η,δmax为材料已知常数,只需测得裂纹扩展速度v及焦散斑最大直径Dmax则可获得动态能量释放率G。
2 试验结果与分析
2.1 裂纹扩展路径分析
图5为30°预制裂隙和45°预制裂隙试件,在双孔同时爆破条件下破坏后的照片。从图5可以明显看出,双孔同时起爆后,由于受到预制裂隙尖端的影响,炮孔外侧的一条爆生主裂纹沿最小抵抗线(与预制裂隙近垂直)的方向扩展;预制裂隙尖端产生的衍生裂纹受到炮孔及其压碎区的导向作用[8],与爆生主裂纹相向扩展。爆生主裂纹与衍生裂纹之间最终并非直接相遇,而是以“勾连状”贯通止裂。最终含45°预制裂隙试件左右主裂纹分别扩展45.6,41.6 mm,含30°预制裂隙试件左、右主裂纹分别扩展20.4,18.5 mm。
对比2个试件发现,45°预制裂隙试件爆生主裂纹与衍生裂纹尖端之间围成的碎裂面积大于30°预制裂隙试件;45°预制裂隙尖端距离炮孔的最短距离较30°预制裂隙远,爆生主裂纹及衍生裂纹扩展的距离较长;由于试件边界无约束,成为裂纹扩展的自由面,因此除与预制裂隙尖端相互作用的爆生主裂纹,其余主裂纹向试件边界方向扩展,且两个试件炮孔外侧的爆生主裂纹数量相同,均为5条。

图5 含30°和45°预制裂隙试件破坏
Fig.5 Failure of 30° and 45° prefabricated fissure specimen
图6为含30°预制裂隙试件各个时刻的焦散斑图像。从图6可以看出,炸药起爆后,爆炸冲击波迅速产生并扩展到预制裂隙近端尖端附近,在预制裂隙尖端积聚能量,出现应力集中现象,同时在炮孔周围产生明显的塑性区(压碎区),主裂纹尖端开始产生未成形的焦散斑,并沿着最小抵抗线的方向(即与预制裂隙垂直的方向)扩展。在13.3 μs时,预制裂隙尖端受到之前应力波的绕射、反射等作用,产生应力集中现象,出现“月牙状”的焦散斑,此时预制裂隙尖端受到压缩波的作用,焦散斑水平方向受挤压,竖直方向向外扩张,且沿炮孔及压碎区方向扩展。随后炮孔产生的应力波波阵面在炮孔连线中心位置相遇,衍生裂纹尖端应力开始集中,焦散斑面积明显变大且趋于圆形,该时间段内焦散斑位置变化较快。之后主裂纹及衍生裂纹受到来自远端炮孔应力波的抵消作用,焦散斑的位置变化不明显。在39.9 μs时,受压缩波和剪切波的共同作用,主裂纹焦散斑出现扭曲,并产生复合型焦散斑。在66.5 μs时,主裂纹尖端的焦散斑与衍生裂纹尖端的焦散斑之间二者相向扩展,在预制裂纹尖端附近“勾连”贯通。
图7为含45°预制裂隙试件焦散斑图像。从图7可以看出,在26.6 μs时,两侧炮孔产生的应力波波前在炮孔连线中间位置相遇,在53.2 μs时出现明显的复合型焦散斑,此时受到压缩波和剪切波的共同作用。随后应力波作用减小,爆生主裂纹及衍生裂纹尖端主要受爆生气体的准静压作用,在此作用下焦散斑位置变化先变快后变慢,焦散斑面积也先变大后减小。爆生主裂纹在气楔作用下沿最小抵抗线方向扩展,衍生裂纹受到爆生气体的作用沿炮孔及压碎区方向扩展,二者最终非直接相遇,呈“勾连状”贯通止裂。

图6 含30°预制裂隙试件焦散斑图像
Fig.6 Caustic spots of 30° prefabricated fissure specimen

图7 含45°预制裂隙试件焦散斑图像
Fig.7 Caustic spots of 45° prefabricated fissure specimen
由此可见,衍生裂纹与爆生主裂纹之间相向扩展,最终并非直接相遇,而是以“勾连状”贯通止裂。 45°预制裂隙试件模型在双孔起爆后,裂纹扩展前期主要受到爆炸应力波的作用,焦散斑位置变化较快,焦散斑面积较大,裂纹扩展后期主要受爆生气体的准静压作用,焦散斑位置变化慢,焦散斑面积小,呈振荡式变化;相较而言,30°预制裂隙试件模型裂纹扩展主要受到爆炸应力波的作用。
2.2 裂纹扩展速度分析
图8(a)为含30°预制裂隙试件裂纹扩展速度变化曲线。由于30°预制裂隙两尖端与炮孔距离较近,裂纹扩展时间较短。从图8(a)可以看出,在26.6 μs时,左主裂纹裂纹扩展速度达到峰值,444.63 m/s,随后开始下降。在39.9 μs时,右主裂纹裂纹扩展速度达到峰值461.26 m/s,峰值速度与左主裂纹峰值速度大致相同,随后开始下降,直至贯通止裂。预制裂隙尖端产生的衍生裂纹扩展速度与主裂纹裂纹扩展速度变化趋势大致相同,总体呈先增大后减小的趋势,代表着应力波与裂纹尖端相互作用的变化情况。在26.6 μs时,左衍生裂纹速度达到峰值441.60 m/s,之后开始减小。右衍生裂纹在39.9 μs时到达峰值268.01 m/s,随后减小至贯通止裂。对比含30°预制裂隙试件衍生裂纹与主裂纹裂纹扩展速度,可见衍生裂纹扩展速度峰值小于主裂纹裂纹扩展速度峰值,且衍生裂纹与同侧主裂纹扩展速度同时达到峰值。

图8 含30°和45°预制裂隙试件裂纹扩展速度变化曲线
Fig.8 Crack propagation velocity of 30° and 45° prefabricated fissure specimen
图8(b)为含45°预制裂隙试件裂纹扩展速度变化曲线。从图8(b)可以看出,左主裂纹在39.9 μs时到达第1个峰值532.94 m/s,之后继续扩展,在66.5 μs时达到第2个峰值531.70 m/s,随后在爆生气体的作用下裂纹扩展速度明显减小,且呈振荡式变化,直至裂纹贯通止裂。右主裂纹尖端随着能量的积累,在裂纹起裂后迅速释放,裂纹扩展速度由峰值537.31 m/s开始减小,在93.1 μs后,在爆生气体准静压作用下,裂纹几乎稳定扩展直至贯通。衍生裂纹扩展时间较短,右衍生裂纹与左衍生裂纹扩展速度变化趋势一致,这主要与应力波与裂纹尖端的相互作用有关。衍生裂纹裂纹扩展速度先增大后减小,在53.2 μs时分别达到峰值,分别为452.12 m/s和456.74 m/s。随着应力波能量的衰减,裂纹扩展速度逐渐减小直至贯通。可见模型的对称设计,致使主裂纹之间及衍生裂纹之间扩展速度几乎相同,由于两炮孔的装药结构及装药量等参数可能存在人为操作误差,造成主裂纹之间及衍生裂纹之间裂纹扩展速度的微小差别。
对比含45°预制裂隙试件与含30°预制裂隙试件裂纹扩展速度变化曲线,可以看出,预制裂隙在一定倾斜范围内,随着角度的增加,爆生主裂纹的扩展速度峰值更大,裂纹扩展时间更长,且裂纹扩展后期,在爆生气体的准静压作用下,裂纹扩展速度较低,且呈振荡式变化,直至贯通止裂。
2.3 裂纹尖端应力特征分析
应力强度因子反映裂纹尖端应力场的变化情况,其根据焦散斑最大直径及裂纹扩展速度确定,图9分别为30°预制裂隙试件裂纹尖端应力强度因子KI,KII变化曲线。从图9(a)可以看出,主裂纹尖端应力强度因子KI随时间先增大后减小,表明双孔起爆后,主裂纹裂纹尖端应力场受到爆炸应力波的作用逐渐增强,在裂纹尖端能量发生积累,产生应力集中,应力强度因子逐渐变大。之后,应力波作用开始衰减,主裂纹尖端应力强度因子开始减小。左主裂纹在53.2 μs时达到峰值1 257.9 kN/m3/2,随后开始减小。右主裂纹在39.9 μs时达到峰值938.2 kN/m3/2,之后减小至贯通止裂。在39.9 μs时,左、右主裂纹尖端出现应力强度因子KII,表明此时剪切波与裂纹尖端相互作用,左、右主裂纹尖端应力强度因子KII峰值分别为877.1,792.6 kN/m3/2。衍生裂纹在受到应力波的反射、绕射及透射等作用,形成复杂的尖端应力场,应力强度因子逐渐增大,随后能量开始释放,应力强度因子减小。左衍生裂纹尖端应力强度因子KI在53.2 μs时达到峰值990.7 kN/m3/2。右衍生裂纹时,左、右衍生裂纹尖端应力强尖端应力强度因子KI在39.9 μs时达到峰值1 089.0 kN/m3/2。在13.3 μs时,左、右衍生裂纹尖端出现应力强度因子KII,此时裂纹尖端产生剪应力,应力强度因子KII峰值分别为698.3,712.9 kN/m3/2。从图9可以看出,对于同一条裂纹尖端复合型应力强度因子,同一时间应力强度因子KII均小于KI,可以说明同一时刻压缩波的作用大于剪切波。

图9 含30°预制裂隙试件KI和KII变化曲线
Fig.9 Relation curves between dynamic stress intensity factorsKI and KII of 30° prefabricated fissure tips and time

图10 含45°预制裂隙试件KI,KII变化曲线
Fig.10 Relation curves between dynamic stress intensity factors KI,KII of 45° prefabricated fissure tips and time
图10分别为含45°预制裂隙试件裂纹尖端应力强度因子KI,KII变化曲线。由于裂纹扩展前期,裂纹尖端所受应力波作用与含30°预制裂隙试件相似,故裂纹尖端所受的应力波作用在此不再赘述。从图10可以看出,在79.8 μs时,左主裂纹尖端应力强度因子KI达到峰值1 092.0 kN/m3/2。在26.6 μs时,右主裂纹尖端应力强度因子KI达到峰值1 598.7 kN/m3/2,随后开始减小。在裂纹扩展后期应力强度因子KI出现振荡式变化,这主要与爆生气体的气楔作用有关。左、右主裂纹尖端应力强度因子KII分别在53.2,39.9 μs时产生,出现较晚,表明与压缩波相比,剪切波扩展速度较慢,作用较晚。在66.5 μs时,左、右主裂纹尖端应力强度因子KII同时达到峰值,分别为965.2,861.4 kN/m3/2,随后下降,后期呈振荡式变化。衍生裂纹在扩展前期受应力波的反射、折射等作用,在53.2 μs度因子KI同时达到第1个峰值,分别为1 669.4 kN/m3/2和1 575.2 kN/m3/2。随后在79.8 μs时受到反射拉伸波的作用,左、右衍生裂纹尖端应力强度因子KI同时出现第2个峰值,分别为1 234.0 kN/m3/2和1 265.0 kN/m3/2,之后下降直至贯通止裂。在39.9 μs时,左、右衍生裂纹出现应力强度因子KII,随后在79.8 μs时达到峰值,分别为918.4,872.0 kN/m3/2。由图10可知,在裂纹扩展前期,裂纹尖端主要受应力波的作用,应力强度因子较大;裂纹扩展后期,在爆生气体的作用下,裂纹尖端应力强度因子较小,且呈振荡式变化。与含30°预制裂隙试件相同,对于同一时刻裂纹尖端复合型应力强度因子,KII均小于KI,剪切波的作用小于压缩波。
对比2个试件裂纹尖端的应力强度因子变化规律,可以看出,在一定范围内,随着预制裂隙角度的增加,裂纹尖端应力强度因子峰值更大、裂纹扩展时间更长且裂纹扩展后期受爆生气体的作用,应力强度因子呈振荡式变化。
2.4 裂纹尖端能量释放率
裂纹尖端的能量释放率代表着裂纹扩展单位面积时整个系统能量的下降率,反映驱动裂纹向前扩展的能力。双孔起爆后,爆炸应力波在传播过程中携带着能量,应力波与裂纹尖端相互作用,能量释放率的提高代表着应力波的加载过程,减小代表应力波的衰减过程。由于裂纹未起裂之前,系统的能量转化为弹性应变能,在裂纹起裂后,弹性应变能释放,一部分克服裂纹扩展阻力,另一部分转化为裂纹表面的表面能,而能量释放率由于应力波与裂纹尖端的相互作用,不断的积累与释放,驱动裂纹向前扩展。
图11(a)为含30°预制裂隙试件能量释放率变化曲线。由图11(a)可知,裂纹尖端能量释放率随时间先增大后减小,反映应力波对裂纹运动的影响,左主裂纹尖端能量释放率在53.2 μs时达到峰值203.0 N/m。右主裂纹尖端能量释放率在39.9 μs时达到峰值131.2 N/m。左衍生裂纹尖端能量释放率峰值在26.6 μs时达到峰值180.4 N/m。右衍生裂纹尖端能量释放率峰值在39.9 μs时达到峰值195.0 N/m。

图11 含30°,45°预制裂隙试件能量释放率变化曲线
Fig.11 Relation curves between energy release rate of 30° and 45° prefabricated fissure tips and time
图11(b)为含45°预制裂隙试件能量释放率变化曲线。由图11(b)可知主裂纹尖端能量释放率先增大后减小,其之间的差值体现着能量释放率对裂纹扩展的驱动能力,随后呈振荡式变化,直至贯通止裂。左主裂纹尖端能量释放率峰值在79.8 μs时达到峰值424.3 N/m。右主裂纹尖端能量释放率峰值在26.6 μs时达到峰值490.5 N/m。主裂纹能量释放率的变化主要分2个阶段:第1阶段以应力波作用为主,其传播过程中携带的能量在裂纹尖端积累与释放,应力波的加载过程致使能量释放率提高,其衰减过程致使能量释放率减小;第2阶段以爆生气体为主,其携带的能量较低,作用时间较长,在裂纹尖端形成复杂的应力场,致使能量释放率呈振荡式变化。左、右衍生裂纹尖端能量释放率出现2个峰值,第1个峰值分别为521.1 N/m和598.0 N/m,第2个峰值分别为271.0 N/m和378 N/m。衍生裂纹的第1峰值反映着应力波的加载过程,之所以出现第2峰值是由于反射拉伸波在裂纹尖端的作用。
对比2个试件尖端能量释放率的变化曲线,可以发现,在一定范围内,随着预制裂隙角度的增加,裂纹尖端能量释放率峰值更高,代表裂纹扩展的驱动力更大;除此之外,结合能量释放率的公式,能量释放率是应力强度因子的函数,从试验曲线也可以看出能量释放率的变化与裂纹尖端应力强度因子的变化趋势整体一致。
3 结 论
(1)双孔同时爆破条件下,炮孔产生的主裂纹与预制裂隙尖端产生的衍生裂纹之间非直接相遇,而是以 “勾连”形式贯通止裂。
(2)裂纹扩展速度、应力强度因子及能量释放率等特征量整体变化趋势为先增大后减小,在一定范围内,随着预制裂隙倾斜角度的增加,裂纹扩展速度、应力强度因子及能量释放率峰值更高;爆生主裂纹和衍生裂纹扩展的时间更长,扩展的距离更远。
(3)双孔同时起爆后,随着预制裂隙倾斜角度的增加,爆生主裂纹与衍生裂纹尖端之间最终围成的破坏面积更大,爆炸荷载与预制裂隙尖端作用更加明显。
(4)含45°预制裂隙模型裂纹扩展前期主要受应力波的动荷载作用,裂纹扩展速度较快、应力强度因子较大、能量释放率更高;扩展后期主要受爆生气体的准静压作用,裂纹扩展速度较慢,应力强度因子较小、能量释放率较低,且呈振荡式变化。
(5)应力波与衍生裂纹相互作用,形成复杂的奇异应力场,且同一时刻应力强度因子KI大于KII,说明压缩波的作用大于剪切波,裂纹尖端主要以压缩波产生的拉应力作用而扩展。
[1] LONG Nguyen Quoc,BUCZEK Micha M,HIEN LA Phu,et al.Accuracy assessment of mine walls’ surface models derived from terrestrial laser scanning[J].International Journal of Coal Science & Technology,2018,5(3):328-338.
M,HIEN LA Phu,et al.Accuracy assessment of mine walls’ surface models derived from terrestrial laser scanning[J].International Journal of Coal Science & Technology,2018,5(3):328-338.
[2] MAI Ngoc Luan,ERTEN Oktay,TOPAL Erkan.A new generic open pit mine planning process with risk assessment ability[J].International Journal of Coal Science & Technology,2016,3(4):407-417.
[3] HOLLOWAY D C.Application of holographic interferometry to stress wave and crack propagation problems[J].Optical Engineering,1982,21(5):769-792.
[4] BHANDARI S,BADAL R.Post-blast studies of jointed rocks[J].Engineering Fracture Mechanics,1990,35(1):439-445.
[5] 张志呈.定向断裂控制爆破机理综述[J].矿业研究与开发,2000,20(5):40-42.
ZHANG Zhicheng.Summary of the mechanism of directional fracture controlled blasting[J].Mining Research & Development,2000,20(5):40-42.
[6] 张志呈.定向断裂控制爆破[M].北京:冶金工业出版社,2000.
[7] 黄涛,陈鹏万,张国新,等.岩石双孔爆破过程的流形元法模拟[J].爆炸与冲击,2006,26(5):434-440.
HUANG Tao,CHEN Pengwan,ZHANG Guoxin,et al.Numerical simulation of two-hole blasting using numerical manifold method[J].Explosion and Shock Waves,2006,26(5):434-440.
[8] FENDER M L,LECHENAULT F,DANIELS K E,et al.Universal shapes formed by two interacting cracks[J].Physical Review Letters,2010,105(12):1-4.
[9] YANG R,WANG Y,XUE H,et al.Dynamic behavior analysis of perforated crack propagation in two-hole blasting[J].Procedia Earth & Planetary Science,2012,5:254-261.
[10] YANG R S,WANG Y B,GUO D M,et al.Experimental research of crack propagation in polymethyl methacrylate material containing flaws under explosive stress waves[J].Journal of Testing and Evaluation,2016,44(1):56-60.
[11] 杨仁树,王雁冰,岳中文,等.定向断裂双孔爆破裂纹扩展的动态行为[J].爆炸与冲击,2013,33(6):631-637.
YANG Renshu,WANG Yanbing,YUE Zhongwen,et al.Dynamic behaviors of crack propagation in directional fracture blasting with two holes[J].Explosion and Shock Waves,2013,33(6):631-637.
[12] 杨仁树,王雁冰,杨立云,等.双孔切槽爆破裂纹扩展的动焦散试验[J].中国矿业大学学报,2012,41(6):868-872.
YANG Renshu,WANG Yanbing,YANG Liyun,et al.Dynamic caustic experimental study of crack propagation in two borehole cut blasting[J].Journal of China University of Mining & Technology,2012,41(6):868-872.
[13] YUE Z W,YANG L Y,WANG Y B.Experimental study of crack propagation in polymethyl methacrylate material with double holes under the directional controlled blasting[J].Fatigue & Fracture of Engineering Materials & Structures,2013,36(8):827-833.
[14] 王雁冰,商禹智,石震鑫,等.定向断裂双孔爆破含缺陷介质裂纹扩展的动焦散试验[J].爆破,2018,35(1):15-20.
WANG Yanbing,SHANG Yuzhi,SHI Zhenxin,et al.Dynamic caustics experiment on crack propagation in defective medium by directional breaking with double hole blasting[J].Blasting,2018,35(1):15-20.
[15] 王雁冰,杨仁树,丁晨曦,等.双孔爆炸应力波作用下缺陷介质裂纹扩展的动焦散试验[J].煤炭学报,2016,41(7):1755-1761.
WANG Yanbing,YANG Renshu,DING Chenxi,et al.Dynamic caustics experiment on crack propagation of defective medium under the effect of explosive stress waves of double holes[J].Journal of China Coal Society,2016,41(7):1755-1761.
[16] 李清,于强,朱各勇,等.不同药量的切缝药包双孔爆破裂纹扩展规律试验[J].岩石力学与工程学报,2017,36(9):2205-2212.
LI Qing,YU Qiang,ZHU Geyong,et al.Experimental study of crack propagation under two-hole slotted cartridge blasting with different amounts of charge[J].Chinese Journal of Rock Mechanics and Engineering,2017,36(9):2205-2212.
[17] 沈世伟,廖文旺,徐燕,等.不同节理间距条件下岩体双孔爆破动焦散试验研究[J].煤炭学报,2018,43(8):2180-2186.
SHEN Shiwei,LIAO Wenwang,XU Yan,et al.Dynamic caustics test of rock mass under different joint spacing conditions with two-hole blasting[J].Journal of China Coal Society,2018,43(8):2180-2186.
[18] 杨立云,杨仁树,岳中文,等.数字激光动态焦散线试验系统[P].中国专利:201120458198X,2012-08-29.
YANG Liyun,YANG Renshu,YUE Zhongwen,et al.Experimental system of digital laser dynamic caustics[P].China Patent:201120458198X,2012-08-29.
[19] PAPADOPOULOS G A.Fracture mechanics:The experimental method of caustics and det-criterion of fracture[J].Springer-Verlag,1993,4:156-184.
[20] ROSSMANITH H P,DAEHNKE A,KNASMILLNER R E K,et al.Fracture mechanics applications to drilling and blasting[J].Fatigue and Fracture Engineering Materials and Structures,1997,20(11):1617-1636.
[21] YUE Z W,YANG L Y,WANG Y B.Experimental study of crack propagation in polymenthyl methacrylate material with double holes udder the directional controlled blasting[J].Fatigue & Fracture of Engineering Materials & Structures,2013,36(8):827-833.
[22] 徐颖,孟益平,程玉生.装药不耦合系数对爆破裂纹控制的试验研究[J].岩石力学与工程学报,2002,21(12):1843-1847.
XU Ying,MENG Yiping,CHENG Yusheng.Study on control of blast crack by decoupling charge index[J].Chinese Journal of Rock Mechanics and Engineering,2002,21(12):1843-1847.
[23] TAKAHASHI K,ARAKAWAK.Dependence of crack acceleration on the dynamic stress-intensity factor in polymers[J].Experimental Mechanics,1987,27(2):195-199.
[24] IRWIN G R.Analysis of stresses and strains near the end of a crack traversing a plate[J].Journal of Applied Mechanics,1957,24:361-364.
[25] 李世愚.岩石断裂力学导论[M].合肥:中国科学技术大学出版社,2010.
[26] LAGARDE A.Static and dynamic photoelasticity and caμstics recent developments[M].NewYork:Springer-Verlag,1987:407-522.
[27] FREUND L B.Dynamic fracture mechanics[M].Edinburgh:Cambridge University Press,1990.
