煤炭作为人类生活和经济发展的主要能源之一，在世界能源消费结构中占据非常重要的地位。虽然随着全球清洁能源不断推广，煤炭在一次能源中的占比不断下降，但煤炭仍是世界一次能源消耗结构的主要组成部分(29.2%)[1]。在我国，煤炭在一次能源结构中一直占据主体地位，预计到2030年，煤炭占比仍将保持在50%以上[2]。煤炭开采虽然能获得有效的资源，但同时会伴随着地表塌陷、公路和铁路变形、建(构)筑物损坏等灾害的发生，对人民生命财产安全构成了巨大威胁。因此，研究煤炭开采引起的地表变形规律和特征，用于进行灾害预测、控制和防治，具有非常重要的意义[3-4]。

常用的研究煤炭开采地表移动变形的方法包括:典型曲线法、剖面函数法和概率积分法等[5]。其中，概率积分法由刘宝琛、廖国华等学者在波兰学者LITWINISZYN提出的随机介质理论的基础上发展而来，通过建立理论结构模型，推导并计算出了地表变形的最大值和分布情况的解析公式，现已成为研究开采沉陷变形规律使用最广泛的方法之一[5]。该方法的基本假设是地表变形符合概率积分非线性模型，该模型中存在的待求参数，需采用一定的数学方法进行反演，以确定模型的具体表达式，进而分析变形规律和特征。

由于不同的参数反演方法得到的结果各异，因此选择合适的参数反演方法至关重要。现有的参数反演方法大体可归为两类:一类是传统的优化算法，包括线性最小二乘法、模矢法等[6];一类是智能优化算法，包括遗传算法(genetic algorithm，GA)、粒子群算法和模拟退火算法等。其中，传统的优化算法适合解决非线性程度较低的模型参数反演问题，但对于非线性程度较高的概率积分模型，其存在初始值要求高、求解过程易发散和易陷入局部最优解等问题。智能优化算法作为解决非线性模型参数反演的重要工具，一定程度上克服了传统优化算法求解过程易发散的缺陷，并在概率积分模型参数反演中得到了广泛关注和讨论[7]。查剑锋等[8]采用遗传算法进行概率积分法的预计参数反演，验证了该算法相较于最小二乘法和模矢法在参数反演准确性和可靠性方面具有明显优势;随后，模拟退火算法[9]、粒子群算法[10]等分别被用于进行概率积分模型的参数反演，均取得了较为理想的效果。然而，智能优化算法是一种基于生物进化的随机全局优化算法，其参数反演结果具有一定的随机性，即基于同一数据，采用同一智能优化算法(参数设置固定)，反演的参数存在一定差异，这就为后续参数的使用造成了一定的困扰，有必要引入新的算法进行概率积分模型中预计参数的反演。

考虑到概率积分模型的非线性特征，本文尝试引入最优化算法进行参数反演，采用使用较为广泛的BFGS算法，进行相关问题的论述和数据处理。BFGS算法是一种解决非线性方程无约束问题的最优化算法，由BROYDEN，FLETCHER，GOLDFARB和SHANNO在20世纪60年代从不同的角度独立提出，现已成为最有效的拟牛顿算法之一。该方法是利用相邻两迭代点之间的位移和对应目标函数的梯度差构造近似的Hesse矩阵，然后基于牛顿方程产生搜索方向，继而通过非精确线搜索完成迭代过程。此过程不需要计算目标函数的Hesse矩阵，理论上求解参数具有较强的稳定性，其主要优点是处理非线性问题时具有超线性收敛性和自校正能力[11-12]。目前，该算法已成功运用到许多领域，例如地表三维形变监测[13]、航空电磁反演[14]、 微电网潮流计算[15]等。

笔者拟通过概率积分模型建立目标函数，将其转化为无约束最优化问题，然后引入BFGS算法进行概率积分模型的参数反演，验证BFGS算法在开采沉陷参数反演中的可行性，并通过大量的仿真实验，与常用的传统优化算法中的模矢法和智能优化算法中的遗传算法反演的参数进行对比分析，验证新算法在统计意义上的性能优势;最后，采用实际工程应用案例，进一步验证BFGS算法的参数反演的可靠性与性能。

1 算法描述

1.1 概率积分法预计模型

概率积分法是一种计算地表移动和变形的预测方法，其地表任意点下沉值预计的基本数学模型为

(1)

式中，W(x,y)为(x,y)位置的下沉值;x和y为地表任意点的横、纵坐标;W0为地表最大下沉值;Wo(x)为倾向方向充分采动时走向主断面上横坐标为x的下沉值;Wo(y)为走向方向充分采动时倾向主断面上纵坐标为y的下沉值。计算公式分别为

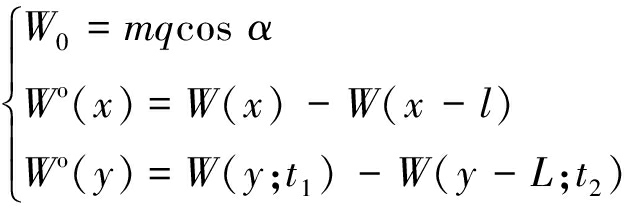
(2)

式中，m为法向采厚;q为下沉系数;α为煤层倾角;W(x)为横坐标为x的地表点的下沉值;l为走向工作面的计算长度;L为倾向工作面的计算长度;W(y;t1)和W(y-L;t2)中y为函数W中的变量，t1和t2为函数W中的参数， t1为下山方向的主要影响半径r1，t2为下山方向的主要影响半径r2。

式(2)中相关参数的计算公式为

(3)

l=D3-s3-s4

(4)

(5)

其中，du为煤层的单元厚度;D1为工作面倾向长度;D3为工作面走向长度;θ0为开采影响传播角;s1，s2，s3，s4分别为下山边界、上山边界、左边界和右边界的拐点偏移距;r为主要影响半径，可表示为

(6)

式中，H为开采边界采深;tan β为主要影响角正切。

同理，概率积分法对于任意点水平移动值预计的基本数学模型为

Uo(y)Wo(x)sin φ]

(7)

式中，φ为从x轴的正向逆时针到指定方向的角度值;Uo(x)和Uo(y)分别为走向主断面上和倾向主断面上的水平移动值，可表示为

(8)

式中，U(x)为横坐标为x的地表点的水平移动值;和中y为函数U中的变量，和为函数U中的参数，其中，代表下山方向的水平移动系数b1和下山方向的主要影响半径代表上山方向的水平移动系数b2和上山方向的主要影响半径r2。

U(x)的计算公式为

(9)

式中，b为水平移动系数。

将式(4)～(6)，(9)代入式(8)，并加上由于煤层倾斜所引起的水平移动和水平变形的分量，可得

(10)

式中，b1，b2分别为下山和上山方向水平移动系数;H0，H1，H2分别为平均采深、下边界采深和上边界采深;tan β1，tan β2分别为下山方向和上山方向的主要影响角正切值。

1.2 基于BFGS算法的概率积分法预计参数的反演

采用BFGS算法反演概率积分预计公式中的参数，需通过概率积分公式建立目标函数模型，将其转化为无约束最优化问题，可表示为

(11)

式中，N为地面观测点数;Wi为下沉测量值;Ui为水平移动测量值。

将式(1)，(7)代入式(11)，得到目标函数:

[Erf(y)-Erf(y-L)]][Erf(x)-Erf(x-

(12)

式中，

BFGS算法的迭代过程开始于计算新的迭代解，即

Xk+1=Xk+αkdk

(13)

式中，Xk为待求参数的第k次的迭代解;dk为第k次的搜索方向;αk为步长因子，其数值应当服从于Wolfe步长规则。

dk可表示为

(14)

式中，为对目标函数式(12)中q，b，tan β，θ0，s1，s2，s3和s4八个待求参数分别求偏导，有

(15)

(16)

Erf(y-L)][xErf′(x)-(x-l)Erf′(x-l)]+[Erf(x)-Erf(x-l)][yErf′(y)-(y-L)×

(17)

(18)

(19)

(20)

同时，式(14)中的Bk为目标函数第k次迭代的Hesse矩阵的近似矩阵，表达式为

(21)

式中，

Wolfe步长规则为

(22)

式中，σ1和σ2为步长规则限制参数，且0<σ1<σ2<1。

利用BFGS算法反演概率积分模型中的参数，即求取目标函数式(12)中的待求参数，其算法步骤:① 输入工作面观测点的坐标、下沉值、水平移动值和地质采矿条件，给定BFGS算法中的步长规则限制参数σ1和σ2(0<σ1<σ2<1)，计算概率积分公式中待求参数初始值X0，给出终止误差ε，初始对称正定矩阵B0，并令k=0。② 计算目标函数的梯度函数。若则停止计算，输出Xk为近似极小值点。③ 由式(14)计算得到dk，确定算法的搜索前进方向。④ 利用式(22)得到满足Wolfe准则的搜索步长因子αk。⑤ 利用校正公式(21)，计算得到Hesse矩阵的近似矩阵Bk。⑥ 令k=k+1，转至步骤②。终止准则停止后求得的Xk即为概率积分模型中待求参数的最优解。

2 仿真实验与结果统计分析

2.1 设计工作面地质采矿条件及沉陷预计参数

设计开采工作面的地质采矿条件和概率积分参数，法向采厚m=4 m、煤层倾角α=3°、倾向长D1=300 m、走向长D3=670 m、开采深度H=260 m，用全部垮落法管理顶板。概率积分参数设计值为:下沉系数q0=0.64、水平移动系数b0=0.3、主要影响角正切tan β0=2.37、开采影响传播角θ0=88.5°、拐点偏移距分别为s10=s20=s30=s40=52 m。设计工作面走向线上监测点44个(E1～E44)，倾向线上监测点25个(N1～N25)，共计69个监测点，分布如图1所示。

为了比较不同算法的性能优劣，分别采用模矢法、GA算法和BFGS算法进行参数反演，其中，模矢法的参数设置为:参数的终止步长定为10-5;GA算法的参数设置为:迭代的最高次数为200，初始种群的规模为100，交叉概率为0.9，变异概率为0.001[7];BFGS算法的参数设置为:σ1=0.4，σ2=0.55，最大迭代次数为500，终止误差ε=10-5[16]。此外，为了测试不同初始值条件下，3种算法的参数反演性能，每次反演参数的初始值在如下范围内随机产生:q∈[q0-0.25, q0+0.25];b∈[b0-0.05, b0+0.05];tan β∈[tan β0-0.4, tan β0+0.4];θ0∈[80°,90°];s1∈[s10-20, s10+20];s2∈[s20-20, s20+20];s3∈[s30-20, s30+20];s4∈[s40-20, s40+20]。

2.2 不同误差水平下的参数反演比较与分析

受测量手段、观测环境等因素的影响，采集的数据中必然含有随机误差，因此，有必要测试在不同水平随机误差条件下，不同算法反演概率积分参数的性能。将设计的地质采矿条件和沉陷预计参数带入到概率积分模型中，计算该工作面中设计观测点的下沉值和水平移动值，并将其作为真值，在真值上加入中误差为5 mm(10～20 mm)的随机误差，即可产生一组仿真数据。分别在5，10，和20 mm三种随机误差水平下，仿真100组仿真数据，用于算法的验证和分析。

分别采用模矢法、GA算法和BFGS算法，对上述仿真数据进行参数反演，每组参数反演的初始值大小在设置范围内随机产生。表1给出了不同随机误差水平下，3种算法得到的100次参数反演结果与设计值差值绝对值的平均值。

由表1可知:① 在不同中误差的随机误差下，BFGS算法反演参数的效果总体良好。其中主要参数q，b，tan β和θ0与对应设计值差值绝对值的平均值均小于0.1，相对误差均在0.5%以内，表明BFGS算法反演的q，b，tan β和θ0与设计值基本一致;② 随着随机误差的增大(中误差由5～20 mm)，3种算法反演参数的误差并没有明显的变化，表明随机误差的大小对概率积分方程的拟合度的影响不大;③ 比较3种算法的反演结果:对于q，b，tan β和θ0四个主要参数，BFGS算法的反演精度高出模矢法和GA算法1个数量级，表现出了更为优越的参数反演性能;对于s1，s2，s3和s4四个参数，3种算法的反演精度基本相当，BFGS算法有较小的优势。此外，BFGS算法得到的总体拟合的验后单位权中误差明显小于其他两种算法，表明BFGS算法可以获得更高精度的拟合效果。

进一步分析了不同算法反演参数的分布特征，限于篇幅，仅给出中误差为10 mm的100组仿真数据的反演结果(图2)。由图2可知:① 在设计范围内随机产生待反演参数的初始值的基础上，BFGS算法反演的100组参数q，b，tan β和θ0的结果接近一条直线，其反演参数的收敛性明显好于其他两种方法，表现出了较强的稳定性;② 3种算法反演得到的s1，s2，s3和s4四个参数均在一定的范围内摆动，且波动范围基本相当。综上分析，相较于模矢法和GA算法，BFGS算法对概率积分参数的反演效果表现出了统计意义上的优势，对于不同的初始值，其参数反演的精确度和稳定性均最优。

2.3 算法对粗差的抗干扰能力

受人为因素、外在环境因素等影响，大量观测值中可能存在粗差，需要在不同粗差条件下，进一步测试BFGS算法进行参数反演的性能。考虑到粗差的数量通常不超过所有观测值的5%～10%[17]，因此，本文选取7%的粗差作为最大比例，即粗差数目不超过5个(监测点共69个)，进行相关数据处理。具体做法如下:在2.2节100组中误差为10 mm的下沉值和水平移动值的基础上，每组随机选取0～5个点加入粗差作为新的测试数据，粗差由中误差大小为(5～20)σ(σ=10 mm)正态分布函数随机产生。

表1 3种算法反演参数计算结果(不同中误差水平)
Table 1 Statistical results of inversed parameters by three methods under different error levels

注:Mean(|q-q0|)是100组反演参数q与真值q0差值取绝对值的平均值;相对误差(q)=Mean(|q-q0|)/q0，其他参数指标类同。

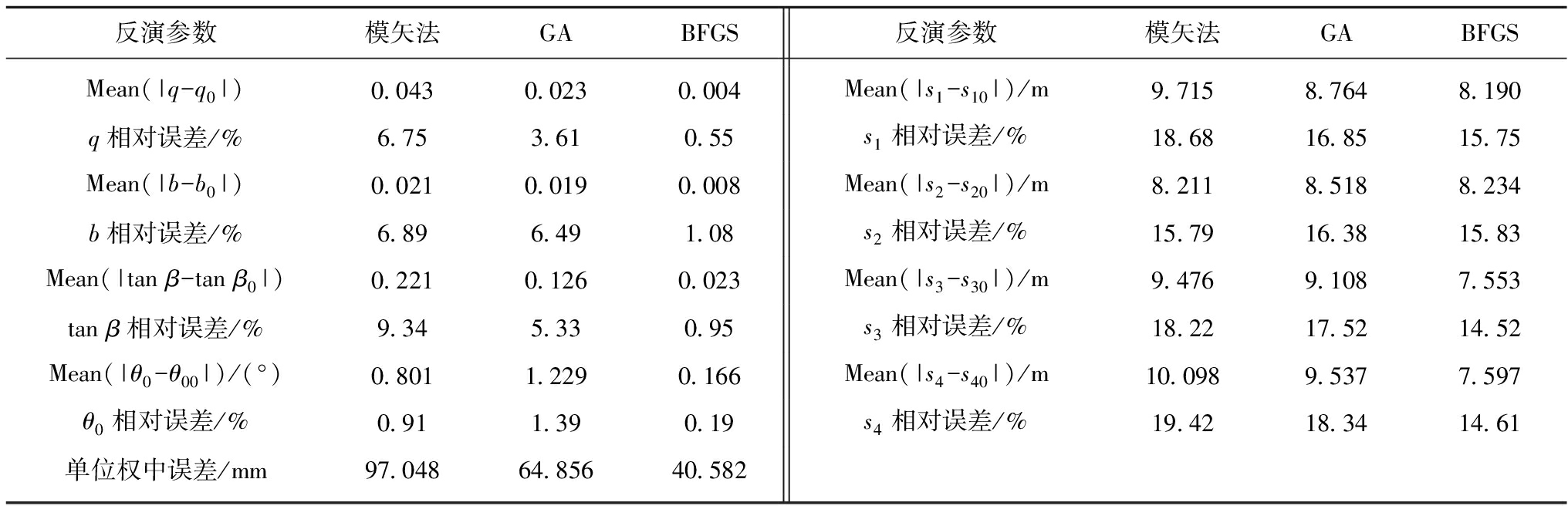
分别采用模矢法、GA算法和BFGS算法反演概率积分模型中的参数，表2给出了3种算法反演的参数与设计值之差绝对值的平均值及其相对误差，由表2可知:① 与表1中仅加入10 mm随机误差的结果相比，加入粗差后，BFGS算法的反演的q，b，tan β和θ0四个参数的误差有所增大，但其相对误差仍可基本保持在1%以内，s1，s2，s3和s4四个参数的误差基本保持不变;② BFGS算法得到q，b，tan β和θ0四个主要参数的误差仍显著小于模矢法和GA算法;③ 由于粗差的存在，概率积分模型误差增大，不同参数反演方法对整体拟合结果影响程度减弱，使得BFGS算法的验后单位权中误差虽然仍明显小于其他两种算法，但相较于仅含有10 mm随机误差的结果，其程度有所减弱。综上分析，虽然在含有粗差的情况下，BFGS算法参数反演的精度有所降低，但其仍然表现出了较好的鲁棒性，其算法对粗差具有较好的抗干扰能力。

表2 3种算法反演参数计算结果(含有粗差)
Table 2 Statistical results of inversed parameters by three methods with gross errors

2.4 算法对观测点缺失的抗干扰能力

通常进行矿区地表变形监测时，需要布设大量的地面监测点，进行长时间重复性观测，监测点不可避免地受到人为破坏、地下水渗出和其他不可控因素的影响，造成监测点的损坏或无法测量，进而引起监测数据的缺失。为了验证在不同程度数据缺失情况下各算法参数反演的性能，随机删除100组中误差为10 mm的下沉值和水平移动值中10%，30%和50%的数据，数据删除的位置随机，进而进行概率积分参数的反演。

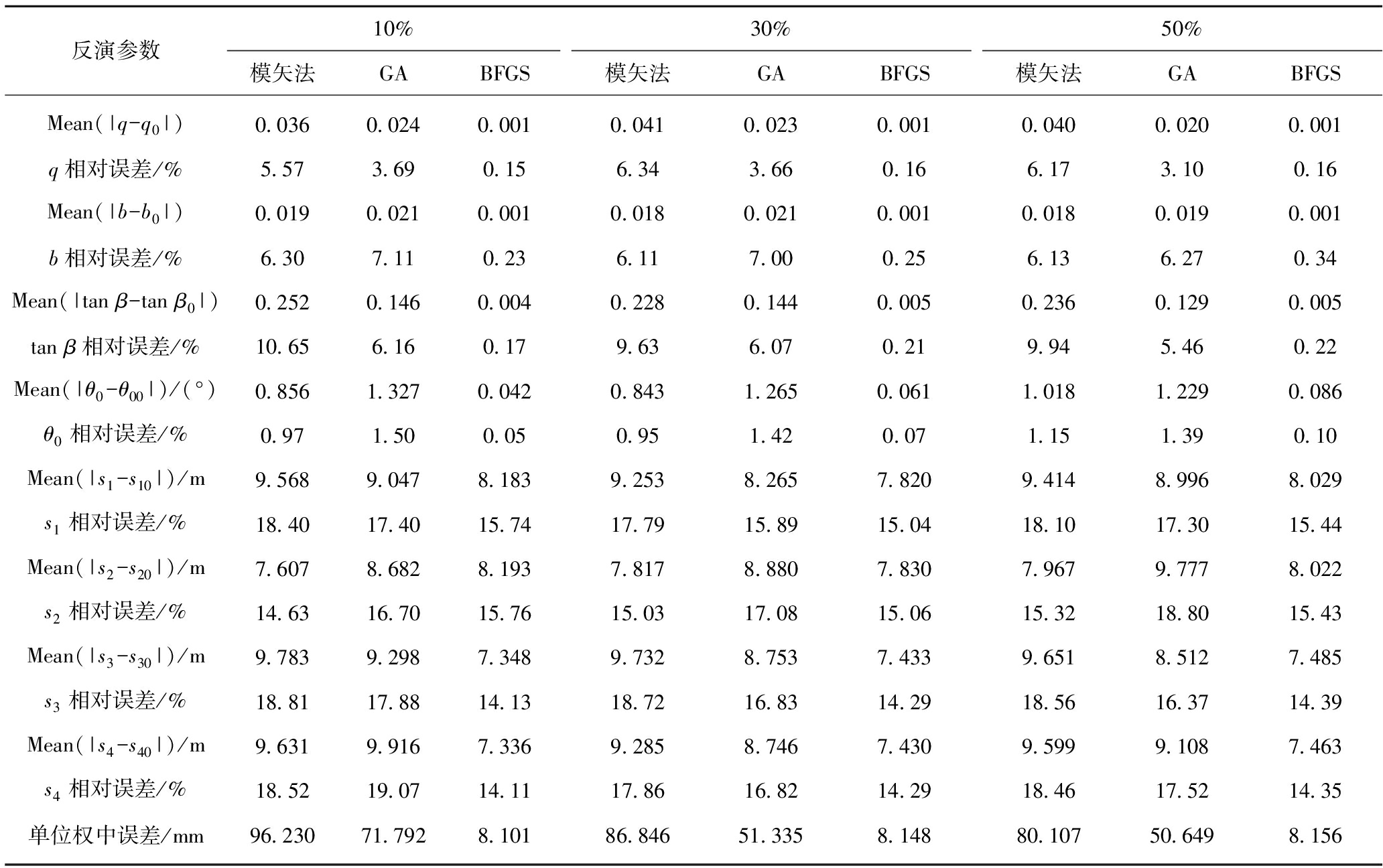
不同数据缺失情况下，模矢法、GA和BFGS 3种算法得到的100次参数反演结果与设计值之差绝对值的平均值及其相对误差见表3。由表3可知:① 对于无数据缺失(表1)和不同程度的数据缺失，3种算法反演的8个参数及其验后单位权中误差，均无显著变化，说明在仅含有随机误差的概率积分模型中，数据的缺失对本文采用的3种反演方法影响较小;② 在相同的数据缺失条件下，BFGS算法反演的4个主要参数q，b，tan β和θ0的误差明显小于模矢法和GA算法，且其验后单位权中误差表现出了同样的优势。说明在不同程度数据缺失的情况下，BFGS仍具有相对较好的参数反演性能，其对观测点缺失具有一定的抗干扰能力。

表3 3种算法反演参数计算结果(不同程度的数据缺失)
Table 3 Statistical results of inversed parameters by three methods with different losses of observation points

3 工程应用与结果分析

进一步验证不同算法的性能，采用实际工程应用案例，进行相关数据的处理和分析。试验矿区位于内蒙古自治区准格尔旗薛家湾镇，数据采集区域为101-2工作面(图3)，倾向长300 m，走向长1 985 m。采掘煤层为6上煤层，该煤层位于石炭系太原组第二岩段上部，煤层厚度平均12.70 m;可采区储量利用厚度11.09 m;煤层厚度变化不大，总体由东北向西南变薄。煤层顶板多为粗粒砂岩、细粒砂岩，局部为泥岩;底板多为泥岩、砂质黏土岩，局部为粗粒砂岩。煤层倾角3°～5°，平均采深260 m。

101-2工作面地表布设1条走向线和2条倾向线，由于外在因素破坏，剩余可用观测点83个(图3)。观测数据为观测点的下沉值，分别采用模矢法、GA算法和BFGS算法，对工作面的概率积分预计参数进行反演。考虑到传统优化算法对初值要求较高且智能优化算法的反演结果在一定范围内具有随机性，故将每种算法分别反演10次，并取其平均值作为最终的反演参数，结果见表4。同时，采用反演的参数求取下沉值并绘制拟合曲线(图4)。

由表4和图4可知:① 不同算法反演的参数有所差异。其中，GA算法和BFGS算法反演得到的主要参数q，tan β和θ0基本一致，但与模式法的反演结果有较大差异;3种算法反演的s1，s2，s3和s4四个参数存在显著差异;② BFGS算法的单位权中误差小于模矢法和GA算法，且其下沉曲线的整体拟合效果优于模矢法和GA算法(图4)。虽然BFGS算法的验后单位权中误差小于模矢法和GA算法，但其程度明显小于仿真数据(表1)，其主要由于实测数据受到矿区沟壑地形的影响，采用概率积分模型进行拟合，其存在系统性函数模型误差，使得不同参数反演方法对整体拟合精度的影响减弱，但BFGS算法仍表现出了一定程度的优势。

表4 3种算法对101-2工作面实测数据的参数反演结果
Table 4 Results of inversion parameters of three methods in the working face 101-2

4 结 论

(1)BFGS算法可以有效地反演概率积分模型中参数，在一定的初始值范围内，BFGS算法的反演结果具有较强的稳定性;同时，在不同水平的随机误差下，BFGS算法反演参数的精度基本一致。

(2)在不同水平的随机误差、不同的数目和大小的粗差和不同数目观测点缺失条件下，与常用的模矢法和GA算法相比较，BFGS算法均可以获得更高精度的反演参数，表现出了良好的参数估计性能和较强的抗干扰能力。同时，工程实例中参数反演结果和下沉拟合曲线也说明了BFGS算法具有一定的优势。

(3)比较仿真实验和实测数据结果，BFGS算法的优势有所差异，说明了在地表变形变化较为剧烈的矿区，采用概率积分模型描述地表变形特征具有一定的局限性，其函数模型误差较大，仅研究参数反演方法，难以获得更为精细的变形规律。

需要指出，工程应用时单纯的通过拟合中误差和下沉曲线拟合程度并不能保证参数的准确性，因为模型中的参数还受到地质采矿条件、地形等有因素的影响。因此，为了获得更好的拟合效果，除了采用有效的参数反演方法，还需要根据实际工程案例制定具体的参数反演方案。另外，本文仅对采用BFGS算法进行概率积分模型中参数的反演问题，进行了初步的公式推导和算法测试，还需要对诸如BFGS算法存在解的非唯一性、函数内部参数的优化设置、概率积分模型中初始参数范围的优化设置、目标函数模型的改进等问题，进行进一步研究。

参考文献

[1] 袁亮.煤炭精准开采科学构想[J].煤炭学报,2017,42(1):1-7.

YUAN Liang.Scientific conception of precision coal mining[J].Journal of China Coal Society,2017,42(1):1-7.

[2] 葛世荣,刘洪涛,刘金龙,等.我国煤矿生产能耗现状分析及节能思路[J].中国矿业大学学报,2018,47(1):9-14.

GE Shirong,LIU Hongtao,LIU Jinlong,et al.Energy consumption analysis and energy saving strategies for coal mine production in China[J].Journal of China University of Mining and Technology,2018,47(1):9-14.

[3] DARMODY Robert G,BAUER R,BARKLEY D,et al.Agricultural impacts of longwall mine subsidence:the experience in Illinois,USA and Queensland,Australia[J].International Journal of Coal Science and Technology,2014,1(2):207-212.

[4] HU Zhenqi,CHEN Chao,XIAO Wu,et al.Surface movement and deformation characteristics due to high-intensive coal mining in the windy and sandy region[J].International Journal of Coal Science and Technology,2016,3(3):339-348.

[5] 何国清,杨伦,凌赓娣,等.矿山开采沉陷学[M].徐州:中国矿业大学出版社,1991:116-120.

[6] 吴侃,葛家新,王铃丁,等.开采沉陷预计一体化方法[M].徐州:中国矿业大学出版社,1998:88-91.

[7] 查剑锋,冯文凯,朱晓峻.基于遗传算法的概率积分法预计参数反演[J].采矿与安全工程学报,2011,28(4):655-659.

ZHA Jianfeng,FENG Wenkai,ZHU Xiaojun.Research on parameters inversion in probability integral method by genetic algorithm[J].Journal of Mining and Safety Engineering,2011,28(4):655-659.

[8] 朱晓峻,郭广礼,方齐.概率积分法预计参数反演方法研究进展[J].金属矿山,2015,44(4):173-177.

ZHU Xiaojun,GUO Guangli,FANG Qi.Recent progress on parameter inversion of probability integral method[J].Metal Mine,2015,44(4):173-177.

[9] 苏军明,朱建军,伍雅晴,等.模拟退火算法在概率积分法参数反演中的应用[J].工程勘察,2015,43(12):76-79.

SU Junming,ZHU Jianjun,WU Yaqing,et al.Application of simulated annealing algorithm to parameters inversion in probability integral method[J].Geotechnical Investigation and Surveying,2015，43(12):76-79.

[10] 徐孟强,查剑锋,李怀展.基于PSO算法的概率积分法预计参数反演[J].煤炭工程,2015,47(7):117-119.

XU Mengqiang,ZHA Jianfeng,LI Huaizhan.Parameters inversion in probability integral method by particle swarm optimization[J].Coal Engineering,2015,47(7):117-119.

[11] NOCEDAL J,WRIGHT S J.Nonlinear Equations[M].New York:Springer,2006:194-201.

[12] 王宜举,修乃华.非线性最优化理论与方法[M].北京:科学出版社,2012:68-111.

[13] 胡俊,李志伟,朱建军,等.基于BFGS法融合InSAR和GPS技术监测地表三维形变[J].地球物理学报,2013,56(1):117-126.

HU Jun,LI Zhiwei,ZHU Jianjun,et al.Measuring three-dimensional surface displacements from combined InSAR and GPS data based on BFGS method[J].Chinese Journal of Geophysics,2013,56(1):117-126.

[14] 刘云鹤,殷长春.三维频率域航空电磁反演研究[J].地球物理学报,2013,56(12):4278-4287.

LIU Yunhe,YIN Changchun.3D inversion for frequency-domain HEM data[J].Chinese Journal of Geophysics,2013,56(12):4278-4287.

[15] 彭寒梅,曹一家,黄小庆.基于BFGS信赖域算法的孤岛微电网潮流计算[J].中国电机工程学报,2014,34(16):2629-2638.

PENG Hanmei,CAO Yijia,HUANG Xiaoqing.Power flow calculation of islanded microgrids based on BFGS trust region method[J].Proceedings of the CSEE,2014,34(16):2629-2638.

[16] 马昌凤.最优化方法及其Matlab程序设计[M].北京:科学出版社,2010:53-60.

[17] 周江文,黄幼才,杨元喜,等.抗差最小二乘法[M].武汉:华中理工大学出版社,1997:1-2.

BFGS method based inversion of parameters in probability integral model

YANG Jingyu1,LIU Chao1,WANG Bin2

(1.School of Geomatics,Anhui University of Science and Technology,Huainan 232001,China; 2.School of Geomatics Science and Technology,Nanjing Tech University,Nanjing 211816,China)

Abstract:Probability integral model is an important mathematical model to describe the surface deformation law caused by coal mining.Usually the traditional optimization algorithm and intelligent optimization algorithm are used to invert the unknown parameters in the probability integral model to determine the explicit surface defor-mation characteristics.In this paper,the authors propose to adopt the optimization methods to perform the inversion of the parameters.Specifically,the BFGS method is used as an example of a widely used unconstrained op-timization method.Based on the BFGS method,the authors can utilize the displacement between two adjacent iteration points to generate the search direction by Newton equation.On this basis,the iterative process is completed through inexact line search to obtain the optimal parameters.In the experimental part,the authors employ the pattern search method and genetic algorithm as the representatives of the traditional optimization algorithm and intelligent optimization algorithm.The simulation results show that the BFGS method can effectively invert all parameters,and the parameter inversion accuracy of BFGS method is significantly higher than the pattern search method and genetic algorithm under different error levels.In addition,the parameter inversion accuracy of BFGS algorithm is still better than the other two algorithms under different gross error levels and data missing conditions,which,to some extent,illustrates the feasibility and superiority of introducing BFGS method for parameter inversion in probability integral model.In the engineering case,the fitting curves of the inversion results and the sinking values further verify the reliability and accuracy of the new algorithm.However,the unit weight error in the case is significantly larger than that in the simulation experiment.Taking the actual factors of the case into consideration,the main reason for the large difference of the unit weight error is the large surface fluctuations in the mining area,which causes the larger model error of the probability integral method.Therefore,for the specific engineering case,in addition to the effective parameter inversion method,it is necessary to determine a reasonable inversion scheme according to the actual situation,in order to achieve better parameter inversion effect.

Key words:probability integral method;parameters inversion;BFGS method;pattern search method;genetic algorithm

杨靖宇，刘超，王彬.基于BFGS算法的概率积分模型的参数反演[J].煤炭学报,2019,44(10):3058-3068.doi:10.13225/j.cnki.jccs.2018.1543

YANG Jingyu,LIU Chao,WANG Bin.BFGS method based inversion of parameters in probability integral model[J].Journal of China Coal Society,2019,44(10):3058-3068.doi:10.13225/j.cnki.jccs.2018.1543

中图分类号:TD325

文献标志码:A

文章编号:0253-9993(2019)10-3058-11

收稿日期:2018-11-20

修回日期:2019-04-02

责任编辑:陶 赛

基金项目:国家自然科学基金资助项目(41474026);江苏省自然科学基金资助项目(BK20180720)

作者简介:杨靖宇(1994—)，男，安徽宿州人，硕士研究生。E-mail:yangjingyu716@126.com

通讯作者:刘 超(1985—)，男，陕西蒲城人，副教授，博士。E-mail:chaoliu0202@gmail.com