拉斗铲常用于露天煤矿煤层上部岩石的剥离，能够同时完成松散岩石的采掘、运输及排弃作业，将岩石直接倒堆至内排土场，能够减少生产环节，降低生产成本低，因此在国内外得到了广泛的应用[1-3]。受矿层赋存条件、露天矿产量规模等多种因素的影响，我国露天煤矿采用拉斗铲倒堆工艺时，拉斗铲通常采用扩展平台倒堆方式[4-6]。
拉斗铲作业平台参数(作业平台高度Hz和作业平台宽度Bz)影响单斗挖掘机及推土机辅助作业平台的工程量，并影响拉斗铲的重复倒堆量及作业效率。拉斗铲作业平台高度及宽度设计不合理将可能增大辅助工程量，降低拉斗铲的作业效率，提高露天煤矿的生产成本[7-9]。此外，作业平台由松散岩石构成，稳定性差，且拉斗铲自重大，拉斗铲在作业平台上走行、作业时存在安全隐患[10]。因此，应综合考虑经济、安全等因素，提出拉斗铲作业平台参数的优化方法，以保障拉斗铲的作业安全，提高拉斗铲的作业效率，降低倒堆系统的生产成本。
目前，作业平台参数多根据拉斗铲的技术参数确定，如根据拉斗铲底盘直径、尾端回转半径确定最小作业平台宽度;根据拉斗铲作业半径、挖掘深度等确定作业平台高度[11]。国内外学者针对拉斗铲倒堆工艺的研究主要集中在拉斗铲设备故障[12]、拉斗铲作业方式[13]、作业周期[14]、作业效率[15]、拉斗铲生产自动化[16]等方面，在拉斗铲作业平台参数优化方面的研究较少。相关成果主要有:Baafi等分析了作业平台宽度对拉斗铲重复倒堆率、作业效率的影响，认为拉斗铲重复倒堆率、作业效率随着作业平台宽度的增大而降低[17]。梅晓仁等揭示了推土机推土距离与推土机降段高度等之间的近似关系，以年作业总费用最小为目标，提出了抛掷爆破爆堆降段高度的优化模型[18]。王平亮综合考虑拉斗铲剥离能力、煤层厚度、露天煤矿生产任务等因素，提出了拉斗铲站立水平动态调整方法[19]。程鹏等通过实测数据的统计分析，得出了拉斗铲小时生产能力与作业平台高度间的近似函数关系，推导出了作业平台高度的计算公式，结果表明:为使拉斗铲的生产能力不低于3 850 m3/h，要求作业平台高度应为10.0～16.5 m[20]。
以上研究考虑了单个作业平台参数对拉斗铲作业效率的影响，提出了单个作业平台参数的优化确定方法，忽略了平台高度与平台宽度之间的相互影响、相互制约关系，研究结果仅能保证特定条件下单个参数最优，并不能保证优化的作业平台参数全局最优。因此，笔者以平台宽度、平台高度为变量，以倒堆工艺系统年剥离总费用最小为目标函数，在考虑安全、经济等约束条件下，提出拉斗铲作业平台参数的综合优化方法。
1 拉斗铲作业效率与作业平台参数关系
1.1 拉斗铲走行距离
(1)拉斗铲单向走行
图1中，Lhlmin为拉斗铲铲斗至回拉滚筒的最小距离;R为拉斗铲作业半径，受Lhlmin及R的限制，在避免拉斗铲回拉绳与作业平台岩石发生摩擦的情况下，拉斗铲能够剥离的岩石仅为图1中ABC区域内的岩石[21]。
图1 单向走行条件下拉斗铲最大挖掘深度示意
Fig.1 Sketch map of maximum stripping depth under one-way walking condition
根据图1中的几何关系:
Lhlminsin ψc+Rgtcos ψc=Hgt
(1)
Rmin=Lgt+Lhlmincos ψc-Rgtsin ψc
(2)
式中，ψc为回拉绳与水平面的最大夹角，(°);Rgt为拉斗铲回拉滚筒半径，m;Lgt为回拉滚筒至回转中心的水平距离，m;Hgt为回拉滚筒中心高度，m;Rmin为拉斗铲的最小挖掘半径，m。
根据式(1)可求得回拉绳与水平面的最大夹角ψc，进而利用式(2)求得拉斗铲的最小挖掘半径Rmin，则初始条件下拉斗铲的最大挖掘深度Hcmax=(R-Rmin)tan ψc。
通常拉斗铲采用迈步式的行走机构，假设其走步长为Lxz，走行距离为Lzx，为了减少拉斗铲的走行时间，一般Lzx=nLxz，n为拉斗铲走铲一次反向移动次数。
令
其中，B3为拉斗铲勺斗宽度;h为煤层厚度;δ为排弃物料自然安息角;β为煤台阶坡面角。当Hzz≤(Hcmax-Lxztan ψc)时，仅单向走行拉斗铲便能剥离所有岩石。此时的拉斗铲单次走行距离可利用式(3)计算。
(3)
式中，⎣」为向下取整符号。
(2)拉斗铲往返走行
当Hzz>Hcmax-Lxztan ψc时，拉斗铲前进并倒堆剥离其后侧的岩石后，必须向相反方向移动才能剥离所有岩石，如图2所示[22]。图中ψhh为回拉绳与部分岩石摩擦时的最大倾角，(°)；lby为拉斗铲基与平台坡顶线的安全距离，m；Hhmax为ψh>δ条件下拉斗铲的最大挖掘深度，m；Hhhmax为ψh>δ条件下拉斗铲的最大挖掘深度，m。
图2 反向移动后拉斗铲最大挖掘深度示意
Fig.2 Sketch map of maximum stripping depths after dragline moving back
反向移动距离最大为
(4)
式中，Lfxmax为反向移动最大距离，m;Rjz为拉斗铲基座半径，m;lbymin为拉斗铲基座边缘与平台坡顶线的最小安全距离，m。
在拉斗铲回拉绳与作业平台岩石不摩擦的条件下，反向移动后拉斗铲能够剥离图2中DEF区域内的岩石。此时，回拉绳最大倾角ψh(图3)满足:
Rgtcos ψh+Lhl(ψh)sin ψh=Hgt+hch
(5)
式中，
hch=tan ψc[Lhl(ψh)cos ψh-(Rjz-Lgt+Rgtsin ψh+lby)]。
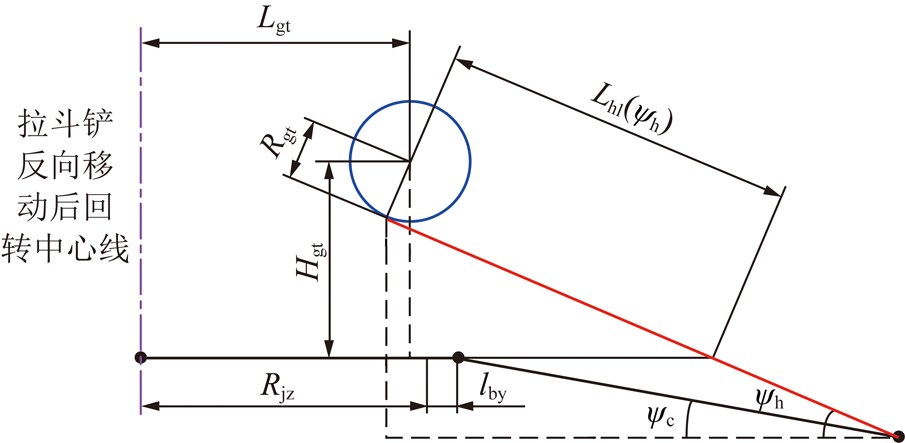
图3 回拉绳最大倾角示意
Fig.3 Maximum inclining angle of dragline tripping line
ψh是lby的函数，利用式(5)计算可得ψh，若ψh>δ，则以步长Lxz增大lby，直至ψh≤δ。
该条件下拉斗铲的最大挖掘深度为
Hhmax=[-(Hgt-Rgtcos ψh)cot ψh+R+
Rgtsin ψh-Lgt]tan ψh
(6)
如果Hzz≤Hhmax-Lxztan ψh，则在保证拉斗铲回拉绳与岩石之间不摩擦的条件下，拉斗铲利用往返走行即能剥离所有岩石。此时，拉斗铲的正向走行距离:
(7)
如果Hzz>Hhmax-Lxztan ψh,lby=lbymin且ψh<δ，则在保证回拉绳不磨损的条件下，拉斗铲剥离所有岩石。拉斗铲回拉绳必须与平台坡顶附近的部分岩石摩擦才能增大拉斗铲的挖掘深度。此时，拉斗铲的最大挖掘深度为图2中的Hhhmax，此种情况较少出现，且走行距离推导过程与前相似，在此不再赘述。
1.2 拉斗铲走行时间
拉斗铲倒堆一幅剥离物的走行时间
其中，tzy为拉斗铲作业过程中的走行时间，为拉斗铲作业过程中的走行距离Lzy与作业过程中的走行速度vzy之比;tkc为拉斗铲空程返回时间，为拉斗铲空程走行距离Lkc与空程走行速度vkc之比。
若拉斗铲沿单中心线单向走行(图4(a))，其剥离一幅采掘带内岩石的作业走行距离Lzy等于抛掷爆破台阶工作线长度L。
图4 拉斗铲工作面走行路线示意
Fig.4 Walking directions of dragline in working face
若拉斗铲沿单中心线往返走行(图4(b))，则
若拉斗铲沿双中心线往返走行(图4(c))，则
(8)
式中，Bzx为两作业中心线间的垂直距离;n为拉斗铲走铲一次反向移动次数。
1.3 拉斗铲作业周期
拉斗铲的挖掘循环主要由挖掘满斗、铲斗提升回转、铲斗卸载、反转下放铲斗4个环节组成，除铲斗卸载时间外，其余3个环节时间均受作业平台参数的较大影响[23-25]。
(1)铲斗提升回转时间
拉斗铲挖掘满斗后同时进行铲斗提升和回转动作，其用时定义为提升回转时间:
(9)
式中，δn为拉斗铲的内回转角度，(°);δw为外回转角度，(°);Hts拉斗铲铲斗的平均提升高度，m;ωz为拉斗铲铲斗提升回转过程中的平均回转角速度，rad/s;vts为拉斗铲铲斗的平均提升速度，m/s。
根据图5中的几何关系可知，δn=arcsin(ln/R)，δw=arcsin(lw/R)，ln,lw如图5所示。当拉斗铲作业位置及作业方式一定时，ln,lw主要受Bz的影响，设ln=λnBz,lw=λwBz，λn,λw可根据几何关系计算得出。
图5 拉斗铲回转角示意
Fig.5 Sketch map of dragline rotation angle
(2)反转下放铲斗时间
拉斗铲将剥离的岩石卸载至内排土场之后，进行回转的同时也下放铲斗准备挖掘岩石，其用时即为反转下放铲斗时间。通常拉斗铲的回转时间较长，反转下放铲斗时间为
(10)
式中，ωk为拉斗铲反转下放铲斗过程中的平均回转角速度，rad/s。
(3)挖掘满斗时间
假设作业平台高度为Hz0时拉斗铲的挖掘机满斗时间最小为twmin，挖掘满斗时间随着平台高度的增大先减小后增大，则拉斗铲的挖掘满斗时间tw=kw|Hz-Hz0|+twmin。其中，kw为挖掘满斗时间随作业平台高度变化的系数。
拉斗铲作业周期tz=tw+th+tx+tf=tz(Hz,Bz)。其中，tx为拉斗铲卸载时间。
1.4 拉斗铲作业效率
假设拉斗铲的斗容为E，满斗系数为km，松散系数为ks，则拉斗铲小时生产能力Qh=3 600Ekm/(tzks)。拉斗铲倒堆一幅剥离物所需时间为
(11)
式中，A为采掘带宽度,m；H为抛掷爆破台阶高度，m;L为工作线长度，m;tzb为准备拉斗铲作业平台等所需时间，h;kz为拉斗铲倒堆率，其计算见2.1节。
因此，拉斗铲的平均作业效率:
(12)
2 作业平台参数优化模型
2.1 相关变量计算方法
利用抛掷爆破爆堆的三维扫描数据可得抛掷爆破爆堆纵的剖面(图6)。建立图6中的平面坐标系，可得爆堆曲线方程y=yz(x)及折线ABCDEF的方程y=yz(x)，则爆堆截面积为
Sbd=
[yb(x)-yz(x)]dx=yb(x)dx-
(13)
式中，α为抛掷爆破台阶坡面角，(°);xF,xE分别为点F,E的横坐标值。
图6 抛掷爆破爆堆剖面
Fig.6 Profile map of casting blast muck pile
爆堆岩石松散系数ks=Sbd/AH。
直线EF的方程为:yEF=tan δ(x-xE)，令yb(x)=tan δ(x-xE)可求得xF。同理，D点横坐标
直线DJ的方程为yDJ=tan δ(x-xD)，令yb(x)=tan δ(x-xD)可求得L点的横坐标xL。
则有效抛掷岩石截面积为
Syx=
yDJ(x)dx+
[yb(x)-yz(x)]dx=
xE)2tan δ
(14)
有效抛掷率k1=Syx/Sbd。
同理，多边形AGK的面积为
多边形KLMH的面积为
SKLMH=
[yGH-yb(x)]dx+
[yHI-yb(x)]dx
假设辅助设备做扩展平台宽度为Btt，即图6中P点横坐标为xP=xK+Btt，则拉斗铲扩展平台宽度为Bd=xH-xP，辅助扩展平台面积为
Stt=
[yGH-yb(x)]dx+
[yPQ-yb(x)]dx
(15)
式中，yPQ=-tan δ(x-xP)+h+Hz。
拉斗铲扩展平台面积Sd=SKLMH-Stt。
当xQ≤xL时，辅助设备做作业平台内岩石均需2次剥离，没有有效剥离量，拉斗铲所做作业平台内的有效剥离面积为
Sdy=SLMN=
[yDJ-yb(x)]dx+
[yHI-yb(x)]dx
当xQ>xL时，直线PQ与DJ相交于R点，辅助扩展平台内的有效剥离面积为
Stty=
[yDJ-yb(x)]dx+
[yPQ-yb(x)]dx
辅助扩展平台有效剥离率kky=Stty/Sbd。此时，拉斗铲扩展平台内的有效剥离面积Sdy=SLMN-Stty。拉斗铲重复倒堆率k2=(Sd-Sdy)/Sbd。
拉斗铲作业平台宽度满足要求后爆堆内多余岩石可由卡车排弃至排土场，从而产生辅助剥离量，辅助剥离面积Sf =SAGK-Stt，辅助剥离率kf=Sf/Sbd。则拉斗铲倒堆率kz=1-k1+k2-kf-kky。
2.2 模型建立
2.2.1 目标函数
辅助扩展平台量Vtt=LDStt/(ksA)，单斗卡车辅助剥离量Vf=LDSf/(ksA)，拉斗铲倒堆量Vd=LDkzSbd/(ksA)。其中，D为露天煤矿年推进度，m;A为抛掷爆破台阶采掘带宽度，m。
假设在抛掷爆破爆堆上最多可布置m台单斗挖掘机、n台推土机。其中，单斗挖掘机可做辅助扩展平台，并可辅助剥离岩石，推土机平整爆堆并辅助做扩展平台。假设单台推土机的年推土能力为Qta，单台单斗挖掘机的年生产能力为Qwa，单斗挖掘机用于做扩展平台的生产能力与总生产能力的比值为ηw，推土机完成扩展平台量与生产能力的比值为ηt。
如果
则ηw=0，推土机扩展平台量为Vtk=Vtt，单斗挖掘机扩展平台量Vwk=0;如果
则
倒堆工艺系统年剥离总费用为
Pbs=Vdcd+Vtkctk+Vwkcwk+Vfcf
(16)
式中，cd为拉斗铲倒堆成本，元/m3;cwk为单斗挖掘机扩展平台成本，元/m3;ctk为推土机扩展平台成本，元/m3;cf为辅助剥离成本，元/m3。
cd,ctk,cwk均是作业平台参数的函数。假设拉斗铲生产效率为Qd0时的倒堆剥离成本为cd0，倒堆剥离成本与拉斗铲生产效率成反比关系，拉斗铲生产效率为Qp时的倒堆成本cd=Qd0cd0/Qp。
假设推土机扩展平台成本与推土距离成正比，推土距离为Ltk0时的推土机扩展平台成本为ctk0，推土机扩展平台成本ctk = Ltkctk0 /Ltk0，其中推土机推土距离Ltk≈0.5(xP-xG)。
单斗挖掘机扩展平台成本cwk= cw+cyLky+cp，其中，cw为挖掘成本，元/m3;cy为运输成本，元/(m3·km);cp为排弃成本，元/m3; Lky为做扩展平台的运输距离，Lky≈0.5(xP-xG)+4Ra，m;Ra为卡车回转半径。
模型目标函数为
min Pbs=Vdcd+Vtkctk+Vwkcwk+Vfcf
2.2.2 约束条件
(1)作业安全约束
为了保证拉斗铲作业安全，要求作业平台宽度最小为
Bmin=1.5Rjz+Rr+Δ
(17)
式中，Rr为拉斗铲尾部回转半径，m;Δ为安全距离，m。
此外，倒堆内排土台阶高度与作业平台高度均不能大于其临界高度，即
(18)
(2)拉斗铲线性尺寸约束
① 倒堆距离约束
受拉斗铲作业半径等影响，拉斗铲排弃岩石高度有限。根据图7中的几何关系可得
Hkp=(Bz-Hzcot α+R-Ls-hcot β-A)tan δ
(19)
式中，Hkp为拉斗铲可排弃物料最大高度，m;Ls为拉斗铲作业中心线至平台坡顶线的距离，m。
图7 拉斗铲倒堆范围示意
Fig.7 Sketch map of dragline working range
其中，受拉斗铲最大排弃高度Hdp限制，Hkp≤Hdp+Hz+h。
内排土场可倒堆排土横断面面积
为使内排土场能容纳倒堆剥离量，Hkp必须满足:
② 挖掘深度约束
拉斗铲在作业平台上部进行下采，为了避免回拉绳磨损，且受拉斗铲线性尺寸限制，拉斗铲挖掘深度有限。由2.1节可知，若Hzz>Hhmax-Lxztan ψh且ψh=δ，或Hzz>Hhhmax-Lxztan ψhh，则拉斗铲作业平台高度偏大，导致拉斗铲不能剥离所有岩石。所以作业平台高度必须满足:
(20)
式中，Hhmax≤Hdmax，Hhhmax≤Hdmax，Hdmax为拉斗铲最大挖掘深度，m。
(3)设备生产能力约束
① 拉斗铲生产能力约束
受拉斗铲生产能力Qp的限制，拉斗铲的剥离任务量Vd≤QpTa。
② 辅助设备生产能力限制
爆堆上能够同时作业的单斗挖掘机、推土机台数受空间限制，辅助设备生产能力也因此受限。辅助设备在保证做一定宽度的扩展平台的情况下，单斗卡车的辅助剥离量Vf≤(1-ηw)mQwa。
2.3 模型求解方法
作业平台参数优化模型为典型的约束非线性规划模型。模型直接求解较为困难，但模型中仅有两个变量，且变量取值范围较小，计算精度也要求不高，可采用穷举法进行求解。求解流程如图8所示。
3 工程实例
3.1 拉斗铲作业效率
以黑岱沟露天煤矿为例，该矿生产能力为34 Mt/a，抛掷爆破台阶高度为38.0 m，采掘带宽度为85.0 m，抛掷爆破工作线长度2 200.0 m，台阶坡面角为65.0°，排弃物料自然安息角38.0°，煤台阶坡面角75.0°，煤层厚度28.8 m。
其抛掷爆破台阶爆破后，先采用推土机平整爆堆顶部，然后利用液压挖掘机剥离抛掷爆破台阶坡面处的岩石并倒堆至爆堆靠内排土场一侧。之后利用单斗挖掘机采用端工作面的方式进行降段作业，为拉斗铲做作业平台。当拉斗铲作业平台宽度满足要求时，拉斗铲进入作业平台开始剥离作业。拉斗铲相关参数见表1。
图8 求解流程
Fig.8 Flow chart of solution
表1 拉斗铲相关参数
Table 1 Relevant parameters of dragline m
参数RRrDjzHdpLsLbyminRrRjzLxzLhlminLxzRgtHgtLgt数值100.029.521.345.120.05.029.510.652.320.02.31.6256.69.0
露天煤矿抛掷爆破之后，利用三维激光扫描仪扫描爆堆可获得其三维空间数据。沿工作线按一定间隔作爆堆纵剖面线(图9)。对爆堆剖面线数据进行多项式拟合得到其方程:
yb(x)=-3.59×10-9x5+1.858×10-6x4-3.199×
10-4x3+1.985×10-2x2-0.524 3x+59.75
图9 多项式拟合
Fig.9 Polynomial fitting
计算可得抛掷爆破爆堆截面积为4 014.36 m2，有效抛掷岩石截面积为1 195.50 m2，爆破后岩石松散系数为1.24，抛掷爆破有效抛掷率为29.78%。
令Hz在10～22内取值，Bz在108～130内取值，将基础数据代入式(12)，可得拉斗铲作业效率与平台高度、平台宽度间的关系，如图10所示。
图10 拉斗铲作业效率与平台高度、平台宽度关系
Fig.10 Relationships between Bz,Hz and Qp
随着作业平台高度Hz、作业平台宽度Bz的增大，拉斗铲作业效率均先增大后降低。通过计算可知，Hz=13.3 m，Bz=118.1 m时，拉斗铲作业效率取最大值4 043.02 m3/h。
3.2 工作面参数优化
代入相关数据可以确定黑岱沟露天矿拉斗铲作业平台参数优化模型为
利用Matlab编写代码，代入相关基础数据，计算可求得最优作业平台高度为14.6 m，平台宽度为118 m，此时倒堆工艺系统年剥离总费用最小为15 771.5万元，与作业平台高度15.0 m，平台宽度120 m相比，每年可节省剥离费用371.7万元。
表2 各生产环节相关指标
Table 2 Relevant indices of each production link
参数数值拉斗铲作业效率为3 469 m3/h时的倒堆成本/(元·m-3)3.00单斗挖掘机挖掘成本/(元·m-3)2.00卡车运输成本/(元·(m3·km)-1)2.00排弃成本/(元·m-3)1.20推土距离为45 m时的推土机扩展平台成本/(元·m-3)11.23卡车回转半径/m14.20单台推土机的年推土能力/(104 m3·a-1)150.00单台单斗挖掘机的年生产能力/(104 m3·a-1)675.00可布置单斗挖掘机数量/台2可布置推土机数量/台4
4 结 论
(1)拉斗铲作业平台高度与平台宽度之间相互影响、相互制约，不能对单个参数进行独立优化，而需要以2者为变量，建立优化模型，提出拉斗铲作业平台参数的综合优化方法。
(2)揭示了拉斗铲作业效率与作业平台高度、作业平台宽度间的函数关系，通过计算可知，拉斗铲作业效率随着作业平台宽度、作业平台高度的增大均先增大后降低。黑岱沟露天煤矿的拉斗铲在作业平台宽度118.1 m、作业平台高度13.3 m时作业效率取最大值4 043.02 m3/h。
(3)以倒堆工艺系统年剥离总费用最小为目标，以作业安全、拉斗铲线性尺寸、设备生产能力为约束，建立了拉斗铲作业平台高度、作业平台宽度综合优化模型，提出了模型的求解方法。并对黑岱沟露天煤矿拉斗铲作业平台参数进行了优化，研究结果表明其最优作业平台高度为14.6 m，作业平台宽度为118 m，优化后每年可节省剥离费用371.7万元。
[1] PANISHEV S V,KAIMONOV M V.Technical approach to prediction of dragline productiveness in blasted rock handling at open pit mines in permafrost zone[J].Journal of Mining Science,2017,53(4):702-707.
[2] PONNUSAMY M,MAITY T.Recent advancements in dragline control systems[J].Journal of Mining Science,2016,52(1):160-168.
[3] GÖLBAʂ I O,DEMIREL N.Optimisation of dragline inspection intervals with time-counter algorithm[J].International Journal of Mining Reclamation & Environment,2016,31(6):412-425.
[4] ZHANG Weishi,CAI Qingxiang,CHEN Shuzhao.Optimization of transport passage with dragline system in thick overburden open pit mine[J].International Journal of Mining Science and Technology,2013,23(6):901-906.
[5] PANDEY P,MUKHOPADHYAY A K,CHATTOPADHYAYA S.Reliability analysis and failure rate evaluation for critical subsystems of the dragline[J].Journal of the Brazilian Society of Mechanical Sciences & Engineering,2018,40(2):1-11.
[6] 孙健东,张瑞新,武海龙,等.露天矿拉斗铲倒堆工艺作业方式与参数优化[J].煤炭学报,2018,43(5):1312-1321.
SUN Jiandong,ZHANG Ruixin,WU Hailong,et al.Operation method and parameters optimization of dragline overcast stripping technology in surface mine[J].Journal of China Coal Society,2018,43(5):1312-1321.
[7] 周伟,才庆祥,尚涛.拉斗铲倒堆综合开采工艺的配合模式[J].采矿与安全工程学报,2013,30(2):285-288.
ZHOU Wei,CAI Qingxiang,SHANG Tao.Match mode of combined system with dragline oriented system[J].Journal of Mining and Safety Engineering,2013,30(2):285-288.
[8] MCINNES C H,MEEHAN P A.Trajectory optimization of a mining dragline using the method of lagrange multipliers[J].International Journal of Robust and Nonlinear Control,2011,21(14):1677-1692.
[9] 白润才,孙磊,吴东海,等.拉铲倒堆工艺采掘带宽度优化研究[J].金属矿山,2014,43(12):49-52.
BAI Runcai,SUN Lei,WU Donghai,et al.Optimization of the cut width in dragline stripping system[J].Metal Mine,2014,43(12):49-52.
[10] 马力,李克民,孙健东,等.抛掷爆破-拉斗铲倒堆工艺台阶采掘带宽度优化[J].煤炭学报,2017,42(11):2867-2874.
MA Li,LI Kemin,SUN Jiandong,et al.Optimization of mining panel width for stripping technology of blast casting-dragline working bench[J].Journal of China Coal Society,2017,42(11):2867-2874.
[11] 肖双双,李克民,丁小华,等.拉斗铲倒堆工艺技术特征分析及应用[J].中国科技论文,2017,12(15):1745-1748.
XIAO Shuangshuang,LI Kemin,DING Xiaohua,et al.Analysis and application of technical characteristics of dragline stripping technology[J].China Sciencepaper,2017,12(15):1745-1748.
[12] UZGOREN N,UYSAL O,ELEVLI S,et al.Reliability analysis of draglines’ mechanical failures[J].Eksploatacja I Niezawodnosc-Maintenance and Reliability,2010,12(4):23-28.
[13] ERDEM B,DURAN Z,ÇELEBI A.A model for direct dragline casting in a dipping coal-seam[J].Journal South African Institute of Mining and Metallurgy,2004,104(1):9-16.
[14] MOHAMMADI M,RAI P,SINGH U,et al.Investigation of cycle time segments of dragline operation in surface coal mine:A statistical approach[J].Geotechnical and Geological Engineering,2016,88(1):1-10.
[15] DEMIREL N.Effects of the rock mass parameters on the dragline excavation performance[J].Journal of Mining Science,2011,47(4):441-449.
[16] MEEHAN P A,AUSTIN K J.Prediction of chaotic instabilities in a dragline bucket swing[J].International Journal of Non-Linear Mechanics,2006,41(2):304-312.
[17] BAAFI E Y,MIRABEDINY H,WHITCHURCH K.Computer simulation of complex dragline operations[J].International Journal of Surface Mining Reclamation and Environment,1997,11(1):7-13.
[18] 梅晓仁,王永军.拉铲倒堆开采工艺推土机降段高度优化[J].辽宁工程技术大学学报(自然科学版),2009,28(3):355-358.
MEI Xiaoren,WANG Yongjun.Dozer-lowered height optimization of dragline stripping system[J].Journal of Liaoning Technical University(Natural Science),2009,34(11):1456-1459.
[19] 王平亮.吊斗铲倒堆工艺系统动态调整方法研究[J].露天采矿技术,2010,25(5):1-4.
WANG Pingliang.Research on dynamic adjustment method of dragline stripping technology system[J].Opencast Mining Technology,2010,25(5):1-4.
[20] 程鹏,肖双双.黑岱沟露天煤矿拉斗铲扩展平盘高度确定[J].煤炭工程,2015,47(6):14-17.
CHENG Peng,XIAO Shuangshuang.Determination of extended bench height of dragline in heidaigou opencast coal mine[J].Coal Engineering,2015,47(6):14-17.
[21] 肖双双.抛掷爆破—拉斗铲倒堆工艺参数优化理论研究[D].徐州:中国矿业大学,2016:49-63.
XIAO Shuangshuang.Research on optimization theories of parameters in blast casting-dragline stripping technology[D].Xuzhou:China University of Mining and Technology,2016:49-63.
[22] 张瑞新,孙健东,温晓可,等.黑岱沟露天矿拉斗铲挖掘作业方式研究[J].煤炭工程,2016,48(1):10-13.
ZHANG Ruixin,SUN Jiandong,WEN Xiaoke,et al.Research on rational operation mode of dragline in Heidaigou surface mine[J].Coal Engineering,2016,48(1):10-13.
[23] 孙健东,张瑞新,马新根,等.拉斗铲一次作业循环效率提升研究[J].采矿与安全工程学报,2016,33(4):721-727.
SUN Jiandong,ZHANG Ruixin,MA Xingen,et al.Study on efficiency promotion of dragline with single-operation cycle[J].Journal of Mining and Safety Engineering,2016,33(4):721-727.
[24] 马新根,孙健东.拉斗铲旋转-耗时分析及旋转作业效率级别划分[J].煤炭科学技术,2015,43(S1):51-54.
MA Xingen,SUN Jiandong.Analysis on dragline rotation time-consuming and efficiency division[J].Coal Science and Technology,2015,43(S1):51-54.
[25] MOHAMMADI M,RAI P,GUPTA S.Improving productivity of dragline through enhancement of reliability,inherent availability and maintainability[J].Acta Montanistica Slovaca,2016,21(1):1-8.
