我国西北地区煤炭资源丰富,是当前和未来我国主要的煤炭生产区[1]。近年来,在西北侏罗纪煤炭资源开采中发生了多次侏罗系风化基岩突水事故,使人们逐渐认识到掌握侏罗系风化基岩富水性在矿井防治水中的重要意义。但侏罗系风化基岩富水性在空间上极不均一,如何评价预测侏罗系风化基岩的富水性就成为矿井防治水中亟待解决的问题。在矿井水害防治中含水层的富水性评价预测是重要的基础工作[2],众多学者对此进行了研究,提出了多因素综合分析法[3-6],即在分析含水层富水性影响因素的基础上,建立含水层富水性的定量评价预测模型,对研究区含水层的富水性做出评价预测。在建立含水层富水性评价预测模型时,各因素的权重确定非常重要(权重不同富水性预测结果不同)且往往根据层次分析法(Analytic Hierarchy Process,简称AHP)来确定。但层次分析法在对富水性影响因素指标权重确定时大多由专家依照T L SAATY创立的1~9标度法进行打分,并计算出各因素指标权重,但这种权重确定方法没有充分利用实测数据且计算的权重具有主观性[4,7]。章海波等[8]提出了一种改进的AHP指标权重确定方法,该方法在确定各指标权重时除考虑专家的打分外,也考虑了各指标实测数据的标准差,在一定程度上提高了应用效果。为了克服AHP赋权的主观性,马荣等[9]采用熵权法来计算各因素指标的权重,并对含水层的非均质性进行了预测。该方法的优点是一种根据各指标实测数据确定其权重的客观评价方法,但缺点是在确定各指标权重时未考虑专家的经验。因此,单独使用任何一类方法都会存在一定的局限性。笔者以陕北侏罗纪煤田柠条塔井田南翼为例,探讨利用改进的AHP和熵权法耦合来确定风化基岩富水性影响因素指标权重的富水性预测方法。即在指标权重确定时将改进AHP和熵权法以合理的数学方法耦合起来,使所确定的权重既考虑专家经验,也考虑实测数据特征,从而使富水性评价预测结果更加符合实际。
1 研究区地质概况
陕北侏罗纪煤田是晋陕蒙地区煤炭主产区之一,煤炭资源约占全国保有量的14%。研究区位于陕北侏罗纪煤田神府矿区南部、陕西省神木市西部柠条塔井田南翼(面积约为68.57 km2)。研究区地形总体上呈中部高、南部和北部低的特点,地表大多被现代风积沙(约占南翼总面积的90%)所覆盖,局部出露第四系黄土及新近系红土。据钻孔揭露及地质填图资料,区内地层由老至新依次有:三叠系上统永坪组(T3y),侏罗系中统延安组(J2y)、直罗组(J2z),新近系上新统保德组(N2b),第四系中更新统离石组(Q2l),萨拉乌苏组(Q3s),第四系全新统风积沙![]() 和冲积层
和冲积层![]() 含煤地层为侏罗系中统延安组,含5个煤组可采煤层8层,分别为1-2上,1-2,2-2上,2-2,3-1,4-2,4-3,5-2煤层,其中主要可采煤层为2-2,3-1,4-2和5-2煤层,1-2上,1-2,2-2上和4-3为次要可采煤层。
含煤地层为侏罗系中统延安组,含5个煤组可采煤层8层,分别为1-2上,1-2,2-2上,2-2,3-1,4-2,4-3,5-2煤层,其中主要可采煤层为2-2,3-1,4-2和5-2煤层,1-2上,1-2,2-2上和4-3为次要可采煤层。
井田南翼煤层上覆隔水层主要为离石组黄土和保德组红土,厚0~115.43 m。煤层上覆含水层主要为第四系松散层孔隙潜水含水层,直罗组风化基岩裂隙承压含水层和延安组裂隙承压含水层。松散层孔隙潜水含水层局部发育,仅在小侯家母河沟、肯铁岭沟和芦草沟附近厚度较大,常有泉水出露,钻孔单位涌水量可达0.532 4 L/(s·m),富水性中等,但由于其分布范围小水量易于疏干对矿井威胁较小。延安组含水层裂隙发育微弱,岩石致密坚硬,钻孔单位涌水量为0.000 57 L/(s·m),富水性弱;直罗组风化基岩裂隙含水层在南翼普遍分布,厚度2.2~77.92 m,平均厚度26.62 m,钻孔单位涌水量平均为0.118 3 L/(s·m),富水性弱到中等,是矿井主要充水含水层,对矿井安全生产威胁较大。
2 风化基岩富水性控制因素
影响风化基岩裂隙含水层富水性的因素是多方面的,为了更有效的评价富水性,笔者分析了研究区内对风化基岩含水层进行过抽水试验的41个水文孔资料,发现研究区内风化基岩的富水性主要受风化基岩顶面标高、岩性、风化程度和岩芯采取率4个因素控制,即就是可以利用这4个因素进行风化基岩富水性预测。其中岩性和风化程度是一种定性指标,不便将其与基岩顶面标高、岩性采取率两个定量指标融合使用,笔者先对其按类别进行量化,然后用岩性组合指数和风化指数来定量表示。
(1)风化基岩顶面标高级别指数。
根据钻孔抽水试验资料分析,研究区风化基岩的富水性与其顶面标高存在一定的相关性,即在风化基岩顶面标高较高的地区,钻孔单位涌水量要小于标高较低的地区。如钻孔BK42,K3-1,BK28的单位涌水量分别为0.105 1,0.122 0和0.005 0 L/(s·m),对应的风化基岩顶面标高为1 180.40,1 218.32和1 242.62 m。为了比较清楚地表示这种相关关系,将研究区基岩标高按15 m高差进行分级,并对其按级别进行量化赋值,其值越大富水性越强(表1)。
表1 风化基岩顶面标高级别赋值
Table 1 Elevation grades assignment to weathered bedrock top surface

标高/m>1 2401 225~1 2401 210~1 2251 195~1 210<1 195量化值12345
(2)岩性组合指数。
研究区风化基岩岩性不同,富水性不同。据抽水钻孔资料可知,风化砂岩比风化泥岩富水性强,同样风化砂岩其粒径大的较粒径小的富水性强。如风化强度相同的SK2和J7钻孔,前者单位涌水量为0.194 8 L/(s·m),而后者为0.046 4 L/(s·m),究其原因为SK2钻孔的岩性主要为中粒砂岩,J7钻孔的岩性以细粒砂岩为主、粉砂岩次之。同样风化基岩顶面标高相同,风化程度和岩芯采取率相近的K7-3和BK49钻孔,前者的单位涌水量为0.138 0 L/(s·m),后者为0.014 9 L/(s·m),究其原因为K7-3钻孔的岩性以中粒砂岩为主、粗砂岩次之,BK49钻孔的岩性以中粒砂岩、粉砂岩为主,砂质泥岩次之。
根据岩性组合对富水性的贡献大小将其量化(表2),然后构建表征岩性组合富水性强弱的岩性组合指数r,r值越大则富水性越强。
r=∑rimi∑mi
(1)
式中,ri为岩性类别;mi为不同岩性岩层的厚度,m。
(3)风化指数。
区内基岩风化程度可划分为弱风化(Ⅰ)、中等风化(Ⅱ)和强风化(Ⅲ)3类。风化程度越强富水性越好,例如岩性组合相同、风化基岩顶面标高和岩芯采取率相近的J15和ZK2钻孔,前者单位涌水量为0.446 1 L/(s·m),后者为0.062 6 L/(s·m),分析其钻孔柱状,J15钻孔风化程度强的层段16.3 m,而ZK2钻孔仅为2.7 m。导致富水性差异的原因是岩石在遭受风化后其结构发生破坏风化裂隙发育,致使岩石的透水性增强。对岩石风化程度按类别进行量化,见表3。
表2 风化基岩岩性等级赋值
Table 2 Rock type assignment of weathered bedrock

岩性类别泥岩砂质泥岩粉砂岩细砂岩中砂岩粗砂岩砾岩量化值11.523456
表3 基岩风化程度赋值
Table 3 Weathering degree assignment of bedrock

风化程度弱风化中等风化强风化量化值123
相同岩性和风化程度的风化基岩,其厚度不同,富水性一般也不同。因此构建风化指数w这一指标来刻画风化基岩的风化程度和厚度对富水性的影响。其值越大则富水性越强。
w=∑wihi∑hi
(2)
式中,wi为不同岩性岩石的风化程度;hi为不同岩性风化基岩的厚度。
(4)岩芯采取率指数。
钻孔采取的岩芯长度与相应实际钻探进尺比值,是表征岩体完整性的一种岩石质量指标,其值越低说明岩石越破碎,储水空间越大,富水性越好。例如J9和SK1钻孔,其风化基岩顶面标高、岩性组合指数和风化指数均相近,但前者岩芯采取率指数为0.66后者为0.936,表现为J9钻孔的单位涌水量为0.111 7 L/(s·m)而SK1钻孔仅为0.010 8 L/(s·m)。
各钻孔风化基岩的岩芯采取率是通过构建岩芯采取率指数c来计算的,其从侧面反映了风化基岩的富水性。其值越小则富水性越强。
c=∑cihi∑hi
(3)
式中,ci为岩层采取率。
综上,可以采用风化基岩顶面标高级别指数、岩性组合指数、风化指数和岩芯采取率指数4个指标进行风化基岩富水性预测,其层次结构模型如图1所示。

图1 风化基岩含水层富水性预测的层次结构模型
Fig.1 Hierarchy model for predicting water-richness of weathered bedrock aquifer
对研究区这4个指标进行统计,在ArcGIS中生成各指标空间变化图,如图2所示。
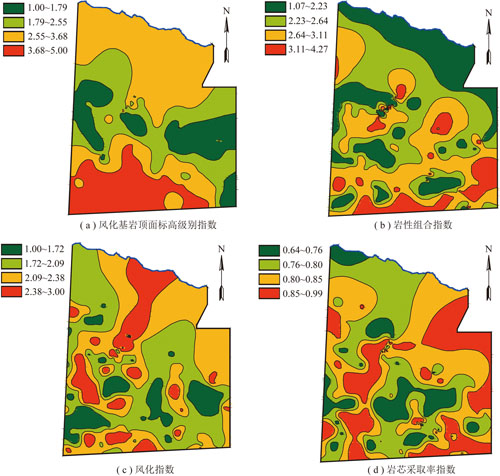
图2 富水性预测指标的空间变化
Fig.2 Spatial change of water rich prediction index
3 基于改进AHP和熵权法耦合的富水性指标权重确定方法
鉴于改进AHP在确定指标权重时重专家经验而对指标实测数据特征考虑不够,及熵权法在确定指标权重时重客观数据而未顾及专家经验的不足,如果通过数学方法将改进AHP和熵权法耦合起来,使指标权重确定时既考虑专家经验又考虑客观数据,就会使所确定的指标权重更加符合实际。下面在介绍改进AHP、熵权法指标权重确定方法的基础上,给出耦合两者的权重计算方法。
3.1 改进AHP指标权重确定方法
传统的AHP权重确定方法在构建判断矩阵时,指标之间相对重要程度的判断,会因专家不同而存在差异,具有一定的主观性,同时对定量指标应用不够充分也是一个明显的不足之处[10]。
改进的层次分析法具体内容为:对于n个指标首先分别计算其样本标准差然后两两进行比较,依据重要程度的传递性法则进行排序,依次可得到判断矩阵其他元素的值[11],即如果知道p1,2=a1,p2,3=a2,…,p(n-1),n=a(n-1),则![]() 从而构造一个改进的判断矩阵Bn×n[12]。
从而构造一个改进的判断矩阵Bn×n[12]。
从评价的角度出发,某一指标内部的变化程度越大,则其传递的综合评价的信息就越丰富[13]。因此,可以采用各评价指标的样本标准差S(i)(i=1~n)来反映各评价指标对含水层富水性的影响程度,并用于构造判断矩阵Bn×n,其i指标相对j指标重要性标度bij的计算公式为

(4)
其中,S(i),S(j)分别为i指标和j指标的样本标准差;Smax和Smin分别为{S(i)|i=1~n}的最大值和最小值;相对重要程度参数值bm=min{9,int[Smax/Smin+0.5]},min和int分别为取最小和取整函数。根据矩阵求出最大特征根λmax所对应的特征向量uj,即
首先计算每一行元素的乘积Mi,然后计算Mi的n次方根![]() 然后对向量
然后对向量![]() 做归一化处理即可得到所求的特征向量uj。
做归一化处理即可得到所求的特征向量uj。
![]()
(5)
![]()
(6)
鉴于多阶判断矩阵的复杂性,判断矩阵中某些数值可能会出现前后矛盾的情况,为此需要对判断矩阵进行一致性检验,保证最后评价的一致性,一致性检验计算公式为
CI=(λmax-n)/(n-1)
(7)
随机一致性比率RI为
RI=CI/CR
(8)
其中,uj为改进的AHP计算的权重;n为判断矩阵的阶数(也是评价指标个数);λmax为最大特征值;CR为判断矩阵平均随机一致性指标,当CR<0.1时,判断矩阵B满足一致性检验,否则需对其进行调整。对于1~9标度来说,其对应的RI=0.9。
3.2 熵权法指标权重确定方法
熵是热力学中的概念,被C E SHANNON引入到信息论中,用来对信息量进行度量。不确定性与信息量成负相关,因而可以用熵值来度量不确定性情况。指标对结果的影响程度随着其集中程度增高而降低,即一个系统越有序,信息熵就越低;系统越无序,信息熵就越高[14]。熵权法是一种客观确定权重的方法,使用时根据指标的变异程度来确定指标权重,能够尽可能消除人的主观干扰[15]。
在具体的风化基岩富水性分区评价预测中,相对于某个指标,其在整个研究区内分布不均,其值在网格节点处分布差异较大,说明各节点的非均质性强弱存在较大差异,则该指标的熵值越小,相应的熵权就越大。具体步骤如下:
(1)对原始数据进行标准化处理。
n个评价对象,m个评价指标构成的原始数据矩阵为

(9)
对X实施标准化处理可得
Y=(yij)n×m
(10)
其中,yij为第j个评价指标在第i个评价对象上的标准值,yij,y′ij∈[0,1]。指标评价:评价指标一般可分为正向指标yij(指标值越大越好)和负向指标y′ij(指标值越小越好)。
![]()
(11)
![]()
(12)
(2)评价指标的熵。
在有n个评价对象,m个评价指标的评估问题中,第j个指标的熵定义为
![]()
(13)
其中,![]() 当fij=0时,fijln fij=0。熵值越小,说明该指标向决策者提供了越有用的信息。
当fij=0时,fijln fij=0。熵值越小,说明该指标向决策者提供了越有用的信息。
(3)评价指标的熵权。
在(n,m)评价问题中,第j个指标的熵权定义为
![]()
(14)
式中,![]() 即为熵权法计算的权重。
即为熵权法计算的权重。
3.3 改进AHP和熵权法耦合的指标权重确定方法
通常算法组合的典型方法有幂平均合成法和最优化方法[15]。笔者采用最优化方法中的最小二乘法对改进AHP和熵权法进行耦合,形成一种主客观赋权法。对评价对象的所有指标而言,主客观赋权下的富水性评价值的偏差应越小越好。据此,建立最小二乘法优化组合权重模型:
[(vj-wj)zij]2}
(15)
约束条件为
用矩阵表示为
![]()
(16)
式中,A为m×m对角阵;e,W,B均为m×1向量。
![]()
(17)
e=[1,1,…,1]T wj=[w1,w2,…,wm]T
![]()
(18)
求解上面的矩阵方程,得
![]()
(19)
式中,wj即为改进的AHP和熵权法耦合计算的权重;zij为具有m个评价指标、n个评价对象的标准化后的数据矩阵。
4 柠条塔井田南翼风化基岩富水性预测
由图1层次结构模型可知,柠条塔井田南翼风化基岩含水层富水性预测指标有风化基岩顶面标高级别指数、岩性组合指数、风化指数和岩芯采取率指数4个预测指标。柠条塔井田南翼共有172个钻孔,其中风化基岩抽水试验钻孔41个,可用于风化基岩富水性预测方法的试验、比较与优选。
4.1 富水性指标权重计算
依据上述钻孔数据计算的各指标值,运用改进AHP、熵权法和耦合其两者的方法分别计算富水性预测指标的权重。
4.1.1 基于改进AHP的指标权重计算
首先统计172个钻孔4个预测指标的值,再利用改进的AHP指标权重计算方法,对研究区内风化基岩富水性预测指标权重进行计算,根据式(4)计算的判断矩阵B4×4为

该判断矩阵为一四阶矩阵,经一致性检验式(7),(8)计算,该判断矩阵的最大特征值λmax=4.151 3,CR=0.056<0.1,因此,该判断矩阵满足一致性检验。通过计算求得指标层的权重(uj):风化基岩顶面标高级别指数权重(u1)为0.619 7、岩性组合指数权重(u2)为0.201 6、风化指数权重(u3)为0.137 2、岩芯采取率指数(u4)为0.041 5(表4)。
表4 不同方法计算的风化基岩富水性预测指标权重
Table 4 Weighted prediction index of weathered bedrock calculated by different methods
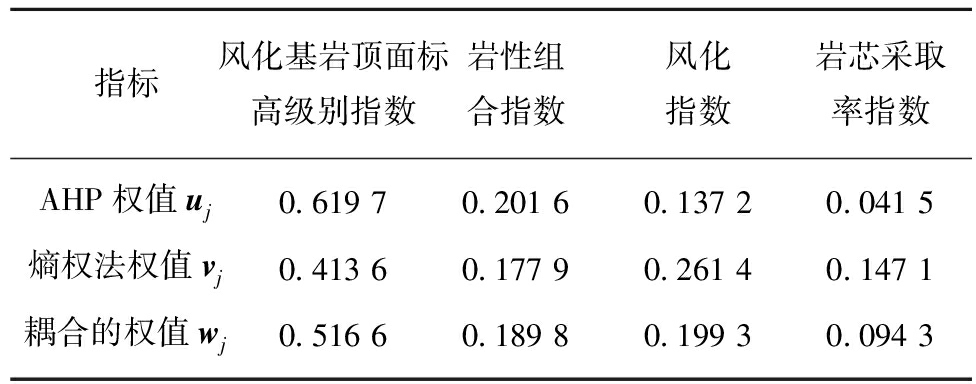
指标风化基岩顶面标高级别指数岩性组合指数风化指数岩芯采取率指数AHP权值uj0.619 70.201 60.137 20.041 5熵权法权值vj0.413 60.177 90.261 40.147 1耦合的权值wj0.516 60.189 80.199 30.094 3
4.1.2 基于熵权法的指标权重计算
利用已统计的172个钻孔风化基岩富水性预测指标值(除岩芯采取率指数为负向指标,其余3个指标均为正向指标),结合式(10)将各指标值构成的原始数据矩阵进行标准化处理。
标准化后的矩阵如下所示:

将标准化后的矩阵在Matlab中利用式(13)和(14)进行熵值和熵权计算,得到各指标的权重(vj):风化基岩顶面标高级别指数(v1)为0.413 6、岩性组合指数(v2)为0.177 9、风化指数(v3)为0.261 4、岩芯采取率指数(v4)为0.147 1(表4)。
4.1.3 基于改进AHP和熵权法耦合的指标权重计算
采用最小二乘法把改进AHP和熵权法偶合起来,由式(17)可知A为4×4的对角阵,有

同样在Matlab中利用式(18)和(19)对其进行计算,最终得到指标层的优化权重(wj):风化基岩顶面标高级别指数(w1)为0.516 6、岩性组合指数(w2)为0.189 8、风化指数(w3)为0.199 3、岩芯采取率指数(w4)为0.094 3(表4)。
4.2 富水性预测
4.2.1 富水性分区预测方法
富水性分区预测时要涉及富水性等级的划分。富水性等级的划分一般是根据钻孔单位涌水量的大小,按照《煤矿防治水细则》(以下简称《细则》)给出的划分标准(表5)进行划分。对柠条塔井田南翼进行过风化基岩抽水试验的41个钻孔分析发现,其最大单位涌水量为0.446 1 L/(s·m),属富水性中等,未见富水性强和极强的钻孔,其中富水性弱的钻孔占56.10%。为了使富水性分区预测结果更便于矿井防治水工作开展,可将富水性弱这一级别进一步细分,即将《细则》中的弱富水性(q≤0.1 L/(s·m))进一步划分为极弱(q≤0.01 L/(s·m))和弱(0.01~0.1 L/(s·m))。
表5 《细则》中含水层富水性等级划分
Table 5 Classification of aquifer water abundance in coal mine water control detailed rules

富水性等级弱中等强极强《细则》划分标准/(L·(s·m)-1)≤0.10.1~11~5>5
富水性预测分区时,首先要计算富水性综合指数。其方法是根据对柠条塔井田南翼172个钻孔4个预测指标的统计值,将其进行标准化处理,然后在Surfer软件中栅格化,再将各指标的网格图导入ArcGIS中,运用栅格计算器,结合改进AHP、熵权法和耦合两者计算的权重,通过线性权重加和的方式得到富水性综合指数wk:
![]()
(20)
式中,i为指标序号;n为指标个数;Pi为第i个指标的权重值;Ai为第i个指标的标准值。
其次,采用自然间断法对通过式(20)计算出的各钻孔富水性综合指数进行分级分类。自然间断法可对富水性综合指数进行最恰当地分类(组),并可使各个类之间的差异最大化。柠条塔井田南翼富水性综合指数的间断法分类见表6,即按中断值(K)可以将研究区富水性划分I,II,III,IV共4个类别,结合进行过风化基岩抽水试验的41个钻孔发现间断法划分的风化基岩富水性预测分区范围和风化基岩抽水钻孔富水性存在对应关系,即由Ⅰ至Ⅳ,富水性由弱至强。Ⅰ和Ⅱ分别对应富水性极弱和弱。Ⅲ和Ⅳ对应富水性中等,但预测分区的Ⅳ相较于Ⅲ富水性更强一点。
表6 中断值(K)和预测分区对应关系
Table 6 Correspondence of interrupt value and predicted partition

中断值K<0.399 60.399 6~0.544 90.544 9~0.702 90.702 9~0.930 4预测分区ⅠⅡⅢⅣ抽水钻孔富水性极弱弱中等中等
柠条塔井田南翼基于改进AHP、熵权法和改进AHP与熵权法耦合的富水性分区预测结果如图3所示。
4.2.2 富水性预测结果比较
为了比较基于改进AHP、熵权法和改进AHP与熵权法耦合的3种富水性分区预测方法的优劣,将区内风化基岩抽水钻孔富水性等级与图3中的预测类别进行比较,如果一致,则认为两者吻合,表明预测结果是正确的,反之则不正确,这样就验证了3种方法富水性预测结果的正确性。41个风化基岩抽水钻孔的孔号、风化基岩厚度、单位涌水量和3种方法富水性类别预测结果见表7,表中钻孔单位涌水量等级Ⅰ,Ⅱ,Ⅲ分别对应富水性极弱、弱和中等。通过对比发现基于改进AHP权重确定方法、熵权法权重确定方法和耦合两者的权重确定方法所预测的富水性类别与41个抽水钻孔的富水性吻合度分别为68.29%,70.73%和92.68%,即就是利用最小二乘法耦合计算权重进行富水性分区预测的方法最好。

图3 基于改进AHP的富水性分区预测
Fig.3 Water abundance partition prediction based on improved AHP
表7 抽水钻孔的单位涌水量类型和3种方法富水性预测结果对照
Table 7 Comparison of units-inflow types in pumping holes and three methods for predicting water abundance

钻孔孔号风化基岩厚度/m单位涌水量/(L·(s·m)-1)(类型)预测结果(是否符合)AHP熵权法耦合钻孔孔号风化基岩厚度/m单位涌水量/(L·(s·m)-1)(类型)预测结果(是否符合)AHP熵权法耦合BK2847.500.005 0(Ⅰ)Ⅰ(是)Ⅰ(是)Ⅰ(是)SB2622.180.001 8(Ⅰ)Ⅱ(否)Ⅲ(否)Ⅰ(是)BK4217.400.105 1(Ⅲ)Ⅲ(是)Ⅲ(是)Ⅲ(是)J135.250.087 2(Ⅱ)Ⅰ(否)Ⅱ(是)Ⅱ(是)BK4917.700.014 9(Ⅱ)Ⅰ(否)Ⅱ(是)Ⅱ(是)J229.900.256 1(Ⅲ)Ⅱ(否)Ⅲ(是)Ⅲ(是)ZK119.000.151 0(Ⅲ)Ⅳ(是)Ⅳ(是)Ⅲ(是)J314.700.310 8(Ⅲ)Ⅰ(否)Ⅱ(否)Ⅱ(否)ZK218.000.062 6(Ⅱ)Ⅱ(是)Ⅱ(是)Ⅱ(是)J463.100.008 9(Ⅰ)Ⅰ(是)Ⅰ(是)Ⅰ(是)ZK322.800.036 1(Ⅱ)Ⅱ(是)Ⅲ(否)Ⅱ(是)J566.700.028 3(Ⅱ)Ⅱ(是)Ⅱ(是)Ⅱ(是)ZK48.500.047 4(Ⅱ)Ⅱ(是)Ⅲ(否)Ⅱ(是)J620.050.135 3(Ⅲ)Ⅰ(否)Ⅱ(否)Ⅱ(否)ZK555.500.106 0(Ⅲ)Ⅱ(否)Ⅲ(是)Ⅲ(是)J728.010.046 4(Ⅱ)Ⅱ(是)Ⅲ(否)Ⅱ(是)ZK626.000.097 5(Ⅱ)Ⅰ(否)Ⅱ(是)Ⅰ(否)J849.000.089 7(Ⅱ)Ⅱ(是)Ⅱ(是)Ⅱ(是)ZK721.000.005 2(Ⅰ)Ⅰ(是)Ⅰ(是)Ⅰ(是)J924.500.111 7(Ⅲ)Ⅲ(是)Ⅲ(是)Ⅲ(是)ZK818.700.045 9(Ⅱ)Ⅱ(是)Ⅲ(否)Ⅱ(是)J1027.540.063 9(Ⅱ)Ⅱ(是)Ⅱ(是)Ⅱ(是)SK176.990.010 8(Ⅱ)Ⅱ(是)Ⅱ(是)Ⅱ(是)J1122.260.145 8(Ⅲ)Ⅳ(是)Ⅳ(是)Ⅲ(是)SK211.130.194 8(Ⅲ)Ⅲ(是)Ⅲ(是)Ⅲ(是)J1232.200.291 1(Ⅲ)Ⅳ(是)Ⅳ(是)Ⅲ(是)SK361.460.389 1(Ⅲ)Ⅰ(否)Ⅱ(否)Ⅲ(是)J1321.150.313 9(Ⅲ)Ⅲ(是)Ⅲ(是)Ⅲ(是)SK626.510.078 2(Ⅱ)Ⅲ(否)Ⅱ(是)Ⅱ(是)J1434.630.109 2(Ⅲ)Ⅳ(是)Ⅳ(是)Ⅳ(是)SK718.400.088 7(Ⅱ)Ⅲ(否)Ⅲ(否)Ⅱ(是)J1516.300.446 1(Ⅲ)Ⅳ(是)Ⅳ(是)Ⅳ(是)SK823.330.034 6(Ⅱ)Ⅱ(是)Ⅱ(是)Ⅱ(是)J1715.100.411 9(Ⅲ)Ⅳ(是)Ⅳ(是)Ⅳ(是)SK284.200.018 2(Ⅱ)Ⅱ(是)Ⅲ(否)Ⅱ(是)K3-15.560.122 0(Ⅲ)Ⅱ(否)Ⅲ(是)Ⅲ(是)SK295.640.022 8(Ⅱ)Ⅱ(是)Ⅲ(否)Ⅱ(是)K5-321.000.195 0(Ⅲ)Ⅲ(是)Ⅲ(是)Ⅲ(是)SK3011.700.092 9(Ⅱ)Ⅲ(否)Ⅱ(是)Ⅱ(是)K7-36.200.138 0(Ⅲ)Ⅲ(是)Ⅲ(是)Ⅲ(是)SB0117.610.029 3(Ⅱ)Ⅱ(是)Ⅲ(否)Ⅱ(是)
5 结 论
(1)陕北侏罗纪煤田风化基岩裂隙含水层是矿井主要的充水含水层,其富水性在空间上变化较大,可以选用风化基岩顶面标高级别指数、岩性组合指数、风化指数和岩芯采取率指数共4个指标对风化基岩含水层富水性进行预测。
(2)建立的基于改进AHP和熵权法耦合的富水性预测方法是一种相对较好的方法,它比改进AHP和熵权法单独使用时的预测效果更符合实际。
[1] 陈大鹏,姜霞.陕北能源重化工基地社会经济与环境协调发展研究——以榆林市为例[J].环境科学与管理,2007(9):186-191.
CHEN Dapeng,JIANG Xia.Research on coordinated development between socioeconomic system in Northern Shaanxi Energy & Chemical Industry Base[J].Environmental Science and Management,2007(9):186-191.
[2] 奚砚涛,冯春莉,郭英海,等.钻孔单位涌水量换算的理论与实践[J].煤田地质与勘探,2015,43(1):48-51.
XI Yantao,FENG Chunli,GUO Yinghai,et al.The theory and practice of conversion about specific capacity[J].Coal Geology & Exploration,2015,43(1):48-51.
[3] 代革联,杨韬,周英,等.神府矿区柠条塔井田直罗组地层富水性研究[J].安全与环境学报,2016,16(4):144-148.
DAI Gelian,YANG Tao,ZHOU Ying,et al.Exploration of the water-abundant sandstone geological features of Ningtiaota Zhiluo Formation in Shenfu mining area[J].Journal of Safety and Environment,2016,16(4):144-148.
[4] 武强,樊振丽,刘守强,等.基于GIS的信息融合型含水层富水性评价方法——富水性指数法[J].煤炭学报,2011,36(7):1124-1128.
WU Qiang,FAN Zhenli,LIU Shouqiang,et al.Water-richness evaluation method of water-filled aquifer based on the principle of information fusion with GIS:Water-richness index method[J].Journal of China Coal Society,2011,36(7):1124-1128.
[5] 侯恩科,童仁剑,王苏健,等.陕北侏罗纪煤田风化基岩富水性Fisher模型预测方法[J].煤炭学报,2016,41(9):2312-2318.
HOU Enke,TONG Renjian,WANG Sujian,et al.Prediction method for the water enrichment of weathered bedrock based on Fisher model in Northern Shaanxi Jurassic coalfield[J].Journal of China Coal Society,2016,41(9):2312-2318.
[6] 王生全,牛建立,刘洋,等.锦界煤矿矿井涌水规律及其控制因素分析[J].煤矿安全,2014,45(2):145-147,150.
WANG Shengquan,NIU Jianli,LIU Yang,et al.Gushing water law and its control factors analysis of Jinjie Coal Mine[J].Safety in Coal Mines,2014,45(2):145-147,150.
[7] 郭金玉,张忠彬,孙庆云.层次分析法的研究与应用[J].中国安全科学学报,2008,18(5):148-153.
GUO Jinyu,ZHANG Zhongbin,SUN Qingyun.Study and applications of analytic hierarchy process[J].China Safety Science Journal(CSSJ),2008,18(5):148-153.
[8] 章海波,骆永明,赵其国,等.香港土壤研究Ⅵ.基于改进层次分析法的土壤肥力质量综合评价[J].土壤学报,2006(4):577-583.
ZHANG Haibo,LUO Yongming,ZHAO Qiguo,et al.Hong Kong soil researches Ⅳ.Integrated evaluation of soil fertility quality based on the improved analytic hierarchy process[J].Acta Pedologica Sinica,2006(4):577-583.
[9] 马荣,石建省,刘继朝.熵权耦合随机理论在含水层非均质综合指数研究中的应用[J].吉林大学学报(地球科学版),2011,41(5):1520-1528.
MA Rong,SHI Jiansheng,LIU Jichao.Application of entropy weight and stochastic theory to study the heterogeneity synthetic index of aquifer[J].Journal of Jilin University(Earth Science Edition),2011,41(5):1520-1528.
[10] 吴殿廷,李东方.层次分析法的不足及其改进的途径[J].北京师范大学学报(自然科学版),2004,40(2):264-268.
WU Dianting,LI Dongfang.Shortcomings of analytical hierarchy process and the path to improve the method[J].Journal of Beijing Normal University(Natural Science),2004,40(2):264-268.
[11] 黄德才,郑河荣.AHP方法中判断矩阵的标度扩展构造法[J].系统工程,2003(1):105-109.
HUANG Decai,ZHENG Herong.Scale-extending method for constructing judgment matrix in the analytic hierarchy process[J].Systems Engineering,2003(1):105-109.
[12] 潘寒尽,张多林.AHP方法存在的问题及改进方法[J].航空兵器,2003(6):16-17.
PAN Hanjin,ZHANG Duolin.Problems and improvement methods of AHP method[J].Aero Weaponry,2003(6):16-17.
[13] 翟立林,张庆洪.应用决策分析[M].上海:同济大学出版社,1994.
[14] 邓红雷,戴栋,李述文.基于层次分析-熵权组合法的架空输电线路综合运行风险评估[J].电力系统保护与控制,2017,45(1):28-34.
DENG Honglei,DAI Dong,LI Shuwen.Comprehensive operation risk evaluation of overhead transmission line based on hierarchical analysis entropy weight method[J].Power System Protection and Control,2017,45(1):28-34.
[15] 孔尚萍,张海瑞,廖选平,等.基于AHP与熵权法的空中目标威胁评估方法[J].战术导弹技术,2018(1):79-84.
KONG Shangping,ZHANG Hairui,LIAO Xuanping,et al.Aerial targets threat assessment based on AHP and entropy weight method[J].Tactical Missile Technology,2018(1):79-84.
