泡沫浮选法是一种高效的细粒矿物分选技术,原理是利用不同矿物颗粒与气泡间相互作用的差异,使矿物颗粒能够选择性的黏附在气泡上并随气泡上浮至矿浆表面,从而实现有用矿物与脉石矿物的分离[1-3]。
颗粒与气泡间的相互作用是泡沫浮选的基础,二者间的相互作用直接影响浮选结果,目前其研究方法可分为两类:热力学方法和动力学方法[4-5]。热力学方法主要通过测定颗粒与气泡黏附前后自由能的变化,进而判断颗粒与气泡的黏附状态;动力学法立足于颗粒与气泡的相对运动过程,将该过程细化为碰撞、黏附和脱附3个子过程并逐一研究[6]。
早期研究通常假设颗粒随流线运动,通过求解不同流态下的流线方程研究颗粒与气泡间的相对运动,该方法对惯性较小的颗粒适应性较好[7-9]。随颗粒惯性增大,颗粒会挣脱流线束缚,LANGMUIR和BLODGETT[10]通过Stokes数量化了惯性力对颗粒运动的影响。SCHULZE[11]考虑了截流效应、重力以及惯性力3个因素对颗粒与气泡间相对运动的影响,并分别推导了各因素作用下碰撞概率的计算公式,然而上述研究缺乏对颗粒负惯性作用的认识,因此碰撞概率的计算结果往往偏大。DAI等[12-13]在SUTHERLAND的研究基础上考虑了颗粒负惯性作用和气泡表面流动性的影响,推导了GSE(Generalized Sutherland Equation)方程,并通过试验发现,当颗粒直径为7~60 μm,Stokes数小于0.27时,理论推导结果与试验结果吻合度较高。NGUYEN[14-15]等利用Galileo数量化了重力对颗粒运动的影响,结果显示,对细颗粒而言(直径<20 μm),碰撞概率随颗粒密度的增大而减小,分析认为这是由于颗粒负惯性作用造成的,对粗颗粒而言,碰撞概率随颗粒密度的增大而增大。
除颗粒性质外,气泡表面流动性同样会影响颗粒与气泡的相对运动。目前常用“滞留帽”模型描述气泡表面的流动性[16],即认为气泡表面吸附的污染物会被气泡周围流体扫到气泡底部,气泡上半球可视为流动性表面,下半球为非流动性表面。气泡表面流动性常用清洁角θclean量化,HUANG等[17]在LEGENDRE等[18]的研究基础上提出了临界角θcrit,认为若θclean>θcrit,颗粒掠过轨迹只能与气泡在流动性表面碰撞,若θclean<θcrit,则掠过轨迹的碰撞点没有这一限制。
上述研究多为理论推导,目前关于颗粒与气泡间相对运动的试验研究较为匮乏,且试验对象多为形状规则,表面性质均匀的颗粒(玻璃微珠、玻璃纤维),与实际浮选对象差异较大[19]。笔者以煤为研究对象,通过小筛分和小浮沉试验得到粒级为0.100~0.074 mm,密度级分别为-1.3,1.4~1.5和+1.7 g/cm3的试样,并利用自行设计搭建的试验装置追踪了大量颗粒与气泡间的相对运动过程,研究了颗粒从沉降到最终与气泡碰撞过程中的运动行为,将该过程细分为颗粒自由沉降阶段、颗粒轨迹受气泡影响发生偏离阶段和颗粒与气泡碰撞阶段3个子过程逐一研究。
1 试验装置及材料
1.1 试验装置
目前颗粒与气泡间相对运动的试验研究多采用颗粒沉降法,即通过摄像机直接观察颗粒与气泡的相对运动过程。该方法具有较强的直观性和准确性,故逐渐在研究中被使用。
本次试验装置为实验室自行设计搭建的颗粒与气泡碰撞、黏附行为测量装置[20-22],试验装置三维图如图1所示。
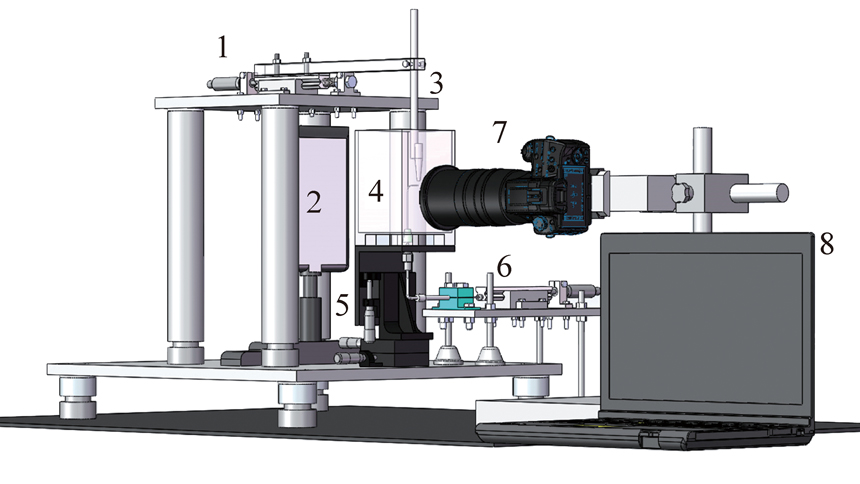
图1 试验装置三维图
Fig.1 3-dimensional graph of the experimental apparatus
1—漏斗微移模块;2—LED阵列光源;3—入料定位漏斗;4—观察室;
5—气泡微移模块;6—气泡产生调节模块;7—摄像机;8—计算机
试验装置主体由漏斗微移模块、LED阵列光源、入料定位漏斗、观察室、气泡微移装置、气泡产生调节模块、摄像机、计算机等部分构成。试验过程中计算机与摄像机连接,用于实时显示并记录颗粒的运动过程;漏斗微移模块和气泡微移装置用于精确调节颗粒和气泡的相对位置,使颗粒能够与气泡在不同位置处碰撞;气泡产生调节模块用于产生并调节气泡大小,气泡直径可在0.5~2.0 mm精确调节;观察室尺寸为80 mm×90 mm×150 mm,材料为聚甲基丙烯酸甲酯(PMMA),透光率为92%;LED阵列光源用于提供照明,由8×12颗高亮LED灯珠构成,光通量为1 250 Lm。
试验过程分3步:① 调节试验装置,包括建立像素点和实际距离的换算关系,调节气泡大小和入料定位漏斗与气泡的相对位置以及相机参数;② 颗粒经入料定位漏斗给入观察室与气泡进行碰撞及黏附,并利用摄像机记录该过程;③ 使用在Matlab平台上自行开发的颗粒多目标追踪软件逐帧分析试验视频,得到颗粒运动特征参数。
1.2 试验材料
试验煤样取自内蒙古公乌素矿区16号煤层,试验时首先对该煤样湿筛,得到0.1~0.074 mm粒级的试样,随后通过小浮沉试验得到密度级为-1.3,1.4~1.5和+1.7 g/cm3的煤颗粒。
试验液体环境为去离子水,电导率0.25 μS/cm,观察室中加入去离子水600 mL。每次试验取5 mg煤样置于烧杯中,加入200 mL去离子水,用磁力搅拌器分散成悬浮液,磁力搅拌器转速为1 500 rad/min。拍摄过程中视频分辨率为1 280×720,感光度ISO取100,帧率FPS取50,光圈值取5.6,快门速度取1/500。每次试验拍摄视频约5 h,经软件处理得到有效颗粒1 000~1 500个,液体温度为25±1 ℃。
2 结果与讨论
2.1 颗粒沉降末速
速度是衡量颗粒运动状态的重要参数,对颗粒与气泡间的相对运动有重要影响,颗粒沉降末速主要受颗粒粒度和密度的影响。样品处理阶段通过湿筛得到了粒级0.100~0.074 mm的颗粒,然而湿筛结果显然无法准确反映试样的粒度分布,本次试验过程中利用颗粒当量直径表征颗粒粒度,颗粒当量直径是指与颗粒投影面积相同圆的直径。试验共统计了3 000个颗粒的当量直径,分布如图2所示。

图2 颗粒当量直经分布
Fig.2 Distributions of particle equivalent diameter
由图2可知,颗粒当量直径在0.06~0.12 mm,中间粒级颗粒数较多,两侧粒级颗粒数较少。统计结果显示,颗粒当量直径均值为0.092 mm,主分布区间为0.07~0.10 mm,该区间颗粒比例为69.61%。当量直径小于0.07 mm和大于0.11 mm的颗粒比例分别为4.13%和8.72%,表明颗粒当量直径的分布范围与湿筛结果相差不大。对于两侧当量直径超出湿筛范围的颗粒,分析认为主要是两种原因造成的:一是当量直径和筛分粒径定义上的区别,颗粒形状的不规则性会造成当量直径与筛分粒径之间的差异;二是湿筛过程中存在细长颗粒透筛,导致当量直径较大的颗粒进入产品,且试验过程中颗粒在磁力搅拌器的分散作用下会被破碎成微细颗粒。
颗粒沉降过程中主要受重力、浮力、流体阻力、附加质量力、惯性力的影响,假设颗粒为规则球体,其受力方程[23]为

(1)
将式(1)进行整理:
![]()
(2)
求解式(2),得到静水下颗粒速度随时间的变化关系:
(3)
式中,Rp为颗粒半径;ρp为颗粒密度;ρl为液体密度;V为颗粒速度;Cd为阻力系数;μ为液体黏度;t为时间。
根据式(3)分别绘制直径0.074 mm和0.10 mm两种情况下各密度颗粒速度随时间变化情况,由图3可知,颗粒经一个短暂的加速阶段(小于10 ms)后速度逐渐趋于平稳,此时颗粒达到沉降末速。结果表明,本次试验中可忽略颗粒加速阶段,认为所有颗粒在与气泡碰撞前速度已达到沉降末速。

图3 颗粒速度随时间变化
Fig.3 Graph of particle velocity versus time
煤样准备阶段将试样分成了-1.3,1.4~1.5和+1.7 g/cm3三个密度级,分别代表低密度级煤样、中间密度级煤样和高密度级煤样。图4为3组煤样的沉降末速分布图,每个密度级约统计1 500个颗粒。

图4 三密度级煤样颗粒沉降末速分布
Fig.4 Distribution of terminal velocity of three densitiy coal samples
由图4可知,3组煤样颗粒沉降末速分布均是中间多两侧少,与颗粒当量直径分布规律类似,表明颗粒沉降末速的变化主要是颗粒粒度变化引起的。对于高密度级煤样,颗粒沉降末速分布范围更广,表明高密度级煤样密度分布范围大于低密度级和中间密度级煤样。根据式(2)计算可知,高密度级煤样的密度分布为1.7~2.2 g/cm3。试验测得3组煤样的沉降末速均值按密度由低至高依次为1.61,2.15,4.75 mm/s,颗粒沉降末速分布范围依次为1.04~2.19,1.47~2.83,2.41~7.10 mm/s。
2.2 密度对颗粒运动轨迹的影响
利用流线方程研究颗粒与气泡的相对运动是一种常用方法。本次试验在静止的去离子水中进行,流体绕气泡的流线方程[2]为
![]()
(4)
其中,r和φ分别是极坐标下的极径和极角。由式(4)得到气泡周围流线分布如图5(a)所示。

图5 流线图和颗粒运动轨迹
Fig.5 Diagram of streamline and particle trajectory
试验追踪了大量煤颗粒的运动轨迹,并将颗粒按初始沉降位置分成5个区间,每个区间长度0.1 mm,距气泡中心轴的距离分别是0~0.1,0.1~0.2,0.2~0.3,0.3~0.4和0.4~0.5 mm。为体现流线和颗粒运动轨迹间的差异,图5(b)选取了试验观测到的5个煤颗粒与气泡碰撞时的运动轨迹,颗粒密度均在1.4~1.5 g/cm3。
由图5可知,流体和颗粒距气泡较远时均沿竖直方向下落,随二者与气泡间距离不断减小,流线和颗粒运动轨迹均偏离原运动方向。为量化气泡对颗粒运动轨迹的影响范围,引入了轨迹偏离点,即颗粒运动轨迹偏离原运动方向的角度达到3°时的位置。试验过程中每组煤样统计2 000个颗粒的轨迹偏离点,并按初始沉降区间对各区间轨迹偏离点至气泡中心的距离求均值,3组煤样由不同初始沉降位置下落时轨迹偏离点到气泡中心的距离如图6所示。

图6 流线和煤样轨迹偏离点到气泡中心的距离
Fig.6 Distance of streamline and coal samples from trajectory deviation point to bubble center
由图6可知,流线和煤样的轨迹偏离点到气泡中心的距离均随初始沉降区间向外扩展而增大,该现象主要是水平方向煤样初始沉降位置远离气泡造成的。初始沉降位置相同时,流线偏离点距气泡中心的距离要远大于煤样轨迹偏离点至气泡中心的距离,表明流线更易受气泡影响。分析认为,该现象主要是颗粒惯性力造成的,随着颗粒与气泡间距离不断减小,气泡逐渐影响颗粒的运动,然而受惯性力的影响,颗粒具有维持原运动方向的趋势,气泡对颗粒运动轨迹影响较小。上述研究与NGUYEN等[24-26]的研究吻合,NGUYEN等认为,当颗粒与气泡间距离减小至与颗粒粒径相当时,气泡会影响颗粒的运动轨迹。
试验进一步发现,除颗粒粒径外,颗粒密度同样影响颗粒和气泡间的相对运动。由图6可知,初始沉降位置相同时,高密度煤样轨迹偏离点到气泡中心的距离小于低密度煤样轨迹偏离点到气泡中心的距离。分析认为,初始沉降位置相同时,水平方向上煤样运动轨迹的偏离距离相同,故上述现象是煤样运动轨迹在竖直方向上的偏离差异造成的。因此进一步统计了初始沉降区间相同时同组煤样中所有颗粒轨迹偏离点距气泡最高点平面的竖直距离并求均值,如图7所示。

图7 煤样轨迹偏离点到气泡的竖直距离
Fig.7 Vertical distance from coal samples trajectory deviation point to bubble
由图7可知,同一初始沉降区间内,随煤样密度增大,颗粒轨迹偏移点距气泡的竖直距离减小,表明颗粒密度会影响颗粒轨迹偏移的位置。分析认为,颗粒粒径相同时,随颗粒密度增大,颗粒质量和惯性增大,抵抗气泡影响的能力增强,且颗粒沉降速度随密度的增大而增大,故需要沉降更大距离才能达到轨迹偏离点。
2.3 密度对碰撞点处颗粒速度的影响
颗粒运动轨迹偏离一段距离后,随颗粒与气泡间距离不断减小,颗粒与气泡碰撞。颗粒和气泡的碰撞位置用碰撞角表示,碰撞角是指碰撞点和气泡中心连线与竖直方向的夹角。试验统计了3组试样与气泡的碰撞角,每组试样统计1 500个颗粒,统计时以10°为1个统计区间,将气泡表面分成了9个碰撞区间,各碰撞区间内3组煤样颗粒比例的分布如图8所示。

图8 各碰撞角区间内3组煤样的颗粒分布
Fig.8 Distribution of particles in each collision angles of the three coal samples
由图8可知,3组煤样中颗粒与气泡的碰撞角主要分布在20°~50°,该区间内颗粒数占颗粒总数的比例均在80%以上,表明该区间是碰撞发生的主要区间。碰撞角小于10°时,受气泡对颗粒切向阻力的影响,颗粒偏离原运动方向,导致初始沉降位置距气泡中轴较近的颗粒难以在较小的碰撞角区间内发生碰撞。碰撞角大于50°时,与气泡碰撞的颗粒数急剧减小,碰撞角大于70°时,颗粒已经很难与气泡在该区间发生碰撞。分析认为,当颗粒初始沉降区间距气泡中轴较远时,运动轨迹的偏离使得颗粒难以与气泡碰撞。图9是密度级1.4~1.5 g/cm3的试样由不同初始沉降区间沉降时碰撞角的分布。

图9 不同初始沉降区间内碰撞角的分布
Fig.9 Distribution of collision angle in different initial settlement interval
由图9可知,颗粒比例随初始沉降区间向外扩展呈现2个变化规律:① 碰撞角区间不断向外扩展,② 颗粒集中分布区间不断向外扩展。当颗粒初始沉降区间由0~0.1 mm扩展至0.1~0.2 mm时,碰撞角分布区间由0°~40°增大至10°~50°。当颗粒在初始沉降区间0~0.1 mm沉降时,颗粒无法与气泡在碰撞角小于10°的区间内发生碰撞,随初始沉降区间不断向外扩展,颗粒碰撞区间随之不断向外扩展。此外,颗粒集中分布区间也随着初始沉降区间的增大而增大,各初始沉降区间内颗粒碰撞角均值按初始沉降区间由小至大依次为18.44°,29.82°,38.04°,42.83°,49.29°。
试验发现,颗粒与气泡碰撞前速度会逐渐减小,颗粒速度在碰撞点处降至最低值[20]。本次研究进一步发现,碰撞点处的颗粒速度减小量与碰撞角有关,3组煤样碰撞点处颗粒速度减小比例与碰撞角间的关系如图10所示。
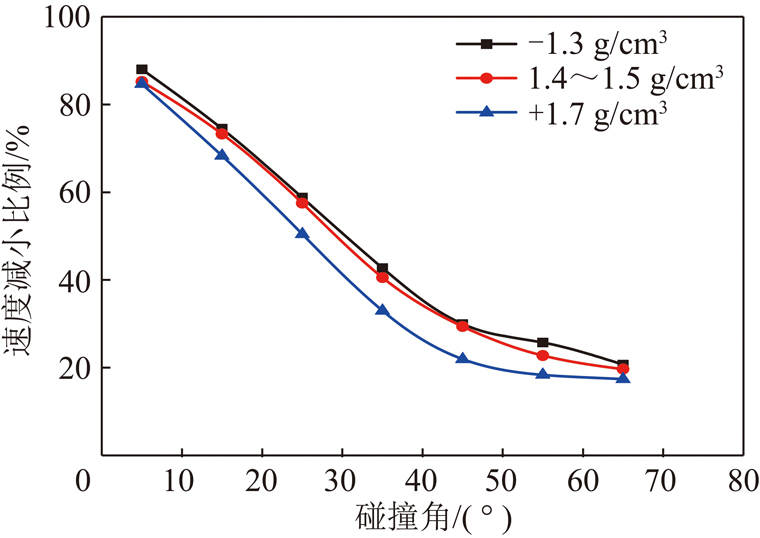
图10 碰撞角和碰撞点处速度减小比例关系
Fig.10 Relationship between collision angle and particle velocity reduction ratio
碰撞角小于50°时,碰撞点处颗粒速度减小比例随碰撞角增大近似直线减小,碰撞角大于50°时,碰撞点处的颗粒速度减小比例趋于平稳。试验表明,碰撞点处颗粒速度减小比例受颗粒密度的影响,低密度颗粒的速度减小量大于高密度级颗粒的速度减小量,然而差异并不明显。
前面2.1节中已经对颗粒进行了受力分析,然而随颗粒不断沉降,当颗粒与气泡间的距离减小至与颗粒粒径相当时,气泡会影响颗粒的运动轨迹。为此,引入了阻力系数f用于描述气泡对颗粒的影响,颗粒受力如图11所示。

图11 颗粒受力示意
Fig.11 Schematic of force acting on particles
图11中Fg为颗粒重力,Fb为浮力,Fd为颗粒所受阻力,颗粒受力方程如式(5)所示[27]。
![]()
(5)
将颗粒速度分解为径向速度Vr和切向速度Vt,图11中α角为颗粒速度方向与竖直方向的夹角,θ角为颗粒中心与气泡中心连线与水平方向的夹角。由式(5)得到颗粒在径向和切向上的受力方程:

(6)
其中,fr和ft分别为阻力系数f在径向和切向的分量。因试验在去离子水中进行,气泡表面未受污染,与流动性表面较为接近,故计算时采用了NGUYEN等[23]提出的阻力系数计算方法:
fr=[1+(Rp/4h)0.719]1.394
(7)
ft=[1.106+(h/Rp)]/[1.501+(h/Rp)]
(8)
其中,h为颗粒与气泡间的距离。将式(7)和式(8)代入式(6)。利用Matlab编程求解式(6),求解过程中式中Rp取0.05 mm,ρp分别取1.3,1.4和1.7 g/cm3,ρl取1.0 g/cm3,μ取0.894 9 mPa·s,综合考虑到数据容量和的运算精度的影响,两点间的时间间隔取为3×10-5 s。
颗粒距气泡较远时阻力系数fr和ft约为1,意味着气泡对颗粒影响较小。随着颗粒与气泡间距离不断减小,阻力系数fr增大,fr减小,颗粒径向速度Vr减小,切向速度Vt增大,颗粒速度V减小,将颗粒速度降至最低点处的速度记为理论碰撞速度。分别求解了颗粒从不同初始位置沉降时的理论碰撞速度,如图12所示。

图12 理论碰撞速度与初始沉降区间的关系
Fig.12 Relation between theoretical collision velocity and initial settlement interval
由图12可知,颗粒初始沉降位置距气泡中轴较近时,颗粒理论碰撞速度较小,即颗粒速度减小量大,随颗粒初始沉降位置向外扩展,颗粒理论碰撞速度增大,且初始沉降区间大于0.25 mm后理论碰撞速度趋于平稳,与试验结果较为吻合。
3 结 论
(1)颗粒当量直径主要分布在0.06~0.12 mm,当量直径均值为0.092 mm,颗粒经过短暂的加速阶段后达到沉降末速,3组颗粒沉降末速均值按密度级由低至高(-1.3,1.4~1.5,+1.7 g/cm3)依次为1.61,2.15,4.75 mm/s,颗粒沉降末速分布范围依次为1.04~2.19,1.47~2.83,2.41~7.10 mm。
(2)流线和颗粒距气泡较远时均沿竖直方向下落,随二者与气泡间的距离减小,气泡会影响流线和颗粒运动轨迹。同一初始沉降区间内,煤样轨迹偏移点距气泡的竖直距离随煤样密度的增大而减小。
(3)颗粒与气泡碰撞角主分布在20°~50°,随初始沉降区间向外扩展,碰撞角区间和颗粒集中分布区间均向外扩展。碰撞角小于50°时,碰撞点处颗粒速度减小比例随碰撞角增大近似直线减小,碰撞角大于50°时,碰撞点处的颗粒速度减小比例趋于平稳。碰撞点处颗粒速度减小比例受颗粒密度影响,低密度颗粒的速度减小量大于高密度级颗粒的速度减小量,然而差异并不明显。理论计算表明,颗粒初始沉降位置距气泡中轴较近时理论碰撞速度较小,且颗粒理论碰撞速度随颗粒初始沉降位置向外扩展而增大。
[1] FUERSTENAU M C,JAMESON G,YOON R H.Froth flotation:A century of innovation[M].American:Society for Mining Metallurgy & Exploration,2007.
[2] NGUYEN A V,SCHULZE H J.Colloidal science of flotation[M].London:CRC Press,2004.
[3] SHAHBAZI B,CHELGANI S.Modeling of fine coal flotation separation based on particle characteristics and hydrodynamic conditions[J].International Journal of Coal Science & Technology,2016,3(4):429-439.
[4] 陈泉源,张泾生,王淀佐.气泡与颗粒作用研究新进展[J].国外金属矿选矿,2001,38(2):17-19.
[5] 王梦霞,车晓宇,吕梦璇,等.无机盐与表面活性剂在低阶煤表面的协同吸附[J].洁净煤技术,2019,25(1):77-85.
WANG Mengxia,CHE Xiaoyu,LÜ Mengxuan,et al.Synergistic adsorption of inorganic salt and surfactants on the surface of low rank coal[J].Clean Coal Technology,2019,25(1):77-85.
[6] 程宏志,蔡昌凤,张孝钧,等.浮选微观动力学和数学模型[J].煤炭学报,1998,23(5):545-549.
CHENG Hongzhi,CAI Changfeng,ZHANG Xiaojun,et al.Flotation microscopic kinetics and mathematical model[J].Journal of China Coal Society,1998,23(5):545-549.
[7] SUTHERLAND K L.Physical chemistry of flotation.XI.kinetics of the flotation process[J].Journal of Physical & Colloid Chemistry,1948,52(2):394.
[8] FLINT L R,HOWARTH W J.The collision efficiency of small particles with spherical air bubbles[J].Chemical Engineering Science,1971,26(8):1155-1168.
[9] YOON R H,LUTTRELL G H.The effect of bubble size on fine particle flotation[J].Mineral Processing & Extractive Metallurgy Review,1989,5(1-4):101-122.
[10] LANGMUIR I,BLODGETT K.Mathematical investigation of water droplet trajectories[J].Atmospheric Phenomena,1961:335-347.
[11] SCHULZE H J.Probability of particle attachment on gas bubbles by sliding[J].Advances in Colloid & Interface Science,1992,40:283-305.
[12] DAI Z,DUKHIN S,FORNASIERO D,et al.The inertial hydrodynamic interaction of particles and rising bubbles with Mobile Surfaces[J].Journal of Colloid & Interface Science,1998,197(2):275.
[13] DAI Z,FORNASIERO D,RALSTON J.Particle-bubble collision models-a review[J].Advances in Colloid & Interface Science,2000,85(2):231-256.
[14] NGUYEN A V,KMET’ S.Collision efficiency for fine mineral particles with single bubble in a countercurrent flow regime[J].International Journal of Mineral Processing,1992,35(3-4):205-223.
[15] NGUYEN A V.The Collision between fine particles and single air bubbles in flotation[J].Journal of Colloid & Interface Science,1994,162(1):123-128.
[16] DUKHIN S S,KRETZSCHMAR G,MILLER R.Dynamic of adsorption at liquid interfaces[M].Amsterdam:Elsevier,1995.
[17] HUANG Z,LEGENDRE D,GUIRAUD P.Effect of interface contamination on particle-bubble collision[J].Chemical Engineering Science,2012,68(1):1-18.
[18] LEGENDRE D,SARROT V,GUIRAUD P.On the particle inertia free collision with a partially contaminated spherical bubble[J].International Journal of Multiphase Flow,2009,35(2):163-170.
[19] 张世杰.煤泥浮选过程中颗粒与气泡碰撞、黏附规律研究[D].北京:中国矿业大学(北京),2015:6.
ZHANG Shijie.Study on collision and attachment behavior between particle and bubble in coal slime flotation[D].Beijing:China University of Mining & Technology(Beijing),2015:6.
[20] 卓启明,刘文礼,刘伟,等.煤颗粒与气泡黏附行为的试验研究[J].煤炭学报,2018,43(7):2029-2035.
ZHUO Qiming,LIU Wenli,LIU Wei,et al.Experimental study on the attachment behavior of coal particles and bubbles[J].Journal of China Coal Society,2018,43(7):2029-2035.
[21] 卓启明,刘文礼,王东辉,等.颗粒与气泡碰撞、吸附行为测量装置及方法[P].中国专利,ZL201610444525.3.
[22] ZHUO Qiming,LIU Wenli,XU Hongxiang.The effect of collision angle on the collision and adhesion behavior of coal particles and bubbles[J].Processess,2018,6(11):1-15.
[23] NGUYEN A V.Hydrodynamics of liquid flows around air bubbles in flotation:A review[J].International Journal of Mineral Processing,1999,56(1):165-205.
[24] NGUYEN A V.One-step analysis of bubble-particle capture interaction in dissolved-air flotation[J].International Journal of Environment & Pollution,2007,30(2):227-249.
[25] NGUYEN A V.Particle-bubble encounter probability with mobile bubble surfaces[J].International Journal of Mineral Processing,1998,55(2):73-86.
[26] NGUYEN A V,EVANS G M.Exact and global rational approximate expressions for resistance coefficients for a colloidal solid sphere moving in a quiescent liquid parallel to a slip gas-liquid interface[J].Journal of Colloid & Interface Science,2004,273(1):262-270.
