随着我国煤炭资源的大规模持续开采,硬质煤层和黏性煤层的比例不断上升,导致破煤岩难度加大[1-2]。预裂辅助冲击截齿针对复杂煤岩条件,在牵引截割过程中加入截齿的高强度往复冲击运动,以使煤体内部实现同步预裂,降低硬煤的截割阻抗或黏煤的黏性,从而令采煤工作的效率得到提升,因此对预裂辅助冲击截齿这种新型技术进行其破煤特性的研究具有重要意义。目前国内外对于破煤岩性能评价的研究大多集中在传统截齿的角度,张强等[3]基于ABAQUS软件得到了不同初始地应力条件下凿岩机破岩效率的变化规律;刘春生[4]基于分形理论,给出了评价截割阻力曲线的分形维数等特征量的实际物理含义;李德根等[5]从混沌分形的角度给出了截割动力系统的截割性能评价指标和系统演变混沌状态的数学关系;张倩倩等[6]分析了破岩机制及不同截线间距对破岩效果的影响;李祥松[7]通过比能耗、截齿损耗率及截齿受力等多角度全面评价了不同截割头的实际性能;李晓豁等[8]利用切削图分析了掘进机的截割性能;于彬等[9]基于煤的破碎度研究了截割阻力的影响因素;江红祥[10]研究了高压水射流冲击和机械刀具的破岩性能;杜玉昆[11]研究了超临界二氧化碳射流的破煤岩性能;徐广举[12]研究了振动式掘进机振动截割时的截齿截割性能;乔时和[13]研究了高压气液两相射流瞬态动力的破煤特性;付林[14]研究了新型钻式采煤机钻具的截割性能;刘春生等[15]采用熵理论研究了煤岩截割性能的评价方法。
对于预裂辅助冲击截齿,由于破煤机制与传统截齿不同,其截齿与齿座整体形成一个闭式液压回路[16],截齿在液压驱动作用下进行切线方向上的冲击运动,故无法按照传统截齿或气液射流等方式的破煤机理进行分析,且目前较为缺乏在复杂煤层条件下的破煤性能评价体系,需要针对新型破煤技术及新的煤层地质条件进行综合分析。
笔者以预裂辅助冲击截齿为研究对象,利用理论分析和数值模拟的方法,考虑截齿的回转、牵引和冲击运动,确定截齿的破煤运动轨迹,并基于离散元方法建立截齿破煤模型,对传统截齿与预裂辅助冲击截齿的破煤特性进行对比分析。
1 预裂辅助冲击截齿破煤轨迹分析
在分析预裂辅助冲击截齿的破煤特性前,首先应确定截齿破煤的作用形式,即截齿的运动轨迹,为使结果更贴近实际工况,设定截齿以滚筒为载体,综合截齿的回转运动、牵引运动以及冲击运动建立截齿的破煤轨迹模型,得到破煤作用范围的解析解,与单独设定截齿只进行牵引运动或回转运动相比,虽同为分析单个截齿的破煤轨迹,但将3种截齿的运动状态综合考虑对于预裂辅助冲击截齿这一新型破煤方式更有实际意义,且对后续破煤仿真分析中的截齿运动轨迹控制具有一定的理论参考依据。
图1为预裂辅助冲击截齿的实际破煤轨迹曲线,其中,r为滚筒的筒毂半径;h为预裂辅助冲击截齿的齿座高度;l为截齿长度;v为截齿进给速度;n为截割转速。为建立截齿破煤的轨迹模型,首先假定截齿只进行回转运动,经t s后运动至a点,由于截齿的回转运动与牵引行进运动同步进行,故以a点出发在滚筒的牵引方向上延长至b点,ab的距离是滚筒经t s后的行进距离。在破煤轨迹的局部放大图中,以b为终点的破煤轨迹曲线上的弧形突起则为截齿的往复冲击作用形成的微小破坏,最终局部放大图中以a,b为终点曲线围成的面积即为预裂辅助冲击截齿的破煤作用面积S。
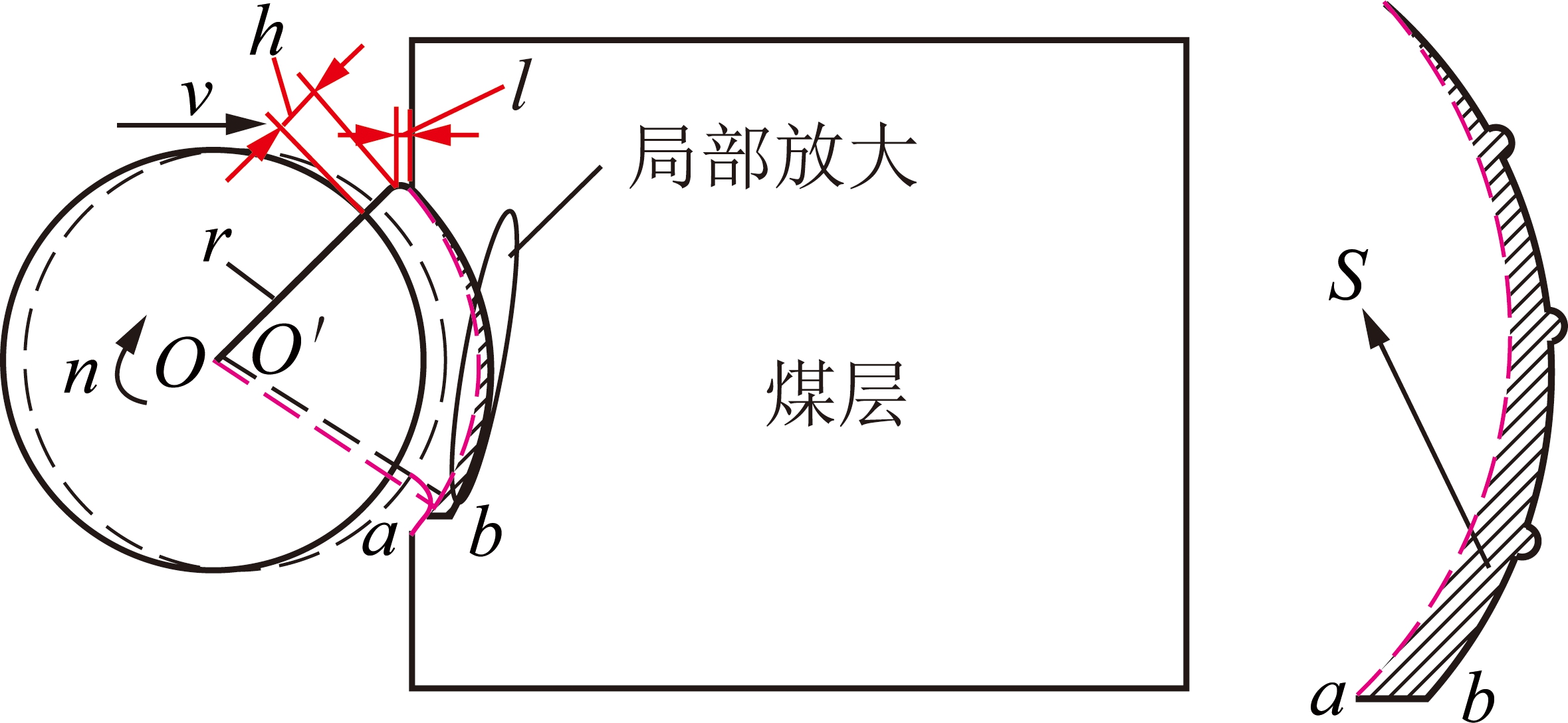
图1 预裂辅助冲击截齿的破煤轨迹模型
Fig.1 Coal breaking trajectory model of hydraulic assisted impact pick
为计算出截齿在时间t s内的理论破煤面积S,将图1的破煤轨迹简化并分为若干便于计算的区域,建立出数学模型如图2所示。

图2 截齿破煤轨迹的数学模型
Fig.2 Mathematical model of coal cutting trajectory of pick
图2中,α为截齿截割角度;β为截齿安装角度。设滚筒筒毂中心至截齿齿尖的距离为R,以t s后筒毂的中心O′到截齿齿尖作辅助圆,由于滚筒是以匀速回转和牵引行进,则面积S必然是环形abcd面积的一半。
以O点为中心建立直角坐标系,将环形abcd分为cde,degf,fhi,gibj,abi五个区域,分别计算各区域面积,最终将各面积相加即可得到环形区域的面积。
图2中c点是截齿齿尖与煤体的最初接触点,计算S1的面积,首先应确定c点、d点的坐标,以x,y轴为基准,设c点的横纵坐标分别为A和B,则A,B的值分别为
![]()
(1)
式中,θ为齿座与筒毂中心的连线与y轴(垂直方向)的夹角。
设圆O的解析表达式为
x2+y2=R2
(2)
图2中ab和OO′的长度为滚筒牵引行进距离,由前述内容可知滚筒牵引速度v与截割时间t,设行进距离为C,则C的表达式和圆O′的方程为

(3)
式中,C为滚筒牵引行进距离,m;v为滚筒牵引速度,m/min;t为截割时间,s。
由于c点、d点纵坐标的值同为B,根据圆O′方程可得到d点横坐标,故利用定积分可求出区域cde的面积S1为
![]()
(4)
由图2可知g点坐标为(R,0),则根据坐标关系利用定积分求出区域edfg的面积S2为
![]()
(5)
根据f点横坐标可由圆O′方程求出f点纵坐标的值,将扇形O′if面积减去三角形O′if面积即可得到区域ifh的面积S3为
![]()
(6)
确定b点坐标需要根据截齿在t时间内转过的角度计算,由图1已知滚筒的转速n,将截齿旋转角度以D表示,则D的值为
D=6nt
(7)
式中,n为滚筒转速,r/min;D为滚筒旋转角度,(°)。
已知c点坐标,则由截齿旋转角度D可以得到b点的横纵坐标,进而利用定积分求得区域bjgi的面积S4为
![]()
(8)
通过b点坐标易得a点坐标,则利用定积分求出区域abj的面积S5为

(9)
经上述计算求解可得到传统破煤方式的单截齿在时间t内的破煤理论面积。而在图1中预裂辅助冲击截齿的往复冲击作用还额外造成了煤体的破坏,为计算截齿截割过程中由于冲击运动产生的额外破煤面积,首先应确定截齿在时间t内的冲击次数λ,设截齿的冲击频率为μ,则截齿的冲击次数为
λ=[μt]
(10)
式中,[μt]为不超过两数乘积的最大整数。
由于截齿每次往复冲击运动的时间极短,在截齿单次冲击过程中滚筒牵引及回转运动对其运动方向的变化几乎没有影响,且考虑到截齿的冲击运动是为了对煤体产生预裂作用,而非截割作用,故可以将截齿每次冲击后的额外破煤区域简化为等腰梯形如图3所示。

图3 额外破煤面积的数学模型
Fig.3 Mathematical model of extra coal breaking area
图中梯形的上底d1是截齿齿尖合金头达到最大冲击行程后与煤体接触的部分,因已将截齿冲击产生的额外破煤区域简化为等腰梯形,即忽略掉极短时间内滚筒牵引与回转运动对其产生的影响,故可将d1长度认定为截齿齿尖合金头的直径,θ是由截齿在冲击的过程中继续进行回转运动所产生,图3中的两个θ相加即为截齿在单次往复运动的时间内旋转的角度,设截齿的单次往复冲击时间为t1,则可得到θ的表达式为
θ=3nt1
(11)
图3中梯形两腰是由截齿最大冲击行程l1和截齿单次冲击至最大行程用时内牵引行进的距离叠加而成,故易得梯形面积,设截齿长度为l,截齿末端直径为d,则根据截齿在时间t内的冲击次数可进一步求得因冲击运动造成煤体额外破坏的总面积S6为
(l1+vt1)cos θ
(12)
最终综合以上表达式,得到预裂辅助冲击截齿在时间t内的破煤轨迹曲线所围成的二维面积S为
![]()
(13)
对截齿破煤作用面积理论分析的意义在于,根据理论面积与截齿三维模型的实际截割厚度可以得到截齿破煤的理论破煤体积,经理论公式计算得到的破煤体积必然比粗略计算破煤体积的准确度高很多,因为预裂辅助冲击截齿是新型破煤方式,针对的是硬煤、黏煤的恶劣煤质工况,所以对此进行精确的分析才更有实际意义。另一方面,将后文仿真得到的模拟破煤体积与理论破煤体积进行比对,可以得到不同工况下的破煤颗粒实际占比,也从侧面提出了一种新的截割性能评价。
2 预裂辅助冲击截齿破煤的离散元模型建立
2.1 单截齿滚筒建模及煤壁模型设计
2.1.1 单截齿滚筒模型建立
由于对截齿的破煤轨迹分析从回转、牵引和冲击3种运动方式综合考虑,则对单个截齿的破煤特征分析应以滚筒为载体,同时因离散元模拟中关于几何体三维模型的分析较为理想化,不会产生偏载现象而进一步影响仿真结果,故利用Solidworks软件建立单截齿简化模型如图4所示。
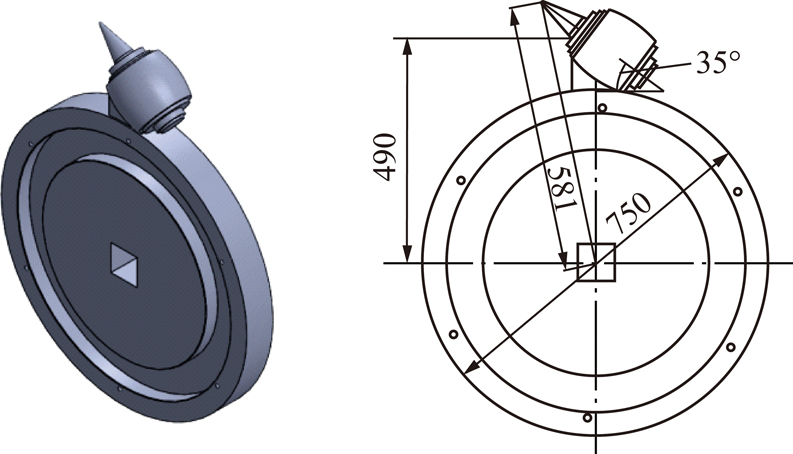
图4 单截齿滚筒模型
Fig.4 Model of single pick drum
单截齿滚筒的模型尺寸参数如图4所示,其中筒毂直径为750 mm,齿座距滚筒中心的垂直距离为115 mm,截齿齿尖至滚筒中心的长度为581 mm,截齿安装角度为35°。
2.1.2 煤壁整体形状设计与模拟方案确定
在截齿破煤特征分析的离散元模拟中,另一主要研究对象是由若干颗粒元堆积而成的煤壁模型,在建立煤壁模型前,应设计煤壁的整体形状,考虑到破煤工具为单截齿滚筒,为了在防止筒毂本身直接接触到煤体的条件下,保证较好的模拟效果,故设定煤壁已被理想化截割一定时间,其破坏区域恰好为单截齿滚筒的大小,根据单截齿滚筒的尺寸参数,得到仿真所采用煤壁模型的形状如图5所示。

图5 煤壁整体形状
Fig.5 Whole shape of coal wall
2.1.3 煤壁模型预填充
为建立单截齿滚筒的截割模型,且保证每种工况下除煤体内部参数外均完全相同,首先需要在EDEM离散元分析软件中预先生成对应形状的颗粒集合体。
(1)全局设置
接触模型Hertz-Mindlin方式,添加2种材料分别为煤与钢,为防止这一情况颗粒元接触重叠量过大,将煤材料的剪切模量设定为80 GPa,煤与煤之间的两项摩擦因数均设定为0.001。
(2)粒子模型设置
颗粒元半径设置为25 mm,接触半径通常为颗粒元半径的1.1倍[17],故设为27.5 mm。
(3)几何体模型设置
在Sections处导入图5所示的煤壁整体模型,设定模型的材料为煤,其余保持默认。
(4)颗粒工厂设置
添加几何体设置中导入的煤壁三维模型为颗粒工厂,其余保持默认。
设定时间步长为30%,网格大小设定为3Rmin,最终得到稳定填满的煤壁模型如图6所示。

图6 煤壁模型
Fig.6 Coal wall model
2.2 煤壁硬度与黏度的参数设定
2.2.1 EDEM的颗粒接触模型选择
预填充的煤壁模型虽较为规整,但颗粒元仅在边界条件约束下紧凑堆积,若去掉边界条件会导致颗粒集合体松散破坏,为使各颗粒元共同构成完整的煤壁模型,同时表达出煤壁的坚硬特征或黏性特征,需要重新设定颗粒接触模型。
采用颗粒间内力代替边界约束力来限制颗粒运动的方法,在所有接触模型中,Hert-Mindlin with bonding与Linear Cohesion可在颗粒元间生成黏结键,若黏结键被破坏,则恢复弹性接触模型自由运动。由于Linear Cohesion模型只计算黏结键所受法向力,与煤壁实际物理特征不符,所以选择Hert-Mindlin with bonding作为颗粒元的黏结模型。该模型生成的黏结键可同时受到外力的法向和切向作用,黏结键产生后会随模拟过程中外力的作用实时更新黏结力F与力矩T,其计算方法[17]为

(14)
式中,vn,vt为颗粒的法向、切向速度,m/s;Sn,St为黏结键的法向、切向刚度,N/m3;R为黏结半径,m;δt为时间步长,s;A为单位接触面积,mm2;J为极惯性矩,mm4;wn为颗粒元的法向旋转角速度;wt为颗粒元的切向旋转角速度;Tn为黏结键的法向力矩;Tt为黏结键的切向力矩;Fn为黏结键的法向黏结力;Ft为黏结键的切向黏结力。
随着黏结力与力矩的不断更新,当黏结键受力超过所设定的极限法向应力σmax或切向应力τmax时即被破坏,其判断条件的计算方法为

(15)
综合式(14)和(15)可知,对于单截齿滚筒的破煤仿真,截齿接触煤壁将力传递到煤壁模型内部后,根据牛顿第二定律,力的传导作用会引起若干颗粒元的加速度变化,进而改变法向、切向的运动速度,最终通过离散元计算方法判断黏结键是否被破坏,即煤壁是否被破坏,若破坏区域在煤壁内部且范围不大,则反映的是煤壁内部产生裂隙破坏,若破坏区域延伸至煤壁外部,则反映的是块煤产生剥离破坏。
2.2.2 硬度黏结参数的确定
煤体的硬度属性主要以普氏系数f值作为衡量标准,为使本文研究更具实际意义,以f4,f5,f6做为煤壁模型的硬度值,并以这3个硬度普氏系数为参考建立相关黏结参数。
黏结键法向刚度Sn与弹性模量E关联,切向刚度St与剪切模量G关联,其计算方法为

(16)
式中,L为颗粒间距,m。
由于颗粒元的接触半径为27.5 mm,颗粒间距为两个相邻颗粒元中心的距离,则与式(16)所对应的颗粒间距为0.055 m。另一方面,黏结键的极限法向强度即表示煤体的极限抗压强度σy,可根据普氏系数与抗压强度的经验关系式[18]求得3种煤壁硬度下的极限抗压强度分别为40,50,60 MPa,同时又有:
σy:σl:τ=100:(3~10):(10~40)
(17)
式中,σl为极限抗拉强度;τ为极限抗剪强度。
由式(17)可得到其余两种极限强度的范围,至此确定了所有黏结参数的设定标准,但考虑到仅有煤体的硬度值作为已知量,故而从煤体的三向极限强度切入,在常见煤层地质条件中选取极限强度在合理范围内的煤系为参考,进而得到模拟中煤材料的本构参数及各硬度下的黏结参数。
表1为某矿区的煤层力学参数,在三向极限应力强度的选择上,由于表中只给出煤体的抗拉强度,故首先确定不同硬度下煤体的抗拉强度取值范围,根据式(17),得到硬度值为f4时抗拉强度取值范围是1.2~4.0 MPa,硬度值为f5时取值范围是1.5~5.0 MPa,硬度值为f6时取值范围是1.8~6.0 MPa。为使不同硬度的煤壁模型更具对比性,进一步将3种硬度下的抗拉强度取值范围缩小到3~4,4~5,5~6 MPa,若表中超过一种煤系符合取值范围,则选择弹性模量即煤体刚度更大的煤系序号。
表1 煤系力学参数
Table 1 Mechanical parameters of coal measures

序号密度/(kg·m-3)弹性模量/GPa剪切模量/GPa泊松比黏聚力/MPa内摩擦角/(°)抗拉强度/MPa11 4204.201.7200.222.1129.55.6021 4102.120.8200.300.1820.03.2031 2801.300.4900.321.2532.01.1541 4603.801.6200.172.6027.84.3051 4602.430.9300.310.5024.02.3561 4202.200.9560.151.8824.23.7771 3902.300.8800.310.4224.04.3081 3703.151.2000.310.6027.00.4091 4202.400.9300.290.2020.00.28101 4001.490.5400.381.2020.00.64111 4000.990.3800.311.0028.00.50121 4301.200.4600.301.2028.00.60131 4200.500.1900.320.8020.00.01141 3000.400.1450.390.3430.00.20
最终确定分别以6,4,1号煤系作为硬度值分别为f4,f5和f6的煤质条件。为排除由煤颗粒密度不同造成煤壁模型结构产生较大变化的因素,设定3种硬度下的煤颗粒密度相同,故最终得到不同硬度条件下黏结键参数见表2。
2.2.3 黏度黏结参数的确定
本文研究的黏性煤既非原煤燃烧时的黏性,也非煤层开采时碎煤附着于截齿表面的黏性,而是指煤体内部韧性的程度,即煤壁受到变形破坏后不一定产生剥离破坏。传统机械破煤方式往往很难完全破坏煤体内部的黏性,若盲目增加截割功率无疑会提高破煤工作的成本,预裂辅助冲击截齿可以利用截齿高强度的往复冲击不断破坏煤体内部黏性,虽然在煤体内部的黏性阻力下,其裂隙发育程度可能减弱,但截齿的冲击作用已令黏性失效,进而达到高效开采的效果。
表2 不同硬度下的材料参数与黏结参数
Table 2 Material parameters and bonding parameters under different hardness

硬度f4f5f6泊松比0.150.170.22剪切模量/GPa0.9561.6201.720密度/(kg·m-3)1 4201 4201 420恢复系数0.450.450.45静摩擦因数0.480.480.48滚动摩擦因数0.180.180.18单位法向刚度/(GN·m-3)4068.9276.31单位切向刚度/(GN·m-3)17.3929.4531.27临界法向应力/MPa405060临界切向应力/MPa162024黏结半径/m0.0250.0250.025
罗汀、姚仰平等[19]基于SMP准则得到了适用于黏性固体材料的平面应变强度公式,通过引入材料的黏聚力和摩擦角计算出黏性材料的三向极限应力值,即
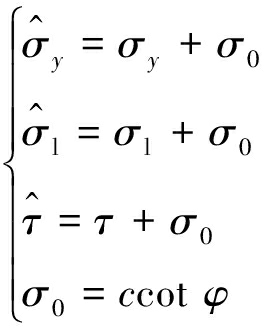
(18)
式中,c为黏聚力,MPa;φ为摩擦角,![]() 为黏性条件下的新极限抗压强度;
为黏性条件下的新极限抗压强度;![]() 为黏性条件下的新极限抗拉强度;σ0为黏性条件下的额外三向强度值;
为黏性条件下的新极限抗拉强度;σ0为黏性条件下的额外三向强度值;![]() 为黏性条件下的新极限抗剪强度。
为黏性条件下的新极限抗剪强度。
根据式(18)并结合表1可知,各序号煤系之间的σ0相差不大,为突出煤壁模型的黏性属性,应尽量选择硬度较低、黏聚力较大且摩擦角较小的煤系序号,再从表中筛选3个最大的黏聚力数值做为3种黏度,最终确定以序号10煤系为煤壁模型的材料参数标准,选择摩擦角为20°,3种黏度下的黏聚力分别为1.20,1.88和2.60 MPa。
将3种黏度下的黏聚力和摩擦角代入式(18),得到不同黏度下的σ0约为3.297,5.165和7.143 MPa。在煤体三向极限强度的确定上,根据式(17)计算出合理范围内最大的强度值,根据序号10煤系的抗拉强度σl为0.64 MPa,得到该条件下煤体的σy,τ约为21.333 MPa和8.533 MPa。将各项本构参数代入式(16)求得煤体的刚度,并通过式(18)得到三向应力强度的新值,最终确定了不同黏度下的材料参数与黏结参数见表3。
表3 不同黏度下的材料参数与黏结参数
Table 3 Material parameters and bonding parameters under different viscosity
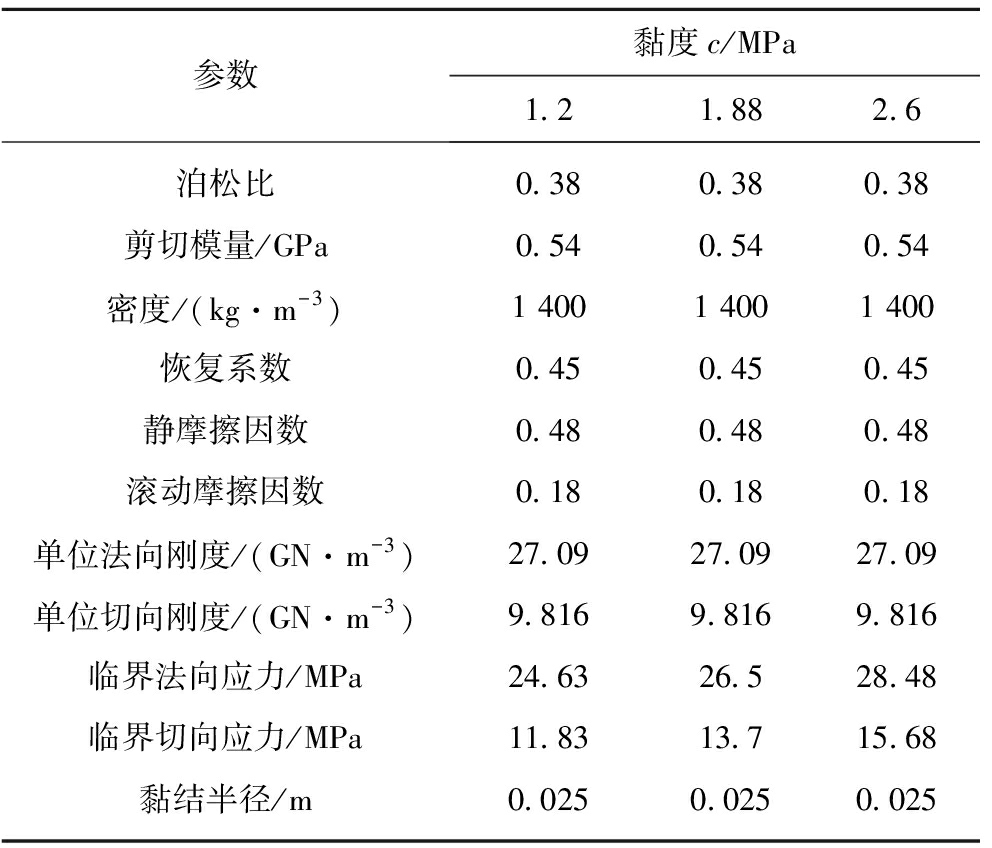
参数黏度c/MPa1.21.882.6泊松比0.380.380.38剪切模量/GPa0.540.540.54密度/(kg·m-3)1 4001 4001 400恢复系数0.450.450.45静摩擦因数0.480.480.48滚动摩擦因数0.180.180.18单位法向刚度/(GN·m-3)27.0927.0927.09单位切向刚度/(GN·m-3)9.8169.8169.816临界法向应力/MPa24.6326.528.48临界切向应力/MPa11.8313.715.68黏结半径/m0.0250.0250.025
2.3 单截齿滚筒的运动参数设置
将滚筒三维模型导入,在设定两项参数前需重新定义钢的材料参数见表4。
表4 钢的材料参数
Table 4 Material parameters of steel

泊松比剪切模量/GPa密度/(kg·m-3)恢复系数静摩擦因数滚动摩擦因数0.36837 8500.350.480.08
调整截齿和滚筒其他部分的位置坐标参数,设置截齿和滚筒其他部分的运动速度为12 m/min;旋转运动即单截齿滚筒的回转截割运动,调整截齿和滚筒其余部分的旋转中心并设定转速为30 r/min。
对于预裂辅助冲击截齿滚筒,需在截齿部分额外添加一项直线运动来表示截齿的往复冲击运动,通过设置相关运动参数,使截齿能够在其运动轨迹的切线方向做出额外线性运动,即冲击动作。而EDEM的几何体直线运动参数中只有速度或加速度的设置,利用牛顿第二定律,以加速度a表示截齿冲击力F,并根据加速度a求得截齿的冲击运动时间t,即

(19)
式中,m为截齿、齿套和冲击活塞总质量,kg;l1为截齿最大冲击行程,m。
m值约为4.5 kg,设油液压力约为10 kN,截齿最大冲击行程为10 mm,则截齿加速度约为2 222.2 m/s2,加速时间约为0.003 s,同时由加速度和加速时间可进一步得到当截齿达到最大冲击行程后的瞬时速度约为6.67 m/s,符合实际的活塞杆运动速度,故而可以在EDEM中采用加速度代替冲击力的方法使截齿做冲击运动。
设定滚筒运动时间为1 s,此时滚筒旋转半周,牵引行进距离为0.2 m,在得到一定破煤效果的基础上保证了筒毂不会接触到煤体。另一方面,为实现截齿的往复冲击运动,需在截齿达到最大冲击行程后重新调整截齿的运动方向使其复位,设截齿的冲击频率为4 Hz,则需要在每间隔0.25 s后调整截齿的运动方向做下一次冲击运动,达到最大行程后同样进行截齿的复位运动参数设定,如此循环便实现了液压冲击技术单截齿滚筒的运动控制。
为提高模拟精度,设定仿真时间步长为5%,网格大小为2Rmin,最终得到单截齿滚筒的离散元破煤模型如图7所示。

图7 单截齿滚筒的破煤模型
Fig.7 Coal breaking model of single pick drum
3 传统截齿与预裂辅助冲击截齿的破煤对比
3.1 单截齿破煤仿真的动态过程分析
3.1.1 传统截齿的破煤仿真过程分析
图8为传统截齿滚筒的破煤过程,从0.2,0.5,1.0,2.0 s四个时刻进行分析,可以看出,滚筒截割至0.2 s时,截齿刚刚侵入煤体,煤壁模型内有些许颗粒脱落,对应到实际工况即表示该阶段煤体的破坏形式基本为碎煤脱落;截割至0.5 s时,破煤产生初步效果,煤壁模型内开始有块煤脱落的破坏形式;截割至1 s时,即截割过程结束的时间点,此时截齿已经完全脱离煤体部分,但由于单截齿滚筒模型无法将脱落的块煤及时输送至外部,使得仍有部分已脱落的颗粒元在仿真计算范围内,当全部颗粒元脱离仿真区域后,得到图8(d)的最终破煤效果。

图8 传统技术破煤仿真过程
Fig.8 Simulation process of coal breaking by tradi-
tional technology
图8(d)中,连接破坏区域内每一处最外端未被破坏颗粒的中心,可以看到所形成的连线与实际破煤的月牙形相似,但在单截齿滚筒截割的前半个阶段内破煤形状较为粗糙,究其原因是由于复杂煤层条件下,传统机械破煤截割方式易出现碎煤脱落,这种情况在截齿最初的破煤工作阶段更为明显,直至截齿逐渐深入煤体后,碎煤比率减小,最后破煤形状接近于理想的月牙形。
3.1.2 预裂辅助冲击截齿的破煤仿真过程分析
图9为预裂辅助冲击截齿滚筒的破煤过程,从截齿应进行冲击的4个阶段进行分析,图9(a),9(c)为截齿第1次往复冲击过程,此时滚筒刚刚开始运动,截齿先对煤体进行冲击作用,使煤体内部产生裂隙,降低截割阻力;图9(b)为截齿第1次冲击的局部放大图;图9(d),9(e)分别为截齿第2次和第3次冲击过程的某一时刻,图9(f)为原本设定中应进行第4次进行冲击运动的时间点,但从图中可以看出,当滚筒截割至该位置时,位于截齿切线方向上的煤体均已被破坏,此时已不需进行第4次冲击,保持滚筒的初始运动即可。

图9 液压冲击技术破煤仿真过程
Fig.9 Simulation process of coal breaking by hydraulic assisted impact technology
同样将最外端颗粒中心连接起来,可以看出连线形状与图1极为相似,其中A,B两点是由截齿冲击作用额外截割所形成,若忽略该部分,可以观察到此处连线与图8(b)相比更为光滑,在连线两侧的多余颗粒元数量明显减少,说明预裂辅助冲击截齿有效降低了复杂煤层条件的截割难度,使截齿在最初进行破煤工作时的碎煤量大为降低。
故从单截齿滚筒破煤的宏观动态过程分析,预裂辅助冲击截齿可以取得较为良好的效果。
3.2 不同煤体硬度下的破煤特征对比分析
由于复杂煤层条件与传统优质煤层条件不同,复杂煤层开采难度大,国内外对此研究较为受限,故本文需要提出更多的破煤特征评价方式来提升研究的可信度,考虑到煤壁离散元模型与实际煤体的关联性,颗粒集合体可以表示出煤壁的形状,黏结键可以进一步为颗粒集合体赋予实际煤体的机械性质,因此可以将破煤颗粒实际占比与破煤难易程度作为特征评价,其中破煤颗粒实际占比由剩余颗粒总数确定,即剩余颗粒数越少,破煤颗粒实际占比越高;破煤难易程度由剩余黏结键总数确定,即剩余黏结键总数越少,破煤越容易。
3.2.1 破煤颗粒实际占比的对比
统计各工况下的剩余颗粒数,煤壁模型内颗粒总数为12 782,则剩余颗粒总数见表5。
表5 剩余颗粒总数
Table 5 Total number of remaining particles

破煤方式剩余颗粒总数f4硬度煤壁f5硬度煤壁f6硬度煤壁预裂辅助冲击截齿12 14612 19212 220传统截齿12 20912 31612 441
由于煤壁内颗粒总数基数较大,而截齿实际能接触的煤体较小。为更好地分析截割效率,需要确定截齿在破煤过程中实际能接触到煤壁体积V1与煤壁模型的整体体积V2,则可进一步得到滚筒破煤实际接触颗粒数量a1与煤壁模型内颗粒总数a2的比例关系为
![]()
(20)
其中,V1可由截齿破煤运动轨迹模型求得,由于仿真过程中单截齿滚筒转动180°,根据式(4)~(6),(12)可得传统截齿破煤面积SA与预裂辅助冲击截齿破煤面积SB分别为
![]()
(21)
筒毂至齿座与y轴夹角θ为10°,截齿截割角度β为30°,截齿安装角度α为40°,筒毂中心至截齿齿尖长度R约为578 mm,并已知液压冲击技术单截齿滚筒破煤过程中截齿进行了3次往复冲击运动,将数据代入上式,得到SA和SB的值分别约为0.517 8,0.518 1 m2,因此根据单截齿滚筒宽度为170 mm,可进一步得到V1与V2的值分别约为0.088 0,0.088 1 m3,显然液压冲击技术下的截齿冲击额外破煤面积可以忽略不计,因此最终确定2种破煤方式下的理论破煤体积均为0.088 m3。
另一方面,由图5可求得煤壁模型的实际体积约为1.6 m3,已知煤壁模型内颗粒总数a2为12 782个,故根据式(20),得到截齿实际接触颗粒数量a1约为703个。由表5可知各工况下破煤颗粒数量x,则定义各工况下的单截齿滚筒破煤颗粒实际占比η为
![]()
(21)
故得出各工况下的破煤颗粒实际占比见表6。
表6 破煤颗粒实际占比
Table 6 Actual proportion of broken coal particles

破煤方式破煤颗粒实际占比/%f4硬度煤壁f5硬度煤壁f6硬度煤壁预裂辅助冲击截齿90.4783.9379.94传统截齿81.5166.2948.51
由表6可以看出,截齿在加入往复冲击运动后,破煤颗粒实际占比明显高于普通牵引切削截割,并且随着煤岩硬度的提高,预裂辅助冲击截齿的破煤颗粒实际占比优势会更加明显,在硬度达到f6时才略低于传统技术在硬度值为f4时的破煤颗粒实际占比,并且比传统技术下在硬度为f6的破煤颗粒实际占比高出约31%。为得到2种破煤方式下各自效率的定量分析,将硬度与破煤颗粒实际占比的数据导入Matlab,可得到变化拟合曲线如图10所示。
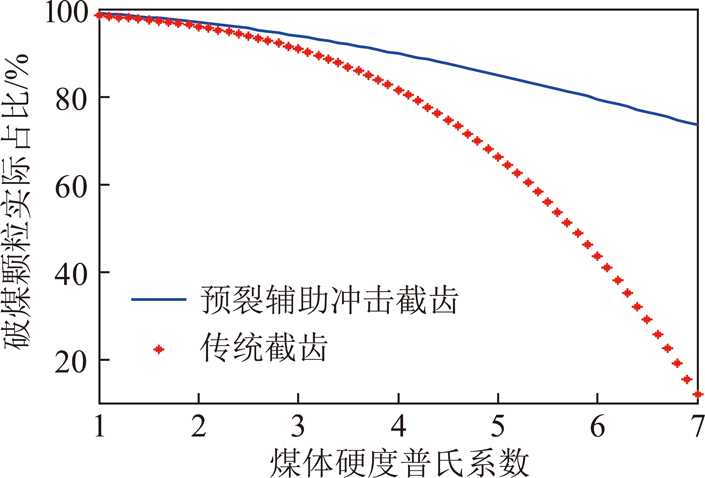
图10 截齿破煤颗粒实际占比随煤岩硬度的变化拟合曲线
Fig.10 Fitting curves of actual proportion of broken coal particles with change of coal hardness
从图10可以看出,预裂辅助冲击截齿的截割效率在煤岩硬度增加后的下降趋势更为平缓,普通牵引切削方式截割受硬度影响较强烈。设预裂辅助冲击截齿的破煤颗粒实际占比为η1,传统截齿的破煤颗粒实际占比为η2,煤体硬度值为h,则两条曲线对应的拟合表达式为

(22)
因此从破煤颗粒实际占比的角度分析,预裂辅助冲击截齿在面对坚硬煤质时,相对传统机械破煤方式有显著性提升,且当煤壁硬度值超过f8时,其破煤颗粒实际占比仍可以超过60%,更加凸显了液压冲击技术的优越性。
3.2.2 破煤难易程度的对比
统计各工况下的剩余黏结键数,煤壁模型内黏结键总数为51 188,则剩余黏结键总数见表7。
表7 剩余黏结键总数
Table 7 Total number of remaining bonds
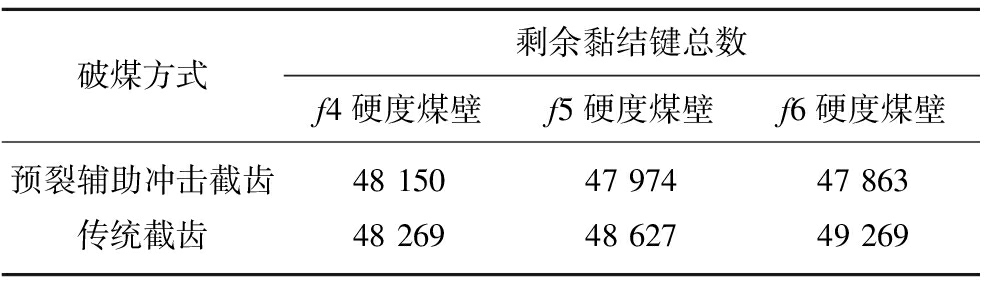
破煤方式剩余黏结键总数f4硬度煤壁f5硬度煤壁f6硬度煤壁预裂辅助冲击截齿48 15047 97447 863传统截齿48 26948 62749 269
同样根据式(20)求得单截齿滚筒破煤的理论黏结键总数b1约为2 815个,由于黏结键与颗粒数的意义不同,黏结键相对颗粒元较为微观,每个颗粒元四周可能有多个黏结键存在,不仅在颗粒元脱离煤壁时涉及到黏结键的断裂,在滚筒破煤过程中裂隙发育同样与黏结键的断裂有关,也就是说黏结键断裂不一定代表颗粒元脱离,但能反映出煤体内部产生一定程度的破坏,进而降低单截齿滚筒破煤时的难度。因此,设破煤难易程度为ε,已断裂键数为x,则定义破煤难易程度为
![]()
(23)
规定难易程度ε值为100%时标准程度,即表示截齿对煤体的破坏全部体现成脱离破坏;若ε值大于100%,则说明截齿可以对煤体造成裂隙破坏,数值越大,煤体内部的裂隙发育越良好,破煤越容易;若ε值小于100%,则说明该工况下的截齿破煤难度较大,易导致截齿磨损,降低破煤颗粒实际占比。根据式(23),得出各工况下的破煤难易程度见表8。
表8 破煤难易程度
Table 8 Difficulty of coal breaking

破煤方式难易程度/%f4硬度煤壁f5硬度煤壁f6硬度煤壁预裂辅助冲击截齿107.92114.17118.10传统截齿103.6990.9868.17
由表8可知,预裂辅助冲击截齿可以极大降低硬质煤层开采的难度,且随着煤体硬度升高,其截齿冲击带来的预裂效果越好。而传统截齿在截割f4硬度的煤体时表现尚可,但硬度的加大使其破煤难度急剧上升,在硬度值为f6时,两种破煤方式下的破煤难易程度甚至相差50%,已接近于2倍。将硬度值与破煤难易程度的数据导入Matlab,可得到变化拟合曲线如图11所示。

图11 截齿破煤难度随煤岩硬度的变化拟合曲线
Fig.11 Fitting curves of the difficulty with change of the hardness of coal
由图11可知,传统截齿在硬度值约为f3.5以下时能够有效降低破煤难度,但超过该硬度后破煤难度迅速加大,当硬度值超过f4后,其难易程度大幅衰减,而预裂辅助冲击截齿的破煤难度较为稳定,即使在硬度值达到f7时仍能有效降低破煤难度。设预裂辅助冲击截齿的破煤难度为ε1,传统截齿的破煤颗粒实际占比为ε2,煤体硬度值为h,则2条曲线对应的拟合表达式为

(24)
从破煤难易程度的角度分析,预裂辅助冲击截齿针对坚硬煤质可以有效降低破煤难度,且预裂性能稳定,适用于各种硬质煤系的开采环境,但在煤体硬度较低时,传统截齿的预裂性能表现也尚可。
3.2.3 截齿受力的对比
图12为各工况下截齿所受合力随时间的变化趋势,可以看出,预裂辅助冲击截齿的截齿受力峰值均比同种硬度下的传统截齿受力峰值低,但除此之外没有其他较为明显的规律。
为使不同工况下的截齿受力区别更明显,此处根据截齿受力图像上的每一个离散点,利用积分公式求出单截齿滚筒有效破煤阶段内的受力均值F,设各工况下截齿脱离煤体后的时间为T,则
F=![]() f(t)dt
f(t)dt
(25)
式中,t为截割时间。
利用Matlab将图15中的各离散点导入,最终求得各工况下的截齿受力均值见表9。

图12 各工况下截齿受力随时间变化趋势
Fig.12 Changing trend of the stress with time under various working conditions
表9 截齿受力均值
Table 9 Average force of pick

破煤方式截齿平均受力/Nf4硬度煤壁f5硬度煤壁f6硬度煤壁预裂辅助冲击截齿21 86527 23734 715传统截齿26 54834 39937 118
可以看出,煤体经截齿的冲击作用后,减小了截齿牵引切削时的截割阻力,而传统截齿只能利用牵引切削和回转截割的方式克服截割阻力,两种截齿的最大受力差距接近7 000 N,因此从截齿受力来看,预裂辅助冲击截齿在硬质煤层条件下,可以更好地防止截齿由于受力过大而产生磨损。
综合破煤颗粒实际占比、破煤难易程度和截齿受力分析,预裂辅助冲击截齿在其冲击预裂作用的帮助下,可以获得更高的破煤颗粒实际占比,有效降低破煤难度,并能够减小截齿所受阻力,防止截齿磨损,同时煤系硬度越高,越优于传统截齿的破煤性能。
3.3 不同煤体黏度下的破煤特征对比分析
3.3.1 破煤颗粒实际占比的对比
黏性煤壁模型的颗粒总数同为12 782,统计出各工况下的剩余颗粒总数见表10。
表10 剩余颗粒总数
Table 10 Total number of remaining particles

破煤方式剩余颗粒总数黏聚力1.20 MPa黏聚力1.88 MPa黏聚力2.60 MPa预裂辅助冲击截齿12 24612 25812 347传统截齿12 26212 32212 446
已知单截齿滚筒破煤实际接触颗粒数量a1约为703个,同样利用式(21)得出各工况下的破煤颗粒实际占比见表11。
表11 破煤颗粒实际占比
Table 11 Coal breaking efficiency

破煤方式破煤颗粒实际占比/%黏聚力1.20 MPa黏聚力1.88 MPa黏聚力2.60 MPa预裂辅助冲击截齿76.2474.5461.88传统截齿73.9765.4347.80
由表11可以看出,随着煤体黏性增加,传统截齿的破煤颗粒实际占比下降较多,而预裂辅助冲击截齿相较于传统截齿可以更好保证破煤颗粒实际占比,在黏聚力为1.88 MPa时,预裂辅助冲击截齿的破煤颗粒实际占比比传统截齿在黏聚力为1.2 MPa工况下的破煤颗粒实际占比依然高出近1%,在煤体黏聚力为2.6 MPa时,两种截齿的破煤颗粒实际占比差距甚至达到了近14%,将表示煤体黏性的黏聚力和破煤颗粒实际占比数据导入Matlab,得到效率随煤壁黏度的变化拟合曲线如图13所示。

图13 截齿破煤颗粒实际占比随煤岩黏度的变化拟合曲线
Fig.13 Fitting curves of coal breaking efficiency with change of coal viscosity
由图13可知,在煤体黏度较低时,两种技术下的破煤颗粒实际占比差距不大,传统截齿的破煤颗粒实际占比还略优于预裂辅助冲击截齿,但当煤体黏聚力超过1 MPa后,传统截齿的破煤颗粒实际占比迅速下降,而预裂辅助冲击截齿在黏聚力为1~2 MPa的工况下破煤性能较为稳定,在黏聚力超过2 MPa后,预裂辅助冲击截齿的破煤颗粒实际占比开始有所降低,但依然能够保证破煤颗粒实际占比优于传统截齿。设预裂辅助冲击截齿的破煤颗粒实际占比为η1,传统截齿的破煤颗粒实际占比为η2,煤体黏聚力为j,则两条曲线对应的拟合表达式为
![]()
(26)
从破煤颗粒实际占比角度分析,预裂辅助冲击截齿在煤体黏性较大的工况下,能够有效保证破煤颗粒实际占比的稳定性,究其原因是由于预裂辅助冲击截齿的高强度高频率冲击作用可以破坏煤体黏性,从而降低截割难度,在煤体黏度黏聚力低于2 MPa时的破煤颗粒实际占比较优。
3.3.2 破煤难易程度的对比
黏性煤壁模型的黏结键总数同为51 188,统计出剩余黏结键总数见表12。
表12 剩余黏结键总数
Table 12 Total number of remaining bonds

破煤方式剩余黏结键总数黏聚力1.20 MPa黏聚力1.88 MPa黏聚力2.60 MPa预裂辅助冲击截齿48 34148 42748 910传统截齿48 45148 75648 923
已知单截齿滚筒破煤实际接触黏结键数量a1约为2 815个,利用式(23)得出各工况下的破煤难易程度见表13。由表13可以看出,对于黏性煤壁来说,在煤体黏聚力为1.2 MPa时,预裂辅助冲击截齿还能够对煤体起到一定的预裂作用,当黏聚力继续增加时,预裂辅助冲击截齿也很难继续对煤体起到预裂作用,但仍可有效破坏与截齿有直接接触煤体的黏性,相对传统截齿更能够降低黏性煤层的开采难度,在黏聚力为1.88 MPa时,两种截齿的破煤难易程度相差约为12%,但当黏聚力为2.6 MPa时,两种截齿的破煤难度相近。将煤体黏度值与破煤难易程度的数据导入Matlab,可得到变化拟合曲线如图14所示。
表13 破煤难易程度
Table 13 Difficulty of coal breaking

破煤方式难易程度/%黏聚力1.20 MPa黏聚力1.88 MPa黏聚力2.60 MPa预裂辅助冲击截齿101.1498.0880.92传统截齿97.2386.3980.46

图14 截齿破煤难度随煤岩黏聚力的变化拟合曲线
Fig.14 Fitting curves of the difficulty with change of the hard-
ness of viscosity
可以看出,在黏聚力不超过2 MPa工况下,预裂辅助冲击截齿可以稳定降低破煤难度,尤其适用于黏聚力为1.0~2.5 MPa内的工况,传统截齿在煤体黏度小于1 MPa的工况下能够对煤体造成更大程度的预裂,由于建立黏性煤壁的离散元模型时选取的煤系硬度较低,在f1~f2内,当煤体黏度越低,越接近条件较好的低硬度煤体,传统截齿可以对煤体产生更优秀的预裂作用。设预裂辅助冲击截齿的破煤难度为ε1,传统截齿的破煤颗粒实际占比为ε2,煤体黏度值为j,则两条曲线对应的拟合表达式为
![]()
(27)
从破煤难易程度的角度分析,预裂辅助冲击截齿适用于煤体黏度黏聚力在2.5 MPa以下的工况,能够保证较良好的稳定性,但在煤体黏度较低时,传统截齿的预裂性能表现也尚可。
3.3.3 截齿受力的对比
图15表示各工况下截齿所受合力随时间的变化趋势。

图15 各工况下截齿受力随时间变化趋势
Fig.15 Changing trend of the stress with time under various working conditions
利用式(25),将各离散点导入Matlab,得到各工况下的截齿受力均值见表14。
表14 截齿受力均值
Table 14 Average force of pick
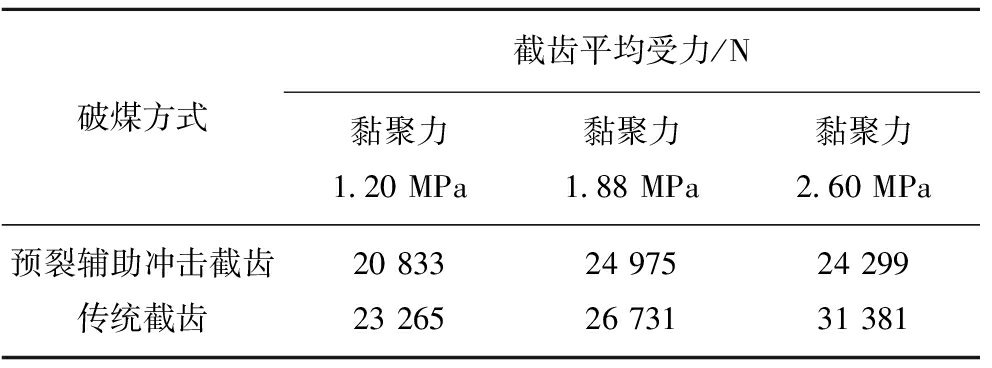
破煤方式截齿平均受力/N黏聚力1.20 MPa黏聚力1.88 MPa黏聚力2.60 MPa预裂辅助冲击截齿20 83324 97524 299传统截齿23 26526 73131 381
可以看出,预裂辅助冲击截齿经截齿的冲击运动后,相对传统截齿减小了截齿受力,且在黏聚力达到2.6 MPa时,两种截齿的受力相差约为7 000 N,已经接近该工况下预裂辅助冲击截齿本身受力的28%,极大程度减少了截齿磨损。
综合破煤颗粒实际占比、破煤难易程度和截齿受力分析,黏性煤壁与硬质煤壁的破煤过程有很大不同,使得预裂辅助冲击截齿的破煤表现有所影响,但相对于传统截齿仍具有较为稳定优秀的破煤性能。
4 结 论
(1)从破煤颗粒实际占比、破煤难易程度和截齿受力3个角度分别对比分析了不同煤体硬度下,两种截齿的破煤特征,在破煤颗粒实际占比上,截齿在加入往复冲击运动后的破煤颗粒实际占比明显提高,在煤体硬度同为f6时提高了31%;在破煤难易程度上,预裂辅助冲击截齿可以极大降低硬质煤层开采的难度,且煤体硬度越大,预裂效果越好,在硬度值为f6时,两种破煤技术下的破煤难度相差50%;在截齿受力上,预裂辅助冲击截齿可以减小截割阻力,两种截齿的最大受力差距接近7 000 N。
(2)从破煤颗粒实际占比、破煤难易程度和截齿受力分析了不同煤体黏度下截齿的破煤特征,在破煤颗粒实际占比上,随着煤体黏性增加,传统截齿的破煤颗粒实际占比下降较多,而预裂辅助冲击截齿可以更好保证破煤颗粒实际占比,当煤体黏聚力为2.6 MPa时,两种截齿的破煤颗粒实际占比差距达到近14%;在破煤难易程度上,预裂辅助冲击截齿能够降低黏性煤层的开采难度,在黏聚力为1.88 MPa时,两种截齿的破煤难易程度相差约为12%;在截齿受力上,预裂辅助冲击截齿能够有效降低截齿所受阻力,在黏聚力达到2.6 MPa时,两种截齿的受力相差接近7 000 N。
[1] 张强,王海舰,吴泽光,等.滚筒式采煤机煤岩截割力学特性及测试系统研究[J].工程设计学报,2017,24(4):459-464,479.
ZHANG Qiang,WANG Haijian,WU Zeguang,et al.Research of coal-rock cutting mechanical characteristic and test system for drum shearer[J].Chinese Journal of Engineering Design,2017,24(4):459-464,479.
[2] 张强,王海舰,郭桐,等.基于截齿截割红外热像的采煤机煤岩界面识别研究[J].煤炭科学技术,2017,45(5):22-27.
ZHANG Qiang,WANG Haijian,GUO Tong,et al.Study on coal-rock interface recognition of coal shearer based on cutting infrared thermal image of picks[J].Coal Science and Technology,2017,45(5):22-27.
[3] 张强,索江伟,王海舰,等.基于ABAQUS的凿岩机钻头破岩数值模拟分析[J].振动与冲击,2018,37(1):136-141.
ZHANG Qiang,SUO Jiangwei,WANG Haijian,et al.Numerical simulation analysis on the drill bit rock breaking process based on ABAQUS[J].Journal of Vibration and Shock,2018,37(1):136-141.
[4] 刘春生.采煤机截齿截割阻力曲线分形特征研究[J].煤炭学报,2004,29(1):115-118.
LIU Chunsheng.Fractal characteristic study of shearer cutter cutting resistance curves[J].Journal of China Coal Society,2004,29(1):115-118.
[5] 李德根,刘春生.镐型截齿截割煤岩动力系统的混沌特征[J].黑龙江科技学院学报,2011,21(6):458-462.
LI Degen,LIU Chunsheng.Chaotic characteristic of dynamics system of concial pick cutting coal[J].Journal of Heilongjiang Institute of Science and Technology,2011,21(6):458-462.
[6] 张倩倩,韩振南,刘炜煌.不同螺旋线数纵向截割头截割性能的比较分析[J].矿山机械,2013,41(5):12-16.
ZHANG Qianqian,HAN Zhennan,LIU Weihuang.Comparison and analysis of cutting performance of longitudinal cutting heads with various numbers of helical lines[J].Mining & Processing Equipment,2013,41(5):12-16.
[7] 李祥松.掘进机截割头性能评价试验分析[J].煤炭技术,2015,34(4):261-263.
LI Xiangsong.Performance evaluation test analysis of roadheader cutting head[J].Coal Technology,2015,34(4):261-263.
[8] 李晓豁,隗金文,刘利.横向截割头摆动截割时切屑图的模拟研究[J].辽宁工程技术大学学报(自然科学版),2002,21(1):76-78.
LI Xiaohuo,KUI Jinwen,LIU Li.Simulation study of grooving section patterns for a horizontal cutting header when swing and cutting[J].Journal of Liaoning Technical University (Natural Science Edition),2002,21(1):76-78.
[9] 于彬,仲崇军,于信伟.影响煤截割阻力的因素[J].煤炭技术,1998,17(3):6-8,11.
YU Bin,ZHONG Chongjun,YU Xinwei.Factors affecting the cutting resistance of coal[J].Coal Technology,1998,17(3):6-8,11.
[10] 江红祥.高压水射流截割头破岩性能及动力学研究[D].徐州:中国矿业大学,2015.
JIANG Hongxiang.Study on rock fragmentation performance of high-pressure water-jets cutting head and its dynamics[D].Xuzhou:China University of Mining and Technology,2015.
[11] 杜玉昆.超临界二氧化碳射流破岩机理研究[D].青岛:中国石油大学(华东),2012.
DU Yukun.Study on the rock-breaking mechanism of supercritical carbon dioxide jet[D].Qingdao:China University of Petroleum,2012.
[12] 徐广举.新型截齿振动截割性能研究[D].长沙:中南大学,2011.
XU Guangju.The study of the new pick vibrational cutting performance[D].Changsha:Central South University,2011.
[13] 乔时和.高压气液两相射流瞬态动力破煤特性及微观致裂机制研究[D].徐州:中国矿业大学,2016.
QIAO Shihe.Study on the characteristics and microscopic mechanism of coal-breaking caused by the transient dynamic of high-pressure gas-liquid wwo-phase jet[D].Xuzhou:China University of Mining and Technology,2016.
[14] 付林.新型钻式采煤机钻具截割与输送性能研究[D].徐州:中国矿业大学,2016.
FU Lin.Study on cutting and conveying performance of novel auger miner drilling tool[D].Xuzhou:China University of Mining and Technology,2016.
[15] 刘春生,袁昊,李德根,等.载荷谱细观特征量与截割性能评价的熵模型[J].煤炭学报,2017,42(9):2468-2474.
LIU Chunsheng,YUAN Hao,LI Degen,et al.Meso-feature of load spectrum and entropy model for cutting performance evaluation[J].Journal of China Coal Society,2017,42(9):2468-2474.
[16] 张强,刘永凤,田莹,等.一种煤岩预裂与截齿联合破碎系统[P].中国专利:CN106677774A,2017-05-17.
ZHANG Qiang,LIU Yongfeng,TIAN Ying,et al.A combined crushing system of coal and rock pre-splitting and pick[P].China Patent,CN106677774A,2017-05-17.
[17] 王国强,赫万军,王继新.离散单元法及其在EDEM上的实践[M].西安:西北工业大学出版社,2010:1-5,16-18.
[18] 曾锐.滚筒式采煤机—高压水射流联合截割系统的设计与研究[D].徐州:中国矿业大学,2014.
ZENG Rui.Design and research on combined cutting system of drum shearer & high pressure water jet[D].Xuzhou:China University of Mining and Technology,2014.
[19] 罗汀,姚仰平,松岡元.基于SMP准则的土的平面应变强度公式[J].岩土力学,2000,21(4):390-393.
LUO Ting,YAO Yangping,SONG Gangyuan.Soil strength equation in plane strain based on SMP[J].Rock and Soil Mechanics,2000,21(4):390-393.
